Оптимизационное моделирование. Поиск решения

Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения, который особенно удобен для решения так называемых "задач оптимизации".

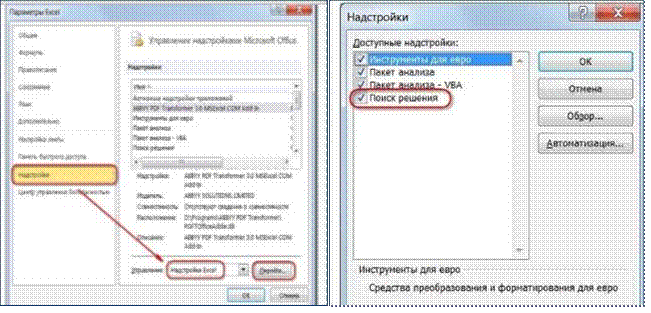
Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные. Для отображения этой кнопки выполните следующую настройку: 

Параметры Excel – Надстройки – Надстройки Excel – Поиск решения

Разберѐм порядок работы Поиска решения на простом примере.

Пример 1. Распределение премии

Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.

Первым делом создаѐм таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат - это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).

  Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:

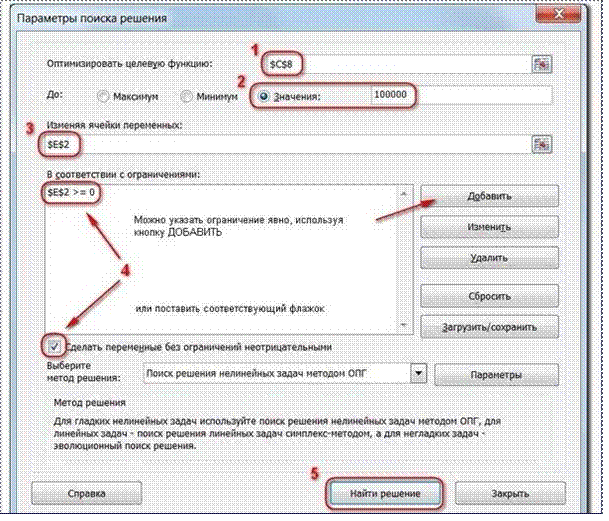
Целевая ячейка, в которой должен получиться желаемый результат. Целевая ячейка может быть только одна

Варианты оптимизации:  максимальное возможное значение, минимальное возможное значение или конкретное значение. Если требуется получить конкретное значение, то его следует указать в поле ввода

Изменяемых ячеек может быть несколько: отдельные ячейки или диапазоны. Собственно, именно в них Excel перебирает варианты с тем, чтобы получить в целевой ячейке заданное значение Ограничения задаются с помощью кнопки Добавить. Задание ограничений, пожалуй, не менее важный и сложный этап, чем построение формул. Именно ограничения обеспечивают получение правильного результата. Ограничения можно задавать как для отдельных ячеек, так и для диапазонов. Помимовсем понятных знаков =, >=, <=, при задании ограничений можно использовать варианты цел (целое), бин (бинарное или двоичное, т.е. 0 или 1), раз (все разные - только начиная с версии Excel 2010).

В данном примере ограничение только одно: коэффициент должен быть положительным. Это ограничение можно задать по-разному: либо установить явно, воспользовавшись кнопкойДобавить, либо поставить флажок Сделать переменные без ограничений неотрицательными.

Для версий до Excel 2010 этот флажок можно найти в диалоговом окне Параметры Поиска решения, которое открывается при нажатии на кнопку Параметры

Кнопка, включающая итеративные вычисления с заданными параметрами.

После нажатия кнопки Найти решение Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.  

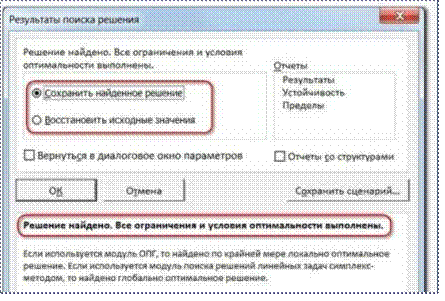
Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.

 Решение данной задачи выглядит так

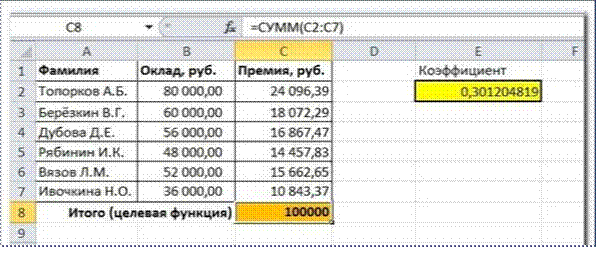
Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.

Разберѐм еще одну задачу оптимизации (получение максимальной прибыли)

Пример 2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных книжных полок.

Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В - 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В - 30 мин. в неделю можно использовать 160 ч машинного времени.

Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В - 120 руб. прибыли?

Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке

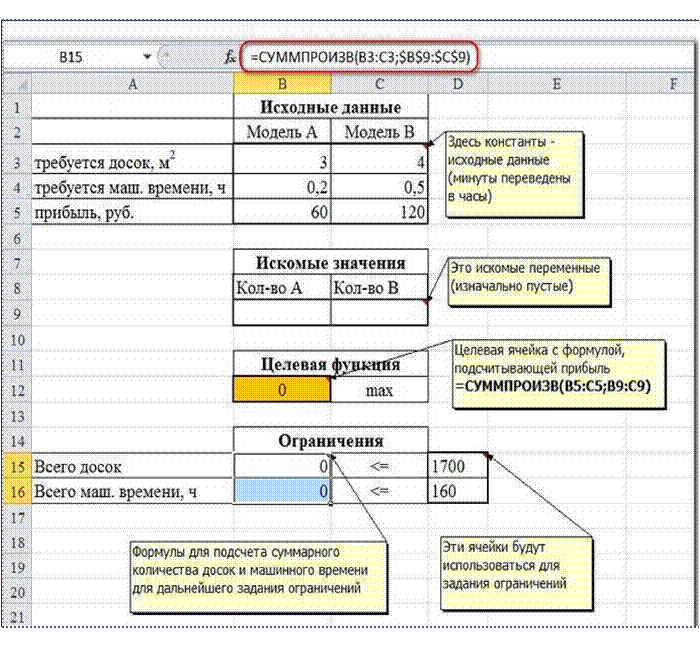
 Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры

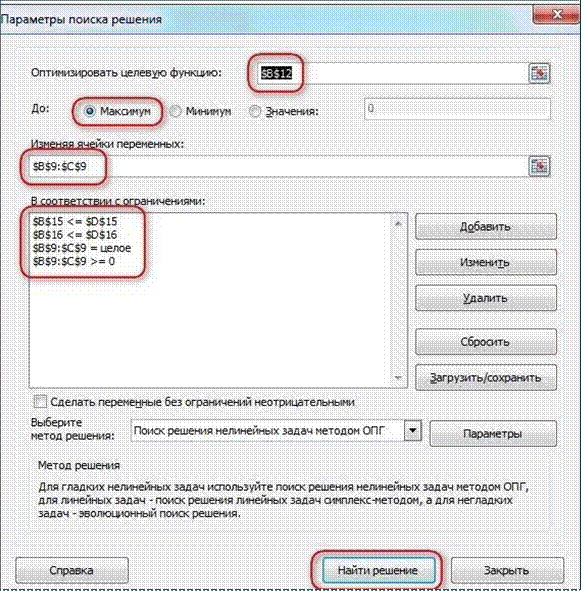
Целевая ячейка B12 содержит формулу для расчѐта прибыли

Параметр оптимизации - максимум

Изменяемые ячейки B9:C9

Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице

Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат

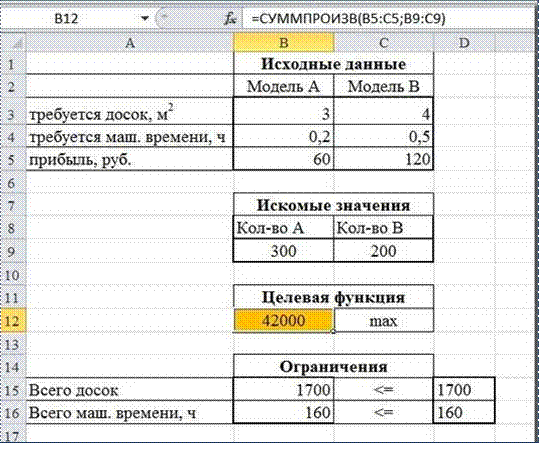
 Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:

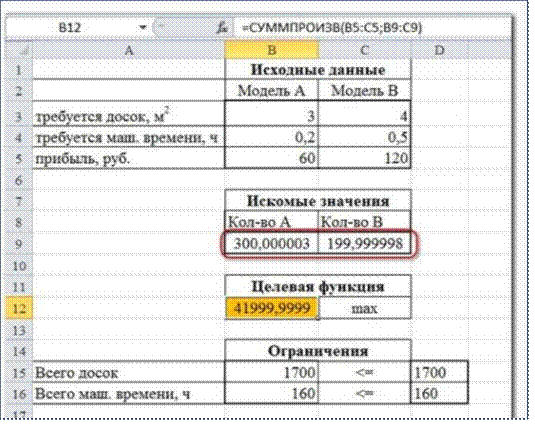
И это несмотря на то, что было задано ограничение целое. В таких случаях можно попробовать настроить параметры Поиска решения. Для этого в окне Поиск решения нажимаем кнопкуПараметры и попадаем в одноимѐнное диалоговое окно

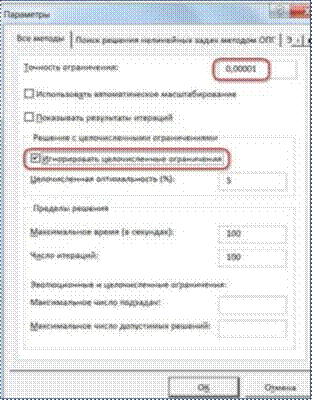
Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае - целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даѐт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.

Пример 3. Транспортная задача (минимизация затрат)

На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта,  поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.

Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

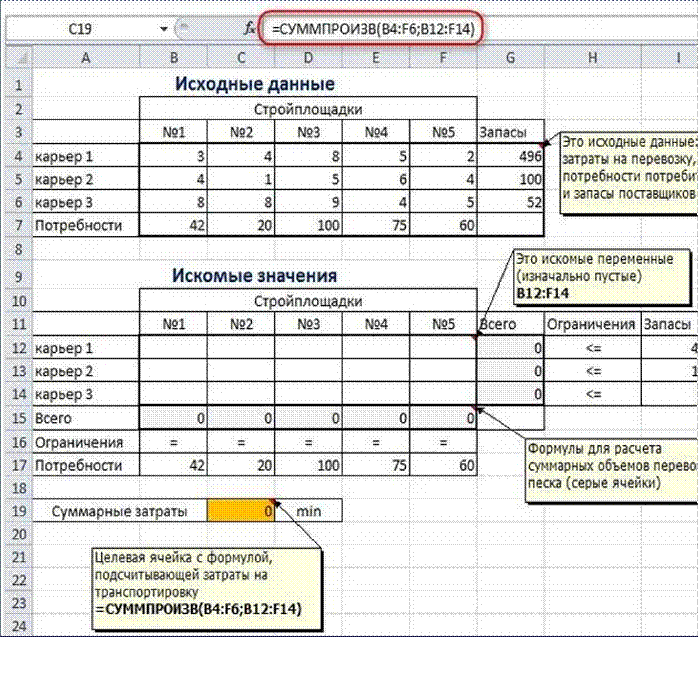
В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчѐта общих затрат на транспортировку.

Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)

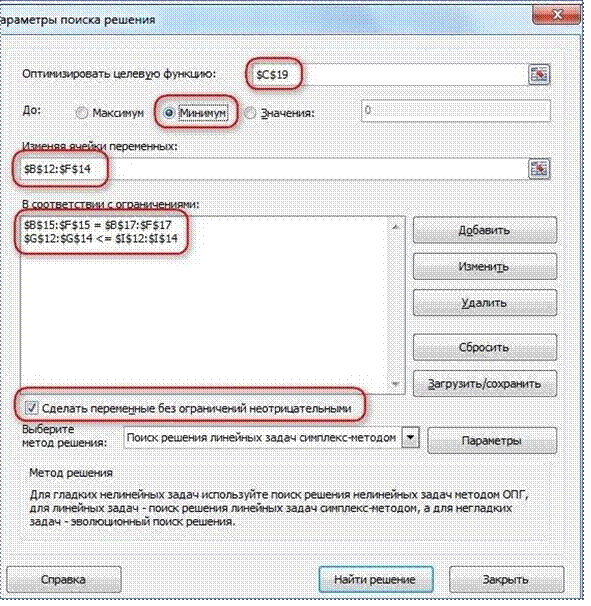
 Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже

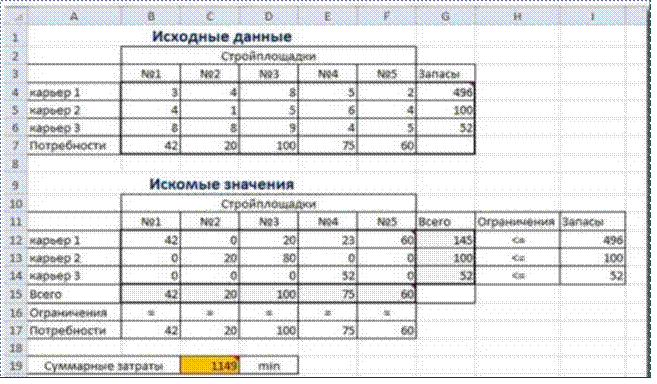
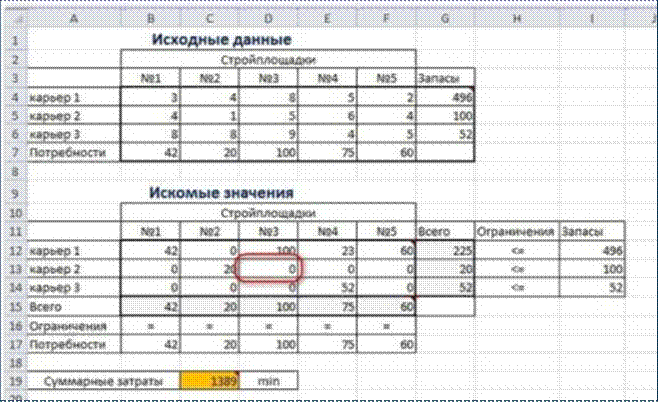
 Иногда транспортные задачи усложняются с помощью дополнительных ограничений. Например, по каким-то причинам невозможно возить песок с карьера 2 на стройплощадку №3. Добавляем ещѐ одно ограничение $D$13=0. И после запуска Поиска решения получаем другой результат

И последнее, на что следует обратить внимание, это выбор метода решения. Если задача достаточно сложная, то для достижения результата может потребоваться подобрать метод решения

Задача 4.(Старинная задача)

Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телѐнок 50 копеек. Сколько быков, коров и телят купил крестьянин?