Методическая разработка урока по математике на тему: Закрепление основных разделов алгебры

Министерство образования и науки Российской Федерации

Негосударственное образовательное учреждение среднего профессионального образования «Владивостокский морской техникум»

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКАЯ  РАЗРАБОТКА

 

По дисциплине «Математика»

   Закрепление основных разделов из курса

«Алгебра и начала анализа. 10 – 11 класс»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Автор (разработала):           идентификатор

преподаватель математики  и информатики НОУ СПО ВМТ  А.С.Кантаева       213-371-932

 

 

 

 

г.Владивосток

Аннотация

 

Методическая разработка по предмету «Математика» рекомендована для работы с учащимися первых курсов средних учебных заведений. Здесь рассмотрен нетрадиционный вид урока – урок-игра «Математический бой». В данной разработке урока затронуты все основные разделы учебника «Алгебра и начала анализа»:

- тригонометрические функции

- производная

- первообразная и интеграл

- показательная и логарифмическая функции.

Разработка соответствует Государственным требованиям и минимуму содержания и уровню подготовки выпускников  всех специальностей среднего профессионального образования.

 

Содержание (Слайд 3)

 

	Стр.
Введение	4
Структура урока	5
1. Организационный момент	5
2. Постановка целей	5
3. Основная часть	5
3.1. Представление команд	5
3.2. Разминка	5
3.3. Логические задачи	6
3.4. Теоретические вопросы - «Правила учим и знаем»	6
3.5. Конкурс «Домашнее задание»	6
3.6.  Задание на скорость – «Правила знаем – задачи решаем!»	6
3.7.  Задание на доске	7
3.8. Конкурс капитанов	7
3.9.  Задание на доске	9
Заключение	10
Список использованной литературы	11
Приложение А
Приложение Б
Приложение В
Приложение Г
Приложение Д
Приложение Е
Приложение Ж

 

 

 

 

 

Введение.

 

«Учить надо не мыслям, а мыслить»

И.Кант.

 

Для подавляющего большинства учащихся основная трудность при изучении математики в том, что язык математики для них чужой. Для них изучение математики – это изучение чужого и жестокого языка. И вести это обучение надо осторожно. Для математиков (особенно профессоров и академиков) язык математики естественный (родной). Как правило,   им не понятно, как можно его не понимать.

Математическое образование предполагает усвоение не только определенной суммы знаний, но и формирование системы математических методов (приемов) мышления. С психологической точки зрения, методы мышления – это различные виды познавательной деятельности. Знания являются информационными компонентами этой деятельности. Они не существуют сами по себе, а всегда с чем то связаны. К сожалению, в практике усвоение понятий нередко ограничивается заучиванием определения понятия и иллюстрацией одним – двумя примерами.

Изучение математики направлено на достижение, в первую очередь, целей интеллектуального развития учащихся, формирование качеств мышления, характерной для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.

Многие преподаватели говорят о том, что учащиеся с трудом усваивают учебный материал, не могут применить знания и т.д. С точки зрения деятельностного подхода к обучению, учащихся следует вооружать системой общих и специфических приемов деятельности – как умственной, так и  практической. Очевидно, что логические умения являются важнейшим компонентом мыслительной деятельности. Стало быть, учителя чаще всего не владеют в полной мере умениями развивать логическое мышление, организовывать учебную деятельность по усвоению материала, заинтересовывать учащихся к своему предмету, т.е. проводить так называемые нестандартные уроки.

Любой педагог, пробуждая интерес к своему предмету, не просто осуществляет передачу опыта, но и укрепляет веру в свои силы у каждого учащегося. Но для создания глубокого интереса к предмету, для развития их познавательной активности, необходим поиск дополнительных средств, стимулирующих развитие общей активности, самостоятельности, личной инициативы и творчество учащихся.

Следовательно, высокая познавательная активность возможно только на интересном для учащихся уроке, когда ему интересен предмет изучения и в какой форме это проходит.

Структура урока

 

1.      Организационный момент (2-3 мин.).

На этом этапе создается мотивация учебной деятельности на данном уроке, преподавателю важно актуализировать сложившиеся ранее познавательные мотивационные установки, укрепить их и поддержать («вы все хорошо усвоили материал, каждой команде есть чем поразить соперника, ваши силы равны»). Также преподаватель создает условие для появления новых мотивационных установок: обратить внимание на то, что от результата работы каждого курсанта на уроке зависит результат работы всей команды.

 

2.   Постановка целей учебной деятельности. Слайд 5

Преподаватель объясняет учащимся, что этот урок поможет обобщить и систематизировать материал, научит работать совместно.

Методическая цель: повысить интерес учащихся к изучаемому предмету. Развить логическое мышление, сообразительность, познавательную активность. Обобщить и систематизировать умения и навыки овладения математическими знаниями, необходимыми в повседневной жизни.

Воспитательная цель: воспитать средствами математики культуру личности, взаимопомощь, взаимовыручку; чувство сплоченности, единства.

 

3.      Основная часть (1 час 10 мин.) Слайд 6

Команды сидят каждая за общим столом. Приготовлены черновики, ручки, рабочие тетради. Объявляется начало «боя», называется состав жюри из приглашенных на урок.

 

3.1.Представление команд, девиза, капитанов, жюри. («РИТМ» - решать, искать, творить, мечтать, «XYZ» - хотеть, уметь, знать). Максимальное количество баллов за представление – 3. Слайд 7-9

 

3.2. Разминка. Несложные задания устного характера. Задается по одному вопросу каждой команде, в случае неправильного ответа – возможность ответить переходит к другой команде. За каждый полный ответ команда получает по 2 балла, неполный – 1  балл, неправильный ответ – 0 баллов. Слайд 10-22

Цель: отработка навыков быстрого и правильного ответа, развитие внимательности.

·               Числа 1,2,3,4,5… называются … числами?   (Натуральными)

·               Функции синус, косинус, тангенс, котангенс называются …?  (Тригонометрическими)

·               Как называется график функции синус? (Синусоида)

·               Как называется разность  ? (Приращением аргумента)

·               Что называется производной? (Производной функции f в точке  называется число, к которому стремится разностное отношение , при  , стремящемся к нулю)

·               Уравнения, в которых под знаком корня содержится переменная, называются …? (Иррациональными)

·               Что называется первообразной?  (Функция F называется первообразной для функции f на заданном промежутке, если для всех  из этого промежутка )

·               Как называются уравнения, в которых переменная содержится в степени? (Показательными)

·               Как называется знак ? По какой формуле вычисляется площадь криволинейной трапеции?()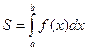

·               Как называется функция, заданная формулой ? (Логарифмической)

 

3.3. Логические задачи. Задания можно записать на доске или подготовить большие карточки, чтобы учащимся было хорошо видно (заранее). Слайд 23-38

Цель: развить логическое мышление.

a)        Определите следующие два члена числовой последовательности:

1.      2,4,6,8 …  (10,12)

2.      3,6,4,7,5 … (8,6)

3.      16,14,17,13,18 … (12,19)

4.      174,171,57,54,18,15 … (5,2)

5.      230,225,45,40 … (8,3)

b)        Найдите лишнее число:

1.      12,45,678,94,3456  (45-нечетное)

2.      75,225,952,3651,25931  (952-четное)

c)        Найдите лишнюю фигуру (приложение А):

1.     Круг, ромб, квадрат, треугольник, отрезок.     (Отрезок)

2.     Параллелепипед, цилиндр, квадрат, куб.   (Квадрат)

3.     Из четырех фигур – одна лишняя, используйте параллельный перенос.   (4 фигура)

 

3.4.Правила  учим и знаем. Каждый ученик команды отвечает на один вопрос теории. Вопросы готовятся на отдельных карточках, их выбирает капитан. За каждый ответ по 1 баллу. (Приложение Б). Слайд 39

Цель: межпредметная связь «Культура речи», развитие памяти и мышления.

 

3.5. Конкурс «Домашнее задание» состоит из двух  основных частей:  из заданий, которые были заданны на дом преподавателем и задания, которое команды придумали    соперникам. (Приложение В). Слайд 40-47

Цель: развить творчество, смекалку, познавательную активность; воспитать чувство ответственности, самоконтроля; формировать интерес к изучению математики.

1.                  Устное задание, на скорость. Основные формулы производных и логарифмов.

2.                   Нужно обрезать нитки так, чтобы на основной нити остались цифры  от 1 до 9. (За правильный ответ по 1 баллу)

3.                  Запишите подряд 22 пятерки. Поставьте между всеми цифрами знаки арифметических действий так, чтобы в результате получилось число 2006.

(5*5*5*5+5*5*5*5+5*5*5*5+5*5*5+5*5-5*5+5+5/5=2006)

(максимальное количество баллов-3)

4.                  Запишите подряд 25 пятерок. Поставьте между некоторыми цифрами знаки арифметических действий так, чтобы в результате получилось число 2006.

(555+555+555+55+55+55+55+55+55+5+5+5/5=2006)

(максимальное количество баллов-3)

5.                  Каждая команда предоставляет свои задания сопернику.

(максимальное количество баллов-3)

 

3.6. «Правила знаем – задачи решаем!» Слайд 48

Каждая команда получает одинаковую карточку с заданием. Это  задание на скорость, отводится 15-20 мин., в зависимости от количества и сложности задач.

Цель: отработка навыков совместных действий, нахождения производных, вычисление неопределенного интеграла, решения  показательных уравнений.

1.      Найдите производные функций:

·        

·        

·        

·        

·        

2.      Вычислить неопределенный интеграл:

·        

·        

·        

·        

·        

3.      Решить уравнения:

·        

·        

·        

·        

·        

4.    Запишите три правила нахождения первообразных.

 

5.    Запишите основное логарифмическое тождество.

 

3.7.  Задание на доске. Слайд 49-51

В следующих числовых рядах числа записаны в определенной закономерности. В каждом ряду своя закономерность. Установите ее и запишите в свободные  три клетки еще по три числа.

19, 20, 22, 25, 29	34	40	47
5, 8, 14, 26, 50	98	194	386
253, 238, 223, 208, 193	178	163	148
12, 11, 16, 16, 20, 21, 24	26	28	31
15, 29, 56, 109, 214	423	840	1673

 

3.8. Конкурс капитанов. Слайд 52-54

Капитаны получают задания на карточке, решив их, выходят к доске и выполняют еще одно логическое задание. Кто выходит первым, имеет право выбора. Максимальное количество баллов – 6. В это время команды отгадывают кроссворд, зарабатывая тем самым дополнительные баллы. За каждое угаданное слово по 1 баллу. (Приложение 4)

Цель: развить смекалку, чувство ответственности, самоконтроля; отработка навыков совместных действий.

1.      Какая из нижеприведенных функций описывает график:

·      y=kx

·      y=ax+bx+c

·      y=k/x

·      y=1x1

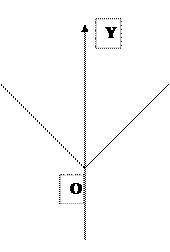
2.      Определите вид фигуры, используя для этого нанесенные данные:

·      Прямоугольник

·      Ромб

·      Параллелограмм

·      Трапеция

 

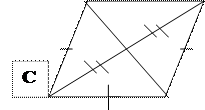
3.      Среди данных функций выберите степенные:

·       

·       

·       

·        

·        

4.      Запишите формулу для вычисления  определенного интеграла. (Формулу Ньютона - Лейбница)

5.      Что называется арксинусом числа а?

6.      Что называется арккосинусом числа а?

3.9. Задания на доске. Слайд 55-62

Заполните пустые клетки каждого квадрата буквами из числа уже имеющихся в нем так,  чтобы ни в одной из горизонталей, вертикалей или диагоналей квадрата буквы не повторялись.

 

К	О	Л	Б	А
О	Б	А	Л	К
Л	К	Б	А	О
Б	А	К	О	Л
А	Л	О	К	Б

 

 

В	А	Л	Е	Т
Т	Л	Е	В	А
А	В	Т	Л	Е
Л	Е	А	Т	В
Е	Т	В	А	Л

 

 

Д	О	С	К	А
А	С	Д	О	К
О	А	К	Д	С
С	К	О	А	Д
К	Д	А	С	О

 

 

 

Р	У	Ч	К	А
А	Ч	Р	У	К
У	Р	К	А	Ч
Ч	К	А	Р	У
К	А	У	Ч	Р

 

 

 

Заключение. Слайд 63-64

Вопросы этого «Математического боя» затронули все основные разделы учебника «Алгебра и начала анализа»:

- тригонометрические функции

- производная

- первообразная и интеграл

- показательная и логарифмическая функции.

Урок-игра «Математический бой» отличается от традиционных нестандартностью проведения, атрибутикой (эмблемы, плакаты и др.), атмосферой соревнования.

К положительным  моментам урока можно отнести то, что ученики готовятся  к нему. Каждая команда старается показать безукоризненные знания, умения, навыки, понимание математических символов, формул, терминов и т.д. В предлагаемом варианте происходит  чередование устных и письменных заданий, что очень важно для предупреждения утомляемости.

Доказано, если использование соревновательных ситуаций носит не случайный, а систематизированный характер, тесно связанный с изучаемым материалом, то на фоне деятельности учащиеся легче поймут и запомнят способы решения примеров, задач, теоретический материал, который быть может, недостаточно был усвоен на предыдущих уроках.

Урок «Математический бой» выполняет познавательные и воспитательные функции. На нем учащиеся применяют приобретенные знания, открывают новые приемы и способы решений, рассуждений; развивается логическое мышление, смысловая  образная память.

Обязательность четкого, правильного и наиболее полного объяснения решения той или иной задачи также является положительной чертой этого урока. Соревновательность активизирует мыслительную деятельность, возбуждает ее. Учащиеся преображаются на глазах, с огромным удовольствием показывают свои знания и умения.

Диалоговое взаимодействие (при обсуждении того или иного задания) способствует выработке у учащихся аргументировано доказывать свою точку зрения, отстаивать свою позицию; прислушиваться к мнению других, коллективно находить правильные решения. Развивает чувство взаимопомощи и взаимоуважения; формирует осознанные нормы поведения, умение оценивать и направлять свои действия с учетом позиций других членов коллектива; учит внимательности, терпимости, самоуправлению и самообладанию.

Такой урок способствует развитию различных качеств личности учащегося: честности, находчивости, сообразительности, критичности мышления, скорости в отыскании ответа и т.д.

Так как вопросы «боя» содержат различный уровень сложности, то смогли отличиться и “слабые”  курсанты. В результате такого урока был повышен уровень обучения математики, сформированы умения и навыки самообразования, сформированы умения работать в групповой деятельности, обобщены и систематизированы знания по всему курсу «Алгебра и начала анализа». Проверена общая эрудиция и способность к логическому и комплексному математическому мышлению каждого учащегося.

В заключение хотелось бы отметить, что такая форма урока, как «Математический бой», позволяет разносторонне развиваться личности учащегося. Этот урок-игра стал важной частью учебного процесса для курсантов первого курса.

 

 

 

 

 

Список использованной литературы. Слайд 65-67

1. Арсланьян В. Психологические «штучки» на уроке математики.: Учебно–методическая газета Первое сентября. Приложение математика. №18, 2006.
2. Блинков А. Весенний турнир Архимеда.: Учебно–методическая газета Первое сентября. Приложение математика. №15, 2006.
3. Колмагоров А. и др. Алгебра и начала анализа: Учебник для 10 -11 классов средней школы. – М.: Просвещение, 1990.
4. Муравин Г., Муравина О. Контрольные работы.: Учебно–методическая газета Первое сентября. Приложение математика. №31, 2004.
5. Никифоров С. Использование тестов в теме «Решение тригонометрических уравнений».: Учебно–методическая газета Первое сентября. Приложение математика. №13, 2005.
6. Нилова Н. Задания в карточках.: Учебно–методическая газета Первое сентября. Приложение математика. №33, 2004.
7. Обрубов А. и др. 14 турнир Архимеда: Новогодний аттракцион.: Учебно–методическая газета Первое сентября. Приложение математика. №10, 2005.
8. Свеклина А. Активизация познавательной деятельности учащихся.: Учебно–методическая газета Первое сентября. Приложение математика. №32, 2004.
9. Стандарт среднего (полного) общего образования по математике.: Учебно–методическая газета Первое сентября. Приложение математика. №14, 2006.
10. Тумашева О. Кроссворд.: Учебно–методическая газета Первое сентября. Приложение математика. №5, 2005.
11. Федотова Л. Повышение вычислительной культуры учащихся.: Учебно–методическая газета Первое сентября. Приложение математика. №36, 2004.
12. Федотова Л. Повышение вычислительной культуры учащихся.: Учебно–методическая газета Первое сентября. Приложение математика. №40, 2004.
13. Юрченко О. Методы мотивации и стимулирования деятельности учащихся.: Учебно–методическая газета Первое сентября. Приложение математика. №1, 2005.
14. Яковлева Т. Значение уроков «Математический лабиринт».: Учебно–методическая газета Первое сентября. Приложение математика. №4, 2005.
15. Яковлева Т. Математический лабиринт - нестандартный урок, организация и методика проведения.: Учебно–методическая газета Первое сентября. Приложение математика. №3, 2005.