Методические материалы по решению планиметрических задач на построение с помощью программы Geogebra

Методические материалы по решению планиметрических задач на построение с помощью программы Geogebra

 

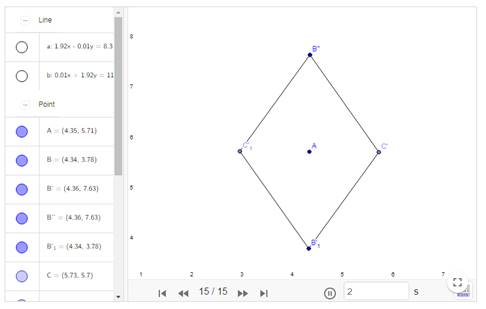
Задача 1. Построить квадрат, сохраняющий свои свойства при смещении вершин. Построить квадрат с использованием кругов.

Пошаговое построение.

1.                 Создайте произвольный отрезок АВ. Он будет радиусом кругов и одной из сторон квадрата.

2.                 Постройте круг с центром в точке А и радиусом АВ. Аналогичным образом постройте второй круг с центром в точке В и радиусом АВ. В результате получим два круга из одинаковым пересекающимся радиусом. Центры кругов лежат на краях отрезка АВ

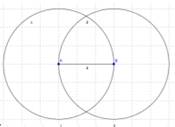
3.                 Через точки А и В проведите две прямые, перпендикулярные отрезку АВ. Подсказка: инструментом Перпендикулярная прямая нужно выделить точку и отрезок в любом порядке.

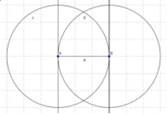
4.                 Чтобы получить точки пересечения полученных перпендикуляров с кругами. Воспользуйтесь инструментом Сечение. Получим точки C и D

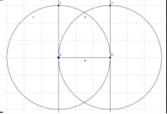
5.                 Постройте отрезок CD.

Выделите нужную фигуру инструментом Многоугольник. Мы получили идеальный квадрат

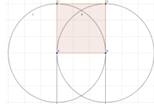
6.Спрячьте вспомогательные элементы конструкции и наблюдайте результат.

Учебное исследование 1. Исследовать поведение полученного квадрата. Попытайтесь двигать вершины полученного квадрата. Ответьте на следующие вопросы:

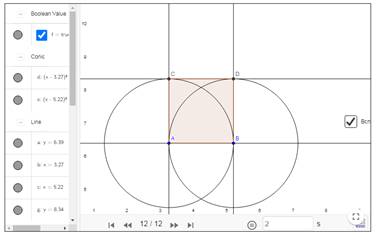
1. Какие точки можно двигать, а какие остаются неподвижными? Почему определенные точки квадрата нельзя передвигать напрямую курсором?

 

Задача 2. Построить квадрат, сохраняющий свои свойства при смещении вершин. Построение квадрата с использованием инструмента «Правильный многоугольник».

Пошаговое построение.

1. Инструментом Правильный многоугольник создайте на графическом холсте две точки (или выделите уже существующие), в диалоговом окне введите количество вершин – четыре и нажмите «Ок». Квадрат готов.

Примечание: При построении учитывайте, что вершины правильного многоугольника будут строиться против часовой стрелки, направлении построения или выделения двух основных точек.

Таким же образом можно построить верный многоугольник с любым количеством вершин.

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельные, то есть лежащие на параллельных прямых. Частные случаи параллелограмма представляет собой прямоугольник, квадрат и ромб.

Задача 3. Построить параллелограмм по двум смежным сторонам.

Пошаговое построение.

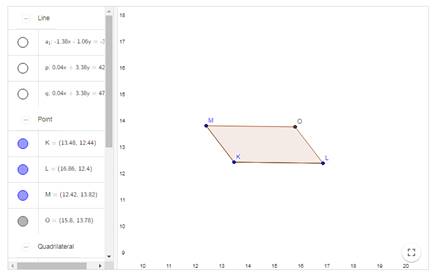
1. Произведите два произвольных отрезка с одной общей вершиной, которые будут образовывать две смежные стороны и три вершины параллелограмма.

2. Проведите параллельные прямые относительно каждого отрезка через противоположную вершину параллелограмма.

3. Найдите последнюю вершину на пересечении построенных прямых.

4. Спрячьте прямые и постройте недостающие стороны.

На модели можно изменять угол параллелограмма и длину его сторон, при этом противоположные углы и стороны всегда остаются равными.

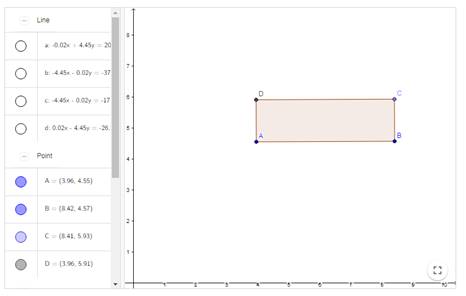
Задача 4. Построить прямоугольник, учитывая, что Прямоугольник – это параллелограмм, у которого все углы прямые.

Пошаговое построение.

1. Постройте точку А в любом месте на холсте.

2. Проведите через т. А произвольную прямую АВ.

3. Постройте перпендикуляр через т. А и т. В относительно прямой.

4. Постройте параллельную прямую на перпендикуляре через т. А или т. В относительно прямой АВ.

Альтернативно можно провести еще один перпендикуляр к уже существующему.

5. Найдите точку пересечения параллельной прямой и перпендикуляра для того чтобы определить последнюю вершину.

6. Спрячьте все прямые и соедините точки отрезками. Прямоугольник готов, и вышедшая фигура будет сохранять его свойства при передвижении вершин.

 

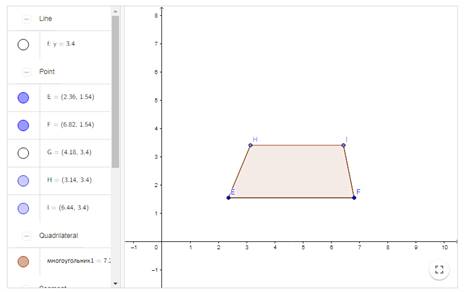
Задача 5. Используя вышеперечисленные инструменты, построить динамическую модель трапеции. Модель должна давать возможность изменять длины всех сторон трапеции с сохранением параллельности ее оснований.

  Напомним, что трапеция – это четырехугольник, у которого две противоположные стороны параллельны – они являются основами трапеции; две другие боковые стороны не параллельны.

 

Задача 6. Построить ромб.

Напомним, что ромб – это  параллелограмм, у которого все стороны равны, а диагонали пересекаются под прямым углом. Ромб с прямыми углами называется квадратом.

Пошаговое построение.

1. Постройте точку А в любом месте на холсте.

2. Проведите прямую АВ: т. А будет центром ромба, т. В – одной из его вершин.

3. Проведите перпендикуляр к прямой АВ через т. а. Эти прямые содержащие диагонали ромба, которые всегда пересекаются под прямым углом.

4. Постройте точку С на построенном перпендикуляре.

5. Произведите отрезок BC. Это одна из сторон ромба.

6. Так как все стороны ромба равны, нужно установить зависимость между ними на чертеже. Это можно сделать, отразив их от одной стороны ВС. Таким образом, все они будут производными одной стороны, сохраняя пропорции при деформации.

Учебное исследование 2. Установите, какие точки можно передвигать, чтобы трансформировать ромб. Почему другие точки не доступны для непосредственного передвижения с помощью курсора?

 

Треугольник – одна из основных фигур, изучаемых в геометрии. Он является очень интересной фигурой с множеством свойств, которые, вполне возможно, еще не до конца исследованы.  Рассмотрим разные способы построения разных видов треугольников.

Так же, как в случае с квадратом, треугольник удобно построить с помощью свободных отрезков. Это будет хорошей иллюстрацией для произвольного треугольника, однако такие разновидности, как прямоугольный, равнобедренный, равносторонние треугольники, требуют  особого подхода. Ниже описаны алгоритмы их построения. Для удобства демонстрации можно построить все виды треугольников на одном холсте, контролируя их видимость с помощью инструмента Флажок.

Флажки в GeoGebra – удобный способ контролировать видимость отдельных объектов чертежа. Чтобы создать флажок, нужно кликнуть одноименным инструментом в любом месте полотна, затем в диалоговом окне указать его имя и перечислить объекты чертежа. Объекты можно выбрать из списка в диалоговом окне или непосредственно выделить их на чертеже. Они будут отображаться только при значении флажка true.

Флажок – это логическое значение, переменное типа Boolean. Чтобы включить еще один объект под действие уже существующего флажка, необходимо в свойствах объекта поставить имя логического переменного флажка в строку «Условие отображение объекта». Имя переменного флажка можно узнать, переведя на него курсор.

 

Задача 7. Построить прямоугольный треугольник.

Пошаговое построение.

1. Постройте точку А в любом месте на холсте.

2. Проведите через т. А произвольную прямую АВ.

3. Постройте перпендикуляр через т. А относительно прямой АВ

4. Постройте на перпендикуляре третью вершину С и проведите гипотенузу ВС. Спрячьте вспомогательные прямые и проведите катеты треугольника. Выделите прямой угол с помощью соответствующего инструмента.

Учебное исследование 3. Установить, почему при передвижении т. В сохраняется пропорция длин катетов, а также можно поворачивать треугольник, а передвижение т. С такого эффекта не дает?

Задача 8. Построить треугольник с контролируемым углом.

Пошаговое построение.

1. Произведите произвольный отрезок.

2. Создайте слайдер для контроля угла. Так как он будет определять величину угла треугольника, укажите интервал от 0° до 180°.

3. Теперь нужно создать угол на отрезке. Поочередно выделите точки отрезка инструментом «Угол заданной величины» и в диалоговом окне укажите переменную созданного слайдера. Появится новая точка, положение которой можно контролировать с помощью слайдера.

Примечание. Данная точка является третьей вершиной только в случае, если необходимо получить равнобедренный треугольник. Чтобы контролировать длины его сторон, необходимо выполнить следующие действия:

4. Проведите луч через полученную точку и спрячьте ее.

5. Постройте точку на луче – это третья вершина треугольника. Спрячьте луч и проведите к точке отрезки.

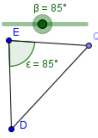
По желанию, таким же образом можно сделать и вторую точку треугольника контролируемой.

 

Задача 9. Построить равнобедренный треугольник.

Пошаговое построение.

1. Произведите произвольный отрезок.

2. Постройте срединный перпендикуляр к отрезку с помощью одноименного инструмента.

3. Постройте точку на срединном перпендикуляре и спрячьте его.

4. Проведите стороны равнобедренного треугольника из точки к концам выходного отрезка и выделите их насечкой (Настройки> Стиль> Оформление).

 

Задача 10. Построить равносторонний (правильный) треугольник.

Пошаговое построение.

1. Произведите произвольный отрезок.

2. Постройте две окружности через концы отрезка с центрами в них

Найдите точку пересечения кругов.

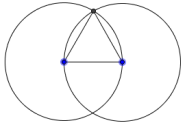
Треугольник в данном построении будет равносторонним, потому что его стороны будут радиусами двух равных окружностей.

 

Задача 11. Построить равносторонний треугольник с помощью инструмента «Правильный многоугольник».

Учебное исследование 4. Постройте треугольник, который при передвижении вершин всегда будет оставаться тупоугольным/остроугольным. Попытайтесь найти несколько способов построения.

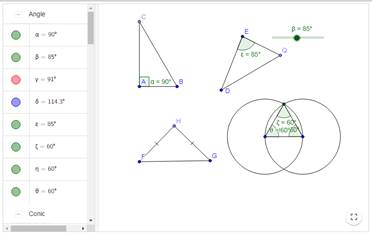
Решение классической задачи на построение равностороннего треугольника на трех параллельных прямых

 

Задача 12. Построить правильный треугольник так, чтобы его вершины лежали на трех параллельных прямых (классическая логическая и геометрическая задача, которая решается исключительно с помощью карандаша, циркуля и линейки). В этом построении описан алгоритм решения этой задачи с использованием соответствующих инструментов GeoGebra.

Пошаговое построение.

1. Постройте точку в любом месте чертежа и проведите через нее прямую, параллельную оси Ох. Спрячьте оси. Проведите еще две прямые, параллельные первой.

2. Постройте вторую вершину треугольника на средней параллели. Постройте верный треугольник на этих двух точках. Для этого постройте два круга с центрами в двух известных точках, вершинах треугольника и радиусом, равным его стороне. Сечение этих кругов даст третью вершину треугольника. Это не решение задачи, поскольку третья, зависимая вершина треугольник не будет лежать на третьей параллели.

3. Подвигайте вершины треугольника по параллелям. Что может сказать о положении третьей вершины?

Примечание: При изменениях треугольника третья вершина двигается по одной линии. Это можно увидеть, включив функцию точки «Оставлять следует» (включить функцию можно из-за свойств объекта).

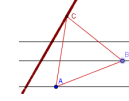
4. Чтобы получить более точное геометрическое место точек положения т. с, можно построить локус. Для этого подходящим инструментом поочередно выделите точки С и В.

5. Можно заключить, что искомое положение т. С находится на пересечении локуса и третьей параллели. Однако найти точку пересечения с локусом невозможно, поэтому необходимо построить соответствующую ему прямую. Для этого постройте еще один правильный треугольник рядом с первым (см. шаг 2).

6. Проведите прямую через зависимые вершины двух треугольников. Она должна совпадать с локусом. Локус спрячьте или удалите.

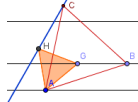
7. Найдите точку пересечения построенной прямой с третьей параллелью. Это будет правильным положением третьей вершины правильного треугольника.

8. Постройте правильный треугольник на произвольной точке, которая принадлежит нижней параллели, и полученной точке пересечения с третьей параллелью.

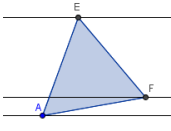
Спрячьте вспомогательные объекты конструкции. Задача решена. При передвижении параллелей вершины треугольника всегда будут им принадлежать.

 

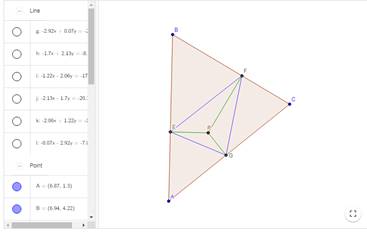
Задача 13. Построить динамическую иллюстрирующую модель теорему Морлея.

Теорема Морлея (Морли)

Теорема. Трисектрисы углов любого произвольного треугольника пересекаются в точках, образующих вершины равностороннего треугольник.

Трисектрисами угла называются два луча, делящих угол на три уровня части. В GeoGebra нет соответствующего встроенного инструмента, однако можно разделить любой угол на три равные части с помощью инструмента «Поворот вокруг точки».

Пошаговое построение.

1. Постройте случайный треугольник АВС.

2. Определите все три его угла с помощью соответствующего инструмента. На панели объектов появятся величины α, β, γ.

3. Теперь поверните точку С относительно точки А на угол α/3. Появится новая точка С', производная от С. Луч из АС' отделит треть от угла ВАС.

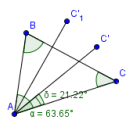
Таким же образом отложите угол С'А С'1 и поделите другие углы треугольника на три части, построив трисектрисы.

Заметьте, что т. С и т. С', хоть и обозначены стандартным синим цветом, однако не будут недоступны для непосредственного передвижение.

4. Найдите точки пересечения трисектриса (крайней с крайней) и постройте на них треугольник DFE. Это треугольник Морлея, который при любом исходном треугольнике всегда будет оставаться правильным.

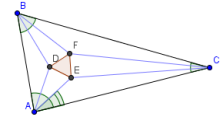
Оформите чертежи: спрячьте производные точки и отрезки к ним, затем проведите отрезки от вершин треугольника до точек пересечения трисектрис.

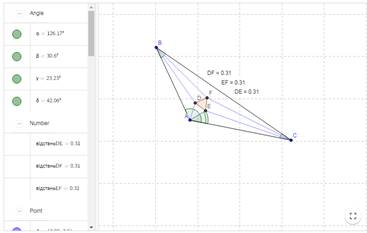
Учебное исследование 1. Докажите правильность треугольника DFE. Для этого определите длины сторон треугольника DFE с помощью соответствующего инструмента, чтобы проверить его правильность.

 

Задача 14. Построить срединные перпендикуляры треугольника.

Напомним, что прямую, проходящую через середину отрезка и перпендикулярную к нему, называют срединным перпендикуляром к отрезка.

Пошаговое построение.

1. Постройте произвольный треугольник любым удобным для вас способом.

2. Проведите к каждой из сторон треугольника срединные перпендикуляры (хотя для определения точки их пересечения хватит всего двух перпендикуляров). Это можно сделать с помощью инструментов «Середина или центр» и «Перпендикулярная прямая», или же сразу использовать специальный инструмент «Серединный перпендикуляр».

3. Определите точку пересечения перпендикуляров.

4. Постройте круг с центром в точке пересечения. Можно ли построить вписанную или описанную окружность треугольника из центром в этой точке?

Задача 15. Построить биссектрису треугольника.

Напомним, что биссектриса угла – это луч, исходящий из его вершины, проходит между его сторонами и делит данный угол пополам.

Биссектрисой треугольника называется отрезок биссектрисы углы треугольника, который соединяет вершину с точкой на противоположной стороне этого треугольника.

Пошаговое построение.

1. Постройте биссектрисы углов треугольника и найдите точку их пересечения. Можно ли построить вписанную или описанную окружность треугольник с центром в этой точке?

2. Выделите построенные объекты цветом и создайте флажок для контроля видимости элементов чертежа.

3. Постройте вписанный круг с центром в точке пересечения биссектрис. Чтобы построить круг, необходимо провести высоту (перпендикуляр) с точки пересечения биссектрис на любую сторона треугольника. Высота будет радиусом окружности.

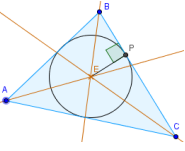
Задача 16. Построить медианы треугольника.

Напомним, что медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны этого треугольника.

Пошаговое построение.

1. Проведите медианы ко всем сторонам треугольника (найдите середину стороны и проведите к ней отрезок с противоположной вершины) и найдите точку их пересечения.

2. Выделите построенные объекты цветом и создайте флажок для контроля видимости элементов чертежа

Учебное исследование 3. Исследуйте построение и сделайте выводы о свойствах медианы, а именно:

1) Медиана разбивает треугольник на два треугольника одинаковой площади.

2) Все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении  2:1, считая от вершины. Эта точка называется центром тяжести треугольника или его центроидом.

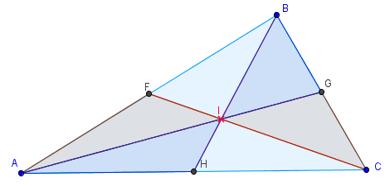
  4. Исследуйте построение и определите на сколько треугольников разделяется треугольник своими медианами. Какие треугольники равны между собой и почему?

 

Задача 16. Построить высоты треугольника.

Напомним, что высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.

Пошаговое построение.

1. Продлите стороны треугольника дополнительными прямыми.

2. Проведите высоты ко всем сторонам треугольника и найдите точку их пересечения

3. Выделите построенные объекты цветом и создайте флажок для контроля видимости элементов чертежа

 

Задача на построение 17. Построить ортотреугольник.

Пошаговое построение.

1. Найдите точки пересечения высот треугольника с его сторонами.

2. Соедините эти точки отрезками – это и есть ортотреугольник.

Высоты исходного треугольника являются биссектрисами углов его ортотреугольника, соответственно, их сечение является центром вписанного в ортотреугольник круга.

3. Опустите перпендикуляр из пересечения высот исходного треугольника на одну из сторон ортотреугольника и найдите точку их пересечения.

4. Постройте вписанный в ортотреугольник круг с центром в точке пересечения высот.

Заметьте, что ортотреугольник существует только при условии, что точка пересечения высот исходного треугольник лежит внутри него.

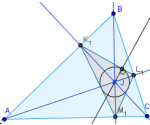
Примечание: Согласно задаче Фаньяно, ортотреугольник произвольного треугольника АВС имеет наименьший периметр из всех видов вписанных треугольников

 

Задача 18. Построить точку Шпикера, внешневписанные окружности и точку Бевена.

Напомним, что внешневписанная окружность треугольника – это окружность, затрагивающая одну из сторон треугольника и продолжения двух других его сторон. Для любого треугольника существует три внешневписанных окружности.

Пошаговое построение.

1. Продлите стороны треугольника прямыми.

2. Постройте на полученных прямых точках так, чтобы они находились у вершин треугольника и вне его сторон (всего должно получиться шесть точек). Это вспомогательные точки, которые можно затем скрыть.

3. С помощью построенных на продолженных сторонах точек, постройте биссектрисы для наружных углов треугольника (для применение инструмента «Биссектриса угла» необходимо выделить по три точки, которые определяют каждый угол).

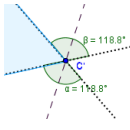
Всего нужно построить три биссектрисы – на каждую пару углов нужно по одной, так как углы являются смежными.

4. Найдите три точки пересечения построенных биссектрис – это центры вне вписанных кругов. Они всегда лежат вне треугольника

5. Опустите с точек пересечения биссектрис перпендикуляры на стороны треугольник. Точки пересечения перпендикуляров и сторон треугольника являются точками прикосновения от вписанных кругов к треугольнику.

6. Постройте внешневписанные окружности.

7. Отрезки, соединяющие центры внешневписанных окружностей и противоположные им вершины треугольника, являются биссектрисами его углов.

Точка пересечения этих отрезков называется точкой Шпикера. Она же есть радикальным центром внешневписанных окружностей.

 

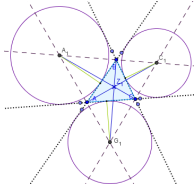
Примечание. Радикальный центр трех окружностей – единственная точка, которая ставится в соответствие любым трем окружностям на евклидовой плоскости.

Определяется пересечением радикальных осей всех трех окружностей. Центр круга, проходящего через центры внешневписанных окружностей, называют точкой Бевена.

8. Построить точку Бевена можно, проведя круг через три центра внешневписанных окружностей (инструмент «Круг через три точки») и определив ее центр (инструмент «Середина или центр»).

9. Выделите построенные объекты цветом и создайте флажки для контроля видимости элементов чертежа.

 

Задача 19. Построить точку Жергона.

Напомним, что точка Жергонна – точка пересечения соединяющих отрезков вершины треугольника с точками соприкосновения противоположных сторон треугольника с вписанной в него окружностью.

Пошаговое построение.

1. Найдите точки касания вписанного круга (порядок построения см. в задачи на построение биссектрис) и сторон треугольника.

2. Проведите к точкам отрезки из вершин треугольника и найдите точку пересечения этих отрезков.

3. Выделите построенные объекты цветом и создайте флажки для контроля видимости элементов чертежа.

 

Задача 20. Построить точку Негеля.

Напомним, что точка Нагеля – точка пересечения отрезков, соединяющая вершины треугольника с точками соприкосновения противоположных сторон с соответствующими внешневписанными окружностями.

Пошаговое построение.

1. Найдите точки соприкосновения всех внешневписанных окружностей со сторонами треугольника.

2. Произведите отрезки от точек до вершин треугольника и найдите точку пересечения отрезков.

 

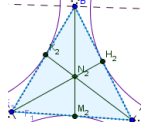
Задача 21. Построить внешние треугольники и точки Торричелли.

Пошаговое построение.

1.                 С помощью инструмента «Правильный многоугольник» выделите концы стороны треугольника и в диалоговом окне укажите количество вершин (три). Чтобы в результате внешний правильный треугольник не был построен «внутри» основного, вершины необходимо выделять против часовой стрелки.

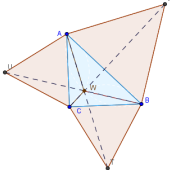
2. Постройте правильные внешние треугольники на всех сторонах исходного треугольника.

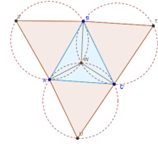
3. Первый способ:

Постройте три окружности  вокруг каждого из внешних треугольников (инструмент «Окружность по трем точкам»).

Найдите точку пересечения трех кругов, что описывают внешние треугольники. Проведите вспомогательные отрезки от вершин треугольника к найденной точке пересечения.

Второй способ:

Соедините отрезками свободные вершины внешних правильных треугольников с противоположными вершинами выходного треугольник.

Найдите точку пересечения этих отрезков. Это первая точка Торричелли.

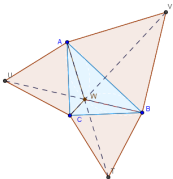
4. Выделите построенные объекты цветом и создайте флажки для контроля видимости элементов чертежа. Вторая точка Торричелли строится подобным образом. Различие в том, что правильные треугольники на сторонах исходного строятся не наружу, а внутрь.

 

Задача 22. Построить точку Брокара.

Напомним, что точка Брокара – особая точка внутри треугольника, названа в честь Анри Брокара, французского математика.

Пошаговое построение.

1. Постройте (или отобразите уже построенные) срединные перпендикуляры сторон треугольника.

2. Постройте перпендикуляры: к стороне ВС через т. С, к АВ через т. В, к СА через т. А.

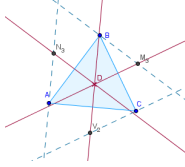
Найдите точки пересечения этих перпендикуляров с срединным перпендикуляром.

2.                 Постройте круги с центрами в точках пересечения и через близлежащие вершины треугольник.

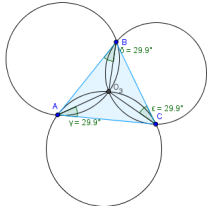
Точка пересечения этих  окружностей является точкой Брокара.

Учебное исследование 7.

Исследуйте свойства точки Брокара. Какие выводы можно сделать о углах, что формируются отрезком, который соединяет т. брокара и прилегающей против часовой стрелки стороной треугольника? (Они всегда равны и называются углами Брокара.)

С какой точкой в правильном треугольнику совпадает точка Брокара? (с точкой пересечения медиан.)

Учебное исследование 8. Докажите, что угол Брокара ≥ 30°. В каких случаях он будет равен 30°?

 

Задача 23. Построить точку Лемуана (Гребе).

Напомним, что у точки Лемуана существует два определения:

-                   точка пересечения прямых, соединяющих каждую вершину треугольника с точками пересечения касающихся описанной окружности, проведенных из двух других вершин.

-                   точка пересечения симедиан треугольника.

Пошаговое построение.

1. Отразите описанную окружность и проведите к ней касательные относительно вершин треугольника (инструментом «Касательная» выделите круг и точку).

2. Найдите точки пересечения соприкасающихся и соедините их отрезками с противоположными вершинами треугольника.

Точка пересечения этих отрезков является точкой Лемуано.

Симедиана – это луч, который симметричен к лучу медианы относительно биссектрисы угла, проведенной из той же вершины.

3. Отобразите на чертеже медианы и биссектрисы.

Инструментом «Отражение относительно прямой» отобразите биссектрису относительно медианы, проходящей через ту же вершину треугольник.

Таким образом, точка пересечения симедиан треугольника является точкой Лемуано.

Совпадают ли две данные точки Лемуано?

 

 

 

 

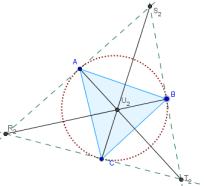
Задача 24. Построить точки Аполлония.

Напомним, что точки Аполлония (изодинамические центры) – две такие точки, расстояние от которых до вершин треугольника обратно пропорционально противоположным этим вершинам сторонам.

Круги, построенные на трех точках – вершине треугольника и сечениях биссектрис внутреннего и наружного угла при этой вершине с прямой, что содержит противоположную сторону треугольника, пересекающуюся в двух точках, которые являются точками Аполлония.

Пошаговое построение.

1. Постройте биссектрисы треугольника и биссектрисы его внешних углов (см. задачу на построение точки Шпикера).

2. Проведите окружность через:

-       вершину треугольника;

-       точку пересечения биссектрисы внутреннего угла при этой вершине с противоположной стороной;

-       точку пересечения биссектрисы внешнего угла с продолженной противоположной стороной.

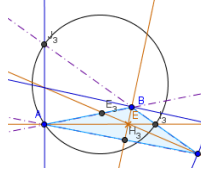
3. Постройте такие круги на двух других вершинах треугольника.

Сечение этих трех кругов дадут две точки Апполония.

4. Проведите прямую через точки Аполлония.

Точки Аполлония лежат на прямой, соединяющей центр описанного круга с точкой Лемуана. Эта прямая называется осью Брокара (выделена зеленым пунктиром).

 

 

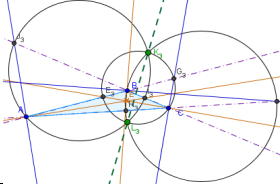
Учебное исследование 9. Отразите построенную ранее точку Лемуана, описанную окружность, и проверьте, действительно ли центр описанного окружности и точка Лемуана лежат на оси Брокара.

 

 

Скачано с www.znanio.ru