УДК 372.8:[512+517]

ББК 74.262.21

П64

Серия «МГУ — школе» основана в 1999 году

Потапов М. К.

П64 Алгебра и начала математического анализа. Методические рекомендации. 10 класс : пособие для учителей общеобразоват. организаций / М. К. Потапов, А. В. Шевкин. — М. : Просвещение, 2013. — 191 с. : ил. — (МГУ — школе).

В книге рассмотрена концепция и структура учебника «Алгебра и начала математического анализа, 10» авторов С. М. Никольского, М. К. Потапова, Н. Н. Решетникова, А. В. Шевкина, приведено 4 варианта примерного тематического планирования, даны методические рекомендации по изучению курса и комментарии к решению наиболее трудных задач, а также рекомендации по использованию дидактических материалов к учебнику (авторы: М. К. Потапов, А. В. Шевкин).

Книга предназначена учителям, работающим по учебнику «Алгебра и начала математического анализа, 10» С. М. Никольского и др.

УДК 372.8:[512+517]

ББК 74.262.21

Издательство «Просвещение», 2013

О пособии для учителей

Данная книга адресована учителям, работающим по учебнику «Алгебра и начала математического анализа, 10» (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Этот учебник предназначен как для базового, так и для углубленного уровня обучения и является частью учебного комплекта для 10—11 классов. Он продолжает серию учебников «МГУ — школе» тех же авторов для 5—9 классов и нацелен на подготовку учащихся к поступлению в вуз и к обучению в вузе.

В учебный комплект для 10 класса входят:

1) Алгебра и начала математического анализа. 10 класс. Учебник для общеобразоват. организаций: базовый и углубленный уровни (С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2008—2013);

2) Алгебра и начала математического анализа. Дидактические материалы. 10 класс (М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2005—2013);

Алгебра и начала математического анализа. Тематические тесты. 10 класс (Ю. В. Шепелева. — М.: Просвещение, 2011—2013).

4) Алгебра и начала математического анализа. Методические рекомендации. 10 класс. Пособие для учителей общеобразоват. организаций (М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2008—2013).

В данной книге рассмотрены концепция учебников алгебры и начал математического анализа для 10—11 классов, их структура, приведено 4 варианта примерного тематического планирования, даны методические рекомендации по изучению основных тем курса 10 класса и комментарии к решению некоторых трудных задач. Здесь же даны рекомендации по использованию дидактических материалов. Практически для всех пунктов учебника в книге для учителя имеются рубрики Решения и комментарии и Промежуточный контроль. В первой из них приведены условия многих задач и их решения или даны рекомендации, помогающие найти решение. При этом даны пояснения, помогающие обучению школьников. Во второй рубрике указаны номера самостоятельных работ по дидактическим материалам.

Концепция учебников для 10 и 11 классов серии

«МГУ — школе»

Авторами учебников разработана концепция многоуровневых учебников математики. Приведем основные положения этой концепции.

^•Математика едина и может быть изложена в одном учебнике для работы по разным программам. Содержание учебника должно соответствовать научной точке зрения на изучаемые вопросы.

^•Учебник должен сочетать в себе научность, стройность, экономность и логичность изложения материала с доступностью для учащихся его учебных текстов.

^•Учебник не должен ограничиваться интересами среднего ученика, он должен удовлетворять интересам всех учащихся — от слабых до сильных.

^•Учебник должен быть пригоден для организации дифференцированного обучения и обеспечивать любой желаемый уровень глубины изучения материала.

^•Способ изложения материала в учебнике, организация учебных текстов и системы упражнений должны обеспечивать достижение различных целей обучения при работе по разным программам.

Структура учебников «Алгебра и начала математического анализа» для 10 и 11 классов и их методический аппарат отвечают основным положениям этой концепции. Авторы учебников серии «МГУ — школе» считают принципиально важным обучать школьников, выбравших разные профили, по одним и тем же учебникам. Тогда учащиеся, заинтересованные в более глубоком изучении математики, могут углублять свои познания в математике самостоятельно или под руководством учителя, который получает реальную возможность для организации дифференцированного обучения и подготовки учащихся к поступлению в вузы. Кроме того, переход с одной программы обучения на другую не будет вызывать трудностей ни для учащихся, ни для учителей.

Эти особенности учебников в полной мере отвечают требованиям ФГОС, нацеливающих учебный процесс на формирование у учащихся в процессе изучения курса математики общеучебных (надпредметных) умений при выполнении универсальных учебных действий, предусмотренных ФГОС.

Каждый из двух учебников обладает цельностью и завершенностью своего содержания, а вместе они составляют единый курс. Для каждого из учебников разработана авторская рабочая программа, соответствующая ФГОС.

В учебниках параграфы без звездочки соответствуют ФГОС (базовый уровень). Параграфы со звездочкой и специально выделенный в параграфах без звездочки материал предназначены учащимся, изучающим математику на углубленном уровне.

Каждая глава учебников для 10 и 11 классов завершается историческими сведениями. В конце учебников помещены разделы «Задания для повторения», содержащие задания для повторения изученного в 10 или 11 классе и за предыдущие годы. В этот раздел включены задания школьных выпускных экзаменов и конкурсных экзаменов в различные вузы страны прошлых лет, а также задания Единого государственного экзамена (ЕГЭ). Это позволит учителю организовать целенаправленную подготовку учащихся к экзаменам начиная с 10 класса.

На базовом уровне дополнительные материалы и сложные задачи, специально выделенные в учебниках, можно не рассматривать. Пропуск необязательных пунктов и задач не нарушает целостности курса. Уменьшается лишь глубина погружения учащихся в теоретические вопросы, уменьшается число доказываемых фактов, число технически или идейно сложных задач.

При углубленном изучении математики за счет дополнительных пунктов и отдельных задач со звездочкой содержание изучаемого материала расширяется и углубляется до объема, соответствующего программе для классов с углубленным изучением математики.

Учебник для 10 класса включает следующий материал: действительные числа, рациональные уравнения и неравенства, корень степени n, степень положительного числа, логарифмы, формулы тригонометрии, показательные, логарифмические, тригонометрические функции, уравнения и неравенства, а также элементы теории вероятностей.

Учебник для 10 класса охватывает почти весь материал по алгебре и началам математического анализа, необходимый для поступления в вузы со средним уровнем требований по математике.

Учебник для 11 класса включает все вопросы программы, связанные с исследованием функций и построением их графиков, с производной и первообразной, с решением уравнений, неравенств, их систем, а также с комплексными числами. Здесь углубляются знания учащихся по ранее изученным вопросам до уровня, необходимого для поступления в вузы, предъявляющие повышенные требования к математической подготовке школьников.

О работе по учебнику и дидактическим материалам для

10 класса

Работать по учебнику для 10 класса можно после обучения в 9 классе по любому из учебников. В начале учебника повторяются основные вопросы программы девятилетней школы, что позволит систематизировать изученное ранее и подготовиться к изучению нового материала.

Главы учебника называются:

I. Корни, степени, логарифмы.

II. Тригонометрические формулы. Тригонометрические функции.

III. Элементы теории вероятностей.

Так как материалы глав I и II практически не связаны друг с другом, то желательно изучать эти главы параллельно, отводя на изучение каждой главы определенное число часов в неделю. Такое изучение оправдано еще и тем, что во многих школах в 9 классе продолжают изучать тригонометрический материал. В этом случае откладывать изучение тригонометрии на второе полугодие 10 класса было бы нелогичным. Параллельное изучение этих глав позволяет в конце 10 класса одновременно подойти к изучению функций и решению уравнений и неравенств: показательных, логарифмических и тригонометрических, что будет способствовать лучшему усвоению этих важных тем.

В главе I изучение линии числа начинается с повторения действительных чисел, а завершается изучением степени с любым действительным показателем и логарифмов. Линия уравнений и неравенств начинается с повторения способов решения рациональных уравнений и неравенств, а завершается изучением показательных и логарифмических уравнений и неравенств. Отметим особенность методики обучения решению неравенств и их систем, принятой в учебнике. Сначала рассматриваются строгие неравенства, потом нестрогие. Такая последовательность изучения материала позволяет предупредить появление ошибок при решении неравенств в сложных случаях, когда множество решений содержит изолированные точки.

В главе I должное внимание уделено и линии преобразования числовых и буквенных выражений, и линии функций.

При изучении функций используется понятие функции, непрерывной на промежутке, опирающееся на интуитивное представление о функции, график которой является непрерывной линией. Определение непрерывной функции через непрерывность ее графика не требует от учащихся каких-либо особых усилий для его понимания. Рассматривая непрерывный график, легко убедить учащихся в том, что приведенное определение равносильно и такому определению: функция непрерывна на промежутке, если она определена в каждой точке этого промежутка и малому изменению аргумента x соответствует малое изменение функции f (x). При этом не стоит пытаться как-либо пояснить это аналитически. В 11 классе в связи с рассмотрением общих свойств функций будут рассмотрены и непрерывность функции в точке, и разрывные функции.

В главе II приведено изложение всего тригонометрического материала: от введения понятия угла, тригонометрических функций угла, формул тригонометрии до тригонометрических уравнений и неравенств, при этом все тригонометрические формулы доказываются. Вводятся понятия арксинуса, арккосинуса, арктангенса, арккотангенса. После рассмотрения формул сложения и их следствий вводятся тригонометрические функции числового аргумента. Глава завершается изучением способов решения тригонометрических уравнений и неравенств.

В главе III представлены элементы теории вероятностей. Тем самым выполнено требование ФГОС о формировании у учащихся умения воспринимать и критически оценивать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, решать простейшие вероятностные задачи прикладного характера.

В данной книге приведены методические рекомендации по изучению всех тем, включенных в учебник и в дидактические материалы для 10 класса, с решениями наиболее трудных задач. Иногда комментарии к близким по содержанию пунктам объединены. При этом не обсуждается время, отводимое на изучение пункта, — в каждом профиле оно окажется своим, а в отдельных профилях некоторые пункты вообще не изучаются. В комментариях для учителя не выделяется обязательный и необязательный материал, так как в учебнике есть соответствующие обозначения. Во многих пунктах книги для учителя методические комментарии даны в расчете на возможно более глубокое изучение вопроса, поэтому при подготовке к уроку учитель должен отобрать главное, что будет изложено учащимся на уроке, решить, каким будет закрепление материала в классе и дома, каким и когда будет контроль изученного. При этом не надо стремиться донести до учащихся все подробности и тонкости изучаемого материала, если учащиеся существенно ограничены во времени изучения темы. Если учитель считает необходимым дать необязательный для своего класса материал, то не следует входить во все подробности изложения такого материала. На некоторые места достаточно обратить внимание учащихся и посоветовать им внимательно прочитать объяснение или доказательство, имеющееся в учебнике, но опущенное при обсуждении в классе.

При организации повторения курса алгебры за 10 класс необходимо обратить особое внимание на наиболее трудные темы курса для данного класса, постараться учесть индивидуальные пробелы учащихся.

При повторении теории необходимо выделять основные теоретические факты, изученные за год, давая иллюстрации их применения на наиболее характерных примерах, в том числе на примерах задач школьных выпускных экзаменов, а также вступительных экзаменов в вузы (ЕГЭ). При этом можно использовать задачи из раздела «Задания для повторения».

Примерное тематическое планирование для 10 класса

Из приведенных четырех вариантов примерного тематического планирования варианты I и II предназначены для базового уровня. Варианты III и IV предназначены для углубленного уровня. В зависимости от уровня подготовки класса и при наличии дополнительных учебных часов учитель вносит коррективы в примерное планирование, увеличивая время изучения трудных тем и число изучаемых вопросов.

Справа от параграфа или пункта указано число часов, отведенных на его изучение при каждом из вариантов планирования I, II, III, IV, рассчитанных соответственно на 2,5, 3, 4 и 5 недельных часов в течение года. Тексты контрольных работ приведены в дидактических материалах.

I			II	III	IV
1. Действительные числа 7			7	12	13
1.1. Понятие действительного числа 2			2	2	2
1.2. Множества чисел. Свойства действительных чисел 2			2	2	2
1.3. Метод математической индукции —			—	1	1
1.4. Перестановки 1			1	1	1
1.5. Размещения 1			1	1	1
1.6. Сочетания 1			1	1	1
1.7. Доказательство числовых неравенств —			—	1	2
1.8. Делимость целых чисел —			—	1	1
	I	II		III	IV
1.9. Сравнения по модулю m	—	—		1	1
1.10. Задачи с целочисленными неизвестными	—	—		1	1
2. Рациональные уравнения и неравенства	12	14		18	25
2.1. Рациональные выражения 2.2. Формулы бинома Ньютона, суммы и разности	1	1		1	1
степеней 2.3. Деление многочленов с остатком. Алгоритм	1	1		2	3
Евклида	—	—		—	2
2.4. Теорема Безу	—	—		—	1
2.5. Корень многочлена	—	—		—	2
2.6. Рациональные уравнения	1	2		2	2
2.7. Системы рациональных уравнений	1	2		2	2
2.8. Метод интервалов решения неравенств	2	2		3	3
2.9. Рациональные неравенства	2	2		3	3
2.10. Нестрогие неравенства	2	2		3	3
2.11. Системы рациональных неравенств	1	1		1	2
Контрольная работа № 1	1	1		1	1
3. Корень степени n	6	9		12	14
3.1. Понятие функции и ее графика	1	1		1	1
3.2. Функция у = хⁿ	1	1		2	2
3.3. Понятие корня степени n	1	1		1	1
3.4. Корни четной и нечетной степеней	1	1		2	2
3.5. Арифметический корень	1	2		2	2
3.6. Свойства корней степени n	1	2		2	2

3.7. Функция y =ⁿx, х ≥ 0 — — 1 1 3.8. Функция y =ⁿx — — — 1

3.9. Корень степени n из натурального числа —	—	—	1
Контрольная работа № 2 —	1	1	1
4. Степень положительного числа 8	10	13	14
4.1. Степень с рациональным показателем 1	1	1	1
4.2. Свойства степени с рациональным показателем 1	2	2	2
4.3. Понятие предела последовательности 1	2	2	2
4.4. Свойства пределов —	—	2	2
4.5. Бесконечно убывающая геометрическая прогрессия 1	1	1	2
4.6. Число е 1	1	1	1
4.7. Понятие степени с иррациональным 1 показателем	1	1	1
4.8. Показательная функция 1	1	2	2
Контрольная работа № 3 1	1	1	1
5. Логарифмы 5	6	6	8
5.1. Понятие логарифма 2	2	2	2

	I	II	III	IV
5.2. Свойства логарифмов	2	3	3	3
5.3. Логарифмическая функция	1	1	1	1
5.4. Десятичные логарифмы	—	—	—	1
5.5. Степенные функции 6. Показательные и логарифмические уравнения	—	—	—	1
и неравенства	7	7	11	13
6.1. Простейшие показательные уравнения	1	1	1	2
6.2. Простейшие логарифмические уравнения 6.3. Уравнения, сводящиеся к простейшим заменой	1	1	1	2
неизвестного	1	1	2	2
6.4. Простейшие показательные неравенства	1	1	2	2
6.5. Простейшие логарифмические неравенства 6.6. Неравенства, сводящиеся к простейшим	1	1	2	2
заменой неизвестного	1	1	2	2
Контрольная работа № 4	1	1	1	1
7. Синус и косинус угла	7	7	7	11
7.1. Понятие угла	1	1	1	1
7.2. Радианная мера угла	1	1	1	1
7.3. Определение синуса и косинуса угла	1	1	1	1
7.4. Основные формулы для sin α и cos α	2	2	2	2
7.5. Арксинус	1	1	1	2
7.6. Арккосинус	1	1	1	2
7.7. Примеры использования арксинуса и арккосинуса	—	—	—	1
7.8. Формулы для арксинуса и арккосинуса	—	—	—	1
8. Тангенс и котангенс угла	4	4	6	10
8.1. Определение тангенса и котангенса угла	1	1	1	1
8.2. Основные формулы для tg α и ctg α	1	1	2	2
8.3. Арктангенс	1	1	1	2
8.4. Арккотангенс 8.5. Примеры использования арктангенса и	—	—	1	2
арккотангенса	—	—	—	1
8.6. Формулы для арктангенса и арккотангенса	—	—	—	1
Контрольная работа № 5	1	1	1	1
9. Формулы сложения	5	8	11	13
9.1. Косинус разности и косинус суммы двух углов	1	2	2	2
9.2. Формулы для дополнительных углов	1	1	1	1
9.3. Синус суммы и синус разности двух углов	1	2	2	2
9.4. Сумма и разность синусов и косинусов	1	2	2	2
9.5. Формулы для двойных и половинных углов	1	1	2	2
9.6. Произведение синусов и косинусов	—	—	1	2

	I	II	III	IV
9.7. Формулы для тангенсов 10. Тригонометрические функции	—	—	1	2
числового аргумента	7	8	9	9
10.1. Функция у = sin x	2	2	2	2
10.2. Функция у = cos x	2	2	2	2
10.3. Функция y = tg x	1	2	2	2
10.4. Функция y = ctg x	1	1	2	2
Контрольная работа № 6 11. Тригонометрические уравнения	1	1	1	1
и неравенства 11.1. Простейшие тригонометрические	5	8	12	16
уравнения 11.2. Уравнения, сводящиеся к простейшим заменой	2	2	2	2
неизвестного 11.3. Применение основных тригонометрических	1	2	2	3
формул для решения уравнений	1	2	2	2
11.4. Однородные уравнения 11.5. Простейшие неравенства для синуса	1	1	1	1
и косинуса 11.6. Простейшие неравенства для тангенса и	—	—	1	1
котангенса 11.7. Неравенства, сводящиеся к простейшим	—	—	1	1
заменой неизвестного	—	—	1	2
11.8. Введение вспомогательного угла	—	—	1	2
11.9. Замена неизвестного t = sin x + cos x	—	—	—	1
Контрольная работа № 7	—	1	1	1
12. Вероятность события	4	4	6	6
12.1. Понятие вероятности события	2	2	3	3
12.2. Свойства вероятностей событий 13. Частота. Условная вероятность	2 —	2 —	3 2	3 3
13.1. Относительная частота события	—	—	1	2
13.2. Условная вероятность. Независимые события 14. Математическое ожидание. Закон больших	—	—	1	1
чисел	—	—	—	—
14.1. Математическое ожидание	—	—	—	—
14.2. Сложный опыт	—	—	—	—
14.3. Формула Бернулли. Закон больших чисел	—	—	—	—
Повторение Повторение курса алгебры и начал математического	8	10	11	15
анализа за 10 класс	7	9	10	13
Итоговая контрольная работа № 8	1	1	1	2

В этой главе повторяются, расширяются и систематизируются известные учащимся из курса алгебры основной школы сведения о действительных числах, вводятся понятия корня степени n, степени с рациональным показателем, а затем и с действительным показателем, понятие логарифма числа. Тем самым завершается линия развития понятия числа. Дальнейшее расширение множества чисел — введение комплексных чисел — завершается в учебнике для 11 класса (профильное обучение).

Функциональная линия в первой главе строится следующим образом. Сначала повторяется классическое определение функции по Лобачевскому — Дирихле, изучается функция у = х^п, затем функция y = ⁿx. После введения понятия степени с действительным показателем вводится показательная функция, а после введения логарифмов и логарифмическая функция.

Линия уравнений и неравенств начинается повторением изученного в девятилетней школе — повторяются способы решения рациональных уравнений и неравенств. Завершается глава решением показательных и логарифмических уравнений и неравенств.

На углубленном уровне предусмотрено изучение дополнительных тем, связанных с решением алгебраических уравнений высших степеней.

В результате изучения главы I учащиеся должны знать основные определения и свойства, связанные с понятиями действительного числа, корня степени n, степени с действительным показателем и логарифма, уметь преобразовывать несложные выражения, содержащие корни степени n, степени с дробным показателем и логарифмы, знать свойства и уметь строить графики функций у = хⁿ, y = ⁿx, показательной и логарифмической; уметь решать простейшие показательные, логарифмические, а также сводящиеся к ним уравнения и неравенства.

§ 1. Действительные числа

1.1. Понятие действительного числа 1.2. Множества чисел. Свойства действительных чисел

Материал первых двух пунктов § 1 нацелен на повторение с некоторым обобщением известных учащимся сведений о действительных числах, модуле числа, системе координат на прямой и плоскости. Надо обратить внимание учащихся на то, что множество чисел может быть замкнутым относительно некоторой операции, например, множество натуральных чисел замкнуто относительно операций сложения и умножения: сумма и произведение любых двух натуральных чисел являются натуральными числами, а разность и частное не обязательно являются натуральными числами. Стремление «усовершенствовать» множество чисел, сделать выполнимыми в «новом» множестве операции, не всегда выполнимые в «старом», является побудительной причиной для расширения первоначально освоенных множеств чисел. Здесь можно напомнить учащимся некоторые не всегда выполнимые операции, которые стали всегда выполнимыми после расширения множества чисел.

Надо напомнить учащимся, что наряду с бесконечными десятичными периодическими дробями существуют и бесконечные десятичные непериодические дроби, которые называют иррациональными числами. Рациональные и иррациональные числа составляют множество всех действительных чисел.

Сравнивают действительные числа, записанные в виде бесконечных десятичных дробей, поразрядно, т. е. по тем же правилам, по которым сравнивают конечные десятичные дроби.

Имеется особый случай — дроби с периодом 9. Такие дроби есть другая форма записи конечных десятичных дробей, которые можно записать еще и как бесконечные десятичные дроби с периодом 0. В учебнике приведен пример записи дроби 2,4 в виде дробей с периодами 0 и 9:

2,4 = 2,4000... = 2,4(0) и 2,4 = 2,3999... = 2,3(9).

Дроби с периодом 9 обычно не рассматривают, в частности, чтобы избежать путаницы при сравнении бесконечных десятичных дробей, например, дробь 2,4(0) может оказаться «больше самой себя», но записанной в виде 2,3(9).

Пункт 1.1 учебника завершается представлением действительных чисел точками координатной прямой, системой координат на плоскости.

При повторении материала данного пункта надо обратить внимание учащихся на мнемоническое правило записи бесконечной десятичной периодической дроби в виде обыкновенной дроби:

для того чтобы записать периодическую десятичную дробь в виде обыкновенной дроби, надо в числителе записать разность числа до второго периода и числа до первого периода, в знаменателе записать столько девяток, сколько цифр в периоде, и приписать к ним столько нулей, сколько цифр между запятой и первым периодом.

Это правило сформулировано в п. 1 дидактических материалов, там же приведены примеры его применения. Применение этого правила можно заменить рассуждениями, которые продемонстрируем на примере.

Пример. Запишем бесконечную периодическую десятичную дробь 2,1(45) в виде обыкновенной дроби. Обозначим дробь буквой х:

x = 2,1(45),

тогда

10x = 21,454545...,

1000x = 2145,454545...,

1000x − 10x = 2145 − 21,

990x = 2145 − 21, x =, x =

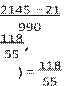значит, 2 1 45, (.

Замечание 1. Часто возникает вопрос об обосновании мнемонического правила и рассуждений в приведенном примере. Трудность здесь заключена в том, что неясно, что ученик понимает под бесконечной периодической дробью.

Под бесконечной периодической дробью можно понимать результат деления уголком числителя на знаменатель несократимой дроби, имеющий простой делитель, отличный от 2 и 5. При таком подходе невозможно получить дробь с периодом 9 и можно убедиться в правильности ответа в приведенном примере, разделив уголком 118 на 55, но трудно обосновать мнемоническое правило в общем виде.

Замечание 2. Под бесконечной периодической дробью α₀,α₁α₂α₃...α_k... можно понимать сумму ряда α ₀+ + + ^α+ ^α33 +... + ^αkk +... .

10 10 10

При таком подходе надо изучать свойства рядов и доказывать на их основе мнемоническое правило и правило умножения бесконечной десятичной дроби на 10ⁿ, что достаточно трудно. Однако в случае простых периодических дробей можно доказать, например, равенство 2,3(9) = 2,4.

Действительно, периодическую дробь 2,3(9) можно записать в виде суммы ряда

2,3 + 0,09 + 0,009 + 0,0009 + ...,

являющегося суммой числа 2,3 и суммы бесконечно убывающей геометрической прогрессии 0,09 + 0,009 + 0,0009 + ..., равной = 0 1, . Поэтому 2,3(9) = 2,4 (отметим, что фор-

мула суммы бесконечно убывающей геометрической прогрессии уже изучалась в 9 классе и будет обоснована в п. 4.5 учебника).

Вот почему нам кажется, что здесь не стоит углубляться в теорию: определять периодическую дробь, обосновывать мнемоническое правило и правило умножения бесконечной десятичной дроби на 10ⁿ. Достаточно, если у учащихся будет сформировано интуитивное представление о периодической дроби, а при записи ее в виде обыкновенной дроби они сумеют либо воспользоваться мнемоническим правилом, либо провести рассуждения, как в приведенном выше примере, и совсем хорошо, если они убеждаются в правильности полученного ответа, разделив уголком числитель дроби на ее знаменатель.

Пункт 1.2 посвящен знакомым учащимся обозначениям числовых множеств. Обратим внимание на то, что в девятилетней школе термины «отрезок», «интервал», «полуинтервал» для обозначения числовых множеств в большинстве учебников не используются.

На с. 13—14 учебника приведены свойства действительных чисел. Надо подчеркнуть, что все другие свойства действительных чисел, различные неравенства и многие теоремы могут быть доказаны с опорой на эти основные свойства.

При работе с материалами пп. 1.1—1.2 можно использовать задачи из раздела «Задания для повторения» для организации повторения и выявления пробелов в подготовке десятиклассников. С той же целью можно использовать самостоятельные работы 1—4 из дидактических материалов. Способы использования этих и многих других самостоятельных работ могут быть различными. Например, по работе 1 может быть дано такое задание: самостоятельно повторить теоретический материал (раздел I, с. 4—5) и выполнить самостоятельную работу С—1 (раздел II, с. 64—65).

Решения и комментарии

1.17. а) Решите уравнение | | x |− 2 | = 10.

Решение. Решая это уравнение, надо начинать с ответа на вопрос: «Какое число имеет модуль 10?» Ответ на него приводит к необходимости решить два уравнения:

| x | − 2 = 10 и | x | − 2 = −10

или равносильные им уравнения:

| x | = 12 и | x | = −8.

Первое уравнение имеет два корня: 12 и −12, а второе — не имеет корней. Следовательно, исходное уравнение имеет два корня: 12 и −12.

1.18. а) Докажите, что расстояние между точками А (х₁) и В (x₂) вычисляется по формуле АВ = | х₁− х₂|.

б) Докажите, что расстояние между точками А (х₁; у₁) и В (x₂; y₂) вычисляется по формуле AB = (x₁− x₂)²+(y₁− y₂)².

в) Докажите, что координата точки С (х) — середины отрезка АВ, где A (x₁) и В (x₂), вычисляется по формуле:

x = x1 + x2 .

г) Докажите, что координаты точки С (х; у) — середины отрезка АВ, где А (х₁; y₁) и В (х₂, у₂), вычисляются по формулам: x = x1 + x2 ; y = y1 + y2 .

2 2

д) Докажите, что если точка С (х) принадлежит отрезку АВ, где А (х₁) и В (x₂), и делит этот отрезок в отношении AC : CB = m : n, то координата точки С вычисляется по формуле x = nx1 + mx2 . m n+

е) Докажите, что если точка С (х; у) принадлежит отрезку АВ, где А (х₁; у₁) и В (х₂, у₂), и делит этот отрезок в отношении АC : CВ = m : n, то координаты точки С вычисny¹+ my²ляются по формулам: x.

m n+ Решение. а) Если x₁> x₂, то АВ = х₁− х₂= | х₁− х₂|.

Если х₁< х₂, то АВ = х₂− х₁= | х₁− х₂|.

б) В случае у₁≠ у₂и x₁≠ x₂требуемое равенство получаем из теоремы Пифагора. Если же у₁= y₂, то доказываемое равенство тоже верно, так как |x₁− x₂| = (x₁− x₂)²+0²(см. п. «а»). Доказательство в случае х₁= х₂аналогично.

в) Пусть для определенности x₁< x₂, тогда х₁< х < х₂и из условия, что С — середина отрезка АВ, следует, что х₂− х = x − x₁, откуда и получаем требуемое равенство. Доказательство в случае ^х₁> ^х₂аналогично.

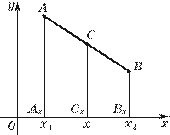
г) Через точки А, В и С проведем прямые, перпендикулярные оси Ох (рис. 1). На пересечении их с осью Ох получим точки А_х(x₁), В_х(x₂) и С_х(х). Так как по теореме Фалеса А_xС_x= В_xС_x, то из п. «в» следует, что

x = x1 + x2 . Доказательство вто- Рис. 1

2 рой формулы аналогично.

д) Пусть х₁< х < х₂. Так как AC : CB = m : n, то верно равенство x x− ¹= ^x²⁻^x, из которого получаем требуемое m n

равенство x = nx1 + mx2 . m n+

Доказательство в случае x₁> x > х₂аналогично.

е) Пусть точка С (х; у) принадлежит отрезку АВ, где

А (х₁; у₁) и В (x₂; y₂), и делит этот отрезок в отношении AC : CB = m : n. Через точки А, В и С проведем прямые, перпендикулярные оси Ох. На пересечении их с осью Ох получим точки А_х(x₁), B_x(x₂) и С_х(х). Так как по теореме о пропорциональных отрезках АC : CВ = А_xС_x: C_xВ_x, то A_xC_x: C_xB_x= m : n. Тогда x ₌^nx¹+ ^mx²(см. п. «д»). Доказаm n+

тельство второй формулы аналогично.

1.19. Доказательство иррациональности корней степени n в общем виде дано в комментариях к п. 3.9.

1.28. а) Установите взаимно-однозначное соответствие между элементами множеств N и Z; N и Q.

б) Покажите, что между множествами всех точек прямой и всех точек интервала (0; 1) можно установить взаимно-однозначное соответствие.

Решение. а) Сначала установим взаимно-однозначное соответствие между элементами множеств N и Z.

Поставим в соответствие каждому натуральному числу единственное целое число по правилу: единице соответствует нуль, каждому четному натуральному числу 2п соответствует число n, а следующему за ним натуральному числу 2п + 1 соответствует число −п.

Также можно указать правило, по которому каждому целому числу соответствует вполне определенное натуральное число: нулю соответствует единица, каждому положительному целому числу n соответствует натуральное число 2n, а противоположному ему числу −n соответствует натуральное число 2n + 1. Взаимно-однозначное соответствие между элементами множеств N и Z установлено:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...

•

0, 1, −1, 2, −2, 3, −3, 4, −4, 5, ...

Теперь установим взаимно-однозначное соответствие между элементами множеств N и Q. Выпишем рациональные числа в виде дробей так, чтобы сумма числителя и знаменателя положительной дроби была равна 1, потом 2, потом 3, ..., и записывая после каждого положительного рационального числа противоположное ему рациональное число. При этом пропускаются дроби, равные записанным ранее дробям. Так задается правило, по которому каждое рациональное число получит свой определенный номер члена бесконечной последовательности дробей. Каждой дроби будет соответствовать свое натуральное число (номер члена последовательности), а каждому натуральному числу — своя дробь. Взаимно-однозначное соответствие между элементами множеств N и Q установлено:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ...

•

01, 11, ₋11, 21, ₋21, 21, ₋21, 31, ₋31, 31, ₋31, 41, ₋41, _...

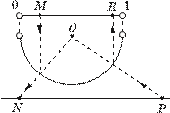б) Взаимно-однозначное соответствие между множествами всех точек прямой и всех точек интервала (0; 1) установлено на рисунке 2.

Здесь показан способ отыскания точки N прямой, соответствующей точке М интервала, а

Рис. 2 также точки R интервала, соответствующей точке Р прямой.

Промежуточный контроль. С—1.

1.3*. Метод математической индукции

Методом математической индукции называют способ доказательства истинности некоторого утверждения для любого натурального числа n. Этот способ основан на принципе математической индукции, сформулированном в учебном тексте. Прежде чем приступить к обсуждению способа изложения материала на уроке, приведем шуточный пример, помогающий учащимся понять суть нового метода доказательства.

Представьте, что вы подошли к кинотеатру и видите огромную очередь желающих купить билет на новый фильм. Вы становитесь в конец очереди, и к вам подходит человек со словами: «Я прошел от начала очереди и заметил, что в очереди после каждой женщины стоит женщина». Можно ли на основании услышанного утверждать, что в очереди стоят одни женщины? Обычно учащиеся легко справляются с этим вопросом, отвечая, что для истинности утверждения «В очереди стоят только женщины» надо быть уверенным, что первая в очереди женщина. Тогда после каждой женщины стоит женщина и утверждение «В очереди стоят только женщины» будет истинным. Но если первым в очереди стоит мужчина, то это утверждение будет ложным.

Вторым примером, которым можно предварить объяснение нового материала, может быть разбор решения задачи 1.45.

1.45. На один из трех штырьков насажены п различных колец так, что большее кольцо лежит ниже меньшего (на рисунке 3 п = 3). За один ход разрешается перенести одно кольцо с одного штырька на другой, при этом не разрешается большее кольцо класть на меньшее. Докажите, что наименьшее число ходов, за которое можно перенести все кольца с одного штырька на другой, равно 2ⁿ− 1. Рис. 3

Условие этой задачи учителю лучше сформулировать самому. Тогда у учащихся будет возможность поучаствовать в поиске формулы, выражающей зависимость числа ходов от числа колец, и убедиться, что, даже найдя эту формулу, они пока что не могут доказать ее для любого натурального n, так как натуральных чисел бесконечно много.

Рассуждения можно провести так.

Одно кольцо (п = 1) можно перенести на новый штырек за 1 ход.

Два кольца (п = 2) можно перенести за 3 хода (первое кольцо перенести на второй штырек, второе — на третий, затем первое — на третий).

Три кольца (п = 3) можно перенести за 3 + 1 + 3 = 7 ходов, перенеся сначала два верхних кольца за 3 хода, потом нижнее кольцо за 1 ход, потом снова два кольца за 3 хода.

Аналогично можно перенести 4, 5, 6 колец за 15, 31, 63 ходов соответственно.

Наблюдательные учащиеся могут заметить, что для п колец число ходов меньше п-й степени числа 2 на единицу, т. е. выражается формулой 2ⁿ− 1.

Следовательно, получена гипотеза о выражении числа ходов через n, которую еще нужно доказать для любого натурального n. Но что значит доказать формулу для любого натурального n? Очевидно, что проверить истинность формулы для всех п невозможно. Необходимо соглашение, позволяющее считать, что при выполнении некоторых условий доказываемое утверждение истинно для любого натурального n.

После обсуждения рассмотренных примеров учащиеся будут подготовлены к тому, что если истинность некоторого утверждения, зависящего от натурального n, установлена для п = 1 и доказано, что из истинности этого утверждения для некоторого п = k следует его истинность для следующего значения п, равного k + 1, то считается, что это утверждение истинно для любого натурального п (такое соглашение и называют принципом математической индукции).

Пример 1 из учебника достаточно прост, чтобы, не отвлекаясь на технические сложности, освоить идею доказательства методом математической индукции.

При обсуждении примера 2 можно упомянуть, что выдающийся математик XX столетия А. Н. Колмогоров (1903—1987) еще в детстве проявлял необыкновенные математические способности. В возрасте пяти лет он установил, что: 1 + 3 = 2², 1 + 3 + 5 = 3², 1 + 3 + 5 + 7 = 4²и т. д., т. е. выдвинул гипотезу, что сумма n первых нечетных натуральных чисел равна п². Доказательство истинности этой гипотезы требует применения метода математической ин-

дукции.

Обратим внимание на имеющееся в учебнике важное замечание о недопустимости пропуска любого из двух шагов в доказательстве методом математической индукции и об ошибках, к которым может привести такой пропуск.

В учебнике имеется достаточное число примеров для обучения доказательству справедливости равенств и неравенств, а после задания 1.35 имеется указание, с помощью которого можно немного сократить запись доказательства некоторых утверждений. Рассмотрим пример применения этого способа оформления доказательства.

Докажем равенство

1 1 1 1 n

+ + +... + = . (1)

1⋅ 4 4⋅ 7 7 ⋅ 10 (3n − 2) ⋅ (3n + 1) 3n + 1

Обозначим A n( ) = ¹+ ¹+ ¹+... + ¹,

1⋅ 4 4⋅ 7 7 ⋅ 10 (3n − 2) ⋅ (3n + 1)

B n( ) = ⁿ.

3n + 1

Сначала убедимся в справедливости равенства А (1) = В (1).

Так как A, B, то равенство

А (1) = В (1) доказано, т. е. при п = 1 равенство (1) справедливо.

Теперь вычислим разность A (k + 1) − А (k), равную (k + 1)-му слагаемому суммы А (k + 1):

A k( ) A( )k ,

и разность В (k + 1) − В (k), равную

B _k₍+ ₎− _{B k}_{( )}= − = (k + 1)(3 k + 1) − k k(3 + 4) =

Тем самым мы доказали равенство

A (k + 1) − A (k) = B (k + 1) − B (k). (2)

Предположим теперь, что при п = k равенство (1) справедливо, т. е. что A (k) = В (k), тогда из справедливости равенства (2) следует справедливость равенства A (k + 1) = В (k + 1), т. е. справедливость равенства (1) при п = k + 1.

Итак, равенство (1) справедливо при п = 1, и из его справедливости для п = k следует его справедливость для п = k + 1, тогда согласно принципу математической индукции равенство (1) справедливо для любого натурального n.

Решения и комментарии

1.31. а) Докажите методом математической индукции, что 0ⁿ= 0 для любого натурального числа n.

Хотя это утверждение и кажется очевидным, но тем не менее оно должно быть доказано методом математической индукции.

Доказательство. При п = 1 справедливо равенство 0¹= 0.

Предположим, что для некоторого натурального числа п = k справедливо равенство 0^k= 0, и докажем, что тогда справедливо равенство 0^k^{+ 1}= 0.

Используя равенство 0^k= 0, имеем: 0^k^{+ 1}= 0^k⋅ 0 = = 0 ⋅ 0 = 0.

Следовательно, равенство 0ⁿ= 0 справедливо для любого натурального числа n.

1.38. б) Докажите по индукции, что для любого натурального п справедливо неравенство

Доказательство. Так как левая часть неравенства для n любого натурального числа n равна дроби (доказано 3n + 1

по индукции выше), а n = 1 1 < 31 для любого нату3n + 1 3 +

рального числа n, то из справедливости равенства (1) для любого натурального числа n следует справедливость доказываемого неравенства для любого натурального числа n.

Замечание. Обычно в 9 классе формулы n-го члена и суммы первых п членов арифметической и геометрической прогрессий не доказывают с помощью метода математической индукции, а лишь проводят рассуждение, подводящее к гипотезе. На это нужно обратить внимание учащихся. Для осознания нового уровня владения материалом они должны научиться доказывать эти формулы с помощью метода математической индукции (задание 1.32).

1.43. г) Докажите, что для любого натурального числа п 3ⁿ+ 4ⁿ− 1 делится на 6.

Доказательство. Доказываемое утверждение справедливо при п = 1, так как 3¹+ 4¹− 1 = 6, т. е. делится на 6.

Предположим, что при п = k сумма 3^k+ 4^k− 1 делится на 6, и докажем, что при п = k + 1 сумма 3^k^+
1+ 4^k^{+ 1}− 1 делится на 6. (Успех доказательства зависит от умения учащихся в сумме 3^k^{+ 1}+ 4^k^{+ 1}− 1 выделить сумму 3^k+ 4^k− 1, которая по нашему предположению делится на 6.)

3^k^{+ 1}+ 4^k^{+ 1}− 1 = 3 ⋅ 3^k+ 4 ⋅ 4^k− 1 = 3 ⋅ 3^k+ 3 ⋅ 4^k− 3 + 4^k+ 2 = = 3 ⋅ (3^k+ 4^k− 1) + (4^k+ 2).

Слагаемое 3 ⋅ (3^k+ 4^k− 1) последней суммы делится на 6, так как один из его множителей делится на 6 по нашему предположению. Осталось доказать, что и слагаемое 4^k+ 2 также делится на 6. Применим метод математической индукции еще раз.

Очевидно, что при k = 1 сумма 4¹+ 2 = 6 делится на 6.

Предположим, что при k = т сумма 4^m+ 2 делится на 6, и докажем, что при k = т + 1 сумма 4^m^+
1+ 2 делится на 6. 4^m^+
1+ 2 = 4 ⋅ 4^m+ 2 = 4 ⋅ 4^m+ 8 − 6 = 4 ⋅ (4^m+ 2) − 6.

Слагаемое 4 ⋅ (4^m+ 2) делится на 6, так как один из его множителей делится на 6 по нашему предположению, число 6 тоже делится на 6, поэтому и разность 4 ⋅ (4^m+ 2) − 6, а значит, и сумма 4^m^+
1+ 2 тоже делятся на 6.

Тем самым доказано, что сумма 4^k+ 2 делится на 6 для любого натурального k. Но тогда и 3^k^{+ 1}+ 4^k^{+ 1}− 1 делится на 6.

Итак, выражение 3ⁿ+ 4ⁿ− 1 делится на 6 при п = 1; из предположения, что это выражение делится на 6 при п = k, следует, что оно делится на 6 и при п = k + 1. Это означает, что выражение 3ⁿ+ 4ⁿ− 1 делится на 6 при любом натуральном числе п.

Промежуточный контроль. С—8.

1.4. Перестановки

1.5. Размещения 1.6. Сочетания

Материал пп. 1.4—1.6 подробно изложен в учебнике со всеми необходимыми обоснованиями. Он обычно вызывает затруднения у учащихся, которые плохо понимают, чем размещения из п элементов по k отличаются от сочетаний из п элементов по k. Надо отметить, что для первых важен порядок следования выбранных k элементов, а для вторых этот порядок не важен. При этом можно воспользоваться примерами 1—3 из п. 9 раздела I дидактических материалов (с. 12), дающими запоминающиеся образы:

P₄— количество мелодий, которые можно сыграть, используя 4 различные ноты (без повторения);

A⁴₇— количество мелодий, которые можно сыграть, используя 4 различные ноты из данных семи нот (без повторения);

C⁴₇— количество аккордов, которые можно сыграть, используя 4 различные ноты из данных семи нот (без повторения). Ноты в аккорде звучат одновременно, порядок следования нот не важен.

Чтобы подготовить учащихся к введению определений и формул для вычисления числа перестановок из п элементов, числа размещений из п элементов по k, числа сочетаний из п элементов по k, надо, следуя учебнику, решить приведенные в нем простые задачи с двумя, тремя, четырьмя элементами.

Например, формула подсчета числа перестановок из п элементов может быть получена сначала для нескольких малых натуральных чисел п.

Для п = 3 рассуждение можно провести так. На первое место можно поставить любой из трех элементов (3 возможности). Если один элемент мы уже поставили на первое место, то на второе место можно поставить один из двух оставшихся элементов (2 возможности). Тогда первые два места можно занять шестью способами (3 ⋅ 2 = 6), в каждом из которых оставшееся третье место можно занять одним способом одним оставшимся элементом (1 возможность). Тогда число перестановок из трех элементов равно Р₃= 3 ⋅ 2 ⋅ 1 = 6. Приведенное рассуждение учащиеся легко применят для четырех элементов и могут выдвинуть гипотезу, что справедлива формула

Р_n= n ⋅ (n − 1) ⋅ (n − 2) ... 3 ⋅ 2 ⋅ 1 = n!

Эту гипотезу можно доказать методом математической индукции (с. 23 учебника).

Решения и комментарии

1.54. Множество, состоящее из шести элементов x₁, x₂, x₃, x₄, x₅, x₆, упорядочили всеми возможными способами.

Сколько таких способов? В скольких случаях:

а) элемент x₁будет первым по порядку;

б) элемент х₁не будет ни первым, ни последним?

Решение. Всех способов упорядочить 6 элементов Р₆= 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720.

а) Поставим элемент x₁на первое место. Упорядочить оставшиеся элементы можно Р₅= 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120 способами. Поэтому элемент x₁будет на первом месте в 120 случаях.

б) Всех способов упорядочить 6 элементов Р₆= 720. Из них элемент х₁будет на первом месте в 120 случаях, аналогично элемент х₁будет на последнем месте в 120 случаях. Поэтому элемент х₁не будет ни первым, ни последним в 720 − 2 ⋅ 120 = 480 случаях.

1.55. Сколькими различными способами можно усадить в ряд трех мальчиков и трех девочек так, чтобы никакие два мальчика и никакие две девочки не оказались рядом?

Решение. Перенумеруем шесть мест посадки в ряд: 1, 2, 3, 4, 5, 6. Места мальчиков и девочек должны чередоваться так, чтобы никакие два мальчика и никакие две девочки не оказались рядом, поэтому у нас есть две возможности для посадки девочек: на четные места или на нечетные, а в каждой из них — Р₃= 3 ⋅ 2 ⋅ 1 = 6 способов. Всего способов усадить девочек в ряд будет 6 ⋅ 2 = 12, а в каждом из них — Р₃= 3 ⋅ 2 ⋅ 1 = 6 способов посадки мальчиков. Всего имеется 12 ⋅ 6 = 72 способа посадки девочек и мальчиков согласно условиям задачи.

1.56. Задача-шутка. Как-то раз в воскресенье семеро друзей зашли в кафе, уселись за один столик и заказали мороженое. Хозяин кафе сказал, что если друзья в каждое следующее воскресенье будут садиться по-новому и перепробуют все способы посадки, то с этого момента он обещает кормить их мороженым бесплатно. Удастся ли друзьям воспользоваться предложением хозяина кафе?

Решение. Чтобы перепробовать все Р₇= 7 ⋅ 6 ⋅ 5 × × 4 ⋅ 3 ⋅ 2 ⋅ 1 = 5040 способов посадки, потребуется более 96 лет. Маловероятно, что хозяин кафе сумеет исполнить свое обещание через 96 лет.

1.60. Сколькими различными способами можно распределить между шестью лицами: а) две; б) три разные путевки в санатории?

Решение. а) Число способов распределить две разные путевки между шестью лицами равно A 30 (первую путевку можно распределить шестью способами; в каждом из них вторую путевку можно распределить пятью способами среди лиц, не получивших первую путевку).

б) Число способов распределить три разные путевки между шестью лицами равно A 120 (первую путевку можно распределить шестью способами; в каждом из них вторую путевку можно распределить пятью способами среди лиц, не получивших первую путевку; в каждом из 6 ⋅ 5 = 30 способов распределить две первые путевки третью можно распределить между четырьмя оставшимися лицами четырьмя способами).

1.65. Сколькими способами можно распределить две одинаковые путевки между пятью лицами?

Решение. Число способов распределить две одинаковые путевки между пятью лицами равно C (оно в

2 раза меньше числа способов распределить две разные путевки между пятью лицами, так как порядок получения путевок не важен).

1.71. При встрече п друзей обменялись рукопожатиями. Определите число рукопожатий.

Решение. Каждый из п друзей пожмет п − 1 руку. При этом каждое рукопожатие считается дважды — каждым из двух друзей, жмущих друг другу руки. Поэтому всех рукоn n

пожатий будет , что и требовалось до-

казать.

1.72. В турнире по шахматам каждый участник сыграл с каждым по одной партии, всего было сыграно 36 партий. Определите число участников турнира.

Решение. Все п участников турнира сыграли ^{n n}⁽⁻¹⁾пар-

2 n n( − 1)

тий, что равно 36. Составим уравнение = 36. Оно

имеет единственный положительный корень 9, поэтому число участников равно 9.

1.73. В классе имеется 6 сильных математиков. Сколькими способами из них можно составить команду на районную олимпиаду по математике, если от класса можно послать команду: а) из 4 человек; б) от 2 до 4 человек?

Решение. а) Число способов выбрать 4 человека из 6 (без учета порядка выбираемых) равно C.

б) Число способов выбрать от 2 до 4 человек из 6

(без учета порядка выбираемых) равно

C C C .

1.74. Найдите число всех подмножеств данного множества, содержащего п элементов (п — любое натуральное число).

Решение. Напомним, что принято считать, что пустое множество, т. е. множество, не содержащее ни одного элемента, является подмножеством любого множества. Пустое множество обозначают знаком ∅.

Пусть данное множество М содержит п элементов. Тогда из этих элементов можно составить подмножество, содержащее:

0 элементов (пустое множество) — C_n⁰= 1 способом;

1 элемент — C п способами;

2 элемента — C способами; ...; п элементов — C_nⁿ 1 способом.

Следовательно, множество М имеет:

одно — C_n⁰— подмножество, содержащее 0 элементов

(пустое множество);

C_n¹подмножеств, содержащих 1 элемент; C_n²подмножеств, содержащих 2 элемента; ...; C_п^пподмножеств, содержащих п элементов.

Поэтому число всех подмножеств множества М равно

Cn0 + Cn1 + Cn2 + ... + Cnn.

Докажем методом математической индукции, что справедливо равенство

Cn0 + Cn1 + Cn2 + ... + Cnn = 2n. (1)

1) Если п = 1, то равенство (1) справедливо, так как C⁰₁= C₁¹= 1, и поэтому C₁⁰+ C¹₁= 2¹.

2) Предположим, что при п = k справедливо равенство

Ck0 + Ck1 + Ck2 + ... + Ckk = 2k. (2)

3) Используя это, покажем, что при п = k + 1 справедливо равенство

C0k + 1 + Ck1+ 1 + Ck2 + 1 + ... + Ckk++11 = 2k + 1. (3)

Рассмотрим сумму в левой части равенства (3).

Так как C, Ckk++11 = 1 = Ckk, а Cmk + 1 = Ckm − 1 + Cmk для 1 ≤ т ≤ k, то получаем, что справедливо равенство

... + Ckk Ckk

Используя равенство (2), получаем, что справедливо равенство (3).

Согласно принципу математической индукции это означает, что равенство (1) справедливо для любого натурального числа п.

Отметим, что далее равенство (1) доказано также с помощью бинома Ньютона.

Промежуточный контроль. С—9.

1.7*. Доказательство числовых неравенств

Обратим внимание на то, что к десятому классу большинство учащихся имеют весьма смутные представления о доказательствах в алгебре. Саму процедуру доказательства они часто понимают неправильно. Поясним сказанное на примере. Если ученика попросят доказать, что для любых чисел а и b справедливо неравенство а²+ b²≥ 2ab, то можно ожидать такое «доказательство»:

«а²+ b²≥ 2ab, a²− 2ab + b²≥ 0, (a − b)²≥ 0,

что и требовалось доказать».

Ученики обычно удивляются, что приведенное «доказательство» доказательством не является. Да и не требовалось доказать, что (а − b)²≥ 0.

Приведенное рассуждение всего лишь анализ, помогающий найти путь доказательства, которое проводится в обратном порядке, а именно так:

рассмотрим неравенство, справедливое для любых чисел а и b:

(a − b)²≥ 0;

применим формулу квадрата разности

а²− 2ab + b²≥ 0;

в полученном верном неравенстве перенесем слагаемое −2ab в правую часть неравенства и получим новое верное неравенство, что и требовалось доказать.

Доказательство может содержать приведенные выше шаги:

а²+ b²≥ 2ab, (1)

а²− 2ab + b²≥ 0,

(а − b)²≥ 0, (2)

но тогда оно должно заканчиваться фразой: «Рассуждая в обратном порядке, из справедливости неравенства (2) получим справедливость неравенства (1), что и требовалось доказать».

В учебнике показаны различные приемы решения задач на доказательство неравенств, опираясь на которые можно доказать многие неравенства из данного пункта.

В дидактических материалах (п. 7) приведены методы доказательства неравенств, не отмеченные в учебнике.

Есть еще один метод доказательства числовых равенств и неравенств, связанный со сравнением чисел.

Скажем, что два числовых равенства равносильны, если из справедливости одного из них следует справедливость другого. Аналогично определяются равносильные неравенства. Для записи равносильности двух равенств или неравенств часто используют знак ⇔.

Если под знаком ∨ будем понимать один из пяти знаков сравнения: =, >, <, ≥, ≤, под знаком ∧ — знак, противоположный знаку ∨, т. е. =, <, >, ≤, ≥ соответственно, то многочисленные утверждения о равносильности числовых равенств и неравенств можно сформулировать так:

1. a ∨ b ⇔ a + c ∨ b + c для любого c ∈ R.

2. a ∨ b ⇔ ас ∨ bc для любого с > 0.

3. a ∨ b ⇔ aⁿ∨ b^пдля любых а > 0, b > 0, n ∈ N.

4. a ∨ b ⇔ ас ∧ bc для любого с < 0.

Знак ∨ используется в задачах на сравнение и доказательство числовых равенств и неравенств. Если мы хотим выяснить, какой из знаков сравнения (=, >, <, ≥, ≤) надо поставить между данными числовыми выражениями, то между ними можно поставить знак ∨, сделать несколько равносильных преобразований, используя утверждения 1—4 и прийти в итоге к очевидному равенству или неравенству. Тогда если использовались только свойства 1—3, то получившийся знак сравнения надо поставить вместо знака ∨ в сравнении данных числовых выражений. Использования свойства 4 лучше избегать, чтобы уменьшить число допускаемых ошибок.

Пример 1. Сравним числа 11 + 2 и 3 + 3.

Используя утверждения 1—3, напишем цепочку равносильных сравнений:

11 + 2 ∨ 3 + 3,

( 11 + 2)²∨ (3 + 3)²(по утверждению 3),

13 + 2 22 ∨ 12 +6 3,

1 +2 22 ∨ 6 3 (по утверждению 1),

(1 +2 22)²∨ (6 3)²(по утверждению 3),

89 +4 22 ∨ 108,

4 22 ∨ 19 (по утверждению 1), (4 22)²∨ 19²(по утверждению 3), 352 ∨ 361.

Так как 352 < 361, то в последнем сравнении должен стоять знак <. Поэтому и во всех предыдущих сравнениях должен стоять тот же знак. Следовательно, 11 + 2 <3+ 3. Пример 2. Докажем справедливость равенства

3 + 3 + ³10 +6 3 = 3 +1.

Напишем цепочку равносильных сравнений:

3 + 3 + ³10 +6 3 ∨ 3 +1,

( 3 + 3 + ³10 +6 3)²∨ ( 3 +1)²(по утверждению 3),

3 + 3 + ³10 +6 3 ∨ 4 +2 3,

³10 +6 3 ∨ 1 + 3 (по утверждению 1),

( 10³+6 3)³∨ (1 + 3)³(по утверждению 3), 10 +6 3 ∨ 1 +3 3 +3( 3)²+( 3)³.

В правой и левой частях последнего сравнения одно и то же число 10+6 3. Это означает, что в нем, а также в каждом предыдущем сравнении должен стоять знак =. Следовательно, этот знак будет стоять и в первом сравнении, что и требовалось доказать.

Пример 3. Докажем, что для любого а ∈ R справедливо a2 1 неравенство ^≤.

₁+ _a4 ₂

Напишем цепочку равносильных сравнений:

a2 1

∨ ,

1 + a4 2

2а²∨ 1 + а⁴(по утверждению 2), 0 ∨ 1 − 2а²+ а⁴(по утверждению 1), 0 ∨ (1 − a²)².

Так как (1 − а²)²≥ 0 для любого а ∈ R, то в последнем сравнении должен стоять знак ≤. Поэтому в каждом предыдущем сравнении должен стоять знак ≤. Следовательно, этот знак должен стоять и в первом сравнении, а это и требовалось доказать.

Решения и комментарии

1.77. к) Для любых действительных чисел а и b докажите, что если 0 < а < b, то а³< b³.

Доказательство. По условию задачи а < b и а > 0, поэтому а²< ab. Так как а < b и b > 0, то аb < b². Из транзитивности неравенств имеем а²< b².

Так как а²< b²и а > 0, то а³< а²b. Так как а²< b²и b > 0, то а²b < b³. Из транзитивности неравенств имеем а³< b³, что и требовалось доказать.

1.78. Докажите, что сумма кубов катетов прямоугольного треугольника меньше куба гипотенузы.

Доказательство. Для катетов a, b и гипотенузы с прямоугольного треугольника верно равенство а²+ b²= с². Умножив обе части этого равенства на с, получим новое верное равенство а²с + b²с = с³, в котором заменим слагаемые а²с и b²с на меньшие слагаемые а³и b³соответственно. Левая часть равенства уменьшится, и мы получим верное неравенство а³+ b³< c³. Это и требовалось доказать.

1.79. а) Докажите, что .

Доказательство. Обозначим:

A; B.

Так как , то А < В. Так

как А > 0, то А²< АВ, а так как AB = 81¹= ^⎛_⎜⎝ 9¹^⎞_⎟⎠ ², то A²< ⎝^⎜⎛ ₉¹^⎟⎠⎞². Откуда, учитывая, что A > 0, получаем, что A < . Это и требовалось доказать.

1.81. Задача Евклида (III в.). Докажите, что если а — наибольшее из четырех положительных чисел а, b, с, d и a ⁼^c, то справедливо неравенство а + d > b + с. b d

Доказательство. Так как по условию задачи а > с, то из

верного равенства a = c ^⋅^bследует, что ^b>1, откуда получаd d

ем, что b > d. Аналогично показывается, что из условия задачи следует, что c > d.

Умножим обе части верного числового неравенства b > d на положительное число с − d, получим верное неравенство b (с − d) > d (c − d), которое перепишем в виде

bc + d²> dc + bd.

Заменим в этом последнем неравенстве произведение bc равным ему произведением ad, получим неравенство:

ad + d²> dc + bd.

Разделим обе части этого верного неравенства на положительное число d и получим верное неравенство а + d > с + b,

что и требовалось доказать.

Замечание. Во времена Евклида многие факты в математике доказывались геометрическим способом. Приведем геометрическое доказательство того же неравенства.

На отрезке AD, длина которого равна а + d, построим окружность как на диаметре (рис. 4). Отметим точку М, такую, что AM = a, DM = d. Так как а > d, то центр О

окружности принадлежит отрезку AM. Так как а > b, то, построив окружность с центром М и радиусом b, получим точку В на первой окружности, такую, что ВМ = b. На пересечении прямой ВМ с первой окружностью получим точку С. Из теоремы о пересекающихся хордах следует, что ad = b ⋅ MC, а из условия задачи следует, что ad = bc, поэтому

МС = с. Так как длина хорды, не Рис. 4 проходящей через центр окружности, меньше ее диаметра, то AD > ВС, т. e. a + d > b + c, что и требовалось доказать.

1.82. Докажите, что для любого натурального числа п справедливо неравенство:

a) ; (3)

в) ; (4)

г) . (5)

Доказательство. а) Так как ,

, ..., , то 1 + ¹+ ¹+...

3 ⋅ 4

Так как > 0 для любого натурального числа п и n + 1

1 ⁻¹< 1, то получаем, что справедливо неравенство (3).

n + 1

в) Так как

= ⋅ + + + + (4′)

4 1 5 5 9 9 13

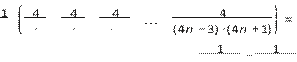= 14 ⋅ ⎛⎜⎝ 11 − 51 + 51 − 91 + 91 − 131 +... + 4n − 3 4n + 1⎠⎟⎞ = 14 ⋅⎜⎝⎛1 − 4n1+ 1⎞⎠⎟ и 14 ⋅^⎜⎝⎛1⁻_4n¹+ ₁⎞^⎟⎠ ^<¹₄, то получаем, что справедливо неравенст-

во (4).

г) Так как

= 1 ⋅ ⎛⎜⎝ 11 − 31 + 31 − 51 + 51 − 71 +... + 2n1− 1 − 2n1+ 1⎟⎞⎠ = 21 ⋅⎝⎜⎛1− 2n1+ 1⎞⎠⎟, 2

т. е. так как 12 + 12 + 12 +... + 1 2 < 1 ⋅⎛⎜1 − 1+ 1⎟⎠⎞ (5′)

2 4 6 (2n) 2 ⎝ 2n

и 21 ⋅⎜⎝⎛1 − 2n1+ 1⎞⎟⎠ < 21,

то получаем, что справедливо неравенство (5).

Отметим, что приведенные доказательства справедливости неравенств (3), (4) и (5), строго говоря, не являются полноценными, так как для полноценности этих доказательств требуется доказать справедливость равенств (3′) и (4′) и неравенства (5′) методом математической индукции.

1.83. а) Докажите, что для любых действительных чисел а и b, если а + b = 3, то а²+ b²≥ 4,5.

Доказательство. Пусть а = 1,5 + с, b = 1,5 − с. Тогда а²+ b²= (1,5 + с)²+ (1,5 − с)²= 2,25 + 3с + с²+ 2,25 − 3с + с²= = 4,5 + 2с²≥ 4,5, что и требовалось доказать.

Промежуточный контроль. С—7.

1.8*. Делимость целых чисел

Материал о делимости целых чисел — новый в программе старших классов, поэтому он подробно описан в учебнике. Сначала рассматривается вопрос о делимости (без остатка) натуральных чисел, затем о делимости целых чисел

(с остатком).

В учебнике принято обозначение (m, п) — наибольший общий делитель чисел m и n; сформулированы основная теорема арифметики, свойство делимости суммы и разности (теорема 1), теорема о единственности деления с остатком для целых чисел (теорема 2).

Решения и комментарии

1.84*. а) Определите целые числа m, n, k и р, для которых справедливо равенство:

2m + n ⋅ 3k + 1 ⋅ 57 ⋅ 712 = 27 − n ⋅ 37 ⋅ 5m + p ⋅ 7m + n + k. (1) Решение. По основной теореме арифметики каждое натуральное число, большее 1, можно представить единственным образом в виде произведения степеней простых чисел. Поэтому из равенства (1) следует, что показатели степеней простых множителей в правой и левой частях этого равенства равны, т. е. m + n = 7 − n, k + 1 = 7, m + p = 7, m + n + k = 12.

Решив систему четырех уравнений с четырьмя неизвестными, получим: m = 5, п = 1, k = 6, р = 2.

Замечание. Идея решения задачи 1.84 используется при решении задачи 276 из раздела «Задания для повторения».

276. (МГУ, экон. ф-т.) За время хранения вклада в банке в конце каждого месяца начисляли на счет проценты от суммы вклада, которая находилась на счету в начале месяца, сначала в размере 5% в месяц, затем 11%, потом 7 % и, наконец, 12% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на 180%. Определите срок хранения вклада.

Решение. Пусть в банк положили а р. (а ≠ 0). Ежемесячно на счет начислялось сначала 5% m месяцев, затем 11% n месяцев, потом 7 % k месяцев и, наконец, 12% p месяцев от суммы вклада, которая находилась на счету в начале месяца. После m + n + k + p месяцев на счету оказалось

⎛ 5 ⎞ m ⎛ 100 ⎞ n ⎛ 50 ⎞k ⎛ 12 ⎞ p

a⎜⎝1 + 100 ⎟⎠ ⎜⎝1 + 900 ⎟⎠ ⎜⎝1 + 700 ⎠⎟ ⎜⎝1 + 100 ⎟⎠ =

= a⎜⎝⎛ 2021⎞⎟⎠ m ⎛⎜⎝ 109 ⎞⎟⎠ n ⎝⎜⎛ 1514⎟⎞⎠k ⎛⎜⎝ 2825 ⎞⎟⎠ p p.

или по условию задачи a ⎜⎝⎛1 ⁺¹⁸⁰₁₀₀⎞⎟⎠ = a ⋅¹⁴5 p.

Следовательно, справедливо равенство:

a ⎜⎝⎛ 2021⎞⎟⎠ m ⎛⎜⎝ 109 ⎞⎟⎠ n ⎝⎛⎜ 1514⎟⎠⎞k ⎜⎝⎛ 2825 ⎞⎟⎠ p = a ⋅ 145 .

Разделив полученное равенство на а (а ≠ 0) и умножив его на 20^m⋅ 9ⁿ⋅ 14^k⋅ 25^p⋅ 5, получим равносильное ему равенство

5 ⋅ 21^m⋅ 10ⁿ⋅ 15^k⋅ 28^p= 20^m⋅ 9ⁿ⋅ 14^k⁺¹⋅ 5^2p.

Разложив обе части равенства на простые множители, перепишем его в виде:

2n+ 2p ⋅ 3m+k ⋅ 5n+k+ 1 ⋅ 7m+p = 22m+k+ 1 ⋅ 32n ⋅ 5m+ 2p ⋅ 7k+ 1.

Из единственности разложения числа на простые множители (основная теорема арифметики) следует, что

⎧n +2p = 2m + k +1

⎪m + k = 2n

^⎨⎪n + k +1 = m +2 p ⎩m + p = k +1.

Решив систему из четырех полученных уравнений, получим, что m = 2, п = 3, k = 4, р = 3, т. е. деньги были вложены в банк на 2 + 3 + 4 + 3 = 12 месяцев.

1.85. а) Докажите, что числа 1997 и 1999 являются взаимно простыми.

Доказательство. Предположим, что числа 1997 и 1999 не являются взаимно простыми, т. е. оба делятся на натуральное число d ≠ 1. Тогда и их разность 2 делится на d, т. е. d = 2. Но каждое из этих чисел не делится на 2, следовательно, предположение, что числа 1997 и 1999 не являются взаимно простыми, неверно. Значит, они взаимно простые, что и требовалось доказать.

1.86. а) Докажите, что дробь несократимая.

Доказательство. Так как числа 1997 и 1999 взаимно простые (см. задание 1.85), то дробь несократимая.

1.87. а) Докажите, что произведение двух последовательных натуральных чисел делится на 2.

Доказательство. Пусть п и п + 1 — два последовательных натуральных числа. При делении на 2 натуральное число п может иметь только два остатка: 0 и 1.

Если n = 2k (k ∈ N), то п (п + 1) = 2k (2k + 1).

Если п = 2k + 1 (k ∈ N), то п (п + 1) = 2 (2k + 1) (k + 1).

Следовательно, произведение двух последовательных натуральных чисел делится на 2, так как содержит множитель 2 в каждом из двух возможных случаев.

1.88. Найдите все целые числа, которые при делении и на 4, и на 3, и на 2 дают остаток 1.

Решение. Все целые числа, которые при делении на 12 дают остаток 0, можно записать в виде 4 ⋅ 3 ⋅ k = 12k, где k ∈ Z.

При делении на 12 любого целого числа т может получиться один из 12 остатков: 0, 1, 2, ..., 11. Следовательно, множество всех целых чисел можно разбить на 12 непересекающихся классов А_r, где А_r— множество всех целых чисел, имеющих вид 12k + r, где r = 0, 1, 2, ..., 11. Нетрудно убедиться, что лишь для чисел из класса A₁выполняется условие: остаток от деления этих чисел и на 4, и на 3, и на 2 равен 1. Следовательно, все искомые числа можно записать в виде 12k + 1, где k ∈ Z.

1.89. Найдите все целые числа, которые при делении на 4 дают остаток 3, при делении на 3 дают остаток 2, при делении на 2 дают остаток 1.

Решение. Все целые числа, которые при делении на 4 дают остаток 0, при делении на 3 дают остаток 0, при делении на 2 дают остаток 0, можно записать в виде 4 ⋅ 3 ⋅ k = 12k, где k ∈ Z.

При делении на 12 любого целого числа m может получиться один из 12 остатков: 0, 1, 2, ..., 11. Следовательно, множество всех целых чисел можно разбить на 12 непересекающихся классов А_r, где А_r— множество всех целых чисел, имеющих вид 12k + r, где r = 0, 1, 2, ..., 11.

Нетрудно убедиться, что лишь для чисел из класса А₁₁выполняется условие: остаток от деления этих чисел на 4 равен 3, при делении на 3 равен 2, при делении на 2 равен 1.

Следовательно, все искомые числа можно записать в виде 12k + 11, где k ∈ Z.

Замечание к заданиям 1.88 и 1.89. Условия заданий проверяются лишь на числах r, так как искомые остатки получаются только при делении r на соответствующее число.

1.90. Докажите, что сумма кубов трех последовательных натуральных чисел делится на 9.

Доказательство. Пусть М = п³+ (п + 1)³+ (п + 2)³, где п — любое натуральное число. При делении на 3 числа п может получиться один из трех остатков: 0, 1, 2. Следовательно, множество всех натуральных чисел можно разбить на три непересекающихся класса чисел, имеющих вид 3m, где m ∈ N, 3m + 1 или 3m + 2, где m = 0,1,2,... .

Докажем, что если число п относится к любому из этих трех классов, то число М делится на 9.

1) Пусть п = 3m, где m ∈ N. Тогда

М = (3m)³+ (3m + 1)³+ (3m + 2)³= 27m³+ 27m³+ 27m²+ + 9m + 1 + 27m³+ 54m²+ 36m + 8 = 9k, где k ∈ N.

2) Пусть п = 3m + 1, где т = 0, 1, 2, ... . Тогда М = (3m + 1)³+ (3m + 2)³+ (3 (m + 1))³= 9p, где р ∈ N.

3) Пусть n = 3m + 2, где m = 0, 1, 2, ... . Тогда

М = (3m + 2)³+ (3 (m + 1))³+ (3 (m + 1) + 1)³= 9q, где q ∈ N.

Следовательно, в каждом случае натуральное число М делится на 9, что и требовалось доказать.

1.9*. Сравнения по модулю m

Материал о сравнении по модулю m также новый в программе для старших классов и поэтому подробно описан в учебнике. Введено понятие сравнения по модулю m и соответствующее обозначение, сформулированы 4 свойства сравнений. Рассмотренная теория применена для доказательства делимости 6²²− 1 на 7, нахождения остатка от деления 2²⁹на 11, доказательства признака делимости на 9.

Решения и комментарии

1.92. Сформулируйте признак делимости на 11 и докажите его.

Сформулируем признак делимости на 11: если разность суммы цифр числа, стоящих на четных местах, и суммы цифр, стоящих на нечетных местах, делится на 11, то и число делится на 11.

Верно и обратное утверждение:

если число делится на 11, то разность суммы его цифр, стоящих на четных местах, и суммы цифр, стоящих на нечетных местах, делится на 11.

Доказательство. Так как 10 ≡ −1(mod11), то 10²ⁿ≡ ≡ −( 1)²ⁿ(mod11) ≡1(mod11), а 10²ⁿ^+
1≡ −( 1)²ⁿ^+
1(mod11) ≡ ≡ −1(mod11).

Рассмотрим доказательство признака делимости на 11

на примере 6-значного натурального числа ^{a a a a a a a}_{6 5 4 3 2 1 0}. Для него справедливы сравнения:

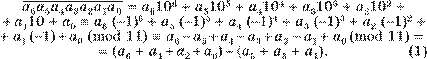
Справедливость обоих утверждений следует из равенства (1).

1.95. Определите остаток от деления числа 3²⁵на:

а) 10; б) 11; в) 13.

Решение. а) Так как 3²= 9 ≡ −1(mod10), то 3²⁵= (3^2
12) ⋅3 ≡ ≡ −( 1)¹²⋅3(mod10) = 3. Следовательно, 3 — остаток от деления числа 3²⁵на 10.

б) Так как 3⁵= 243 = 22 11⋅ +1 ≡1(mod11), то 3²⁵= (3^5
5) ≡ ≡1⁵(mod11) =1. Следовательно, 1 — остаток от деления числа 3²⁵на 11.

в) Так как 3³= 27 = 2 13⋅ +1 ≡1(mod13), то 3²⁵= (3^3
8) ⋅3 ≡ ≡ 3(mod13). Следовательно, 3 — остаток от деления числа 3²⁵на 13.

1.96. Не выполняя деления, определите остаток от деления числа 200420052006200720082009 на 9.

Решение. 200420052006200720082003 — наибольшее число, не превосходящее данного и делящееся на 9, оно на 6 меньше данного, поэтому 200420052006200720082009 ≡ ≡ 6 (mod 9). Следовательно, 6 — остаток от деления данного числа 200420052006200720082009 на 9.

1.97. Пусть Р₃(х) = х³− 4х²+ 5х + 1. Определите последнюю цифру числа Р₃(10²⁰⁰⁵).

Решение. Так как 10²⁰⁰⁵≡ 0(mod10), то P₃(10²⁰⁰⁵) ≡ ≡ P₃( )(0 mod10) = 0³− 4 ⋅ 0²+ 5 ⋅ 0 + 1 = 1. Следовательно, при делении числа Р₃(10²⁰⁰⁵) на 10 получается остаток 1, а это означает, что последняя цифра числа P₃(10²⁰⁰⁵) (в его десятичной записи) есть 1.

1.98. Пусть Р2004 (x) = x2004 − x2003 + x2002 − x2001 ... − х + 1. Определите последнюю цифру числа P₂₀₀₄(100²⁰⁰⁵).

Решение. Так как 100²⁰⁰⁵≡ 0(mod10), то P₂₀₀₄(100²⁰⁰⁵) ≡ ≡ P (0) (mod 10) = 02004 − 02003 + 02002 − 02001... − 0 + 1 = 1.

) на 10 по-

лучается остаток 1, а это означает, что последняя цифра числа Р₂₀₀₄(100²⁰⁰⁵) (в его десятичной записи) есть 1.

1.99. Докажите, что квадрат любого натурального числа либо делится на 9, либо при делении на 3 дает остаток 1.

Доказательство. Любое натуральное число п при делении на 3 дает только один из трех остатков: 0, 1, 2. Поэтому возможен лишь один из трех случаев: 1) n ≡ 0(mod 3); 2) n ≡1(mod 3); 3) n ≡ 2(mod3).

1) Если n ≡ 0(mod3), то п = 3m, где m ∈ N. Тогда п²= 9m², т. е. n²делится на 9.

2) Если n ≡1(mod3), то n²≡1²(mod3) ≡1(mod3), т. е.

п²при делении на 3 дает остаток 1.

3) Если n ≡ 2(mod3), то n²≡ 4(mod3) ≡1(mod3), т. е.

n²при делении на 3 дает остаток 1.

Таким образом, утверждение полностью доказано.

1.100. Найдите последнюю цифру числа 9⁹⁹.

Решение. Так как число 9⁹= 2п + 1, где п ∈ N и

9 ≡ −1(mod10), то 9²ⁿ^{+ 1}≡ −1(mod10) ≡ 9(mod10). Следовательно, при делении числа 9⁹⁹на 10 получится остаток 9, а это означает, что 9 — последняя цифра числа 9⁹⁹.

1.10*. Задачи с целочисленными неизвестными

Задачи с целочисленными неизвестными демонстрируют практическое применение материала о делимости натуральных (целых) чисел. В данном пункте рассмотрены диофантовы уравнения и старинные задачи, решаемые с их помощью. Учащиеся должны научиться находить частное решение диофантова уравнения первой степени, полное его решение, решать задачи с помощью диофантовых уравнений. Отметим, что на конкурсных экзаменах иногда встречаются задачи такого содержания, поэтому освоение материала данного пункта окажется полезным учащимся, готовящимся к конкурсным испытаниям.

Решения и комментарии

1.101. Подберите частное решение диофантова уравнения первой степени и запишите общее решение этого уравнения:

а) х + у = 5; б) 8x − y = 15.

Решение. а) Частным решением диофантова уравнения х + у = 5 является, например, пара чисел х = 1, у = 4. Общее решение этого уравнения: x = 1 + n, у = 4 − п, где п ∈ Z.

б) Частным решением диофантова уравнения 8х − у = 15 является, например, пара чисел х = 2, у = 1. Общее решение этого уравнения: х = 2 + п, у = 1 + 8n, где п ∈ Z. 1.102. а) Объясните, почему не имеет решений в целых числах уравнение 3x + 12y = 5.

Решение. Так как (3, 12) = 3, а 5 не делится на 3, то уравнение 3х + 12у = 5 не имеет решений в целых числах, так как если бы существовало решение (x₀; у₀) этого уравнения, то было бы справедливо числовое равенство 3x₀+ 12у₀= 5, в котором левая часть делится на 3, а правая не делится, что, естественно, невозможно.

1.103. Задача Леонардо Пизанского (Фибоначчи, 1180—1240). Некто купил 30 птиц за 30 монет, из числа этих птиц за каждых трех воробьев заплачена 1 монета, за каждые две горлицы — также 1 монета и, наконец, за каждого голубя — по 2 монеты. Сколько было птиц каждой породы?

Решение. Пусть купили х воробьев по монеты, у горлиц по монеты и 30 − х − у голубей по 2 монеты. Будем предполагать, что птиц каждой породы купили не менее одной, т. е. х, у и (30 − х − у) — натуральные числа. Составим уравнение

¹x ¹2 30 ⁽¹⁾

+ y + ( − x − y) = 30_.

3 2

Умножив уравнение (1) на 6 и перенеся неизвестное у в правую часть уравнения, получим уравнение, равносильное уравнению (1):

10x = 9(20 − у). (2)

Так как правая часть равенства (2) делится на 9, то и левая его часть делится на 9. Так как 10 не делится на 9, то, применяя лемму (с. 36 учебника), получаем, что х делится на 9, т. е. х = 9х₁, где x₁∈ N. Перепишем уравнение (2) в

виде

9y = 10(18 − x). (3)

Так как правая часть равенства (3) делится на 10, то и левая его часть делится на 10. Так как 9 не делится на 10, то, применяя ту же лемму, получаем, что у делится на 10, т. е. у = 10y₁, где y₁∈ N. Перепишем уравнение (2) в виде 10 ⋅ 9x₁+ 9 ⋅ 10y₁= 180.

Разделив это уравнение на 90, получим равносильное ему уравнение х₁+ у₁= 2,

имеющее единственное решение в натуральных числах: x₁= 1, y₁= 1.

Теперь найдем соответствующие значения х и у: x = 9x₁= 9, y = 10y₁= 10.

Тогда 30 − x − y = 30 − 9 − 10 = 11. Итак, купили 9 воробьев, 10 горлиц и 11 голубей.

1.104. Из «Арифметики» Л. Ф. Магницкого (1669—

1739). Купил некто на 80 алтын гусей, утят и чирков. Гуся покупал по 2 алтына, утку по 1 алтыну, чирка же по 3 деньги, а всех куплено 80 птиц. Спрашивается, сколько каких птиц он купил. (1 алтын = 3 к., 1 деньга = 0,5 к.)

Решение. Пусть купили х гусей по 6 к., у уток по 3 к., 80 − x − у чирков по 1,5 к. Будем предполагать, что птиц каждой породы купили не менее одной, т. е. х, у и

(80 − х − у) — натуральные числа. Составим уравнение

6x + 3y + 1,5(80 − х − y) = 240. (4)

Разделив уравнение (4) на 1,5 и перенеся неизвестные в одну часть уравнения, а известные — в другую, получим уравнение, равносильное уравнению (4):

3x + y = 80. (5)

Так как х = 0, у = 80 — частное решение уравнения (5), то общее решение этого уравнения: х = 0 + п = п, у =80−3n, где п ∈ Z, но тогда 80 − х − у = 2п.

Так как мы рассматриваем решения уравнения (4) в натуральных числах и число птиц каждого вида меньше 80, то x ≥ 1, y ≥ 1, откуда 1 ≤ п ≤ 26. Таким образом, задача имеет 26 решений. Всего купили: п гусей, 80 − 3п уток, 2п чирков, где n ∈ N, п ≤ 26.

Приведем одно из 26 решений задачи: купили 1 гуся, 77 уток и 2 чирка.

1.107. Решите в целых числах уравнение:

a) x²+ y²− 2x + 4y = −5;	(6)
в) xy + 4x − 2y − 11 = 0.	(7)

Решение. а) Перепишем уравнение (6) в виде (x − 1)²+ (y + 2)²= 0.

Это уравнение имеет единственное решение х = 1, у = −2, поэтому пара (1; −2) — единственное решение уравнения (6).

в) Перепишем уравнение (7) в виде

(x − 2)(у + 4) = 3. (8)

Так как x − 2 и у + 4 — целые числа, то решениями уравнения (8) являются только те пары целых чисел (x; у), которые являются решениями хотя бы одной из систем:

⎧x − 2 =1 ⎧x − 2 = −1 ⎧x − 2 = 3 ⎧x − 2 = −3

⎨⎩y +4 = 3 или ⎨⎩y +4 = −3 или ⎨⎩y +4 =1 или ⎨⎩y +4 = −1.

Решив каждую из четырех систем, получим все решения уравнения (6) в целых числах: (3; −1), (1; −7), (5; −3), (−1; −5).

1.108. Докажите, что уравнение:

а) х²− 4х + у²+ 4y + 8 = 0

имеет единственное целочисленное решение;

(9)

б) x²− 4x + y²+ 4y + 9 = 0

(10)

не имеет решений.

Доказательство. a) Перепишем уравнение (9) в виде

(x − 2)²+ (y + 2)²= 0. (11)

Уравнение (11) имеет единственное решение х = 2, у = −2, так как при любых других значениях х и y сумма (х − 2)²+ (у + 2)²положительна. Следовательно, и уравнение (9) имеет единственное целочисленное решение.

б) Перепишем уравнение (10) в виде

(x − 2)²+ (y + 2)²+ 1 = 0. (12)

При любых значениях x и у сумма (х − 2)²+ (у + 2)²+ + 1 ≥ 1, следовательно, уравнение (12), а значит, и уравнение (10) не имеют решений.

Задача-шутка. Докажите, что существует решение уравнения

29x + 30y + 31z = 366 (13)

в натуральных числах.

Решение. В високосном году 366 дней и имеется 1 месяц, содержащий ровно 29 дней, 4 месяца, содержащих ровно 30 дней, и 7 месяцев, содержащих ровно 31 день, поэтому тройка чисел х = 1, у = 4, z = 7 является решением уравнения (13). Это означает, что существует решение уравнения (13) в натуральных числах.

§ 2. Рациональные уравнения и неравенства

2.1. Рациональные выражения

В данном пункте повторяются сведения о рациональных выражениях, действия с алгебраическими дробями, вводится понятие симметрического многочлена. Для выполнения заданий из этого пункта необходимо повторить формулы сокращенного умножения, способы разложения многочлена на множители, изученные в основной школе.

Решения и комментарии

2.10. а) Упростите выражение

⎛ a b ⎞ a³+ 8b³

⎜⎝a − 2b + a + 2b⎟⎠ ⋅ a³+ 3a b²− 2ab²

и найдите его значение при a = 0,5, b = −1.

Решение. а) A = ⎜⎝⎛a−a2b + a +b2b⎞⎟⎠ ⋅ a3 +a33a b+2 8−b32ab2 =

₌a²(a+ 2−ab ab2b a)(+ + 2−b2)b²_⋅(a +a a2( b a2)(+²3−_ab2−ab2+_b24)b²) =

(a²+ 3ab − 2b a²)( + 2b a)( ²− 2ab + 4b²) a²− 2ab + 4b²4b²

= (a − 2b a)( + 2b a a) ( 2 + 3ab − 2b2) = a2 − 2ab =1+a2 − 2ab.

При а = 0,5, b = −1 A .

2.13. Докажите, что если f (x; у) — симметрический многочлен и пара различных чисел (х₀; у₀) является решением уравнения f (x; y) = 0, то пара чисел (у₀; x₀) также является решением уравнения.

Решение. Если пара (x₀; y₀) различных чисел является решением уравнения f (x; y) = 0, то справедливо числовое равенство f (x₀; y₀) = 0. Так как многочлен f (x; у) симметрический, то для пары чисел (х₀; y₀) справедливо равенство f (x₀; y₀) = f (y₀; x₀). Это означает, что пара чисел (у₀; x₀) также является решением уравнения f (x; y) = 0, что и требовалось доказать.

Промежуточный контроль. С—2, С—4.

2.2. Формулы бинома Ньютона, суммы и разности

степеней

Возведение двучлена а + b в степень с показателем 2, 3, 4, 5 и треугольник Паскаля не вызывают затруднений у учащихся. Чтобы формула бинома Ньютона также не вызвала у них затруднений, надо показать, как находить коэффициенты разложения с помощью треугольника Паскаля, выполнить возведение двучлена в 5-ю, 6-ю, 7-ю степень с помощью треугольника Паскаля. Затем выполнить задание 2.14, позволяющее повторить правило вычисления чисел С^k_nи сравнить их с соответствующими коэффициентами разложений (а + х)^пдля п = 2, 3, 4.

Только теперь можно привести общую формулу бинома Ньютона. Доказательство этой формулы не является обязательным для обычных классов.

Приведем второе доказательство равенства

Cn0 + Cn1 + C2n + ... + Cnn = 2n, (1)

рассмотренного при решении задачи 1.74. Формула бинома Ньютона имеет вид:

(a + b)n = Cп0ап + Cn1an − 1b + Cn2аn − 2b2 + ... + Cппbn. (2) Подставив в равенстве (2) число 1 вместо каждого из чисел а и b, получим равенство

2n = Cn0 + Cn1 + Cп2 + ... + Cпn,

доказывающее равенство (1).

Решения и комментарии

2.15. Сколько членов в формуле бинома Ньютона при:

а) п = 3; б) п = 5?

Решение. Разложение по формуле бинома Ньютона для (а + х)ⁿсодержит п + 1 член.

а) При п = 3 в формуле бинома Ньютона 4 члена.

б) При п = 5 в формуле бинома Ньютона 6 членов.

2.16. Сколько членов в формуле бинома Ньютона при:

а) п = 2l; б) п = 2l + 1, где l — натуральное число? В каком из этих случаев имеется средний член в формуле бинома Ньютона?

Решение.

а) Если п = 2l, l ∈ N, то число членов 2l + 1.

б) Если п = 2l + 1, l ∈ N, то число членов 2l + 2.

В случае «а» число членов нечетное и имеется средний член C2llаlxl.

Промежуточный контроль. С—10.

2.3*. Деление многочленов с остатком. Алгоритм Евклида

Основное назначение данного пункта — обучение учащихся делению уголком многочлена на ненулевой многочлен, которое будет использоваться при решении уравнений высших степеней и в других случаях. Алгоритм Евклида используется для нахождения наибольшего общего делителя двух многочленов, для доказательства сократимости (несократимости) алгебраической дроби и т. д.

Решения и комментарии

2.31. а) Докажите, что дробь ^xx34 ⁺+ ¹₁несократима.

Доказательство. Применив алгоритм Евклида к многочленам х⁴+ 1 и x³+ 1, получим последний отличный от нуля остаток 2. Это означает, что наибольший общий делитель этих многочленов — любое действительное число. Пишут НОД (x⁴+ 1, х³+ 1) = 1. Поэтому дробь несократима, что и требовалось доказать.

2.4*. Теорема Безу

Основное назначение данного пункта — обучение учащихся применению теоремы Безу для отыскания остатка от деления многочлена на двучлен х − а; обучение краткой записи процедуры деления многочлена на двучлен х − а с помощью схемы Горнера.

В учебнике описан алгоритм нахождения коэффициентов частного (неполного частного) и остатка при делении уголком и при использовании схемы Горнера. Но учащиеся не всегда понимают, почему схему Горнера надо заполнять именно так и как эти действия связаны с процессом деления многочленов уголком. Остановимся на этом подробнее.

В примере 1 из учебника требуется разделить многочлен 3х³− 2х − 20 = 3x³+ 0x²− 2х − 20 на двучлен х − 2. Выполним деление уголком (рис. 5; подробное описание действий приведено в учебнике).

Запишем в верхней строке таблицы коэффициенты делимого, а перед второй строкой число 2 (рис. 6).

Рис. 5

Так как первый коэффициент делителя равен 1, то первый коэффициент частного равен 3 (сносим 3 в первую клетку нижней строки таблицы на рисунке 6). Далее при делении уголком коэффициент при х²находится так: из 0 вычитаем 3 ⋅ (−2), получаем 6, т. е. 0 − 3 ⋅ (−2) = 6, что равно 2 ⋅ 3 + 0. Число 6 пишем во вторую клетку нижней строки таблицы (рис. 7).

2 ⋅ 3 + 0 = 6 2 ⋅ 6 + (−2) = 10 2 ⋅ 10 + (−20) = 0

Рис. 7 Рис. 8 Рис. 9

Аналогично получаем числа для следующих клеток нижней строки таблицы:

10 = −2 − 6 ⋅ (−2), что равно 2 ⋅ 6 + (−2) (рис. 8), 0 = −20 − 10 ⋅ (−2), что равно 2 ⋅ 10 + (−20) (рис. 9).

Итак, нижняя строка таблицы (рис. 9) дает коэффициенты при х², при х и свободный член частного, а в последней клетке — остаток от деления многочлена на двучлен х − 2.

Решения и комментарии

2.35. а) С помощью теоремы Безу найдите остаток от деления многочлена 3x³− 2x²− 4x − 5: на х − 1; на x − 2; на х − 3.

Решение. Остаток от деления многочлена P₃(х) = 3х³−

− 2х²− 4х − 5 на двучлен х − 1 равен Р₃(1) = 3 ⋅ 1³− − 2 ⋅ 1²− 4 ⋅ 1 − 5 = −8.

Остаток от деления многочлена P₃(x) = 3x³− 2х²− − 4х − 5 на двучлен х − 2 равен Р₃(2) = 3 ⋅ 2³− 2 ⋅ 2²− − 4 ⋅ 2 − 5 = 3.

Остаток от деления многочлена Р₃(х) = 3х³− 2х²− − 4x − 5 на двучлен х − 3 равен Р₃(3) = 3 ⋅ 3³− 2 ⋅ 3²− − 4 ⋅ 3 − 5 = 46.

2.36. а) С помощью теоремы Безу докажите, что многочлен 17х³− 13x²− 4 делится на двучлен x − 1 без остатка.

Доказательство. Так как для многочлена P₃(х) =

= 17x³− 13x²− 4 верно равенство Р₃(1) = 0, то остаток от деления многочлена Р₃(х) на двучлен x − 1 равен 0, т. е. многочлен Р₃(x) делится на двучлен x − 1 без остатка.

2.5*. Корень многочлена

В данном пункте приводится теорема 1, позволяющая по коэффициентам а_пи а₀многочлена Р_п(х) п-й степени с целыми коэффициентами найти все рациональные корни многочлена Р_n(х) (если они существуют). Следствие из этой теоремы (для а_п= 1) позволяет найти все целые корни многочлена Р_n(х) (если они существуют).

Решения и комментарии

2.41. а) Разложите многочлен Р (х) = 2х³− х²− 8х + 4 на линейные множители, если это возможно.

Решение. Для разложения многочлена Р (х) на линейные множители найдем все рациональные корни этого многочлена (если они существуют).

Здесь a₃= 2, а₀= 4, поэтому, если многочлен Р (х) имеет p рациональный корень (p ∈ Z, q ∈ N), то по теореме 1 чис-

ло 4 делится на р, а число 2 делится на q.

Число p может быть равно одному из чисел: 1, −1, 2, −2,

4, −4; число q может быть равно одному из чисел: 1, 2;

корень может быть равен одному из чисел: 1, −1, 2,

−2, 4, −4, ¹, − ¹.

2 2

Выясним, какое из этих чисел является корнем многочлена Р (х):

P (1) = 2 ⋅ 1³− 1²− 8 ⋅ 1 + 4 = −3 ≠ 0,

Р (−1) = 2 ⋅ (−1)³− (−1)²− 8 ⋅ (−1) + 4 = 9 ≠ 0, Р (2) = 2 ⋅ 2³− 2²− 8 ⋅ 2 + 4 = 0.

Найден первый корень многочлена Р (x) — число 2. Разложив многочлен Р (x) на множители, получим Р (x) = 2x³− x²− 8x + 4 = (х − 2) (2х²+ 3х − 2).

Решив уравнение 2х²+ 3х − 2 = 0, найдем его корни х₁= −2, x₂= , они и будут корнями многочлена 2х²+ 3х − 2.

Следовательно, 2х²+ 3х − 2 = 2(х + 2)^⎜⎝⎛x ⁻₂¹⎠^⎟⎞ = (x + 2)(2x −1).

Поэтому P (x) = 2x³− x²− 8x + 4 = (x − 2) (x + 2) (2x − 1).

2.43. а) Найдите все корни многочлена, если многочлен Р (x) = x³− 5х²+ ах + b делится на х − 3 без остатка, а при делении на х + 3 дает остаток −42.

Решение. По теореме Безу Р (3) = 0, а Р₃(−3) = −42, поэтому верны равенства

3³− 5 ⋅ 3²+ 3a + b = 0, (1)

(−3)³− 5 ⋅ (−3)²− 3а + b = −42. (2)

Решив систему уравнений (1) и (2) относительно а и b, получим а = −2, b = 24. Так как х₁= 3 — корень многочлена Р (х), то многочлен Р (x) разлагается на множители:

Р (x) = x³− 5x²− 2х + 24 = (х − 3) (x²− 2х − 8).

Так как −2 и 4 — корни многочлена x²− 2х − 8, то 3, −2 и 4 — все корни многочлена Р (х).

Промежуточный контроль. С—11.

2.6. Рациональные уравнения

В данном пункте повторяются известные из основной школы сведения о способах решения рациональных уравнений. Отметим некоторые особенности терминологии и способов оформления решения, принятых в учебнике.

Уравнение вида А (x) ⋅ В (x) = 0, где А (x) и В (x) — многочлены, называют распадающимся, множество его корней есть объединение множеств корней уравнений А (x) = 0 и В (x) = 0. При этом понятие совокупности уравнений и соответствующее обозначение пока не используются.

A x( )

Уравнение вида = 0 предлагается решать так: сна-

B x( )

чала решить уравнение А (x) = 0, затем отобрать из найденных чисел те, которые не обращают в нуль знаменатель

A x( )

В (x) дроби. Они и будут корнями уравнения = 0. При

B x( )

⎧A x( ) = 0

этом переход к системе ^⎨⎩ _{B x}_{( )}≠ _0,равносильной данному

уравнению, не используется, так как в учебниках тех же авторов для основной школы такие системы не рассматривались. Если же учащиеся учились по учебникам, в которых такие переходы уже выполнялись, то, объяснив учащимся, какое число называют решением такой системы, учитель может использовать и упомянутый переход.

После рассмотрения примера 3 из учебника можно сформулировать правило: для решения рационального уравнения надо перенести все его члены в левую часть, затем, применяя правила сложения и вычитания алгебраических дробей, записать левую часть как алгебраическую дробь и решить полученное уравнение.

Замечание. Отклонение от этого правила может привести к потере или к приобретению корней, посторонних для данного уравнения.

Пример. Решим уравнение

(x − 2)(x − 3)

=1. (1)

x − 3 Решение. Применив данное правило к уравнению (1), получим равносильное ему уравнение

(x − 3)²

= 0. (2) x − 3

Оно не имеет корней. Следовательно, уравнение (1) тоже не имеет корней.

Однако если мы, отклоняясь от правила, сократили бы дробь в левой части уравнения (1) на x − 3, то получили бы уравнение

x − 2 = 1, (3)

которое имеет корень х = 3. Но х = 3 не является корнем уравнения (1) — при х = 3 левая часть уравнения (1) превращается в выражение, не имеющее смысла.

Следовательно, при таком «способе решения» мы приобрели лишний корень уравнения (1).

Если же сначала будет дано уравнение (3), а мы вопреки x − 2

правилу умножим числитель и знаменатель дроби на

ненулевой многочлен х − 3, то придем к уравнению (1), которое не имеет корней. Значит, при таком «способе решения» потерян корень уравнения (2).

При решении примера 4 (с. 68 учебника) показан достаточно сложный прием замены неизвестного. Другие приемы замены рассмотрены в п. 6 дидактических материалов.

Решения и комментарии

2.49. Решите уравнение, используя замену неизвестного:

в) (x²− 2x)²− 2 (x − 1)²− 1 = 0; ж) ^x⁺¹₊^6x⁻⁶− 5 = 0. x − 1 x + 1

Решение. в) Сначала надо раскрыть вторые скобки в левой части уравнения:

(x²− 2x)²− 2 (x²− 2x + 1) − 1 = 0. (4)

Теперь, сделав замену неизвестного t = х²− 2х, перепишем уравнение (4) в виде t²− 2 (t + 1) − 1 = 0.

Это уравнение имеет два корня: t₁= −1 и t₂= 3. Объединив все корни двух уравнений х²− 2х = −1 и х²− 2х = 3, получим все корни исходного уравнения: x₁= 1, x₂= −1 и x₃= 3.

ж) Перепишем исходное уравнение в виде

x + 1 6(x − 1)

+ − 5 = 0. (5) x − 1 x + 1

Сделав замену неизвестного t = ^x⁺¹, перепишем уравнеx − 1

ние (5) в виде

t + ⁶− 5 = 0. (6) t

Уравнение (6) имеет два корня: t₁= 2 и t₂= 3. Объединив x + 1 x + 1

все корни двух уравнений = 2 и = 3, получим все

x − 1 x − 1

корни исходного уравнения: х₁= 2 и х₂= 3.

2.52. Решите уравнение:

а) + ^x= 2 ²;

x a+ x a− 3

2x 12x²b x−

в) + = ; x b− b²− x²x b+

x 1 b 2

^б)+ ax bx− + a x abx²− = a b− ^;a

г) + x a− = a x(3x2 −+a22a), x a+

x a− x a+

где а и b — данные числа.

Решение. а) Перенеся все члены уравнения в левую часть и выполнив сложение алгебраических дробей, перепишем уравнение в виде

x2 − 4a2 2 − a2 = 0.

Уравнение х²− 4а²= 0 имеет два корня: х₁= 2а, x₂= −2а.

Если а = 0, то эти корни совпадают, но тогда знаменатель дроби 4а²− а²равен нулю, т. е. при а = 0 исходное уравнение не имеет корней.

Если а ≠ 0, то для каждого из корней х₁и х₂знаменатель дроби 4а²− а²отличен от нуля, т. е. при а ≠ 0 исходное уравнение имеет два корня: 2а и −2а.

Итак, исходное уравнение не имеет корней, если а = 0; имеет два корня: х₁= −2а, x₂= 2а, если а ≠ 0.

б) Перенеся все члены уравнения в левую часть и выполнив сложение алгебраических дробей, перепишем уравнение в виде

(a b x− ) ²− 2ax a b+ +

= 0.

ax a b( − )

Если а (а − b) = 0, то это уравнение не имеет корней.

Если же а (а − b) ≠ 0, то уравнение (а − b) х²− 2ах + + а + b = 0 квадратное и имеет два корня: х₁= 1 и x₂= ^{a b}⁺. a b− Очевидно, что для х₁условие ах₁(а − b) ≠ 0 выполняется для всех а и b, таких, что а (а − b) ≠ 0, а для x₂= усло-

вие ах₂(а − b) ≠ 0 выполняется для всех а и b, таких, что а (а − b) ≠ 0 и (а + b) ≠ 0, т. е. при а (а − b) ≠ 0 и (а + b) ≠ 0 исходное уравнение имеет два корня x₁и х₂. Если же а (а − b) ≠ 0 и а + b = 0, то ах₂(а − b) = 0, т. е. исходное уравнение имеет единственный корень x₁= 1.

Итак, исходное уравнение не имеет корней, если а = 0, b — любое число или если а = b; имеет два корня: х₁= 1, x₂= , если а ≠ 0, а ≠ b, а ≠ −b; имеет единственный корень x₁= 1, если а ≠ 0, а = −b.

в) Перенеся все члены уравнения в левую часть и выполнив сложение алгебраических дробей, перепишем уравнение в виде

9x2 − b2 2 − b2 = 0.

Уравнение 9х²− b²= 0 имеет два корня: x₁⁼^b, x₂^{= −}^b.

3 3

Если b = 0, то эти корни совпадают, но тогда знамена-

тель дроби ^b²− b²равен нулю, т. е. при b = 0 исходное урав-

9 нение не имеет корней.

Если b ≠ 0, то для каждого из корней х₁и х₂знамена-

тель дроби ^b²− b²отличен от нуля, т. е. при b ≠ 0 исходное

b b уравнение имеет два корня: и − .

3 3

Итак, исходное уравнение не имеет корней, если b = 0; имеет два корня x₁⁼^b, x₂^{= −}^b, если b ≠ 0.

3 3

г) Перенеся все члены уравнения в левую часть и выполнив сложение алгебраических дробей, перепишем уравнение в виде

2x²− 3ax 2 − a2 = 0. x

Уравнение 2х²− 3ах = 0 имеет два корня: х₁= 0 и х₂= 1,5а.

Если а = 0, то эти корни совпадают и равны нулю, но тогда знаменатель дроби равен нулю, т. е. при а = 0 исходное уравнение не имеет корней.

Если же а ≠ 0, то знаменатель дроби х²− а²отличен от нуля и для x = x₁, и для x = x₂, т. е. при а ≠ 0 исходное уравнение имеет два корня: 0 и 1,5а.

Итак, исходное уравнение не имеет корней, если а = 0; имеет два корня: x₁= 0, х₂= 1,5а, если а ≠ 0.

Промежуточный контроль. С—3, С—5, С—6.

2.7. Системы рациональных уравнений

В данном пункте повторяются известные из основной школы сведения о способах решения систем рациональных уравнений. Здесь рассмотрены способ подстановки, способ сложения уравнений, применение замены неизвестных при решении систем уравнений, а также прием решения системы уравнений с двумя неизвестными, одно из уравнений которой однородное.

Решения и комментарии

2.57. Решите систему уравнений:

⎧y²− 3xy = −2 ⎧ x²− 8y +31 = 0

^а)^⎨⎩x²+5xy =11; ^в)^⎨⎩y²− 2x −14 = 0.

Решение. а) Сложив уравнения исходной системы, получим равносильную ей систему ⎧y²− 3xy = −2

⎨⎩(x + y)2 = 9. (1)

Все решения системы (1) получим, объединив все решения двух систем

⎧y²− 3xy = −2 ⎧y²− 3xy = −2 ^⎨⎩ x + y = 3 ^и^⎨⎩x + y = −3.

⎛ 11 1⎞

Первая из этих систем имеет решения ⎜⎝ 4 ; 4⎟⎠ и (1; 2), а

⎛ 11 1⎞

вторая — ^⎜⎝⁻₄; ⁻₄^⎟⎠ и (−1; −2). Следовательно, исходная

⎛ 11 1⎞ ⎛ 11 1⎞

система имеет четыре решения: ⎜⎝ 4 ; 4⎟⎠ , (1; 2), ⎜⎝− 4 ; − 4⎟⎠ ,

(−1; −2).

в) Сложив уравнения исходной системы, получим равносильную ей систему

⎧x²− 8y +31 = 0

^⎨⎩(x −1)²+(y − 4)²= 0. ⁽²⁾

Второе уравнение системы (2) имеет единственное решение (1; 4), которое является также решением первого уравнения этой системы. Следовательно, система (2) и равносильная ей исходная система имеют единственное решение (1; 4).

2.58. Решите систему уравнений:

⎧⎪ x + x + 3 = 17 ^⎧⎪2x + 2y − 3x − 3y = ₅

^а)⎨x + 3 x 4 ^в)⎨ x y− x y+

⎪⎩x²− 4xy +4y²= 0; ⎪⎩x²+ y²= 90;

⎧x2 + y2 = 5

^д)^⎨⎩xy + x + y = 5.

Решение. а) Сделав замену неизвестного t = ^x, найx + 3

дем корни уравнения t ⁺¹⁼¹⁷, их два: t₁= и t₂= 4. Все t 4

корни первого уравнения исходной системы найдем, объx 1 x единив корни двух уравнений = и = 4. Первое

x + 3 4 x + 3

имеет единственный корень х₁= 1, а второе — единственный корень x₂= −4.

Подставляя х₁, а затем х₂во второе уравнение исходной системы, получим, что y₁= , у₂= −2. Следовательно, ис-

⎛ 1⎞

ходная система имеет два решения: ^⎜⎝1^;₂^⎟⎠ и (−4; −2).

в) Сделав замену неизвестного, найдем корни

уравнения 2t ⁻³= 5, их два: t₁= − t₂= 3. Все решения

исходной системы найдем, объединив решения двух систем

⎧⎪x y⁺= − 1 ^⎧⎪ x y⁺= ₃

⎨x y− 2 ^и⎨ x y−

⎪⎩x²+ y²= 90 ⎪⎩x²+ y²= 90.

Первая из них имеет решения (3; −9) и (−3; 9), а вторая — (6 2; 3 2) и (−6 2; −3 2). Следовательно, исходная система имеет четыре решения: (3; −9), (−3; 9), (6 2; 3 2) и (−6 2; −3 2).

д) Умножив второе уравнение исходной системы на 2 и сложив полученное уравнение с первым уравнением системы, получим систему, равносильную исходной системе:

⎧x2 + y2 = 5

^⎨⎩x²+2xy + y²+2(x + y) =15.

Перепишем систему в виде

⎧x2 + y2 = 5

^⎨⎩(x + y)²+2(x + y) =15.

Сделав замену неизвестных t = х + у, найдем корни уравнения t²+ 2t = 15, их два: t₁= −5 и t₂= 3. Все решения исходной системы найдем, объединив решения двух систем

⎧x2 + y2 = 5 ⎧x2 + y2 = 5 ^⎨⎩x + y = −5 ^и^⎨⎩x + y = 3.

Первая из них не имеет решений, а вторая имеет два решения: (1; 2) и (2; 1).

Следовательно, исходная система имеет те же два решения: (1; 2) и (2; 1).

Замечание. Ту же систему можно решить с помощью замены неизвестных и = х + у, v = ху.

2.59. Решите систему уравнений:

⎧9x²−10xy +4y²= 3 ⎧ x²+ y²=1

^а)^⎨⎩2xy − 3x +2y =1; ^ж)^⎨⎩x³+ y³= −1.

Решение. а) С помощью замены неизвестных и = 3х − 2у, v = xy перепишем исходную систему в виде

⎧u²+2v = 3 ^⎨⎩2v − u =1.

Эта система имеет два решения u₁= 1, v₁= 1 и u₂= −2, v₂= −.

Все решения исходной системы найдем, объединив ре-

шения двух систем:

⎧3x − 2y =1

^⎨xy =1

⎩

⎧⎪3x − 2y = −2 ^⎨xy = − ¹.

⎪⎩ 2

⎛ 2 3 ⎞

Первая из них имеет два решения: (1; 1) и ⎜⎝− 3 ; − 2 ⎟⎠, а вторая не имеет решений. Следовательно, исходная система имеет те же два решения: (1; 1) и ⎜⎝⎛− 32 ; − 32 ⎞⎟⎠.

ж) С помощью замены неизвестных и = х + у, v = ху перепишем исходную систему в виде

⎧u²− 2v =1

⎨⎩u₃− 3uv = −1. (3)

Из первого уравнения системы (3) получим, что u2 − 1 u2 − 1

v = ; подставив выражение вместо v во второе

2 2

уравнение, перепишем систему (3) в виде

⎧⎪ u²− 2v3=1

⎨⎪⎩_u3 − 3u 2− 3u +₁= _0.(4)

Второе уравнение системы равносильно уравнению u³− 3u − 2 = 0, имеющему очевидный корень и₁= −1, другие корни этого уравнения получим, разложив его левую часть на множители: (и + 1) (и²− и − 2) = 0. Найдя корни u₂= 2, u₃= −1 уравнения u²− u − 2 = 0 и учитывая, что u₁= u₃, получим, что второе уравнение системы (4) имеет два различных корня: u₁= −1 и u₂= 2.

Поэтому система (4) имеет два решения: u₁= −1, v₁= 0 и и₂= 2, v₂= 1,5. Все решения исходной системы найдем, объединив решения двух систем

⎧x + y = −1 ⎧x + y = 2

^⎨⎩xy = 0 ^и^⎨⎩xy =1,5.

Первая из них имеет решения (−1; 0) и (0; −1), а вторая не имеет решений.

Следовательно, исходная система имеет те же два решения: (0; −1) и (−1; 0).

2.8. Метод интервалов решения неравенств

Метод интервалов решения неравенств, рассматриваемый в данном пункте, знаком учащимся. Подчеркнем, что он основывается на свойстве двучлена х − а обращаться в нуль в точке х = а, принимать положительные значения для всех x > а и отрицательные значения для всех х < а. В п. 2.8 рассматриваются лишь строгие неравенства, содержащие произведения двучленов (неравенства с алгебраическими дробями рассматриваются в следующем пункте).

Все учащиеся должны научиться решать неравенства, левая часть которых является произведением различных двучленов. Более сложный случай применения метода интервалов связан с наличием одинаковых двучленов. Метод решения таких неравенств назван в учебнике общим методом интервалов.

Явного применения непрерывности функций здесь нет, этот прием будет рассмотрен только в 11 классе.

Решения и комментарии

2.72. Решите неравенство:

а) (x²− 4)(х²− 5х + 6) > 0;

д) x³+ x²− 8x − 12 > 0.

Решение. а) Разложив левую часть исходного неравенства на множители, перепишем неравенство в виде

(x − (−2)) (x − 2)²(x − 3) > 0. (1)

Исследуем знак многочлена А (x) = (х − (−2)) (х − 2)²(х − 3) на интервалах (−∞; −2), (−2; 2), (2; 3), (3; +∞). На интервале (3; +∞) каждый множитель положителен, поэтому А (x) > 0; при переходе через корень многочлена x = 3 меняет знак только один линейный множитель х − 3, следовательно, меняет знак и А (x), т. е. A (x) < 0 при x ∈ (2; 3); при переходе через корень многочлена х = 2 меняют знак сразу два линейных множителя х − 2 и х − 2, следовательно, А (x) не меняет знак, т. е. A (x) < 0 при x ∈ (−2; 2); при переходе через корень многочлена х = −2 меняет знак только один линейный множитель х − (−2), следовательно, меняет знак и А (x), т. е. А (x) > 0 при Рис. 10 х ∈ (−∞; −2) (рис. 10).

Следовательно, все решения исходного неравенства составляют множество (−∞; −2) ∪ (3; +∞).

д) Здесь сначала надо переписать неравенство, разложив многочлен на множители: (х − (−2))²(х − 3) > 0, а затем применив описанную выше процедуру решения неравенства, получить, что все решения исходного неравенства составляют интервал (3; +∞).

Дополнительное задание (С3, ЕГЭ, 2007). Найдите все значения x, которые удовлетворяют неравенству (2а − 1) x²< (а + 1) x + 3а при любом значении параметра а, принадлежащем промежутку (1; 2).

Это задание можно выполнить, если применить метод интервалов.

Решение. Перепишем исходное неравенство в виде

(2а − 1) x²− (а + 1) x − 3a < 0. (2)

При каждом а ∈ (1; 2) имеем 2а − 1 > 0, поэтому в левой части неравенства (2) записан квадратный трехчлен с положительным коэффициентом при старшем члене, имеющий

два корня х₁= −1 и x₂⁼^3a, такие, что х₁< х₂. Определив 2a − 1

знак трехчлена на интервалах (рис. 11), получим, что при каждом значении a ∈ (1; 2) неравенство (2) равносильно двойному Рис. 11 неравенству

−1 < x < ^3a. (3)

2a − 1

3a 2 − a 3a

Так как = 2 + и = 3 − , а для каждо-

2a − 1 2a − 1 2a − 1

го a ∈ (1; 2) справедливы неравенства ²⁻^a> 0 и > 0, 2a − 1

то для каждого a ∈ (1; 2) справедливо двойное неравенство

. (4)

Из неравенств (3) и (4) (рис. 12) следует, что любое число x₀, такое, что −1 < x₀≤ 2, удовлетворяет неравенству (3) при любом а ∈ (1; 2). Покажем, что других таких х нет.

Ясно, что ни одно число х вне промежутка (−1; 3) не удовлетворяет неравенству (3) при любом

a ∈ (1; 2). Рис. 12 Покажем, что любое x₁, такое, что 2 < x₁< 3, также не удовлетворяет неравенству (3) _{Рис. 13}при любом a₁∈ (1; 2) (рис. 13).

Для этого рассмотрим значеx + 2 3a₁

ние а = а₁, такое, что верно равенство ¹= , тогда

a₁= x1 + 2 и 2 < 3a1 < x1. Так как 1 1 и

2(x₁− 1) 2a₁− 1 2 2(x₁−1)

2 < x₁< 3, то ¹+ ³<a₁< ¹+ ³, т. е. а₁∈ (1; 2).

2 4 2 2

Итак, для числа х₁нашлось такое значение а = a₁∈ (1; 2), что число х₁не удовлетворяет неравенству (3) при этом значении а.

Следовательно, неравенству (3) при любом значении параметра a ∈ (1; 2) удовлетворяют лишь значения x, такие, что −1 < х ≤ 2. Следовательно, искомые значения х есть х, удовлетворяющие неравенствам −1 < х ≤ 2.

2.9. Рациональные неравенства

В данном пункте применение метода интервалов для решения неравенств расширяется на случай, когда левая часть неравенства — алгебраическая дробь. Здесь рассматриваются лишь строгие неравенства, поэтому процедура решения неравенства практически повторяет процедуру, описанную в предыдущем пункте.

Дело в том, что знаки выражений А (x) ⋅ В (x) и ^{A x}^{( )}

B x( )

совпадают для всех тех х, для которых В (x) — ненулевой

многочлен, поэтому неравенства А (x) ⋅ В (x) > 0 и ^{A x}^{( )}> 0

B x( )

(или A (x) ⋅ B (x) < 0 и ^{A x}^{( )}< 0) равносильны. Это обстоя-

B x( )

A x( ) тельство позволяет заменять решение неравенства > 0

B x( )

A x( )

(или < 0) решением неравенства А (x) ⋅ В (x) > 0 (или

B x( )

А (x) ⋅ В (x) < 0).

Все учащиеся должны научиться решать неравенства, левая часть которых является алгебраической дробью, числитель и знаменатель которой содержат произведения различных двучленов. И здесь более сложный случай применения метода интервалов связан с наличием одинаковых двучленов.

Решения и комментарии

2.77. б) Решите неравенство ^x²⁻⁹> 0.

(x + 3)(x − 1) Решение. Разложив числитель алгебраической дроби в левой части исходного неравенства на множители, перепишем неравенство в виде

> 0. (1)

Решим неравенство

(x − 3)(x − 1)(х + 3)²> 0, (2)

равносильное неравенству (1).

Применяя к неравенству (2) общий метод интервалов (рис. 14),

получим, что множество всех ре-

Рис. 14

шений неравенства (2), а значит, и равносильного ему неравенства (1) есть объединение интервалов (−∞; −3), (−3; 1), (3; +∞).

Следовательно, все решения исходного неравенства составляют множество (−∞; −3) ∪ (−3; 1) ∪ (3; +∞).

Замечание. При решении неравенства (1) учащиеся иногда сокращают дробь, заменяя неравенство (1) неравносильx − 3

ным ему неравенством > 0, имеющим решением число x − 1

−3, которого не имеет неравенство (1), т. е. приобретают лишнее решение −3. Чтобы избегать таких ошибок, учащиеся не должны сокращать дроби при решении неравенств.

2.79. а) Решите неравенство x²− 6x ⁺2 ¹⁷<0. x − 6 x + 8

Решение. Обозначив t = х²− 6х + 8, перепишем исходное неравенство в виде

t²− 8t + 17

<0. (3)

Так как t²− 8t + 17 = (t − 4)²+ 1 > 0 для каждого t, то все решения неравенства (3) есть все t < 0, следовательно, множество решений исходного неравенства есть множество решений неравенства х²− 6х + 8 < 0, т. е. множество (2; 4).

2.10. Нестрогие неравенства

Особенность изложения материала о нестрогих неравенствах заключается в том, что они рассматриваются после изучения способов решения строгих неравенств. Для решения нестрогого неравенства требуется решить уравнение, затем строгое неравенство и объединить все найденные решения (см. решение неравенства 2.91).

Решения и комментарии

2.91. а) Решите неравенство x2 −24x + 3 ≥ 0. x − 9

Решение. Разложив числитель и знаменатель алгебраической дроби в левой части исходного неравенства на множители, перепишем его в виде

. (1)

Сначала решим уравнение

= 0. (2)

Оно имеет единственный корень х₁= 1. Теперь решим строгое неравенство

> 0. (3)

Оно равносильно неравенству

(x + 3) (x − 1) (x − 3)²> 0. (4)

Применяя к неравенству (4) общий метод интервалов

(рис. 15), получим, что множество всех решений неравенства (4), а значит, и равносильного ему неравенства (3) есть объединение интервалов (−∞; −3), (1; 3), (3; +∞).

Объединив решения уравнения (2) и неравенства (3) (рис. 16), получим множество Рис. 16 решений исходного неравенства: (−∞; −3) ∪ [1; 3) ∪ (3; +∞).

Следовательно, все решения исходного неравенства составляют множество (−∞; −3) ∪ [1; 3) ∪ (3; +∞).

Замечание. Описанный выше переход от неравенства (3) к неравенству (4) можно применять только для строгих неравенств. Иногда учащиеся по ошибке переносят такой способ рассуждения и на нестрогие неравенства. Например, они могут заменить неравенство (1), имеющее множество решений

(−∞; −3) ∪ [1; 3) ∪ (3; +∞) (см. рис. 16), неравенством (х + 3) × × (х − 1) (x − 3)²≥ 0, которое имеет множество решений (−∞; −3] ∪

∪ [1; +∞) (рис. 17), т. е. приобре-

Рис. 17 сти два лишних решения: −3 и 3. Промежуточный контроль. С—12, С—13.

Задания из этих самостоятельных работ могут использоваться выборочно как для выполнения самостоятельной работы на оценку, так и для домашних самостоятельных работ. К заданиям на решение систем неравенств можно вернуться при изучении следующего пункта учебника.

2.11. Системы рациональных неравенств

В данном пункте напоминается, что называют решением системы рациональных неравенств и что значит решить систему рациональных неравенств. Далее разобраны примеры решения систем, содержащих строгие и нестрогие неравенства.

В учебнике имеются также пример 4 на решение уравнения и пример 5 на решение неравенства, приводящие к необходимости решить систему рациональных неравенств. В них рассмотрены частные случаи решений уравнения и неравенства, для которых применен метод рассуждений с числовыми значениями. Суть его заключается в том, что мы предполагаем, что уравнение (неравенство) имеет решение, обозначаем его x₀и составляем верное числовое равенство (неравенство).

В первом случае используется тот факт, что числовое равенство | и | + | v | = и + v справедливо тогда и только тогда, когда одновременно выполняются два условия: u ≥ 0 и v ≥ 0, а во втором — что числовое выражение u + v определено тогда и только тогда, когда одновременно выполняются два условия: и ≥ 0 и v ≥ 0, что и приводит оба раза к необходимости решать систему.

В первом случае все решения системы и есть решения исходного уравнения, а во втором случае только если система имеет конечное число решений, то можно проверить, удовлетворяют они исходному неравенству или нет. И только тогда можно найти решение исходного неравенства. В других случаях этот метод решения не даст результата.

Решения и комментарии

2.101—2.103. С идеей решения подобных заданий можно познакомиться при разборе решений примеров 1 и 2 из п. 15 дидактических материалов.

Промежуточный контроль. С—14, С—15.

Контрольная работа К—1.

§ 3. Корень степени п

3.1. Понятие функции и ее графика

В данном пункте напоминаются определения функции и ее графика. Поскольку функция определена как некоторый закон, то, например, функция у = х²может быть задана формулами у = t², и = v², ..., x = у²(здесь закон выражает правило: для получения значения функции надо значение аргумента возвести в квадрат, поэтому то, какими буквами обозначены функция и аргумент, не важно). Эта особенность трактовки понятия функции поможет в 11 классе легче усвоить понятие обратной функции.

Решения и комментарии

3.4—3.7. Здесь требуется построить графики некоторых функций с применением известных преобразований графиков: переносы, использование модулей. Делать выводы для общего случая, например о получении графика функции у = f (x − а) из графика функции у = f (x), необязательно. Этому будут посвящены специальные пункты учебника для 11 класса.

3.7. Постройте график функции: а) y ₌^x²⁻⁴; б) y ₌^{| x}⁻^1|.

x − 2 x − 1

Решение. а) Область определения функции y есть

все х ≠ 2, функцию можно задать так: у = х + 2, х ≠ 2. Ее график — прямая у = х + 2 с «выколотой» точкой (2; 4) (рис. 18).

б) Область определения функции y = ^{| x}⁻^1|есть все х ≠ 1, x − 1

функцию можно задать так: y = ⎧⎨⎩¹−^,1,^еслиесли^x_x>¹<1. Ее график —

пара лучей без начальной точки: y = 1, х > 1 и y = −1, x < 1

(рис. 19).

Рис. 18 Рис. 19

3.2. Функция y хⁿ

В данном пункте рассматриваются функции вида у = хⁿдля п ∈ N, n ≥ 2, затем формулируются и обосновываются свойства функции у = хⁿсначала для неотрицательных, затем для любых значений аргумента. Лишь после этого с опорой на изученные свойства строятся графики функций изучаемого вида. Главное назначение изучаемого материала заключается в подготовке к введению понятия корня степени п, а для этого нужно обратить особое внимание на непрерывность графика функции, которая будет использоваться при доказательстве существования корня степени п, указать на различия графиков для n = 2k и n = 2k + 1, k ∈ N. Решения и комментарии

3.17. а) Выясните, какой из графиков двух функций: у = х или у = х²— расположен выше другого на интервале (0; 1).

Решение. Для любых х ∈ (0; 1) из справедливости неравенства 1 > х следует справедливость неравенства х > х², поэтому для любых х ∈ (0; 1) график функции у = х расположен выше графика функции у = х².

3.19. а) Выясните, какой из графиков трех функций: у = х, у = x³, у = x⁵— расположен выше, а какой ниже других на интервале (−1; 0).

Решение. Умножим двойное неравенство −1 < х < 0 сначала на положительное число −х, а потом на положительное число х², получим два верных двойных неравенства x < −х²< 0 и −x²< x³< 0, из справедливости которых следует, что если −1 < х < 0, то х < x³. Аналогично показывается, что x³< x⁵. Это означает, что на промежутке (−1; 0) выше других расположен график функции у = x⁵, a ниже других — график функции у = х.

3.3. Понятие корня степени n

Обратим внимание, что в пункте 3.3 дано лишь словесное описание тех чисел, которые называют корнями степени п из неотрицательного числа. Здесь пока нет обозначений для этих корней, пояснения даются на примерах.

3.4. Корни четной и нечетной степеней

В пункте доказывается, что существует, и притом единственный, корень нечетной степени из любого действительного числа; что существуют два и только два корня четной степени из любого положительного числа; что существует, и притом единственный, корень четной степени из нуля, равный нулю; что не существует корня четной степени из отрицательного числа. Для доказательства существования корней используется графический метод и непрерывность функций у = х^п. Здесь вводятся обозначения ²ⁿa, п ∈ N, для а a, n ∈ N, для а ∈ R.

3.5. Арифметический корень

В данном пункте дается определение арифметического корня степени п из неотрицательного числа (это неотрицательный корень из неотрицательного числа), доказываются первые свойства арифметических корней:

(ⁿa)ⁿ= a, ⁿaⁿ= a, . (1)

Подчеркнем, что здесь а и b неотрицательны, а в последнем равенстве b > 0.

Следует обратить внимание учащихся на замечание в конце пункта. Оно говорит о том, что если п = 2т + 1 (т ∈ N) — нечетное число, то свойства (1) справедливы и для любых чисел а и b (в последнем равенстве b ≠ 0).

Для корней нечетной степени часто применяют свойство 2m +12m +1 −a = − a, a ∈ R.

Традиционно сложными для учащихся являются преобразования выражений, содержащих корни степени п, — освобождение от иррациональности в знаменателе дроби, вынесение множителя за знак корня и внесение множителя под знак корня, особенно если выражение содержит буквы. Эти преобразования разобраны в п. 16 дидактических материалов.

Решения и комментарии

3.63. Упростите выражение:

в) 30⋅3 ¹+ ⁷⋅3 ²+5⋅³144; ж) ⁴81⋅(4 − 17)⁴.

12 2 3

Решение. в) 30⋅³¹+ ⁷⋅³²+5⋅³144 = 30⋅³¹+ ⁷⋅³⁸+

12 2 3 12 2 12

+5⋅³12³⋅ ¹= 30⋅³¹+7 ⋅³¹+60⋅³¹= 97 ⋅³¹.

12 12 12 12 12

Здесь важно было заметить, что второй и третий корни

можно выразить через 3 ¹. Ответ можно преобразовать,

избавившись от иррациональности в знаменателе:

97 ⋅3 1 = 97 ⋅3 183 = 976 ⋅3 18 =16 61 ⋅3 18.

12 6

ж) ⁴81⋅(4 − 17)⁴= ⁴81 ⋅⁴(4 − 17)⁴= 3⋅⁴( 17 − 4)⁴= = 3( 17 − 4).

Здесь важно подчеркнуть, что свойство ²ⁿa²ⁿ= а, n ∈ N, справедливо лишь для неотрицательных чисел, поэтому потребовалось преобразование под знаком корня:

(4 − 17)⁴= ( 17 − 4)⁴.

3.6. Свойства корней степени n

В пункте доказаны новые свойства арифметических корней степени п (теоремы 1—3), приведены примеры их применения. Этот теоретический материал должен быть хорошо усвоен, так как с опорой на него будут вводиться понятие степени с рациональным показателем и доказываться соответствующие свойства.

Например, пользуясь свойством ²ⁿa²ⁿ= | а |, a ∈ R, n ∈ N, и определением модуля для отрицательного числа, решение примера 3.63ж можно записать иначе:

⁴81⋅(4 − 17)⁴= ⁴81 ⋅⁴(4 − 17)⁴= 3 4| − 17 | = 3 ( 17 − 4). Надо обратить внимание учащихся на свойства 2n a2n = |a| и 2n +1 a2n +1 = a, a ∈ R, n ∈ N.

В дальнейшем они будут часто использоваться.

Решения и комментарии

3.79. Упростите числовое выражение:

г) 2⁴4 4; д) 2³2 :³2 2; е) ³32⁴4 ⋅ 2⁴4³4.

Решение. г) 2⁴4 4 = 2⁴8 = ⁴128 = ⁸128.

д) 2³2 :³2 2 = ³8 2⋅ :³4 2⋅ = ⁶16:⁶8 = ⁶16 8: = ⁶2.

е) ³32⁴4 ⋅ 2⁴4³4 = 2³4 2 ⋅ 2^4
34⁴= 2³32 ⋅ 2¹²4⁴=

= 2⁶32 ⋅ 2³4 = 2⁶32 ⋅ ³32 = 2⁶32 ⋅⁶32 = 2(⁶32)²= 2³32 = = 2³8 4⋅ = 2 2⋅ ³4 = 4³4.

Промежуточный контроль. С—16.

3.7. Функция y = ⁿx, x 0 3.8. Функция y = ⁿx

В пункте 3.7 изучаются свойства функции y = ⁿx только для x ≥ 0, а в пункте 3.8 — для любых х. Отметим особенность доказательства непрерывности функции y = ⁿx (х ≥ 0).

Так как графики функций y x 0) и х = у^п

(у ≥ 0, х ≥ 0) совпадают, то непрерывность функции y = ⁿx

(х ≥ 0) следует из уже доказанной ранее непрерывности функции х = у^п(у ≥ 0), т. е. доказательство непрерывности функции y = ⁿx, по сути дела, опирается на непрерывность обратной функции x = у^п, но так как понятие обратной функции еще не вводилось (это материал 11 класса), то в учебнике такая терминология не используется.

Решения и комментарии

3.85. Известно, что: а) ³a >1; б) ³a < 1. Верно ли, что а > 1; а > 0?

Решение. а) Так как ³a > 1, т. е. ³a > ³1, то из возрастания функции y = ³x следует, что а > 1, а так как 1 > 0, то справедливы оба неравенства: а > 1 и а > 0.

б) Так как ³a < 1, т. е. ³a < ³1, то из возрастания функции y = ³x следует, что а < 1, т. е. неравенство а > 1 неверно. Из неравенства ³a < 1 не следует, что а > 0, хотя в данном пункте мы рассматриваем функцию y = ³x только для х ≥ 0. Например, для а = −1 неравенство ³a < 1 верно, а неравенство а > 0 неверно. Следовательно, неравенство а > 0 неверно.

Замечание. Покажем, как можно доказать, что из неравенства ³a >1 и возрастания функции y = ³x следует, что а > 1.

По определению возрастающей функции из справедливости неравенства а > 1 следует, что ³a > 1, а нам надо доказать обратное: что из справедливости неравенства ³a >1 следует, что а > 1. Докажем это методом от противного.

Пусть ³a >1. Предположим, что а < 1, тогда из возрастания функции y = ³x и из справедливости неравенства а < 1 следует, что ³a <1, а это противоречит условию ³a >1. Значит, предположение, что а < 1, неверно.

Пусть ³a >1. Предположим, что а = 1, тогда ³a =1, а это противоречит условию ³a >1. Значит, предположение, что а = 1, неверно.

Для чисел а и 1 выполняется, и притом только одно, из соотношений а > 1, а < 1 и а = 1 (свойство порядка действительных чисел, см. п. 1.2), поэтому если неверно, что а < 1 и а = 1, то а > 1, что и требовалось доказать.

Приведенные здесь рассуждения учащиеся не должны воспроизводить в обязательном порядке. Но будет полезно для них узнать о применении рассуждения от противного в непривычной ситуации, когда возможны не два взаимно исключающие друг друга случая (параллельны и не параллельны и др.), а три случая (а > 1, а < 1 и а = 1).

3.93. Постройте график функции:

а) y = ³x ; б) y = ³−x; в) y = ³|x|;

г) y = ³x − 2; д) y = ³x − 2; е) y = ³2 − x;

ж) y = |³x − 2|; з) y = ³2 − |x|; и) y = |³2 − |x| −1|.

Здесь на конкретных примерах повторяются известные преобразования графиков: переносы, использование модулей. Графики функций изображены на рисунке 20, а—и.

Промежуточный контроль. С—17.

Контрольная работа № 2.

3.9*. Корень степени n из натурального числа

В данном пункте имеется утверждение: «Арифметический корень степени п (п ≥ 2) из натурального числа может быть или натуральным числом, или иррациональным числом». В учебнике сказано, что доказательство этого утверждения при любом п ≥ 2 аналогично доказательству для п = 2.

Приведем доказательство иррациональности числа ³2 (задание 3.102а).

Предположим, что число ³2 — рациональное, т. е. предp положим, что существует несократимая дробь , такая, что q

справедливо равенство ³2 ⁼^p, где p ∈ N, q ∈ N. Тогда спраq

ведливо равенство 2q₃= _p3_{. (1)}

Так как левая часть равенства (1) делится на 2, то и правая часть равенства, т. е. p³, делится на 2.

Число р при делении на 2 может иметь два остатка: 1 или 0.

В первом случае р = 2п + 1, где п = 0,1,2, ..., тогда равенство 2q³= 8n³+ 12n²+ 6n + 1 не выполняется ни при каком натуральном q, так как левая его часть делится на 2, а правая — нет. Значит, число р при делении на 2 не может иметь остаток 1.

Во втором случае р = 2п, где п ∈ N, тогда 4n³= q³. Аналогично показывается, что число q при делении на 2 не может иметь остаток 1, и оно делится на 2.

Рис. 20

Следовательно, каждое из чисел р и q делится на 2. Получилось противоречие с предположением, что число

³2 = ^p, где дробь ^pнесократимая. Следовательно, предпоq q

ложение неверно, а верно утверждение, что число ³2 — иррациональное.

Заметим, что доказательство иррациональности числа 3

29 тем же способом окажется громоздким, так как потребуется рассмотреть не 2 случая, как в предыдущем задании, а 29. Поэтому приведем другой способ доказательства иррациональности корней степени п из натуральных чисел, не являющихся n-й степенью натурального числа.

Теорема. Если натуральное число m не является n-й степенью (п ∈ N, п ≥ 2) какого-либо натурального числа, то

n m — иррациональное число.

Доказательство. Предположим противное, т. е. предположим, что ⁿm — число рациональное. Это означает, что

p существует несократимая дробь (p ∈ N, q ∈ N), такая, что

n m = ^p. Но тогда справедливо равенство

qⁿm = pⁿ. (2)

Левая часть равенства (2) делится на q, поэтому и правая часть делится на q, т. е. число рⁿделится на q.

Если р = 1, то рⁿ= 1 и рⁿделится на q, только если q = 1, но тогда из равенства (2) следует, что m = 1, что противоречит условию теоремы.

Если р > 1, то по основной теореме арифметики число р разлагается на простые множители:

p = p1α1 p2α2 ... pkαk , (3)

где p₁, p₂, ..., p_k— различные простые числа, α₁, α₂, ... ..., α_k— натуральные числа.

Если число q имеет делитель d и d — простое число, то p

так как дробь несократимая, то среди чисел ^р₁, ^р₂, ..., ^p_kq

нет числа d. Из равенства (3) следует равенство

pn = p1nα1 p2nα2 ... pknαk . (4)

По основной теореме арифметики разложение каждого натурального числа на простые множители единственно. Поэтому правая часть равенства (4) есть (единственное) разложение числа рⁿна простые множители. Так как среди чисел р₁, р₂, ..., p_kнет числа d, то рⁿне делится на d, а значит, не делится и на q, имеющие простой делитель d.

Отсюда следует, что так как pⁿделится на q, то число q может быть только равно 1. Тогда из равенства (2) следует, что т = рⁿ, а это противоречит условию, что m не является n-й степенью какого-либо натурального числа.

Полученное противоречие означает, что сделанное предположение неверно, т. е. ⁿm — иррациональное число.

§ 4. Степень положительного числа

4.1. Степень с рациональным показателем

В данном пункте вводится понятие степени положительp ного числа а с рациональным показателем , где р — целое q

число, q — натуральное число, q ≥ 2, и с помощью свойств корня q-й степени доказываются первые свойства степени с рациональным показателем:

p ⎛ 1 ⎞ p p pk pq

1) a ^q= ⎜a ^q⎟ , 2) a ^q= a ^qk(k ∈ N), 3) a ^p= a ^q.

⎝ ⎠

Замечание. Подчеркнем, что рациональная степень числа а определена только для положительного числа а. Однако если рациональное число r положительно, то, применив к нему определение степени с рациональным показателем,

получим, что 0^r= 0^q= ^q0^p= ^q0 = 0.

Напомним, что записи 0⁰и 0^−r(r > 0) не имеют смысла. Также не имеет смысла запись а^r, где а < 0 и r — рациональное число, не являющееся целым числом.

Рассмотрим задание, при выполнении которого используется это замечание.

Пример. Для каждого значения параметра а решим уравнение

(ax) = − ³a. (1)

Решение. 1) Если а = 0, то для любого x ∈ R имеем:

(0 )x = 0 = 0, так как > 0, и ³0 = 0 по определению корня третьей степени. Следовательно, любое x ∈ R является решением уравнения (1) в этом случае.

2) Если а > 0, то − ³a <0. Для любого х < 0 имеем ах < 0.

Поэтому запись (ax) не имеет смысла, т. е. среди х < 0 нет решений уравнения (1). Для х = 0 имеем ах = 0 и , т. е. x = 0 не является решением уравнения (1). Для любого х > 0 по определению степени с рациональным показателем , и так как − ³a <0, то ни для одного х > 0 уравнение (1) не превращается в верное равенство (слева в нем положительное число, а справа — отрицательное). Следовательно, уравнение (1) не имеет решений в этом случае. 3) Если а < 0, то − ³a = ³−a = ³|a| > 0.

Для любого x > 0 имеем ах < 0, и поэтому запись (ax) не имеет смысла, т. е. среди х > 0 нет решений уравнения (1).

Для х = 0 имеем ах , т. е. x = 0 не является решением уравнения (1) в этом случае.

Для любого x < 0 имеем ах = (−а) (−х) = | a | | x | > 0. Поэтому имеет смысл запись (ax) , и так как в этом случае

(ax) = (|a||x|) = ³|a||x| = ³|a| ³|x|, то уравнение (1) перепишется в виде

³|a| ³|x| = ³|a|. (2)

Так как ³|a| ≠ 0, то уравнение (2) равносильно уравнению ³|x| =1, которое (учитывая, что х < 0) имеет единственный корень −1.

Следовательно, уравнение (1) не имеет корней для каждого а > 0; любое число х является его корнем для а = 0; имеет единственный корень −1 для каждого а < 0. 4.2. Свойства степени с рациональным показателем

В данном пункте доказаны новые теоремы о свойствах степени с рациональным показателем, из которых следует, что свойства степеней, известные ранее для целых показателей, справедливы и для рациональных показателей.

Решения и комментарии

4.22. б) Упростите выражение

B = ⎜⎝⎛a1 5, 4− 8 − a +a20 5,a0 5−, 2+ 4⎞⎟⎠ ⋅ a2a−−816a0 5, − a40 5,a0 5+, 4.

Решение.

4 a0 5, − 2 4 (a0 5, − 2)2

¹⁾a1 5, − 8 ⁻a + 2a0 5, + 4 ⁼a1 5, − 8 ⁻(a0 5, − 2)(a + 2a0,5 + 4) =

= a1 5, 4− 8 − a −a41 5,a0 5−, 8+ 4 = −aa1 5+, 4−a80 5, ;

²⁾−aa+ 4a0 5, ^⋅a2 − 8a0 5, ⁼−a1 5,0 5,−(a80 5),⋅ (a−0 54, ) a−0 54, )((aa1 50 5,, −+84)) a −a ;

1 5, − 8 a − 16 (a = _{0 5,}+ ₄

³⁾B = 0 5,−a+ 4 − a40 5,a0 5+, 4 = − a0 5,a(0 5a, 0 5,+ 4+ 4) = − a0 5, .

Подчеркнем, что все преобразования выражения B здесь проведены для тех а, для каждого из которых все рассматриваемые выражения имеют смысл, т. е. для любых а, таких, что а ≥ 0, а ≠ 4, а ≠ 16.

4.23. а) Может ли значение выражения

x − x −1,5 0

A = _{1 2}+ 0,25 − 9(x − 2)

−

x3 − x 3

равняться 1?

Решение. Сначала преобразуем выражение А, полагая, что x > 0, x ≠ 1, x ≠ 2, так как в противном случае это выражение не определено:

1 −3

A = xx x−323((x−−11)) + ⎜⎝⎛ 14⎟⎞⎠ 2 − 9 1⋅ = x +8 − 9 = x −1.

Теперь выясним, существует ли такое х, удовлетворяющее условиям х > 0, х ≠ 1, x ≠ 2, при котором

x − 1 = 1. (1)

Уравнение (1) имеет единственный корень x = 2. Это означает, что не существует такого x, удовлетворяющего условиям x > 0, x ≠ 1, x ≠ 2, при котором верно равенство (1). Следовательно, выражение А не может равняться 1.

Промежуточный контроль. С—18.

4.3. Понятие предела последовательности

В данном пункте сначала вводится понятие бесконечно малой (последовательности или переменной), при этом на базовом уровне не формализуется термин «стремиться», достаточно научить школьников из предложенных переменных правильно находить бесконечно малые. Формальное определение бесконечно малой на языке «ε − N» в учебнике имеется, вводится также понятие бесконечно большой. Они предназначены для углубленного изучения математики. Понятие предела последовательности формируется с помощью понятия бесконечно малой.

Обратим внимание на то, что некоторым учащимся задания 4.25 и 4.29 могут показаться сложными, так как они не умеют делить многочлен на одночлен, двучлен. Надо посоветовать им представлять данные дроби в виде суммы дробей.

В дидактических материалах (п. 19) разобран ряд примеров на понятие предела последовательности.

Решения и комментарии

4.25. Представьте переменную α_nв виде суммы постоянной и бесконечно малой, если:

а) α n = n + 1; в) α n = n2 +24n. n n

Решение. а) α _n= ⁿ⁺¹= ⁿ+ ¹=1 + ¹; n n n n

в) α n = n2 +24n = n22 + 4n2 =1 + 4. n n n n

1 4

Здесь и — бесконечно малые. n n

Эти преобразования необходимо освоить, чтобы в аналогичных случаях находить пределы последовательностей. 4.29. д) Найдите предел переменной, представив ее в n + 2

виде суммы постоянной и бесконечно малой: lim.

n→ +∞ n + 1

Решение. nlim→ +∞ nn++21 =nlim→ +∞⎛⎜n ++ 11 + n 1+ 1⎠⎞⎟ =nlim→ +∞⎜⎝⎛1 + n 1+ 1⎟⎞⎠ = 1, ⎝n

так как выражение является суммой числа 1 и бес-

1 конечно малой .

n + 1

4.30. Для заданного положительного ε укажите такое число N, что для переменной а_пдля всех натуральных п > N выполняется неравенство |α_n| < ε, если:

а) α _n= ¹; б) α _n= ². n n

Решение. При выполнении этого задания достаточно ограничиться подбором числа N для выбранного числа ε.

а) Если ε = 0,1, то при п > 10 справедливо неравенство |α_n| < ε, т. е. N = 10; если ε = 0,01, то при п > 100 справедливо неравенство |α_n| < ε, т. е. N = 100. Для любого ε > 0 при n > справедливо неравенство |α_n| < ε, т. е. N = .

б) Если ε = 0,1, то при п > 20 справедливо неравенство |α_n| < ε, т. е. N = 20; если ε = 0,01, то при п > 200 справедливо неравенство |α_n| < ε, т. е. N = 200. Для любого ε > 0 при n > справедливо неравенство |α_n| < ε, т. е. N = .

В каждом из рассмотренных заданий учащиеся могут привести еще несколько примеров, главное назначение которых — показать, что для любого ε > 0 в данном примере можно подобрать такое число N, что при всех п > N справедливо неравенство |α_n| < ε.

4.31. Используя определение бесконечно малой величины (через ε и N), докажите, что переменная α_n— бесконечно малая величина, если:

б) α n = 2000 ; в) α n = 2n . n + 10 n + 1

Решение. б) Пусть задано число ε > 0. Найдем все такие п, для которых справедливо неравенство | α_n| < ε, т. е. справедливо неравенство

2000

<ε. (1) n + 10

Так как п > 0, то неравенство (1) перепишем в виде

2000

<ε. (2) n + 10

Так как п > 0 и ε > 0, то неравенство (2) равносильно неравенству

n > −10.

Таким образом, неравенство (1) справедливо тогда и только тогда, когда n > −10. Если в качестве числа N возьмем −10 (для ε < 200), то для любого выбранного ε > 0 из неравенства п > N следует неравенство |α_n| < ε, а по определению это означает, что α_n— бесконечно малая.

Здесь полезно выбрать несколько значений ε, чтобы пояснить смысл сказанного.

Если ε = 0,2, то при n > −10 = 10 000 − 10 = 9990

справедливо неравенство |α_n| < ε, т. е. N = 9990;

если ε = 0,1, то при n > −10 = 20 000 − 10 = 19 990

справедливо неравенство |α_n| < ε, т. е. N = 19 990; если ε = 0,01, то при n > −10 = 200 000 − 10 = 199 990

справедливо неравенство |α_n| < ε, т. е. N = 199 990.

Здесь учащихся нужно подвести к выводу: если в качестве ε выбрать сколь угодно малое положительное число, то по формуле N = −10 всегда найдется такое число N,

что из неравенства п > N следует неравенство |α_n| < ε.

в) Это задание сложнее предыдущего. Здесь неравенство |α_n| < ε приводит к неравенству εn²− п + ε > 0, решая которое в предположении, что 0 < ε < 0,5 и n ∈ N, получим

1 − 1 − 4ε²

0 < n <и n > . Отсюда следует, что если в

2ε

качестве числа N взять , то для любого 0 < ε < 0,5

2ε

из неравенства п > N будет следовать неравенство |α_n| < ε.

В качестве примера удобно взять ε = 0,4, тогда N = 2; если взять ε = 0,3, то N = 3; если же взять ε = 0,1, то n > 9,8..., т. е. N = 9.

4.32. Для заданного числа М > 0 укажите такое число N, что для всех натуральных п > N выполняется неравенство | x_n| > М, если:

в) x_n= ⁿ; г) x_n= n²; д) x_n= −3n; е) x_n= ⁿ².

100 2000

Решение. При решении этого задания достаточно ограничиться подбором числа N для выбранного числа М.

в) Если М = 10, то при п > 1000 справедливо неравенство | x_n| > М, т. е. N = 1000; если М = 200, то при п > 20 000 справедливо неравенство | x_n| > M, т. е. N = 20 000. Для любого М > 0 при n > 100М справедливо неравенство | x_n| > М, т. е. N = 100M.

г) Если М = 400, то при п > 20 справедливо неравенство | x_n| > М, т. е. N = 20; если М = 2500, то при п > 50 справедливо неравенство | х_n| > М, т. е. N = 50. Для любого М > 0 при n > M справедливо неравенство | x_n| > М, т. е.

N = M.

д) Если М = 100, то при п > 33 справедливо неравенство | x_n| > М, т. е. N = 33; если М = 600, то при п > 200 справедливо неравенство | x_n| > М, т. е. N = 200. Для любого

М > 0 при n ^>^Mсправедливо неравенство | x_n| > М, т. е.

N = M.

е) Если М = 5, то при п > 100 справедливо неравенство | х_n| > М, т. е. N = 100; если М = 20, то при п > 200 справедливо неравенство | x_n| > М, т. е. N = 200. Для любого М > 0 при n > 2000M справедливо неравенство | x_n| > М, т. е. N = 2000M.

В каждом из рассмотренных заданий учащиеся могут привести еще несколько примеров, главное назначение которых — показать, что для любого М > 0 в данном примере можно подобрать такое число N, что при всех п > N справедливо неравенство | x_n| > М.

4.33. Используя определение бесконечно большой величины (через М и N), докажите, что переменная х_п— бесконечно большая величина, если:

в) xn = n + 5; е) xn = n2 − 9.

3 n

Доказательство. в) Пусть дано число М > 0. Найдем все такие n, для которых справедливо неравенство | x_n| > М, т. е. справедливо неравенство

ⁿ⁺⁵> M. (3)

Так как п > 0, то неравенство (3) перепишем в виде n + 5

> M. (4)

Неравенство (4) равносильно неравенству n > 3М − 5.

Таким образом, неравенство (3) справедливо тогда и только тогда, когда п > 3М − 5. Если в качестве числа N возьмем наибольшее из чисел 0 и 3М − 5, то для любого выбранного М > 0 из неравенства п > N следует неравенство | х_n| > М, а по определению это означает, что х_n— бесконечно большая.

Здесь полезно выбрать несколько значений М, чтобы пояснить смысл сказанного.

Если М = 1, то при п > 0 справедливо неравенство

| x_n| > М, т. е. N = 0; если М = 10, то при п > 30 − 5 = 25 справедливо нера-

венство | x_n| > М, т. е. N = 25; если М = 200, то при п > 600 − 5 = 595 справедливо не-

равенство | x_n| > М, т. e. N = 595.

Здесь учащихся нужно подвести к выводу: если в качестве М выбрать сколь угодно большое положительное число, то по формуле N = 3М − 5 мы всегда найдем такое число N, что из неравенства п > N следует неравенство | x_n| > М.

е) Это задание сложнее предыдущего. Здесь неравенство | x_n| > М надо решать, считая, что п > 3 (так как п → +∞). Тогда неравенство | x_n| > М равносильно неравенству п²− Мп − 9 > 0, решая которое получим, что

M + M²+ 36

n >(решения n < не удовлетворя-

ют условию п > 3).

Если в качестве числа N взять , то для лю-

бого М > 0 выполнено условие п > 3 и из неравенства п > N следует неравенство | x_n| > М.

В качестве примера удобно взять М = 8, тогда N = 9; если взять М = 10, то п > 10,8..., т. е. N = 10; если взять М = 20, то n > 20,4..., т. е. N = 20.

4.4*. Свойства пределов

В данном пункте приведены свойства пределов суммы, разности, произведения и частного и свойство вынесения постоянного множителя за знак предела. Доказательства этих свойств не предусмотрены программой и в учебнике не приведены.

Решения и комментарии

4.35. Найдите предел:

2n + 1 n³+ n

в) lim ; ж) lim ; з) . n→ +∞ 5 − 3n n→ +∞ n²− 1 n

Решение.

2n + 1 2 + n1 = nlim→ +∞⎜⎝⎛2 + n1 ⎞⎟⎠;

в) nlim→ +∞ 5 − 3n = nlim→ +∞ 5 − 3 nlim ⎝⎛^⎜_n5 − 3⎞^⎟⎠

_n_→
+∞

ж) nlim n3²+−n1 n→ +∞ ₁n−+ n = +∞;

→ +∞ n = lim 5

2 1

з) lim 2 − n = lim n2 − n = 0 = 0. n→ +∞ 3 − n2 n→ +∞ 3 − 1 −1

4.37. Найдите предел: a) lim (n³−10n²+2n); n→ +∞

в) lim ( n +1 − n). n→ +∞

Решение. a) nlim (→ +∞ n³−10n²+2n) ⁼nlim→ +∞ n³⎝^⎜⎛1 − ¹⁰_n2 ⁺_n²⎞^⎟⎠ =

⁼nlim n³⋅ lim ⎜⎛1 − ¹⁰+ ²^⎞⎟⎠ = +∞;

При вычислении предела в задании 4.37в использовано свойство предела lim x_n= lim x_n, не доказанное в учеб-

n→ +∞ n→ +∞

нике, но доказанное в дидактических материалах (п. 19).

Промежуточный контроль. С—19.

4.5. Бесконечно убывающая геометрическая прогрессия

В данном пункте напоминается формула п-го члена геометрической прогрессии, формула суммы первых п ее членов. Обратим внимание на особенность терминологии: не всякая бесконечно убывающая прогрессия является убывающей прогрессией. Если −1 < q < 0, то прогрессия не является убывающей, например, геометрическая прогрессия

1, − ¹, ¹, − ¹, ... не убывающая, но она является бесконечно

2 4 8

убывающей прогрессией, так как q = − и | q | < 1.

С бесконечно убывающей прогрессией связана известная психологическая трудность, которую учащимся трудно преодолеть: буквой S обозначили сумму бесконечного числа слагаемых а + aq + aq²+ ..., бесконечный процесс сложения завершить невозможно, однако сумма существует и a вычисляется по формуле .

1 − q

Приведем два примера, которые позволят примирить учащихся с мыслью, что бесконечный процесс сложения может иметь конечный результат.

1) Если длину отрезка м выразить десятичной дробью, то получится 0,3333... м, или 0,3 + 0,03 + 0,003 + + 0,0003 + ... м.

2) Если площадь квадрата равна 1 и закрашивают сначала половину квадрата, потом половину незакрашенной части, потом половину оставшейся незакрашенной части квадрата и т. д., то процесс закрашивания бесконечен, но очевидно, что «в пределе» площадь закрашенной части квадрата равна площади квадрата, т. е. равна 1. Это подтверждает и применение формулы суммы бесконечно убывающей прогрессии:

+2 + ¹3 +... ==1 (см. задание 4.38а).

Решения и комментарии

4.40. а) Докажите, что число 0,(3) есть сумма ряда 0,3 + 0,03 + 0,003 + ... .

Решение. Сумма бесконечно убывающей геометрической прогрессии 0,3 + 0,03 + 0,003 + ... равна дроби 0 3, 1

= , а дробь равна бесконечной периодической деся-

1 − 0 1, 3 тичной дроби 0,(3). Таким образом, сумма ряда 0,3 + 0,03 + + 0,003 + ... = 0,(3).

Задачи 4.43 и 4.44 являются задачами для самостоятельных расчетов. Практика показывает, что находится мало десятиклассников, способных самостоятельно наметить план решения таких задач. Чаще всего этот план приходится намечать учителю или решать с учащимися первую задачу в расчете на то, что кто-то из них сможет решить вторую.

4.43. Стороны квадрата (рис. 21, а) разделили на 3 равные части. На каждой средней части во внешнюю область построили новый квадрат и эту среднюю часть удалили. Получилась фигура, изображенная на рисунке 21, б. Затем каждую сторону полученной фигуры разделили на 3 равные части. На каждой средней части построили новый квадрат во внешнюю область и эту среднюю часть удалили. Получилась фигура, изображенная на рисунке 21, в. Тем же способом получили третью фигуру (рис. 21, г) и т. д.

а) Определите площадь S_nфигуры, полученной после

п-го преобразования, если а — сторона исходного квадрата.

б) Определите предел, к которому стремится площадь S_nфигуры при n → +∞.

Дополнительные задания. в) Определите периметр Р_nфигуры, полученной после п-го преобразования, если а — сторона исходного квадрата.

г) Определите предел, к которому стремится периметр Р_пфигуры при п → +∞.

Решение. Обозначим данную фигуру F₀, a F_n— фигуру, полученную после п-го (n ∈ N) преобразования. На рисунке 21, а—г изображены фигуры F₀, F₁, F₂, F₃.

При каждом преобразовании число с_nсторон замкнутой ломаной, ограничивающей фигуру, увеличивается в 5 раз, так как вместо каждого отрезка появляется 5 отрезков. Поэтому с_n= 4 ⋅ 5ⁿ. При этом длина а_потрезков, составляющих границу фигуры, при каждом преобразовании уменьa шается в 3 раза, поэтому a_n⁼n . Тогда периметр фигуры

F_nесть P_n= a_n⋅ c_n⁼3^an ⋅4 5⋅ ⁿ= 4a ^⋅⎜⎛ ⁵^⎟⎠⎞ ⁿ. Очевидно, что ⎝ ₃

Р_n→ +∞ при п → +∞, так как ⁵3 >1 и поэтому ⎛^⎜⎝ ⁵₃^⎟⎠⎞ ⁿнеограниченно возрастает при п → +∞.

Рис. 21

Число k_nновых квадратов, образующихся после n-го преобразования, равно числу сторон фигуры ^F_n₋1, т. е. k_n= ^с_п− 1 = 4 ⋅ 5ⁿ^{− 1}, тогда сумма ^s_nплощадей новых квадратов, полученных после n-го преобразования, равна

2 n− 1 ⎛ a ⎞2 4 2 ⎛ 5 ⎞ n − 1 sn = kn ⋅ (an) = 4 ⋅ 5 ⋅⎜⎝ 3n ⎠⎟ = 9a ⋅⎜⎝ 9⎟⎠ ⋅

Сумма площадей всех новых квадратов, полученных в преобразованиях с 1-го по n-е, есть сумма первых n членов геометрической прогрессии, она равна s1 + s2 + s3 + ... + sn = 94 a2 + 94 a2 ⋅ 59 + 94 a2 ⋅⎜⎛⎝ 59⎠⎞⎟2 + ...

... + 94 a2 ⋅⎛⎝⎜ 5₉⎞⎟⎠ n − 1 ₉4 2 ⎜⎝⎜⎛1 + 59 + ⎝⎜⎛ 95 ⎟⎞⎠2 + ... + ⎛⎝⎜ 95⎞⎠⎟n −1⎠⎟⎟⎞ =

= a

⎛ 5 ⎞ⁿ

= 94 a2 ⋅ 1 − ⎜⎝ 9⎟⎠ = a2 ⋅⎜⎛1 − ⎝⎛⎜ 59⎟⎠⎞ n ⎠⎟⎞⎟ = a2 − a2 ⋅⎜⎝⎛ 59 ⎟⎠⎞ n .

⎜⎝

Тогда площадь S_nфигуры F_nесть S_n= а²+ а²− а²⋅ ⎛⎝^⎜ ₉⁵⎞^⎟⎠ n , она стремится к а²+ а²= 2а²при п → +∞.

2 2 ⎛ 5 ⎞ n 2 ⎛ 5 ⎞ n

Ответ. a) S_n= 2а − а ⋅ ⎜⎝ ₉⎟⎠ ; б) 2а ; в) P_n= 4a ⋅⎝⎜ ₃⎟⎠ ;

г) Р_n→ +∞ при n → +∞.

4.6. Число е

В данном пункте без доказательства приведены теоремы

1 и 2 о пределе ограниченной переменной. В примере 3 рас-

⎛ 1 ⎞ ⁿ

сматривается переменная u_n= ^⎜⎝1 ⁺_n^⎟⎠ , п ∈ N. Утверждает-

ся, что эта переменная имеет предел — некоторое число. Это число принято обозначать буквой е. Число е иррациональное, оно записывается в виде бесконечной непериодической десятичной дроби 2,718281828459045... . Обычно используют приближение числа е, равное 2,7. Для запоминания большего числа знаков обратим внимание на то, что со второго десятичного знака в записи числа е два раза повторяется год рождения Л. Н. Толстого (1828).

Отметим, что Даниилу Бернулли (1700—1782) принад-

⎛ 1 ⎞ ⁿ1 1 1

лежит доказательство равенства ⎜⎝1 + n⎟⎠ =1 + 1! + 2! + 3! +...,

дающего закон для вычисления десятичных знаков числа е с любой точностью.

Для мотивировки рассмотрения переменной и_пможно рассмотреть ситуацию, описанную в задании 4.48. Здесь можно показать, что для числа п − 1 перевложений сумма

⎛ 1 ⎞ ⁿ

на вкладе в конце года увеличится в ⎜⎝1 + n⎟⎠ раз.

Решения и комментарии

4.48. Представим себе, что некоторый банк платит по вкладам 100% годовых независимо от срока хранения

1 1 100% вклада, т. е. за 1 год 100%, за года 50%, за года ,

2 3 3

за года 25% и т. д. Составьте формулу, по которой можно найти число, показывающее, во сколько раз увеличилась вложенная сумма к концу года, если проводилось п − 1 пе1 ревложений суммы на часть года. К чему стремится это n

число при п → +∞?

Решение. Пусть на счет положили а р. из расчета 100% годовых. Тогда через 1 год на счете окажется

a a a р. Сумма увеличится за год в и₁= 2 раза.

Если положить ту же сумму на года из расчета 100% годовых, то за года сумма увеличится на % и составит a + a 100²= a ⋅⎜⎝1 + ₂⎞⎟⎠ р. Если деньги и доход не снимать со счета, то согласно условиям задачи к концу года сумма увеличится еще раз на 100% от суммы a ⋅^⎜⎝⎛1 ⁺₂¹⎞^⎟⎠ р. Тогда через ₂

1 год на счете окажется a ⋅^⎜⎝⎛1 ⁺₂¹⎞^⎟⎠²р. Сумма увеличится за

⎛ 1⎞²

год в u₂= ^⎜⎝1 ⁺₂^⎟⎠ = 2,25 раза.

Если теперь положить ту же сумму на года из расчета

100% годовых и не снимать деньги со счета, то к концу

⎛ 1⎞³

года на счете окажется a ⋅^⎜⎝1 ⁺₃^⎟⎠ р. Сумма увеличится за

⎛ 1⎞³10

год в u₃= ^⎜⎝1 ⁺₃^⎟⎠ = 2 ₂₇≈ 2,37 раза.

Если же положить ту же сумму на часть года из расчеn

та 100% годовых и не снимать деньги со счета, то к концу года на счете окажется a ⋅^⎜⎝⎛1 ⁺_n¹⎞^⎟⎠ ⁿр. Сумма увеличится за

⎛ 1 ⎞ ⁿгод в u_n= ^⎜⎝1 ⁺_n^⎟⎠ раз.

Может сложиться впечатление, что с увеличением частоты перевложений суммы в течение года первоначальная сумма может неограниченно увеличиваться. Это не так. Переменная и_nявляется возрастающей, но ограничена сверху числом 3, т. е. сумма не может увеличиться более чем в 3 раза. При п → +∞ переменная u_nстремится к числу e.

4.7. Понятие степени с иррациональным показателем

Основное содержание этого пункта связано с введением понятия степени с иррациональным показателем. Сначала разъясняется, что понимается под числом 3², затем — что понимается под числом а^α, где а > 0, а ≠ 1, α — иррациональное число. Наконец, делается вывод, что определена любая действительная степень положительного числа.

Более подробно этот вопрос можно разъяснять так. Рассмотрим 5 случаев.

1) Если а > 1, α > 0, то стремящейся к α неубывающей последовательности рациональных чисел ^r₁, ^r₂, ..., ^r_k, ... — десятичных приближений числа α с недостатком, где r₁= [α], соответствует неубывающая последовательность a^r1, a^r2 , ..., a^rk , ... степеней числа а, ограниченная сверху числом a^r1⁺¹. По теореме 1 (п. 4.6) эта последовательность имеет предел. Под числом а^αи понимают этот предел.

2) Если 0 < а < 1, α > 0, то стремящейся к α неубывающей последовательности рациональных чисел r₁, r₂, ..., r_k, ... — десятичных приближений числа α с недостатком, где r₁= [α], соответствует невозрастающая последовательность a^r1, a^r2 , ..., a^rk , ... степеней числа а, ограниченная снизу числом a^r¹⁺¹. По теореме 2 (п. 4.6) эта последовательность имеет предел. Под числом а^αи понимают этот предел.

3) Если а > 1, α < 0, то стремящейся к α невозрастающей последовательности рациональных чисел ^r₁, ^r₂, ..., ^r_k, ... — десятичных приближений числа α с избытком, где r₁= [α], соответствует невозрастающая последовательность a^r1, a^r2 , ..., a^rk , ... степеней числа а, ограниченная снизу числом a^r¹⁻¹. По теореме 2 (п. 4.6) эта последовательность имеет предел. Под числом а^αи понимают этот предел.

4) Если 0 < а < 1, α < 0, то стремящейся к α невозрастающей последовательности рациональных чисел r₁, r₂, ... ..., r_k, ... — десятичных приближений числа α с избытком, где r₁= [α], соответствует неубывающая последовательность a^r1, a^r2 , ..., a^rk , ... степеней числа а, ограниченная сверху числом a^r¹⁻¹. По теореме 1 (п. 4.6) эта последовательность имеет предел. Под числом а^αи понимают этот предел.

5) Если а = 1 и α — иррациональное число, то стремящейся к α последовательности рациональных чисел r₁, r₂, ..., r_k, ... — десятичных приближений числа α соответ-

r r r ствует последовательность чисел 1 ¹, 1 ², ..., 1 ^k, ..., состоящая из одних единиц, так как 1^r= 1 для любого рационального числа r. Эта последовательность имеет предел, равный 1, т. е. 1^α= 1.

Можно доказать, что стремящуюся к α последовательность рациональных чисел ^r₁, ^r₂, ..., ^r_n, ... можно выбрать любым способом (не обязательно так, как в рассмотренных случаях), все равно последовательность a^r1, a^r2 , ..., a^rn , ... будет иметь предел и этот предел не зависит от выбора последовательности r₁, r₂, ..., r_n, ... .

Стоит еще раз отметить, что 0^α= 0 при любом α > 0, а записи 0⁰и 0^−α(α > 0) не имеют смысла.

Без доказательства в учебнике приведены 5 свойств степени с действительным показателем. Некоторые из них будут использоваться при выполнении задания 4.51.

Решения и комментарии

4.49. Между какими двумя соседними натуральными числами заключено число 2 ²?

Так как1 < 2 <2, то 2¹<2 ²<2², т. е. 2 <2 ²<4. Но правое неравенство можно уточнить. Так как 1,4 < 2 <1,5, то 2²<2^1
5,. Так как 2^1,5= 2 2 = 2 8, ... <3, то 2 ²< 3.

Итак, 2 <2²< 3.

4.50. Постройте неубывающую последовательность, пределом которой является число 2^π(π = 3,1415926...).

Ответ. 23, 23,1, 23,14, 23,141, 23,1415, ... .

Дополнительный вопрос. Почему построенная последовательность является неубывающей, а не строго возрастающей?

Ответ. Потому что в каком-то разряде числа π может встретиться цифра 0, тогда два соседних члена последовательности окажутся равными.

4.51. а) Вычислите 2 ³⋅2²^{− 3}.

Решение. Преобразуем произведение, используя свойство 1 степени:

2 3 ⋅22 − 3 = 2 3 + 2 − 3 = 22 = 4.

4.8. Показательная функция

В пункте вводится функция у = а^x, где a > 0, а ≠ 1, х ∈ R, рассматриваются свойства этой функции и ее график. Эти свойства будут использоваться в дальнейшем при доказательстве свойств логарифмической функции, при решении показательных уравнений и неравенств.

Решения и комментарии

4.59. Определите графическим способом, сколько корней имеет уравнение 2^х= х².

При решении этой задачи учащиеся обычно ограничиваются рассмотрением графиков функций в привычных пределах для у ≤ 10 и находят только две точки пересечения графиков. А их три (рис. 22). Поэтому уравнение 2^х= х²имеет три корня, один из которых отрицательный, а два других положительные: х = 2 и x = 4.

Промежуточный контроль.

Контрольная работа № 3.

§ 5. Логарифмы

5.1. Понятие логарифма

В пункте вводится понятие логарифма. Прежде чем давать определение логарифма, можно предложить учащимся устные задания, в которых часто будет звучать оборот «показатель степени, в которую надо возвести ..., чтобы получить ...». Например, «назовите показатель степени, в которую надо возвести 2, чтобы получить 8», «назовите показатель степени, в которую надо возвести 3, чтобы получить 9».

Ответы на несколько таких вопросов надо записать на доске в виде равенств:

2³= 8, 3²= 9, ...

Затем надо сказать, что показатель степени, в которую надо возвести 2, чтобы получить 8, называют логарифмом числа 8 по основанию 2 и обозначают log₂8; показатель степени, в которую надо возвести 3, чтобы получить 9, называют логарифмом числа 9 по основанию 3 и обозначают log₃9 и т. п. По ходу разговора на доске добавляются новые записи:

2³= 8,	log₂8 = 3;
3²= 9,	log₃9 = ...

Следует заметить, что основание логарифма и основание степени в каждой строчке — одно и то же число. Теперь учащиеся будут подготовлены к введению определения логарифма числа b по основанию а.

В учебнике графически обосновывается, что для любого b > 0 и любого а (а > 0, а ≠ 1) существует, и притом единственное, число α, такое, что b = а^α. Его называют логарифмом числа b no основанию а и обозначают log_ab, при этом число а (а > 0, а ≠ 1) называют основанием логарифма. Из определения логарифма следует, что a^loga ^b= b.

Здесь же вводятся обозначения для десятичных и натуральных логарифмов.

Решения и комментарии

5.4. а) Вычислите log₂4.

Решение. Вычисляя log₂4, нужно подобрать показатель степени, в которую надо возвести число 2, чтобы получить 4: так как 2²= 4, то log₂4 = 2.

5.5. Вычислите: а) 2log23; г) 2log23+ log25.

Решение. а) Применяя равенство a^loga ^b= b, имеем:

2log23 = 3.

г) Применяя свойство степени и равенство a^loga ^b= b,

имеем:

2log23+ log25 = 2log23 ⋅ 2log25 = 3 5⋅ =15.

5.9. Вычислите: з) е^{2 ln 5}; л) 10^{2 lg 3}.

Решение. з) е2 ln 5 = (eln 5)2 = 52 = 25;

л) 102 lg 3 = (10lg 3)2 = 32 = 9.

5.2. Свойства логарифмов

В пункте доказываются основные свойства логарифмов (логарифм произведения, дроби, степени), формула перехода логарифмов от одного основания к другому и следствия из нее. Свойство логарифмов log_ab = log_aγ b ^γсформулировано в задании 5.21. В дидактических материалах (п. 20) доказано еще одно свойство логарифмов, выражаемое равенством a^logb ^c= c^logb ^a(a > 0, b > 0, b ≠ 1, c > 0).

Доказательства этих последних свойств не входят в программу обучения на базовом уровне, их может привести учитель, а учащиеся могут применять их при выполнении сложных заданий на преобразование выражений, содержащих логарифмы (см., например, задание 126 из раздела «Задания для повторения»).

Отметим еще одно полезное свойство логарифмов — равенство log_bb^α= α, α ∈ R, которое непосредственно следует из определения логарифма, но можно также считать, что это частный случай свойства логарифмов log_а^b^α= α log_ab (при b = а). Этим свойством часто пользуются при решении логарифмических уравнений (неравенств), заменяя, например, число 3 числом log₂2³.

Решения и комментарии

5.21. Докажите, что для b > 0, a > 0, а ≠ 1 и любого γ

(γ ≠ 0)

log_ab = log_aγ ^b^γ.

Доказательство. Пусть log_аb = с, тогда b = а^cи b^γ= (а^с)^γ= (а^γ)^с, откуда по определению логарифма следует, что c = log_aγ ^b^γ. Но тогда справедливо равенство log_ab = log_aγ b ^γ, что и требовалось доказать.

Пользуясь указанным свойством, вычислим:

а) log52 1252 = loge5 125 = 3; ж) log100 102π = log10 10π = π;

з) log₄2^e= log₂22 = ^e;

и) log₃9^π= log₃9²^π= log₃3⁴^π= 4π.

5.26. а) Вычислите A.

Решение. A.

5.27. а) Вычислите A .

Решение. A = 3log₉43 +2log₄16 = 3log₃23 +22 = 23 +4 =12. 126. (Задания для повторения.)

Здесь сокращены равные множители 2^log5³и 3^log5²(свойство a^logbc= c^logba, приведенное выше).

Промежуточный контроль. С—20.

5.3. Логарифмическая функция

В пункте вводится логарифмическая функция у = log_aх, где а > 0, а ≠ 1, x > 0, рассматриваются свойства этой функции и ее график. Отметим особенность доказательства непрерывности функции у = log_aх. Так как графики функций у = log_ах (х > 0) и х = а^усовпадают, то непрерывность функции y = log_ax следует из уже отмеченной ранее непрерывности функции х = а^у, т. е. доказательство непрерывности функции y = log_aх, по сути дела, опирается на непрерывность обратной функции х = а^у, но так как понятие обратной функции еще не вводилось (это материал 11 класса), то в учебнике такая терминология не используется.

Свойства логарифмической функции будут использоваться в дальнейшем для решения логарифмических уравнений и неравенств.

Решения и комментарии

5.33. Используя свойства логарифмической функции, сравните: a) log₂3 и log₂5; в) log₁3 и log5.

Решение. а) Так как функция у²= log₂xвозрастает на промежутке (0; +∞), то из неравенства 3 < 5 следует неравенство log₂3 < ^log₂5.

в) Так как функция y = log x убывает на промежутке

(0; +∞), то из неравенства 3 < 5 следует неравенство

> .

Дополнительное задание. Сравните числа:

а) log₂3 и log₃5; б) log₃4 и log₄5. Решение. а) Умножим данные числа на 2:

2 log₂3 = log₂9, 2 log₃5 = log₃25

и напишем очевидные неравенства, следующие из возрастания функций у = log₂х и у = log₃х на промежутке (0; +∞):

3 = log₂8 < log₂9 < log₂16 = 4;

2 = log₃9 < log₃25 < log₃27 = 3.

Так как log₂9 > 3, а 3 > log₃25, то log₂9 > log₃25, но тогда log₂3 > log₃5.

б) Умножим данные числа на 4:

4 log₃4 = log₃256 и 4 log₄5 = log₄625

и напишем очевидные неравенства, следующие из возрастания функций у = log₃х и у = log₄х на промежутке (0; +∞):

5 = log₃243 < log₃256 < log₃729 = 6;

4 = log₄256 < log₄625 < log₄1024 = 5.

Так как log₃256 > 5, a 5 > log₄625, то log₃256 > log₄625, но тогда log₃4 > log₄5.

5.4*. Десятичные логарифмы

Десятичные логарифмы уже введены в п. 5.1. Данный пункт посвящен использованию десятичных логарифмов и таблиц логарифмов и антилогарифмов в практических вычислениях. Здесь вводится понятие характеристики и мантиссы десятичного логарифма. Содержание данного пункта имеет скорее общекультурную и историческую направленность, так как в практических вычислениях логарифмы вытеснены калькуляторами.

В качестве исторического экскурса учащимся можно показать выполнение несложных вычислений с использованием таблиц логарифмов и антилогарифмов.

Вычислим приближенно значение выражения

A .

Сначала с помощью таблиц логарифмов вычислим логарифм A: lg A lg lg 3,48 + lg 5,239 − lg 3,24 − lg 4,31 ≈

≈ 0,5416 + 0,7192−0,5105−0,6345=0,1158, т. е. lg A ≈0,1158.

Теперь с помощью таблиц антилогарифмов вычислим A ≈ 10^0,1158≈ 1,305 ≈ 1,31 (результат приближенных вычислений должен содержать не более трех значащих цифр).

Для сравнения вычислим значение выражения А с помощью калькулятора. Получим А ≈ 1,3055856 ≈ 1,31.

5.5*. Степенные функции

В данном пункте рассматриваются степенные функции, т. е. функции вида y = x^β, где β — данное действительное число. Область определения этих функций зависит от того, каков показатель степени β. Но любая из них определена на интервале (0; +∞). Это позволяет для x ∈ (0; +∞) записать, что x^β= (е^ln
x)^β= e^{β ln x}. Применяя это равенство, легко получить свойства степени с любым показателем β ∈ R, например: (x₁⋅ x₂)^β= (x₁)^β⋅ (x₂)^βпри х₁> 0 и х₂> 0.

§ 6. Показательные и логарифмические уравнения и неравенства

6.1. Простейшие показательные уравнения

Простейшими показательными уравнениями названы уравнения вида а^x= b, где а — данное положительное, не равное 1 число, b — данное действительное число. В учебнике приведены три примера решения простейших показательных уравнений и два примера решения показательных уравнений, сводящихся к простейшим уравнениям.

Решения и комментарии

6.7. а) Решите уравнение

3^x= 4. (1)

Решение. Так как 4 > 0, то уравнение (1) имеет единственный корень x₁= log₃4.

6.8. а) Решите уравнение

9 ⋅ 5^x− 25 ⋅ 3^x= 0. (2)

Решение. Уравнение (2) является однородным показательным уравнением первой степени. Так как 3^x≠ 0, то уравнение (2) можно переписать в виде 3x ⎛⎜⎜⎝⎛⎜⎝ 5₃⎞⎟⎠ x − 25₉⎞⎟⎟⎠ = 0, откуда следует, что уравнение (2) равносильно уравнению

⎛ 5 ⎞ ^x25

⎜⎝ ₃^⎟⎠ ⁻₉= 0, (3)

имеющему единственный корень х₁= 2. Следовательно, уравнение (2) имеет единственный корень х₁= 2.

Замечание. Обычно переход от уравнения (2) к равносильному ему уравнению (3) осуществляют делением уравнения (2) на выражение 9 ⋅ 3^x, отличное от нуля при любом x. Именно таким способом будем решать в дальнейшем однородные показательные уравнения (и неравенства).

Дополнительное задание. Решите уравнение:

⎛ 1 ⎞ ^x⎛ 2 ⎞ ^x_x

а) ⎜⎝ 2 + 1⎟⎠ = 3 − 2 2; б) ⎜⎝ 3 + 1⎠⎟ +( 3 −1) = 8 − 4 3. Решение. а) Пользуясь равенствами

2 −1 и 3 − 2 2 = ( 2 −1)²,

перепишем исходное уравнение в виде

( 2 −1)^x= ( 2 −1)². (4)

Так как 2 −1 > 0 и 2 −1 ≠1, то уравнение (4) и равносильное ему исходное уравнение имеют по единственному корню x₁= 2.

б) Пользуясь равенствами

2 2( 3 − 1)₂

= = 3 −1 и 8 − 4 3 = 2 4( − 2 3) = 2( 3 −1) , 3 + 1 3 − 1

перепишем исходное уравнение в виде

( 3 −1)^x= ( 3 −1)². (5)

Так как 3 −1 > 0 и 3 −1 ≠1, то уравнение (5) и равносильное ему исходное уравнение имеют по единственному корню x₁= 2.

6.2. Простейшие логарифмические уравнения

Простейшими логарифмическими уравнениями названы уравнения вида log_ax = b, где а — данное положительное, не равное 1 число, b — данное действительное число. В учебнике приведены три примера решения простейших логарифмических уравнений и два примера решения логарифмических уравнений, сводящихся к простейшим уравнениям.

Решения и комментарии

6.11. а) Решите уравнение log₂(log₂x) = 1.

Решение. Хотя идея замены неизвестного при решении логарифмических уравнений будет изучаться в следующем пункте, здесь имеется возможность подготовить учащихся к использованию этой идеи.

Не делая формально замены t = log₂x, можно заметить, что логарифм по основанию 2 некоторого числа равен 1 тогда и только тогда, когда это число равно 2. Следовательно, исходное уравнение равносильно уравнению

log₂x = 2. (1)

Так как уравнение (1) имеет единственный корень х₁= 4, то и равносильное ему исходное уравнение имеет тот же корень.

6.12. Решите уравнение:

a) log₁₆x + log₄х + log₂x = 7;

в) 2 log₂(log₂x) + log_0,5(log₂x) = 1.

Решение. а) Так как log₄x = ^log2^x= ^log2^x= ¹log₂x и log₂4 2 2

log₁₆x = ^log2^x= ^log2^x= ¹log₂x, то исходное уравнение можlog₂16 4 4

но переписать в виде

⎛ 1 1 ⎞

⎜⎝ ₄⁺₂+1^⎟⎠ log₂x = 7. (2)

Уравнение (2) равносильно уравнению

log₂x = 4,

имеющему единственный корень х₁= 16. Следовательно, и равносильное ему исходное уравнение имеет тот же корень.

log (log^{2 2}x) = log (log^{2 2}x) =

в) Так как log_{0 5,}(log₂x) =

log₂0 5, −1

= −log (log_{2 2}x), то исходное уравнение можно переписать в виде

log₂(log₂x) = 1. (3)

Уравнение (3) имеет единственный корень х₁= 4 (см. задание 6.11a). Следовательно, и равносильное ему исходное уравнение имеет тот же корень.

6.14. а) Решите уравнение log₂х + log₃x = log₃6. Решение. Так как log₂x = ^log3^x, то исходное уравнение

log₃2

можно переписать в виде

log3 x +log3 x = log3 6. (4) log₃2

Так как log3 x +log3 x = ⎜⎝⎛ log13 2 +1⎠⎞⎟ log3 x = 1 log+ log3 23 2 log3 x = log3 2

= ^log3⁶log₃x, то уравнение (4) можно переписать в виде log₃2

log log . (5)

Так как , то, разделив обе части уравнения (5)

на число , получим уравнение

log₃x = log₃2, (6)

равносильное исходному. Так как уравнение (6) имеет единственный корень x₁= 2, то и равносильное ему исходное уравнение имеет тот же корень.

6.15. а) Решите уравнение

log²₂x + 5 log₃x log₄x + log²₅x = 0.

Решение. Пользуясь формулой перехода к новому основанию, преобразуем левую часть исходного уравнения, получим равносильное ему уравнение:

log + ^x+ ^x= . (7)

log₂3 ⋅ log₂4 log₂5

Перепишем уравнение (7) в виде

⎛ 5 1 ⎞

log 1 + + 0. (8)

⎝

Так как число, записанное в скобках, отлично от нуля, то уравнение (8) равносильно уравнению

log₂²x = 0, (9)

имеющему единственный корень х₁= 1. Следовательно, исходное уравнение, равносильное уравнению (9), имеет тот же корень.

6.3. Уравнения, сводящиеся к простейшим заменой неизвестного

В пункте приведены приемы решения уравнений, которые после замены неизвестного сводятся к простейшим по казательным или логарифмическим уравнениям.

Решения и комментарии

6.19. а) Решите уравнение 3^4x2^−
6x^+
3−10 3⋅ ^2x2^{− 3x}^{+ 1}+3 = 0. Решение. Перепишем исходное уравнение в виде

3 3⋅ 2 2( x2 − 3x + 1) −10 3⋅ 2x2 − 3x + 1 +3 = 0. (1)

Введя новое неизвестное t =3 ^2x2^{− 3x}^{+ 1}, перепишем уравнение (1) в виде

3t²− 10t + 3 = 0.

Это уравнение имеет два корня: t₁= 3, t₂= , следовательно, чтобы найти все корни уравнения (1), надо объединить все корни двух уравнений:

32x2 − 3x + 1 = 3 и 32x2 − 3x + 1 = .

Первое из этих уравнений равносильно уравнению 2х²− 3х + 1 = 1, которое имеет корни 0 и 1,5, а второе уравнение равносильно уравнению 2х²− 3х + 1 = −1, которое корней не имеет. Следовательно, исходное уравнение имеет только два корня: 0 и 1,5.

6.24. а) Решите уравнение 3^x^{+ 1}− =1.

Решение. Введя новое неизвестное t = 3^х^{+ 1}, перепишем исходное уравнение в виде

t − ²=1. (2) t − 2

Уравнение (2) имеет два корня: t₁= 3, t₂= 0, следовательно, чтобы найти все корни исходного уравнения, надо объединить все корни двух уравнений:

3х + 1 = 3 и 3х + 1 = 0.

Первое из этих уравнений имеет единственный корень 0, а второе корней не имеет. Следовательно, исходное уравнение имеет только один корень 0.

Особое внимание нужно уделить однородным показательным уравнениям. Выше уже разобраны решения однородного показательного уравнения первой степени (задание 6.8). В данном пункте учебника разобрано решение однородного уравнения второй степени. Для подготовки к самостоятельной работе С—23 (после изучения однородных неравенств) можно использовать следующие задания. Дополнительные задания. Решите уравнение:

1. а) 9 ⋅ 2^х− 4 ⋅ 3^х= 0; б) 125 ⋅ 4^х− 64 ⋅ 5^x= 0;

в) 2^x^+
4+ 11 ⋅ 2^x= 8 ⋅ 3^х; г) 25 ⋅ 7^х= 2 ⋅ 5^х^{+ 2}− 5^х.

2. а) 12^х+ 18^х= 2 ⋅ 27^х; б) 2 ⋅ 5^2х+ 10^х= 15 ⋅ 4^х;

в) 52x + 1 + 6 ⋅ 20x = 42x + 1,5; г) 4 ⋅ 8х − 12x = 18x + 1.

3. а) ;

б) ;

в) ;

г) .

Ответы. 1. а) 2; б) 3; в) 3; г) 2.

2. а) 0; б) 1; в) −1; г) −2.

3. а) 1, ; б) 1, ; в) 1, ; г) .

Промежуточный контроль. С—21.

6.4. Простейшие показательные неравенства

Простейшими показательными неравенствами названы неравенства вида а^х> b и а^х< b, где а — данное положительное, не равное 1 число, b — данное действительное число. В учебнике найдены решения простейших показательных неравенств a^x> a^x0 и a^x< a^x0 . А именно, в учебнике доказана равносильность неравенств:

a^x> a^x0 и x > x₀при а > 1;	(1)
a^x> a^x0 и х < x₀при 0 < а < 1;	(2)
a^x< a^x0 и х < х₀при а > 1;	(3)
a^x< a^x0 и х > x₀при 0 < a < 1.	(4)

Наряду с приведенным в учебнике доказательством для доказательства, например, равносильности неравенств (1) можно рассуждать и так.

Пусть число x₁— любое решение неравенства х > х₀, тогда справедливо числовое неравенство x₁> х₀и из возрастания функции у = а^x(а > 1) следует справедливость числового неравенства a^x1 > a^x0. Но это означает, что любое решение неравенства x > x₀является решением неравенства

a^x> a^x0.

Пусть теперь число x₁— любое решение неравенства a^x> a^x0 (а > 1), тогда справедливо числовое неравенство a^x1 > a^x0. Докажем, что тогда x₁> x₀. Доказательство проведем от противного.

Предположим, что х₁= х₀, тогда a^x1 = a^x0, что противоре чит условию a^x1 > a^x0. Значит, это предположение неверно.

Предположим, что х₁< х₀, тогда из возрастания функции у = а^x(а > 1) следует справедливость числового неравенства a^x1 < a^x0, что противоречит условию a^x1 > a^x0. Значит, это предположение неверно.

Для чисел x₁и х₀возможно только одно из трех соотношений x₁= х₀, х₁< x₀и х₁> x₀(п. 1.2). Поэтому, если неверно, что x₁= x₀и x₁< x₀, то x₁> x₀. Но это означает, что любое решение неравенства a^x> a^x0 является решением неравенства x > x₀.

Следовательно, неравенства a^x> a^x0 и х > х₀равносильны при а > 1.

Равносильность неравенств (2)—(4) доказывается аналогично.

Решения и комментарии

6.34. а) Решите неравенство 2^x^{+ 2}+ 2^х> 20.

Решение. Перепишем исходное неравенство в виде

2^x(2²+ 1) > 20

или в виде

2^x> 2². (5)

Решениями неравенства (5), а значит, и исходного неравенства являются все х > 2.

6.35. е) Решите неравенство 625 ⋅ 3^х− 81 ⋅ 5^х< 0.

Решение. Это однородное показательное неравенство первой степени. Разделив его на 625 ⋅ 5^хи перенеся второе слагаемое в правую часть неравенства, перепишем исходное неравенство в виде

⎛ 3 ⎞ x

⎜⎝ 5 ⎟⎠

< ⎜⎝ 35 ⎞⎟⎠4. ⎛

(6)

Так как 0 < <1, то решениями неравенства (6), а зна-

чит, и равносильного ему исходного неравенства являются все х > 4.

6.5. Простейшие логарифмические неравенства

Простейшими логарифмическими неравенствами названы неравенства вида log_ax > b и log_ax < b, где а — данное положительное, не равное 1 число, b — данное действительное число. В учебнике доказана равносильность неравенств:

log_ax > log_ax₀и х > х₀для а > 1;

log_ax > log_ax₀и 0 < х < х₀для 0 < а < 1; log_ax < log_ax₀и 0 < х < х₀для а > 1; log_ax < log_ax₀и х > x₀для 0 < a < 1.

Другими словами, найдены решения простейших логарифмических неравенств.

Решения и комментарии

6.42. а) Решите неравенство log₂x + log₄x + log₁₆x > 3,5.

Решение. Так как log₄x = ^log2^x= ^log2^x= ¹log₂x, a log₂4 2 2

log²x = log²x = ¹log₂x, то исходное неравенство

log₁₆x =

log₂16 4 4

⎛ 1 1⎞

можно переписать в виде ⎜⎝1 + 2 + 4⎟⎠ log2 x > 3 5,

или в виде

log₂x > log₂4. (1)

Неравенство (1), а значит, и равносильное ему исходное неравенство имеют решения: все x > 4.

6.44. а) Решите неравенство log₂х + log₃х < log₃6.

Решение. Так как

= log3 x⎜⎝⎛ log13 2 +1⎞⎟⎠ = 1 log+ log3 23 2 ⋅log3 x = loglog33 26 ⋅log3 x, то исходное

неравенство можно переписать в виде

. (2)

log³2

Умножив неравенство (2) на положительное число ,

log₃6

получим равносильное ему неравенство

log₃x < log₃2,

все решения которого, а значит, и равносильного ему исходного неравенства составляют промежуток 0 < х < 2.

6.6. Неравенства, сводящиеся к простейшим заменой неизвестного

В пункте приведены приемы решения неравенств, которые после замены неизвестного сводятся к простейшим по казательным или логарифмическим неравенствам.

Решения и комментарии

6.48. а) Решите неравенство 125 ⋅ 3^2х^{− 7}− 27 ⋅ 5^2х^{− 7}> 0.

Решение. Так как 5^2х^{− 7}> 0 для любого действительного x, то, разделив исходное неравенство на 125 ⋅ 5^2х^{− 7}, ⎛ ₃⎞2x − 7 ₂₇

получим неравенство ^⎜⎝ ₅^⎟⎠ ⁻₁₂₅> 0, равносильное исходному неравенству. Перепишем это неравенство в виде

⎛ 3 ⎞2x − 7 ⎛ 3 ⎞3

⎜⎝ ₅⎟⎠ > ⎜⎝ ₅⎟⎠ . (1)

Обозначив t = 2х − 7, перепишем неравенство (1) в виде простейшего показательного неравенства

⎛ 3 ⎞t ⎛ 3 ⎞3

⎜⎝ ₅⎟⎠ > ⎜⎝ ₅⎟⎠ . (2)

Так как 0 < <1, то неравенство (2) равносильно неравенству t < 3, следовательно, все решения неравенства (1) составляют множество решений неравенства 2х − 7 < 3, т. е. промежуток (−∞; 5). Замечание. При решении таких неравенств часто замену неизвестного не записывают в явном виде, переходя от неравенства (1) к равносильному ему неравенству 2х − 7 < 3.

6.54. а) Решите неравенство log₂(х²− 5x + 4) < 2.

Решение. Введя новое неизвестное t = х²− 5х + 4 и заменив число 2 на log₂4, перепишем исходное неравенство в виде

log₂t < log₂4. (3)

Так как 2 > 1, то все решения неравенства (3) составляют промежуток 0 < t < 4. Следовательно, все решения исходного неравенства есть решения двойного неравенства

0 < x²− 5x + 4 < 4. (4)

Решив двойное неравенство (4), найдем все его решения: х ∈ (0; 1) ∪ (4; 5). Они являются также решениями равносильного ему исходного неравенства.

6.55. а) Решите неравенство log₂(log₃х) > 1.

Решение. Введя новое неизвестное t = log₃х и заменив число 1 на log₂2, перепишем исходное неравенство в виде

log₂t > log₂2. (5)

Так как 2 > 1, то неравенство (5) равносильно неравенству t > 2. Поэтому все решения исходного неравенства являются решениями неравенства

log₃x > 2. (6)

Неравенство (6) имеет множество решений (9; +∞), следовательно, и равносильное ему исходное неравенство имеет те же решения.

6.59. а) Решите неравенство

1 2

+ > −1.

lg (3x + 1) lg (3x + 1) + lg0 01,

Решение. Введя новое неизвестное t = lg (3x + 1) и заменив lg 0,01 числом −2, перепишем исходное неравенство в виде

1 2

+ > −1. (7) t t − 2

Неравенству (7) удовлетворяют все t < −2, все t > 2 и все t из промежутка 0 < t < 1. Следовательно, множество решений исходного неравенства есть объединение множеств решений трех неравенств:

lg (3x + 1) < −2, lg (3х + 1) > 2,

0 < lg (3x + 1) < 1.

Эти неравенства имеют множества решений — соответственно ^⎜⎝⎛⁻₃¹; −0 33, ⎞^⎟⎠, (33; +∞) и (0; 3). Поэтому множество решений исходного неравенства есть объединение этих про-

⎛ 1 ⎞ межутков: ^⎜⎝⁻₃; −0 33, ^⎟⎠ ∪ (0; 3) ∪ (33; +∞).

6.62. б) Решите неравенство 3 ⋅ 9^x− 5 ⋅ 6^x+ 2 ⋅ 4^x< 0.

Решение. Так как 4^x> 0 для любого действительного х, то, разделив исходное неравенство на 4^x, получим неравенство

⎛ 3 ⎞2x ⎛ 3 ⎞ x

3⋅⎜⎝ ₂⎟⎠ − 5⋅⎜⎝ ₂⎟⎠ +2 <0, (8)

равносильное исходному неравенству.

⎛

Введя новое неизвестное t = ^⎜⎝ ₂3 ^⎟⎠⎞ x, перепишем неравенст-

во (8) в виде

3t²− 5t + 2 < 0. (9)

Множество решений неравенства (9) есть промежуток

< t <1. Поэтому, чтобы найти все решения неравенства

(8), надо решить двойное неравенство ⎛ 3 ⎞ −1 ⎛ 3 ⎞ x ⎛ 3 ⎞ 0

⎜⎝ 2 ⎟⎠ < ⎜⎝ 2 ⎟⎠ < ⎜⎝ 2 ⎟⎠ . (10)

Множество решений неравенства (10) есть интервал (−1; 0). Следовательно, множество решений исходного неравенства (8) есть тот же интервал.

Особое внимание надо уделить однородным показательным неравенствам. Выше было показано решение однородного показательного неравенства первой степени (задание 6.35), а в данном пункте учебника показан способ решения однородных показательных неравенств второй степени (задание 6.62; см. также п. 23 дидактических материалов).

Промежуточный контроль. С—22, С—23.

Контрольная работа № 4.

Особенностью изложения материала главы II является то, что сначала (в параграфах 7—9) изучаются тригонометрические функции угла с опорой на геометрические иллюстрации и факты. Подчеркнем, что аргументом у этих функций является угол. Все их свойства доказываются для углов, решаются задачи на нахождение всех углов, удовлетворяющих некоторым равенствам и неравенствам. Только в параграфах 10 и 11 речь идет о тригонометрических функциях числового аргумента и о решении тригонометрических уравнений и тригонометрических неравенств, в которых неизвестным является число, а не угол.

Изложение тригонометрического материала в учебнике таково, что все формулы доказываются с минимальной опорой на геометрию сначала для синуса и косинуса, а потом для тангенса и котангенса.

Все формулы сложения и следствия из них в учебнике доказаны, но термин «формулы приведения» в учебнике не используется по двум причинам. Во-первых, эти формулы появляются постепенно по мере их доказательства, а во-вторых, правило для запоминания формул (мнемоническое правило) является лишь методическим приемом, который описан в дидактических материалах и будет применяться учителем тогда, когда он посчитает это целесообразным.

Функциональная линия учебника продолжается изучением тригонометрических функций, их свойств и графиков. Линия уравнений и неравенств — решением тригонометрических уравнений и неравенств.

На углубленном уровне предусмотрено изучение арксинуса, арккосинуса, арктангенса, арккотангенса; формул для них, следствий из формул сложения, не предусмотренных при обучении на базовом уровне, а также специальных приемов решения тригонометрических уравнений и неравенств.

Отметим, что в стандарте эти понятия не предназначены для изучения на базовом уровне. Но совершенно очевидно, что, не сформировав у учащихся представления об арксинусе, арккосинусе и арктангенсе, нельзя считать, что мы научили их решать даже простейшие тригонометрические уравнения, которые на базовом уровне должны изучаться.

Нельзя считать ученика обученным решению простейших тригонометрических уравнений, если он умеет решать уравнение sin x = 0,5, но не умеет решать уравнение sin x = 0,6.

В результате изучения главы II учащиеся должны знать основные определения, свойства и формулы, связанные с тригонометрическими функциями, уметь по значению одной из функций находить значения остальных, преобразовывать несложные выражения, содержащие тригонометрические функции, применяя изученные формулы, знать свойства и уметь строить графики функций у = sin x, у = cos x, у = tg x, у = ctg x, уметь решать простейшие тригонометрические и сводящиеся к ним уравнения и неравенства.

§ 7. Синус и косинус угла

7.1. Понятие угла

В пункте вводятся понятия положительных и отрицательных углов, нулевого угла.

При рассмотрении данного пункта удобно использовать окружность единичного радиуса, которая в п. 7.3 будет названа единичной окружностью. Учащимся надо показать прием построения «табличных» углов (30°, 45°, 60°, 90°) и связанных с ними углов без транспортира, что позволит в дальнейшем быстрее находить значения тригонометрических функций, сводимых к значениям функций для «табличных» углов, а позднее хорошо решать простейшие тригонометрические уравнения и неравенства. Покажем, как это можно сделать.

Учащиеся должны сначала научиться отмечать на единичной окружности точки, соответствующие углам:

а) 0°, 90°, 180°, 270° (рис. 23, а), т. е. точки, получаемые при пересечении осей координат с единичной окружностью;

б) 45°, 135°, 225°, 315°, т. е. точки, получаемые при пересечении биссектрис координатных углов с единичной окружностью (рис. 23, б);

в) 30°, 150°, 210°, 330°, т. е. точки, получаемые при пересечении прямых y = и y = − с единичной окружностью

(рис. 23, в);

г) 60°, 120°, 240°, 300°, т. е. точки, получаемые при пересечении прямых x = и x = − с единичной окружностью

(рис. 23, г).

Умея строить указанные точки, легко построить соответствующие им углы и тем самым выполнить задание 7.11. При этом нужно отметить требуемые углы дугами (как на рисунке 76 учебника) или, обозначив построенные точки буквами, сделать поясняющие записи в виде ∠AOB = 90° (см. рис. 23, а).

Чтобы обосновать, что точка В, изображенная на рисунке 23, в, соответствует углу 30°, достаточно опустить из этой точки перпендикуляр ВС на ось Ох (рис. 23, д). Тогда в прямоугольном треугольнике ВОС катет ВС равен половине гипотенузы ОB. Поэтому угол СОВ, лежащий против этого катета, равен 30°. Аналогично дается обоснование для рисунка 23, г.

Решения и комментарии

7.13. Представьте следующие углы в виде α + 360° ⋅ п, где 0° ≤ α < 360°, n — некоторое целое число:

в) 600°; г) −900°.

Решение. в) 600° = 240° + 360° ⋅ 1; г) −900° = 180° + 360° ⋅ (−3).

7.2. Радианная мера угла

Сначала напомним старинное мнемоническое правило^{^[1]}, позволяющее воспроизводить первые десятичные знаки иррационального числа π. В следующей фразе число букв в каждом слове дает цифру десятичной записи числа π: «Кто, и шутя и скоро, стремится пи узнать — число уже готово». Получается π = 3,1415926536.

При изучении данной темы обычно наблюдается недопонимание учащимися необходимости выражать радианную меру угла через число π. Чтобы снять всякие сомнения на этот счет, можно провести такое рассуждение.

Отметим на единичной окружности точки, соответствующие углам в 1, 2, 3, 4, 5, 6 радиан. Для этого надо откладывать от точки А в направлении против часовой стрелки на окружности 1, 2, 3, 4, 5, 6 раз дугу, длина которой равна радиусу окружности. Так как длина окружности радиуса 1 равна 2π ≈ 6,28, то полный оборот содержит больше 6 радиан (рис. 24, а).

Если продолжить откладывание в том же направлении на этой окружности дуг длиной в 1 радиус, то возникает иллюзия, что через некоторое (возможно, большое) число шагов новое деление на окружности, соответствующее углу в некоторое число радиан, совпадет с каким-нибудь из отмеченных ранее делений. Однако этого не произойдет, как бы долго мы ни продолжали откладывать в том же направлении эти дуги. Докажем это методом от противного.

Предположим, что на п-м шаге мы отметили на окружности точку N, соответствующую углу в п радиан, п — натуральное число (рис. 24, б). Затем продолжили откладывание в том же направлении дуг длиной в 1 радиус и на каком-то шаге обнаружили, что точка, соответствующая углу в т радиан, совпала с уже отмеченной точкой N. Для этого пришлось сделать k (k ≠ 0) полных оборотов. Тогда справедливо равенство т − п = 2kπ, k ∈ N, из которого следует, что π = m n− . 2k

Получено противоречие: число π оказалось равным обыкновенной дроби. Но как известно, число π — иррациональное число, т. е. оно не может быть равным обыкновенной дроби. Следовательно, предположение, что на каком-то шаге новое деление, соответствующее углу в т радиан, совпадет со старым делением, соответствующим углу в п радиан (т и п — натуральные числа), неверно.

Заметим, что в приведенном рассуждении мы нигде не пользовались тем, что т и п — натуральные числа, т. е.

1 если точка N получена при откладывании p раз части дуги q

в 1 радиан, то она не может совпасть ни с какой другой точ-

1 кой, полученной при откладывании r раз части дуги в

p r

1 радиан ( ≠ , где p, q, r, s — натуральные числа). Такое q s рассуждение можно провести при решении задачи 7.39б.

Теперь становится ясным, что при использовании радианной меры без числа π и его долей обойтись невозможно. На рисунке 24, в показаны точки, которые на рисунке 23, а соответствовали углам 90°, 180°, 270°, 360°. Теперь они соответствуют углам , π, , 2π радиан. Запоминанию этих

углов (и следующих за ними) помогает считалочка: показывая точки на окружности, говорим: «Раз пи на два, два пи на два, три пи на два, ...». Аналогичный прием помогает при поиске точек, соответствующих углам π, π, 3π, π, ... радиан.

4 2 4

Теперь, установив равенство: π радиан = 180° — и разделив его сначала на π, потом на 180, получим соотношения, которые надо запомнить:

1 радиан = ¹⁸⁰ радиан = 1°.

С их помощью можно переводить градусную меру в радианную и обратно. Например, 135° = диан = радиан; радиан радиан.

В этих равенствах слово «радиан» обычно опускают и пишут коротко: 135°= ³^π_,⁵^π=150°.

4 6

Решения и комментарии

7.22. Запишите в виде α + 2πп, где п — некоторое целое число (0 ≤ α < 2π), следующие углы: а) 6,5π; б) π;

в) −12 π; г) .

Решение. а) 6,5π = 0,5π + 6π; б) ;

в) ; г) .

Промежуточный контроль. С—24, С—25.

Эти работы рассчитаны на обучение «чтению» точек единичной окружности, соответствующих «табличным» углам, а также на подготовку учащихся к записи ответов при решении простейших тригонометрических уравнений. При выполнении самостоятельной работы С—25 учащиеся могут писать лишь правильные ответы, не делая пояснений, аналогичных тем, что имеются в п. 25 раздела I дидактических материалов. 7.3. Определение синуса и косинуса угла

В данном пункте нужно сначала повторить все сведения из тригонометрии прямоугольного треугольника, необходимые в дальнейшей работе: определения тригонометрических функций острого угла прямоугольного треугольника, нахождение двух сторон этого треугольника по одной его стороне и острому углу, вывод табличных значений синуса и косинуса для углов 30°, 45°, 60°. При этом надо обратить внимание учащихся на тот факт, что большая часть тригонометрического материала, которую действительно лучше помнить, легко усваивается с опорой на наглядные образы, различные мнемонические правила, что запоминание фактов тригонометрии в виде таблиц является наименее продуктивным и опасным с точки зрения правильного воспроизведения запомненного.

В учебнике вводится понятие единичной окружности, синуса и косинуса угла α, рассматриваются свойства синуса и косинуса как функций угла α.

Для того чтобы в дальнейшем успешно решать простейшие тригонометрические уравнения, учащиеся должны научиться правильно изображать на единичной окружности точки, соответствующие значениям тригонометрических функций, и в случае табличных значений уметь определять соответствующие значения аргументов этих функций. Достижению этой цели способствует самостоятельная работа С—26.

Обратите внимание учащихся на то, что точки первой четверти, соответствующие табличным значениям синуса и косинуса, надо строить так, как показано на рисунке 25. Эти точки находятся на пересечении с единичной окружностью осей координат, биссектрисы угла АОВ, прямых x = и y = . Поэтому в

тетради нужно рисовать единичную окружность радиусом 1 см или 2 см, чтобы было удобно де- _{Рис. 25}

лить пополам их радиусы с помощью клетчатой бумаги.

Применяя теорему Пифагора, из прямоугольных тре-

угольников ОМK и ONE найдем, что OK = NE ⁼³. Поэто-

му cos 30° = sin 60° =

Аналогично CF = OF = . Поэтому sin 45° = cos 45° = ².

2 2

Следующий этап изучения тригонометрических функций — формирование понятий синуса и косинуса произвольного угла.

Для успешного освоения тригонометрии произвольного угла важно научить школьников определять значения тригонометрических функций по точке единичной окружности, соответствующей углу, по значениям тригонометрических функций угла отмечать на единичной окружности точки и определять соответствующие им углы. Последнее умение, по сути, есть умение решать простейшее тригонометрическое уравнение. Только пока ставится задача не решить уравнение, а найти, например, все такие углы α, для каждого из которых справедливо равенство sin α = 0 (см. задание 7.26a).

Решения и комментарии

7.30. Вычислите, сделав рисунок: a) sin 120°; в) sin 135°. Решение. Сделав рисунок

(см. рис. 26, а, б), учащиеся поймут, что sin 120° = sin 60°, sin 135° = sin 45°. Затем, пользуя табличные значения, получат ответ: sin 120°=

sin 135°= ².

2 Рис. 26

Представляется целесообразным научить школьников решению таких задач до того, как они научатся на следующих уроках применять формулы при преобразованиях.

7.35. а) Найдите синусы и косинусы углов +2πk, где k — любое целое число.

Решение. Сначала по записи данных углов учащиеся должны построить точку единичной окружности, соответствующую углам α_k= +2πk, где k ∈ Z, а потом определить,

что sin α_k= 1, cos α_k= 0.

7.46—7.47. При выполнении этих заданий надо опираться на умение строить точки единичной окружности, соответствующие данным углам, и находить значения синуса или косинуса данного угла исходя из определения, так как свойства sin (−α) = −sin α и cos (−α) = cos α еще не изучены.

Для закрепления знания свойств функций угла: sin α и cos α здесь полезно рассмотреть задания 7.65а, б, 7.66а, б,

7.67а.

7.65. а) Сравните sin 91° и sin 92°.

Решение. 91° и 92° — углы второй четверти, в которой большему углу соответствует меньший синус, поэтому sin 91° > sin 92°.

7.66. а) Сравните cos 101° и cos 157°.

Решение. 101° и 157° — углы второй четверти, в которой большему углу соответствует меньший косинус, поэтому cos 101° > cos 157°.

7.67. а) Сравните cos 1,6π и cos 1,68π.

Решение. 1,6π и 1,68π — углы четвертой четверти, в которой большему углу соответствует больший косинус, поэтому cos 1,6π < cos 1,68π.

Промежуточный контроль. С—26.

7.4. Основные формулы для sin и cos

В данном пункте с опорой на ранее изученные факты — уравнение окружности, свойства координат точек единичной окружности, симметричных относительно оси Ох, относительно начала координат, — доказаны основное тригонометрическое тождество

и формулы		sin²α + cos²α = 1	(1)
		sin (−α) = −sin α,	(2)
		cos (−α) = cos α,	(3)
	sin (α + 2πk) = sin α, k ∈ Z,		(4)
	cos (α + 2πk) = cos α, k ∈ Z,		(5)
	sin (π + α) = −sin α,		(6)
	cos (π + α) = −cos α.		(7)

Некоторые другие формулы, например sin (π − α) = sin α, cos (π − α) = −cos α, могут быть доказаны как следствия формул (2)—(7) (см. задание 7.68). Например, sin (π − α) = sin (π + (−α)) = −sin (−α) = sin α.

В самостоятельной работе С—27 проверяется умение школьников находить значения одной из заданных функций угла α (sin α или cos α) по заданному значению другой и выполнять упрощения выражений с применением формул (1)—(7).

Решения и комментарии

7.54. а) Вычислите sin α, если cos α = , 0 < α < .

Решение. Поскольку 0 < α < , то sin α > 0. Так как

sin²α = 1 − cos²α = 1 − ¹= ¹⁵, то sinα =.

16 16

При решении этой и аналогичных задач лучше избегать записи: sin α = ± 1 − cos²α, так как, имея опыт вычисления

−b ± D

корней квадратного уравнения по формуле, уча-

щиеся могут подумать, что имеется два значения sin α, отвечающих условию задачи, а это не так.

7.64. а) Расположите в порядке возрастания числа: sin (−55°), sin 600°, sin 1295°.

Решение. Выразим синусы данных углов через синусы углов из первой четверти: sin (−55°) = −sin 55°; sin 600° = sin (240° + 360°) = sin 240° = sin (180° + 60°) =

= −sin 60°; sin 1295° = sin (215° + 3 ⋅ 360°) = sin 215° = sin (180° + 35°) = = −sin 35°.

Так как углы 55°, 60° и 35° принадлежат первой четверти, в которой большему углу соответствует больший синус, то sin 35° < sin 55° < sin 60°. Но тогда −sin 35° > −sin 55° > > −sin 60°, поэтому sin 1295° > sin (−55°) > sin 600°.

7.67. г) Сравните sin 1 и cos 1.

Решение. Так как ^π<1 < ^π, то угол в 1 радиан находится

4 2

в I четверти, поэтому sin 1 > sin = cos > cos 1, следовательно, sin 1 > cos 1.

7.71—7.72. Эти задания готовят учащихся к решению простейших тригонометрических уравнений для «табличных» углов.

7.73—7.74. Эти задания готовят учащихся к введению понятий арксинуса и арккосинуса числа. Для выполнения заданий «д» и «е» лучше брать единичную окружность радиуса 1,5 см или 3 см. Тогда точки единичной окружности, соответствующие углу α, будут указаны точнее.

Промежуточный контроль. С—27.

7.5. Арксинус

В данном пункте учебника дано определение арксинуса числа а (| a | ≤ 1), из которого получается формула sin (arcsin a) = а, справедливая для каждого числа а, такого, что −1 ≤ а ≤ 1.

Отметим, что перед введением понятия арксинуса и для мотивации его введения полезно давать задания типа 7.75: «Найдите угол из промежутка ⎡⎢⎣− 2π; 2π⎤⎥⎦, синус которого

равен: а) 1; б) −1; в) 0; г) ; д) − ²; е) ³».

2 2

После нескольких таких заданий надо сказать, что для упрощения этих формулировок оборот «угол из промежутка ⎡⎢⎣− 2π; 2π⎤⎥⎦, синус которого равен числу а» заменяют на бо-

лее короткий: «arcsin а». Теперь те же задания можно формулировать короче:

«Найдите: arcsin 1; arcsin (−1) и т. д.».

Далее рассмотрена задача 1: для данного числа а, такого, что | а | < 1, найти все углы α, для каждого из которых sin α = a.

Ясно, что это другая формулировка задачи: для данного числа а, такого, что | а | < 1, решить уравнение sin α = а, где неизвестное — угол α. (Отметим, что углы измеряются обычно в радианах, хотя их можно измерять и в градусах.) Здесь впервые получены формулы для таких углов: α = arcsin a + 2πп, п ∈ Z и α = π − arcsin a + 2πk, k ∈ Z.

Эти формулы в дальнейшем будут использованы для решения простейших тригонометрических уравнений. Здесь не стоит форсировать объединение получаемых формул в одну. Сначала учащиеся должны научиться решать уравнения, только потом (и даже не всегда) оказывается полезным объединять получаемые формулы в одну.

Затем в пункте рассмотрены задачи, аналогичные задаче 1, но для | а | = 1 и | a | > 1.

Решения и комментарии

7.77. а) Имеет ли смысл запись arcsin ? Решение. Здесь учащиеся нередко не видят подвоха. Они так часто вычисляли sin и еще не привыкли к тому, что arcsin а существует лишь для таких а, что −1 ≤ а ≤ 1, поэтому иногда они считают, что это выражение существует. Между тем >1, поэтому arcsin не существует и, следовательно, запись arcsin не имеет смысла.

7.80. Сравните с нулем: a) arcsin 3¹; б) arcsin ⎛^⎜⎝− ₃¹⎞^⎟⎠.

Решение. Если учащиеся обозначат α₁= arcsin и, взглянув на рисунок 27, ответят: arcsin > 0, то получат верный

ответ, которого достаточно, если они отвечают на вопросы теста. Если же от них требуется обоснованное решение, то оно будет опираться на следующие рассуждения.

Для любых углов α₁и α₂, таких, что , справедливо неравенство sin α₁< < sin α₂(п. 7.3 учебника).

Для сравнения углов докажем обратное утверждение:

Для любых углов α₁и α₂из промежутка ⎡⎢⎣− 2π; 2^π^⎤⎥⎦, таких, что

sin α₁< sin α₂, справедливо неравенство α₁< α₂.

Доказательство проведем методом «от противного»:

если α₁= α₂, то sin α₁= sin α₂,

что противоречит условию

sin α₁< sin α₂; Рис. 27

если α₁> α₂, то sin α₁> sin α₂, что противоречит усло-

вию sin α₁< sin α₂; следовательно, α₁< α₂, что и требовалось доказать.

Таким образом, доказано, что для любых углов α₁и α₂из промежутка ⎡− π; π⎤⎥⎦ равносильны неравенства:

⎢⎣ 2 2

sin α₁< sin α₂и α₁< α₂.

Применим это утверждение.

а) Обозначим α₁= arcsin . Так как углы 0 и α₁из про-

межутка ⎡− π; π⎤⎥⎦ и sin arcsin⎛⎜⎝ 31⎞⎠⎟ = 31 > 0 = sin0, то arcsin 31 > 0

⎢⎣ 2 2

(см. рис. 27).

б) Обозначим α₂= arcsin^⎜⎝⎛⁻₃¹⎞^⎟⎠. Так как углы 0 и α₂из промежутка ⎡− π; π⎤⎥⎦ и sin arcsin⎛⎜⎝ ⎛⎜⎝− 31⎠⎟⎞⎞⎟⎠ = − 31 < 0 = sin0, то

⎢⎣ 2 2

⎛ 1⎞

arcsin^⎜⎝⁻₃^⎟⎠ <0 (см. рис. 27).

7.83. Задайте формулами все углы α, для каждого из которых: д) sinα = ²; з) sinα = − ²; л).

2 2

Ответ. д) k, k ∈ Z; n, п ∈ Z

(рис. 28);

з) α_k= − +2πk, k n, n ∈ Z (рис. 29);

Рис. 28 Рис. 29

л) α_k= arcsin^⎜⎝⎛− ²₃⎞^⎟⎠ +2πk, k ∈ Z; α _n= π − arcsin^⎜⎝⎛− ²₃^⎞⎟⎠ +2πn, n ∈ Z

(рис. 30).

Дополнительные задания.

1. Сравните arcsin с углом .

Решение. Так как arcsin и

— углы из промежутка

⎡− π; π⎥⎤⎦ и так как sin arcsin⎛⎜⎝ 31⎠⎞⎟ = 31 < 22 = sin π4, то arcsin 31 < π4

⎢⎣ 2 2

(по доказанному выше утверждению).

2. Существует ли число x, такое, что:

a) arcsin x = ; б) arcsin x = ?

Если существует, то найдите его.

Решение. а) x = ; б) так как ,

то такого числа x не существует.

7.6. Арккосинус

Введение понятия арккосинуса можно мотивировать так же, как и введение понятия арксинуса. Для этого можно использовать задание 7.84. Только надо подчеркнуть принципиальное отличие: arccos a (| а | ≤ 1) — это угол из промежутка [0; π]. Из определения арккосинуса получается формула cos (arccos a) = а, справедливая для каждого числа а, такого, что −1 ≤ а ≤ 1.

Далее рассмотрена задача 1: для данного числа а, такого, что | а | < 1, найти все углы α, для каждого из которых cos α = а.

Здесь впервые получены формулы α = arccos a + 2πn, n ∈ Z и α = −arccos a + 2πk, k ∈ Z.

Эти формулы в дальнейшем будут использованы для решения простейших тригонометрических уравнений. И здесь не стоит форсировать объединение получаемых формул в одну.

Затем рассмотрены задачи, аналогичные задаче 1, но для | а | = 1 и | а | > 1.

Решения и комментарии

7.89. Сравните с числом 0,5π: a) arccos ¹; б) arccos⎛^⎜⎝⁻1₄⎞^⎟⎠. 4

Решение. Для любых углов α₁и α₂, таких, что 0 ≤ α₁< α₂≤ π, справедливо неравенство cos α₁> cos α₂(п. 7.3 учебника). Для сравнения углов методом от противного можно доказать обратное утверждение: для любых углов α₁и α₂из промежутка [0; π], таких, что cos α₁> cos α₂справедливо неравенство α₁< α₂.

Таким образом, можно доказать, что для любых углов α₁и α₂из промежутка [0; π] равносильны неравенства: cos α₁< cos α₂и α₁> α₂. Применим это утверждение.

а) Обозначим α₁= arccos. Так как углы 0,5π и α₁принадлежат промежутку [0; π] и cos α₁= > 0 = cos 0,5π, то arccos <05, π (рис. 31).

б) Так как углы 0,5π и α₂= arccos ^⎜⎝⎛⁻¹₄⎞^⎟⎠ принадлежат

промежутку [0; π] и cos α₂= − < 0 = cos 0,5π, то

⎛ 1⎞

arccos ^⎜⎝⁻₄^⎟⎠ > 0 5, π (см. рис. 31).

7.90. а) С помощью арккосинуса выразите углы из про^{межутка}⎡⁻^π^;^π^⎤⎥⎦, соответствующие отмеченным точкам

⎢⎣ _{2 2}единичной окружности (рис. 32).

Ответ. а) α₁= arccos, α₂= −arccos.

Рис. 31 Рис. 32

7.93. Задайте формулами все углы α, для каждого из которых:

е) cos α = ³; з) cos α = − ²; м).

2 2

Ответ. е) k, k ∈ Z; n, n ∈ Z;

з) Z; n, n ∈ Z;

м) Z; n, n ∈ Z.

Дополнительные задания.

1. Сравните с нулем .

Решение. Так как 0 ≤ arccos а ≤ π для любого а ∈ [−1; 1] и , то .

2. Существует ли число x, такое, что:

a) ; б) arccos x = − ?

Если существует, то найдите его.

Решение. а) x ;

б) так как 0 ≤ arccos х ≤ π, а , то такого числа х

не существует.

Промежуточный контроль. С—28.

7.7*. Примеры использования арксинуса и арккосинуса

В пункте рассмотрено применение арксинуса и арккосинуса для нахождения всех углов, для каждого из которых справедливо неравенство sin α > a (sin α < a); cos α > a (cos α < а). Тем самым подготовлена база для изучения решения простейших тригонометрических неравенств для синусов и косинусов. Ясно, что это другая формулировка задачи: для данного числа а решите неравенство sin α > a (sin α < а); cos α > a (cos α < а), где неизвестное — угол α. Отметим, что углы здесь обычно измеряют в радианах, хотя их можно измерять и в градусах.

Главная трудность в решении рассматриваемых задач заключается в правильном изображении соответствующих точек единичной окружности — границ промежутков и в правильном чтении получаемых промежутков.

Решения и комментарии

В заданиях 7.94—7.96, по сути, требуется решить простейшие тригонометрические неравенства, но задача формулируется в других терминах. Здесь использованы все табличные значения sin α и cos α, а в задании 7.97 надо использовать арксинус или арккосинус числа.

7.97. а) Найдите все такие углы α, для каждого из которых sinα > . Решение. Сначала найдем углы из промежутка [0; π], для каждого из которых sinα = . Это углы

α₁= arcsin и α₂= π − arcsin

(рис. 33).

Теперь найдем все искомые углы α, для каждого из которых

Рис. 33 sin α > (им соответствуют точки

единичной окружности, выделен-

ные на рисунке 33 жирной дугой):

arcsin + 2πk < α < π − arcsin + 2πk, k ∈ Z. 7.98. а) Найдите все такие углы α, для каждого из которых sin α < 1.

Решение. Очевидно, что условию sin α < 1 удовлетворяют все углы α, кроме таких α = α_n, для которых sin α_n= 1, т. е. кроме α _n= +2πn, n ∈ Z (на рисунке

34 точки единичной окружности, соответствующие таким углам, выделены жирной дугой). Итак, α — любой угол, отличный от углов α_n, или коротко:

n, n ∈ Z.

Ответ можно записать иначе, как в учебнике: ^π+2πn <α < ^π+2πn, n ∈ Z.

Рис. 34

7.8*. Формулы для арксинуса и арккосинуса

В данном пункте доказаны формулы:

arcsin (−a) = −arcsin a, | a | ≤ 1,

arccos (−a) = π − arccos a, | a | ≤ 1,

arcsin (sin α) = α, α ∈ −^⎡_⎢⎣₂^π; ₂^π^⎤_⎥⎦,

arccos (cos α) = α, α ∈ [0; π].

Здесь же приведены решения задач, связанных с вычислением arcsin (sin α) для α ∉ −^⎡⎢⎣ ₂^π; ₂^π^⎤⎥⎦, а также arccos (cos α) для α ∉ [0; π].

Решения и комментарии

7.103. Вычислите: г) arccos cos⎜⎛⎝ ^⎜⎝⎛− ^π₄⎞^⎟⎠⎞⎟⎠ ;

⎛ 5π⎞

д) arcsin sin⎜⎝ ₆⎟⎠ .

⎛ ⎛ ^π⎞⎞ ⎛ ^π⎞ ^π, так как

Решение. г) arccos cos⎜⎝ ^⎜⎝− ₄^⎟⎠⎟⎠ = arccos cos^⎜⎝ ₄^⎟⎠ = ₄

];

д) arcsin sin⎜⎝⎛ 56π⎟⎠⎞ = arcsin sin⎜⎝⎛ 6π⎟⎠⎞ = 6π, так как 6π ∈ −⎡⎢⎣ 2π; 2π⎤⎥⎦.

7.104. Вычислите: a) arcsin (sin 9); б) arccos (cos 9).

Решение. a) arcsin (sin 9) = arcsin (sin (3π − 9)) = 3π − 9,

так как 3π − 9∈ −^⎡⎢⎣ ₂^π; ₂^π^⎤⎥⎦;

б) arccos (cos 9) = arccos (cos (9 − 2π)) = 9 − 2π, так как 9 − 2π ∈ [0; π]. Дополнительное задание. Вычислите:

a) arccos (sin 0,8π); б) arcsin (cos 2).

Решение. а) Выразим sin 0,8π через косинус угла из

промежутка [0; . Так

как 0,3π ∈ [0; π], то arccos (sin 0,8π) = arccos (cos 0,3π) = 0,3π.

б) Выразим cos 2 через синус угла из промежутка

^⎡⎢⎣− 2^π; 2^π^⎤⎥⎦: cos2 = sin^⎜⎛⎝₂^π− 2^⎟⎠⎞. Так как ₂^π− 2∈ −⎢⎣^⎡ ₂^π; ₂^π^⎤⎥⎦, то

arcsin (cos 2) = arcsin ⎜⎛⎝sin ⎜⎝⎛ ₂^π− 2⎞⎟⎠⎟⎠⎞ = ₂^π− 2.

§ 8. Тангенс и котангенс угла

8.1. Определение тангенса и котангенса угла

Введению тангенса и котангенса произвольного угла должно предшествовать повторение определений тангенса и котангенса для острого угла, повторение табличных значений тангенса и котангенса для углов 30°, 45°, 60°

⎛ π π π ⎞

⎜⎝ ₆, ₄, ₃радиан^⎟⎠ .

В данном пункте учебника вводятся понятия тангенса и котангенса угла α, показывается применение осей тангенса и котангенса для наглядного представления числовых значений этих функций угла α. Здесь, как и при введении синуса и косинуса угла, надо начать с определений этих функций для острого угла прямоугольного треугольника, получить все табличные их значения, показать эти значения на оси тангенса и оси котангенса (рис. 35, 36). Учащиеся должны научиться по заданному табличному значению tg α и ctg α показать соответствующие точки единичной окружности, уметь записать один из углов, соответствующих этой точке, и все такие углы.

Решения и комментарии

8.9. Отметьте на оси тангенсов точки, соответствующие числам 0; 1; −1; 2; −2; ³;

Решение. Пользуясь единичной окружностью и клетчатой бумагой, учащиеся должны расположить данные числа на оси Рис. 35 тангенсов, как на рисунке 35.

8.13. Отметьте на оси котангенсов точки, соответствующие числам 0; 1; −1; 2; −2; 3; − 3; ³; − ³.

3 3

Решение. Пользуясь единичной окружностью и клетчатой бумагой, учащиеся должны расположить данные числа на оси котангенсов так, как на рисунке 36.

Умение решать задания 8.9 и 8.13 поможет учащимся научиться решать простейшие тригонометрические уравнения tg x = а и ctg x = а, а также усвоить новые понятия — арктангенса числа и арккотангенса числа. 8.16. Сравните: д) tg 1 и tg 2; е) tg 2 и tg 3; ж) ctg 1 и ctg 2; з) ctg 2 и ctg 3; и) tg 1 и ctg 2.

Решение. д) Так как угол в 1 радиан — угол первой четверти, а угол в 2 радиана — угол второй четверти, то tg 1 > 0, a tg 2 < 0, поэтому tg 1 > tg 2;

е) так как углы в 2 и 3 радиана — углы из промежутка ⎛ π 3π⎞

^⎜⎝ ₂; ₂^⎟⎠, где функция tg α возрастает и 2 < 3, то tg 2 < tg 3;

ж) так как углы в 1 и 2 радиана — углы из промежутка (0; π), где функция ctg α убывает и 1 < 2, то ctg 1 > ctg 2;

з) так как углы в 2 и 3 радиана — углы из промежутка

(0; π), где функция ctg α убывает и 2 < 3, то ctg 2 > ctg 3;

и) так как угол в 1 радиан — угол первой четверти, а угол в 2 радиана — угол второй четверти, то tg 1 > 0, a ctg 2 < 0, поэтому tg 1 > ctg 2.

Лучшему усвоению изученного материала помогает самостоятельная работа С—29 из дидактических материалов.

Промежуточный контроль. С—29.

8.2. Основные формулы для tg и ctg

В этом пункте доказаны основные формулы для tg α и ctg α:

k, k ∈ Z,

ctg (−α) = −ctg α, α ≠ πk, k ∈ Z, ctg (α + πn) = ctg α, n ∈ Z, α ≠ πk, k ∈ Z, tg α ⋅ ctg α = 1, α _≠^π^k, k ∈ Z,

k, k ∈ Z,

k, k ∈ Z.

В упражнениях к этому пункту предлагаются задания на упрощение выражений с помощью изученных формул, на нахождение по заданному значению одной из функций sin α, cos α, tg α и ctg α значений остальных функций.

Решения и комментарии

8.22. Вычислите: в) sin α, tg α и ctg α, если π < α <

и cos α = −0,6.

Решение. Так как cos α = −0,6, то sin²α = 1 − cos²α = = 1 − 0,36 = 0,64.

Так как π <α < , то sin α < 0, поэтому

= −0 8, .

tgα = ; ctgα = ^{^[2]}= ³.

tgα 4

И здесь лучше избегать записи sin α = ± 1 − cos²α по описанной выше причине.

8.24. Упростите выражение¹:

ж) ; з) .

з) ^{2 2}₂

sin α − tg ^αsin2α − csinos2α^αsin2α ^⎛⎜⎝1 ⁻_cos12α^⎞⎟⎠

8.27. Вычислите:

a) tg (−80°) + tg (−70°) + tg (−60°) + ... + tg 60° + tg 70° +

+ tg 80°;

в) tg (−80°) tg (−70°) tg (−60°) ... tg 60° tg 70° tg 80°. Решение.

a) tg (−80°) + tg (−70°) + tg (−60°) + ... + tg 60° + tg 70° +

+ tg 80° = −tg 80° − tg 70° − tg 60° − ... + tg 60° + tg 70° + + tg 80° = 0, так как сумма каждой пары слагаемых − tg α + tg α равна нулю, а средний член суммы tg 0° тоже равен нулю.

в) tg (−80°) tg (−70°) tg (−60°) ... tg 60° tg 70° tg 80° = 0, так как средний множитель в произведении tg 0° равен нулю.

Промежуточный контроль. С—30.

8.3. Арктангенс

В данном пункте учебника дано определение арктангенса числа а, из которого получается формула tg (arctg a) = а,

справедливая для каждого числа a ∈ R.

Введение понятия арктангенса можно мотивировать так же, как и введение понятия арксинуса. Это можно сделать при выполнении задания 8.30.

Далее рассмотрена задача: для данного числа a ∈ R найти все углы α, для каждого из которых tg α = а. Здесь впервые получена формула α = arctg a + πп, n ∈ Z.

Эта формула в дальнейшем будет использована при решении простейших тригонометрических уравнений.

Решения и комментарии

8.34. Сравните с нулем: б) arctg 2; д) arctg (−2).

Решение. Можно доказать (как при выполнении задания 7.80), что для любых углов α₁и α₂из промежутка

⎛ π π⎞

^⎜⎝⁻₂; ₂^⎟⎠ равносильны неравенства: tg α₁< tg α₂и α₁< α₂.

Применим это утверждение.

б) Так как arctg 2 и 0 — углы из промежутка ⎜⎝⎛− 2π; 2π⎞⎟⎠ и

tg (arctg 2) = 2 > 0 = tg 0, то из неравенства tg (arctg 2) > > tg 0 следует, что arctg 2 > 0.

д) Так как arctg (−2) и 0 — углы из промежутка ⎛ π π⎞

^⎜⎝⁻₂; ₂^⎟⎠ и tg (arctg (−2)) = −2 < 0 = tg 0, то из неравенства

tg (arctg (−2)) < tg 0 следует, что arctg (−2) < 0.

8.36. Найдите все углы α, для каждого из которых:

ж) tgα = − ³; л).

Ответ. ж) k, k ∈ Z (рис. 37, а);

л) (рис. 37, б).

Дополнительное задание. Существует ли число x, такое, что: a) ; б) arctg x = − ?

Если существует, то найдите его.

Решение. а) х = −1;

б) так как − ^π<arctg x < ^π, а − ²^π< − ^π, то такого числа х

2 2 3 2

8.4*. Арккотангенс

Введение понятия арккотангенса можно мотивировать так же, как и введение понятия арксинуса. Это можно сделать при выполнении задания 8.37.

Надо подчеркнуть принципиальное отличие: arcctg a — это угол из промежутка (0; π). Из определения арккотангенса получается формула ctg (arcctg a) = а, справедливая для каждого числа a ∈ R.

Далее рассмотрена задача: для данного числа a ∈ R найти все углы α, для каждого из которых ctg α = а. Здесь впервые получена формула α = arcctg a + πп, п ∈ Z.

Эта формула в дальнейшем будет использована для решения простейших тригонометрических уравнений.

Решения и комментарии

8.41. Сравните с числом 0,5π: б) arcctg 2; д) arcctg (−2).

Решение. Можно доказать (как при выполнении задания 7.80), что для любых углов α₁и α₂из промежутка (0; π) равносильны неравенства: ctg α₁< ctg α₂и α₁> α₂.

Применим это утверждение.

б) Так как arcctg 2 и 0,5π — углы из промежутка (0; π) и сtg (arcсtg 2) = 2 > 0 = сtg 0,5π, то из неравенства сtg (arcсtg 2) > сtg 0,5π следует, что arcсtg 2 < 0,5π.

д) Так как arcctg (−2) и 0,5π — углы из промежутка (0; π) и сtg (arcсtg (−2)) = −2 < 0 = сtg 0,5π, то из неравенства сtg (arcсtg (−2)) < сtg 0,5π следует, что arcсtg (−2) > 0,5π.

8.43. Найдите все углы α, для каждого из которых:

ж) ctg α = − ³; л).

Ответ. ж) k, k ∈ Z (рис. 38, а);

л) k, k ∈ Z (рис. 38, б).

Рис. 38

Дополнительное задание. Существует ли число х, такое, что: a) arcctg x = ; б) arcctg x = ?

Если существует, то найдите его.

Решение. а) х = 1;

б) так как 0 < arcctg x < π, a > π, то такого числа х не существует.

Промежуточный контроль. С—31.

8.5*. Примеры использования арктангенса и арккотангенса

В данном пункте рассмотрено применение арктангенса и арккотангенса для нахождения всех углов, для каждого из которых справедливы неравенства tg α > a (tg α < а); ctg α > a (ctg α < а). Тем самым подготовлена база для изучения решения простейших тригонометрических неравенств для тангенсов и котангенсов.

Решения и комментарии

В заданиях 8.45—8.47, по сути, требуется решить простейшие тригонометрические неравенства, но задача формулируется в других терминах. Здесь использованы все табличные значения tg α и ctg α, а в задании 8.47 надо использовать арктангенс и арккотангенс.

8.47. в) Найдите все углы α, для каждого из которых tg α > 2.

Решение. Сначала найдем угол α₁∈ ^⎜⎝⎛⁻₂^π; ₂^π⎞^⎟⎠ , такой, что

tg α₁= 2. Это α₁= arctg 2

(рис. 39). Теперь найдем все искомые углы α, для каждого из которых tg α > 2 (им соответствуют точки единичной окружности, выделенные на рисунке 39 жирной дугой):

arctg 2 + πk < α < + πk, k ∈ Z.

Рис. 39

8.6*. Формулы для арктангенса и арккотангенса

В данном пункте учебника доказаны формулы: arctg (−a) = −arctg a,

arcctg (−a) = π − arcctg a,

arctg (tg α) = α, α ∈ ^⎜⎝⎛⁻₂^π; ₂^π^⎞⎟⎠, arcctg (ctg α) = α, α ∈ (0; π).

Здесь же приведены решения задач, связанных с вычислением arctg (tg α) для α ∉ ^⎜⎝⎛⁻₂^π; ₂^π⎞^⎟⎠ , а также arcctg (ctg α) для α ∉ (0; π).

Решения и комментарии

8.52. Вычислите: г) arcctg ctg^⎜⎛ ^⎜⎝⎛− ^π₄⎞^⎟⎠⎞^⎟⎠ ; д) arctg ^⎜⎝⎛tg ⁵₆^π⎞^⎟⎠ .

⎝

Решение. г) arcctg ctg⎜⎛ ^⎜⎝⎛− ^π₄⎞^⎟⎠⎞⎟⎠ = arcctg ctg^⎜⎝⎛ ³₄^π⎞^⎟⎠ = ³₄^π, так ⎝

как );

д) arctg tg^⎜⎝⎛ 5₆π^⎟⎠⎞ = arctg tg^⎜⎝⎛ ^⎜⎝⎛⁻₆^π⎞^⎟⎠⎠⎞^⎟ ^=
−₆^π, так как

− 6π ∈ ⎛⎜⎝− 2π; 2π⎞⎟⎠ .

8.53. Вычислите: a) arctg (tg 5); б) arcctg (ctg 5).

Решение. a) arctg (tg 5) = arctg (tg (5 − 2π)) = 5 − 2π, так как 5 − 2π ∈ ⎜⎝⎛− 2π; 2π⎞⎟⎠;

б) arcctg (ctg 5) = arcctg (ctg (5 − π)) = 5 − π, так как 5 − π ∈ (0; π).

Дополнительные задания.

1. Вычислите sin (arctg а).

Решение. Так как arctg а существует для любого числа a ∈ R, то далее будем считать, что а — любое число. Обозначим β = arctg а, тогда tg β = a.

Вычислим cos²β ⁼2 ¹⁼2¹.

tg β + 1 a + 1

Так как − ^π<β < ^π, то cos β > 0, поэтому

2 2 cosβ = .

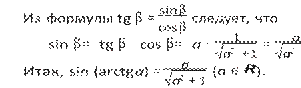
2. Вычислите tg (arcsin a).

Решение. Обозначим β = arcsin а, тогда sin β = а.

Так как tg β не определен для , то ,

поэтому в этой задаче a — любое число, такое, что а ∈ (−1; 1). Вычислим cos²β = 1 − sin²β = 1 − a².

Так как , то cos β > 0, поэтому cosβ = 1 − a².

Теперь вычислим .

Итак, tg(arcsin a) =

Промежуточный контроль.

Контрольная работа № 5.

§ 9. Формулы сложения

9.1. Косинус разности и косинус суммы двух углов

Отметим, что основной формулой, из которой получаются остальные, является формула

cos (α − β) = cos α cos β + sin α sin β. (1)

Она доказывается с помощью скалярного произведения векторов.

Для доказательства формулы

cos (α + β) = cos α cos β − sin α sin β (2)

достаточно выполнить преобразование cos (α + β) = cos (α − (−β)) и применить формулу косинуса разности двух углов и свойства синуса и косинуса.

Решения и комментарии

9.7. Докажите справедливость равенства:

a) cos⎜⎝⎛α − 2π⎞⎟⎠ = sinα; г) cos⎝⎜⎛ 32π +α⎠⎞⎟ = sin α.

Здесь надо доказать формулы, аналогичные формулам для дополнительных углов из п. 9.2, поэтому способ доказательства, основанный на применении формул (1)—(2), должен быть усвоен учащимися.

Решение. a) cos^⎜_⎝⎛α ⁻₂^π^⎞⎟_⎠= cos α ⋅cos ₂^π+ sin α ⋅ sin ₂^π=

= cos α ⋅ 0 + sin α ⋅ 1 = sin α;

⎛ 3π ⎞ ³^π⋅cos α − sin ³^π⋅ sin α =

г) cos ^⎜⎝ ₂+α^⎟⎠ = cos _{2 2}

= 0 ⋅ cos α − (−1) ⋅ sin α = sin α.

9.12. Вычислите: а) cos 135°; б) cos 15°.

Решение. а) cos 135° = cos (90° + 45°) = cos 90° ⋅ cos 45° −

− sin 90° ⋅ sin 45° = 0⋅ ²−1⋅ ²= − ²;

2 2 2

б) cos 15° = cos (45° − 30°) = cos 45° ⋅ cos 30° +

+ sin 45° ⋅ sin 30° = ²⋅ ³+ ²⋅ ¹₌⁶⁺².

2 2 2 2 4

9.13. а) Вычислите cos 75° + cos 15°.

Решение. cos 75° + cos 15° = cos (45° + 30°) + cos (45° − 30°) =

= cos 45°⋅ cos 30°− sin 45°⋅ sin 30°+cos 45°⋅ cos 30°+

+sin 45°⋅ sin 30° = 2 cos 45° ⋅ cos 30° = 2 ⋅ ²⋅ ³= ⁶.

2 2 2

9.14. Упростите выражение:

а) cos (45° + α) cos (45° − α) − sin (45° − α) sin (45° + α);

б) cos ⎜⎝⎛ 2₃π +α⎟⎠⎞ +cos ⎜⎝⎛ ²₃^π− α^⎞⎟⎠ +cosα;

в) cos²(60° + β) + cos²(60° − β) + cos²β. Решение.

а) cos (45° + α) cos (45° − α) − sin (45° − α) sin (45° + α) = = cos (45° + α + 45° − α) = cos 90° = 0;

б) cos ⎜⎝⎛ 23π +α⎟⎠⎞ +cos ⎜⎝⎛ 23π − α⎠⎞⎟ +cos α = cos 23π cosα −

=2cos ²3^πcos α +cos α = 2⋅ −⎛⎝⎜ ₂¹⎟⎞⎠ cosα +cosα = 0;

в) cos²(60 ) + cos²(60

9.18. а) Найдите наибольшее и наименьшее значения выражения cos α − 3 sinα.

Решение. Сначала преобразуем данное выражение: cos α − 3 sinα = 2 ⎜⎝⎛ ₂¹cos α − ₂sin α⎞⎟⎠ =

= 2 ⎜⎝⎛cos cos α − sin ₃^πsin α⎠⎟⎞ = 2cos ⎜⎛⎝ ₃^π+α⎞⎟⎠.

Так как наибольшим и наименьшим значениями выра-

⎛ π ⎞ жения ^cos^⎜⎝ ₃+α^⎟⎠ являются числа 1 и −1 соответственно, то

наибольшим и наименьшим значениями выражения

cosα − 3 sinα являются числа 2 и −2 соответственно.

9.2. Формулы для дополнительных углов

В этом пункте доказаны две формулы:

⎛ π ⎞ ⎛ π ⎞

cos ⎜⎝ ₂− α⎟⎠ = sin α и sin ⎝⎜ ₂− α⎠⎟ = cos α,

которые очень часто используются в дальнейшем.

Решения и комментарии

9.22. Упростите выражение: а) sin (90° − 13°);

б) sin (−90° + 24°).

Решение. а) sin (90° − 13°) = cos 13°;

б) sin (−90° + 24°) = −sin (90° − 24°) = −cos 24°.

9.23. Выразите число через синус или косинус положительного угла, не превышающего 45°: е) sin 1859°; ж) cos 444°. Решение. е) sin 1859° = sin (5 ⋅ 360° + 59°) = sin 59° =

= sin (90° − 31°) = cos 31°;

ж) cos 444° = cos (360° + 84°) = cos 84° = cos (90° − 6°) = = sin 6°.

9.24. Выразите число через синус или косинус положительного угла, не превышающего :

e) cos; ж) sin.

Решение. е) cos 14π = cos ⎛⎜⎝2π + 45π⎞⎟⎠ = cos 45π = sin ⎜⎛⎝ 2π − 45π⎞⎟⎠ =

= sin ⎜⎝⎛− 310π⎞⎠⎟ = − sin 310π = − sin⎝⎜⎛ 2π − 5π⎞⎟⎠ = −cos 5π.

ж) sin 24π = sin ^⎜⎝⎛4π − ⁴₇^π⎞⎠⎟ = sin ^⎜⎛⎝− ⁴₇^π⎠^⎟⎞ = − sin ⁴₇^π=

₇

= −cos ⎜⎝⎛ 2π − 47π⎞⎟⎠ = −cos ⎛⎜⎝− 14π ⎞⎠⎟ = −cos 14π .

9.3. Синус суммы и синус разности двух углов

В данном пункте учебника доказаны формулы синуса суммы и синуса разности двух углов:

sin (α − β) = sin α cos β − cos α sin β, sin (α + β) = sin α cos β + cos α sin β.

Обратим внимание на то, что в учебнике уже доказаны формулы для sin (π + α), cos (π + α) (п. 7.4), cos ^⎜⎝⎛ ₂^π− α⎞^⎟⎠ и

⎛ π ⎞

sin ^⎜⎝ ₂− α^⎟⎠ (п. 9.2). Только с доказательством формул для cos (α ± β) и sin (α ± β) появилась возможность доказать формулы для ^cos^⎜⎝⎛ π₂k ±α^⎟⎠⎞ и ^sin^⎜⎝⎛ ^π₂^k±α⎞^⎟⎠ для любого целого k.

Так как значения синуса и косинуса не изменяются от прибавления (вычитания) 2π к аргументу, то синус (косинус) любого из указанных выше аргументов нетрудно свести к синусу (косинусу) аргументов − α, +α, π − α, π +α, − α, +α, которые можно привести к аргументу α, при-

меняя формулы синуса (косинуса) суммы (разности) двух углов.

Выпишем все 12 формул для указанных выше шести аргументов:

⎛ π ⎞ ⎛ π ⎞

sin ⎜⎝ ₂− α⎟⎠ = cos α, sin ⎜_⎝₂+α⎟_⎠= cos α, sin (π − α) = sin α,

⎛ π ⎞ ⎛ π ⎞

cos ⎜⎝ ₂− α⎟⎠ = sin α, cos ⎜_⎝₂+α_⎠⎟= − sin α, cos (π − α) = −cos α,

⎛ 3π ⎞ ⎛ 3π ⎞

sin ⎜⎝ ₂− α⎟⎠ = −cos α, sin ⎜⎝ ₂+α⎟⎠ = −cos α, sin (π + α) = −sin α,

cos ^⎜_⎝⎛ 3₂π − α^⎟_⎠⎞ = − sin α, cos _⎝⎛^⎜ ³₂^π+α_⎠^⎟⎞= sin α, cos (π + α) = −cos α.

Все эти формулы можно воспроизводить с помощью следующего мнемонического правила:

1) Если первое слагаемое аргумента есть или , то в правой части формулы надо заменить синус на косинус (косинус на синус). Если первое слагаемое аргумента π, то менять синус (косинус) не надо.

2) В правой части формулы надо поставить знак «−», только если для острого угла α значение синуса (косинуса) в левой части формулы отрицательно.

Эти формулы называют часто формулами приведения (аргумента к более простому виду). Но специального пункта «Формулы приведения» в учебнике нет. Однако стоит уделить внимание известному мнемоническому правилу, позволяющему правильно воспроизводить любую из формул приведения. Это правило отвечает на два вопроса: 1) менять или не менять наименование функции (синус на косинус, косинус на синус); 2) ставить или нет в правой части формулы знак «−»?

Но известен и менее формальный его вариант, который учителя математики передают из поколения в поколение. Обычно рассказывают такую историю.

В старые добрые времена жил рассеянный математик, который при поиске ответа на вопрос 1 смотрел на свою ученую лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента ±α, π ±α, ±α, ... . Если лошадь кивала

головой вдоль оси Оу, то математик считал, что получен ответ «да, менять», если вдоль оси Ox — «нет, не менять».

Можно посоветовать учащимся, за неимением ученой лошади, самим кивать головой вдоль той оси координат, которой принадлежит точка, соответствующая первому слагаемому аргумента. Так они получат ответ на вопрос 1. Разумеется, они должны понимать, что это шутка, что формулы доказаны, а «лошадиное» правило лишь помогает им определить функцию угла α для правой части формулы.

Ответ на вопрос 2 получается так. Хотя формулы приведения доказаны для любого угла α, достаточно определить знак левой части формулы для острого угла α и поставить его перед sin α или cos α в правой части формулы.

Например, ^sin^⎜⎝⎛ 3₂π − α^⎟⎠⎞ = −cosα; ^cos^⎜⎛⎝³₂^π+α⎞^⎟⎠ = sinα.

Решения и комментарии

9.30. Упростите выражение:

а) 3 sin α − cos α; б) ²(cos α − sin α).

При решении этого задания формулы (1) и (2) применяются для формирования умения преобразовывать тригонометрические выражения с помощью вспомогательного угла. Тот же прием используется при решении задания

9.33.

Решение.

а)sinα − 2¹cosα = cos 6^πsinα − sin 6^πcosα = sin ⎝⎜⎛α − ₆^π⎞⎟⎠ ;

б)(cos α − sin α) = cos ^π4 cos α − sin ^π4 sin α = cos ⎝⎜⎛ ^π₄+α⎞⎟⎠ . ₂

9.33. б) Найдите наибольшее и наименьшее значения выражения 5 cos α + 12 sin α.

Решение. Так как 5²+12²=13, то 5 cos α + 12 sin α =

=13^⎜⎝⎛ ₁₃⁵cosα + ¹²₁₃sinα⎞^⎟⎠ = A.

⎛ 5 ⎞2 ⎛ 12 ⎞2

Так как ⎜⎝ ₁₃⎟⎠ + ⎜⎝ ₁₃⎟⎠ =1, то найдется угол β, такой, что

sin β = , а cos β = . Тогда

A = 13 (sin β cos α + sin α cos β) = 13 sin (β + α).

Так как наибольшее и наименьшее значения выражения sin (β + α) равны 1 и −1 соответственно, то наибольшее и наименьшее значения выражения А равны 13 и −13 соответственно.

Промежуточный контроль. С—32, С—33.

9.4. Сумма и разность синусов и косинусов

В данном пункте учебника доказаны формулы:

sin α + sin β = 2sin ^{α
+ β}cos ^{α − β}, (1)

2 2

sin α − sin β = 2sin ^{α
− β}cos ^{α + β}, (2)

2 2

cos α +cos β = 2cos ^{α
+ β}_cos ^{α
− β}, (3)

2 2

cos α − cos β = −2sin ^{α
− β}sin ^{α + β}. (4)

2 2

Для лучшего запоминания формул (1)—(4) надо обратить внимание учащихся на то, что в левой части каждой из них стоят суммы или разности одноименных функций от α и β, а справа — удвоенные произведения двух функций от полусуммы или полуразности этих углов. Воспроизводить эти формулы будет легче, если учащиеся запомнят идею их доказательства: надо сложить или вычесть sin (x + у) и sin (x − у) или cos (x + у) и cos (x − у).

В правой части каждой из формул (1)—(4) знак между α и β в числителе первого аргумента совпадает со знаком между функциями в левой части формулы.

Не рекомендуем правую часть формулы (4) записывать β −α α + β

без знака «минус»: 2sin sin . Учащиеся должны за-

2 2

помнить, что знак «−» в правой части формул (1)—(4) ставится только при вычитании косинусов.

Решения и комментарии

9.38. а) Докажите справедливость равенства

sin 50° + sin 10° − cos 20° = 0.

Решение. sin 50° + sin 10° − cos 20° = 2 sin 30° cos 20° −

что и требовалось доказать.

9.40. а) Докажите справедливость равенства

Решение. cos 512π +cos 712π = 2cos 2π cos ⎛⎜⎝− 12π ⎟⎠⎞ =

= 2 0⋅ ⋅cos ^⎜⎝⎛⁻₁₂^π⎞^⎟⎠ = 0, что и требовалось доказать.

9.41. в) Вычислите .

Решение. Формулы для cos α cos β, sin α sin β, sin α cos β еще будут изучаться в п. 9.6, необязательном для изучения на базовом уровне. Здесь же воспользуемся равенством cos (х + у) + cos (x − у) = 2 cos x cos у, полученном при доказательстве формул (1)—(4). Из него нетрудно получить формулу cos x cos у = (cos (х + у) + cos (x − y)), с помощью которой выполним вычисления:

cos 752° ⋅cos 152° = 21 ⎛⎜cos ⎛⎜⎝ 752° + 152°⎠⎟⎞ +cos ⎝⎜⎛ 752° − 152°⎠⎟⎞⎞⎟⎠ = ⎝

= 21 (cos 45° +cos 30° =) 21 ⎛⎜⎝ 22 + 23 ⎠⎞⎟ = 2 +4 3 .

Промежуточный контроль. С—34.

9.5. Формулы для двойных и половинных углов

В данном пункте учебника доказаны формулы:
sin 2α = 2 sin α cos α,	(1)
cos 2α = cos²α − sin²α,	(2)

sin²α 1 − cos α, (3)

cos². (4)

Идею доказательства формул (1)—(2) — в формулах для sin (α + β) и cos (α + β) заменить β на α — учащиеся должны обязательно знать.

Не рекомендуем формулы (3) и (4) записывать в виде sin α = ± 1 − cosα, cos α = ± ¹⁺^cos^α,

2 2 2 2

так как учащиеся могут подумать, что для каждого α существует два значения sin или cos, а это не так.

Решения и комментарии

9.62. а) Докажите справедливость равенства

(sin α + sin β)²+ (cos α + cos β)²= 4 cos².

Доказательство. (sin α + sin β)²+ (cos α + cos β)²= sin²α +

+ 2 sin α sin β + sin²β + cos²α + 2 cos α cos β + cos²β =

= 2 + 2sinα sin β + 2 cos α cos β = 2 + 2 (cos α cos β + sin α sin β) = = 2 + 2 cos (α − β) = 2 (1 + cos (α − β)) = 4 cos²,

что и требовалось доказать.

9.63. а) Докажите справедливость равенства sin 2α (sin 2α + sin 2β) + cos 2α (cos 2α + cos 2β) = 2 cos²(α − β). Доказательство. sin 2α (sin 2α + sin 2β) +

+ cos 2α (cos 2α + cos 2β) = sin²2α + sin 2α sin 2β + cos²2α + + cos 2α cos 2β = 1+ cos (2α − 2β) = 2 cos²(α − β), что и требовалось доказать.

9.64. а) Вычислите cos ^πcos ^πcos ^π.

Решение. Для решения этой задачи умножим и разделим выражение на 8 sin π ⎛⎜sin π ≠0⎞⎟ и преобразуем получен-

9 ⎝ 9 ⎠

ную дробь, применяя 3 раза формулу синуса двойного угла:

⎛ ⎛ π π⎞ 2π⎞ 4π

2 ⎜2 ⎜ π π π ⎝ ⎝2sin 9 cos 9 ⎟⎠ cos 9 ⎟⎠ cos 9

cos coscos==

⁹8sin

⎛ 2π 2π⎞ 4π π cos 4π sin8π

= 2 ⎜_⎝2sin 9 cos 9 ⎟_⎠cos ₉= 2sin ₉₌₉^π= ⁸1_,

8sin 8_sin 8sin 9

так как sin 89π = sin ⎛^⎜⎝π ⁻₉π⎞^⎟⎠ = sin ₉^π.

Применение рассмотренного приема в следующем задании не так очевидно.

Дополнительное задание. Вычислите cos ^π− sin ^π.

Для решения задачи сначала приведем данное выражение к разности одноименных функций:

cos 25π − sin 310π = sin ⎛⎝^⎜₂π ⁻2₅π⎠⎞^⎟ − sin 3₁₀π = sin ₁₀π − sin 3₁₀π.

Теперь, применив формулу разности синусов, получим:

sin π − sin 3π = 2sin ⎛⎜⎝− 10π ⎟⎠⎞ cos 210π = −2sin 10π cos 210π.

10 10

Умножим и разделим полученное произведение на 2cos

⎛ π ⎞

⎜⎝cos ₁₀≠ 0⎟⎠ и применим два раза формулу синуса двойного

угла:

⎛ π π ⎞ 2π 2π cos2π

2 ⎜⎝2sin10cos10 ⎟⎠ cos10 2sin

−2sin ^πcos ²^π= − = − 10 10 =

^{10 10}2cos 2cos

⁴^π⎛ π π ⎞

sin sin⎜ − ⎟ _cos^π

⎝ 2 10 ⎠

= − = − = − = −.

2cos 2cos 2cos

Итак, cos π − sin ^π= − .

Промежуточный контроль. С—35.

9.6*. Произведение синусов и косинусов

В этом пункте доказаны три формулы: sin α cos β =(sin (α + β) + sin (α − β)), cos α cos β =(cos (α + β) + cos (α − β)),

sin α sin β = (cos (α − β) − cos (α + β)).

Эти формулы относятся к таким, которые проще вывести заново, если они не запомнились надежно. И здесь запоминанию формул способствует опора на чередование функций для синуса суммы или разности двух углов, косинуса суммы или разности двух углов.

Решения и комментарии

9.65. а) Преобразуйте в сумму или в разность cos 3α cos α.

Решение. cos 3α cosα = (cos (3α +α +) cos (3α − α)) =

= (cos 4α +cos 2α) = cos 4α + cos 2α.

9.66. а) Докажите, что

sin 9π cos 5π − sin ⁶^πcos ^π= ¹− ¹sin ^π.

28 28 35 35 2 2 5

Доказательство.

sin 928π cos 528π − sin 635π cos 35π = 21 ⎛⎜⎝sin⎛⎜⎝ 928π + 528π⎠⎞⎟ + sin ⎜⎝⎛ 928π − 528π⎟⎞⎠⎟⎠⎞ −

− 1 ⎛⎜sin ⎛⎝⎜ 635π + 35π ⎠⎞⎟ + sin ⎜⎝⎛ 635π − 35π ⎠⎞⎟⎟⎞⎠ = 21 ⎛⎜⎝sin 2π + sin 7π⎟⎞⎠ −

2 ⎝

− 2¹⎛^⎜⎝sin ₅^π+ sin ₇^π⎞^⎟⎠ ⁼₂¹⁻₂¹sin ₅^π, что и требовалось доказать.

Докажите, что если α, β, γ — углы треугольника, то выполняется равенство (9.69—9.71):

9.69. а) 4_cos^α_cos^β_cos^γ= sin α + sin β + sin γ.

2 2 2

Доказательство. Преобразуем правую часть равенства, учитывая, что γ = 180° − (α + β):

+2sin cos = 2sin ⎜cos +cos ⎟ =

2 2 2 2 2

= 2sin 2 ⋅2cos ^α2 cos = 4sin ⎜⎝90° − ₂⎠⎟ ⋅cos ^α₂cos ₂=

₂

, что и требовалось доказать.

9.70. а) sin²α + sin²β + sin²γ = 2 + 2 cos α cos β cos γ. Доказательство. Сначала преобразуем отдельно левую

(А) и правую (В) части доказываемого равенства, учитывая, что γ = 180° − (α + β).

А = sin²α + sin²β + sin²γ = sin²α + sin²β +

+ sin²(180° − (α + β)) = sin²α + sin²β + sin²(α + β) = sin²α +

+ sin²β + (sin α cos β + sin β cos α)²= sin²α + sin²β + + sin²α cos²β + 2sin α cos α sin β cos β + sin²β cos²α.

В = 2 + 2 cos α cos β cos γ =

= 2 + 2 cos α cos β cos (180° − (α + β)) =

= 2 − 2 cos α cos β cos (α + β) =

= 2 − 2 cos α cos β (cos α cos β − sin α sin β) =

= 2 − 2 cos²α cos²β + 2 sin α sin β cos α cos β =

= 2 − cos²α (1 − sin²β) − (1 − sin²α) cos²β +

+ 2 sin α sin β cos α cos β = 2 − cos²α + sin²β cos²α − cos²β+

+ sin²α cos²β + 2 sin α sin β cos α cos β = sin²α + sin²β + + sin²α cos²β + 2 sin α cos α sin β cos β + sin²β cos²α.

Таким образом, А = В, что и требовалось доказать. 9.71. а) sin 2α + sin 2β + sin 2γ = 4 sin α sin β sin γ.

Доказательство. Преобразуем левую часть доказываемого равенства, учитывая, что γ = 180° − (α + β).

sin 2α + sin 2β + sin 2γ = 2sin (α + β) cos (α − β) +

+ 2 sin γ cos γ = 2 sin (180° − γ) cos (α − β) +

+ 2sin γ cos (180° − (α + β)) = 2sin γ cos (α − β) − − 2sin γ cos (α + β) = 2sin γ (cos (α − β) − cos (α + β)) = = 2sinγ ⎜⎝⎛−2sin α − β 2− α − β sin α − β +2 α + β ⎟⎞⎠ = 4 sinα sinβ sinγ,

что и требовалось доказать.

Промежуточный контроль. С—36.

9.7*. Формулы для тангенсов

В этом пункте доказаны формулы:

⎛ π ^πn, n ∈ Z, α +β ≠ 2^π+ πm, m ∈ Z^⎞⎟_⎠,

⎜⎝

⎛ π Z, β ^≠^π+ πn, n ∈ Z, α − β ^≠^π+ πm, m ∈ Z),

^⎜_⎝k, k ∈ _{2 2}

⎛ π ⎞ Z), tg ⎜_⎝₂− α⎟_⎠= ctgα (α ≠ πk, k ∈ tg 2 α = 12tg α2 ⎛⎜⎝α ≠ π4 + π2k k, kn, n ∈ Z⎟⎠⎞, − tg α

n, n ∈ Z), n, n ∈ Z),

а также формулы

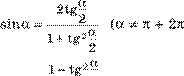n, n ∈ Z),

n, n ∈ Z).

Заметим, что каждая из этих формул справедлива не для всех значений α и β, а лишь для тех, которые записаны в скобках после каждой формулы.

Здесь же приведены примеры применения этих формул.

Решения и комментарии

9.78. а) Докажите справедливость равенства tg π + tg ³^π+ tg ^πtg ³^π=1.

16 16 16 16

Доказательство. Пользуясь формулой

tg α + tg β = tg (α + β) (1 − tg α tg β), (1)

которая следует из формулы для tg (α + β), преобразуем левую часть доказываемого равенства:

16 16 16 16 16

Докажите, что если α, β, γ — углы треугольника, то выполняется равенство (9.84—9.85):

9.84. а) tg α + tg β + tg γ = tg α tg β tg γ.

Доказательство. Преобразуем левую часть равенства, используя формулу (1) и учитывая, что γ = 180° − (α + β):

tg α + tg β + tg γ = tg α + tg β + tg (180° − (α + β)) =

= tg α + tg β − tg (α + β) = tg (α + β) (1 − tg α tg β) − tg (α + β) =

= tg (α + β) (1 − tg α tg β − 1) = tg (180° − γ) (−tg α tg β) = = − tg γ (−tg α tg β) = tg α tg β tg γ,

что и требовалось доказать.

Здесь α, β и γ — углы треугольника и подразумевается, что имеют смысл tg α, tg β и tg γ. Следовательно, рассматриваются лишь треугольники, в которых нет прямых углов, и для углов таких треугольников проведенные выкладки справедливы.

9.85. а) ctg α ctg β + ctg α ctg γ + ctg β ctg γ = 1.

Доказательство. Здесь α, β и γ — углы треугольника и подразумевается, что имеют смысл ctg α, ctg β и ctg γ. Рассмотрим два случая: 1) среди этих углов нет прямого угла; 2) один из этих углов прямой.

В первом случае имеют смысл tg α, tg β и tg γ, и так как α, β и γ — углы треугольника, то tg α ≠ 0, tg β ≠ 0 и tg γ ≠ 0. Поэтому для таких углов, учитывая, что γ = 180° − (α + β), справедливы следующие равенства:

ctg α ctg β + ctg α ctg γ + ctg β ctg γ =

= ctg α ctg β + (ctg α + ctg β) ctg γ =

= ctg α ctg β + (ctg α + ctg β) ctg (180° − (α + β)) = = ctg α ctg β − (ctg α + ctg β) ctg (α + β) =

⎛ ⎞

⋅ =

что и требовалось доказать.

Следовательно, в первом случае равенство доказано.

Во втором случае есть один прямой угол, например, угол α — прямой. Тогда углы β и γ = − β — острые. Так как ctg α = 0, то доказываемое равенство перепишется в виде ctgβctg ^⎜⎝⎛ ₂^π− β⎞^⎟⎠ =1.

⎛ π ⎞

Так как ^ctg^⎜⎝ ₂− β^⎟⎠ = tg β и ctg β tg β = 1, то и во втором

случае требуемое равенство доказано. Следовательно, равенство ctg α ctg β + ctg α ctg γ + ctg β ctg γ = 1 справедливо для любого треугольника.

9.86. Для углов α, таких, что ⁿ, n ∈ Z, докажи-

те справедливость равенства

. (2)

Доказательство. Для любых α справедливы равенства sin 3α = sin 2α cos α + sin α cos 2α = 2 sin α cos²α +

+ sin α (cos²α − sin²α) = 3 sin α cos²α − sin³α, cos 3α = cos 2α cos α − sin α sin 2α = (cos²α − sin²α) cos α −

− 2 sin²α cos α = cos³α − 3 sin²α cos α,

т. е. справедливы равенства

sin 3α = 3 sin α cos²α − sin³α, (3) cos 3α = cos³α − 3 sin²α cos α.

Так как для , n ∈ Z, имеет смысл tg 3α, что, в

частности, означает, что cos 3α ≠ 0 для этих углов, то, используя равенства (3), получаем, что справедливы равенства

. (4)

Так как cos α ≠ 0 для ⁿ, n ∈ Z, то, разделив чис-

литель и знаменатель дроби в правой части равенства (4) на cos³α, получим, что справедливо равенство

3tg α − tg³α tg α (3 − tg²α) tg 3α ⁼2 ⁼2 .

1 − 3tg α 1 − 3tg α

Тем самым требуемое равенство (2) доказано для всех α ≠ ^π+ ^πⁿ, n ∈ Z, что и требовалось доказать.

6 3

Промежуточный контроль. С—37.

§ 10. Тригонометрические функции числового аргумента

В этом параграфе учебника изучаются тригонометрические функции не угла, а числа. Изучение всех тригонометрических функций числового аргумента опирается на изученные ранее свойства тригонометрических функций угла и строится по одной и той же схеме. Сначала формулируются и обосновываются свойства функции, затем строится ее график.

Перед п. 10.1 даны определения периодической функции и ее главного периода. Обратим внимание на то, что в определении периодической функции f (x) с периодом T (T ≠ 0) требуется, чтобы для любого значения x из области определения функции числа x + Т и x − Т (Т ≠ 0) также принадлежали этой области определения и выполнялось равенство f (x + T) = f (x). Далее в учебнике доказано, что из данного определения следует справедливость равенства f (x − Т) = f (x), что иногда требуется по определению.

Определение периодической функции можно дать иначе: если для любого значения x из области определения функции f (x) справедливы равенства

f (x + T) = f (x − T) = f (x), (1)

то функцию f (x) называют периодической с периодом Т (Т ≠ 0). При таком определении проверять принадлежность х + Т и x − Т области определения функции f (x) не требуется, так как, естественно, подразумевается, что если справедливы равенства (1), то имеют смысл выражения f (x + Т) и f (х − Т), поэтому x + Т и x − Т принадлежат области определения функции f (x).

10.1. Функция у sin x

В данном пункте дано определение функции у = sin x, сформулированы и обоснованы ее свойства, строится ее график. При построении графика можно рекомендовать учащимся использовать один и тот же единичный отрезок, равный 1 см, по осям Ох и Оу. Тогда точка π на оси Ох будет правее точки 3. При правильном построении графика прямая у = х должна оказаться касательной к графику функции у = sin х в точке О (0; 0) (рис. 40). Этот факт можно сообщить учащимся для самоконтроля. Он будет до-

Рис. 40

казан позже, при вычислении производной функции у = sin х в точке х = 0 (в 11 классе). Главным периодом функции у = sin х является число Т = 2π, что будет доказано в п. 10.2.

Решения и комментарии

10.7. Сравните: а) sin и sin ; г) sin и sin.

Решение. а) Числа принадлежат промежутку

^⎡⎢⎣⁻2^π; ^π^⎤⎥⎦, на котором функция y = sin x возрастает, ₇^π< ³₇^π, ₂следовательно, sin π < sin ^π.

г) Числа 3π и принадлежат промежутку ⎡π; 3π⎤, на

5 5 ⎢⎣2 2 ⎥⎦

котором функция у = sin x убывает, ³^π< ⁴^π, следовательно,

5 5

sin π > sin ^π. 10.8. Постройте график функции:

а) y = |sin x |; б) у = sin (π − х); в) y = 2_sin^x_cos^x;

2 2

г) y = sin | x |; д) y = |sin x − 0,5|; е) у = sin х − 1.

Решение. а) Чтобы построить график функции у = |sin x |, нужно сохранить точки графика функции у = sin x, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки графика функции y = sin x, расположенные ниже оси Ох (рис. 41).

б), в) Учащиеся должны обнаружить, что данную функцию можно записать в виде у = sin x, поэтому ее график — синусоида (см. рис. 40).

г) Чтобы построить график функции у = sin | x |, нужно сохранить точки графика функции у = sin x, расположенные правее и на оси Оу, и, симметрично отразив эту часть

Рис. 41

графика функции у = sin x относительно оси Оу, получить вторую часть искомого графика функции (рис. 42).

д) Чтобы построить график функции у = |sin x − 0,5|, нужно перенести график функции у = sin x на 0,5 единицы вниз, затем сохранить точки полученного графика, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки, расположенные ниже оси Ох (рис. 43).

е) График функции у = sin x − 1 получен переносом

графика функции у = sin x на 1 единицу вниз (рис. 44).

10.9. Сколько корней имеет уравнение:

а) sin x = x²; в) sin x = ^x; г) sin x = ^x?

10 100

Решение. а) Функция f (x) = sin x принимает значения лишь из промежутка [−1; 1], а функция g (x) = х²принимает значения из того же промежутка лишь при x ∈ [−1; 1], поэтому уравнение может иметь корни лишь на отрезке [−1; 1]. Построим графики функций у = sin x и у = х²(рис. 45).

При x ∈ [−1; 0) имеем f (x) < 0, a g (x) > 0, поэтому на этом промежутке графики функций не имеют общих точек, а значит, уравнение sin x = x²не имеет корней.

Так как f (0) = g (0), то x₁= 0 — корень уравнения sin х = х².

На промежутке (0; 1] графи- Рис. 45 ки функций имеют единственную общую точку, значит, уравнение sin x = x²имеет еще один корень.

Итак, уравнение sin x = х²имеет два корня. Замечание. При решении этой задачи мы вынуждены опираться на графики функций. Вывод о существовании точки пересечения графиков на промежутке (0; 1] следует из того, что разность функций f (x) − g (x) в точке положительна, а в точке 1 отрицательна. Значит, есть хотя бы

⎛ π ⎞

одна точка из интервала ⎜⎝ 6 ; 1⎟⎠, где эта разность равна нулю. Вывод о единственности такой точки следует из возрастания обеих функций на промежутке ⎡π; 1⎤ с сохранени⎢⎣6 ⎥⎦

ем выпуклости вверх одного графика и выпуклости вниз другого. Этот материал будет изучаться в 11 классе.

в) Функция f (x) = sin x принимает все значения из

промежутка [−1; 1], а функция g x( ) ⁼^xпринимает все зна-

чения из того же промежутка при x ∈ [−10; 10]. Поэтому уравнение имеет корни лишь на отрезке [−10; 10].

Так как обе функции нечетные, то сначала рассмотрим их на промежутке [0; 10] (рис. 46). На промежутках [π; 2π] и [3π; 10] функция f (x) принимает неположительные зна-

Рис. 46

чения, а функция g (x) — положительные. Поэтому на этих промежутках графики функций не пересекаются. На каждом из промежутков [0; π] и [2π; 3π] графики функций пересекаются в двух точках, следовательно, на промежутке [0; 10] графики функций пересекаются в четырех точках, поэтому на промежутке [0; 10] данное уравнение имеет 4 корня. Столько же корней оно имеет на промежутке [−10; 0]. Но так как корень х = 0 входит в оба эти промежутка (он учтен дважды), то всего исходное уравнение имеет 7 корней. Отметим, что и в этом решении мы вынуждены опираться на графики.

г) Функция f (x) = sin x принимает все значения из

промежутка [−1; 1], а функция g x( ) ⁼^xпринимает все

100

значения из того же промежутка при x ∈ [−100; 100]. Поэтому уравнение имеет корни лишь на отрезке [−100; 100]. Рассмотрим эти функции на промежутке [−100; 100]. В отрезке [0; 100] укладывается 15 полных периодов 2π и один неполный, изображенный на рисунке 47. На каждом из этих 16 промежутков графики функций пересекаются в двух точках. Всего на промежутке [0; 100] имеется 32 точки пересечения, считая и точку x = 0.

В силу симметричности графиков функций относительно начала координат на промежутке [−100; 0] также имеется 32 точки пересечения, считая и точку x = 0, поэтому всего точек пересечения 32 + 32 − 1 = 63 (точка х = 0 была

учтена дважды). Следовательно, уравнение sin x = ^xимеет 100 63 корня. И в этом решении мы вынуждены опираться на графики.

Дополнительное задание. Постройте график функции у = |sin x | + sin x.

Решение. При тех значениях x, для которых sin х ≥ 0, функция задается формулой у = 2sin x; при тех значениях x, для которых sin х < 0, функция задается формулой у = 0. На рисунке 48 график функции у = sin x изображен серой линией, а график функции у = |sin х | + sin x — черной линией.

10.2. Функция у cos х

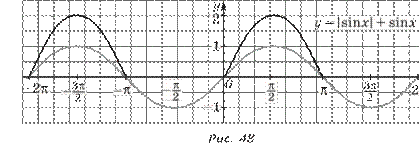
В данном пункте учебника дано определение функции у = cos x, сформулированы и обоснованы ее свойства, строится ее график. При построении графика используется график функции у = sin x. В конце пункта разобраны две задачи, в которых доказывается, что у функций у = sin x и у = cos х не существует положительного периода, меньшего Т = 2π. Тем самым доказано, что Т = 2π является главным периодом функций у = sin х и y = cos x. Решения и комментарии

10.17. Постройте график функции:

а) у = |cos х |; б) у = cos (π − х).

Решение. а) Чтобы построить график функции у = |cos x |, нужно сохранить точки графика функции у = cos х, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки графика функции у = cos x, расположенные ниже оси Ох (рис. 49).

б) Так как cos (π − х) = −cos x, то график функции у = cos (π − х) получится симметричным отражением косинусоиды у = cos x относительно оси Ох.

Рис. 49

10.18. Сколько корней имеет уравнение:

а) cos x = x²; б) cos x = −х²; в) cos x = ^x; г) cos x = ^x?

10 100

Ответ. а) 2 корня; б) нет корней; в) 7 корней;

г) 63 корня.

10.3. Функция у tg x

В данном пункте учебника дано определение функции у = tg x, сформулированы и обоснованы ее свойства, строится ее график. Главным периодом функции у = tg х является число Т = π. Этот факт будет доказан в п. 10.4. При правильном построении графика прямая у = х должна оказаться касательной к графику функции у = tg x в точке О (0, 0). Этот факт можно сообщить учащимся для самоконтроля. Он будет доказан в 11 классе с помощью вычисления производной функции у = tg х в точке x = 0.

Решения и комментарии

10.24. Сравните: а) tg и tg ; г) tg и tg .

Решение. а) Числапринадлежат промежутку ⎛⎜⎝− 2^π; 2^π⎞⎟⎠, на котором функция 7^π_>8^π,

у = tg x возрастает,

следовательно, tg π > tg π.

7 8

г) Числа 1110π и 1310π принадлежат промежутку ⎛^⎜⎝ ₂π; 3₂π⎞^⎟⎠ ,

на котором функция у = tg x возрастает, ¹¹^π_<¹³^π, следова-

10 10

тельно, tg π < tg ^π. 10.25. Постройте график функции:

a) y = |tg x |; б) y = tg | x |; в) y = tg (π − x);

г) y = tg x − 1; д) y = |tg x −1|; е) у = tg x cos x.

Решение. а) Чтобы построить график функции у = |tg x |, нужно сохранить точки графика функции y = tg x, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки графика функции у = tg x, расположенные ниже оси Ох (рис. 50).

б) Чтобы построить график функции у = tg | x |, нужно сохранить точки графика функции у = tg х, расположенные правее и на оси Оу, и, симметрично отразив эту часть графика функции у = tg x относительно оси Оу, получить вторую часть искомого графика функции (рис. 51).

в) Так как tg (π − x) = tg (−x) = −tg x, то график функции у = tg (π − х) получится из графика функции у = tg x с помощью симметрии относительно оси Ох.

г) График функции у = tg x − 1 получится из графика функции у = tg x с помощью переноса на 1 единицу вниз

(рис. 52).

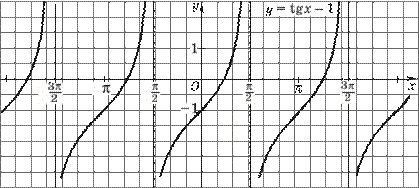
Рис. 52

д) Чтобы построить график функции y = |tg x − 1|, нужно перенести график функции у = tg x на 1 единицу вниз, затем сохранить точки полученного графика, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки графика, расположенные ниже оси Ох (рис. 53).

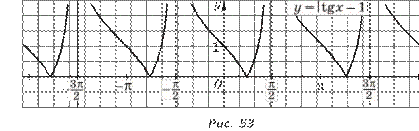
е) Так как функция y = tg x cos x определена для всех х, кроме x n, n ∈ Z, и для всех таких x верно равенство tg x cos x = sin х, то график функции у = tg x cos x есть график функции у = sin x без точек, соответствующих числам x = +πn, n ∈ Z (рис. 54). Они изображены на графике «выколотыми» точками.

10.4. Функция у ctg x

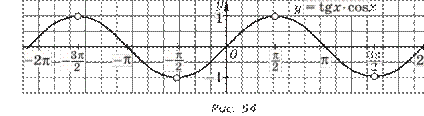
В данном пункте учебника дано определение функции у = ctg x, сформулированы и обоснованы ее свойства, строится ее график. При построении графика используется график функции у = tg x. В конце пункта разобраны две задачи, в которых доказывается, что у функций у = tg x и у = ctg x не существует положительного периода, меньшего, чем Т = π. Тем самым доказано, что Т = π является главным периодом функций у = tg x и у = ctg x.

Решения и комментарии

10.32. Сравните: а) ctg и ctg ; г) ctg и ctg .

Решение. а) Числа принадлежат промежутку

(0; π), на котором функция y = ctg x убывает, ^π< ⁶^π, следо-

7 7

вательно, ctg π > ctg ^π. 7

г) Числа и принадлежат промежутку (π; 2π), на

котором функция y = ctg x убывает, ¹¹^π_<¹³^π, следователь-

10 10

но, ctg π > ctg ^π.

Решение. а) Чтобы построить график функции

y = |ctg x |, нужно сохранить точки графика функции у = ctg x, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки графика функции у = ctg x, расположенные ниже оси Ох (рис. 55).

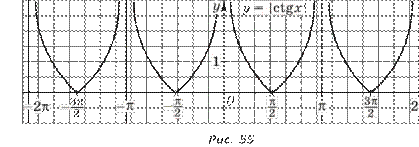
б) Чтобы построить график функции у = ctg | x |, нужно сохранить точки графика функции у = ctg x, расположенные правее оси Оу, и, симметрично отразив эту часть графика функции у = ctg x относительно оси Оу, получить вторую часть искомого графика функции (рис. 56).

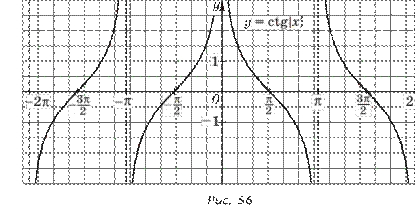
в) Так как функция y = ctg x определена для всех х, кроме х = πn, n ∈ Z, и для таких x верно равенство ctg x sin х = cos х, то график функции у = ctg x sin x есть график функции у = cos x без точек, соответствующих числам x = πn, n ∈ Z (рис. 57).

г) Так как ctg (π − х) = ctg (−x) = −ctg x, то график функции у = ctg (π − х) получится из графика функции у = ctg х с помощью симметрии относительно оси Ох.

д) График функции у = ctg x + 1 получится из графика функции у = ctg x с помощью переноса на 1 единицу вверх

(рис. 58).

е) Чтобы построить график функции у = |ctg x + 1|, нужно перенести график функции у = ctg х на 1 единицу вверх, затем сохранить точки полученного графика, расположенные выше и на оси Ох, и симметрично отразить относительно оси Ох точки графика, расположенные ниже оси Ох (рис. 59).

Промежуточный контроль. С—38.

Контрольная работа № 6.

§ 11. Тригонометрические уравнения и неравенства

При изучении предыдущего тригонометрического материала уделялось внимание подготовке учащихся к решению тригонометрических уравнений и неравенств. Фактически учащиеся уже обучались решать уравнения и неравенства, но вопрос ставился иначе. Например, так: «Укажите все углы α, для каждого из которых справедливо равенство sin α = 0 (или неравенство sin α > 0)». Теперь с опорой на сформированные умения необходимо научить их решать простейшие и сводящиеся к ним тригонометрические уравнения и неравенства, освоить специальные приемы решения некоторых тригонометрических уравнений и неравенств.

11.1. Простейшие тригонометрические уравнения

В данном пункте введены понятия основных тригонометрических функций (у = sin x, у = cos x, у = tg x, у = ctg x) и простейшего тригонометрического уравнения, понятие серии решений, получены формулы для решения простейших тригонометрических уравнений sin х = a, cos х = а, tg x = a, ctg x = а, приведены примеры применения этих формул.

Упражнения к данному пункту учащиеся уже решали ранее, но с другой постановкой задания, например: «Укажите все углы α, для которых справедливо равенство sin α = 1», теперь же требуется решить уравнение sin x = 1.

Обратим внимание на то, что в учебнике не ставится цель сразу написать общую формулу решений уравнения sin x = а (| а | ≤ 1) в виде х = (−1)^karcsin a + πk, k ∈ Z. Практика показывает, что раннее введение такой записи без должного понимания учащимися ее смысла, без объяснения «скрытого» в ней периода 2π приводит к механическому использованию этой записи с характерной ошибкой: (−1)^karcsin a + 2πk, k ∈ Z.

Учитывая, что для многих заданий вполне достаточно давать ответ в виде двух серий решений, на первых порах можно не требовать от учащихся (особенно от слабых) записи ответа в сокращенном виде. А чтобы предупредить указанную выше ошибку, надо обязательно показать учащимся, что при k = 2п или k = 2п + 1, п ∈ Z, ответ будет иметь вид arcsin a + 2πn, n ∈ Z, или π − arcsin a + 2πn, n ∈ Z, соответственно.

Можно посоветовать учащимся не решать простейшее уравнение sin x = а по общим формулам в случаях a = 0, а = 1, а = −1, мотивируя совет тем, что, например, общая формула для решений уравнения sin x = 1 дает повторяющиеся решения. Если ответ записать в виде (−1)^k + πk, k ∈ Z, то, давая k значения 0, 1, 2, 3, ..., получим решения

^π, ^π, ⁵^π, ⁵^π, ... соответственно. Такие же повторы корней

2 2 2 2

дают общие формулы для решений уравнений sin x = −1, cos x = −1.

Учащиеся, как правило, хорошо справляются с предлагаемыми заданиями, но учителю необходимо проследить, чтобы этот начальный этап обучения решению тригонометрических уравнений был освоен каждым учащимся. Проконтролировать умения учащихся решать простейшие тригонометрические уравнения можно с помощью самостоятельной работы С—39 из дидактических материалов.

Решения и комментарии

11.6. Решите уравнение: а) ; б) .

Решение. а) Так как >1, a sin х ≤ 1 для каждого х ∈ R, то уравнение не имеет решений.

б) Так как , то уравнение cos x = − имеет

две серии решений: x_n= arccos ^⎜⎝⎛− ^π₄⎞^⎟⎠ + πn, n ∈ Z;

_k⎛ π⎞ Z. Две серии решений х_nи x

x = −arccos ^⎜⎝⁻₄^⎟⎠ + πk, k ∈ _k

_m⎛ π⎞ Z. можно объединить в одну: x = ±arccos ^⎜⎝⁻₄^⎟⎠ + πm, m ∈

Заметим, что серии решений х_nи x_kможно выразить, употребляя одну букву, что часто делается для краткости ответов в учебнике. Использовать же формулу arccos (−а) = = π − arccos а на первых порах нецелесообразно. Это только усложнит запись ответа.

11.7. При каких значениях а имеет хотя бы одно решение уравнение:

а) sin x = a; б) cos x = a; в) tg x = a; г) ctg x = a?

Решение. а) Уравнение sin x = а имеет хотя бы одно решение при каждом а ∈ [−1; 1].

б) Уравнение cos x = а имеет хотя бы одно решение при

каждом a ∈ [−1; 1].

в) Уравнение tg x = а имеет хотя бы одно решение при

каждом a ∈ R.

г) Уравнение ctg х = а имеет хотя бы одно решение при

каждом а ∈ R.

Промежуточный контроль. С—39.

11.2. Уравнения, сводящиеся к простейшим

заменой неизвестного

В данном пункте рассмотрены приемы решения тригонометрических уравнений, которые после замены неизвестного t = f (x), где f (x) — одна из основных тригонометрических функций, сводятся к квадратному или рациональному уравнению. Здесь же показан прием решения тригонометрических уравнений с помощью замены аргумента у основных тригонометрических функций.

Решения и комментарии

11.14. а) Решите уравнение sin²x = .

Решение. Введя новое неизвестное t = sin x, получим

уравнение t²⁼¹, имеющее два корня: t₁= и t₂^{= −}³. По-

этому множество решений уравнения sin²есть объединение множеств решений двух уравнений:

sinx = ³и sin x = − ³. (1)

3 3

Все решения первого уравнения задаются двумя сериями:

x_n= arcsin ³+2πn, n ∈ Z; x_k= π − arcsin ³+ π2 k, k ∈ Z.

3 3

Все решения второго уравнения задаются двумя сериями: x_p= arcsin ^⎜⎝⎛⁻₃³⎞^⎟⎠ +2πp, p ∈ Z; x_q= π −arcsin ^⎜⎝⎛⁻₃³⎞^⎟⎠ +2πq, q ∈ Z.

Все решения исходного уравнения задаются четырьмя сериями: x_n, x_k, x_р, x_q.

Замечание 1. Описанную выше замену неизвестного обычно делают в уме и сразу находят объединение множеств решений уравнений (1).

Замечание 2. Для наглядной иллюстрации решений исходного уравнения можно изобразить в системе координат uOv единичную окружность (рис. 60). Тогда на пересечении прямой

v = ³и единичной окружности

получим две точки А и B, соответствующие углам, имеющим радианную меру х (далее будем записывать коротко: углам х),

Рис. 60 ₃

для которых sin x =. Анало-

гично получим точки С и D, соответствующие углам x,

для которых sin x = − ³.

Таким образом, точки А и В соответствуют всем реше-

ниям уравнения sin x ⁼³, а точки С и D соответствуют

всем решениям уравнения sin x ^=
−³.

Учитывая симметричность пар точек А и С, В и D относительно точки О, а также симметричность точек А и D относительно оси и, все решения исходного уравнения можно

задать одной серией x_m= ±arcsin ³+ πm, т ∈ Z.

Промежуточный контроль. С—40.

11.3. Применение основных тригонометрических

формул для решения уравнений

В данном пункте рассмотрено применение основного тригонометрического тождества, формул сложения, приемов понижения кратности угла и понижения степени уравнения.

Рассказывая о понижении степени уравнения, можно привести второй способ решения ранее рассмотренного уравнения sin²x = :

sin²x = = ¹⇔cos2x = .

2 3

Все решения последнего в цепочке равносильных уравнений составляют серию решений x_n= ±arccos + πn, n ∈ Z, которые и являются решениями исходного уравнения.

Замечание. При решении одного и того же уравнения (задание 11.4a) разными способами получены ответы, записанные разными способами:

x_m= ±arcsin ³+ πm, m ∈ Z и x_n= ±arccos + πn, n ∈ Z. (1)

Полезно убедиться, что серии ^х_ти ^х_пзадают одну и ту же серию решений. Для этого достаточно доказать, что уг-

лы α = arcsin ³и β = ¹arccos равны. Так как α и β — углы

3 2

⎛ π⎞

из промежутка ⎜⎝0; 2 ⎟⎠, и на этом промежутке функция

у = sin x принимает каждое значение один раз, то для доказательства равенства α и β достаточно доказать, что sin α = sin β.

Так как β ∈ ^⎜⎝⎛0; ₂^π⎞^⎟⎠, то sin β > 0, следовательно,

sinβ = . Так как α ∈ ^⎜⎝⎛0; ₂^π⎞^⎟⎠, то

sin α > 0, поэтому sinα = . Следовательно, sin α = sin β, а

это означает, что α = β.

Итак, обе формулы (1) задают одну и ту же серию решений исходного уравнения.

Полезно обратить внимание учащихся на то, что в зависимости от способа решения уравнения ответ может быть записан в различных формах. Учащиеся должны уметь доказывать, что ответы, записанные разными способами, на самом деле одинаковы, но обязательным элементом решения уравнения это доказательство не является.

Решения и комментарии

11.17. а) Решите уравнение sin x cos ^π+ sin ^πcos x = 0.

3 3

Решение. Используя формулу синуса суммы двух углов, перепишем исходное уравнение в виде sin ^⎜⎝⎛x ⁺₃^π⎞^⎟⎠ = 0.

Множество всех решений последнего уравнения задается формулой x_m+ = πm, m ∈ Z, откуда находим все решения исходного уравнения: x_mm, m ∈ Z.

11.18. Решите уравнение:

а) sin x − cos x = − ;

в) sin x − 3 cos x = 2;

д) sin x + cos x = −1.

Решение. а) Перепишем исходное уравнение в виде sinx cos π − sin π cos x = −,

6 6

⎛ π⎞ 1

sin ⎜⎝x − 6 ⎟⎠ = − 2.

Множество всех решений последнего уравнения задается формулами:

x_m− ^π= − ^π+2πm, m ∈ Z и x_n− ^π= − ^π+2πn, n ∈ Z,

6 6 6

откуда находим все решения исходного уравнения: х_т= 2πт, m ∈ Z; x_n= − +2πn, n ∈ Z.

в) Разделив исходное уравнение на число 2, перепишем его в виде

sin x − ³cos x =1,

sin x cos π − sin π cos x =1,

3 3

⎛ π⎞

sin ⎜⎝x − ₃⎟⎠ =1.

Множество всех решений последнего уравнения задается формулой x_m− ^π= ^π+2πm, откуда находим все решения

3 2

исходного уравнения: x_m= +2πm, т ∈ Z.

д) Умножив исходное уравнение на число, перепи-

шем его в виде

2 2 2

sin x + cos x = − ,

2 2 2

⎛ π⎞ ²

sin ⎜⎝x + 4⎟⎠ ^=
−₂.

Множество всех решений последнего уравнения задается формулами:

x_m+ π = − π +2π m, m ∈ Z и x_n+ ^π= − ^π+2π n, n ∈ Z,

4 4 4

откуда находим все решения исходного уравнения: x_m= − +2π m, т ∈ Z; x_n= −π + π2 n, п ∈ Z.

11.21. а) Решите уравнение

3cos 2х − 5cos x = 1. (1)

Сколько решений это уравнение имеет на отрезке [0; 2π]? Выпишите их.

Решение. Используя формулу косинуса двойного угла, перепишем уравнение (1) в виде

6cos²х − 5cos x − 4 = 0. (2)

Введем новое неизвестное t = cos x, уравнение (2) превратится в квадратное уравнение с неизвестным t:

6t²− 5t − 4 = 0,

имеющее два корня: t₁= − и t₂= .

Следовательно, множество решений уравнения (2) есть объединение множеств решений двух уравнений:

cosx = − и cos x = .

Все решения первого из этих уравнений составляют две серии решений:

x_m= +2π m, m ∈ Z; x_n= − +2πn, п ∈ Z,

а второе уравнение решений не имеет. Следовательно, все решения уравнения (1) составляют те же две серии решений.

Отрезку [0; 2π] принадлежат только одно число из серии х_т(при т = 0) и только одно число из серии х_n(при п = 1), всего два решения: и .

Итак, уравнение (1) имеет две серии решений: +2πm, т ∈ Z; n, n ∈ Z; отрезку [0; 2π] принадлежат только два решения исходного уравнения: и .

11.23. а) Решите уравнение

cos 4x + 6 sin²x = 1. (3)

Решение. Используя тождества cos 4х = 2 cos²2х − 1 и

sin²x = ¹⁻^{cos 2x}, перепишем уравнение (3) в виде

2 cos²2х − 3 cos 2х + 1 = 0. (4)

Введем новое неизвестное t = cos 2x, уравнение (4) превратится в квадратное уравнение с неизвестным t:

2t²− 3t + 1 = 0,

имеющее два корня: ^t₁= и ^t₂= 1.

Следовательно, множество решений уравнения (4) есть объединение множеств решений двух уравнений:

cos2x = и cos 2х = 1.

Все решения первого из этих уравнений составляют одну серию решений x_m= ± + π m, m ∈ Z, а все решения

второго уравнения составляют одну серию решений x_k= πk, k ∈ Z. Следовательно, все решения уравнения (3) составляют те же две серии решений.

Промежуточный контроль. С—41.

11.4. Однородные уравнения

В данном пункте учебника рассмотрены однородные тригонометрические уравнения и способ их решения с помощью перехода к равносильным им уравнениям относительно тангенса, приведены примеры решения однородных уравнений первой, второй и третьей степени.

Решения и комментарии

11.26. а) Решите уравнение sin x − cos x = 0.

Решение. Исходное уравнение равносильно уравнению tg x − 1 = 0, имеющему одну серию решений x_m= + π m, m ∈ Z, следовательно, исходное уравнение имеет ту же серию решений.

11.29. а) Решите уравнение sin²x − 3 sin x cos x + 2 cos²x = 0.

Решение. Исходное уравнение равносильно уравнению

tg²x − 3 tg x + 2 = 0. (1)

Сделав замену неизвестного t = tg x, получим квадратное уравнение t²− 3t + 2 = 0, имеющее два корня: t₁= 1 и t₂= 2.

Следовательно, множество решений уравнения (1) есть объединение множеств решений двух уравнений:

tg x = 1 и tg x = 2.

Все решения первого из этих уравнений составляют серию решений x_m= + π m, т ∈ Z, а все решения второго уравнения составляют серию решений х_n= arctg 2 + πп, п ∈ Z. Следовательно, все решения исходного уравнения, равносильного уравнению (1), составляют те же две серии решений.

11.30. а) Решите уравнение sin³x − 2 sin²x cos x − sin x cos²x + 2 cos³x = 0.

Решение. Исходное уравнение равносильно уравнению

tg³x − 2 tg²x − tg x + 2 = 0. (2)

Сделав замену неизвестного t = tg x, получим уравнение t³− 2t²− t + 2 = 0, имеющее три корня: t₁= −1, t₂= 1, t₃= 2.

Следовательно, множество решений уравнения (2) есть объединение множеств решений трех уравнений: tg x = −1, tg x = 1, tg x = 2.

Решая каждое из этих простейших тригонометрических уравнений, находим, что множество всех решений уравнения (2), а значит, и исходного уравнения состоит из трех серий решений: x_mm, т ∈ Z, x_k= + πk, k ∈ Z,

x_n= arctg 2 + π n, n ∈ Z.

Две первые серии можно объединить в одну: xm ₌^π₊πm, m ∈ Z.

4 2

11.31. а) Решите уравнение 2 cos 4х − cos³х = 2 − 16 cos²x.

Решение. Используя тождества cos 4x = 2 cos²2x − 1 = 2 (2 cos²x − 1)²− 1 =

= 8 cos⁴x − 8cos²x + 1,

перепишем исходное уравнение в виде

16 cos⁴x − cos³x = 0

или в виде

³⎛ 1 ⎞

cos x ^⎜⎝cos x ⁻₁₆^⎟⎠ = 0. (3)

Следовательно, множество решений уравнения (3) есть объединение множеств решений двух уравнений:

cos x = 0 и cos x = .

Все решения первого из этих уравнений составляют серию решений x_m= + π m, т ∈ Z, а все решения второго уравнения составляют серию решений x_n= ±arccos +2π n, п ∈ Z. Следовательно, все решения исходного уравнения составляют те же две серии решений.

Промежуточный контроль. С—42.

11.5*. Простейшие неравенства для синуса и косинуса

В данном пункте учебника рассмотрены неравенства sin х > a, sin x < a, cos х > a, cos x < а. Приведены их решения в общем виде и для конкретных значений а. Опираясь на рисунки учебника с графиками функций у = sin x и y = cos x, надо показать, как читаются промежутки решений (слева направо). Полезно показать и второй способ получения тех же ответов с помощью единичной окружности, читая промежутки от меньшего числа к большему против часовой стрелки. Далее для нескольких неравенств показаны оба способа решения тригонометрических неравенств.

Решения и комментарии

11.34. Решите неравенство: а) sinx > ; ж) sin x < .

Решение. I способ. В системе координат хОу построим графики функций y = sin х и y = , отметим точки пересечения графиков (рис. 61). На оси Ох им соответствуют точπ 5π 13π

а) Все точки графика у = sin х, расположенные выше прямой y ⁼¹, соответствуют таким значениям x, для которых sin x > . Эти точки графика выделены жирной линией, а соответствующие им промежутки значений x, являющиеся решениями неравенства sin x > , выделены штриховкой (см. рис. 61). Эти решения составляют серию

⎛ π 5π ⎞ Z.

промежутков ^⎜⎝ ₆+2πn; ₆+2πn^⎟⎠, n ∈

ж) Все точки графика у = sin x, расположенные ниже прямой y = , соответствуют таким значениям х, для которых sin x < . Эти точки графика изображены тонкой линией, а соответствующие им промежутки значений х, являющиеся решениями неравенства sin x < , не выделены штриховкой (см. рис. 61). Эти решения составляют серию промежутков ^⎜⎝⎛ 5₆π +2πn; ¹³₆^π+2πn⎞^⎟⎠, n ∈ Z.

II способ. В системе координат uOv построим единичную окружность, на которой отметим две точки, соответствующие углам x, для которых sin x = . Они получатся на пересечении прямой v = и единичной окружности.

а) Все точки, расположенные выше прямой v = , соответствуют углам х, для которых sin x >

(эти точки выделены жирной линина рисунке 62). Поэтому все решения исходного неравенства составляют серию промежутков Рис. 62 ⎛⎜⎝ ₆π +2πn; 5₆π +2πn⎞^⎟⎠ , n ∈ Z.

ж) Все точки, расположенные ниже прямой v = , соответствуют углам x, для которых sin x < (эти

выделены жирной линией на рисунке 63). Поэтому все решения исходного неравенства составсерию промежутков

+2πn; ¹³6^π+2πn^⎞⎟⎠ , n ∈ Z.

11.37. Решите неравенство:

Рис. 63

а) cos x >; г) cos x <.

Решение. I способ. Построим в системе координат хОу графики функций y = cos x и y = , отметим точки пересечения графиков (рис. 64). На оси Ох им соответствуют точки α ₀= arccos , α₁= −arccos , α₂= 2π − arccos и т. д.

а) Все точки графика у = cos x, расположенные выше

рых cos x > . Эти точки графика выделены жирной линией, а соответствующие им промежутки значений х, являющиеся решениями неравенства cos x > , выделены штриховкой

(см. рис. 64). Эти решения составляют серию промежутков

⎛ 3 3 ⎞

^⎜⎝−arccos ₄+2πn; arccos ₄+2πn^⎟⎠ , п ∈ Z.

г) Все точки графика у = cos х, расположенные ниже прямой y =, соответствуют таким значениям х, для которых cos x <. Эти точки графика изображены тонкой линией, а соответствующие им промежутки значений х, являющиеся решениями неравенства cos x < , не выделены штриховкой (см. рис. 64). Эти решения составляют серию промежутков ^⎜⎝⎛arccos 3₄+2πn; 2π − arccos ³₄+2πn⎞⎠^⎟, n ∈ Z.

II способ. В системе координат uOv построим единичную окружность, на которой отметим две точки, соответствующие углам х, для которых cos x = . Они получатся на пересечении прямой u = и единичной окружности.

а) Все точки, расположенные правее прямой u = , соответствуют углам x, для которых cosx >

Поэтому все решения исходного неравенства составляют серию промежутков

⎛ 3 3 ⎞

⎜⎝−arccos ₄+2πn; arccos ₄+2πn⎟⎠ ,

п ∈ Z (рис. 65).

г) Все точки, расположенные левее прямой u = , соответствуют углам х, для которых cos x < . По-

этому все решения исходного неравенства составляют серию промежутков

⎛ 3 3

⎜⎝arccos ₄+2πn; 2π − arccos ₄+2πn ,

п ∈ Z (рис. 66). Рис. 66 Замечание. Характерная ошибка учащихся при решении тригонометрических неравенств заключается в том, что при чтении промежутков они не соблюдают главного требования: промежутки читаются от меньшего числа к большему (т. е. на окружности против часовой стрелки). Чтобы избегать таких ошибок, нужно для каждого неравенства делать свой рисунок (см. рис. 62 и 63, рис. 65 и 66).

11.6*. Простейшие неравенства для тангенса и котангенса

В данном пункте учебника рассмотрены неравенства tg x > a, tg x < а, ctg x > a, ctg x < а. Опираясь на рисунки учебника с графиками функций y = tg x и у = ctg x, надо показать, как читаются промежутки решений (слева направо), потом показать, как те же ответы можно получать с помощью единичной окружности, читая промежутки от меньшего числа к большему против часовой стрелки.

Решения и комментарии

11.39. Решите неравенство: а) tg х > 1; ж) tg x < 1.

Решение. I способ. В системе координат хОу построим графики функций у = tg x и у = 1, отметим точки пересечения графиков (рис. 67). На оси Ох им соответствуют точки π, 5π и др.

4 4

а) Все точки графика у = tg x, расположенные выше прямой y = 1, соответствуют значениям x, для которых tg x > 1. Эти точки графика выделены жирной линией, а соответствующие им промежутки значений x, являющиеся решениями неравенства tg x > 1, выделены штриховкой (см. рис. 67). Эти решения составляют серию промежутков

⎛ π π ⎞ _Z_.

ж) Все точки графика у = tg x, расположенные ниже прямой y = 1, соответствуют значениям x, для которых tg x < 1. Эти точки графика изображены тонкой линией, а соответствующие им промежутки значений x, являющиеся решениями неравенства tg x < 1, не выделены штриховкой (см. рис. 67). Эти решения составляют серию промежутков ⎛⎜⎝− 2π + πn; π4 + πn⎞⎟⎠, n ∈ _Z_.

II способ. В системе координат uOv построим единичную окружность, на которой отметим две точки, соответствующие углам х, для которых tg x = 1. Они получатся на пересечении единичной окружности и прямой, проходящей через начало координат и точку 1 оси тангенсов.

а) Все точки единичной окружности, соответствующие углам х, для которых tg x > 1, выделены жирной линией. Все решения исходного неравенства составляют серию промежутков ⎛⎜⎝ π₄+ πn; ₂π + πn⎞⎟⎠ , n ∈ _Z₍рис. 68).

ж) Все точки единичной окружности, соответствующие углам х, для которых tg x < 1, выделены жирной линией. Все решения исходного неравенства составляют серию промежутков ⎛⎜⎝− 2^π+ πn; ^π4 + πn⎞⎟⎠ , n ∈ Z (рис. 69).

11.42. Решите неравенство:

а) ctg x > 2; г) ctg x < 2.

Решение. I способ. а) В системе координат хОу построим графики функций у = ctg x и у = 2, отметим точки пересечения графиков (рис. 70). На оси Ох им соответствуют точки α₀= arcctg 2, α₁= arcctg 2 + π и др.

Все точки графика у = ctg x,

расположенные выше прямой у = 2, соответствуют значениям х,

Рис. 69

для которых ctg x > 2. Эти точки графика выделены жирной линией, а соответствующие им промежутки значений х, являющиеся решениями неравенства ctg x > 2, выделены штриховкой (см. рис. 70). Эти решения составляют серию промежутков (πn; arcctg 2 + πn), n ∈ Z.

г) Все точки графика у = ctg x, расположенные ниже прямой у = 2, соответствуют значениям х, для которых ctg x < 2. Эти точки графика изображены тонкой линией, а соответствующие им промежутки значений х, являющиеся решениями неравенства ctg x < 2, не выделены штриховкой (см. рис. 70). Эти решения составляют серию промежутков (arcctg 2 + πn; π + πn), n ∈ Z.

II способ. В системе координат uOv построим единичную окружность, на которой отметим две точки, соответствующие углам x, для которых ctg x = 2. Они получатся на пересечении единичной окружности и прямой, проходящей через начало координат и точку 2 оси котангенсов.

а) Все точки единичной окружности, соответствующие углам х, для которых ctg x > 2, выделены жирной линией. Все решения исходного неравенства составляют серию промежутков (πn; arcctg 2 + πn), п ∈ Z (рис. 71).

г) Все точки единичной окружности, соответствующие углам х, для которых ctg х < 2, выделены жирной линией. Все решения исходного неравенства составляют серию промежутков (arcctg 2 + πп; π + πn), n ∈ Z (рис. 72).

Рис. 71 Рис. 72

11.7*. Неравенства, сводящиеся к простейшим

заменой неизвестного

В данном пункте учебника рассмотрены приемы решения тригонометрических неравенств, которые после замены неизвестного t = f (x), где f (x) — одна из основных тригонометрических функций, сводятся к квадратному или рациональному неравенству. Здесь же показан прием решения тригонометрических неравенств с помощью замены аргумента у основных тригонометрических функций.

Решения и комментарии

11.44. а) Решите неравенство

sin²x − ²sin x <0. (1)

Решение. Введем новое неизвестное t = sin x. Неравенство (1) перепишется в виде

t²− ²t <0. (2)

Множество всех решений неравенства (2) есть все t из

промежутка 0 < t < ². Поэтому все решения неравенства (1)

есть решения двойного неравенства

0 < sin x < ². (3)

Множество всех решений неравенства (3), а значит, и неравенства (1) есть две серии интервалов

⎛ π ⎞ ⎛ 3π ⎞

⎜⎝2πn; ₄+2πn⎟⎠ ^и⎜⎝ ₄+2πn; π +2πn⎟⎠,

n ∈ Z (рис. 73).

11.47. а) Решите неравенство _Рис.
73sin 2x > 0. (4)

Решение. Введем новое неизвестное t = 2х. Неравенство (4) перепишется в виде

sin t > 0. (5)

Множество всех решений неравенства (5) есть серия интервалов 2πп < t < π + 2πn, n ∈ Z, следовательно, множество всех решений неравенства (4) находим из условий

2πn < 2x < π + 2πп,

оно задается условием

πn < x < + πn, n ∈ Z.

Следовательно, множество решений неравенства (4) есть серия интервалов ^⎜⎝⎛πn; ₂^π+ πn⎞^⎟⎠ , n ∈ Z.

Промежуточный контроль. С—43.

11.8*. Введение вспомогательного угла

В данном пункте учебника рассмотрено введение вспомогательного угла. Применение этого приема показано на примерах решения уравнений и неравенств. В предыдущих пунктах уже решались уравнения вида a sin х + b cos x = 0 и находились наибольшее и наименьшее значения функции y = a sin х + b cos x. Но только теперь применение приема рассматривается в общем виде.

Решения и комментарии

11.50. а) Решите уравнение

4 sin х − 5 cos x = 2. (1)

Решение. Разделив обе части уравнения (1) на число 41, перепишем это уравнение в виде

sin x − cos x = . (2)

Подберем такой угол α, что sinα = , a cosα = , то-

гда уравнение (2) перепишется в виде

sin(x − α =)(3)

Так как −1 < <1, то множество решений уравнения

(3) задается формулами x_n− α = arcsin + π2 n, n ∈ Z и x_k− α = π − arcsin + π2 k, k ∈ Z, откуда получим, что уравнение (1) имеет две серии решений:

x_n= α +arcsin ²+ π2 n, п ∈ Z; x_k= α + π − arcsin + π2 k, k ∈ Z,

где α = arcsin.

11.52. а) Решите неравенство

sin x +cos x > − 2. (4)

Решение. Разделив обе части неравенства (1) на положительное число перепишем это неравенство в виде

cos x > −1. (5)

Так какπ, то неравенство (5) пере-

пишется в виде

⎛ π⎞

sin ⎜⎝x ⁺₄⎟⎠ > −1. (6)

Все решения неравенства (6) задаются условиями:

− ^π+2πn < x + ^π< ³^π+2πn, п ∈ Z (рис. 74),

2 4 2

откуда находим решения неравенства (6):

− ^π+2πn < x < ^π+2πn, n ∈ Z.

Следовательно, все решения неравенства (4) составляют серию интервалов ^⎜⎝⎛⁻3₄π +2πn; ⁵₄^π+2πn⎞^⎟⎠, n ∈ Z.

Замечание. Так как неравенство (6) равносильно неравенству sin ^⎜⎝⎛x + ^π₄⎞^⎟⎠ ≠ −1, то все решения неравенства (6) мож-

но было задать другим условием: xn, п ∈ Z, то-

гда все решения неравенства (4) можно записать и так:

xn, n ∈ Z.

Обратим внимание на то, что однородные тригонометрические уравнения первой и второй степени можно решать двумя способами: 1) введением вспомогательного угла; 2) сведением к равносильному уравнению относительно тангенса (п. 11.4 учебника), причем оба способа одинаково трудоемки.

В то же время однородные тригонометрические неравенства первой и второй степени предпочтительнее решать введением вспомогательного угла, так как сводить их к неравенствам относительно тангенса очень трудоемкая задача.

Например, рассмотрим решение неравенства

sin x − cos x > 0. (7)

I способ. Вводя вспомогательный угол, перепишем неравенство (7) в виде

sin ^⎜⎝⎛x − ^π₄⎞^⎟⎠ > 0. (8)

Множество всех решений неравенства (8) задается условиями

2πn < x − < π +2πn, n ∈ Z.

Откуда находим множество всех решений неравенства (7):

^π+2πn < x < ^π+2πn, n ∈ Z.

II способ. Для решения неравенства (7) вторым способом надо решить три системы:

⎧cos x = 0 ⎧cos x > 0 ⎧cos x <0

¹⁾^⎨⎩sin x > 0, ²⁾^⎨⎩tg x >1, ³⁾^⎨⎩tg x <1 и затем объединить решения трех систем.

Ясно, что первый способ предпочтительнее.

11.54. б) Решите неравенство

3sin²x −2 3 sin x cos x −3cos²x > 0. (9)

Решение. I способ. Перепишем неравенство (9), разложив его левую часть на множители:

(sin x − 3cos x)(3sin x + 3cos x) > 0. (10)

Разделим неравенство (10) на 4 3:

⎛ 1 3 ⎞ ⎛ 3 1 ⎞

⎜⎝ ₂sin x − ₂cos x⎟⎠ ⎜⎝ ₂sin x + ₂cos x⎠⎟ > 0. (11)

Преобразуем левую часть неравенства (11), введя вспомогательный угол: sin⎜⎝⎛x − 3^π⎞⎟⎠ sin ⎛⎜⎝x + ₆^π⎞⎟⎠ > 0. (12)

Далее можно решить две системы неравенств и, объединив множества их решений, получить множество решений неравенства (9).

Применим другой прием. Так как

sin ⎜⎝⎛x + ₆π⎟⎠⎞ = sin ⎜⎝⎛⎜⎝⎛x − ₃π⎠⎟⎞ + ₂^π⎠⎞⎟ = cos ^⎛⎜⎝x − ₃^π⎟⎠^⎞,

то после умножения на 2 неравенство (12) перепишется в виде

2sin ⎜⎝⎛x − ₃π⎟⎠⎞ cos ⎜⎝⎛x − ₃^π⎞⎟⎠ > 0

или в виде

sin 2^⎜⎝⎛ x − ²₃^π⎞^⎟⎠ > 0. (13)

Все решения неравенства (13) задаются условиями

2πn <2x − < π +2πn, n ∈ Z,

откуда находим все решения неравенства (13): ^π+ πn < x < ^π+ πn, n ∈ Z.

Следовательно, все решения неравенства (9) составляют

⎛ π 5π ⎞ Z. серию интервалов ^⎜⎝ ₃+ πn; ₆+ πn^⎟⎠ , n ∈

II способ. 1) Если cos x = 0, т. е. если x_k= + πn, п ∈ Z, то справедливо неравенство

3sin²x_k− 2 3 sin x_kcosx_k− 3cos²x_k> 0.

Это означает, что все числа x_kявляются решениями неравенства (9) (рис. 75, а).

2) Если cos х ≠ 0, т. е. если xn, то неравенство (9)

можно переписать в виде

cos²x (3tg²x − 2 3tg x − 3) > 0. (14)

Так как cos²x > 0, то неравенство (14) равносильно неравенству

3tg²x − 2 3tg x − 3 > 0. (15)

Введя новое неизвестное t = tg x, перепишем неравенство (15) в виде

3t²− 2 3t − 3 > 0. (16)

Множество всех решений неравенства (16) есть все

t ^<
−³и все t > 3. Поэтому множество решений неравенст-

3 ва (9) есть объединение множеств решений неравенств

tg x > 3 и tg x < − ³.

Множество решений первого неравенства есть серия интервалов ^⎜⎝⎛ ₃π + πk; ₂^π+ πk^⎟⎠⎞ , k ∈ Z, a множество решений вто-

⎛ π 5π ⎞

рого неравенства есть серия интервалов ⎜⎝ 2 + πn; 6 + πn⎟⎠ ,

n ∈ Z. Тогда множество решений неравенства (15) есть объединение этих интервалов (рис. 75, б).

3) Объединив все найденные решения, получим множе⎛ π

III способ. Применив формулы синуса и косинуса двойного угла, перепишем неравенство (9) в виде −3cos2x − 3 sin2x > 0.

Разделив обе части этого неравенства на −2 3, перепишем его в виде

cos2x + sin2x <0. (17)

Так как 1 = sin ^π, а ³= cos ^π, то неравенство (17) пере-

2 3 2 3

пишется в виде

sin 2^⎜⎝⎛ x ⁺₃^π⎞^⎟⎠ <0. (18)

Все решения неравенства (18) задаются условиями π +2πn <2x + <2π +2πn, п ∈ Z. Отсюда получим, что все решения неравенства (9) есть серия интервалов

⎛⎜⎝ ₃^π+ πn; ⁵₆^π+ πn^⎟⎠⎞, n ∈ Z (см. рис. 75, в).

Наиболее простым представляется третий способ решения данного неравенства.

Замечание. При выполнении задания 11.54 вторым способом часто пропускают первый шаг решения и, как следствие, теряют решения x_k.

11.9*. Замена неизвестного t sin x cos x

В данном пункте рассмотрен специальный прием решения уравнений и неравенств, содержащих выражения sin x + cos x (или sin x − cos x) и sin x cos x.

Решения и комментарии

11.56. а) Решите уравнение

2 sin x cos x + sin x + cos x = 1. (1)

Решение. Сделаем замену неизвестного t = sin x + cos x и выразим через t выражение 2 sin x cos x: t²= 1 + 2 sin x cos x, откуда 2 sin x cos x = t²− 1, поэтому уравнение (1) перепишется в виде

t²+ t − 2 = 0. (2)

Уравнение (2) имеет два корня: t₁= 1 и t₂= −2, следовательно, множество решений уравнения (1) есть объединение множеств решений двух уравнений: sin х + cos x = 1 и sin x + cos x = −2.

Перепишем эти уравнения с помощью введения вспомогательного угла:

sin ^⎜⎝⎛x + ^π₄⎞^⎟⎠ ⁼₂²и sin ⎛^⎜⎝x + ^π₄⎞^⎟⎠ = − 2.

Первое уравнение имеет две серии решений: х_n= 2πn, n ∈ Z и x_kk, k ∈ Z, а второе уравнение не имеет ре-

шений, так как sin ^⎜⎝⎛x + ^π₄⎞^⎟⎠ ≥ −1 для любого x ∈ R, a − 2 < −1.

Итак, уравнение (1) имеет две серии решений: х_n= 2πn, n ∈ Z и x_kk, k ∈ Z.

11.58. а) Решите уравнение

sin³x + cos³x = sin 2x + 1. (3)

Решение. Перепишем уравнение (3) в виде

(sin x + cos x) (1 − sin x cos x) = 2 sin x cos x + 1. (4) Используя замену неизвестного t = sin x + cos x, перепишем уравнение (4) в виде

⎛ t²− 1⎞ ₂

t ⎜⎝1 − ₂⎟⎠ = t . (5)

Уравнение (5) имеет три корня: t₁= 0, t₂= 1 и t₃= −3, следовательно, множество решений уравнения (3) есть объединение множеств решений трех уравнений:

sin x + cos x = 0, sin x + cos x = 1 и sin x + cos x = −3.

Решим эти уравнения введением вспомогательного угла.

Первое из них имеет одну серию решений: x_nn, n ∈ Z, второе — две серии решений: x_mm, m ∈ Z и

x_k= 2πk, k ∈ Z, а третье не имеет решений, так как sin х + cos х > −2 для любого x ∈ R, a −3 < −2. Итак, уравнение (3) имеет три серии решений: х_т, х_пи x_k.

11.59. а) Решите неравенство

sin 2x − 3 sin x − 3 cos x + 3 < 0. (6)

Решение. Используя замену неизвестного t = sin x +

+ cos x, перепишем неравенство (6) в виде

t²− 3t + 2 < 0. (7)

Все решения неравенства (7) есть все t из промежутка 1 < t < 2, следовательно, множество решений неравенства

(6) совпадает с множеством решений двойного неравенства

1 < sin x + cos x < 2. (8)

Используя введение вспомогательного угла, перепишем это неравенство (8) в виде 22 < sin ^⎜⎝⎛x + ^π₄⎞^⎟⎠ < 2.

⎛ π⎞

Неравенство sin ^⎜⎝x ⁺₄^⎟⎠ < 2 справедливо для любого х ∈ R, а все решения неравенства sin ^⎜⎝⎛x + ^π₄⎞^⎟⎠ ^<₂²задаются условиями π +2πn < x + ^π< ³^π+2πn, п ∈ Z, откуда найдем

4 4 4

все решения неравенства (8):

2πn < x < +2πn, n ∈ Z.

Итак, решения неравенства (6) составляют серии интер-

⎛ π ⎞ Z.

валов ^⎜⎝2πn; ₂+2πn^⎟⎠ , n ∈

Промежуточный контроль.

С—44, С—45 (повторение). Контрольная работа № 7.

В преамбуле к учебнику введены понятия: теория вероятностей, события и случайные события. Для контроля усвоения материала этого параграфа можно использовать задачи из учебника или из других источников.

§ 12. Вероятность события

12.1. Понятие вероятности события

В данном пункте введены понятия равновозможных событий, единственно возможных событий, случая, достоверного события, невозможного события, несовместных событий, вероятности события.

Решения и комментарии

12.2. Бросают игральную кость. Являются ли события А — «выпадание шести очков» и В — «выпадание четного числа очков» равновозможными, единственно возможными?

Решение. События А и В не являются равновозможными, так как событию А благоприятствует один случай (выпадет 6 очков), а событию В — три (выпадет 2, 4, 6 очков). События А и В не являются и единственно возможными, так как, кроме событий А и В, может произойти, например, и событие С — выпадет 5 очков.

12.4. Бросают две монеты. Рассмотрим два события: А — «выпали два орла»; В — «выпала решка» (хотя бы на одной монете). Являются ли события А и В:

а) равновозможными; б) несовместными?

Решение. Для большей наглядности будем считать, что монеты разные — большая и маленькая, всего возможны 4 случая: выпадут два орла (Оо), две решки (Рр), орел на большой монете, решка на маленькой (Ор), решка на большой монете, орел на маленькой монете (Ро).

а) События А и В не являются равновозможными, так как событию А благоприятствует один случай (Оо), а событию В — три (Рр, Ор, Ро).

б) События А и В являются несовместными, так как

они не могут произойти одновременно в одном опыте. 12.8. При игре в лото используются фишки с номерами от 1 до 90. Наудачу вынимается одна фишка. Какова вероятность события:

а) А — «номер вынутой фишки делится на 10»;

б) В — «номер вынутой фишки делится и на 5, и на 9»;

в) С — «номер вынутой фишки меньше 100»;

г) D — «номер вынутой фишки 77»?

Решение. а) Событию А благоприятствуют 9 случаев: будут вынуты фишки с номерами 10, 20, 30, 40, 50, 60, 70, 80, 90. Р (А) = 10 : 90 = 0,1.

б) Событию В благоприятствуют 2 случая: будут выну-

ты фишки с номерами 45, 90. Р (В) = 2 : 90 = .

в) Событию С благоприятствуют 90 случаев: будут вы-

нуты фишки с номерами от 1 до 90. P (С) = 90 : 90 = 1.

г) Событию D благоприятствует 1 случай: будет вынута

фишка с номером 77. Р (D) = 1 : 90 = .

12.10. а) Я задумал двузначное число. Какова вероятность того, что вы угадаете это число с первого раза?

б) Я задумал двузначное число, записанное разными цифрами. Какова вероятность того, что вы угадаете это число с первого раза?

Решение. а) Всех двузначных чисел 99 − 9 = 90. Вероятность угадать одно из них с первого раза равна .

б) Из 90 двузначных чисел 90 − 9 = 81 записаны разными цифрами. Вероятность угадать такое число с первого раза равна .

12.11. Ученик задумал натуральное число, не превышающее 100. Какова вероятность того, что это число:

а) четное; б) делится на 4; в) делится на 10; г) при делении на 10 дает остаток 7?

Решение. Из первых 100 натуральных чисел 50 четных, 25 делящихся на 4, 10 делящихся на 10, 10 дающих при делении на 10 остаток 7, поэтому искомая вероятность равна:

а) 50 : 100 = 0,5; б) 25 : 100 = 0,25; в) 10 : 100 = 0,1;

г) 10 : 100 = 0,1. 12.12. Используя некоторые из цифр 1, 2, 3, 4, 5 без повторения, записали четырехзначное число. Какова вероятность того, что вы угадаете это число с первого раза?

Решение. Таких четырехзначных чисел А

= 120, поэтому искомая вероятность равна 1 : 120 .

12.13. Четырехзначное число записали, используя цифры 1, 2, 3, 4, 5 (цифры числа могут быть одинаковые). Какова вероятность того, что вы угадаете это число с первого раза?

Решение. Таких четырехзначных чисел 5 ⋅ 5 ⋅ 5 ⋅ 5 = 625, поэтому искомая вероятность равна 1 : 625 .

12.14. Один игрок записал четырехзначное число, используя различные цифры, кроме 0. Какова вероятность того, что второй игрок угадает это число с первого раза?

Решение. Таких четырехзначных чисел А × × 7 ⋅ 6 = 3024, поэтому искомая вероятность равна

1 : 3024 = ¹.

3024

12.16. В ящике лежат 6 белых и 8 черных шаров — из них 2 белых и 3 черных шара помечены звездочками. Из ящика наудачу вынимают один шар. Какова вероятность того, что будет вынут белый шар со звездочкой?

Решение. Вероятность вынуть любой из двух белых шаров со звездочкой равна 2 : (6 + 8) = .

12.17. Четыре футбольные команды ^K₁, ^K₂, ^K₃, ^K₄вышли в полуфинал мирового первенства. Специалисты считают, что их силы примерно равны. Какова вероятность события:

а) А — «команды K₁и K₂выйдут в финал»;

б) В — «команда K₁получит «золото», а команда

K₂— «серебро»;

в) С — «команды заняли места с первого по четвертое в

указанном порядке: K₄, K₁, K₃, K₂»?

Решение. а) В финал может выйти любая пара команд:

1) K₁и K₂; 2) K₁и K₃; 3) K₁и K₄; 4) K₂и K₃; 5) K₂и K₄; 6) K₃и K₄. Событию А благоприятствует 1 случай из 6, поэтому P A( ) = .

б) В каждом из рассмотренных 6 случаев (задание «а») имеется два способа распределить «золото» и «серебро». Событию В благоприятствует 1 случай из 12, поэтому P B( ) = .

в) Так как распределение мест с 1-го по 4-е возможно Р₄= 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24 способами, то событию С благоприятствует 1 случай из 24, поэтому P C( ) = .

12.2. Свойства вероятностей событий

В данном пункте учебника определена сумма событий А и В, сумма (объединение) несовместных событий А и В, произведение (пересечение) событий А и В, введены соответствующие обозначения: A ∪ B, A + В, A ∩ B. Здесь же дано определение события, противоположного событию А (обозначение А), введено обозначение А\В для события, заключающегося в том, что происходит событие A, но событие В не происходит.

Решения и комментарии

12.22. Бросают игральный кубик. Событие А заключается в выпадании или 5, или 6 очков; событие В заключается в выпадании четного числа очков. В чем заключаются события А\В и B\А? Вычислите вероятности Р (А\В) и Р (В\А).

Решение. Событие A\В заключается в выпадании 5 очков, Р (А\В) = . Событие B\A заключается в выпадании

или 2, или 4 очков, Р (В\А) = ²= ¹.

6 3

12.24. Однажды к Галилео Галилею явился солдат и спросил: «Какая сумма выпадает чаще при бросании трех игральных костей — 9 или 10?» Галилей правильно решил эту задачу. Что ответил Галилей?

Решение. При бросании трех костей возможны 6 ⋅ 6 ⋅ 6 = 216 случаев, каждому из них соответствует трехзначное число, первая, вторая и третья цифры которого — количества очков, выпавшие соответственно на первом, втором и третьем кубике:

111, 112, 113, 114, 115, 116, 211, ..., 665, 666.

Сумма 9 очков получится только в следующих 25 случаях:

126, 216, 315, 414, 513, 612, 135, 225, 324, 423, 522, 621.

144, 234, 333, 432, 531,

153, 243, 342, 441,

162, 252, 351,

261,

Сумма 10 очков получится только в следующих 27 случаях:

136, 226, 316, 415, 514, 613, 145, 235, 325, 424, 523, 622, 154, 244, 334, 433, 532, 631.

163, 253, 343, 442, 541,

262, 352, 451,

361,

Следовательно, вероятность выпадания 9 очков равна

, а вероятность выпадания 10 очков равна . Поэтому

более вероятно выпадание 10 очков.

12.25. В некотором царстве, в некотором государстве живут правдолюбцы, которые всегда говорят правду, и лжецы, которые могут лгать или говорить правду, но не любят признаваться в этом. Для получения правдивой информации о количестве лжецов было проведено такое исследование. Каждого испытуемого спрашивали: «Вы лжец?» Прежде чем ответить, испытуемый подбрасывал монету так, чтобы результат этого опыта был виден только ему одному. Если выпадал герб, то он должен был сказать «да» (независимо от того, кем он является на самом деле). Если же выпадала решка, то он должен был правдиво ответить на вопрос (в этом случае исследователи не могли знать, кем на самом деле является испытуемый, так как они не знали результата опыта с монетой). В результате исследования выяснилось, что 61% граждан царства-государства ответили «да», остальные — «нет». Сколько процентов граждан этого царства-государства являются лжецами, если были опрошены все граждане?

Решение. Считаем выпадание герба и решки равновероятными событиями, поэтому у 50% всех граждан выпал герб, и они сказали «да». Еще 61 − 50 = 11 (%) всех граждан после выпадания у них решки также сказали «да». Они лжецы. Если считать, что лжецы равномерно распределены между двумя группами испытуемых (первая — те, у которых выпал герб, вторая — те, у которых выпала решка), то и в первой группе лжецы составляют 11% всех граждан. Тогда среди всего населения царства-государства лжецы составляют 22%.

12.26. Имеется 16 игральных карт: 4 валета, 4 дамы, 4 короля и 4 туза. Из колоды наудачу вынимают одну карту. Какова вероятность, что будет вынута или козырная карта, или дама?

Решение. Пусть событие А заключается в том, что будет

вынута козырная карта, P A( ) = ⁴= ¹. Пусть событие В за-

16 4

ключается в том, что будет вынута дама, P B( ) = ⁴= ¹. Со-

16 4

бытие A ∪ В заключается в том, что будет вынута или козырная карта, или дама. Тогда Р (A ∪ B) = Р (А) + + Р (А) − Р (АВ). Событие АВ заключается в том, что будет вынута козырная дама. P AB( ) = .

Итак, P A B , т. е. искомая вероят-

ность равна .

Можно рассуждать и иначе. Так как козырных карт 4 и дам 4 (из них одна козырная), то событию D — «вынута козырная карта или дама» — благоприятствует 7 случаев. Следовательно, P D( ) = .

12.27. Имеется колода из 52 игральных карт. Из колоды наудачу вынимают одну карту. Какова вероятность, что будет вынута или козырная карта, или дама?

Решение. Пусть событие А заключается в том, что будет вынута козырная карта, P A( ) = . Пусть событие В заклю-

чается в том, что будет вынута дама, P B( ) = ⁴= ¹. Событие 52 13 A ∪ B заключается в том, что будет вынута или козырная карта, или дама. Тогда Р (A ∪ B) = Р (А) + Р (А) − Р (АВ). Событие АВ заключается в том, что будет вынута козырная дама. P AB .

Итак, P A B , т. е. искомая вероят-

ность равна .

Можно рассуждать и иначе. Так как козырных карт 13 и дам 4 (из них одна козырная), то событию D —«вынута козырная карта или дама» — благоприятствует 16 случаев.

Следовательно, P D( ) = ¹⁶= ⁴. 52 13

§ 13*. Частота. Условная вероятность

13.1*. Относительная частота события

В данном пункте введены понятия относительной частоты события, статистической устойчивости относительных частот, приведены данные Бюффона и Пирсона о выпадании герба, полученные в больших сериях опытов с подбрасыванием монеты. Здесь же имеется замечание об аксиоматическом построении теории вероятностей, а также о различии между элементарной теорией вероятностей и общей теорией вероятностей.

Решения и комментарии

13.3. Пятеро учащихся при бросании монеты 50 раз получили следующие данные:

Ученик	Число бросаний	Число выпаданий герба	Относительная частота выпадания герба
1	50	27	0,54
2	50	28	0,56
3	50	23	0,46
4	50	26	0,52
5	50	24	0,48

Вычислите относительную частоту выпадания герба во всех 250 опытах.

Решение. Для вычисления относительной частоты выпадания герба во всех 250 опытах разделим количество выпаданий герба в этих опытах на число опытов:

(27 + 28 + 23 + 26 + 24) : 250 = 0,512.

13.2*. Условная вероятность. Независимые события

В пункте введены понятия условной вероятности события В при условии, что произошло событие А. Это отношение числа случаев, благоприятствующих событию АВ, к числу случаев, благоприятствующих событию А. Его обозначают Р_А(В). Далее показана справедливость равенств:

Р (АВ) = Р (А) Р_А(В), Р (АВ) = Р (В) Р_В(А), P_B(A) ₌^{P AB}^{( )}

P B( )

(если Р (В) > 0) и P_A( )B ₌^{P AB}^{( )}(если Р (А) > 0). P A( )

Затем вводится понятие независимых событий А и В.

Это такие события, для которых Р (АВ) = Р (А) ⋅ Р (В).

Решения и комментарии

13.5. Пусть бросают игральную кость. Событие А заключается в выпадании не более 4 очков, событие В — в выпадании нечетного числа очков. Вычислите вероятность:

а) Р (А); б) Р (B); в) Р_В(A); г) Р_А(В).

Решение. Всего равновозможных и единственно возможных случаев 6 (выпадание 1, 2, 3, 4, 5, 6 очков), из них благоприятствующих: событию А — 4 случая (выпадание 1, 2, 3, 4 очков), событию В — 3 случая (выпадание 1, 3, 5 очков), событию АВ — 2 случая (выпадание 1, 3 очков).

P AB( ) = ²= ¹.

6 3

а) P A( ) = ⁴= ²; б) P B( ) = ³= ¹;

6 3 6 2

в) P (A) = P AB( ) = 1 : 1 = 2; г) PA ( )B = P AB( ) = 1 : 2 = 1.

P B( 3 2 3 P A( ) 3 3 2

Замечание. Результаты, полученные при решении этой задачи, можно проиллюстрировать (и даже получить их без изученных формул) с помощью кругов Эйлера (рис. 76).

Вероятность события А при условии того, что наступило

^{Рис. 76}событие В, есть P_B(A) = , так как

событие А происходит в двух случаях из тех, когда произошло событие В.

Вероятность события В при условии того, что наступило

событие А, есть P_A( )B ⁼²⁼¹, так как событие В происхо-

4 2

дит в двух случаях из тех, когда произошло событие A.

13.6. В ящике находятся 15 шаров: 7 белых и 8 черных, из них 3 белых шара и 2 черных помечены звездочками. Опыт состоит в том, что из ящика наугад вынимают один шар. Событие А заключается в том, что «вынут белый шар», событие В — «вынут черный шар», событие С — «вынут шар, помеченный звездочкой». Вычислите вероятность:

а) Р (А); б) Р (B); в) Р (C); г) Р_C(А);

д) Р_C(B); е) Р_A(C); ж) Р_B(C); з) Р_B(А).

Решение. Всего равновозможных и единственно возможных случаев 7 + 8 = 15 (вынут или белый шар, или черный шар, или со звездочкой), из них благоприятствующих: событию А — 7 случаев, событию В — 8 случаев, событию С — 5 случаев, событию АВ — 0 случаев, событию АС — 3 случая, событию ВС — 2 случая. P AC( ) = ,

P BC( ) = .

а)P B( ) =; в) P C( ) = ⁵= ¹;

15 3

г) PC (A) = P AC( = 3 : 1 = 3;

P C( ) 15 3 5

д) PC ( )B = P CB( ) = 2 : 1 = 2;

P C( ) 15 3 5

е) PA ( )C = P AC( ) = 3 : 7 = 3;

P A( ) 15 15 7

ж) PB( )C = P CB( ) = 2 : 8 = 1;

P B( ) 15 15 4

з) PB(A) = P AB( ) = 0 : 8 = 0.

P B( ) 15 15 Рис. 77

Эти результаты можно проиллюстрировать с помощью кругов Эйлера (рис. 77).

13.10. Два стрелка стреляют по мишени. Вероятность поражения мишени первым стрелком равна 0,7, вторым — равна 0,8. Считая, что поражения мишени каждым из стрелков являются независимыми событиями, найдите вероятность следующего события:

а) мишень поразят оба стрелка;

б) мишень поразит первый стрелок, но не поразит второй;

в) мишень поразит второй стрелок, но не поразит

первый;

г) мишень не поразит ни один из стрелков;

д) мишень поразит хотя бы один из стрелков.

Решение. а) Для краткости первого стрелка обозначим А, второго — В. Пусть событие А — «стрелок А попал в мишень», событие В — «стрелок В попал в мишень», событие АВ — «попали оба», тогда событие А — «стрелок А

не попал в мишень», событие В — «стрелок В не попал в

мишень», событие АВ — «попал А, но не попал В», собы-

тие АВ — «попал В, но не попал А», событие АВ — «не попали оба», событие A ∪ В — «попал хотя бы один

стрелок». События А и В, А и В, А и В, А и В независимы, поэтому:

а) Р (АВ) = Р (А) ⋅ Р (В) = 0,7 ⋅ 0,8 = 0,56;

б) Р (АB) = Р (А) ⋅ Р (B) = 0,7 ⋅ (1 − 0,8) = 0,14;

в) Р (AВ) = Р (А) ⋅ Р (В) = (1 − 0,7) ⋅ 0,8 = 0,24;

г) Р (АB) = Р (А) ⋅ Р (B) = (1 − 0,7) ⋅ (1 − 0,8) = 0,06;

д) Р (А ∪ В) = Р (А) + Р (В) − Р (АВ) = 0,7 + 0,8 − 0,56 =

= 0,94.

§ 14*. Математическое ожидание. Закон больших чисел

14.1*. Математическое ожидание

В пункте введено понятие математического ожидания случайной величины х. Это число, обозначаемое M (х), равно сумме произведений значений случайной величины на

m вероятности этих значений, т. е. M x( ) = ∑ x p_{i i}.

i=1

Далее разъясняется, что математическое ожидание называют еще средним значением случайной величины или ее значением «в среднем». Приведены примеры задач, для решения которых используется понятие математического ожидания случайной величины.

Решения и комментарии

14.1. Рулетка имеет 38 номеров, выпадание каждого из которых единственно возможно и равновозможно. Если выпадет номер, на который поставил игрок, то он получает свою ставку обратно плюс ту же сумму в 35-кратном размере, если нет, то теряет свою ставку. Определите, сколько «в среднем» получает каждый игрок в одной игре при ставке в 19 рублей.

Решение. Вероятность выигрыша в рулетку равна , а проигрыша . Будем считать, что игрок получит х р., где х — случайная величина, принимающая значения х₁= 19 ⋅ 36 и x₂= −19 соответственно с вероятностями и

. Тогда математическое ожидание выигрыша равно

M р. Следовательно, каждый иг-

рок получит «в среднем» р., т. е. проиграет 0,5 рубля.

Будем называть игру справедливой, если «в среднем» будет одинаковым число очков или денег, получаемых каждым игроком. Определите, является ли справедливой игра, описанная в задачах (14.3—14.5):

14.3. Подбрасываются две монеты. Игрок А получает 3 очка, если выпадают два герба, 0 очков в других случаях. Игрок В получает 2 очка, если выпадает герб и решка, 0 очков в других случаях.

Решение. Выпишем все исходы, получаемые при броске двух монет: ОО, ОР, РО, PP. Вероятность выигрыша игрока А равна P A( ) = , а игрока В равна P B( ) = . Математическое ожидание выигрыша для игрока А равно M_A, а для игрока B — M_B. M_A< M_B— игра несправедливая.

14.5. Подбрасываются две игральные кости. Игрок А получает 6 очков, если выпадает сумма, не большая 7 очков, 0 очков в других случаях. Игрок В получает 7 очков, если выпадает сумма, большая 7 очков, 0 очков в других^«случаях.

Решение. Исход броска двух кубиков будем обозначать двузначными числами от 11 до 66, в записи которых первая цифра обозначает число очков, выпавшее на первом кубике, вторая — на втором.

Как нетрудно подсчитать, выигрышу игрока А благоприятствует 21 случай из 36: 11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 31, 32, 33, 34, 41, 42, 43, 51, 52, 61.

Выигрышу игрока В благоприятствует 15 случаев из 36: 26, 35, 36, 44, 45, 46, 53, 54, 55, 56, 62, 63, 64, 65, 66.

Вероятность выигрыша игрока А равна P A( ) = ²¹= ⁷, а

36 12

игрока В равна P B( ) = ¹⁵= ⁵. Математическое ожидание

36 12

выигрыша для игрока А равно M_A, а для

игрока B — ^M_B.

Так как M_A>M_B, то игра несправедливая.

14.7. Подбрасываются две монеты. Игрок А получает а очков, если выпадает два герба, 0 очков в других случаях. Игрок В получает b очков, если выпадает герб и решка, 0 очков в других случаях. Найдите отношение а : b, при котором эта игра станет справедливой.

Решение. Вероятности выигрыша игроков А и В равны соответственно P A( ) = и P B( ) = . Математическое ожида-

ние выигрыша для игрока А равно M_Aa , а для игрока В — M_Bb . Чтобы игра стала справедли-

вой, должно выполняться равенство M_A= M_B. Это возможно только в случае а : b = 2 : 1.

14.8. Задача Луки Пачоли (1494 г.). Двое игроков играют до трех выигрышей. После того как первый игрок выиграл две партии, а второй — одну, игра прервалась. Спрашивается, как справедливо разделить ставку 210 ливров (ливр — серебряная монета).

Решение. В задачах на дележ ставки считается, что вероятность выигрыша в каждой партии для каждого игрока равна 0,5. Так как в худшем для первого игрока случае игра закончится после двух партий, то рассмотрим, какие случаи могли бы произойти, если бы игроки сыграли две партии (независимо от первоначальной договоренности):

1) первый игрок выиграет обе партии; 2) первый игрок выиграет первую партию и проиграет вторую; 3) первый игрок проиграет первую партию и выиграет вторую; 4) первый игрок проиграет обе партии.

По первоначальному соглашению всю игру выиграет первый игрок в трех случаях из четырех, второй — лишь в одном. Следовательно, вероятность выигрыша первого игрока равна P, вероятность выигрыша второго игро-

ка — P.

Из ставки С (210 ливров) игрок А получил бы х_Aливров, где х_A— случайная величина, которая принимает значение С с вероятностью и значение 0 с вероятностью , а игрок В получил бы х_Bливров, где х_B— случайная величина, которая принимает значение С с вероятностью и значение 0 с вероятностью .

Найдем математическое ожидание величин ^х_Aи ^х_B, т. е. найдем, сколько «в среднем» получил бы каждый игрок:

M x C C; M x C C.

Следовательно, «в среднем» игроки разделили бы ставку в отношении 3 : 1, поэтому ставку 210 ливров надо разделить в отношении М (х_А) : М (х_B) = 3 : 1. Первый игрок должен получить 157,5 ливров, второй — 52,5.

14.9. Задача Пьера Ферма (1654 г.). Пусть до выигрыша всей встречи игроку А недостает двух партий, а игроку В — трех партий. Как справедливо разделить ставку, если игра прервана?

Решение. Для выигрыша всей встречи игроку А осталось выиграть две партии, а игроку В — три. Для окончания игры достаточно провести 4 партии, так как в худшем для A случае он выиграет одну, а В — две партии и для выявления победителя потребуется еще одна партия. Для перебора всех возможных случаев составим таблицу выигрышей, где выигрыши партий игроками А и В обозначены соответственно буквами а и b.

Из 16 возможных исходов 11 благоприятствуют выигрышу игрока А и 5 — выигрышу игрока В, следовательно, из ставки С (денежных единиц) игрок А получил бы х_Аден. ед., где ^х_A— случайная величина, которая принимает значение С с вероятностью и значение 0 с вероятностью , а игрок В получил бы х_Bден. ед., где х_B— случайная величина, которая принимает значение С с вероятностью и значение 0 с вероятностью .

Найдем математическое ожидание величин ^х_Aи ^х_B, т. е. найдем, сколько «в среднем» получил бы каждый игрок:

M x C C; M x C C.

Поэтому надо разделить ставку в отношении

М (х_А) : М (х_B) = 11 : 5.

Отметим, что такое решение было предложено П. Ферма в 1654 г.

14.2*. Сложный опыт

В данном пункте учебника введены понятия независимых опытов, сложных опытов.

Решения и комментарии

14.11. Что более правдоподобно — выпадание, по крайней мере, одной шестерки при 4-кратном бросании игральной кости или выпадание, по крайней мере, пары шестерок при 24-кратном одновременном бросании двух костей?

Решение. Вероятность того, что при четырехкратном

⎛ 5 ⎞4

бросании одной кости шестерка не появляется, равна ^⎜⎝ ₆^⎟⎠ .

Отсюда следует, что вероятность того, что при четырехкратном бросании одной кости шестерка появится хотя бы

⎛ 5 ⎞4

один раз, равна P₁=1 − ^⎜⎝ ₆^⎟⎠ ≈ 0 518, .

С другой стороны, вероятность того, что при одновременном бросании двух костей случится выпадание двух шестерок, равна , не случится — . Но тогда если этот

опыт с бросанием двух костей повторить 24 раза, то вероятность того, что при этом появится хотя бы один раз пара

⎛ ₃₅⎞24

шестерок, равна P₂=1 − ^⎜⎝ ₃₆^⎟⎠ ≈ 0 491, .

Так как Р₁> Р₂, то первое событие более правдоподобно (вероятнее) второго.

14.12. В каждом из двух ящиков лежат одинаковые шары двух цветов: белые и черные. Опыт заключается в том, что из каждого ящика не глядя берут по одному шару. Известно, что вероятность взять белый шар из первого ящика равна а (0 < a < 1), а вероятность взять белый шар из второго ящика равна b (0 < b < 1). Какова вероятность того, что в результате опыта будут вынуты: а) 2 белых шара; б) 2 черных шара; в) 1 белый шар и 1 черный шар?

Решение. Пусть события А и В заключаются во взятии белого шара из первой и второй урны соответственно. По условию задачи Р (А) = а; Р (В) = b.

а) Нас интересует вероятность события АВ. Так как со-

бытия А и В независимы, то Р (АВ) = Р (А) ⋅ Р (В) = аb.

б) Нас интересует вероятность события А В. Так как события А и В независимы и Р (А) = 1 − Р (А) = 1 − a, Р (В) = 1 − Р (В) = 1 − b, то

P (A B) = (1 − a) (1 − b) = 1 − a − b + ab.

в) Нас интересует вероятность события АВ + АВ. Так как события АВ и АВ несовместны, то Р (АВ + АВ) = = Р (АВ) + Р (АВ), а так как события А и В, А и B независимы, то

P (АВ + АВ) = Р (А) Р (В) + Р (А) Р (В) = = (1 − а) b + а (1 − b) = а + b − 2ab.

14.3*. Формула Бернулли. Закон больших чисел

Решения и комментарии

14.13. Всхожесть семян некоторого растения равна 90%. Найдите вероятность того, что из пяти посеянных семян взойдут: а) 0; б) 1; в) 2; г) 4; д) 5.

Решение. В данном примере р = 0,9, q = 1 − p = 0,1, тогда, применяя формулу (1) (с. 355 учебника), имеем:

а) п = 5, k = 0. Тогда Р

б) n = 5, k = 1. Тогда Р

в) n = 5, k = 2. Тогда Р

г) n = 5, k = 4. Тогда Р

д) п = 5, k = 5. Тогда Р

14.14. Монета подбрасывается 10 раз. Вычислите вероятность выпадания герба:

а) не более чем 2 раза;

б) не более чем 3 раза.

Решение. а) Вероятность того, что при рассматриваемом нами десятикратном повторении опыта событие А (выпадание герба) произойдет 0, 1 или 2 раза, равна

Р₁₀(0) + Р₁₀(1) + Р₁₀(2). Числа Р₁₀(0), Р₁₀(1), Р₁₀(2) вычислим по формуле (1) (с. 355 учебника):

Р; Р; Р.

Итак, Р.

б) Вероятность того, что при рассматриваемом нами десятикратном повторении опыта событие А (выпа- дание герба) произойдет 0, 1, 2 или 3 раза, равна Р₁₀(0) + Р₁₀(1) + Р₁₀(2) + Р₁₀(3). Числа Р₁₀(0), Р₁₀(1) и Р₁₀(2) мы нашли при выполнении задания «а», число Р₁₀(3) вычислим по формуле (1) (с. 355 учебника):

Р.

Итак, Р.

14.16. Имеется тест из четырех заданий. К каждому из заданий даны 5 ответов для выбора. Контролирующее устройство проверяет работу ученика по номерам выбранных ответов и выставляет оценку:

5 — за выбор верных ответов во всех четырех заданиях;

4 — за выбор верных ответов в любых трех заданиях;

3 — за выбор верных ответов в любых двух заданиях; 2 — за выбор верного ответа лишь в одном задании; 1 — за выбор неверных ответов во всех четырех заданиях.

Ученик, не выполняя заданий, решил случайным образом указать номера верных ответов в каждом из них.

Какова вероятность таким способом получить оценку:

а) 5; б) 4; в) 3; г) 2; д) 1?

Решение. Пусть события А, В, С и D заключаются в угадывании ответа в заданиях 1, 2, 3 и 4 соответственно. При случайном выборе ответа Р (А) = Р (В) = Р (С) = P (D) = 0,2, тогда Р (А) = Р (В) = Р (С) = P (D) = 0,8.

а) Р (ABCD) = P (A) ⋅ P (B) ⋅ P (C) ⋅ P (D) = (0,2)⁴= 0,0016.

б) События АВCD, АВCD, ABCD, ABCD независимы, вероятность каждого из них равна 0,8 ⋅ (0,2)³, а вероятность суммы этих четырех событий равна 4 ⋅ 0,8 ⋅ (0,2)³= = 0,0256.

в) События А В CD, ABCD, АВСD, AB CD, АВСD,

АВС D независимы, вероятность каждого из них равна (0,2)²⋅ (0,8)², а вероятность суммы этих шести событий равна 6 ⋅ (0,2)²⋅ (0,8)²= 0,1536.

г) События А В CD, A BCD, ABC D, AB C D независимы, вероятность каждого из них равна 0,2 ⋅ (0,8)³, а вероятность суммы этих четырех событий равна 4 ⋅ 0,2 ⋅ (0,8)³= = 0,4096.

д) Р (А В С D) = (0,8)⁴= 0,4096.

Промежуточный контроль.

Итоговый тест для самоконтроля (с. 149—153) из дидактических материалов.

Введение . . . . . . . . . . . . . . . . . . . . . . . . 3

О пособии для учителей . . . . . . . . . . . . . . . . . . . —

Концепция учебников для 10 и 11 классов серии «МГУ —

школе» . . . . . . . . . . . . . . . . . . . . . . . . . . 4

О работе по учебнику и дидактическим материалам для

10 класса . . . . . . . . . . . . . . . . . . . . . . . . . 5

Примерное тематическое планирование для 10 класса . . . . 8

Глава I. Корни, степени, логарифмы . . . . . . . . . . 12

§ 1. Действительные числа . . . . . . . . . . . . . . . 13

1.1. Понятие действительного числа . . . . . . . . . . . . —

1.2. Множества чисел. Свойства действительных числ . . . —

1.3*. Метод математической индукции . . . . . . . . . . . 19

1.4. Перестановки . . . . . . . . . . . . . . . . . . . . 23

1.5. Размещения . . . . . . . . . . . . . . . . . . . . . —

1.6. Сочетания . . . . . . . . . . . . . . . . . . . . . . —

1.7*. Доказательство числовых неравенств . . . . . . . . . 27

1.8*. Делимость целых чисел . . . . . . . . . . . . . . . 33

1.9*. Сравнения по модулю т . . . . . . . . . . . . . . . 36

1.10*. Задачи с целочисленными неизвестными . . . . . . . 38

§ 2. Рациональные уравнения и неравенства . . . . . . . 41

2.1. Рациональные выражения . . . . . . . . . . . . . . —

2.2. Формулы бинома Ньютона, суммы и разности

степеней . . . . . . . . . . . . . . . . . . . . . . 42

2.3*. Деление многочленов с остатком. Алгоритм Евклида . . 43

2.4*. Теорема Безу . . . . . . . . . . . . . . . . . . . . 44

2.5*. Корень многочлена . . . . . . . . . . . . . . . . . . 45

2.6. Рациональные уравнения . . . . . . . . . . . . . . . 47

2.7. Системы рациональных уравнений . . . . . . . . . . 50

2.8. Метод интервалов решения неравенств . . . . . . . . 54

2.9. Рациональные неравенства . . . . . . . . . . . . . . 56

2.10. Нестрогие неравенства . . . . . . . . . . . . . . . . 57

2.11. Системы рациональных неравенств . . . . . . . . . . 59

§ 3. Корень степени п . . . . . . . . . . . . . . . . . . 60

3.1. Понятие функции и ее графика . . . . . . . . . . . . —

3.2. Функция у = х^п. . . . . . . . . . . . . . . . . . . . 61

3.3. Понятие корня степени п . . . . . . . . . . . . . . . —

3.4. Корни четной и нечетной степеней . . . . . . . . . . —

3.5. Арифметический корень . . . . . . . . . . . . . . . 62

3.6. Свойства корней степени п . . . . . . . . . . . . . . 63

3.7*. Функция y=ⁿx, х ≥ 0 . . . . . . . . . . . . . . . . . —

3.8*. Функция y=ⁿx . . . . . . . . . . . . . . . . . . . —

3.9*. Корень степени п из натурального числа . . . . . . . . 65

§ 4. Степень положительного числа . . . . . . . . . . . .	68
4.1. Степень с рациональным показателем . . . . . . . . .	—
4.2. Свойства степени с рациональным показателем . . . . .	69
4.3. Понятие предела последовательности . . . . . . . . .	70
4.4*. Свойства пределов . . . . . . . . . . . . . . . . . .	75
4.5. Бесконечно убывающая геометрическая прогрессия . . .	76
4.6. Число е . . . . . . . . . . . . . . . . . . . . . . .	79
4.7. Понятие степени с иррациональным показателем . . . .	81
4.8. Показательная функция . . . . . . . . . . . . . . .	82
§ 5. Логарифмы . . . . . . . . . . . . . . . . . . . . .	83
5.1. Понятие логарифма. . . . . . . . . . . . . . . . . .	—
5.2. Свойства логарифмов . . . . . . . . . . . . . . . . .	84
5.3. Логарифмическая функция . . . . . . . . . . . . . .	86
5.4*. Десятичные логарифмы . . . . . . . . . . . . . . . .	87
5.5. Степенные функции . . . . . . . . . . . . . . . . . § 6. Показательные и логарифмические уравнения*	88
и неравенства . . . . . . . . . . . . . . . . . . . .	88
6.1. Простейшие показательные уравнения . . . . . . . . .	—
6.2. Простейшие логарифмические уравнения . . . . . . . 6.3. Уравнения, сводящиеся к простейшим заменой	89
неизвестного . . . . . . . . . . . . . . . . . . . . .	91
6.4. Простейшие показательные неравенства . . . . . . . .	93
6.5. Простейшие логарифмические неравенства . . . . . . . 6.6. Неравенства, сводящиеся к простейшим заменой	94
неизвестного . . . . . . . . . . . . . . . . . . . . . *Глава II.* Тригонометрические формулы.	95
Тригонометрические функции . . . . . . . . .	99
§ 7. Синус и косинус угла . . . . . . . . . . . . . . . .	100
7.1. Понятие угла. . . . . . . . . . . . . . . . . . . . .	—
7.2. Радианная мера угла . . . . . . . . . . . . . . . . .	102
7.3. Определение синуса и косинуса угла . . . . . . . . . .	104
7.4. Основные формулы для sin α и cos α . . . . . . . . . .	106
7.5. Арксинус . . . . . . . . . . . . . . . . . . . . . .	108
7.6. Арккосинус . . . . . . . . . . . . . . . . . . . . .	111
7.7*. Примеры использования арксинуса и арккосинуса . . .	113
7.8*. Формулы для арксинуса и арккосинуса . . . . . . . .	115
§ 8. Тангенс и котангенс угла. . . . . . . . . . . . . . .	116
8.1. Определение тангенса и котангенса угла . . . . . . . .	—
8.2. Основные формулы для tg α и ctg α . . . . . . . . . .	118
8.3. Арктангенс. . . . . . . . . . . . . . . . . . . . . .	119
8.4*. Арккотангенс . . . . . . . . . . . . . . . . . . . .	121
8.5*. Примеры использования арктангенса и арккотангенса . .	122
8.6*. Формулы для арктангенса и арккотангенса. . . . . . .	123
§ 9. Формулы сложения . . . . . . . . . . . . . . . . .	124
9.1. Косинус разности и косинус суммы двух углов . . . . .	—
9.2. Формулы для дополнительных углов. . . . . . . . . .	126
9.3. Синус суммы и синус разности двух углов . . . . . . .	127
9.4. Сумма и разность синусов и косинусов . . . . . . . . .	129

9.5. Формулы для двойных и половинных углов . . . . . . 130

9.6*. Произведение синусов и косинусов. . . . . . . . . . . 132

9.7*. Формулы для тангенсов . . . . . . . . . . . . . . . . 134

§ 10. Тригонометрические функции числового аргумента. . 137

10.1. Функция у = sin x . . . . . . . . . . . . . . . . . . 138

10.2. Функция у = cos x . . . . . . . . . . . . . . . . . . 143

10.3. Функция у = tg x . . . . . . . . . . . . . . . . . . . 144

10.4. Функция у = ctg x . . . . . . . . . . . . . . . . . . 146

§ 11. Тригонометрические уравнения и неравенства . . . . 149

11.1. Простейшие тригонометрические уравнения . . . . . . 150

11.2. Уравнения, сводящиеся к простейшим заменой

неизвестного . . . . . . . . . . . . . . . . . . . . . 151

11.3. Применение основных тригонометрических формул

для решения уравнений. . . . . . . . . . . . . . . . 153

11.4. Однородные уравнения . . . . . . . . . . . . . . . . 157

11.5*. Простейшие неравенства для синуса и косинуса . . . . 158

11.6*. Простейшие неравенства для тангенса и котангенса. . . 162

11.7*. Неравенства, сводящиеся к простейшим заменой

неизвестного . . . . . . . . . . . . . . . . . . . . . 165

11.8*. Введение вспомогательного угла . . . . . . . . . . . . 166

11.9*. Замена неизвестного t = sin x + cos x . . . . . . . . . . 171

Глава III. Элементы теории вероятностей . . . . . . . . 173

§ 12. Вероятность события . . . . . . . . . . . . . . . . —

12.1. Понятие вероятности события . . . . . . . . . . . . . —

12.2. Свойства вероятностей событий . . . . . . . . . . . . 176

§ 13*. Частота. Условная вероятность . . . . . . . . . . . 178

13.1*. Относительная частота события . . . . . . . . . . . . —

13.2*. Условная вероятность. Независимые события. . . . . . 179

§ 14*. Математическое ожидание. Закон больших чисел . . 182

14.1*. Математическое ожидание . . . . . . . . . . . . . . —

14.2*. Сложный опыт . . . . . . . . . . . . . . . . . . . . 185

14.3*. Формула Бернулли. Закон больших чисел . . . . . . . 187

У ч е б н о е и з д а н и е Серия «МГУ — школе»

Потапов Михаил Константинович

Шевкин Александр Владимирович

АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА

Методические рекомендации

10 класс

Пособие для учителей общеобразовательных организаций

Зав. редакцией Т. А. Бурмистрова

Редактор Л. В. Kузнецова

Младший редактор С. В. Дубова

Художники П. С. Барбаринский, О. П. Богомолова

Художественный редактор О. П. Богомолова

Компьютерная графика: Г. М. Дмитриев

Техническое редактирование и компьютерная верстка Н. Н. Репьевой Корректор И. П. Ткаченко

Подписано в печать 27.08.2013. Формат 60 × 90¹/₁₆.

Гарнитура Школьная. Печ. л. 12. Заказ №

Открытое акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.

[1] Название правила происходит от греческого слова mnкmonikon (μνε′μονικον), означающего искусство запоминания.

[2] Здесь и далее углы α и β таковы, что данные числовые выражения имеют смысл.

Методические рекомендации. Алгебра 10 класс

УДК 372.8:[512+517] ББК 74.262

Концепция учебников для 10 и 11 классов серии «МГУ — школе»

ФГОС. Каждый из двух учебников обладает цельностью и завершенностью своего содержания, а вместе они составляют единый курс

Учебник для 11 класса включает все вопросы программы, связанные с исследованием функций и построением их графиков, с производной и первообразной, с решением уравнений, неравенств, их…

Сначала рассматриваются строгие неравенства, потом нестрогие

При этом не обсуждается время, отводимое на изучение пункта, — в каждом профиле оно окажется своим, а в отдельных профилях некоторые пункты вообще не изучаются

Тексты контрольных работ приведены в дидактических материалах

Степень положительного числа 8 10 13 14 4

Определение тангенса и котангенса угла 1 1 1 1 8

Замена неизвестного t = sin x + cos x — — — 1

Завершается глава решением показательных и логарифмических уравнений и неравенств

Сравнивают действительные числа, записанные в виде бесконечных десятичных дробей, поразрядно, т

Замечание 1. Часто возникает вопрос об обосновании мнемонического правила и рассуждений в приведенном примере

Пункт 1.2 посвящен знакомым учащимся обозначениям числовых множеств

Докажите, что координата точки

Пусть х 1 < х < х 2 . Так как

Теперь установим взаимно-однозначное соответствие между элементами множеств

Представьте, что вы подошли к кинотеатру и видите огромную очередь желающих купить билет на новый фильм

Наблюдательные учащиеся могут заметить, что для п колец число ходов меньше п -й степени числа 2 на единицу, т

Обозначим A n ( ) = 1 + 1 + 1 +

Итак, равенство (1) справедливо при п = 1, и из его справедливости для п = k следует его справедливость для п = k + 1,…

Докажите, что для любого натурального числа п 3 n + 4 n − 1 делится на 6

Надо отметить, что для первых важен порядок следования выбранных k элементов, а для вторых этот порядок не важен

Сколько таких способов? В скольких случаях: а) элемент x 1 будет первым по порядку; б) элемент х 1 не будет ни первым, ни последним?

Число способов распределить три разные путевки между шестью лицами равно

Решение. а) Число способов выбрать 4 человека из 6 (без учета порядка выбираемых) равно

Используя это, покажем, что при п = k + 1 справедливо равенство

Доказательство может содержать приведенные выше шаги: а 2 + b 2 ≥ 2 ab , (1) а 2 − 2 ab + b 2 ≥…

Тогда если использовались только свойства 1—3, то получившийся знак сравнения надо поставить вместо знака ∨ в сравнении данных числовых выражений

Следовательно, этот знак будет стоять и в первом сравнении, что и требовалось доказать

Доказательство. Обозначим:

На отрезке AD , длина которого равна а + d , построим окружность как на диаметре (рис

Так как = ⋅ + + + + (4 ′ ) 4 1 5 5 9 9 13 = 1 4 ⋅ ⎛⎜⎝ 1 1…

Докажите, что для любых действительных чисел а и b , если а + b = 3, то а 2 + b 2 ≥ 4,5

Определите срок хранения вклада

Решив систему из четырех полученных уравнений, получим, что m = 2, п = 3, k = 4, р = 3, т

Найдите все целые числа, которые при делении на 4 дают остаток 3, при делении на 3 дают остаток 2, при делении на 2 дают остаток…

Сравнения по модулю m Материал о сравнении по модулю m также новый в программе для старших классов и поэтому подробно описан в учебнике

Решение. 200420052006200720082003 — наибольшее число, не превосходящее данного и делящееся на 9, оно на 6 меньше данного, поэтому 200420052006200720082009 ≡ ≡ 6 (mod 9)

Задачи с целочисленными неизвестными

Составим уравнение 1 x 1 2 30 (1) + y + ( − x − y ) = 30

Разделив уравнение (4) на 1,5 и перенеся неизвестные в одну часть уравнения, а известные — в другую, получим уравнение, равносильное уравнению (4): 3 x +…

Доказательство. a) Перепишем уравнение (9) в виде ( x − 2) 2 + ( y + 2) 2 = 0

Решение. а) A = ⎜⎝⎛ a − a 2 b + a + b 2 b ⎞⎟⎠ ⋅ a 3 + a 3 3 a…

Приведем второе доказательство равенства

Решения и комментарии 2.31. а)

Число 6 пишем во вторую клетку нижней строки таблицы (рис

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

02.04.2020

Методические рекомендации. Алгебра 10 класс

О пособии для учителей

«МГУ — школе»

10 класса

Примерное тематическое планирование для 10 класса

§ 1. Действительные числа

1.1. Понятие действительного числа 1.2. Множества чисел. Свойства действительных чисел

Решения и комментарии

1.3*. Метод математической индукции

Решения и комментарии

1.4. Перестановки

Решения и комментарии

1.7*. Доказательство числовых неравенств

Решения и комментарии

Доказательство. а) Так как ,

1.8*. Делимость целых чисел

Решения и комментарии

1.9*. Сравнения по модулю m

Решения и комментарии

1.10*. Задачи с целочисленными неизвестными

Решения и комментарии

1.104. Из «Арифметики» Л. Ф. Магницкого (1669—

§ 2. Рациональные уравнения и неравенства

2.1. Рациональные выражения

Решения и комментарии

степеней

Решения и комментарии

2.3*. Деление многочленов с остатком. Алгоритм Евклида

Решения и комментарии

2.4*. Теорема Безу

Решения и комментарии

2.5*. Корень многочлена

Решения и комментарии

2.6. Рациональные уравнения

Решения и комментарии

2.7. Системы рациональных уравнений

Решения и комментарии

2.8. Метод интервалов решения неравенств

Решения и комментарии

2.9. Рациональные неравенства

Решения и комментарии

2.10. Нестрогие неравенства

Решения и комментарии

2.11. Системы рациональных неравенств

Решения и комментарии

§ 3. Корень степени п

3.1. Понятие функции и ее графика

Решения и комментарии

3.2. Функция y хn

3.3. Понятие корня степени n

3.4. Корни четной и нечетной степеней

3.5. Арифметический корень

Решения и комментарии

3.6. Свойства корней степени n

Решения и комментарии

3.7*. Функция y = n x, x 0 3.8*. Функция y = n x

Решения и комментарии

3.9*. Корень степени n из натурального числа

§ 4. Степень положительного числа

4.1. Степень с рациональным показателем

Решения и комментарии

4.3. Понятие предела последовательности

Решения и комментарии

Решение. а) α n = n + 1 = n + 1 =1 + 1; n n n n

4.4*. Свойства пределов

Решения и комментарии

4.5. Бесконечно убывающая геометрическая прогрессия

Решения и комментарии

4.6. Число е

Решения и комментарии

4.7. Понятие степени с иррациональным показателем

Решения и комментарии

4.8. Показательная функция

Решения и комментарии

§ 5. Логарифмы

5.1. Понятие логарифма

Решения и комментарии

5.2. Свойства логарифмов

Решения и комментарии

Решение. A = 3log943 +2log416 = 3log323 +22 = 23 +4 =12. 126. (Задания для повторения.)

3.2. Функция y хⁿ

3.7. Функция y = ⁿx, x 0 3.8. Функция y = ⁿx

Решение. а) α _n= ⁿ⁺¹= ⁿ+ ¹=1 + ¹; n n n n

Решение. A = 3log₉43 +2log₄16 = 3log₃23 +22 = 23 +4 =12. 126. (Задания для повторения.)