Методические рекомендации по геометрии для родителей семиклассника

Разработка учителя математики и информатики

 Кузнецовой Т.Ю.

МБОУ «Полазненская СОШ №3»

 

Рекомендации родителям семиклассника

В 7 классе ученики знакомятся с новыми вычислительными операциями:

1) возведение в степень (усвоение этой темы невозможно без знания таблицы умножения, пусть ребенок повторяет всю таблицу умножения);

2) вынесение за скобки общего множителя (необходимо повторять правила деления натуральных чисел, в пределах 100 - устно, знать правила деления степеней);

3) действия с одночленами и многочленами (правила раскрытия скобок, приведения подобных слагаемых, формулы сокращенного умножения, для них лучше всего сделать карточки и постоянно их повторять);

4) решение линейных уравнений (умение находить компоненты действий при сложении, вычитании, умножении и делении; после изучения в 6 классе свойств уравнений тоже применять их к новым видам линейных уравнений);

5) составление уравнения для решения задач (анализ условия, установление логической связи между данными величинами и теми, которые можно найти; до изучения этой темы необходимо заставлять учащегося составлять краткое условие к задаче, делать пояснения к каждому действию, а в числовых выражениях просить объяснять каждое действие).

Это поможет школьнику в решении геометрических задач, ведь теоретические знания помогут школьнику логически записать решение задачи. В геометрии часть решения состоит в правильном построении чертежа, а это значит, что школьнику необходимо уметь анализировать условие задачи.

Школьник при решении геометрической задачи должен уметь:

1) уметь пользоваться линейкой, циркулем, заранее приведенным в рабочее состояние;

2) аккуратно построить чертеж;

3) сопоставить данные условия с чертежом;

4) используя выученный теоретический материал, составить план решения задачи, обосновать теоретическими фактами то или иное утверждение и логически завершить решение;

5) иногда необходимо уметь достраивать дополнительные элементы для данных фигур.

В результате изучения курса планиметрии учащиеся должны уметь решать типичные задачи на вычисление, доказательство и построение.

При решении типичных задач на доказательство учащиеся должны уметь приводить ссылки на теоретические факты из курса, необходимые для доказательства. А при решении задач на вычисление значений геометрических величин они должны уметь применять изученные свойства фигур и формулы, а также соответствующий аппарат алгебры и тригонометрии.

Для успешного усвоения каждой новой темы необходимо повторять предыдущие правила. Это способствует лучшему усвоению нового материала, а также поддержанию приобретенных навыков и умений.

Овладение основными теоретическими фактами необходимо осуществлять сознательно, тогда практически дети будут выполнять задания верно и быстро, при этом будет меньше пробелов и типичных ошибок. Например, при построении графиков ошибки часто возникают из-за незнания того, что является графиком того или иного вида, ведь методика построения прямой и параболы различны.

В результате изучения курса алгебры учащиеся 7-9 должны овладеть следующими умениями, представляющими обязательный минимум:

1) Уметь выполнять арифметические действия над точными и приближенными значениями, находить приближенное значение квадратного корня, вычислять значения синуса, косинуса и тангенса, вычислять по формулам.

2) Ученики должны уметь выполнять тождественные преобразования целых выражений: раскрытие скобок и заключение в скобки, приведение подобных членов, сложение, вычитание и умножение многочленов, разложение многочленов на множители и разложение квадратного трехчлена на множители.

3) Уметь сокращать алгебраические дроби, выполнять сложение, вычитание, умножение и деление дробей.

4) Уметь выполнять преобразования несложных выражений, содержащих степени и корни.

5) Знать тригонометрические формулы и выполнять несложные преобразования в тригонометрических выражениях.

6) Учащиеся должны уметь решать основные виды уравнений (линейных, квадратных, рациональных), применяя в необходимых случаях соответствующие тождественные преобразования, а также овладеть основными приемами решения систем уравнений.

7) Учащиеся должны уметь решать основные виды неравенств и их систем.

8) Ученики должны уметь решать текстовые задачи методом уравнений.

9) Уметь находить значения функции, заданных формулой, графиком, таблицей и строить графики изученных функций.

Часть вопросов, изучаемых в алгебре, требуют повторения материала, изучаемого школьниками в математике начальной школы и в 5-6 классах средней школы.

Памятка по выполнению домашнего задания по математике:

1. Прочитай учебник, параграф, в котором описывается изучаемая тема, даже если тема не новая.
2. Выучи правила, определения, выделенные в этом параграфе жирным шрифтом или находящиеся в рамке.
3. Просмотри в рабочей тетради классную работу: какая тема изучалась, какие задания выполнялись, просмотри алгоритмы выполнения заданий.
4. Повтори правила и определения по тетради (так как учитель может уже упростить правила и алгоритмы, данные в учебнике, показать их наиболее рациональное использование и т.п.).
5. Выполни устные домашние задания.
6. Выполни письменные домашние здания.
7. Повтори определения понятий, алгоритмы и правила без учебника или тетради.

Как видим из памятки, ученик должен хорошо уметь работать с учебным пособием: учебником, справочником, словарем или электронными носителями, содержащими информацию по теме. В современном обществе все больше пользуется спросом дистанционное обучение. И здесь ученик остается наедине с учебником, учебным пособием. Самостоятельное изучение математического материла по учебнику дело сложное. Это зависит, прежде всего, от изложения материала в учебнике. К особенностям учебников математики можно отнести: своеобразный язык математики, абстрактность теории, сжатость и краткость изложения (одна из основных проблем современного учебника), широкое применение символики, преобладание дедуктивного метода изложения информации, тесная связь текста с иллюстрациями и чертежами. Следует отметить, что в текстах учебников математики имеются так называемые «пробелы в тексте» - это ссылки на уже известный материал, формулы или теоремы. Ученики не всегда самостоятельно могут восстановить эти «пробелы текста». В силу изложенных особенностей математического текста самостоятельное чтение приводит к недопониманию прочитанного, тем более неумению применять полученные знания в нестандартных ситуациях.

 

Памятка работы с параграфом учебника математики для учащихся 7-9 классов.

1. Прочитайте заголовок параграфа. Что вы уже знаете об этом? Что вы говорили в классе об этом?
2. Прочитайте текст параграфа.
3. Выучите формулировки теорем, определения, правила, алгоритмы решения заданий.
4. Установите связь между иллюстрациями, рисунками, чертежами и текстом.
5. Разделите текст на части, озаглавьте их, запишите план в тетрадь.
6. Выполните письменное домашнее задание.
7. Перескажите теоретические сведения, прочитанные из параграфа, согласно вашему плану.
8. Приведите собственные примеры в доказательство прочитанного.

 

Определение луча.     Луч   —   это множество точек прямой, которые  
расположены по одну сторону от данной точки. Луч   —   это полупрямая.  
        Если на прямой обозначить точку, например   В ,   то она разделит  
данную прямую на   2   луча,   в данном случае на   ВА   и   ВС.    

  
        Обозначают (называют) луч следующим образом: 

·         названиями точек принадлежащих лучу, причем начальная точка   луча идет первой.   Например,   ВА ,   ВС ;  

·          прописными латинскими буквами, предварительно нанесенными  на чертеж рядом с лучами.     h ,   k .     

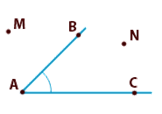
Определение.   Угол   —   это геометрическая фигура, которая  образована двумя лучами, выходящими из одной точки.    
Точка   А   —   это вершина угла,   АВ   и   АС   —   стороны угла.  
Обозначают угол названиями трех точек,  причем вершина угла идет второй.  
Например:   ВАС .    

          Внутренняя область угла образует множество всех точек плоскости,  лежащих между сторонами угла. Точка   N   принадлежит внутренней  
области угла,   точка   M   —   внешней.    
  
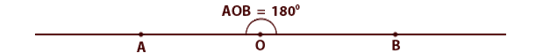
          Определение.   Развернутый угол   —   это угол, стороны которого  
лежат на одной прямой.   Например   АОВ .  

          Углы в геометрии измеряются в градусах.   Величину развернутого угла  
приняли за 180°.   

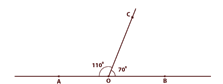
Угол может быть разделен на 2 угла. Точка   С   лежит во внутренней  
области угла   АОВ ,   тогда данный угол разбивается на 2 угла:  
  АОС   и   СОВ.  

            АОС   >   90° ,   значит он тупой.  
            СОВ   <   90° ,   следовательно он острый.    
            АОС   +   СОВ       =       АОВ       =         110°   +     70°       =     180° ,  
            значит     АОВ   —   развернутый угол.    
 
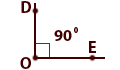
Если градусная мера угла равна   90°   (90 градусов),  то данный угол   (DОE)   —   прямой.    

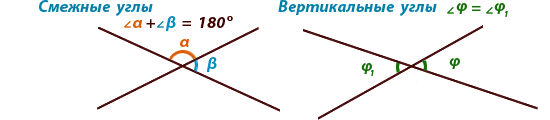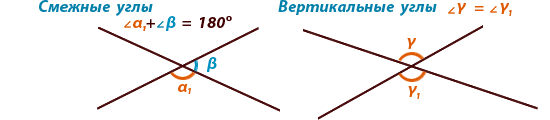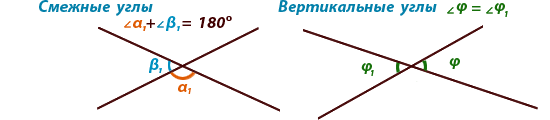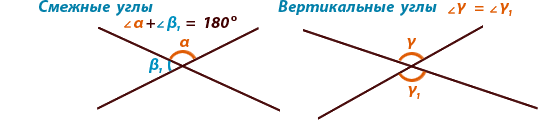 Смежными называются углы, у которых одна сторона общая, а две   другие стороны расположены на одной прямой (являются дополняющими  лучами).  
 Вертикальными называются углы, у которых стороны одного угла  являются продолжением второго угла. 

   
    


         

 Сумма смежных углов равна 180°,  а вертикальные углы равны друг другу.    

 

 

Признаки равенства треугольников. Правила

Треугольник   —   это геометрическая фигура, состоящая из трех точек,  не лежащих на одной прямой, соединенных отрезками.  
         Если треугольники   АВС   и   А 1В 1С 1 можно совместить наложением,  
то они являются равными.   У равных треугольников равны и их  
соответствующие элементы.    

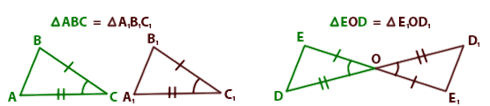Первый признак равенства треугольников:  треугольники равны, если у них равны две стороны и угол между ними.  

 

 

 

 

 

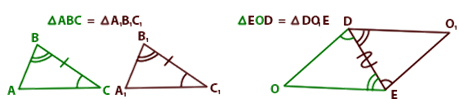Второй признак равенства треугольников:  треугольники равны, если у них равны два угла и сторона между ними.  

 

 

 

 

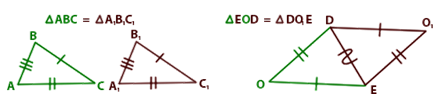Третий признак равенства треугольников:  треугольники равны, если у них равны три стороны.  

 

 

 

 

 

Медиана, биссектриса и высота треугольника.

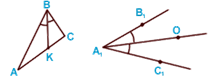
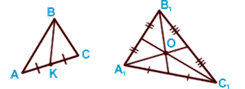Медиана треугольника   —   отрезок, соединяющий вершину  треугольника с серединой противоположной стороны.    
В любом треугольнике можно провести 3 медианы.   Все они  пересекаются в одной точке, в центре (центре тяжести) треугольника.  

  
AK = KC ,  
BK   —   медиана    ABC ,  
О   —   центр    A 1B 1C 1 .    

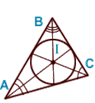Биссектриса треугольника   —   отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой на противолежащей стороне.  
Обратите внимание,   что биссектриса угла   —   это луч, делящий угол  на два равных, а биссектриса треугольника  - это отрезок, часть луча,  ограниченная стороной треугольника.    
BK   —   биссектриса    ABC ,  A 1О   —   биссектриса       C 1A 1B 1 .    
  В каждом треугольнике можно провести  3 биссектрисы, которые пересекаются в одной точке,  обычно обозначаемой латинской буквой   I .  
Точка пересечения биссектрис треугольника ( I )   —   центр вписанной в треугольник окружности.      

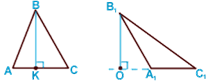  Высота треугольника   —   перпендикуляр, проведенный из вершины  треугольника к прямой, содержащей противоположную сторону.  

  

Равнобедренный треугольник, его свойства и признаки.

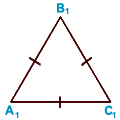 Равнобедренный треугольник   —   треугольник  у которого равны  две стороны, а третья является основанием.  
AB = BC   —   боковые стороны;  
AC   —   основание равнобедренного треугольника.    

  Равносторонний треугольник   —   треугольник  у которого   все стороны   равны.  
  A 1B 1 = B 1C 1 = A 1C 1     —   стороны треугольника.    
 

 Всякий равносторонний треугольник является равнобедренным,  
но не всякий равнобедренный   —   равносторонним.    

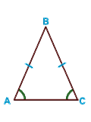Свойства равнобедренного треугольника:

·       в равнобедренном треугольнике углы при основании равны;

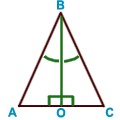
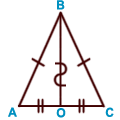
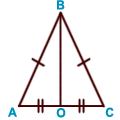·        в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;  

  

 

 

 

 

AB = BC (равнобедренный треугольник),  AO = OC (BO — медиана),   BO — общая сторона  ABO и  CBO.  
 ABO   =    CBO   по 3-му признаку.  
Следовательно:  ABO   =    CBO.  
BO — биссектриса.  

·         в равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой;    

·         в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.    

 

Признаки равнобедренного треугольника:

·         если в треугольнике два угла равны, то он равнобедренный;  

·           если в треугольнике биссектриса является медианой или высотой,  то этот треугольник равнобедренный;  

·         если в треугольнике медиана является биссектрисой или высотой,   то этот треугольник равнобедренный;  

·         если в треугольнике высота является медианой или биссектрисой,  
          то этот треугольник равнобедренный.

 

 

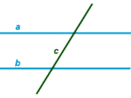
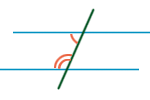
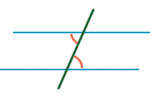
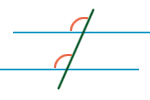
Cоответственные, односторонние, накрест лежащие углы.

 Прямая, пересекающая геометрическую фигуру или две другие прямые, называется секущей прямой.  
c — секущая прямая  
При пересечении секущей двух параллельных прямых образуется восемь углов: 


  •   соответственные углы равны



  •   односторонние углы в сумме равны 180°



  •   накрест лежащие углы равны

 

 

Признаки параллельности прямых

1.       Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

2.       Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

3.       Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Свойства параллельных прямых.

1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.

2. Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.

 

Аксиома параллельных прямых.

В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.

Аксиома, в свою очередь, такая истина, которую не надо доказывать. В каждой науке есть свои аксиомы, на справедливость которых строят все дальнейшие суждения и их доказательства.

 

 

Сумма треугольника равна 180 градусов.

Следствие: в любом треугольнике либо все углы острые, либо два острых угла, а третий тупой или прямой.

Если в треугольнике все углы острые, то он называется остроугольным

Если один из углов треугольника тупой, то он называется тупоугольным.

Если один из углов треугольника прямой, то он называется прямоугольным .

 

 

Прямоугольный треугольник

Треугольник называют прямоугольным, если у него есть прямой угол. 
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой.

Свойство:

o    Сумма двух острых углов прямоугольного треугольника равна 90º

Сумма углов треугольника равна 180º, а прямой угол равен 90º, поэтому сумма двух острых углов прямоугольного треугольника равна 90º.

o Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.

• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º.

 

Признак равенства прямоугольных треугольников:

·         Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

·         Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

·         Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

·         Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

 

Прямоугольный треугольник

Треугольник называют прямоугольным, если у него есть прямой угол. 
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой.

Свойство:

o    Сумма двух острых углов прямоугольного треугольника равна 90º

Сумма углов треугольника равна 180º, а прямой угол равен 90º, поэтому сумма двух острых углов прямоугольного треугольника равна 90º.

o Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.

• Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º.

 

Признак равенства прямоугольных треугольников:

·         Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.

·         Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

·         Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

·         Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.