Методические рекомендации по применению методов решения алгебраических уравнений для учащихся 10 класса (повторение 8-9 класс) Тема: «Решение алгебраических уравнений методом замены переменной»

Оценка 5

Домашнее обучение +6

pdf

математика

8 кл—11 кл

04.07.2021

Методические рекомендации по применению методов решения алгебраических уравнений для учащихся 10 класса (повторение 8-9 класс) Тема: «Решение алгебраических уравнений методом замены переменной»

Методические рекомендации

по применению методов решения алгебраических уравнений для учащихся 10 класса (повторение 8-9 класс)

Тема: «Решение алгебраических уравнений методом замены переменной»

Если в уравнение переменная входит в виде некоторой функции от одного и того же устойчивого выражения, то удобно это одинаковое выражение с переменной обозначить одной буквой (новой переменной). После решения упрощенного уравнения, необходимо произвести обратную замену.

Вид уравнения

Замена (метод или идея решения)

Пример

1.1) Биквадратное уравнение ax⁴+bx²+c=0 ,a≠0

1.2) Рациональное уравнение

Замена: x²=t,t≥0

1. Найти в записи уравнения устойчивое выражение, в составе которого присутсвует переменная.

Для поиска устойчивого выражения иногда нужно преобразовать уравнение.

2. Обозначить устойчивое выражение новой буквой.

x⁴+6 x²−7=0 Решение:

Замена: x²=t t²+6t−7=0⇔ (t−1)(t+7)=0

[ t=1 t=−7<0

Обратная замена: x²=1⇔

[ x=1

x=−1

Ответ:{±1}

(2 x²+3 x−1)²−10x²−15x+9=0 Решение: преобразуем уравнение:

(2 x²+3 x−1)²−5(2x²+3 x−1)+4=0

Замена: 2 x²+3 x−1=t t²−5t+4=0⇔

(t−4)(t−1)=0⇔

[t=1 t=4

Обратная замена:[2x22+3 x−1=1 ⇔

2 x +3 x−1=4

[

2 x²+3 x−2=0

2 ⇔

2 x +3 x−5=0

1 2(x+2)(x− )=0

2 ⇔

2(x−1)(x+)=0

x=−2 x=0,5 x=1

x=−2,5

Ответ: {-2,5; -2; 0,5; 1}

Вид уравнения	Замена (метод или идея решения)		Пример
2.1) Уравнения вида (x±a)⁴+(x±b)⁴=c	Замена: x± ⁺^b=t a 2 («врезаться посередине»)		(x+3)⁴+(x+5)⁴=16 Решение: Замена: x+4=t (t−1)⁴+(t+1)⁴=16⇔ (t⁴−4 t³+6t²−4 t+1) + + (t⁴+4 t³+6t²+4 t+1)=16⇔ 2t⁴+12t²+2=16⇔ t⁴+6t²−7=0⇔ биквадратное уравнение (см п. 1.1) [ t=1 t=−1 Обратная замена: [ x+4=1 ⇔ x=−5 x+4=−1 Ответ: −5;−3 (x+5)³+(x+7)³=8 Решение: Замена: x+6=t (t−1)³+(t+1)³=16⇔ (t³−3t²+3t−1) + + (t³+3t²+3t+1)=8⇔ t³+3t−4=0⇔ (t−1)(t²+t +4)=0⇔t=1 Обратная замена: x+6=1 x=−5 Ответ: −5	-
2.2) Уравнения вида
	Замена:	x± +b=t a 2
(x±a)ⁿ+(x±b)ⁿ=c
	(«врезаться посередине») При разложении выражения вида (a+b)ⁿна множители, биномиальные коэффициенты можно определить с помощью треугольника Паскаля (см. Справочно).

Справочно: Разложение (a+b)ⁿ. Треугольник Паскаля (биномиальные коэффициенты).

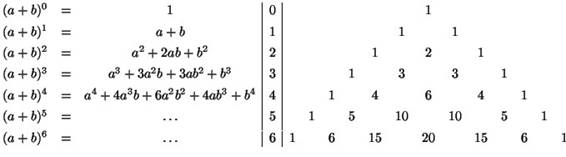
Вид уравнения

Замена (метод или идея решения)

Пример

3) Уравнения вида

(x+a)(x+b)(x+c)(x+d)=f ,f ≠0

1. Перегруппировать сомножители так (если это

(x−1)x(x+1)(x+2)=24

раскрыть скобки.

2. Выполнить замену: x²+(a+d)x=t

(x +x−2)(x +x)=24

Замена: x²+x=t

(t−2)t=24⇔ t²−2t−24=0⇔ (t−6)(t+4)=0⇔ [ ^t⁼⁶t=−4

возможно), чтобы Решение:

выполнялось равенство (x−1)(x+2)x(x+1)=24⇔ a+b=c+d , и попарно ^{2 2}

Обратная замена: x²+x=6 ⇔[x²2+x−6=0⇔

x +x=−4 x +x+4=0

(x+3)(x−2)=0⇔x=−3, x=2

Ответ: {−3;2}

Вид уравнения

Замена (метод или идея решения)

Пример

4.1) Уравнения вида:

Замена: x± ¹=t x

2(x²+ ¹₂)+3(x− ¹x )=4 x

Решение:

a x2 x Замена: x− ¹x=t

(x−¹x) =x²+x¹₂−2x ¹x=x²+ x¹₂−2 x2+x12−2=t2 x2+ 12=t2+2 x

2(t²+2)+3t−4=0⇔ 2t²+3t=0⇔

t(2t +3)=0⇔ Обратная замена:

1 x=−1

x_−
=0

[ ^t⁼⁰⇔ ^x_⇔ [ ^x⁼¹

t=−1,51 x=−2 x− =−1,5

x x=0,5

Ответ: −2;−1;0,5;1

2 x2+ 525+2xx)2=104

(

Решение: выделим в левой части уравнения полный квадрат разности:

x²⇔

1. Выделить квадрат 5+2

4.2) Уравнение вида: разности добавить и

отнять выражение 5+2 x 5+2 x ⇔

f ²(x)+g²(x)=k 2f (x)g(x) ;

2. выполнить замену одинакового выражения.

Замена:t

t²+5t−104=0⇔ (t+13)(t−8)=0⇔

Обратная замена:

⇔

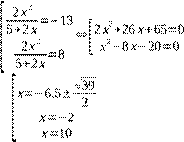Ответ:

Вид уравнения

Замена (метод или идея решения)

Пример

5.1) Уравнения вида:

(px²+nx+g)(px²+mx+g)=cx²,g≠0

Идея: деление обеих частей уравнения на х², х³, ...

4(x+5)(x+6)(x+10)(x+12)=3 x²Решение:

Перегруппируем множители слева: 4(x+5)(x+12)(x+6)(x +10)=3 x²Раскроем скобки попарно умножая первую и вторую, третью и четвертую:

1. Проверить, что x=0 не 4(x²+17 x+60)(x²+16 x+60)=3 x²является корнем уравнения; x=0 не является корнем уравнения,

2. разделим обе части уравнения на разделим обе части уравнения на x²:

x²: (px+^g+n)( px+ ^g+m)=c 4(x+ ⁶⁰+17)(x+⁶⁰+16)=3 x x x x

3. Выполнить замену: px+^gx=t Замена: x _xt

4(t+1)t=3⇔ 4 t²+4t−3=0⇔

⇔

Обратная замена:

⇔

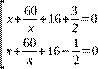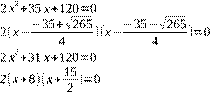решаем квадратные уравнения: отсюда:

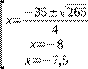
Ответ:

Вид уравнения

Замена (метод или идея решения)

Пример

5.2) Уравнения вида:

ax bx c,с≠0

px²+nx+g)⁺(px²+mx+g)⁼

(

Идея: деление числителя и знаменателя дроби на х, х², х³, ...

1. Проверить, что x=0 не является корнем уравнения; 2. Разделить числитель и знаменатель каждой из дробей левой части уравнения на x :

a b c

24 x 212xx₊2₎5

(2 x2−3 x+4)=(x + +

Решение: разделим числитель и знаменатель дроби в левой части уравнения на 2:

12 x 12x 5

= +

(x²−1,5 x+2) (x²+x+2) x=0 не является корнем уравнения, разделим числитель и знаменатель каждой из дробей слева и справа на х:

12 12 5_⇔

= +

2 2

+ =

п g

(px+ +n) (px+ +m) x x

(x−1,5+ )

(x+1+ )

12 5

3. Выполнить замену:

px+^g=t

= +

2 2

(x+ −1,5) (x+ +1) x x

Замена: x+²=t

− =5⇔

t−1,5 t +1

⇔ 2t²−t−15=0⇔

2(t−3)(t+)=0⇔ [^t⁼⁻^2,5t=3 Обратная замена:

x+ =−2,5 ₂

xx+2=3 _⇔[2xx2−+35xx++24==00 x

первое квадратное уравнение в совокупности не имеет действительных корней, во втором уравнении многочлен в левой части можно разложиь на множители: (x−1)(x−2)=0⇔ отсюда: x=1

[x₌2 Ответ:1;2

Вопросы для контроля:

1. В каком случае используется метод введения новой переменной?

2. Можно ли делить обе части уравнения на выражение, содержащее переменную? Ответ поясните.

3. Какое свойство дроби применяется при решении уравнений вида 5?

Задания для самостоятельного решения:

I. Решите уравнения выполнив эффективную замену (1-7)

1. а) x⁶=7 x³+8 ; б) ₂²¹=6+x²−4 x ;

x −4 x+10

в) (x²+2x)²−(x+1)²=55 ; г) (x²−6 x)²−2(x−3)²=81 .

2. а) (x−2)⁴+(x−3)⁴=1 ; б) (x+6)⁴+(x+4)⁴=82 ;

в) (x−1)⁵+(x+3)⁵=242(x+1) ; г) (x−2)⁶+(x−4)⁶=64 .

3. а) (x−4)(x−5)(x−6)(x−7)=1680 ; б) (x−4)(x+2)(x+8)(x+14)=1204 ;

в) (x−2)(x−3)²(x−4)=20 ; г) x ₂ . x +7 x+12

4 а) 7(x+1x )−2(x²+ x¹₂)=9 ; б) (x²+¹⁶x₂)−x−⁴x−12=0 ;

4 x2+12x+12x + x4₂= x(x(2x++11)2 625

в) 47 ; г) 2=112 .

) 5. а) x²+ ⁸¹x ^x9²2=40 ; б) x²+(_x₋^x₁)²=8 ;

_{( + )}

2 2 2

в) x²+( ^x) =2 ; г) ( ^x) +( ^x) =90 .

2x−1 x−1 x+1

6. а) (2x²−3 x+1)(2x²+5 x+1)=9 x²; б) (2x²−5 x+2)(2x²+7 x+2)=−20 x² ;

в) (x+2)(x+3)(x+8)(x+12)=4 x²; г) (x−4)(x+5)(x+10)(x−2)=18x².

2x 3 x 5 4 x 3x

7. а) 2 + 2 +4=0 ; б) 4 x2−8 x+7+ 4 x2−10x+7=1 ;

x −4 x+2 x +x+2

в) xx22−−106 xx++1515= 2 4 x ; г) x2−3xx+1+ x2−22xx+1=72 .

x −12 x+15

II. Составьте краткий план решения уравнения, укажите замену, которую можно выполнить:

(ax+b)(ax+b+c)(ax+b+2c)(ax+b+3c)=f ,f≠0 .

III. Решите уравнение используя замену переменных^x3 + ⁴⁸2 =10(₃^x−⁴_x) . _x

IV. Решите уравнение используя замену переменных: (xx₂(−x²x++11))₂=10_{9 .}

Домашнее задание

1. Дорешать задания урока для самостоятельного решения.

2. Решить уравнение (уравнения высших степеней):

1. x ³ + 3x ² − 10x − 24 = 0; 3. x ³ − 2x ² − x − 6 = 0;

2. x ³ − 4x ² − 11x + 30 = 0; 4. x ³ + 5x ² + 5x − 3 = 0.

5. x ⁴ + 3x ³− 8x ² − 12x + 16 = 0;

6. x ⁴− 3x ³ + x ² − x − 6 = 0

Проверочная работа

1 вариант 2 вариант Решите уравнение: Решите уравнение:

1. (x−1)(x−5)(x+3)(x+7)=135 ; 1. (x−2)(x−6)(x+1)(x+5)=−180 ;

2 2

2. x²+(x+^x1) =3 ; 2. x²+(x⁴+^x2)₂=5 ;

3. 2(²x−3^x)= x²₂+18^x²+⁴3 ; 3. 12x²+3¹x2+10(2x+3¹x )+11=0 ;

4. (x²−5 x)(x+3)(x−8)+108=0 . 4. (x+4)²(x+10)(x−2)+243=0 .

5. ^x²⁻⁶x^x⁻⁹₌^xx²₂⁻−⁴6x^x⁻−⁹9 ; 5. xx²²−−106 xx++1515=x²−83xx+15

6. ₍2x²₋3 x₊1₎₍2x²₊5 x₊1₎₌9 x². 6. ₍x³₊x²₋3 x₎²₊₍x³₋x²₋3 x₎²₌10 x⁴.

Список литературы:

1. Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательныхорганизаций / А.Г. Мерзляк, В.П. Поляков. - 2-е изд., стереотип. - М.: Вентана-Граф, 2019. 384с. [глава 37]

2. Нелин Е.П. Алгебра. 7-11 классы. Определения, свойства, методы решения задач — втаблицах. Сер. Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). - 4-е изд., испр. - М.: ИЛЕКСА, 2019 — 128 с.

3. Шарыгин И.Ф. Факультативный курс по математике: Решение задач: Учеб. Пособие для 10 кл. сред. шк. - М.: просвещение, 1989. - 252с. [§ 2 Уравнения и системы уравнений]

4. Подготовка к олимпиадам и ЕГЭ по математике и физике: И.В. Яковлев [Электронный ресурс]. - Режим доступа: https://mathus.ru/math/alguzap.pdf [Дата обращения 30.06.2021]

Методические рекомендации по применению методов решения алгебраических уравнений для учащихся 10 класса (повторение 8-9 класс)

Ответ: {-2,5; -2; 0,5; 1}

Вид уравнения Замена (метод или идея решения)

Обратная замена: ⇔ Ответ:

Ответ: Вид уравнения

Ответ: 1 ; 2 Вопросы для контроля: 1

II. Составьте краткий план решения уравнения, укажите замену, которую можно выполнить: ( ax + b )( ax + b + c )( ax + b…

1. 2 ( 2 x − 3 x )= x 2 2 + 18 x 2 + 4 3 ; 3. 12 x 2 +…

Список литературы: 1.

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

04.07.2021