
Министерство образования Оренбургской области
ГАПОУ «БСК» г. Бузулука Оренбургской области
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ
к контрольной работе
по дисциплине «МАТЕМАТИКА»
для студентов I курса заочного отделения
специальности
21.02.01 «Разработка и эксплуатация нефтяных и газовых месторождения»
Бузулук, 2019
Попович М. А.
Методические указания к контрольной работе по дисциплине «Математика» для студентов I курса заочного отделения.- Бузулук: ГАПОУ «Бузулукский строительный колледж», 2018.
Методические указания созданы в помощь студентам Iкурса заочного отделения специальностей «Монтаж и эксплуатация оборудования и систем газоснабжения», «Разработка и эксплуатация нефтяных и газовых месторождения»
. В данном пособии указаны основные требования, предъявляемые к оформлению и выполнению домашней контрольной работы. Даны задания по вариантам для студентов, представлены примеры решения типовых задач, указана рекомендуемая литература и вопросы для самостоятельного изучения.
Ó Попович М.А.
Ó ГАПОУ «Бузулукский строительный колледж», 2018
1. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
2. РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
3. ЗАДАНИЯ ДЛЯ СТУДЕНТОВ
4. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Контрольная работа должна содержать:
1. Титульный лист
2. Рецензия
3. Оглавление
4. Содержание работы
5. Список используемой литературы
Контрольная работа может быть выполнена по усмотрению студента:
- либо в обычной ученической тетради,
- либо на листах формата А4.
Титульный лист.
На титульном листе указывается название учебного заведения; дисциплина; номер группы; номер варианта; Ф. И. О студента, выполнившего контрольную работу; Ф. И. О. преподавателя, проверяющего контрольную работу; нормоконтроль; год выполнения контрольной работы.
Рецензия. Содержит один чистый лист для рецензии работы.
Оглавление. Содержит перечень заданий с указанием номеров страниц.
Содержание работы.
Каждый вариант контрольной работы содержит 10 заданий. Задания выполняются в указанном порядке. Условия заданий должны быть записаны полностью. Каждое задание начинается с новой страницы. В решении задач необходимо указать все используемые формулы; решение должно содержать комментарии или пояснения, указаны все расчеты и показаны все преобразования выполняемые с алгебраическими выражениями.
Список используемой литературы.
Литературные источники приводятся в следующем порядке: по алфавиту фамилии и инициалы авторов, точное название, место издания, издательство, год издания.
Пример: Зотова С. И. Практикум по MS Access. – М.: Финансы и статистика, 2003.
После выполнения контрольная работа сдается в методический кабинет заочного отделения, где регистрируется в журнале контрольных работ.
Далее преподаватель ее проверяет.
Студент должен ознакомиться с результатами проверки работы. Если работе не зачтена, то контрольная работа забирается студентом на доработку и, после устранения недостатков, вновь регистрируется и сдается в методический кабинет.
Номер варианта выбирается по последней цифре зачетной книжки.
|
ЦИФРА |
ВАРИАНТ |
ЦИФРА |
ВАРИАНТ |
|
1 |
1 вариант |
6 |
6 вариант |
|
2 |
2 вариант |
7 |
7 вариант |
|
3 |
3 вариант |
8 |
8 вариант |
|
4 |
4 вариант |
9 |
9 вариант |
|
5 |
5 вариант |
0 |
10 вариант |
Номера задач каждого варианта приведены в таблице:
|
Вариант |
Номера заданий |
|
|||||||||
|
1 |
1 |
11 |
21 |
31 |
41 |
51 |
61 |
71 |
81 |
91 |
|
|
2 |
2 |
12 |
22 |
32 |
42 |
52 |
62 |
72 |
82 |
92 |
|
|
3 |
3 |
13 |
23 |
33 |
43 |
53 |
63 |
73 |
83 |
93 |
|
|
4 |
4 |
14 |
24 |
34 |
44 |
54 |
64 |
74 |
84 |
94 |
|
|
5 |
5 |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
|
|
6 |
6 |
16 |
26 |
36 |
46 |
56 |
66 |
76 |
86 |
96 |
|
|
7 |
7 |
17 |
27 |
37 |
47 |
57 |
67 |
77 |
87 |
97 |
|
|
8 |
8 |
18 |
28 |
38 |
48 |
58 |
68 |
78 |
88 |
98 |
|
|
9 |
9 |
19 |
29 |
39 |
49 |
59 |
69 |
79 |
89 |
99 |
|
|
10 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|
Вопросы для самостоятельного изучения:
Пример 1. Найти производные, пользуясь правилами и формулами дифференцирования.
Решение:
Кроме формул дифференцирования нужно использовать правила дифференцирования (суммы, разности, произведения, частного).
Необходима и теорема о производной сложной функции:
если задана сложная функция
![]() ,
где
,
где ![]() , то есть
, то есть ![]() ; если каждая из функций
; если каждая из функций ![]() и
и ![]() дифференцируема
по своему аргументу, то
дифференцируема
по своему аргументу, то
![]() .
.
1)
![]() ,
, ![]() ,
,
![]()
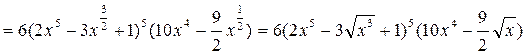 .
.
2)
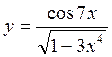 ,
,
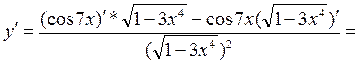
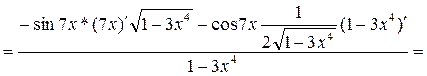
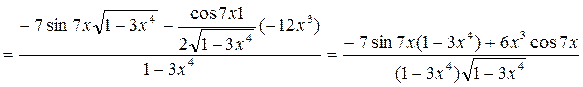
3)
![]()
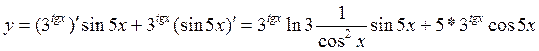
4)
![]()
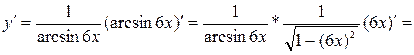
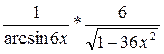
Пример 2. Задан закон s(t) изменения пути движения материальной точки; нужно найти значения скорости и ускорения этой точки в момент времени t0.
Решение:
Пусть ![]() .
.
Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются соответственно значениями в этот момент I и II производных функции, задающей закон изменения пути движения точки.
У нас ![]()
![]() (ед. ск.)
(ед. ск.)
![]()
![]() (ед. уск.)
(ед. уск.)
Пример 3. Имеются три раствора. Первый содержит 80% кислоты и 20% воды, второй-60% соли и 40%воды, третий - по 20%соли и кислоты и 60%воды. Из них необходимо приготовить новый раствор, содержащий 30%воды. Какое наименьшее и какое наибольшее процентное содержание соли может быть в этом новом растворе?
Решение:
1 способ решения: Обозначим за единицу массу нового раствора, х-масса I раствора, у-масса II раствора, z-масса III раствора, х ≥0, у≥0, z ≥0, тогда по условию х+у+z=1.
В новый раствор входит:
из I раствора 0,2х воды и 0,8х кислоты,
из II раствора 0,4у воды и 0,6у соли,
из III раствора 0,2z кислоты; 0,6z воды; 0,2z соли.
Масса воды в новом растворе 1*0,3=0,3
Тогда имеем: 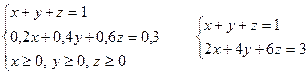
Пусть t – содержание соли в новом растворе, тогда t=0,6y+0,2z
Исключим из системы переменную х
![]()
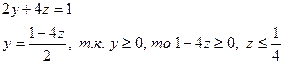
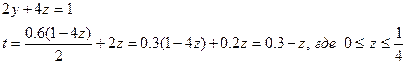
t=0.3-z – убывающая функция, значит наименьшее значение t принимает при z=1/4, а наибольшее
значение - при z=0.
![]()
![]()
Следовательно, ![]()
2 способ решения: Т.к. в новом растворе 30% воды, а во II-м и III-м соответственно 40% и 60%, то требуемый раствор невозможно получить только из II и III растворов, значит масса I-го раствора – ненулевая.
Обозначим за единицу массу первого раствора, х-масса II раствора, у-масса III раствора, x≥0, y≥0.
Тогда масса воды в новом растворе составляет 0,3(1+x+y)=0,2∙1+0,4∙x+0,6∙y ó x=1-3y.
Т.к. x≥0, то 1-3y≥0, y≤1/3.
Пусть Р – процентное
содержание соли в новом растворе, тогда ![]()
![]()
![]()
Найдем производную 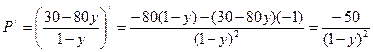
Так как ![]() на интервале
на интервале ![]() , то функция убывает на отрезке
, то функция убывает на отрезке ![]() .
.
Следовательно, наименьшее значение P(y) достигает в точке y=1/3, а наибольшее – в точке y=0.
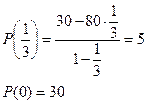
Итак, ![]()
Пример 4. Исследовать функцию методами дифференциального исчисления и начертить график.
Исследование функции и построение графика рекомендуется проводить по следующей схеме:
1) найти область определения функции D(y);
2) найти точки экстремума функции и определить интервалы ее монотонности;
3) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;
4) найти асимптоты графика функции;
5) построить график, используя результаты предыдущих исследований;
6)
дополнительно найти наибольшее и
наименьшее значения на отрезке ![]() .
.
Решение:
Дана функция: ![]()
1)
Областью определения данной
функции являются все действительные значения аргумента х, то есть D(y): ![]() , а это значит,
что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных
асимптот.
, а это значит,
что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных
асимптот.
2) Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
![]()
![]()
![]()
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки I рода х1 = -5, х2 = -1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
|
x |
|
-5 |
|
-1 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
& |
max |
( |
min |
& |
![]()
![]()
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем II производную заданной функции и приравняем ее к нулю:
![]()
![]() , т.е.
, т.е. ![]()
![]()
![]()
![]()
Итак, функция имеет одну
критическую точку 2 рода ![]() . Разобьем
область определения полученной точкой на части, в каждой из которой установим
знак II производной:
. Разобьем
область определения полученной точкой на части, в каждой из которой установим
знак II производной:
|
x |
|
-3 |
|
|
|
- |
0 |
+ |
|
|
|
т.п. |
|
Значение ![]() является
абсциссой точки перегиба графика функции, а ордината этой точки
является
абсциссой точки перегиба графика функции, а ордината этой точки ![]()
4)
Выясним наличие у графика заданной
функции наклонных асимптот. Для определения параметров уравнения асимптоты ![]() воспользуемся
формулами:
воспользуемся
формулами: ![]() .
.
Имеем 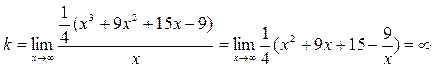 .
.
Таким образом, у графика заданной функции наклонных асимптот нет.
5)
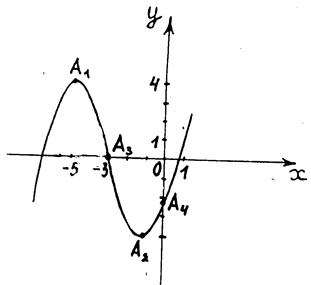 Для построения графика в
выбранной системе координат изобразим точки максимума А1(-5; 4),
минимума А2(-1; -4), перегиба А3 (-3; 0) и точку пересечения
графика с осью Оу А4 (0;
Для построения графика в
выбранной системе координат изобразим точки максимума А1(-5; 4),
минимума А2(-1; -4), перегиба А3 (-3; 0) и точку пересечения
графика с осью Оу А4 (0; ![]() ).
С учетом результатов предыдущих исследований построим кривую.
).
С учетом результатов предыдущих исследований построим кривую.
6)
Найдем наибольшее и наименьшее
значения заданной функции на отрезке ![]() . Для этого
посчитаем значения функции на концах этого отрезка, в критических точках I
рода, попавших на отрезок, и сравним результаты:
. Для этого
посчитаем значения функции на концах этого отрезка, в критических точках I
рода, попавших на отрезок, и сравним результаты:
![]() .
.
Очевидно, что ![]() .
.
Пример 5. Найти неопределенные интегралы
а) способом подстановки
(методом замена переменной) ![]() ,
, ![]() ;
;
б) применяя метод
интегрирования по частям ![]() ,
, ![]() .
.
Решение:
а) ![]() : применим подстановку
: применим подстановку ![]() .
Тогда
.
Тогда ![]() и
и ![]()
![]() : применим подстановку
: применим подстановку ![]() .
Тогда
.
Тогда ![]() ,
,
![]() ,
откуда
,
откуда ![]()
б) ![]() : применим формулу
интегрирования по частям
: применим формулу
интегрирования по частям ![]() .
.
Положим ![]() . Тогда
. Тогда ![]() .
.
Следовательно, ![]() .
.
![]() : положим
: положим ![]() . Тогда
. Тогда ![]() .
.
Отсюда ![]() . Применяя в последнем интеграле
подстановку
. Применяя в последнем интеграле
подстановку ![]() , получаем
, получаем ![]() ,
следовательно,
,
следовательно, ![]() .
.
Отсюда ![]() .
.
Пример 6. Вычислить площадь плоской фигуры, ограниченную параболами.
![]()
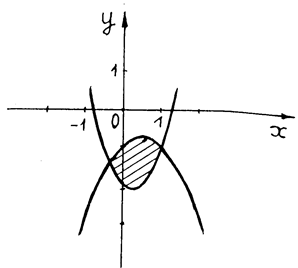 Решение:
Решение:
Найдем абсциссы точек
пересечения заданных парабол. Для этого приравняем правые части их уравнений: ![]() .
.
Решаем полученное квадратное
уравнение: ![]()
![]() .
.
Вычисление площади фигуры
осуществляем по формуле 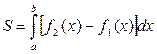 , где
, где ![]() - кривые, ограничивающие фигуру
- кривые, ограничивающие фигуру ![]() .
.
В нашем случае 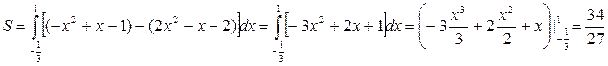 (кв. ед.)
(кв. ед.)
Пример 7. Найти общее решение (общий интеграл)
дифференциального уравнения I порядка 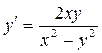 .
.
Решение:
Правая часть уравнения 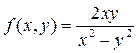 обладает
свойством
обладает
свойством 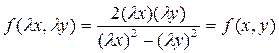 . Поэтому заданное уравнение является
однородным дифференциальным уравнением I порядка.
Совершим замену
. Поэтому заданное уравнение является
однородным дифференциальным уравнением I порядка.
Совершим замену 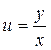 , где
, где ![]() - некоторая функция от аргумента х.
Отсюда
- некоторая функция от аргумента х.
Отсюда ![]() . Исходное уравнение приобретает
вид
. Исходное уравнение приобретает
вид 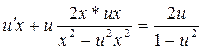 .
.
Продолжаем преобразования: 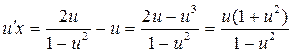 ;
; 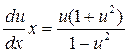 .
.
Производим разделение
переменных: 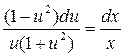 .
.
После интегрирования обеих частей уравнения получаем
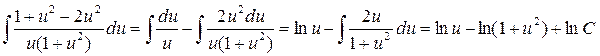 ;
;
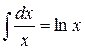 .
.
Таким образом ![]() ;
; 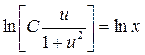 .
.
Потенцируя, находим 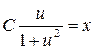 или
или 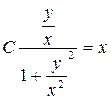 ;
;
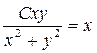 .
.
Итак, общий интеграл исходного уравнения приобретает вид
![]() ,
где С – произвольная постоянная.
,
где С – произвольная постоянная.
Пример 8. Найти
произведение матриц ![]() и
и ![]()
![]()
Пример 9. Вычислить
определитель по правилу треугольников 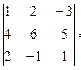 .
.
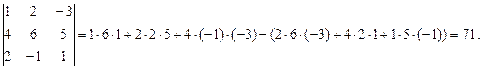
Пример 10. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
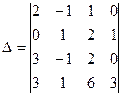
Решение. Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец. Итак, имеем
Полученные в итоге два
определителя третьего порядка вычислим тем же методом. В определителе ![]() нулевых элементов нет,
поэтому можно выбрать для разложения любой из столбцов, например, первый. В
нулевых элементов нет,
поэтому можно выбрать для разложения любой из столбцов, например, первый. В ![]() единственный нулевой
элемент находится на пересечении первого столбца со второй строкой. Для разнообразия
будем разлагать
единственный нулевой
элемент находится на пересечении первого столбца со второй строкой. Для разнообразия
будем разлагать ![]() по
второй строке:
по
второй строке:![]()
![]()
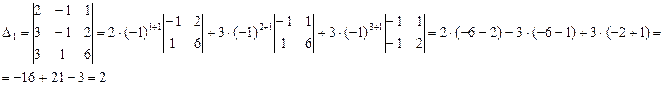
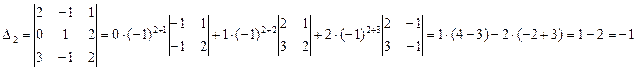
Таким образом окончательно
получим: ![]()
Пример 11. Решить
систему уравнений 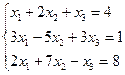 по
формулам Крамера.
по
формулам Крамера.
Составляем главный определитель, элементами которого являются коэффициенты при неизвестных:
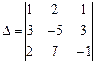
и три вспомогательных определителя:
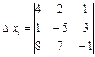 ;
; 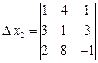 ;
; 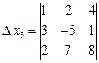 .
.
Определитель ![]() составлен из определителя
составлен из определителя ![]() путем замены элементов первого
столбца свободными членами системы уравнений. В определителях
путем замены элементов первого
столбца свободными членами системы уравнений. В определителях ![]() и
и ![]() соответственно
второй и третий столбцы заменены свободными членами. Вычислим все четыре
определителя.
соответственно
второй и третий столбцы заменены свободными членами. Вычислим все четыре
определителя.
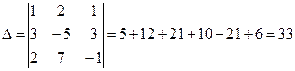 ;
;
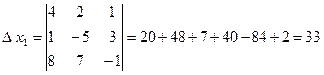 ;
;
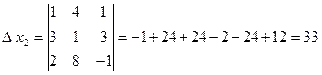 ;
;
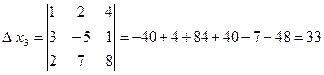 .
.
Неизвестные ![]() ,
, ![]() ,
,
![]() находим по формулам
находим по формулам
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Ответ: ![]() ;
;
![]() ;
; ![]() .
.
Пример 12. Решить
систему уравнений способом Гаусса 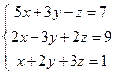 .
.
В результате
элементарных преобразований добиваются того, чтобы в последнем уравнении
системы осталось одно неизвестное (![]() ), во втором – 2
неизвестных (
), во втором – 2
неизвестных (![]() и
и ![]() )
а в первом – 3 неизвестных (
)
а в первом – 3 неизвестных (![]() ,
, ![]() ,
, ![]() ).
За ведущее уравнение берется то, в котором коэффициент при
).
За ведущее уравнение берется то, в котором коэффициент при ![]() равен 1. Если такого уравнения
нет, то его легко получить, разделив любое из уравнений системы на коэффициент
при
равен 1. Если такого уравнения
нет, то его легко получить, разделив любое из уравнений системы на коэффициент
при ![]() .
.
Ведущим уравнением данной системы будет последнее. Перепишем систему так:
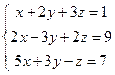 (2)
(2)
Умножаем первое
уравнение на (-2) и складываем со вторым, чтобы избавиться от ![]() во втором уравнении. Результат
сложения записываем на месте второго уравнения. Далее первое уравнение умножаем
на (-5) и складываем с третьим, чтобы избавиться от
во втором уравнении. Результат
сложения записываем на месте второго уравнения. Далее первое уравнение умножаем
на (-5) и складываем с третьим, чтобы избавиться от ![]() в
третьем уравнении. Результат записываем на месте третьего уравнения. Первое
уравнение при этом переписываем без изменений. Получим:
в
третьем уравнении. Результат записываем на месте третьего уравнения. Первое
уравнение при этом переписываем без изменений. Получим:
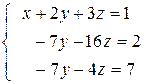 (3)
(3)
Системы уравнений (2) и (3) эквиваленты, т. е. они обе несовместны, или же обе совместны и имеют одни и те же решения.
Умножаем второе
уравнение системы (5) на (-1) и складываем с третьим, чтобы избавиться от ![]() в третьем уравнении. Первое
уравнение при этом не трогаем. Результат записываем на месте третьего
уравнения. Тогда
в третьем уравнении. Первое
уравнение при этом не трогаем. Результат записываем на месте третьего
уравнения. Тогда
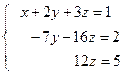 .
.
Из последнего уравнения ![]() . Подставляем это значение
. Подставляем это значение ![]() во втрое уравнение системы и находим
во втрое уравнение системы и находим
![]() :
:
![]()
![]() .
.
В первое уравнение
подставляем значения ![]() и
и ![]() , получаем
, получаем
![]()
![]() .
.
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Пример 13. 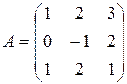 .
.![]() Найти
обратную матрицу
Найти
обратную матрицу ![]() .
.
РЕШЕНИЕ.
1) Составляем и вычисляем определитель
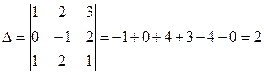 .
.
Определитель вычислен по правилу треугольника.
2) Вычисляем алгебраические дополнения
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
![]() Вычисляем
А11. Вычеркиваем первую строку и первый столбец
Вычисляем
А11. Вычеркиваем первую строку и первый столбец 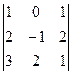 ;
;
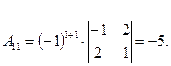
Вычисляем ![]() .
Вычеркиваем первую строку и второй столбец. Составляем определитель второго
порядка из оставшихся элементов.
.
Вычеркиваем первую строку и второй столбец. Составляем определитель второго
порядка из оставшихся элементов.
![]()
![]()
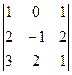 ;
Вычисляем
;
Вычисляем ![]() .
.
Аналогично вычисляем все остальные алгебраические дополнения:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
Составим обратную матрицу
A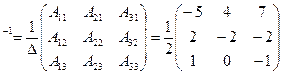
A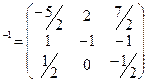
Сделаем проверку
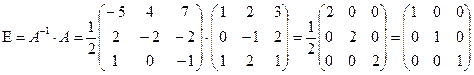
Пример 14. Решить
систему матричным способом 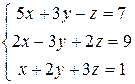 .
.
Из коэффициентов при неизвестных
составим матрицу ![]() :
: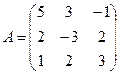 .
.
Из неизвестных составим матрицу –
столбец: 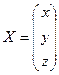 .
.
Из свободных членов составим
матрицу – столбец: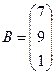 .
.
Тогда система запишется в виде
![]() .
.
Получили матричное уравнение.
Умножаем обе части этого уравнения на ![]() слева.
Получаем:
слева.
Получаем:
![]() .
.
Находим обратную матрицу:
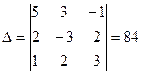 ;
; 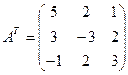 ;
;
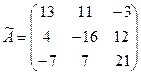 (матрица, составленная из
алгебраических дополнений элементов;
(матрица, составленная из
алгебраических дополнений элементов; 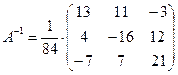 (обратная
матрица).
(обратная
матрица).
Умножая обратную матрицу на ![]() , получаем матрицу
, получаем матрицу ![]() .
. 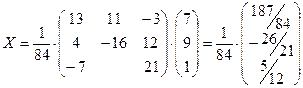 .
.
Отсюда получаем ответ:
![]() ;
; ![]() ;
; ![]() .
.
Пример 15. Дискретная случайная величина Х имеет только два возможных значения х1 и х2 , причем х1 < х2. Найти закон распределения величины Х, если известно, что математическое ожидание М (х) = 1,4, дисперсия D (х) = 0,24 и вероятность р1 того, что Х примет значение х1, равна 0,6.
Решение:
Так как сумма вероятностей всех возможных значений Х равна 1, то вероятность p2 того, что Х примет значение х2, равна p2 = 1 - p1 = 1 – 0,6 = 0,4.
Напишем закон распределения Х:
|
Х |
х1 |
х2 |
|
p |
0,6 |
0,4 |
Для отыскания х1 и х2 составим два уравнения.
Для составления первого уравнения воспользуемся тем, что математическое ожидание
M(x) определяется по формуле M(x) = х1 р1 + х2 р2 + … + хn рn
В нашем случае: M(x) = х1 р1 + х2 р2
Учитывая, что по условию M(x) = 1,4, можем записать первое уравнение:
0,6х1 + 0,4х2 = 1,4.
Учитывая, что по условию D(x) = 0,24, пользуясь формулой D (х) = M (X2) – [M(X)]2, напишем второе уравнение:
0,6 х12 + 0,4 х22 - 1,42 = 0,24, или
0,6 х12 + 0,4 х22 = 2,2.
Решив полученную систему уравнений, найдем два решения:
х1 = 1, х2 = 2 и х1 = 1,8, х2 = 0,8.
По условию, х1 < х2, поэтому задаче удовлетворяет лишь первое решение.
Окончательно получим искомый закон распределения:
|
Х |
1 |
2 |
|
p |
0,6 |
0,4 |
ЗАДАНИЯ ДЛЯ СТУДЕНТОВ
1-10. Найти производную функции одной переменной.
1. ![]() ;
2.
;
2. ![]() ;
;
3. ![]() ; 4.
; 4.
![]() ;
;
5. ![]() ; 6.
; 6.
![]() ;
;
7. ![]() ;
8.
;
8. ![]() ;
;
9. ![]() ;
10.
;
10. ![]() .
.
11-20. Решить задачи с помощью методов математического анализа.
11.а) Точка движется по закону ![]() . Найти величину скорости и ускорения
в момент t=3 с, если путь измеряется в метрах.
. Найти величину скорости и ускорения
в момент t=3 с, если путь измеряется в метрах.
б) Имеются три сплава. Первый сплав содержит 10% золота, 40% серебра и 50% меди, второй сплав- 20% серебра и 80% меди, третий – 20% золота, 30% - серебра и 50 % меди. И них получили новый сплав, содержащий 5% золота. Какое наибольшее и наименьшее процентное содержание серебра может быть в новом сплаве?
12.а) Тело вращается вокруг оси по закону ![]() . Найти угловую скорость вращения в
момент t=1 c; угловое ускорение в момент t.
. Найти угловую скорость вращения в
момент t=1 c; угловое ускорение в момент t.
б) Имеются три раствора. Первый содержит 80% спирта и 20% воды, второй – 40% глицерина, 50% воды и 10% спирта, третий –по 10% спирта и глицерина и 80% воды. Из них необходимо приготовить новый раствор, содержащий 50% воды. Какое наибольшее и наименьшее процентное содержание глицерина может быть в новом растворе?
13.а) Определить скорость движения точки в
конце третьей секунды, если путь, пройденный точкой в t секунд, выражается
формулой ![]() и измеряется в метрах.
и измеряется в метрах.
б) Имеются три раствора. Первый содержит 30% кислоты,30% воды и 40% соли, второй-80% соли и 20%воды, третий - по 40% кислоты и 60% воды. Из них необходимо приготовить новый раствор, содержащий 50%воды. Какое наименьшее и какое наибольшее процентное содержание кислоты может быть в этом новом растворе?
14.а) Температура тела Т изменяется в
зависимости от времени t по закону ![]() . С какой
скоростью нагревается это тело в момент t=4 c?
. С какой
скоростью нагревается это тело в момент t=4 c?
б) Имеются три сплава. Первый сплав содержит 20% золота, 30% серебра и 50% меди, второй сплав- 40% серебра и 60% меди, третий – 10% золота, 20% - серебра и 70 % меди. И них получили новый сплав, содержащий 30% серебра. Какое наибольшее и наименьшее процентное содержание золота может быть в новом сплаве?
15.а) Количество электричества, протекшее
через проводник за t секунд, определяется по формуле ![]() . Найти силу тока в конце четвертой
секунды.
. Найти силу тока в конце четвертой
секунды.
б) Имеются три раствора. Первый содержит 80% спирта и 20% воды, второй – 60% глицерина и 40% воды, третий – 50% спирта, 20% глицерина и 30% воды. Из них необходимо приготовить новый раствор, содержащий 30% воды. Какое наибольшее и наименьшее процентное содержание спирта может быть в новом растворе?
16.а) Тело движется по закону ![]() . Найти, в какие моменты времени
скорости движения тела равны нулю?
. Найти, в какие моменты времени
скорости движения тела равны нулю?
б) Имеются три раствора. Первый содержит 80% кислоты и 20% воды, второй-50% соли и 40%воды, третий - по 30% соли, 40% кислоты и 30%воды. Из них необходимо приготовить новый раствор, содержащий 30%воды. Какое наименьшее и какое наибольшее процентное содержание соли может быть в этом новом растворе?
17.а) Угол поворота шкива определяется из
уравнения ![]() , где t время в секундах. Найти
среднюю угловую скорость в промежутке времени от t=4 до t=6 и угловую скорость
в момент t=6.
, где t время в секундах. Найти
среднюю угловую скорость в промежутке времени от t=4 до t=6 и угловую скорость
в момент t=6.
б) Имеются три сплава. Первый сплав содержит 20% золота, 20% серебра и 60% меди, второй сплав- 40% серебра и 60% меди, третий – 20% золота, 10% - серебра и 70 % меди. И них получили новый сплав, содержащий 30% серебра. Какое наибольшее и наименьшее процентное содержание золота может быть в новом сплаве?
18. а) Тело вращается вокруг оси, причем закон
изменения угла j в зависимости от времени t определяется уравнением ![]() . Найти угловую скорость вращения
тела в момент t=3.
. Найти угловую скорость вращения
тела в момент t=3.
б) Имеются три раствора. Первый содержит 90% спирта и 10% воды, второй – 70% глицерина и 30% воды, третий –по 30% спирта и глицерина и 40% воды. Из них необходимо приготовить новый раствор, содержащий 20% воды. Какое наибольшее и наименьшее процентное содержание глицерина может быть в новом растворе?
19.а) Тело движется по закону ![]() . Найти максимальную скорость движения
тела.
. Найти максимальную скорость движения
тела.
б) Имеются три раствора. Первый содержит 50% кислоты и 30% воды, второй - 70% соли и 30% воды, третий - по 30% соли и кислоты и 40%воды. Из них необходимо приготовить новый раствор, содержащий 40% соли. Какое наименьшее и какое наибольшее процентное содержание кислоты может быть в этом новом растворе?
20.а) Тело, брошенное вертикально вверх со
скоростью v0 м/с, движется по закону ![]() ,
где время t – в секундах, а путь s – в метрах. Найти скорость движения и
ускорение в момент t; в конце третьей секунды, если v0=100 м/с.
,
где время t – в секундах, а путь s – в метрах. Найти скорость движения и
ускорение в момент t; в конце третьей секунды, если v0=100 м/с.
б) Имеются три сплава. Первый сплав содержит 10% золота, 20% серебра и 70% меди, второй сплав- 20% серебра и 80% меди, третий – 30% золота, 50% - серебра и 20 % меди. И них получили новый сплав, содержащий 40% меди. Какое наибольшее и наименьшее процентное содержание золота может быть в новом сплаве?
21-30. Исследовать функцию и построить ее график.
21. ![]() 22.
22.
![]()
23. ![]() 24.
24.
![]()
25. ![]() , 26.
, 26.
![]()
27. ![]() 28.
28.
![]() ,
,
29. ![]() 30.
30.
![]()
31-40. Найти неопределенные интегралы.
31.
![]()
32.

33.

34.
а) 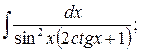 б)
б) 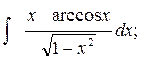
35.
а) 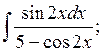 б)
б)
![]()
36. а) 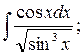 б)
б)
![]()
37.
а) 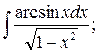 б)
б) ![]()
38.
а) ![]() б)
б) ![]()
39. а)
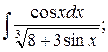 б)
б) ![]()
40.
а) 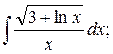 б)
б) ![]()
41-50. Вычислить площадь фигуры, ограниченной заданными линиями. Выполнить рисунок.
41. ![]()
![]() .
.
42. ![]()
![]() .
.
43. ![]()
![]()
44.![]() ,
, ![]() .
.
45. ![]() ,
, ![]() .
.
46. ![]() ,
, ![]() .
.
47. ![]() ,
, ![]() .
.
48. ![]() ,
, ![]() .
.
49. ![]() ,
, ![]() .
.
50. ![]() ,
, ![]() .
.
51-60. . Найти решение дифференциального уравнения первого порядка, удовлетворяющее указанному начальному условию. Сделать проверку.
51. ![]() у(1) = 0.
у(1) = 0.
52. xy | + xey/x – y = 0, y(1) = 1 .
53. 20xdx – 3ydy = 3x2ydy – 5xy2dx, y(1) = 1.
54. xy | = y ln (y/x), y(1) = e.
55. 3(x2y
+ y)dy +![]() = 0, y(0) = 0.
= 0, y(0) = 0.
56. xy | + y = x + 1, y(1) = 0.
57. y |cosx = (y + 1)sinx, y(0) = 0.
58. xy | - y = ![]() y(1) = 0.
y(1) = 0.
59. y | - y/x = x2, y(1) = 0.
50. y | + ycosx
= ![]() y(0) = 0.
y(0) = 0.
61-70. Выполнить действия с матрицами и определителями.
Найти: а) 3A+B б) AB в)A -1 г)A -1A
2).Найти ![]() методом
треугольников,
методом
треугольников, ![]() - разложение по
элементам первого столбца
- разложение по
элементам первого столбца
61. 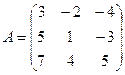
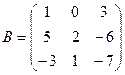
62.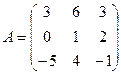
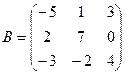
63.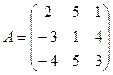
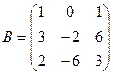
64.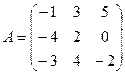
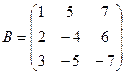
65.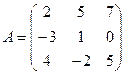
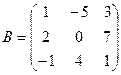
66.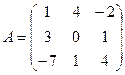
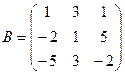
67.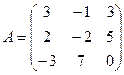
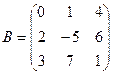
68.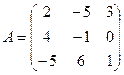
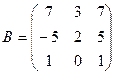
69.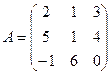
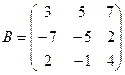
70. 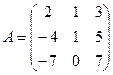
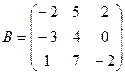
71-80. Решить систему линейных уравнений: а) по формулам Крамера;
б) матричным методом; в) методом Гаусса
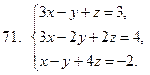
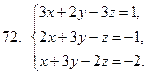
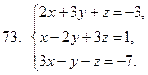
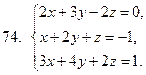
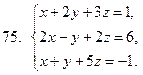
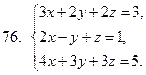
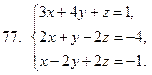
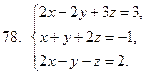
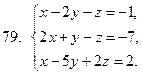
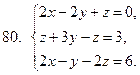
81-90 . Выполнить действия в алгебраической форме и представить полученный результат в тригонометрической и показательной формах.
81. 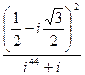 ; 82.
; 82.
![]() ;
;
83. ![]() ; 84.
; 84.
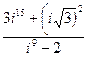 ;
;
85. ![]() ;
86.
;
86. ![]() ;
;
87. ![]() ;
88.
;
88. ![]() ;
;
89. ![]() ;
90.
;
90. ![]() .
.
90-100. а) Решить вероятностные задачи.
б) Найти закон распределения дискретной случайной величины, если известно, что: дискретная случайная величина Х может принимать только два значения х1 и х2 , причем х1 < х2; известна вероятность р1 возможного значения х1, математическое ожидание М (х) и дисперсия D (х)
б) p1 = 0,1; M(x) = 3,9; D(x) = 0,09;
б) p1 = 0,3; M(x) = 3,7; D(x) = 0,21;
б) p1 = 0,5; M(x) = 3,5; D(x) = 0,25;
б) p1 = 0,7; M(x) = 3,3; D(x) = 0,21;
б) p1 = 0,9; M(x) = 3,1; D(x) = 0,09;
б) p1 = 0,9; M(x) = 2,2; D(x) = 0,36;
б) p1 = 0,8; M(x) = 3,2; D(x) = 0,16;
б) p1 = 0,6; M(x) = 3,4; D(x) = 0,24;
б) p1 = 0,4; M(x) = 3,6; D(x) = 0,24;
б) p1 = 0,2; M(x) = 3,8; D(x) = 0,16.
Вопросы к экзамену
для студентов I курса специальности
21.02.01 «Разработка и эксплуатация нефтяных и газовых месторождений»
1. Значение математики в профессиональной деятельности и при освоении ППССЗ Основные математические методы решения прикладных задач в области профессиональной деятельности. Основные понятия и методы математического анализа
2. Понятие числа. Натуральные, целые и рациональные числа. Вещественные числа.
3. Основные понятия теории комплексных чисел. Понятие комплексного числа. Алгебраическая форма комплексного числа
4. Действия над комплексными числами, записанных в тригонометрической форме.
5. Модуль и аргумент комплексного числа
6. Тригонометрическая форма комплексного числа. Действия над комплексными числами.
7. Действия над комплексными числами, заданными в тригонометрической форме. Формула Муавра
8. Показательная форма комплексного числа. Действия над комплексными числами.
9. Формула Эйлера. Показательная форма комплексного числа
10. Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом
11. Основные понятия линейной алгебры. Матрицы.
12. Основные понятия линейной алгебры. Матрицы. Обратная матрица. Ранг матрицы..
13. Матрицы. Операции над матрицами. Невырожденная матрица.
14. Определитель n-го порядка. Свойства определителей. Алгебраические миноры. Вычисление определителей
15. Основные понятия линейной алгебры. Решение систем линейных уравнений.
16. Методы решения систем линейных уравнений. Метод Крамера.
17. Методы решения систем линейных уравнений. Метод Гаусса
18. Методы решения систем линейных уравнений. Матричный метод .
19. Определение функции. Свойства функций. Элементарные функции.
20. Графики функций. Способы задания функций. Элементарные функции.
21. Предел функций. Бесконечно малые и бесконечно большие функции.
22. Основные теоремы о пределах функций. Замечательные пределы.
23. Непрерывность функций. Точки разрыва.
24. Производная функции. Таблица основных формул дифференцирования
25. Производная функции. Ее геометрический и механический смысл Таблица основных формул дифференцирования.
26. Производная сложной функции. Производная: решение прикладных задач в области профессиональной деятельности
27. Производная функции. Таблица основных формул дифференцирования.
28. Дифференциал функции и его приложение к решению задач
29. Признаки возрастания и убывания функции
30. Производная. Экстремумы функции.
31. Выпуклость графика функции. Точки перегиба
32. Асимптоты кривой.
33. Схема исследования функции с помощью производной.
34. Первообразная. Неопределенный интеграл.
35. Таблица интегралов. Методы интегрирования.
36. Определенный интеграл и его геометрический смысл.
37. Приложение определенного интеграла.
38. Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения (виды, способы решения).
39. Дифференциальные уравнения первого порядка с разделяющимися переменными.
40. Линейное дифференциальное уравнение II порядка с постоянными коэффициентами. Теорема Коши.
41. Основные понятия теории вероятностей. Понятие события и вероятности события
42. События. Виды событий. Классическое определение вероятности.
43. Теорема сложение и умножения вероятностей
44. Случайные величины. Числовые характеристики случайных величин.
45. Случайная величина.
46. Дискретная случайная величина.
47. Закон распределения случайной величины.
48. Математическое ожидание и дисперсия случайной величины.
49. Основные понятия математической статистики. Выборка. Представление данных.
50. Основные понятия математической статистики. Основные показатели вариации.
51. Основы интегрального исчисления. Формулы прямоугольников.
52. Основы интегрального исчисления метод трапеций.
53. Основы интегрального исчисления. Метод Симпсона.
54. Основы интегрального исчисления. Абсолютная погрешность при численном интегрировании.
55. Основы дифференциального исчисления. Формулы приближенного дифференцирования, основанные на интерполяционных формулах Ньютона. Погрешность в определении производной
56. Основы дифференциального исчисления. Погрешность в определении производной
1. Богомолов Н.В. Математика: учеб. для ссузов. - М.: Дрофа, 2006. - 395 с.
2. Богомолов Н.В. Практические занятия по математике. - М.: Высш. шк., 2002. - 495 с.
3. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2003. - 208 с.
4. Валуцэ И.И. Математика для техникумов. – М.: Наука. Гл. ред. Физ.мат. лит., 1990 – 576 с.: ил.
5. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2. - М.: ООО "Издательство Оникс", 2006. - 416 с.
6. Кремер Н.Ш. Высшая математика для экономистов - М.: ЮНИТИ, 2002. - 471 с.
7. Пехлецкий И.Д. Математика. - М.: Издательский центр "Академия", 2002. - 304 с.
8. Соловейчик И.Л. Сборник задач по математике с решениями для техникумов. - М.: ООО "Издательский дом "ОНИКС 21 век", 2003. - 464 с.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.