
«Комплект учебно-методических материалов для проведения практических занятий по математике для студентов 2 курса специальностей отделения подготовки специалистов среднего звена»
Дисциплина математического и общего естественнонаучного цикла: «Математика»
Курс обучения: 2
Специальности: 08.02.01 Строительство и эксплуатация зданий и сооружений, 08.02.05 Строительство и эксплуатация автомобильных дорог и аэродромов, 46.02.01 Документационное обеспечение управления и архивоведение
|
|
ФИО автора: Калинина Ирина Валентиновна, |
|
|
преподаватель математики |
2018 г.
Рецензенты:
Крючкова Н.В., к.п.н., доцент кафедры Инфокоммуникационных технологий и безопасности ФГБОУ ВПО «ЧГУ».
Швец Р.П., преподаватель математики высшей квалификационной категории БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Разработала:
Калинина И.В., преподаватель математики высшей квалификационной категории БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
Данный комплект материалов предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практические работы по следующим темам:
1. Векторы в пространстве. Прямые на плоскости.
2. Вычисление пределов функции. Определение непрерывности функции, точек разрыва функции.
3. Вычисление производных сложных функций, производных высших порядков. Понятие дифференциала. Применение дифференциала для приближённых вычислений.
4. Применение производной для исследования функций
5. Неопределённый интеграл. Интегрирование подстановкой и по частям
6. Определённый интеграл. Интегрирование подстановкой и по частям
7. Дифференциальные уравнения.
8. Элементы комбинаторики. Элементы теории вероятностей.
9. Определители и матрицы
Каждые учебно-методические материалы по темам программы состоят из 2-х частей. Первая часть данных материалов содержит теоретическое обоснование и контрольные вопросы по рассматриваемой теме.
Во вторую часть материалов входит практическая работа, которая включает в себя: цели работы, порядок выполнения работы, указания к оформлению и 20 вариантов заданий.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Векторы в пространстве.
Прямые на плоскости
Учебно-методические материалы по дисциплине «Математика» для студентов 2-го курса специальностей отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть 1. Теоретическое обоснование
1. Прямоугольная (декартова) система координат в пространстве
1.1 Введение декартовых координат в пространстве
1.2 Расстояние между двумя точками
1.3 Деление отрезка в данном отношении
2. Векторы в пространстве
2.1 Понятие вектора. Вектора на координатной плоскости
2.2 Действия над векторами
2.3 Скалярное произведение двух векторов. Угол между двумя векторами
3. Прямая на плоскости
3.1 Общее уравнение прямой
3.2 Уравнение прямой с угловым коэффициентом
3.3 Уравнение прямой, проходящей через 2 точки
3.4 Угол между двумя прямыми
3.5 Условия параллельности и перпендикулярности двух прямых
3.6 Расстояние от точки до прямой
4. Контрольные вопросы
Часть 2. Практическая работа
2.1 Цели работы
2.2 Порядок выполнения работы
2.3 Указания к оформлению
2.4 Варианты заданий
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой для студентов 2 курса специальностей отделения подготовки специалистов среднего звена БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина.
Данные материалы содержат теоретическое обоснование и практические работы по темам программы
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данных материалов, т. е. студенты будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
В результате изучения данной темы студент должен:
знать:
-определение декартовой системы координат;
-определение вектора, операции над векторами, свойства, координаты вектора, скалярное произведение;
-уравнение прямой на плоскости;
-общее уравнение прямой;
-условие параллельности и перпендикулярности прямых;
уметь:
-находить координаты точек и строить точки в декартовой системе координат;
-находить координаты векторов, длину вектора, угол между векторами;
-находить модули, скалярное произведение векторов в пространстве;
-составлять общее уравнение прямой, уравнение прямой с угловым коэффициентом.
уметь:
-находить координаты точек и строить точки в декартовой системе координат;
-находить координаты векторов, длину вектора, угол между векторами;
-находить модули, скалярное произведение векторов в пространстве;
-составлять общее уравнение прямой, уравнение прямой с угловым коэффициентом.
Часть 1. Теоретическое обоснование
1.
Прямоугольная (декартова) система
координат в пространстве
 1.1 Введение
декартовых координат в пространстве
1.1 Введение
декартовых координат в пространстве
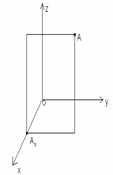
Возьмём три взаимно перпендикулярные прямые х, y,z, пересекающиеся в одной точке О. Проведём через каждую пару этих прямых плоскость. Плоскость, проходящая через прямые х и y, называется плоскостью xy. Две другие плоскости называются соответственно xz, yz. Прямые x, y, z называются координатными осями, точка их пересечения O – началом координат, а плоскости xy, xz, yz – координатными плоскостями. Точка О разбивает каждую из осей координат на две полупрямые – полуоси. Условимся одну из них называть положительной, а другую – отрицательной. Возьмём теперь произвольную точку А и проведём через неё плоскость, параллельную плоскости yz. Координатой х точки А будем называть число, равное по абсолютной величине длине отрезка ОАх: положительное, если точка Ах лежит на положительной полуоси х, и отрицательное, если она лежит на отрицательной полуоси. Аналогично определяются координаты y, z точки А. Точку А обозначают А(x,y,z). Точка О имеет координаты (0,0,0).
1.2 Расстояние между двумя точками
Расстояние d между точками М1(х1, y1, z1) и М2(х2, y2, z2) определяется по формуле:
|
|
В частности, расстояние d от точки М(x,y,z) до начала координат определяется формулой:
|
|
Пример 1:
На оси ОХ найти точку, равноудалённую от точек А(2;-4;5) и В(-3;2;7).
Решение:
Пусть т. М – искомая точка. Так как т. М
лежит на оси Ох, то она имеет координаты (х,0,0). По условию задачи ![]() .
.
![]() ;
;![]() .
.
Приравняем эти равенства и возведём в квадрат:
(х-2)2+41=(х+3)2+53. Решая это уравнение, получим:
10х=-17, х=-1,7. Значит координаты т.М будут (-1,7;0;0)
Ответ: М (-1,7;0;0)
1.3 Деление отрезка в данном отношении
Координаты точки С(х,у,z), делящий отрезок между точками М1(х1; y1; z1) и М2(х2; y2; z2) в заданном отношении λ определяется по формулам:
|
|
В частности, при λ=1 получаются формулы середины отрезка:
|
|
Пример 2:
Точка С (2;3;6) является серединой отрезка АВ. Определить координаты точки А, если В(7;5;8).
Решение:
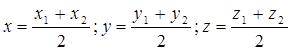
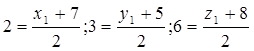
х1=4-7=-3; у1=6-5=1; z1=12-8=4
Ответ: А(-3;1;4)
2. Векторы в пространстве
2.1 Понятие вектора. Вектора на координатной плоскости
В пространстве, как и на
плоскости, вектором называется направленный отрезок и обозначается ![]() . Буквально так же, как и на
плоскости определяются основные понятия для векторов в пространстве: абсолютная
величина вектора, направление вектора, равенство векторов.
. Буквально так же, как и на
плоскости определяются основные понятия для векторов в пространстве: абсолютная
величина вектора, направление вектора, равенство векторов.
Вектор, длина которого равна единице, называется единичным вектором.
Векторы ![]() и
и ![]() называются
коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Обозначение:
называются
коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Обозначение: ![]() II
II
![]() .
.
Свободный вектор ![]() (т.е. такой вектор, который без
изменения длины и направления может быть перенесён в любую точку
пространства), заданный в координатном пространстве 0xyz,
может быть представлен в виде
(т.е. такой вектор, который без
изменения длины и направления может быть перенесён в любую точку
пространства), заданный в координатном пространстве 0xyz,
может быть представлен в виде
|
|
Такое представление
вектора ![]() называется его разложением по осям
координат, или по ортам.
называется его разложением по осям
координат, или по ортам.
Здесь ![]() – проекции вектора
– проекции вектора ![]() на соответствующие оси координат (их
называют координатами вектора
на соответствующие оси координат (их
называют координатами вектора ![]() ),
), ![]() - орты этих осей ( единичные
векторы, направление каждого из которых совпадает с положительным направлением
соответствующей оси).
- орты этих осей ( единичные
векторы, направление каждого из которых совпадает с положительным направлением
соответствующей оси).
Векторы ![]() , в виде суммы которых представлен
вектор
, в виде суммы которых представлен
вектор ![]() , называются составляющими
(компонентами) вектора
, называются составляющими
(компонентами) вектора ![]() по осям
координат.
по осям
координат.
Длина (модуль) вектора ![]() обозначается
обозначается ![]() и определяется по формуле:
и определяется по формуле:
|
|
Вектор ![]() ,
начало которого находится в начале координат, а конец – в точке М(x;y;z) называют
радиусом – вектором точки М и обозначают
,
начало которого находится в начале координат, а конец – в точке М(x;y;z) называют
радиусом – вектором точки М и обозначают ![]() (М)
или просто
(М)
или просто ![]() . Так как его координаты совпадают
с координатами точки М, то его разложение по ортам имеет вид:
. Так как его координаты совпадают
с координатами точки М, то его разложение по ортам имеет вид:
|
|
Вектор ![]() ,
имеющий начало в точке А(х1; y1; z1) и конец в точке
В(х2; y2; z2) может быть
записан в виде
,
имеющий начало в точке А(х1; y1; z1) и конец в точке
В(х2; y2; z2) может быть
записан в виде ![]() =
= ![]() -
-![]() , где
, где ![]() -
радиус- вектор точки А,
-
радиус- вектор точки А, ![]() - радиус –
вектор точки В. Поэтому разложение вектора
- радиус –
вектор точки В. Поэтому разложение вектора![]() по
ортам имеет вид:
по
ортам имеет вид:
|
|
Его длина совпадает с расстоянием между точками А и В:
|
|
Пример 3:
Разложить вектор ![]() по
ортам и найти длину данного вектора, если А(-2;-1;0), В(4;-3;5).
по
ортам и найти длину данного вектора, если А(-2;-1;0), В(4;-3;5).
Решение:
![]() =(4-(-2))
=(4-(-2))![]() +(-3-(-1))
+(-3-(-1))![]() +(5-0)
+(5-0)![]() =6
=6![]() -2
-2![]() +5
+5![]()
![]() =
=![]()
Ответ: ![]() .
.
2.2 Действия над векторами
1.
Если векторы ![]() и
и ![]() заданы их разложениями
по ортам, то их сумма и разность определяются по формулам:
заданы их разложениями
по ортам, то их сумма и разность определяются по формулам:
|
|
Сумма векторов ![]() и
и ![]() начала
которых совмещены, изображается вектором с тем же началом, совпадающим с
диагональю параллелограмма, сторонами которого являются векторы
начала
которых совмещены, изображается вектором с тем же началом, совпадающим с
диагональю параллелограмма, сторонами которого являются векторы ![]() и
и ![]() .
Разность
.
Разность ![]() -
-![]() этих
векторов изображается вектором, совпадающим со второй диагональю того же
параллелограмма,
этих
векторов изображается вектором, совпадающим со второй диагональю того же
параллелограмма,
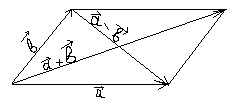
причём
начало этого вектора находится в конце вектора ![]() ,
а конец – в конце вектора
,
а конец – в конце вектора ![]() .
.
2.
Произведение вектора ![]() на постоянный множитель m определяется
формулой:
на постоянный множитель m определяется
формулой:
|
|
Пример 4:
Найти вектор ![]() ,
если
,
если ![]() =
=![]() ,
,
![]() ,
, ![]()
Решение:
![]() ,
, ![]() ,
,
![]()
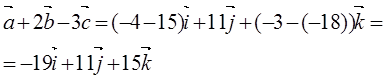
Ответ: ![]()
Условие коллинеарности двух векторов,
заданных своими координатами ![]() (х1;,у1;z1) и
(х1;,у1;z1) и ![]() (х2;,у2;z2) определяется
следующим соотношением:
(х2;,у2;z2) определяется
следующим соотношением:
|
|
Пример 5:
При
каком значении n векторы ![]() и
и ![]() будут коллинеарны?
будут коллинеарны?
Решение:
Составим
пропорцию: 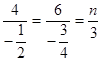 , возьмём 1 и 3 отношения:
, возьмём 1 и 3 отношения: 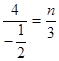 из которого найдём n: n=-24
из которого найдём n: n=-24
Ответ: при n=-24 вектора будут коллинеарны.
2.3
Скалярное произведение двух векторов.
Угол между двумя векторами
Скалярным произведением 2-х ненулевых векторов называется число равное произведению длин этих векторов на косинус угла между ними
Обозначается ![]() ,
т.е. если φ – угол между векторами, то
,
т.е. если φ – угол между векторами, то
|
|
Свойства скалярного произведения:
10.
![]()
20.
![]()
30.
![]()
40.
![]()
Пусть
векторы ![]() и
и ![]() заданы
своими координатами
заданы
своими координатами ![]() ,
, ![]() . Тогда скалярное произведение этих
векторов находится по формуле:
. Тогда скалярное произведение этих
векторов находится по формуле:
|
|
Необходимое
и достаточное условие перпендикулярности 2-х ненулевых векторов ![]() и
и ![]() :
:
|
|
Зная
скалярное произведение 2-х векторов ![]() ,
, ![]() можно найти угол между ними:
можно найти угол между ними:
|
|
Пример 6:
Будет
ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() ?
?
Решение:
Найдём скалярное произведение этих векторов:
![]()
Так как скалярное произведение не равно нулю, то вектора не перпендикулярны.
Ответ: нет.
Пример 7:
Заданы 2 вектора своими координатами
![]() (-4;3;0),
(-4;3;0), ![]() (3;-4;1).
Найти косинус угла между ними.
(3;-4;1).
Найти косинус угла между ними.
Решение:
![]()
Ответ: ![]()
3. Прямая на плоскости
3.1 Общее уравнение прямой
Уравнение первой степени относительно переменных х и у, т.е. уравнение Ах+Ву+С=0
при условии, что коэффициенты А и В одновременно не равны нулю, называется общим уравнением прямой.
Частные случаи общего уравнения прямой Ах+Ву+С=0:
|
Значение |
Вид уравнения |
Положение прямой |
|
С=0, А≠0, В≠0 |
Ах+Ву=0 (у=кх) |
Проходит через начало координат |
|
А=0, В≠0, С≠0 |
Ву+С=0 (у=в) |
Параллельна оси Ох |
|
В=0, А≠0, С≠0 |
Ах+С=0 (х=а) |
Параллельна оси Оу |
|
А=С=0, В≠0 |
Ву=0 (у=0) |
Совпадает с осью Ох (уравнение оси Ох) |
|
В=С=0, А≠0 |
Ах=0 (х=0) |
Совпадает с осью Оу (уравнение оси Оу) |
3.2 Уравнение прямой с угловым коэффициентом
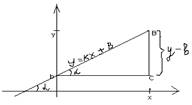 Пусть прямая, не
параллельная оси 0у, пересекает ось 0у в точкеА(0;в), а ось 0х пересекает под
углом α.
Пусть прямая, не
параллельная оси 0у, пересекает ось 0у в точкеА(0;в), а ось 0х пересекает под
углом α.
Выберем на прямой точку В(х;у).Построим прямоугольный треугольник АВС такой, что АС II 0х, ВС II 0у, ВС=у-в, <ВАС=α..
Имеем tgα=![]() , или
, или ![]() .
.
Обозначим tgα=к, получим уравнение прямой с угловым коэффициентом:
|
у=кх+b |
Пример 8:
Составить уравнение прямой, отсекающей на оси 0у отрезок b=3 и образующий с осью 0х угол α=300.
Решение:
Найдём угловой коэффициент к=tgα=tg300=![]() . Подставив k и b в уравнение с
угловым коэффициентом, получим: у=
. Подставив k и b в уравнение с
угловым коэффициентом, получим: у=![]() х+3, или
х+3, или ![]()
Ответ: ![]() .
.
![]() Можно вывести
уравнение с угловым коэффициентом из общего уравнения прямой. В общем уравнении
прямой Ах+Ву+С=0, где В≠0, выразим у. Получим:
Можно вывести
уравнение с угловым коэффициентом из общего уравнения прямой. В общем уравнении
прямой Ах+Ву+С=0, где В≠0, выразим у. Получим: ![]() . Обозначим k=
. Обозначим k=![]() , b=
, b=![]() , тогда
, тогда
уравнение прямой с угловым коэффициентом.
Часто возникает необходимость составить уравнение прямой, зная одну её точку М1(x1, у1) и угловой коэффициент k. Такое уравнение выглядит следующим образом:
|
у-у1=к(х-х1) |
Пример 9:
Составить уравнение прямой, проходящей через точку А(2;-4) и пересекающей ось 0х под углом 450.
Решение:
k=tg450=1, подставим координаты точки А в уравнение с угловым коэффициентом: -4=1*2+b, отсюда b=-4-2=-6. Получим уравнение прямой у=х-6.
Ответ: у=х-6.
3.3 Уравнение прямой, проходящей через 2 точки
Пусть даны 2 точки М1(x1, у1) и М2(x2, у2). Можно составить уравнение прямой, проходящей через эти 2 точки:
|
|
Пример 10:
Составить уравнение прямой, проходящей через точку М1(2;3) и М2(-3;4).
Решение:
Подставим координаты точек в формулу:
![]() ; -5у+15=х-2; 5у+х-17=0- искомая
прямая.
; -5у+15=х-2; 5у+х-17=0- искомая
прямая.
Ответ: 5у+х-17=0
3.4 Угол между двумя прямыми
Угол φ между двумя прямыми, заданными общими уравнениями А1х+В1у+С1=0 и А2х+В2у+С2 =0, вычисляется по формуле:
|
|
Если прямые заданы уравнениями с угловыми коэффициентом у=k1х+b1 и у=k2х+b2, то угол φ между ними вычисляется по формуле:
|
|
Пример 11:
Две прямые, проходящие через начало
координат, образуют между собой, угол равный arctg![]() . Отношение угловых коэффициентов этих
прямых составляет 2:7. Составьте уравнения этих прямых.
. Отношение угловых коэффициентов этих
прямых составляет 2:7. Составьте уравнения этих прямых.
Решение:
у=kх – уравнение прямых, проходящих через начало координат, т.е. чтобы решить задачу, нужно найти угловой коэффициент.
Пусть m – коэффициент пропорциональности, тогда k1=2m, k2=7m. Используем формулу угла между прямыми, заданными уравнениями с угловым коэффициентом:
![]() ;
; ![]() ;
14m2-15m+1=0 .
;
14m2-15m+1=0 .
Решая квадратное уравнение, получаем 2
решения: m1 =1 и m2=![]() .
.
Рассмотрим оба случая.
1 случай. m1 =1: k1=2 и k2=7; уравнения прямых: у=2х и у=7х.
2 случай. m2=![]() : k1=
: k1=![]() и k2=
и k2=![]() ; уравнения прямых: у=
; уравнения прямых: у=![]() х и у=
х и у=![]() .
.
Ответ: у=2х и у=5х; у=![]() х и у=
х и у=![]() .
.
3.5
Условия параллельности и перпендикулярности
двух прямых
Условие параллельности двух прямых, заданных общими уравнениями
А1х+В1у+С1=0 и А2х+В2у+С2 =0, записывается в виде:
|
|
Условие параллельности прямых, заданных уравнениями с угловыми коэффициентами у=к1х+b1 и у=к2х+b2, имеет вид:
|
k2=k1 |
Пример 12:
Составить уравнение прямой, проходящей через точку А(-2;4) параллельно прямой L: 2х-3у+6=0.
Решение:
Преобразуем уравнение прямой L в уравнение с
угловым коэффициентом: у=![]() х+2, угловой
коэффициент k1=
х+2, угловой
коэффициент k1=![]() . Так как прямые параллельны, то k2=k1=
. Так как прямые параллельны, то k2=k1=![]() , следовательно, уравнение прямой L1: у-4=
, следовательно, уравнение прямой L1: у-4=![]() (х+2), или 2х-3у+16=0.
(х+2), или 2х-3у+16=0.
Ответ: 2х-3у+16=0
Условие перпендикулярности двух прямых, заданных общими уравнениями
А1х+В1у+С1=0 и А2х+В2у+С2 =0, записывается в виде:
|
А1А2+ В1В2=0 |
Условие перпендикулярности прямых, заданных уравнениями с угловыми коэффициентами у=k1х+b1 и у=k2х+b2, имеет вид:
|
|
Пример 13:
В ∆АВС точка А(6;2), уравнение прямой ВС: х-4у-7=0. Составить уравнение высоты AN, проведённой из точки А на ВС.
Решение:
Преобразуем ВС в уравнение с угловым
коэффициентом: у=![]() х-
х-![]() ;k1=
;k1=![]() , так как AN
, так как AN![]() ВС, то
ВС, то 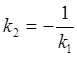 =-4;
следовательно, уравнение прямой AN: у-2=-4(х-6) или у+4х-26=0
=-4;
следовательно, уравнение прямой AN: у-2=-4(х-6) или у+4х-26=0
Ответ: у+4х-26=0
3.6 Расстояние от точки до прямой
Расстояние d от данной точки М(х0;у0) до прямой, заданной общим уравнением Ах+Ву+С=0, определяется формулой:
|
|
Пример 14:
Дана прямая L: 3х-4у+10=0 и точка М(4;3). Найти расстояние от точки М до прямой L.
Решение:
![]() .
.
Ответ: 2
4. Контрольные вопросы
1). Объясните, как получается прямоугольная система координат в пространстве?
2). Объясните, как определяются координаты точки в пространстве?
3). Запишите формулу для определения расстояния между двумя точками, заданными своими координатами?
4). Дайте определение вектора.
5). Какие 2 вектора называются коллинеарными?
6). Запишите разложение вектора по ортам.
7). Что называется ортом?
8). Как найти длину вектора?
9). Что называют радиус-вектором?
10). Дайте определение действий над векторами: сложение, разность, умножение на число.
11). Что называют скалярным произведением 2-х ненулевых векторов?
12). Перечислите свойства скалярного произведения.
13). Сформулируйте необходимое и достаточное условие перпендикулярности 2-х векторов.
14).Сформулируйте необходимое и достаточное условие коллинеарности 2-х векторов.
15). Выразите угол между двумя векторами.
16). Запишите общее уравнение прямой.
17). Исследуйте общее уравнение прямой при А=0, В=0, С=0.
18). Выведите уравнение с угловым коэффициентом из общего уравнения прямой.
19). Что называют угловым коэффициентом прямой?
20). Выведите уравнение прямой с угловым коэффициентом.
21). Запишите уравнение прямой, которая проходит через заданную точку и имеющая угловой коэффициент k.
22). Запишите уравнение прямой, проходящей через 2 точки.
23). Запишите формулу угла между двумя прямыми.
24). Запишите условия параллельности и перпендикулярности двух прямых.
25). Запишите формулу расстояния от точки до прямой.
Часть 2. Практическая работа
2.1 Цели работы
- научиться производить действия над векторами;
- научиться находить скалярное произведение двух векторов, угол между векторами;
- научиться составлять общее уравнение прямой; уравнение прямой с угловым коэффициентом; уравнение прямой, проходящей через 2 точки;
- научиться применять условие параллельности и перпендикулярности 2-х прямых для решения задач.
2.2 Порядок выполнения работы
2.1 Проработать теоретический материал по теме.
2.2 Ответить на контрольные вопросы.
2.3 Получить вариант задания.
2.4 Выполнить задание.
2.5 Оформить отчёт о работе.
2.3 Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
- точное наименование работы;
- цель работы;
- ход работы (условие задачи);
- результаты работы (подробное решение задач);
- вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
2.4 Варианты заданий
Вариант 1
1. Дано: ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
2. Будет ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() .
.
3. При каких
значениях m и n вектор ![]() будет коллинеарен вектору
будет коллинеарен вектору ![]() ?
?
4. Найти ![]() , если
, если ![]() ;
;
![]() .
.
7.
Определить
косинус угла между прямыми L![]() : 3х-2у+6=0;
: 3х-2у+6=0;
L2: х+5у-1=0
Вариант 2
1.
Дано: ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
2. Будет ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() .
.
3. При каких
значениях α и β вектор ![]() будет коллинеарен вектору
будет коллинеарен вектору ![]() ?
?
4. Найти ![]() , если
, если ![]() ;
;
![]() .
.
5. Найти угловой коэффициент прямой, параллельной прямой 2х+5у-1=0.
6. Составить уравнение высоты СК в треугольнике АВС: А(1;2), В(5;-2), С(3;1).
7. Составить уравнение стороны АВ в треугольнике АВС таком же, что и в предыдущем задании.
Вариант 3
1. Дано
![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
7. Определить
угол между прямыми L![]() : 2х-у+9=0; L2: х+2у-1=0
: 2х-у+9=0; L2: х+2у-1=0
Вариант 4
1. Даны вектора ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
2. Будет ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() ?
?
3. Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
4. При каком значении
m вектор ![]() будет коллинеарен вектору
будет коллинеарен вектору ![]() ?
?
5. Найти угловой коэффициент прямой, перпендикулярной прямой 2х-3у+1=0.
6. Найти координаты
точки пересечения прямых L![]() : 3х-2у+3=0; L2: х+2у-7=0.
: 3х-2у+3=0; L2: х+2у-7=0.
7. Составить уравнение прямых, проходящих через точку А(-3;2) перпендикулярно осям координат.
Вариант 5
1. Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
2.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
3.
При каком значении α вектор ![]() будет
перпендикулярен вектору
будет
перпендикулярен вектору ![]() ?
?
4.
Даны вектора ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
5. Составить уравнение прямой, проходящей через точки А(2;1), В(-3;-2).
6. При каком значении
k прямые L1 и L2 перпендикулярны,
если L![]() : у=2х-5; L2: у=kх+1.
: у=2х-5; L2: у=kх+1.
7. Составить уравнение прямой, проходящей через точку А и середину отрезка CD, если А(1;-1), С(2;-3), D(4;-2).
Вариант 6
1.
Дано: ![]() и
и ![]() .
Найти косинус угла между векторами
.
Найти косинус угла между векторами ![]() и(1/3)
и(1/3)![]() .
.
2.
Найти модуль вектора ![]() .
.
3.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
4.
Будет ли вектор ![]() коллинеарен вектору
коллинеарен вектору ![]() ?
?
5. Найти угловой коэффициент прямой, параллельной данной прямой 2х-5у+1=0.
6. Составить уравнение стороны АС в треугольнике АВС: А(2;-2), В(1;3), С(4;-2).
7. Составить уравнение медианы АК в треугольнике АВС таком же, что и в предыдущем задании.
Вариант 7
1.Дано:
![]() и
и ![]() .
Найти косинус угла между векторами
.
Найти косинус угла между векторами ![]() и(1/2)
и(1/2)![]() .
.
2.
Найти модуль вектора ![]() , если
, если ![]() .
.
3.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
4.
Будет ли вектор ![]() коллинеарен вектору
коллинеарен вектору ![]() ?
?
5. Составить уравнение сторон АВ и АС в треугольнике АВС: А(1;2), В(0;-3), С(2;6).
6. Найти угловой коэффициент прямой, параллельной данной прямой 3х-2у-5=0.
7. Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси 0х угол α=300.
Вариант 8
1.
Дано: ![]() и
и ![]() .
Найти косинус угла между векторами
.
Найти косинус угла между векторами ![]() и
и ![]() .
.
2.
Найти модуль вектора ![]() , если
, если ![]() .
.
3.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
4.
Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
5. Составить уравнение прямой, проходящей через точки М(0;1), N(2;-3).
6. Составить уравнение прямых, проходящих через точку P(-2;3) перпендикулярно осям координат.
7.
При каком значении k прямые L1 и L2 перпендикулярны,
если L![]() : у=-5х+1; L2: у=kх-6.
: у=-5х+1; L2: у=kх-6.
Вариант 9
1.
Дано: ![]() и
и ![]() .
Найти косинус угла между векторами
.
Найти косинус угла между векторами ![]() и (1/2)
и (1/2)![]() .
.
2.
Найти модуль вектора ![]() , если
, если ![]() .
.
3.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
4.
Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
5. Составить уравнение прямой, проходящей через середину отрезка АВ перпендикулярно ему, если А(1;3), В(2;5).
6. Составить уравнение стороны АВ в треугольнике АВС: А(-2;-1), В(0;4), С(3;-2).
7. Составить уравнение медианы АК в треугольнике АВС таком же, что и в предыдущем задании.
Вариант 10
1.
Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
2.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
3.
При каком значении β вектор ![]() будет
перпендикулярен вектору
будет
перпендикулярен вектору ![]() ?
?
4.
Даны вектора ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
5. Составить уравнение прямой, проходящей через точки А(-2;1), В(3;-4).
6. Определить угол
между прямыми L![]() : у=3х+4; L2: 2х+у-5=0
: у=3х+4; L2: 2х+у-5=0
7. В треугольнике АВС: А(2;-1), В(-3;-2), точка пересечения высот М(-1;1). Составить уравнение стороны АС.
Вариант 11
1.Дано
![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
2.Дано
![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
3.
При каком значении m и n вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
4.
Даны вектора ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
5. Найти угловой коэффициент прямой, перпендикулярной прямой 3х-2у+7=0.
6. Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси 0х угол α=450.
7.
Определить угол между прямыми L![]() : у=3х+4; L2: у=-2х+1.
: у=3х+4; L2: у=-2х+1.
Вариант 12
1.
Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
2.
Дано ![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
3.
При каком значении α вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() ?
?
4.Даны
вектора ![]() и
и ![]() .Найти
модуль вектора
.Найти
модуль вектора ![]() .
.
5. Найти угловой коэффициент прямой, параллельной прямой 3х-у-5=0.
6. Составить уравнение высоты ВD в треугольнике АВС: А(2;-1), В(-3;2), С(5;4).
7. Составить уравнение стороны АВ в треугольнике АВС таком же, что и в предыдущем задании.
Вариант 13
1.Дано
![]() и
и ![]() .
Найти скалярное произведение
.
Найти скалярное произведение ![]() .
.
2.
Даны вектора ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
3.
При каком значении α и β вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
4.
Дано: ![]() и
и ![]() .
Найти косинус угла между ними.
.
Найти косинус угла между ними.
5. Найти угловой коэффициент прямой, перпендикулярной прямой 5х-7у+1=0.
6.Доказать, что прямые L1║L2, L1: 10х-4у-1=0; L2: у=(5/2)х-1/4.
7. Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси 0х угол 300.
Вариант 14
1.
При каком значении m вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
2.
Будет ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() ?
?
3.
При каком значении α равны между собой модули векторов ![]() ;
; ![]() .
.
4.
Дано: ![]() ;
; ![]() .
Найти
.
Найти ![]() .
.
5. Найти угловой коэффициент прямой, перпендикулярной прямой 5х-2у+7=0.
6. Составить уравнение прямой, проходящей через середину отрезка MN перпендикулярно ему, если M(2;-1), N(5;-2).
7. Составить уравнение медианы АD в треугольнике АВС: А(2;1), В(-3;-1), С(4;-3).
Вариант 15
1.
При каком значении m вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
2.
Будет ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() ?
?
3.
При каком значении α равны между собой модули векторов ![]() ;
; ![]() .
.
4.
Найти ![]() , если
, если ![]() ;
;
![]() .
.
5. Составить уравнение прямой, проходящей через точки А(0;2), В(1;2).
6.
При каком значении k прямые L1 и L2 перпендикулярны, если L![]() : 3х-у+2=0; L2: у=kх+1.
: 3х-у+2=0; L2: у=kх+1.
7. Найти угловой коэффициент прямой 3х-2у-7=0.
Вариант 16
1.
При каком значении m вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
2. Будет
ли вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() ?
?
3.
При каком значении k равны между собой модули векторов ![]() ;
; ![]() ?
?
4.
Дано: ![]() ;
; ![]() .
Найти
.
Найти ![]() .
.
5. Составить уравнение прямой, проходящей через точки А(0;2), В(-3;0).
6.Найти угловой коэффициент прямой, перпендикулярной прямой х=3.
7. Найти угловой коэффициент прямой, параллельной прямой у=2.
Вариант 17
1.Дано:
![]() и
и ![]() .
Найти косинус угла между ними.
.
Найти косинус угла между ними.
2.
При каком значении α и β вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
3.
Дан вектор ![]() . Найти модуль вектора
. Найти модуль вектора ![]() .
.
4.
Дано ![]() . Найти скалярное произведение
. Найти скалярное произведение ![]() .
.
5. Найти угловой коэффициент прямой, параллельной прямой -2х-3у+7=0.
6. Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси 0х угол 600.
7. Составить уравнение прямой, проходящей через точку А отрезка АВ перпендикулярно ему, если А(2;-1), В(-3;-2).
Вариант 18
1.Дано:
![]() и
и ![]() .
Найти косинус угла между ними.
.
Найти косинус угла между ними.
2.
При каком значении α и β вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
3.
Дан вектор ![]() . Найти модуль вектора
. Найти модуль вектора ![]() .
.
4.
Дано: ![]() ;
; ![]() .
Найти
.
Найти ![]() .
.
5.
Определить взаимное положение прямых L1 и L2, если
L![]() : 2х+3у+6=0; L2: 4х+6у-5=0.
: 2х+3у+6=0; L2: 4х+6у-5=0.
6.
Определить тангенс угла между прямыми L![]() : 3х-у+1=0; L2: х+у-5=0.
: 3х-у+1=0; L2: х+у-5=0.
7.
Найти координаты точки пересечения прямых L![]() : х+у-4=0;
: х+у-4=0;
L2: 2х+у-7=0.
Вариант 19
1.Дано:
![]() и
и ![]() .
Найти косинус угла между векторами 2
.
Найти косинус угла между векторами 2![]() и
и ![]() .
.
2.
При каком значении α и β вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
3.
Даны вектора ![]() и
и ![]() .
Найти модуль вектора
.
Найти модуль вектора ![]() .
.
4.
При каком значении α вектор ![]() перпендикулярен
вектору
перпендикулярен
вектору ![]() ?
?
5. Составить уравнение прямой, проходящей через точки А(1;3), В(2;-3).
6. Составить уравнение прямой, проходящей через точку М(3;-1) и имеющую такой же угловой коэффициент, как и прямая 2х-у-6=0.
7.
Доказать, что прямая L1 перпендикулярна прямой L2, если
L![]() : 2х-3у+1=0; L2: 3х+2у-7=0.
: 2х-3у+1=0; L2: 3х+2у-7=0.
Вариант 20
1.
Даны вектора ![]() и
и ![]() .Найти
модуль вектора
.Найти
модуль вектора ![]() .
.
2.
Даны вектора ![]() и
и ![]() .
Будут ли они перпендикулярны?
.
Будут ли они перпендикулярны?
3.
При каком значении m и n вектор ![]() будет
коллинеарен вектору
будет
коллинеарен вектору ![]() ?
?
4.
Найти ![]() , если
, если ![]() ;
;
![]() .
.
5. Составить уравнение прямой, проходящей через начало координат, если она образует с положительным направлением оси 0х угол α=-600.
6.
Определить взаимное положение прямых L1 и L2, если
L![]() : у=(2/5)х-2; L2: 2х-5у+9=0.
: у=(2/5)х-2; L2: 2х-5у+9=0.
7.
Найти координаты точки пересечения прямых L![]() : 3х+у-3=0;
: 3х+у-3=0;
L2: х-у-5=0.
Литература
1 Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.-
М.: Высшая школа, 1997.-250 с.
3. Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4. Данко П. Е. Высшая математика в
упражнениях и задачах,
ч.1-М.: ОНИКС 21 век,2003.-304 с.
5. Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
6. Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
7. Шнейдер В.Е. Краткий курс высшей математики. -М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Вычисление пределов функции
Определение непрерывности функции, точек разрыва функции
Учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть 1. Теоретическое обоснование
1. Числовая последовательность и её свойства
1.1. Понятие числовой последовательности
1.2. Способы задания последовательности
1.3. Свойства числовой последовательности
1.4. Предел числовой последовательности
1.5. Вычисление пределов последовательностей
2. Предел функции
2.1 Предел функции в точке
2.2 Операции над пределами функций
2.3. Предел функции на бесконечности
2.4. Замечательные пределы
2.5. Односторонние пределы
3. Непрерывность функции
3.1. Непрерывность функции в точке
3.2. Непрерывность функции на промежутке
3.3. Точки разрыва функции
4. Контрольные вопросы
Часть 2. Практическая работа
2.1. Цели работы
2.2. Порядок выполнения работы
2.3. Указания к оформлению
2.4. Варианты заданий
2.5. Приложения
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Вычисление пределов функции. Определение непрерывности функции, точек разрыва функции».
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данных материалов, т. е. студенты будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
Критерием успешного усвоения материала является выполнение не менее 2 заданий практической части.
В результате изучения данной темы студент должен
знать:
- определение числовой последовательности и её свойства;
- определение предела последовательности;
- определение предела функции на бесконечности и в точке;
- теоремы о пределах (суммы, разности, произведения, частного, логарифма);
- два «замечательных» предела;
уметь:
- составлять последовательность;
- определять свойства последовательности;
- вычислять пределы последовательности;
- вычислять пределы функции в точке и на бесконечности;
- определять точки разрыва функции.
Часть 1. Теоретическое обоснование
1. Числовая последовательность и её свойства
1.1. Понятие числовой последовательности
Рассмотрим функциональную зависимость у=х2.
|
х |
1 |
2 |
3 |
4 |
5 |
… |
|
у |
1 |
4 |
9 |
16 |
25 |
… |
х - натуральные числа
у - числовая последовательность.
Если каждому натуральному числу n поставлено в соответствие вещественное число хn , то множество вещественных чисел x1, х2, х3,…, хn,… называют числовой последовательностью.
Будем обозначать числовую последовательность {хn}. Числа x1, х2, х3,…, хn ,… -элементы (члены) последовательности,
хn – общий член
последовательности, n- номер, например символ ![]() обозначает
последовательность 1,
обозначает
последовательность 1,![]()
Формула, задающая хn, , называется формулой общего члена последовательности {хn}. С помощью такой формулы можно вычислить любой элемент последовательности.
Пример 1:
Дана формула общего члена последовательности:
![]() . Написать пять первых элементов
последовательности.
. Написать пять первых элементов
последовательности.
Решение
Пусть n=1,2,3,4,5 в общем элементе хn. Получим
![]() .
.
Также, зная несколько элементов последовательности можно написать формулу общего члена последовательности.
Пример 2.
Даны четыре первых членов
последовательности, написать формулу общего члена: ![]()
Решение.
Знаменатели данных элементов образуют последовательность всех нечётных натуральных чисел в квадрате, поэтому можно составить следующую формулу:
![]()
1.2. Способы задания последовательности
1). Последовательность может быть задана словесно, т.е. описанием её членов.
Пример 3.
Дана последовательность {хn}, где хn - половина квадрата натурального числа. Написать первые четыре элемента данной последовательности и формулу общего члена.
Решение.
![]() ,
,
![]() - формула общего члена.
- формула общего члена.
2). Последовательность может быть задана с помощью формулы, указывающей как по номеру n члена последовательности вычислить его значение хn.
Пример 4.
Пусть последовательность {хn} задана формулой
![]() ,
, ![]() .
.
Найти элементы данной последовательности.
Решение.
![]() и т.д. Данная
последовательность имеет вид: 0;1;0;1;…
и т.д. Данная
последовательность имеет вид: 0;1;0;1;…
3). Рекуррентный (индуктивный) способ.
Этот способ состоит в том, что указывается правило (обычно это формула), позволяющее вычислить общий член последовательности через предыдущий и задаётся несколько начальных членов последовательности.
Например, арифметическая
последовательность – числовая последовательность {хn}, заданная
рекуррентными соотношениями ![]() (a,d- заданные числа,
(a,d- заданные числа,
d-разность арифметической прогрессии).
Пример 5.
Выпишите первые пять членов последовательности, заданной рекуррентно: х1=2; хn= 5-хn-1.
Решение.
х2=5-2=3; х3=5-3=2; х4=5-2=3; х5=5-3=2, т.е. получается последовательность: 2;3;2;3;2;…
1.3. Свойства числовой последовательности
Числовая последовательность - частный случай числовой функции, а поэтому некоторые свойства функции рассматриваются и для последовательностей.
Последовательность, все члены которой равны одному и тому же числу, называется постоянной.
Таким образом, для постоянной
последовательности {хn} имеем: ![]()
Последовательность {хn} называют ограниченной сверху, если все её члены не больше некоторого числа.
Например, последовательность -1,-4,-9,-16,…,-n2,… ограничена сверху. В качестве верхней границы можно взять число -1.
Последовательность {хn} называют ограниченной снизу, если все её члены не меньше некоторого числа.
Например, последовательность 1,4,9,16,…, n2,… ограничена снизу. В качестве нижней границы можно взять число 1.
Если последовательность ограничена и сверху, и снизу, то её называют ограниченной.
Например, последовательность ![]() ограничена и сверху, и снизу. В
качестве верхней границы можно взять 1, в качестве нижней-0.
ограничена и сверху, и снизу. В
качестве верхней границы можно взять 1, в качестве нижней-0.
Последовательность {хn} называют возрастающей, если каждый её член больше предыдущего:
![]()
Например, 1,3,5,7,…,2n-1,… - возрастающая последовательность.
Последовательность {хn} называют убывающей, если каждый её член меньше предыдущего:
![]()
Например ![]() -
убывающая последовательность.
-
убывающая последовательность.
Возрастающие и убывающие последовательности объединяют общим термином - монотонные последовательности.
1.4. Предел числовой последовательности
Пусть а – точка прямой, а r – положительное число.
Интервал (а-r; a+r) называют окрестностью точки а, а число r- радиусом окрестности.
![]()
Число а называют пределом последовательности {хn}, если в любой заранее выбранной окрестности точки а содержатся все члены последовательности, начиная с некоторого номера.
Пишут ![]() .
.
Пример 6.
Дана последовательность {хn}: ![]()
Доказать, что ![]() .
.
Решение.
Возьмём любую окрестность точки 0, пусть
её радиус равен r. Ясно, что всегда можно подобрать натуральное число n0 так, чтобы
выполнялось неравенство ![]() . Если,
например, r=0,001, то в
качестве n0 можно взять
1001,поскольку
. Если,
например, r=0,001, то в
качестве n0 можно взять
1001,поскольку ![]() ; если r=
; если r=![]() , то в качестве n0 можно взять 5774,
поскольку
, то в качестве n0 можно взять 5774,
поскольку ![]() , и т.д. Но это значит, что член
последовательности {хn} с номером n0 попадает в
выбранную окрестность точки 0. Тем более в этой окрестности будут находиться
все последующие члены заданной убывающей последовательности
, и т.д. Но это значит, что член
последовательности {хn} с номером n0 попадает в
выбранную окрестность точки 0. Тем более в этой окрестности будут находиться
все последующие члены заданной убывающей последовательности ![]() . В соответствии с определением
предела это и означает, что
. В соответствии с определением
предела это и означает, что
|
|
Можно вычислить аналогично предел
последовательности ![]()
![]() . Этот результат
является частным случаем более общего утверждения:
. Этот результат
является частным случаем более общего утверждения:
|
Если |
Справедливы утверждения:
Если последовательность {хn} имеет своим пределом
число а, говорят также, что эта последовательность сходится
к числу а.
Если последовательность не имеет предела, то говорят, что она расходится. В частности:
Если ![]() ,
то
последовательность
,
то
последовательность ![]() расходится.
расходится.
1.5. Вычисление пределов последовательностей
Выше мы отметили, что ![]() ;
; ![]() если
если
![]() . Добавим ещё одно соотношение:
. Добавим ещё одно соотношение:
![]() .
.
Для вычисления пределов последовательностей в более сложных случаях используется следующая теорема.
Теорема
Если ![]() ,
то
,
то
1) предел суммы равен сумме пределов:
![]() ;
;
2) предел произведения равен произведению пределов:
![]() ;
;
3) предел частного равен частному от пределов:
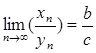 (формула
справедлива, если
(формула
справедлива, если ![]() и
и ![]() для любого n)
для любого n)
4) постоянный множитель можно вынести за знак предела:
![]() .
.
Пример 7.
Найти пределы последовательностей:
а)
![]() ; б)
; б) ![]() ;
;
в)
![]() .
.
Решение.
а). Имеем ![]() .
Применим правило «предел произведения », получим
.
Применим правило «предел произведения », получим
![]() .
.
б). ![]()
в) Применим правило «предел суммы» получим
![]() .
.
Пример 8.
Вычислить: а)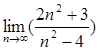 ,
б)
,
б) ![]()
Решение.
В подобных случаях применяют искусственный приём: делят числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n. В данном примере разделим числитель и знаменатель дроби почленно на n2.Получим
а)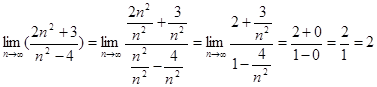 ;
;
б) Домножим и разделим выражение под знаком предела на сопряжённое к нему, после чего воспользуемся формулой разности квадратов:
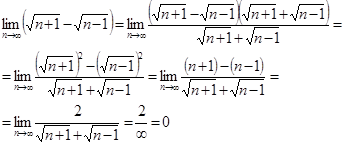
2. Предел функции
2.1 Предел функции в точке
Окрестностью точки х0 называется любой интервал с центром в точке х0.
Пусть функция f(x) определена в некоторой окрестности точки х0 кроме, быть может, самой точки х0.
Число А называется пределом функции f(x) в точке х0,
если для любой последовательности {хn}, сходящейся к х0(![]() ,для любого n),
последовательность {
,для любого n),
последовательность {![]() } соответствующих
значений функции сходится к А.
} соответствующих
значений функции сходится к А.
Обозначается так: ![]()
Пример 9.
Доказать, что ![]()
Доказательство:
Пусть {хn}- произвольная
последовательность, сходящаяся к 2,т.е. такая, что ![]() .
Тогда в соответствии со свойствами пределов последовательностей
.
Тогда в соответствии со свойствами пределов последовательностей ![]() .
.
Так как ![]() для
любой последовательности {хn}, сходящейся к точке
х0 , то по определению предела функции это означает, что
для
любой последовательности {хn}, сходящейся к точке
х0 , то по определению предела функции это означает, что ![]() .
.
2.2 Операции над пределами функций
Пусть функции f(x) и g(x) определены в
некоторой окрестности точки х0 и, кроме того, ![]() ,
,
![]() . Тогда:
. Тогда:
1. Предел суммы ( разности) этих функций равен сумме (разности) их пределов, т.е.
![]() .
.
2. Предел произведения функций равен произведению их пределов, т.е.
![]() .
.
3. Предел частного функции равен частному их
пределов (при условии ![]() ), т.е.
), т.е.
![]() .
.
Отсюда, в частности вытекает, что постоянный множитель можно выносить за знак предела функции, т.е.
![]()
Пример 10.
Используя свойства пределов функций, найти следующие пределы:
1) ![]() ;
2)
;
2) ![]() ;
;
3) ![]() .
.
Решение.
1) Применяя теорему о действиях над пределами функций, получим:
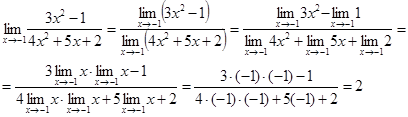
2)
Так
как пределы числителя и знаменателя при ![]() равны
нулю, то мы имеем неопределённость вида
равны
нулю, то мы имеем неопределённость вида ![]() .
.
Избавимся от неё, разложив числитель и знаменатель на множители и сократив их далее на общий множитель х-2
![]() .
.
В полученной дроби знаменатель уже не
стремится к нулю при ![]() , поэтому можно применить
теорему о пределе частного:
, поэтому можно применить
теорему о пределе частного:
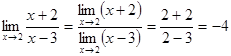 .
.
3)
Здесь
также имеем неопределённость вида![]() . Домножим
числитель и знаменатель дроби на выражение сопряжённое числителю:
. Домножим
числитель и знаменатель дроби на выражение сопряжённое числителю:
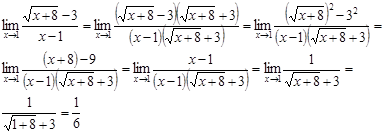
2.3. Предел функции на бесконечности
Пусть функция f(x) определенна на
бесконечном промежутке![]() .
.
Число А называется пределом функции f(x) при ![]() , если для любой положительной
бесконечно большой последовательности {хn} (т.е. хn
, если для любой положительной
бесконечно большой последовательности {хn} (т.е. хn![]() )
последовательность {
)
последовательность {![]() } соответствующих
значений функций сходится к А.
} соответствующих
значений функций сходится к А.
Обозначение: ![]()
Аналогично определяется предел функции f(x) при ![]() .
.
Обозначение:
![]() .
.
Пример 11.
Вычислить ![]() .
.
Решение.
Числитель и знаменатель дроби – бесконечно
большие функции, поэтому здесь имеет место неопределённость ![]() .
.
Раскрывая эту неопределённость, поделим числитель и знаменатель дроби на старшую степень х, т.е. на х2:
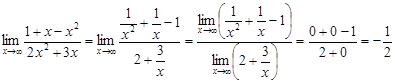
2.4. Замечательные пределы
Первый замечательный предел
![]()
Второй замечательный предел
![]() .
.
Число е≈2,711828 является одной из фундаментальных величин в математике.
Следствия из обоих замечательных пределов:
![]() ;
; ![]() ;
;
![]() ;
;![]() ;
;
Пример 12.
Вычислить пределы:
а) ![]() ;
б)
;
б) ![]() ;
;
в) ![]() ;
г).
;
г). 
Решение.
а) Используя
формулу тригонометрии ![]() , получаем:
, получаем: 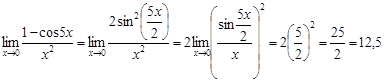
б) Воспользуемся формулой тригонометрии:
cos3x-cos7x=2sin5xsin2x.
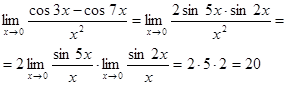
в) Проведём замену переменной
х=2α. При ![]() получаем:
получаем:
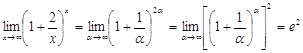 .
.
г) Поделив числитель и знаменатель дроби на х, сведём данный предел к частному пределов:
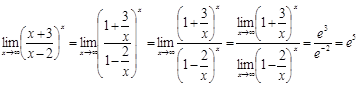
2.5. Односторонние пределы
Число А называется левым пределом функции f(x) в точке х0, если для любой последовательности {хn}, сходящейся
к х0 слева (![]() , для любого n),
последовательность {
, для любого n),
последовательность {![]() }соответствующих значений
функции сходится к А.
}соответствующих значений
функции сходится к А.
Обозначение: ![]()
Число А называется правым пределом функции f(x) в точке х0, если для любой последовательности {хn}, сходящейся
к х0 справа (![]() , для любого n),
последовательность {
, для любого n),
последовательность {![]() }соответствующих значений
функции сходится к А.
}соответствующих значений
функции сходится к А.
Обозначение: ![]()
3. Непрерывность функции
3.1. Непрерывность функции в точке
Функция f(x) называется непрерывной
в точке х0 , если она определена в некоторой окрестности этой
точки и ![]() .
.
Если обозначить х- х0=∆х (приращение аргумента),
f(x)-f(х0)=∆y (приращение функции, соответствующее приращению аргумента ∆х), то это определение можно записать в эквивалентной форме.
Функция f(x) называется непрерывной
в точке х0 , если она определена в некоторой окрестности этой
точки и ![]() .
.
Пример13.
Доказать, что функция у=х2
непрерывна в произвольной точке ![]() .
.
Доказательство.
Пусть ∆х- приращение аргумента в точке х0. Найдём соответствующее приращение функции:
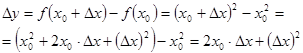
Теперь, применяя теоремы о пределе суммы и произведения функций, получим:
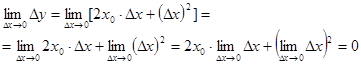
Таким образом ![]() ,
что и означает (по определению) непрерывность данной функции в точке
,
что и означает (по определению) непрерывность данной функции в точке ![]() .
.
Можно доказать, что все элементарные функции непрерывные на своих областях определения.
3.2. Непрерывность функции на промежутке
Функция f(x) называется непрерывной на данном промежутке, если она непрерывна в каждой точке этого промежутка.
В частности, функция f(x) называется непрерывной на отрезке [a;b], если она:
1) непрерывна в каждой точке интервала (a;b);
2) непрерывна справа в точке a.
3) непрерывна слева в точке в.
3.3. Точки разрыва функции
Пусть точка х0 принадлежит области определения функции f(x), или является граничной точкой этой области. Точка х0 называется точкой разрыва функции f(x), если f(x) не является непрерывной в этой точке.
Классификация точек разрыва
Точки разрыва 1-го рода:
1). Если в точке х0 существуют
конечные односторонние пределы![]() и
и
![]() , причём не все три числа
, причём не все три числа ![]() равны между собой, то х0 называется
равны между собой, то х0 называется
точкой разрыва 1-го рода.
Точки разрыва 1-го рода подразделяются на:
а). Точки устранимого разрыва –
![]()
б). Точки скачка- ![]()
2). Если в точке х0 не
существует хотя бы один из односторонних пределов функции![]() или
или ![]() ,
то х0 называется точкой разрыва 2-го рода.
,
то х0 называется точкой разрыва 2-го рода.
Пример 14.
Исследовать на
непрерывность и построить график 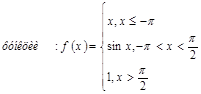
Решение.
Функции у=х, у=sinx, у=1 непрерывны
на всей числовой прямой, поэтому данная функция может иметь разрывы только в
точках, где меняется её аналитическое выражение, т.е. в точках ![]() .
.
Найдём соответствующие односторонние пределы и значения функции.
В точке ![]() имеем:
имеем:
![]() ,
, ![]()
f(-π)=-π.
Таким образом, в этой точке
![]() ,т.е. функция
имеет разрыв 1-го рода и непрерывна слева. Скачок функции f(x) в точке х1=-π
равен π.
,т.е. функция
имеет разрыв 1-го рода и непрерывна слева. Скачок функции f(x) в точке х1=-π
равен π.
Аналогично, для точки ![]() получим:
получим:
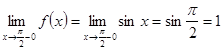 ,
,
![]() ,
,
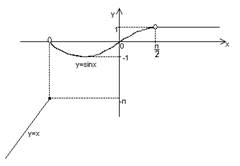 а значение
а значение ![]() не определено. Отсюда следует, что
не определено. Отсюда следует, что
![]() - точка устранимого разрыва для
функции f(x).
- точка устранимого разрыва для
функции f(x).
4. Контрольные вопросы
1).Что называется числовой последовательностью?
2).Какие способы задания последовательности вы знаете? Приведите примеры.
3).Какая последовательность называется возрастающей? Приведите примеры.
4).Какая последовательность называется убывающей? Приведите примеры.
5).Какая последовательность называется постоянной?
6).Какая последовательность называется ограниченной?
7).Приведите примеры неограниченных последовательностей.
8).Что называется пределом последовательности?
9).В чём заключается геометрический смысл предела последовательности?
10).Сформулируйте теорему о пределе суммы, произведения и частного двух последовательностей.
11).Что называется пределом функции в точке?
12).Сформулируйте теорему о пределе суммы, произведения и частного двух функций.
13).Что называется правосторонним пределом функции в точке?
14).Что называется левосторонним пределом функции в точке?
15).Что называется пределом функции на бесконечности?
16).Сформулируйте 1-ый замечательный предел.
17).Сформулируйте 2-ый замечательный предел.
18).Сформулируйте следствия из замечательных пределов.
19).Какая функция называется непрерывной в точке?
20).Какая функция называется непрерывной на промежутке?
21).Какая точка называется точкой разрыва функции?
22).Какие точки разрыва вы знаете?
23).Какие условия должны выполняться, чтобы точка х0 была точкой разрыва 1-го рода?
24). Какие условия должны выполняться, чтобы точка х0 была точкой разрыва 1-го рода?
25).Какие условия должны выполняться, чтобы точка х0 была точкой разрыва 2-го рода?
26).Какая точка называется точкой устранимого разрыва?
27).Какая точка называется точкой скачка?
Часть 2. Практическая работа
2.1. Цели работы
- научиться составлять последовательность;
- научиться находить пределы последовательности;
- научиться вычислять пределы функции в точке и на бесконечности;
- научиться определять точки разрыва функции.
2.2. Порядок выполнения работы
2.1. Проработать теоретический материал по теме.
2.2. Ответить на контрольные вопросы.
2.3. Получить вариант задания.
2.4. Выполнить задание.
2.5. Оформить отчёт о работе.
2.3. Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
- точное наименование работы;
- цель работы;
- ход работы (условие задачи);
- результаты работы (подробное решение задач);
- вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
2.4. Варианты заданий
Вариант 1
1).Напишите первые пять членов последовательности:
![]() .
.
2).Найти пределы:
а)![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
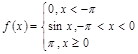
Вариант 2
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.

Вариант 3
1).Выпишите первые пять членов последовательности, заданной рекуррентно:
![]() .
.
2).Найти пределы:
а)![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3)Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
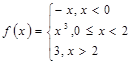
Вариант 4
1).Напишите первые пять членов последовательности:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г)
![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.

Вариант 5
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
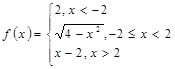
Вариант 6
1).Выпишите первые пять членов последовательности, заданной рекуррентно:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в)
сделать чертёж.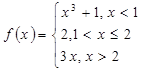
Вариант 7
1).Напишите первые пять членов последовательности:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
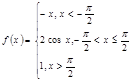
Вариант 8
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыв
в) сделать чертёж.
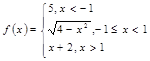
Вариант 9
1).Выпишите первые пять членов последовательности, заданной рекуррентно:
![]() .
.
2).Найти пределы:
а)![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
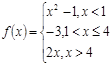
Вариант 10
1).Напишите первые пять членов последовательности:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
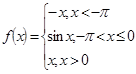
Вариант 11
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыв
в) сделать чертёж.
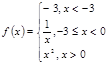
Вариант 12
1).Выпишите первые пять членов последовательности, заданной рекуррентно:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
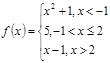
Вариант 13
1).Напишите первые пять членов последовательности:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) 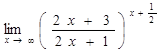 ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
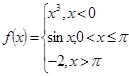
Вариант 14
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыв
в) сделать чертёж.

Вариант 15
1).Выпишите первые пять членов последовательности, заданной рекуррентно:
![]() .
.
2).Найти
пределы: а) ![]() ; б)
; б) ![]() ;
;
в)![]() ; г)
; г) ![]() ;
д)
;
д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
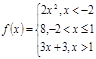
Вариант 16
1).Напишите первые четыре члена последовательности:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
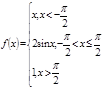
Вариант 17
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а) ![]() ;
б)
;
б) ![]() ; в)
; в) 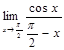 ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыв
в) сделать чертёж.
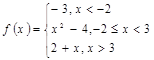
Вариант 18
1).Выпишите первые пять членов последовательности, заданной рекуррентно:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
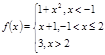
Вариант 19
1).Напишите первые четыре члена последовательности:
![]() .
.
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертёж.
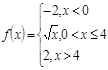
Вариант 20
1).Составьте одну из возможных формул n –го члена последовательности по первым пяти её членам:
![]()
2).Найти пределы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ;
;
г) ![]() ; д)
; д) ![]() .
.
3).Для данной функции f(x) требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыв
в) сделать чертёж.
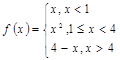
2.5. Приложения
Формулы тригонометрии
Основные тригонометрические тождества
sin2x+cos2x=1;
tg x=![]() ; 1+tg2
x=
; 1+tg2
x=![]() ;
;
tgx ctgx=1; ctg x=![]() ; 1+ctg2x=
; 1+ctg2x=![]() ;
;
Формулы сложения
sin(x+y)=sinx cosy+cosx siny;
cos(x+y)=cosx cosy-sinx sin y; sin(x-y)=sinx cosy-cosx siny;
cos(x-y)=cosx cosy+sinx sin y; tg(x+y)=![]() ;
tg(x-y)=
;
tg(x-y)=![]() .
.
Формулы двойного угла
сos2x=cos2x-sin2x=2; cos2x-1=1-2 sin2x;
sin2x=2sinxcosx;
tg2x=![]() .
.
Формулы половинного угла
![]() ;
;
Переход от суммы к произведению
sinx+siny=2sin![]() cos
cos![]() ;
;
sinx-siny=2sin![]() cos
cos![]() ;
;
сosx+cosy=2cos![]() cos
cos![]() ;
;
сosx-cosy=-2sin![]() sin
sin![]() .
.
Формулы сокращённого умножения
1).
![]()
2).
![]()
3).
![]()
4).
![]()
5).
![]()
6).
![]()
7).
![]()
Разложение квадратного трёхчлена
на простые множители
ах2+вх+с=а(х-х1)(х-х2),
где
х1,х2 – корни квадратного уравнения ах2+вх+с=0
Литература
1. Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.- М.: Высшая школа, 1997.-250 с.
3. Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4. Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5. Лунгу К.Н. Сборник задач по высшей математике. 1 курс- Москва: Айрис- пресс, 2007.- 576 с.
6. Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
7. Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
8. Шнейдер В.Е. Краткий курс высшей математики. -М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Вычисление производных сложных функций, производных высших порядков.
Понятие дифференциала. Применение дифференциала для приближённых вычислений.
Учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть1. Теоретическое обоснование
1. Производная
1.1. Понятие производной
1.2. Таблица производных
1.3. Основные правила дифференцирования
1.4. Производная сложной функции
1.5. Геометрический смысл производной
1.6. Физический смысл производной
1.7. Производные высших порядков
2. Дифференциал
2.1. Понятие дифференциала
2.2. Геометрический смысл дифференциала
2.3. Свойства дифференциала
2.4. Применение дифференциала к приближённым вычислениям
3. Контрольные вопросы
Часть 2. Практическая работа
2.1. Цели работы
2.2. Порядок выполнения работы
2.3. Указания к оформлению
2.4. Варианты заданий
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Вычисление производных сложных функций, производных высших порядков. Понятие дифференциала. Применение дифференциала для приближённых вычислений».
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
- развитие логического и алгоритмического мышления;
- воспитание умений действовать по заданному алгоритму и конструировать новые;
- формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данных материалов, т. е. студенты будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
Критерием успешного усвоения материала является выполнение не менее 4 заданий практической части.
В результате изучения данной темы
студент должен
знать:
- определение производной и дифференциала;
-табличные производные;
-правила дифференцирования;
-физический и геометрический смысл производной и дифференциала;
уметь:
-дифференцировать функции одной действительной переменной;
-вычислять производные сложных функций;
- вычислять производные высших порядков;
-применять дифференциал для приближенных вычислений.
Часть 1. Теоретическое обоснование
1. Производная
1.1. Понятие производной
Пусть функция y=f(x) определена в некоторой окрестности точки х0.
Производной функции y=f(x) в точке х0 называется предел отношения приращения ∆у функции в этой точке
( если он существует) к приращению ∆х
аргумента, когда ![]() .
.
Обозначения: ![]() или
или
![]() .
.
Таким образом,
|
|
Вычисление производных называется дифференцированием функции.
Пример 1.
Пользуясь определением найти производную функции у=3х2.
Решение.
Придадим аргументу х приращение ∆х. Тогда соответствующее приращение ∆у функции будет иметь вид
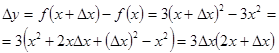
Отсюда
находим предел отношения![]() в точке х при
в точке х при![]() :
:
![]() .
.
Таким
образом ![]()
1.2. Таблица производных
1. ![]() , с- const;
, с- const;
2. ![]() (где
(где ![]() );
в частности,
);
в частности, ![]() ;
;
3. ![]() , а>0; в частности
, а>0; в частности ![]() ;
;
4. ![]() , a>0, a≠1; в
частности ,
, a>0, a≠1; в
частности , ![]()
5. (sinx)’=cosx; 6. (cosx)’=-sinx;
7. ![]() ; 8.
; 8. ![]()
9. ![]() ; 10.
; 10. 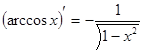
11. ![]() ; 12.
; 12. ![]() ;
;
1.3. Основные правила дифференцирования
Пусть
с – константа, а u(x) и v(x) имеют
производные в некоторой точке х. Тогда функции u(x)![]() v(x), cu(x), u(x)v(x) и
v(x), cu(x), u(x)v(x) и ![]() (где v(x)≠0) также
имеют производные в этой точке, причём
(где v(x)≠0) также
имеют производные в этой точке, причём
1.![]() ;
;
2. ![]() , в частности
, в частности ![]() ;
;
3. 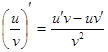 , в частности
, в частности 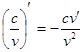
Пример 2.
Пользуясь
основными правилами дифференцирования, найти![]() .
.
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
Решение.
а) Преобразуем функцию к виду
![]() .
.
Отсюда, используя таблицу производных, получим
![]()
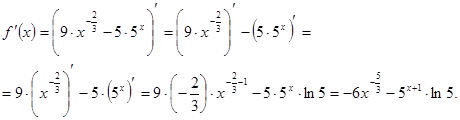
б) Преобразуем функцию к виду
![]() .
.
Воспользуемся формулой для производной произведения:
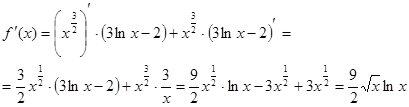
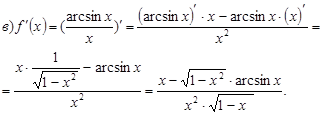
1.4. Производная сложной функции
Пусть дана функция ![]() . Обозначим х2+1 через u.
Тогда
. Обозначим х2+1 через u.
Тогда ![]() зависит от х через
вспомогательную переменную u,
а переменная u является функцией
аргумента х.
зависит от х через
вспомогательную переменную u,
а переменная u является функцией
аргумента х.
Если y=f(u), гдеu=φ(x), т.е. если у зависит от х через посредство промежуточного аргумента u, то у называется сложной функцией от х.
Если у является дифференцируемой функцией от u, а u является дифференцируемой функцией от х, то производная у по х равна произведению производной функции у по u на производную функции u по х.
|
|
Некоторые формулы таблицы производных теперь будут иметь вид:
![]() ,
,
![]() ,
,
![]() и т.д.
и т.д.
Пример 3.
Вычислить производные сложных функций:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() .
.
Решение.
а) Полагая х3=u, найдём:
![]()
![]() ;
;
б) Полагая tgx=u, найдём:
![]() ;
;
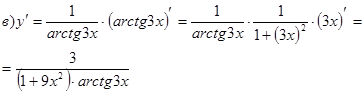
1.5. Геометрический смысл производной
Пусть
функция y=f(x) имеет
производную в точке х0. Тогда существует касательная к графику этой
функции в точке ![]() , уравнение которой имеет
вид:
, уравнение которой имеет
вид:
|
|
При
этом ![]()
![]() ,
где α – угол наклона этой касательной к оси Ох.
,
где α – угол наклона этой касательной к оси Ох.
![]()
Геометрический смысл производной: угловой коэффициент касательной равен производной функции f(x) в точке х0:
|
|
Пример 4.
Написать уравнение касательной к графику функции у=lnx2, x0=e.
Решение.
1). Записываем общее уравнение касательной:
![]() .
.
2).
Находим ![]() :
:
![]() .
.
3). Находим производную:
![]() ;
;
находим
![]()
![]()
![]() :
:
![]() .
.
4). Подставляем найденные значения в общее уравнение касательной:
![]() ;
;
![]() - уравнение касательной.
- уравнение касательной.
1.6. Физический смысл производной
Производная функции f(x) в точке х0 представляет собой скорость изменения функции f(x) относительно её аргумента при данном значении х0.
В частности, если при прямолинейном движении точки задан закон движения s=s(t), то скорость движения в момент t0 есть производная пути по времени:
|
|
Можно дать определение ускорения при прямолинейном движении: ускорение движения в момент времени t0 есть производная скорости по времени:
|
|
Пример 5.
Зависимость пути от времени при прямолинейном движении точки задана уравнением:
![]() (t- в секундах, s- в метрах).
Определить скорость и ускорение движения
(t- в секундах, s- в метрах).
Определить скорость и ускорение движения
в конце второй секунды.
Решение.
Находим производную пути по времени:
![]()
![]() ,
,
при
t=2 имеем: ![]()
![]() Следовательно
Следовательно
![]()
![]() .
.
Находим производную скорости по времени:
![]()
![]() ,
,
при
t=2 имеем: ![]()
![]() Следовательно
Следовательно
![]()
![]() .
.
1.7. Производные высших порядков
Производной второго порядка (второй производной) функции у=f(x) называется производная от её производной.
Вторая производная обозначается так: ![]() , или
, или ![]() .
.
Аналогично
производная третьего порядка функции у=f(x) есть производная
от производной второго порядка: ![]()
![]() .
.
Вообще, производная n-го порядка от функции у=f(x) называется производной
от производной (n-1) порядка: ![]() .
.
Производные высших порядков (вторая, третья и т. д.) вычисляются последовательным дифференцированием данной функции.
Пример 6.
![]()
![]() .
.
Найти
![]()
![]() .
.
Решение.
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
Пример 7.
![]()
![]() .Найти
.Найти
![]() .
.
Решение.
![]()
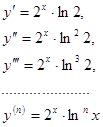
2. Дифференциал
2.1. Понятие дифференциала
Пусть функция у=f(x) определена в некоторой окрестности точки х0. Тогда, если существует такое число А, что приращение ∆у этой функции в точке х0, соответствующее приращению ∆х аргумента, представимо в виде:
∆у=А∆х+α(∆х)∆х,
где![]()
![]() , то функция f(x)
называется дифференцируемой в точке х0. При этом главная,
линейная относительно ∆х, часть этого приращения, т.е. А∆х,
называется дифференциалом функции в точке х0 и
обозначается dy или df(х0).
, то функция f(x)
называется дифференцируемой в точке х0. При этом главная,
линейная относительно ∆х, часть этого приращения, т.е. А∆х,
называется дифференциалом функции в точке х0 и
обозначается dy или df(х0).
Дифференциалом аргумента называется приращение аргумента: dx=∆x.
Функция f(x)
дифференцируема в точке х0 тогда и только тогда, когда в этой точке
существует конечная производная ![]()
![]() ; при этом А=
; при этом А=![]() . Поэтому:
. Поэтому:
Дифференциал функции равен произведению её производной на дифференциал аргумента:
|
|
Отсюда ![]()
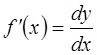 , т.е. производная функции у=f(x) в точке х
равна отношению дифференциала этой функции в данной точке к
дифференциалу независимой переменной.
, т.е. производная функции у=f(x) в точке х
равна отношению дифференциала этой функции в данной точке к
дифференциалу независимой переменной.
Пример 7.
Найти дифференциал функции ![]()
![]() .
.
Решение.
Так как ![]() , то в
данном случае
, то в
данном случае ![]() .
.
Пример 8.
Найти дифференциал функции ![]()
![]() в точке х0=2, если dx=0,1.
в точке х0=2, если dx=0,1.
Решение.
![]() .
.
Теперь найдём dy в точке х0=2, если dx=0,1:
dy=(4-3)0,1=0,1.
2.2. Геометрический смысл дифференциала
![]() Геометрически
приращение ∆у функции f(x)
в точке х – есть приращение ординаты точки на кривой (∆у=NA),
а дифференциал dy функции в этой точке –
приращение ординаты соответствующей точки на касательной( dy=AB).
Геометрически
приращение ∆у функции f(x)
в точке х – есть приращение ординаты точки на кривой (∆у=NA),
а дифференциал dy функции в этой точке –
приращение ординаты соответствующей точки на касательной( dy=AB).
2.3. Свойства дифференциала
Пусть u(x) и v(x) – некоторые функции, дифференцируемые в точке х. Тогда:
1.dC=0, где C – константа.
2. d(αu)=![]() ,где α – константа.
,где α – константа.
3. ![]() .
.
4. ![]() .
.
5. ![]() , где v(x)
, где v(x)![]() .
.
6. Инвариантность формы дифференциала.
Если y=f(u(x)) – сложная функция, то
![]() , или
, или ![]() ,
,
т.е. форма дифференциала не меняется (инвариантна) независимо от того, рассматривается у как функция независимой переменной х или зависимой переменной u.
Пример 8.
Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Решение.
а) 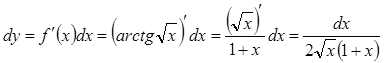 .
.
![]()
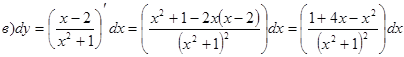 .
.
2.4. Применение дифференциала к приближённым вычислениям
Пусть дана функция у=f(x); приращение этой
функции ∆у=f(x+∆x)-f(x), её дифференциал
![]() . При достаточно малых (близких
к нулю) приращениях аргумента ∆х будем считать, что ∆у≈dy, т.е. что
приращение функции приближённо равно её дифференциалу. Заменив приращение
функции её дифференциалом, а дифференциал аргумента на приращение аргумента
получим
. При достаточно малых (близких
к нулю) приращениях аргумента ∆х будем считать, что ∆у≈dy, т.е. что
приращение функции приближённо равно её дифференциалу. Заменив приращение
функции её дифференциалом, а дифференциал аргумента на приращение аргумента
получим
![]()
![]() ,
,
из чего следует
|
|
Применение этой формулы даёт значительное упрощение вычисления числового значения функции;
геометрически это соответствует замене
участка кривой отрезком касательной.
Пример 9.
Вычислить приближённо:
а) ln1,02; б)![]() ;
в) arcsin 0,51.
;
в) arcsin 0,51.
Решение.
а) Воспользуемся приближённой формулой
![]() .
.
Пусть х0=1, ∆x=0,02.Тогда, подставляя f(x)=lnx,
получим: ![]() ,
,
![]() .
.
Таким образом, ln1,02≈0,02.
б) Учитывая, что ![]() ,
х0=25, ∆x=-1, получим
,
х0=25, ∆x=-1, получим
![]() , т.е.
, т.е.
![]() .
.
Окончательно ![]() ≈4,9.
≈4,9.
в) Полагая f(x)=arcsinx; х0=0,5; ∆x=0,01 получим
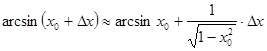 ,т.е.
,т.е.
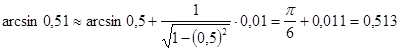 .
.
Таким образом, arcsin 0,51≈0,513.
3. Контрольные вопросы
1). Дайте определение производной функции.
2). Что называется дифференцированием функции?
3). Назовите основные производные.
4). Как вычисляется производная алгебраической суммы функции, произведения и частного функций?
5). Какую функцию называют сложной? Приведите примеры сложных функций.
6). Как вычисляется производная сложной функции?
7). В чём состоит геометрический смысл производной?
8). Напишите общее уравнение касательной.
9). В чём состоит физический смысл производной?
10). Чему равна скорость точки в некоторый момент времени t?
11). Чему равно ускорение точки в некоторый момент времени t?
12). Что называют производной второго порядка? третьего?
13). Что называют производной n-го порядка?
14).Дайте определение дифференциала.
15). Чему равен дифференциал?
16). В чём состоит геометрический смысл дифференциала?
17). Перечислите свойства дифференциала.
18). Напишите формулу для приближённых вычислений с помощью дифференциала.
Часть 2. Практическая работа
2.1. Цели работы
![]() научиться
вычислять производные сложных функций;
научиться
вычислять производные сложных функций;
![]() научиться
находить производные высших порядков;
научиться
находить производные высших порядков;
![]() научиться
вычислять дифференциалы;
научиться
вычислять дифференциалы;
![]() научиться
применять дифференциал
научиться
применять дифференциал
для приближённых вычислений.
2.2. Порядок выполнения работы
2.1 Проработать теоретический материал по теме.
2.2 Ответить на контрольные вопросы.
2.3 Получить вариант задания.
2.4 Выполнить задание.
2.5 Оформить отчёт о работе.
2.3. Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное
наименование работы;
точное
наименование работы;
![]() цель работы;
цель работы;
![]() ход работы
(условие задачи);
ход работы
(условие задачи);
![]() результаты
работы (подробное решение задач);
результаты
работы (подробное решение задач);
![]() вывод
вывод
Отчёт должен быть сдан не позднее 3-х
дней со дня проведения работы.
2.4.
Варианты заданий
Вариант 1
1).Вычислить производную:
а) у=cos5x; б) у=73х-1.
2).Вычислить
производную в точке: ![]() , х0=0.
, х0=0.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=-1.
в точке х0=-1.
5).Найти ускорение тела, движущего по закону
S=0,5sin2t (м), при ![]() с.
с.![]()
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо: (9,06)2
Вариант 2
1).Вычислить производную
а) у=arcsin![]() ; б) у=
; б) у=![]()
2).Вычислить
производную в точке: ![]()
![]() , х0=1.
, х0=1.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
у=4х-х2 в точке пересечения с осью 0х.
5).Тело массой m=1кг движется по закону
S=0,3sin(10t-π) (м). Определить силу, действующую
на
тело при ![]() с.
с.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 3
1).Вычислить производную:
а) у=![]() ; б) у=
; б) у=![]() .
.
2).Вычислить
производную![]()
в точке x0=ln2.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке
(2;3/2).
в точке
(2;3/2).
5).Количество электричества, протекшее через проводник, начиная с момента t=0, определяется формулой
q=2t2+3t+1 (Кл). Найти силу тока в конце 10-ой секунды.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо: (1,012)3
Вариант 4
1).Вычислить производную:
а) у=ln(5x3-x); б) у=![]()
2).Вычислить
производную в точке: ![]() , х0=8.
, х0=8.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
у=![]() в точке х0=3.
в точке х0=3.
5).Движение двух материальных точек задано уравнениями: S1=4t+8t2-16t3 и S2=2t-4t2+t3. Найти, в какой момент времени ускорение одинаково.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённое значение функции:
у=3х2+5х+1 при х0=3, ∆х=0,001.
Вариант 5
1).Вычислить производную:
а) у=![]() ; б) у=
; б) у=![]() .
.
2).Вычислить
производную![]() в точке x0=0.
в точке x0=0.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке (4;0).
в точке (4;0).
5).Маховик вращается по закону φ=8t2-6t+4.
Найти угловую скорость в момент времени t=3c.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо: (0,975)4
Вариант 6
1).Вычислить производную:
а) у=![]() б)
б) ![]()
2).Вычислить
производную в точке: ![]()
![]() ,
х0=0.
,
х0=0.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
у=![]() в точке х0=-2.
в точке х0=-2.
5).Тело, масса которого m=0,5 кг, движется прямолинейно по закону S=2t2+t-3 (м). Найти кинетическую энергию тела через 7 с после начала движения.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 7
1).Вычислить производную:
а) у=![]() ; б) у=
; б) у=![]() .
.
2).Вычислить
производную![]() в точке х0=1.
в точке х0=1.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=4.
в точке х0=4.
5).Точка движется прямолинейно по закону S=2t2+t-3.
В какой момент времени t скорость точки
окажется равной нулю?
6).Найти дифференциал функции:
а) у=![]() ; б) у=
; б) у=![]() .
.
7).Вычислить приближённо: arctg1,05
Вариант 8
1).Вычислить производную:
а) у=![]() б) у=
б) у=![]() .
.
2).Вычислить
производную в точке: ![]()
![]() , x0=2.
, x0=2.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
у=![]() в точке х0=0.
в точке х0=0.
5).Точка движется прямолинейно по закону S=t3+5t2+4 (м). Найти величины скорости и ускорения
в момент времени t=2c.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 9
1).Вычислить производную:
а) у=![]() ; б) у=
; б) у=![]() .
.
2).Вычислить
производную![]() в точке х0=
в точке х0=![]() .
.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точках пересечения с осью 0х.
в точках пересечения с осью 0х.
5). Точка массой m движется по закону S=3t2+7t+9 (м). Докажите, что сила, действующая на точку, постоянна.
6).Найти дифференциал функции:
а) у=![]() ; б) у=
; б) у=![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 10
1).Вычислить производную:
а) у=![]() б) у=
б) у=![]() .
.
2).Вычислить
производную в точке: ![]() , х0=3.
, х0=3.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
у=2х2-12х+16 в точке х0=5.
5).Движение
двух материальных точек задано уравнениями: S1 =![]() и S2 =
и S2 =![]() . В какой момент времени их
скорости равны?
. В какой момент времени их
скорости равны?
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 11
1).Вычислить производную:
а) у=![]() ; б) у=
; б) у=![]() .
.
2).Вычислить
производную![]() в точке x0=2.
в точке x0=2.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке
(4;-3).
в точке
(4;-3).
5). Скорость
точки, движущейся прямолинейно, задана уравнением v=2t2-5t+6. В какой момент
времени ускорение точки будет равно 2![]() .
.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо: arctg1,05
Вариант 12
1).Вычислить производную:
а)![]() ; б)
; б) ![]()
2).Вычислить
производную в точке: ![]() , х0=2.
, х0=2.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=4.
в точке х0=4.
5).Уравнение зависимости температуры T тела от времени:
T= 1/2t2-2t+3. С какой скоростью нагревается тело в момент t=10c.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённое значение функции:
у=х3-х2 +x при х0=2, ∆х=0,01.
Вариант 13
1).Вычислить производную:
а) ![]() ; б)
; б) ![]() .
.
2).Вычислить
производную![]() в точке х0=1.
в точке х0=1.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=-2.
в точке х0=-2.
5).Точка массой 12 кг движется по закону S=t2+2t+3 (м). Найти кинетическую энергию тела
через 5 с после начала движения.
6).Найти дифференциал функции:
а) у=![]() ; б)
; б) ![]()
![]() .
.
7).Вычислить приближённо: (0,988)3
Вариант 14
1).Вычислить производную:
а)![]() б)
б) ![]() .
.
2).Вычислить
производную в точке: ![]() , х0=
, х0=![]() .
.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
у=х2+2х-8 в точке х0=2.
5).Точка движется прямолинейно по закону
S=1/3t3-2t2+3 (м). Найти величины скорости и ускорения
в момент времени t=3c.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 15
1).Вычислить производную:
а) ![]() ; б)
; б) ![]() .
.
2).Вычислить
производную![]() в точке x0=
в точке x0=![]() .
.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке
(2;-5).
в точке
(2;-5).
5).Движение
двух материальных точек задано уравнениями: S1 =![]() и S2 =
и S2 =![]() .
.
В какой момент времени их скорости равны?
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо: (9,95)3
Вариант 16
1).Вычислить производную:
а)![]() ; б)
; б) ![]()
2).Вычислить
производную в точке: ![]() , х0=1.
, х0=1.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=-2.
в точке х0=-2.
5). Cила тока изменяется в зависимости от времени по закону I=3t2+2t+1 (А). Найти скорость изменения силы тока через 8 с.
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённое значение функции:
у=х3-х2 +x-3 при х0=3, ∆х=0,03.
Вариант 17
1).Вычислить производную:
а) ![]() ; б)
; б) ![]() .
.
2).Вычислить
производную![]() в точке x0=
в точке x0=![]() .
.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке x0=-5
в точке x0=-5
5).Движение
двух материальных точек задано уравнениями: S1 =![]() и S2 =
и S2 =![]() .
.
В какой момент времени их скорости равны?
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо: (1,013)4
Вариант 18
1).Вычислить производную:
а)![]() ; б)
; б) ![]()
2).Вычислить
производную в точке: ![]() , х0=
, х0=![]() .
.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=2.
в точке х0=2.
5).Движение
двух материальных точек задано уравнениями: S1 =![]() и S2 =
и S2 =![]() .
.
В какой момент времени их скорости равны?
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённое значение функции:
у=2х2 -3x-1 при х=2,01.
Вариант 19
1).Вычислить производную:
а) ![]() ; б)
; б) ![]() .
.
2).Вычислить
производную![]() в точке x0=e.
в точке x0=e.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке x0=1
в точке x0=1
5).Точка движется прямолинейно по закону
S=t4-2t2 (м). Найти величины скорости и ускорения
в момент времени t=4c.
6).Найти дифференциал функции:
а)![]() ; б)
; б) ![]() .
.
7).Вычислить
приближённо: ![]()
Вариант 20
1).Вычислить
производную: а)![]() ; б)
; б) ![]()
2).Вычислить
производную в точке: ![]() , х0=1.
, х0=1.
3).Найти производные указанных порядков для функции:
![]()
![]()
4).Написать уравнение касательной к кривой
![]() в точке х0=0.
в точке х0=0.
5).Движение
двух материальных точек задано уравнениями: S1 =![]() и S2 =
и S2 =![]()
В какой момент времени их скорости равны?
6).Найти дифференциал функции:
а) ![]() ; б)
; б) ![]() .
.
7).Вычислить приближённо:cos290..
Литература
1.Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.- М.: Высшая школа, 1997.-250 с.
3.Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4.Данко П. Е. Высшая математика в упражнениях и задачах,ч.1-М.: ОНИКС 21 век,2003.-304 с.
5.Лунгу К.Н. Сборник задач по высшей математике. 1 курс- Москва: Айрис- пресс, 2007.- 576 с.
6.Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
7.Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
8. Шнейдер В.Е. Краткий курс высшей математики.
-М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Применение производной для исследования функций.
Учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть 1. Теоретическое обоснование
1.1 Признаки возрастания и убывания функций
1.2 Экстремумы функции
1.3 Выпуклость и вогнутость функции
1.4 Точки перегиба
1.5 Асимптоты
1.6 Построение графиков функций с помощью производной
1.7 Контрольные вопросы
Часть 2. Практическая работа
2.1 Цели работы
2.2 Порядок выполнения работы
2.3 Указания к оформлению
2.4 Варианты заданий
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Применение производной для исследования функций».
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данных материалов, т. е. студенты будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
Критерием успешного усвоения материала является выполнение двух заданий в варианте.
В результате изучения данной темы
студент должен
знать:
-табличные производные;
-правила дифференцирования;
-признаки возрастания и убывания на промежутке;
-правило нахождения экстремумов функции и точек перегиба;
уметь:
-применять производную для исследования функций;
- составлять уравнения асимптот.
Часть 1. Теоретическое обоснование
1.1 Признаки возрастания и убывания функций
Если функция f(x)
дифференцируема на интервале (а;b)
и для любого х из этого интервала выполнено неравенство ![]() (
(![]() ) то f(x)
возрастает (соответственно убывает) на этом интервале.
) то f(x)
возрастает (соответственно убывает) на этом интервале.
Точки, в которых производная равна нулю, и точки в которых функция определена, но производная не существует, называют критическими точками.
Алгоритм нахождения интервалов возрастания и убывания функции:
1).Вычисляем производную ![]() данной функции y=f(x),
а затем находим критические точки.
данной функции y=f(x),
а затем находим критические точки.
2).Критическими точками
область определения функции f(x)
разбивается на интервалы, на каждом из которых производная![]() сохраняет свой знак.
сохраняет свой знак.
3).Определяем знак![]() на каждом из найденных интервалов.
Если на интервале
на каждом из найденных интервалов.
Если на интервале ![]() , то на этом интервале
функция возрастает, если
, то на этом интервале
функция возрастает, если![]() , то функция
убывает.
, то функция
убывает.
Пример 1.
Найти интервалы возрастания и убывания функции:
а) ![]() ; б)
; б) ![]()
в) ![]()
![]() ; г)
; г) ![]() .
.
Решение.
а) D(f)=(-∞;+∞).
Найдём производную:
![]()
![]() .
.
Приравняем её к нулю:
2х-8=0
х=4 - критическая точка.
![]() Нанесём эту точку
на ось 0х:
Нанесём эту точку
на ось 0х:
Ответ: f(x) – возрастает, если ![]() ;
;
f(x) – убывает, если ![]()
![]() .
.
б) D(f)=(-∞;+∞).
Найдём производную:
![]()
![]() .
.
Приравняем её к нулю:
![]() ; x(3x-12)=0
; x(3x-12)=0
x1=0; x2=4 - критические точки.
![]() Нанесём эти точки
на ось 0х:
Нанесём эти точки
на ось 0х:
Ответ: f(x) – возрастает , если ![]() f(x) – убывает, если
f(x) – убывает, если ![]() .
.
в) ![]() .
.
Найдём производную:
![]()
![]() .
.
Приравняем её к нулю:
![]()
х=0 – критическая точка.
Нанесём эту точку на ось 0х:
![]()
Ответ: f(x) – убывает, если ![]() .
.
г) ![]() .
.
Найдём производную:
![]()
![]() .
.
Приравняем её к нулю:
![]() ;
;
х=0 – критическая точка.
Нанесём эту точку на ось 0х:
![]()
Ответ: f(x) – возрастает, если ![]() .
.
1.2 Экстремумы функции
Точка х0 называется точкой локального максимума
(или просто максимума)
функции f(x),
если для любого ![]() в некоторой окрестности
точки х0 верно неравенство f(х0)>f(x).
в некоторой окрестности
точки х0 верно неравенство f(х0)>f(x).
Точка х0 называется точкой локального минимума
(или просто минимума)
функции f(x),
если для любого ![]() в некоторой окрестности
точки х0 верно неравенство f(х0)<f(x).
в некоторой окрестности
точки х0 верно неравенство f(х0)<f(x).
Точки локального экстремума (или просто экстремума) – это точки максимума и минимума.
Экстремум - значение функции в точках экстремума.
![]()
Точки а и с на рисунке – точки максимума;
точки b и d – точки минимума.
Необходимое условие существования экстремума.
Если х0– точка экстремума
функции, то в этой точке производная либо равна нулю (![]() ),
либо не существует.
),
либо не существует.
Достаточное условие экстремума.
Пусть функция f(x) дифференцируема в некоторой окрестности точки х0 и непрерывна в самой этой точке.
Если при переходе через
точку х0 слева направо производная ![]() меняет
знак с плюса на минус, то точка х0 является точкой максимума.
меняет
знак с плюса на минус, то точка х0 является точкой максимума.
Если при переходе через
точку х0 производная ![]() меняет
знак с минуса на плюс, то точка х0 является точкой минимума.
меняет
знак с минуса на плюс, то точка х0 является точкой минимума.
Пример 2.
Найти экстремумы функции:
а) ![]() ; б)
; б) ![]() .
.
Решение.
а) Воспользуемся условием существования экстремума.
D(f)=(-∞;+∞).
Найдём производную:
![]()
![]() .
.
Приравняем её к нулю:
![]()
x1=1; x2=5 - критические точки.
Нанесём эти точки на ось 0х:
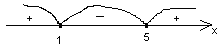
Ответ: x1=1- точка максимума; x2=5 - точка минимума;
f(1)=7 – максимум функции; f(5)=-25 – минимум функции.
б). Воспользуемся условием существования экстремума.
D(f)=(-∞;+∞).
Найдём производную:
![]()
![]() .
.
Приравняем её к нулю:
![]()
x=1- критическая точка.
![]()
Ответ: х=1 - точка минимума; f(1)=e - минимум функции.
1.3 Выпуклость и вогнутость функции
![]() График
функции y=f(x)
называется выпуклым в интервале (а;b),
если он расположен ниже касательной, проведённой в любой точке этого
интервала.
График
функции y=f(x)
называется выпуклым в интервале (а;b),
если он расположен ниже касательной, проведённой в любой точке этого
интервала.
График функции y=f(x) называется вогнутым в интервале (а;b), если он расположен выше касательной, проведённой в любой точке этого интервала.
![]()
Достаточное условие выпуклости (вогнутости) графика функции.
Если ![]() в
интервале (а;b), то график функции является
выпуклым в этом интервале; если же
в
интервале (а;b), то график функции является
выпуклым в этом интервале; если же ![]() ,
то в интервале (а;b) график функции – вогнутый.
,
то в интервале (а;b) график функции – вогнутый.
Пример 3.
Найти промежутки выпуклости кривой ![]()
![]() .
.
Решение.
D(f)=(-∞;+∞).
Находим ![]()
![]() ,
, ![]() .
.
Решаем уравнение ![]() .
.
Вычисляем корни уравнения: x1=0; x2=1.
Нанесём эти точки на ось 0х:
![]()
Ответ: кривая выпукла при ![]() ;
;
кривая вогнута при ![]() .
.
1.4 Точки перегиба
Пусть функция y=f(x) дифференцируема в некоторой окрестности точки х0 . Тогда, если при переходе через точку х0 функция меняет направление выпуклости, то эта точка называется точкой перегиба функции y=f(x).
Необходимое условие точки перегиба.
Если х0 – точка перегиба функции f(x), то в этой точке вторая производная функции либо равна нулю, либо не существует.
Точки, в которых производная равна нулю или не существует, называются критическими точками 2-го рода.
Достаточное условие точки перегиба.
Пусть функция f(x) непрерывна в точке х0 и имеет вторую производную в некоторой окрестности этой точки. Тогда, если при переходе через точку х0 вторая производная меняет знак, то х0 точка перегиба.
Алгоритм нахождения точек перегиба.
1.Найти вторую
производную ![]() .
.
2.Найти критические точки 2-го рода.
3.Определить знак второй производной в промежутках, на которые делят область определения функции f(x) найденные критические точки. Тогда, если при переходе через найденные точки вторая производная меняет знак, то эти точки - точки перегиба.
Пример 4.
Найти точку перегиба кривой:
а) ![]() ; б)
; б) ![]() .
.
Решение.
а) D(f)=(-∞;+∞).
Находим ![]()
![]() ,
, ![]() .
.
Решаем уравнение 12-6х=0.
х=2- критическая точка 2-го рода.
![]()
Т.к. вторая производная в точке х=2 меняет знак, то при х=2 кривая имеет точку перегиба. Находим ординату этой точки: f(2)=16.
Ответ: (2;16) – точка перегиба.
б) D(f)=(-∞;+∞).
Находим ![]()
![]() ,
, ![]() .
.
Решаем уравнение ![]() .
.
х=0- критическая точка 2-го рода.
![]()
Т.к. вторая производная в точке х=0 меняет знак, то
при х=0 кривая имеет точку перегиба. Находим ординату этой точки: f(0)=-![]() .
.
Ответ: (0; -![]() ) – точка
перегиба.
) – точка
перегиба.
1.5 Асимптоты
Асимптоты – это прямые, к которым неограниченно приближается график функции.
Асимптоты бывают трёх видов: вертикальные, горизонтальные и наклонные.
1)
Прямая х=а является вертикальной асимптотой кривой y=f(x), если ![]()
![]() или
или
![]() .
.
![]()
2)
Прямая у=b является
горизонтальной асимптотой кривой y=f(x), если существует
предел ![]()
![]() или
или
![]() .
.
![]()
3) Прямая y=kx+b является наклонной асимптотой кривой y=f(x),если существуют пределы
![]()
![]() , или
, или ![]() .
.
![]()
Пример 5.
Найти асимптоты графика функции ![]() .
.
Решение.
![]() .
.
![]()
![]() , значит х=1 – вертикальная
асимптота.
, значит х=1 – вертикальная
асимптота.
Найдём наклонную асимптоту:
![]()
![]() , откуда
, откуда
![]()
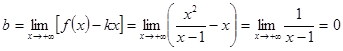 .
.
Таким
образом, прямая у=х – наклонная асимптота графика функции при ![]() . Аналогично получим, что эта
прямая является наклонной асимптотой и при
. Аналогично получим, что эта
прямая является наклонной асимптотой и при![]()
![]() .
.
Найдём горизонтальную асимптоту:
![]() ,
, ![]() ,
,
значит, горизонтальных асимптот нет.
Ответ: х=1 – вертикальная асимптота;
у=х – наклонная асимптота.
1.6 Построение графиков функций с помощью производной
Схема исследования графика функции.
1.Найти область определения функции (D(f)).
2.Определить чётность, нечётность, периодичность.
3.Найти точки пересечения графика функции с осями координат, т.е. решить уравнения х=0 и у=0.
4.Найти интервалы возрастания и убывания.
5.Найти точки экстремума, экстремумы функции.
6.Найти направление выпуклости графика, точки перегиба.
7.Найти асимптоты.
8.Построить график функции.
Пример 6.
Исследовать и построить график функции ![]() .
.
Решение.
1. ![]() .
.
2.
![]() , т.е. функция нечётная. График
данной функции симметричен относительно начала координат.
, т.е. функция нечётная. График
данной функции симметричен относительно начала координат.
Функция непериодическая.
3. Найдём точки пересечения с осью 0х: у=0
![]() , получаем х=0.
, получаем х=0.
Точка (0;0) – точка пересечения с осью 0х.
Аналогично точка (0;0) – точка пересечения с осью оу.
4. Найдём производную:
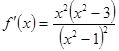 .
.
Приравняем к нулю:
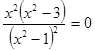 .
.
В точках х=0, х=![]() производная
равна нулю, а в точках х=
производная
равна нулю, а в точках х=![]() производная не
существует. Нанесём полученные точки на ось 0х:
производная не
существует. Нанесём полученные точки на ось 0х:
![]()
f(x) возрастает при ![]() ;
;
f(x) убывает при ![]() .
.
5.Точка
![]() - точка максимума,
- точка максимума, ![]() - максимум функции;
- максимум функции;
точка
![]() - точка минимума,
- точка минимума, ![]() - минимум функции.
- минимум функции.
6.Найдём вторую производную:
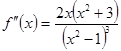 .
.
Приравняем к нулю:
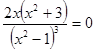 ;
;
В точке х=0 вторая производная равна нулю.
В
точках ![]() вторая производная не существует.
вторая производная не существует.
Однако
точки ![]() не принадлежат области определения
функции, поэтому точка перегиба может быть только в точке с абсциссой х=0.
не принадлежат области определения
функции, поэтому точка перегиба может быть только в точке с абсциссой х=0.
Исследуем знак второй производной и результаты запишем в таблицу:
|
х |
-∞;-1 |
-1;0 |
0 |
0;1 |
1;+∞ |
|
|
- |
+ |
0 |
- |
+ |
|
|
выпукла |
вогнута |
точка перегиба |
выпукла |
вогнута |
7.Найдём асимптоты.
![]()
![]() ,
значит х=-1 – вертикальная асимптота.
,
значит х=-1 – вертикальная асимптота.
![]()
![]() ,
значит х=1 – вертикальная асимптота.
,
значит х=1 – вертикальная асимптота.
![]()
![]() ;
;
![]()
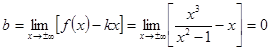 ,
значит
,
значит
у=х – наклонная асимптота.
8.На основе проведённого исследования строим график функции:
![]()
1.7 Контрольные вопросы
1).Объясните, как применяется производная для нахождения интервалов возрастания и убывания функции.
2).Сформулируйте алгоритм нахождения интервалов возрастания и убывания.
3).Какая точка называется точкой локального максимума?
4).Какая точка называется точкой локального максимума?
5).Сформулируйте необходимое условие существования экстремума.
6).Сформулируйте достаточное условие существования экстремума.
7).Какой график называется выпуклым на промежутке?
8).Какой график называется вогнутым на промежутке?
9).Сформулируйте достаточное условие выпуклости графика функции.
10).Сформулируйте достаточное условие вогнутости графика функции.
11).Какая точка называется точкой перегиба?
12).Сформулируйте необходимое условие точки перегиба.
13).Сформулируйте достаточное условие точки перегиба.
14).Дайте определение асимптоты.
15).Какие виды асимптот вы знаете?
16).Что называют вертикальной асимптотой?
17).Что называют горизонтальной асимптотой?
18).Что называют наклонной асимптотой?
19).По какой схеме производится исследование функции?
Часть 2. Практическая работа
2.1 Цели работы
![]() научиться находить
интервалы монотонности функции с помощью производной;
научиться находить
интервалы монотонности функции с помощью производной;
![]() научиться находить точки
экстремума и экстремумы функции;
научиться находить точки
экстремума и экстремумы функции;
![]() научиться находить
промежутки выпуклости и вогнутости функции, точки перегиба;
научиться находить
промежутки выпуклости и вогнутости функции, точки перегиба;
![]() научиться находить
асимптоты графика;
научиться находить
асимптоты графика;
![]() научиться исследовать
функцию с помощью производной и строить графики.
научиться исследовать
функцию с помощью производной и строить графики.
2.2 Порядок выполнения работы
2.1 Проработать теоретический материал по теме.
2.2 Ответить на контрольные вопросы.
2.3 Получить вариант задания.
2.4 Выполнить задание.
2.5 Оформить отчёт о работе.
2.3 Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное наименование работы
точное наименование работы
![]() цель работы;
цель работы;
![]() ход работы (условие задачи);
ход работы (условие задачи);
![]() результаты работы ( подробное
решение задач);
результаты работы ( подробное
решение задач);
![]() вывод
вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
2.4 Варианты заданий
Вариант 1
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]()
Вариант 2
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 3
1.Найти промежутки монотонности и экстремумы функции:
а) ![]() ; б)
; б) ![]() .
.
2. Найти промежутки вогнутости, выпуклости, точки перегиба:
а) ![]() ; б)
; б) ![]() .
.
3. Найти асимптоты графика:
![]() .
.
Вариант 4
1. Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 5
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 6
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 7
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 8
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 9
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3 Найти асимптоты графика:
![]() .
.
Вариант 10
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 11
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 12
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 13
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 14
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 15
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 16
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 17
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 18
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 19
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]() .
.
Вариант 20
1.Найти промежутки монотонности и экстремумы функции:
а)
![]() ; б)
; б) ![]() .
.
2.Найти промежутки вогнутости, выпуклости, точки перегиба:
а)
![]() ; б)
; б) ![]() .
.
3.Найти асимптоты графика:
![]()
Литература
1.Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.- М.: Высшая школа, 1997.-250 с.
3.Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4.Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5.Лунгу К.Н. Сборник задач по высшей математике. 1 курс- Москва: Айрис- пресс, 2007.- 576 с.
6.Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
7.Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
8.Шнейдер В.Е. Краткий курс высшей математики.
-М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Неопределённый интеграл. Интегрирование подстановкой и по частям.
Учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть1. Теоретическое обоснование
1. Первообразная функция
2. Понятие неопределённого интеграла
3. Основные свойства неопределённого интеграла
4.Таблица простейших интегралов
5. Основные способы интегрирования
6.Контрольные вопросы
Часть 2. Практическая работа
1. Цели работы
2. Порядок выполнения работы
3.Указания к оформлению
4. Варианты заданий
5. Приложение
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Неопределённый интеграл. Интегрирование подстановкой и по частям».
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части, т. е. студенты на более высоком уровне овладевают необходимыми умениями и знаниями, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
Критерием успешного усвоения материала является вычисление не менее 5 интегралов в своём варианте.
В результате изучения данной темы
студент должен
знать:
-понятие первообразной;
-таблицу первообразных;
-символику и определение интегрального исчисления;
-свойства неопределенного интеграла;
-методы интегрирования;
уметь:
-вычислять неопределённые интегралы с помощью таблицы первообразных;
-вычислять неопределенные интегралы методом замены переменной;
-вычислять
неопределенные интегралы по частям.
Часть 1. Теоретическое обоснование
1. Первообразная функция
Пусть функция f(x)
определена на некотором (конечном или бесконечном) интервале (a;b).
Тогда функция F(x)
называется первообразной для функции f(x)
на интервале (a;b),
если для всех ![]() :
:
|
|
Например:
функция F(x)=sinx
является первообразной для функции f(x)=cosx
на бесконечном промежутке (-∞;+∞), так как для любых х справедливо ![]() .
.
Если F(x) – первообразная для функции f(x), то функция F(x)+С, где С некоторая постоянная, также первообразная для функции f(x).
2. Понятие неопределённого интеграла
Неопределённый интеграл функции f(x) – это совокупность всех первообразных F(x)+С
для функции f(x).
Обозначается символом
![]() ,
,
где ∫ - знак интеграла; f(x) – подынтегральная функция;
f(x)dx – подынтегральное выражение.
Операция нахождения неопределённого интеграла от данной функции называется интегрированием этой функции.
Пример 1.
Проверить, что ∫3х2dx=x3+C.
Решение.
Дифференцируя
результат интегрирования ![]() , получаем
подынтегральную функцию. Следовательно, интегрирование выполнено верно.
, получаем
подынтегральную функцию. Следовательно, интегрирование выполнено верно.
3. Основные свойства неопределённого интеграла
1. ![]() .
.
2. ![]() .
.
3. ![]() , где
α≠0,
, где
α≠0,
т.е. постоянный множитель можно выносить за знак неопределённого интеграла.
4. ![]() ,
,
т.е. неопределённый интеграл от суммы равен сумме неопределённых интегралов.
5. Если ![]() , то
, то
![]() , где
а≠0.
, где
а≠0.
4.Таблица простейших интегралов
1.![]() .
.
2.![]() .
.
В
частности, ![]() .
.
3.![]()
4.![]()
В
частности, ![]()
5.![]()
6.![]() .
.
7.![]()
8.![]()
9.![]()
В
частности, ![]()
10.![]()
В
частности, ![]()
11.![]()
12.![]()
13.![]()
14.![]()
15.![]()
16.![]()
Пример 2.
Используя таблицу, найти следующие интегралы:
а)
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() ; г)
; г) ![]() ;
д)
;
д) ![]() .
.
Решение.
а) ![]()
б) 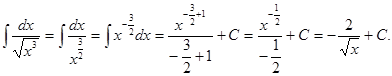
в) ![]()
г) 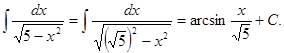
д) ![]() .
.
5. Основные способы интегрирования
1.Метод непосредственного интегрирования
заключается в использовании основных свойств неопределённого интеграла и приведении подынтегрального выражения к табличному виду.
Пример 3.
Используя таблицу и основные свойства неопределённого интеграла, найти интеграл:
а) ![]() ; б)
; б) ![]()
Решение.
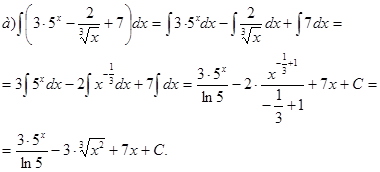
б) Почленно поделим числитель подынтегральной дроби на
знаменатель: ![]() . Отсюда
. Отсюда 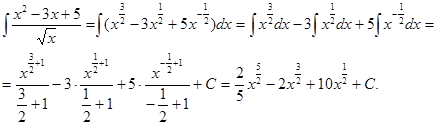
2. Метод подстановки (замена переменной)
Замена переменной в неопределённом интеграле производится с помощью подстановок двух видов:
1). х=φ(t), где φ(t) – монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид
|
|
Из
формулы следует, что для вычисления интеграла ![]()
![]() с помощью подстановки x=φ(t) надо в функции f(x) заменить х
через φ(t) и положить
с помощью подстановки x=φ(t) надо в функции f(x) заменить х
через φ(t) и положить ![]()
![]()
2). u=ψ(x), где u – новая переменная. Формула замены переменной в этом случае имеет вид
|
|
Полученные после применения той или иной подстановки интегралы должны быть более удобны для интегрирования, чем исходные.
Пример 4.
Найти интеграл, используя подходящую подстановку:
а) ![]()
![]() ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
Решение.
а) Применим подстановку t=7x-1. Тогда dt=7dx, откуда dx=1/7dt. Поэтому
![]()
Возвращаясь к переменной х, получим окончательно:
![]()
б) Подынтегральное выражение содержит сложную функцию sin(x3+1), поэтому стоит попробовать подстановку t= x3+1. Тогда dt=d(x3+1)=3x2dx, откуда x2dx=1/3dt. Таким образом,
![]()

в) Сделаем замену t=x2+1, тогда ![]()
![]() ,
,
![]() .
.
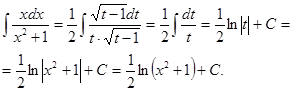
Мы избавились от знака модуля в последнем выражении, так как х2+1>0, для любых х.
Пример 5.
Найти интеграл, используя подходящую подстановку х=φ(t):
а) ![]()
![]() ; б)
; б) ![]() .
.
Решение.
а) Сделаем такую замену х=φ(t), чтобы подкоренное выражение 1-х2 стало полным квадратом. Например, x=sint. Тогда dx=costdt:
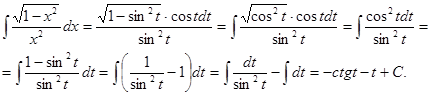 Учитывая, что t=arcsin x, получим
окончательно:
Учитывая, что t=arcsin x, получим
окончательно:
![]() б) Сделаем
замену x=t2, чтобы корни
извлекались нацело, тогда dx=2tdt, t=√x :
б) Сделаем
замену x=t2, чтобы корни
извлекались нацело, тогда dx=2tdt, t=√x :
![]()
3.Интегрирование по частям.
Интегрирование по частям называется нахождение интеграла по формуле
|
|
u=φ(x), v=ψ(x) – непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла
![]() сводится к отысканию другого
интеграла
сводится к отысканию другого
интеграла ![]() ;
;
её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом за u берётся такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так,
например, для интегралов вида ![]() , где P(x) – многочлен, за u следует принять P(x), а за dv – соответственно
выражения
, где P(x) – многочлен, за u следует принять P(x), а за dv – соответственно
выражения ![]() ;
;
для
интегралов вида ![]() за u следует принять
соответственно функции ln x, arcsin x, arcos x, а за dv – выражение P(x)dx.
за u следует принять
соответственно функции ln x, arcsin x, arcos x, а за dv – выражение P(x)dx.
Пример 6.
Найти интегралы, используя интегрирование по частям:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]()
Решение.
а) Обозначим u=x, dv=exdx; тогда du=dx, v=ex:
![]() .
.
б) Обозначим u=lnx, dv=dx; тогда ![]() , v=x:
, v=x:
![]()
в) Обозначим u=x2 , dv=cosx dx; тогда du=2xdx, v=sinx:
![]() .
.
После применения формулы получили более простой интеграл. Но для его вычисления требуется ещё раз применить этот метод:
обозначим u=2x , dv=sinxdx; тогда du=2dx, v=-cosx:
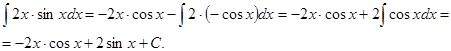 Отсюда
окончательно
Отсюда
окончательно
![]()
Пример 7.
Найти интеграл, используя интегрирование по частям:
![]()
![]()
Решение.
Обозначим u=ex, dv=cosxdx; тогда du= ex dx, v=sinx:
![]()
К интегралу, полученному в правой части равенства снова применим интегрирование по частям.
Обозначим u=ex, dv=sinxdx; тогда du= ex dx, v=-cosx:
![]() Отсюда
Отсюда
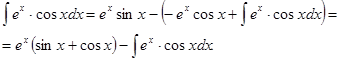
В итоге снова получили исходный интеграл. Перенесём этот интеграл в левую часть равенства, получим
![]()
![]()
Окончательно
![]()
6.Контрольные вопросы
1).Какая функция называется первообразной для данной функции f(x)?
2).Чем отличаются друг от друга различные первообразные функции для данной функции f(x)?
3).Что называется интегрированием?
4).Дайте определение неопределённого интеграла. Дайте определение подынтегральной функции и подынтегрального выражения.
5).Сформулируйте основные свойства неопределённого интеграла.
6).Перечислите основные интегралы.
7).В чем заключается метод непосредственного интегрирования неопределённого интеграла?
8).В чем заключается метод замены переменной в неопределённом интеграле?
9).В чем заключается метод интегрирования по частям в неопределённом интеграле?
Часть 2. Практическая работа
1. Цели работы
![]() научиться
находить первообразные;
научиться
находить первообразные;
![]() научиться
вычислять неопределённые интегралы с помощью таблицы первообразных;
научиться
вычислять неопределённые интегралы с помощью таблицы первообразных;
![]() научиться
вычислять неопределённые интегралы методом замены переменной;
научиться
вычислять неопределённые интегралы методом замены переменной;
![]() научиться
вычислять неопределённые интегралы с помощью интегрирования по частям;
научиться
вычислять неопределённые интегралы с помощью интегрирования по частям;
2. Порядок выполнения работы
2.1. Проработать теоретический материал по теме.
2.2. Ответить на контрольные вопросы.
2.3. Получить вариант задания.
2.4. Выполнить задание.
2.5. Оформить отчёт о работе.
3.Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное
наименование работы;
точное
наименование работы;
![]() цель работы;
цель работы;
![]() ход работы
(условие задачи);
ход работы
(условие задачи);
![]() результаты
работы ( подробное решение задач);
результаты
работы ( подробное решение задач);
![]() вывод
вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
4. Варианты заданий
Вариант 1
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Вариант 2
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Вариант 3
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б)![]() ; в)
; в) ![]() .
.
Вариант 4
1.Вычислить интегралы:
а) 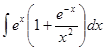 ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
Вариант 5
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)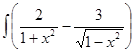 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() .
.
Вариант 6
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)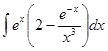 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б)![]() .
.
Вариант 7
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() ;
;
Вариант 8
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)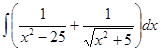 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
![]() .
.
Вариант 9
1.Вычислить интегралы:
а) 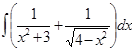 ; б)
; б) ![]() ;
в)
;
в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а)![]() ; б)
; б) 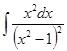 .
.
Вариант 10
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() .
.
Вариант 11
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)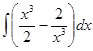 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) 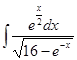 .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() .
.
Вариант 12
1.Вычислить интегралы:
а) ![]() ; б)
; б) 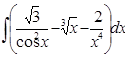 ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() .
.
Вариант 13
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() .
.
Вариант 14
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) 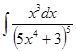 .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() .
.
Вариант 15
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)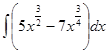 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() .
.
Вариант 16
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]()
Вариант 17
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)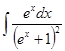 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б)![]() .
.
Вариант 18
1.Вычислить интегралы:
а) ![]() ; б)
; б)![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() .
.
Вариант 19
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)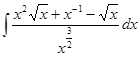 .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б)![]() .
.
Вариант 20
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ; в)
; в)![]() .
.
2.Вычислить интегралы методом подстановки:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.Вычислить интеграл методом интегрирования по частям:
а) ![]() ; б)
; б) ![]() .
.
5. Приложение
Основные производные.
1.![]() , с- const;
, с- const;
2.![]() (где
(где ![]() );
в частности,
);
в частности, ![]() ;
;
3.![]() , а>0; в частности
, а>0; в частности ![]() ;
;
4.![]() , a>0, a≠1; в
частности ,
, a>0, a≠1; в
частности , ![]()
5.(sinx)’=cosx; 6. (cosx)’=-sinx;
7.![]() ; 8.
; 8. ![]()
9.![]() ; 10.
; 10. 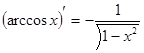
11.![]() ; 12.
; 12. ![]() ;
;
Литература
1.Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.- М.: Высшая школа, 1997.-250 с.
3.Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4.Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5.Лунгу К.Н. Сборник задач по высшей математике. 1 курс- Москва: Айрис- пресс, 2007.- 576 с.
6.Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
7.Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
8.Шнейдер В.Е. Краткий курс высшей математики.
-М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Определённый интеграл. Интегрирование подстановкой и по частям.
Учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть1. Теоретическое обоснование
1. Понятие об определенном интеграле
1.1. Теорема Ньютона–Лейбница
1.2. Основные свойства определённого интеграла
1.3. Интегрирование определенного интеграла методом подстановки
1.4. Интегрирование определенного интеграла по частям
2. Приложения определённого интеграла
2.1. Вычисление площадей плоских фигур
2.2. Вычисление объёмов тел
3.Контрольные вопросы
Часть 2. Практическая работа
2.1 Цели работы
2.2 Порядок выполнения работы
2.3 Указания к оформлению
2.4 Варианты заданий
2.5 Приложение
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Определённый интеграл. Интегрирование подстановкой и по частям».
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части, т. е. студенты будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
Критерием успешного усвоения материала является вычисление не менее 2 заданий в своём варианте.
В результате изучения данной темы
студент должен
знать:
-таблицу первообразных;
- символику и определение интегрального исчисления;
- определение определённого интеграла;
- формулу Ньютона- Лейбница;
- свойства определенного интеграла;
- методы интегрирования;
- геометрический смысл определенного интеграла;
уметь:
- вычислять определённые интегралы по формуле Ньютона- Лейбница;
- вычислять определенные интегралы методом замены переменной;
- вычислять определенные интегралы по частям;
- находить в простых случаях площади фигур и объемы тел вращения.
Часть 1. Теоретическое обоснование
1. Понятие об определенном интеграле
1.1. Теорема Ньютона–Лейбница
Теорема Ньютона – Лейбница.
Пусть f – данная функция, F – её произвольная первообразная. Тогда
|
|
Определённый интеграл – это разность значений любой первообразной функции для f)x) при верхнем и нижнем пределах интегрирования.
Алгоритм
нахождения определённого интеграла 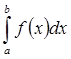 .
.
I. Найти первообразную функцию F(x) для функции f(x).
II.Вычислить значение F(x) при х=b ( b – верхний предел).
III.Вычислить значение F(x) при х=а ( а – нижний предел).
IV. Вычислить разность ![]() .
.
Пример 1.
Вычислить определённые интегралы:
а) ![]() ; б)
; б) 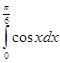 ; в)
; в) 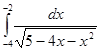 .
.
Решение.
а) 
б) 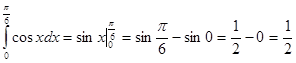 ;
;
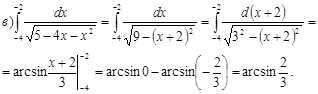
1.2. Основные свойства определённого интеграла
1.При перестановке пределов изменяется знак интеграла:
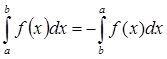 .
.
2.Интеграл с одинаковыми пределами равен нулю:
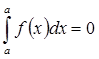 .
.
3.Переменную интегрирования можно обозначать любой буквой:
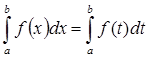 .
.
4.Определённый интеграл суммы функций равен сумме определённых интегралов этих функций:
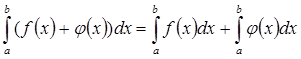 .
.
5.Постоянный множитель подынтегрального выражения можно выносить за знак определённого интеграла:
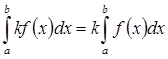 .
.
Пример 2.
Используя свойства определённого интеграла, вычислить интегралы:
а) 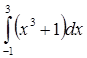 ; б)
; б) 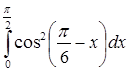 .
.
Решение. 
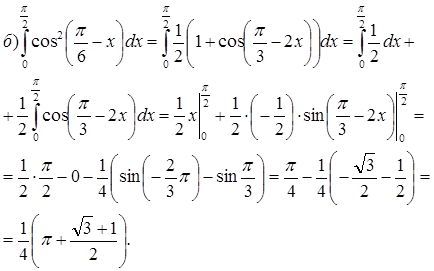
1.3. Интегрирование определенного интеграла методом подстановки
Пусть
для вычисления интеграла 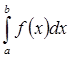 от
непрерывной функции сделана подстановка х=φ(t). Если функция
х=φ(t) и её производная
от
непрерывной функции сделана подстановка х=φ(t). Если функция
х=φ(t) и её производная
![]() непрерывны на отрезке [α,
β], причём a=φ(α), b=φ(β),
то справедлива формула:
непрерывны на отрезке [α,
β], причём a=φ(α), b=φ(β),
то справедлива формула:
|
|
Отметим, что:
1).функцию х=φ(t) следует подобрать так, чтобы, подставив её вместо х в подынтегральное выражение, получить более простой интеграл;
2).при вычислении определённого интеграла методом подстановки возвращаться к старой переменной не требуется;
3) вместо подстановки х=φ(t) применяют и подстановку t=ψ(x).
Пример 3.
С помощью подстановки вычислить интегралы:
а) ![]() ; б)
; б) 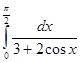 ; в)
; в) ![]() .
.
Решение.
а). Применим подстановку ![]() .
Тогда x=t2; dx=2tdt.
.
Тогда x=t2; dx=2tdt.
Находим новые пределы интегрирования:
|
x |
1 |
9 |
|
t=√x |
1 |
3 |
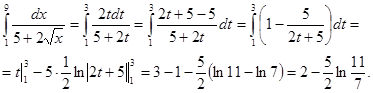
б).
Положим ![]() . Тогда получаем x= 2arctgt, dx=
. Тогда получаем x= 2arctgt, dx=![]()
Находим новые пределы интегрирования:
|
x |
0 |
|
|
t |
0 |
1 |
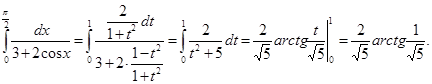 в). Полагая t=3-x, получим: x=3-t, dx=-dt. Пределы
интегрирования:
в). Полагая t=3-x, получим: x=3-t, dx=-dt. Пределы
интегрирования:
|
x |
2 |
3 |
|
t |
1 |
0 |
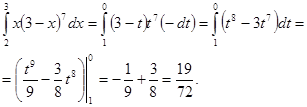
1.4. Интегрирование определенного интеграла по частям
Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a;b], то имеет место формула
|
|
Пример 4.
Вычислить интегралы с помощью формулы интегрирования по частям:
а) ![]() ; б)
; б) 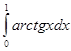 ; в)
; в) 
Решение.
а). Пусть u=lnx, dv=(x+1)dx. Тогда ![]()
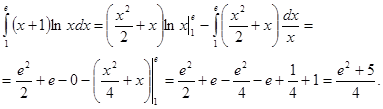
б). Пусть u=arctgx, dv=dx. Тогда ![]() Имеем
Имеем
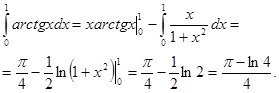
в). Пусть u=x2, dv=sin2xdx, du=2xdx, v=-1/2cos2x.
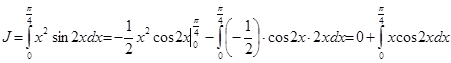 Снова
интегрируем по частям: u=x, dv=cos2xdx, du=dx, v=1/2sin2x.
Снова
интегрируем по частям: u=x, dv=cos2xdx, du=dx, v=1/2sin2x.
![]()
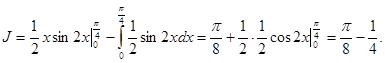
2. Приложения определённого интеграла
2.1. Вычисление площадей плоских фигур
Площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x) (f(x)≥0), слева и справа соответственно прямыми х=а и х=b, снизу отрезком [a;b] оси Ох, вычисляется по формуле
|
|
![]()
В этом и состоит геометрический смысл определённого интеграла: он численно равен площади криволинейной трапеции.
Если f(x)≤0 при хє[a;b], то
|
|
Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x), причём f1(x)≤f2(x), прямыми х=а и х=b вычисляется по формуле
|
|
Пример 5.
Вычислить площадь между кривыми y1=x2 и y2=3x.
Решение.
![]()
Найдём абсциссу точки пересечения графиков данных функций, для этого решаем уравнение: x2=3x.
Отсюда х1=0, х2=3.
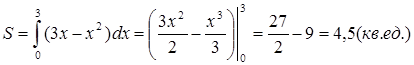
Ответ: 4,5 кв.ед.
2.2. Вычисление объёмов тел
Если криволинейная трапеция, ограниченная кривой y=f(x) и прямыми y=0, x=a, x=b, вращается вокруг оси 0x, то объём тела вращения вычисляется по формуле:
|
|
Пример 6.
Найти объём тела, образуемого вращением вокруг оси 0х сегмента параболы y=x2-4.
Решение.
Найдём точки пересечения параболы y=x2-4 с осью 0х:
x2-4=0; х1=-2, х2=2;
парабола пересекает ось 0х в точках А(-2;0) и В(2;0), построим её.
![]()
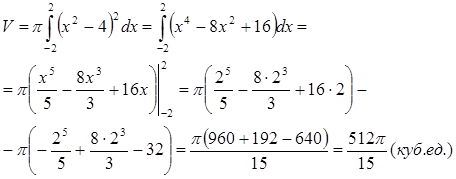 Ответ: V=
Ответ: V=![]()
Пример 7.
Найти объём тела, образованного вращением вокруг оси 0х
фигуры, ограниченной кривой y2=(x-1)3 и прямой х=2.
Решение.
![]()
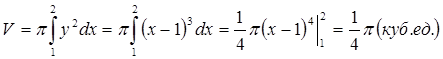 Ответ: V=
Ответ: V=![]() куб.ед.
куб.ед.
3.Контрольные вопросы
1).Сформулируйте теорему Ньютона – Лейбница.
2).Дайте определение определённого интеграла.
3).Перечислите свойства определённого интеграла.
4).При каких условиях справедлива формула замены переменной в определённом интеграле?
5).Почему при замене переменной в определённом интеграле можно не возвращаться к старой переменной?
6).Напишите формулу интегрирования по частям определённого интеграла. При каких условиях она выполняется?
7).Что называется криволинейной трапецией?
8).В чём заключается геометрический смысл определённого интеграла?
9).По какой формуле вычисляется площадь криволинейной трапеции?
10).С помощью какой формулы определяется объём тела вращения?
Часть 2. Практическая работа
2.1 Цели работы
![]() научиться
вычислять определённые интегралы с помощью таблицы первообразных;
научиться
вычислять определённые интегралы с помощью таблицы первообразных;
![]() научиться
вычислять определённые интегралы методом замены переменной;
научиться
вычислять определённые интегралы методом замены переменной;
![]() научиться
вычислять определённые интегралы с помощью интегрирования по частям;
научиться
вычислять определённые интегралы с помощью интегрирования по частям;
![]() научиться
применять определённые интегралы для вычисления площадей фигур;
научиться
применять определённые интегралы для вычисления площадей фигур;
![]() научиться
применять определённые интегралы для вычисления объёмов фигур;
научиться
применять определённые интегралы для вычисления объёмов фигур;
2.2 Порядок выполнения работы
2.1. Проработать теоретический материал по теме.
2.2. Ответить на контрольные вопросы.
2.3. Получить вариант задания.
2.4. Выполнить задание.
2.5. Оформить отчёт о работе.
2.3 Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное
наименование работы;
точное
наименование работы;
![]() цель работы;
цель работы;
![]() ход работы
(условие задачи);
ход работы
(условие задачи);
![]() результаты
работы (подробное решение задач);
результаты
работы (подробное решение задач);
![]() вывод
вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
2.4 Варианты заданий
Вариант 1
1.Вычислить интегралы:
а) ![]() ; б)
; б) 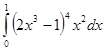 ;
;
в) 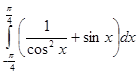 ; г)
; г) ![]() ;
д)
;
д) ![]()
2.Вычислить площадь, ограниченной линиями.
y=x2, у=2х+3.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у=х3, х=0,у=8 вокруг оси 0х.
Вариант 2
1.Вычислить интегралы:
а) 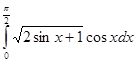 ; б)
; б) ![]() ;
;
в) 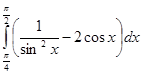 ; г)
; г) 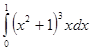 ;
д)
;
д) 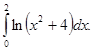
2.Вычислить площадь, ограниченной линиями.
y=x2, у=4х-3.
3.Найти
объём тела, образованного вращением фигуры, ограниченной линиями: у=![]() , х=0,у=0,х=1 вокруг 0х.
, х=0,у=0,х=1 вокруг 0х.
Вариант 3
1.Вычислить интегралы:
а) 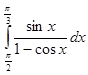 ; б)
; б) 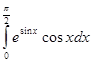 ;
;
в) 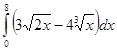 ; г)
; г) 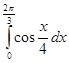 ;
д)
;
д) ![]()
2.Вычислить площадь, ограниченной линиями.
y=![]() ,
у=
,
у=![]() .
.
3.Найти
объём тела, образованного вращением фигуры, ограниченной линиями: у=![]() , х=0,х=ln2 вокруг оси 0х.
, х=0,х=ln2 вокруг оси 0х.
Вариант 4
1.Вычислить интегралы:
а) 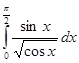 ; б)
; б) 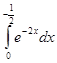 ;
;
в) 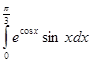 ; г)
; г) 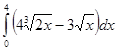 ;
д)
;
д) ![]()
2.Вычислить площадь, ограниченной линиями.
y=![]() ,
у=2х.
,
у=2х.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у=2sinx, 0≤x≤π вокруг оси 0х.
Вариант 5
1.Вычислить интегралы:
а) 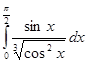 ; б)
; б) 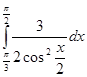 ;
;
в) 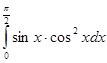 ; г)
; г) ![]() ;
д)
;
д) 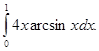
2.Вычислить площадь, ограниченной линиями.
y=x2-4x+5, у=х+5.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у2 =6x, х=3,х=5 вокруг оси 0х.
Вариант 6
1.Вычислить интегралы:
а) 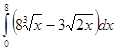 ; б)
; б)  ;
;
в) 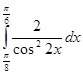 ; г)
; г) 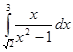 ;
д)
;
д) 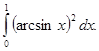
2.Вычислить площадь, ограниченной линиями.
y=x2-8x+16, у=6-х.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у =xex, х=1,y=0 вокруг 0х.
Вариант 7
1.Вычислить интегралы:
а) 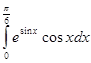 ; б)
; б) 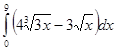 ;
;
в) 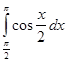 ; г)
; г) 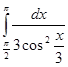 ;
д)
;
д) 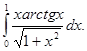
2.Вычислить площадь, ограниченной линиями.
y=x2-6x+9, у=3х-9.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у2 =4x, х=0,х=4 вокруг оси 0х.
Вариант 8
1.Вычислить интегралы:
а) 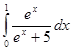 ; б)
; б) 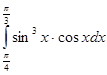 ;
;
в) ![]() ; г)
; г) 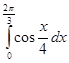 ;
д)
;
д) 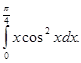
2.Вычислить площадь, ограниченной линиями.
y=![]() , у=3-х.
, у=3-х.
3.Найти
объём тела, образованного вращением фигуры, ограниченной линиями: у =![]() , х=1, x=4, y=0 вокруг 0х.
, х=1, x=4, y=0 вокруг 0х.
Вариант 9
1.Вычислить интегралы:
а) 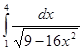 ; б)
; б) 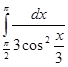 ;
;
в) 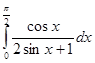 ; г)
; г) 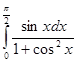 ;
д)
;
д) 
2.Вычислить площадь, ограниченной линиями.
y=x3, у=2х.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у2 =x-1, х=2,х=1 вокруг оси 0х.
Вариант 10
1.Вычислить интегралы:
а) 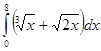 ; б)
; б) 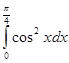 ;
;
в) ![]() ; г)
; г) 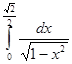 ;
д)
;
д) 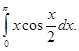
2.Вычислить площадь, ограниченной линиями.
y=-x2, у=-2-х.
3.Найти
объём тела, образованного вращением фигуры, ограниченной линиями: у =![]() , х=1,x=2, y=0 вокруг 0х.
, х=1,x=2, y=0 вокруг 0х.
Вариант 11
1.Вычислить интегралы:
а) 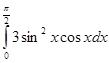 ; б)
; б) 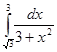 ;
;
в) 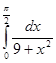 ; г)
; г) ![]() ;
д)
;
д) 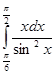
2.Вычислить площадь, ограниченной линиями.
y=sinx, у=cosх, x=0.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у2 =4x, х=2,х=4, y=0 вокруг оси 0х.
Вариант 12
1.Вычислить интегралы:
а) ![]() ; б)
; б) 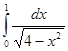 ;
;
в) ![]() ; г)
; г) 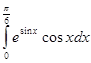 ;
д)
;
д) 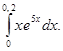
2.Вычислить площадь, ограниченной линиями.
y=1/9x2, у=1/3x+2.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у =-x2+2x, y=0 вокруг 0х.
Вариант 13
1.Вычислить интегралы:
а) 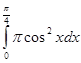 ; б)
; б) 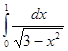 ;
;
в) ![]() ; г)
; г) ![]() ;
д)
;
д) 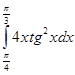
2.Вычислить площадь, ограниченной линиями.
y=x+3, у=х2+1.
3.Найти
объём тела, образованного вращением фигуры, ограниченной линиями: у2
=![]() , х=-1,х=1, y=0 вокруг оси 0х.
, х=-1,х=1, y=0 вокруг оси 0х.
Вариант 14
1.Вычислить интегралы:
а) 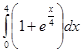 ; б)
; б) ![]() ;
;
в) 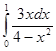 ; г)
; г) 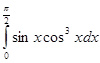 ;
д)
;
д) 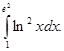
2.Вычислить площадь, ограниченной линиями.
y=x3, у=8, х=0.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у =√х, х=1, y=0 вокруг 0х.
Вариант 15
1.Вычислить интегралы:
а) 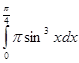 ; б)
; б) 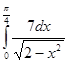 ;
;
в) 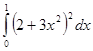 ; г)
; г) 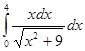 ;
д)
;
д) 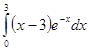
2.Вычислить площадь, ограниченной линиями
y=-x-1, у=1-х2.
3.Найти
объём тела, образованного вращением фигуры, ограниченной линиями: у=sinx, х=![]() , y=0 вокруг оси 0х.
, y=0 вокруг оси 0х.
Вариант 16
1.Вычислить интегралы:
а) ![]() ; б)
; б) ![]() ;
;
в) 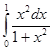 ; г)
; г) 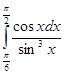 ;
д)
;
д) 
2.Вычислить площадь, ограниченной линиями
y=x2-3x+2, у=x-1.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у =2x-2, х=3, y=0 вокруг 0х.
Вариант 17
1.Вычислить интегралы:
а) 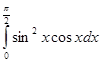 ; б)
; б)  ;
;
в) 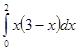 ; г)
; г) 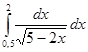 ;
д)
;
д) 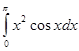
2.Вычислить площадь, ограниченной линиями
y=3-x, у=-х2+2x+3.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у=2x-x2, y=0 вокруг оси 0х.
Вариант 18
1.Вычислить интегралы:
а) ![]() ; б)
; б) 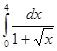 ;
;
в) 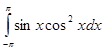 ; г)
; г) 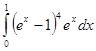 ;
д)
;
д) 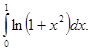
2. Вычислить площадь, ограниченной линиями
y=x2-1, у=2x+2.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у =3x-3, х=2, y=0 вокруг 0х.
Вариант 19
1.Вычислить интегралы:
а) 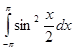 ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) 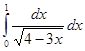 ;
д)
;
д) 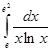
2.Вычислить площадь, ограниченной линиями
y=1-x, у=3-2x, x=0.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у=4x-x2, y=0 вокруг оси 0х.
Вариант 20
1.Вычислить интегралы:
а) ![]() ; б)
; б)  ;
;
в) ![]() ; г)
; г)  ;
д)
;
д) ![]()
2.Вычислить площадь, ограниченной линиями
y=2x, у=x-2, x=4.
3.Найти объём тела, образованного вращением фигуры, ограниченной линиями: у =9-x2, y=0 вокруг 0х.
2.5 Приложение
Основные производные.
1.![]() , с- const;
, с- const;
2.![]() (где
(где ![]() );
в частности,
);
в частности, ![]() ;
;
3.![]() , а>0; в частности
, а>0; в частности ![]() ;
;
4.![]() , a>0, a≠1; в
частности ,
, a>0, a≠1; в
частности , ![]()
5.(sinx)’=cosx; 6. (cosx)’=-sinx;
7.![]() ; 8.
; 8. ![]()
9.![]() ; 10.
; 10. 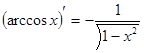
11.![]() ; 12.
; 12. ![]() ;
;
Таблица простейших интегралов.
1.![]() .
.
2.![]() .
.
В
частности, ![]() .
.
3.![]()
4.![]()
В
частности, ![]()
5.![]()
6.![]() .
.
7.![]()
8.![]()
9.![]()
В
частности, ![]()
10.![]()
В
частности, ![]()
11.![]()
12.![]()
13.![]()
14.![]()
15.![]()
16.![]()
Литература
1.Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.- М.: Высшая школа, 1997.-250 с.
3.Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4.Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5.Лунгу К.Н. Сборник задач по высшей математике. 1 курс- Москва: Айрис- пресс, 2007.- 576 с.
6.Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
7.Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
8.Шнейдер В.Е. Краткий курс высшей математики. -М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Дифференциальные уравнения
учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть 1. Теоретическое обоснование
1.Основные понятия
2.Дифференциальные уравнения первого порядка с разделяющимися переменными
3.Линейные дифференциальные уравнения
первого порядка
4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
5.Приложение дифференциальных уравнений к решению различных задач
6.Контрольные вопросы
Часть 2. Практическая работа
1. Цели работы
2. Порядок выполнения работы
3.Указания к оформлению
4. Варианты заданий
5. Приложение
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой по дисциплине «Математика» для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Дифференциальные уравнения».
Основными целями данных материалов являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
- воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данные материалы начинаются с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данных материалов, т. е. студенты будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части.
Критерием успешного усвоения материала является выполнение не менее 4 заданий практической части.
В результате изучения данной темы
студент должен
знать:
-определение дифференциального уравнения;
-понятие решения дифференциального уравнения;
-смысл задачи Коши для дифференциального уравнения;
-план решения дифференциального уравнения с разделяющими переменными;
-план решения линейного дифференциального уравнения первого порядка;
-план решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами;
уметь:
-определять вид дифференциального уравнения;
-решать дифференциальные уравнения с разделяющими переменными;
-решать линейные дифференциальные уравнения I порядка;
-решать линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами;
-показывать, что данная функция является решением дифференциального уравнения.
Часть 1. Теоретическое обоснование
1.Основные понятия
Дифференциальное уравнение – это равенство, содержащее производные или дифференциалы неизвестной функции.
Общий вид дифференциального уравнения:
F(x,y,
![]() )=0 – неявная форма, где х –
независимая переменная, у – неизвестная функция,
)=0 – неявная форма, где х –
независимая переменная, у – неизвестная функция, ![]() её
производные первого, второго и т. д. порядков.
её
производные первого, второго и т. д. порядков.
Например:
![]()
![]() .
.
Если из уравнения можно
выразить ![]() , то оно примет вид:
, то оно примет вид: ![]() =f(x,y)
– явная форма. Это уравнение первого порядка, разрешённое относительно производной.
=f(x,y)
– явная форма. Это уравнение первого порядка, разрешённое относительно производной.
Порядок дифференциального уравнения – это порядок высшей производной, содержащейся в этом уравнении.
Например,
![]() - это дифференциальное
уравнение второго порядка.
- это дифференциальное
уравнение второго порядка.
Решение дифференциального уравнения – это функция y=y(x), определённая на некотором интервале (a,b) удовлетворяющая этому уравнению, которая при подстановке в уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Общее решение – это решение, зависящее от произвольных постоянных. Оно содержит столько независимых переменных, каков порядок уравнения.
Общее решение дифференциального уравнения – это семейство функций y=φ(x,C), удовлетворяющих этому уравнению при произвольном значении постоянных С.
Например,
для дифференциального уравнения ![]() функция у=х2
будет решением, так как при её подстановке левая часть уравнения тождественно
обращается в нуль:
функция у=х2
будет решением, так как при её подстановке левая часть уравнения тождественно
обращается в нуль: ![]()
Частное решение –
это решение, получающееся из общего решения при конкретных определённых
значениях произвольных постоянных ![]() Для нахождения
частных решений задают дополнительные условия.
Для нахождения
частных решений задают дополнительные условия.
Эти условия будут называться начальными, если все они относятся к одному и тому же значению независимой переменной.
Начальные условия или
условия Коши задают значение функции у0 в фиксированной точке
х0. ![]() .
.
Пример 1.
Проверить подстановкой, что дифференциальное уравнение
![]() имеет общее решение в виде
имеет общее решение в виде
![]()
Найти частное решение, удовлетворяющее
условию у=3 при х=0.
Решение.
![]()
Подставим в дифференциальное уравнение:
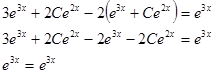
Получили тождество.
Частное решение.
![]() ; 3=е0+Се0
=> С=3
; 3=е0+Се0
=> С=3
![]() - частное решение.
- частное решение.
2. Дифференциальные уравнения первого порядка с разделяющимися переменными
Уравнение первого порядка P(x,y)dx+Q(x,y)dy=0 называется уравнением с разделяющимися переменными, если функции P и Q разлагаются на множители, зависящие каждый только от одной переменной:
![]()
Для решения этого уравнения нужно сначала
разделить переменные, а для этого разделим его члены на ![]() :
:
![]()
а затем проинтегрировать почленно полученное равенство:
![]() .
.
Пример 2.
Найти общее решение уравнения:
![]()
Решение.
Разделим
переменные в данном уравнении, деля его обе части на ![]() :
:
![]() .
.
Проинтегрируем обе части полученного равенства:
![]()
-![]() - общее
решение.
- общее
решение.
Пример 3.
Найти частное решение дифференциального уравнения
![]() при х0=2,
у0=5.
при х0=2,
у0=5.
Решение.
![]()
![]()
![]()
Есть правило: если в решении дифференциального уравнении содержится логарифм, то константу интегрирования С также записываем как lnC.
Так как lne=1, то умножим (0,5х2-х) на lne:
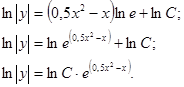
![]() - общее решение дифференциального
уравнения.
- общее решение дифференциального
уравнения.
Найдём частное решение. Для этого вычислим С
при х0=2, у0=5.
5=Се0-0 => С=5.
Частное решение: ![]() .
.
Пример 4.
Найти частное решение дифференциального уравнения
![]() при начальных условиях х0=-4,
у0=2.
при начальных условиях х0=-4,
у0=2.
Решение.
Разделим
переменные, записав предварительно, что ![]()
![]() ,
,
xdy=ydx.
Разделим обе части на ху:
![]()
Проинтегрируем обе части полученного равенства:
![]()
у=Сх – общее решение.
Найдём частное решение. Подставим в полученную формулу х0=-4, у0=2.
2=-4С=>С=-1/2.
Частное решение имеет вид: у=-1/2x.
3.Линейные дифференциальные уравнения
первого порядка
Линейное дифференциальное уравнение первого порядка – это уравнение вида:
![]() ,
,
где Р(х) и q(x) – непрерывные функции.
Линейное однородное уравнение будет, если ![]() , т.е. это уравнение вида:
, т.е. это уравнение вида:
![]()
Это
уравнение с разделяющимися переменными, и его решение будет иметь вид:![]() .
.
Линейное неоднородное уравнение будет, если функция q(x) не равна тождественно нулю:
![]()
Общее решение линейного уравнения первого порядка находится методом вариации постоянной, и имеет вид:
![]() .
.
Пример 5.
Решить
уравнение: ![]() .
.
Решение.
Это линейное неоднородное уравнение первого порядка, где P(x)=х2, и q(x)=x2.
![]() .
.
![]() .
.
Подставляем в уравнение:
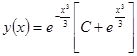 ;
;
![]()
Пример 6.
Решить уравнение: ![]() .
.
Решение.
Разделим на х: ![]() .
Это линейное неоднородное уравнение первого порядка, где P(x)=
.
Это линейное неоднородное уравнение первого порядка, где P(x)=![]() , и q(x)=
, и q(x)=![]() .
.
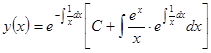
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Пример 7.
Найти частное решение уравнения cosxdy+ysinxdx=dx, если у=1 при х=0.
Решение.
Разделим все члены данного уравнения на cosxdx:
![]() ,
,
Это
линейное неоднородное уравнение первого порядка, где P(x)=tgx, и q(x)=![]() .
.
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
;
Используем начальные условия:
1=sin0+Ccosx, откуда С=1. Таким образом, искомое частное решение имеет вид: y=sinx+cosx.
4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Уравнение ![]() называется линейные однородные
дифференциальные уравнения второго порядка с постоянными коэффициентами.
называется линейные однородные
дифференциальные уравнения второго порядка с постоянными коэффициентами.
Общий интеграл находится
с помощью характеристического уравнения: ![]() ,
которое получается из этого уравнения, если заменить функцию у единицей,
а все её производные заменить соответствующими степенями к.
,
которое получается из этого уравнения, если заменить функцию у единицей,
а все её производные заменить соответствующими степенями к.
При этом:
1. Если все корни характеристического уравнения действительные и различные, то общий интеграл имеет вид:
![]()
2.
Если
характеристическое уравнение имеет корни действительные и равные к1=к2,
то ![]()
3.
Если
корни мнимые ![]() :
: ![]()
4.
Если
корни комплексные ![]() :
:
![]()
Пример 8
Решить уравнение: ![]()
Решение.
Составим характеристическое уравнение:
2k2-5k+2=0,
k1=2, k2=1/2.
Общее решение данного уравнения имеет вид:
![]() .
.
Пример 9.
Решить
уравнение: ![]()
Решение.
Составим характеристическое уравнение:
k2-8k+16=0, k1=k2=4.
Общее решение данного уравнения имеет вид:
![]() .
.
Пример 10.
Найти частное решение уравнения ![]() ,
,
при у(0)=-3, у/(0)=0.
Решение.
Составим характеристическое уравнение:
k2+4k-5=0,
k1=1, k2= -5.
Общее решение данного уравнения имеет вид:
![]() .
.
Подставим у(0)=-3: ![]() .
.
Найдём у/: ![]() .
.
Подставим у/(0)=0: ![]() .
.
Решим систему:
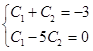
С1= -2,5; С2= -0,5.
Частное решение: ![]() .
.
5.Приложение дифференциальных уравнений к решению различных задач
Пример 11.
Найти закон движения тела по оси Ох, если оно начало двигаться из точки М(4;0) со скоростью v=2t+3t2.
Решение.
При прямолинейном движении скорость есть производная от пути по времени. Обозначив путь через х, имеем v=x/(t);
тогда
![]()
Проинтегрировав, получим х=t2+t3+C. Используя начальные условия, найдём С. Так как х=4 при t=0, то, подставив эти значения в общее решение, находим С=4. Итак, закон движения тела имеет вид х=t2+t3+4.
Пример 12.
Составить уравнение кривой, проходящей через точку М(2;-3) и имеющей касательную с угловым коэффициентом k=4х-3.
Решение.
Согласно условию, имеем
![]()
Проинтегрировав, получим у = 2х2-3х+С. Используя начальные условия, находим С=-5. Следовательно, искомое уравнение имеет вид у = 2х2-3х-5.
Пример 13.
В резервуаре с температурой 200С тело остыло за 20 минут от 100 до 600С. Найти закон охлаждения тела. Через сколько минут оно остынет до 300С? Повышением температуры резервуара пренебречь.
Решение.
Известно, что скорость охлаждения пропорциональна разности температур (закон Ньютона), следовательно,
![]()
или
![]()
откуда
![]()
При t=0 T=1000; отсюда находим, что С=80.
При t=20 минут T=600. Таким образом, ln40=20k+ln80,
откуда k=-1/20ln2.
Окончательно
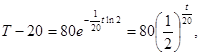
или
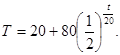
При T=300 имеем
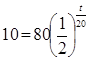
или
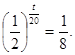
Получим t/20=3, или t=60 минут.
6.Контрольные вопросы
1).Какое уравнение называется дифференциальным?
2).Что называется решением дифференциального уравнения?
3).Какие решения дифференциального уравнения называются общим и частным?
4).Дайте определение дифференциального уравнения первого порядка с разделяющимися переменными.
5).Как решаются дифференциальные уравнения первого порядка с разделяющимися переменными?
6).Какое уравнение называется линейным дифференциальным уравнением первого порядка?
7).Как решаются линейные дифференциальные уравнения первого порядка?
8).Какое уравнение называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами?
9).Как решаются линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами?
Часть 2. Практическая работа
1. Цели работы
![]() научиться решать
простейшие дифференциальные уравнения 1 и 2 порядка.
научиться решать
простейшие дифференциальные уравнения 1 и 2 порядка.
2. Порядок выполнения работы
2.1 Проработать теоретический материал по теме.
2.2 Ответить на контрольные вопросы.
2.3 Получить вариант задания.
2.4 Выполнить задание.
2.5 Оформить отчёт о работе.
3.Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное
наименование работы;
точное
наименование работы;
![]() цель
работы;
цель
работы;
![]() ход
работы (условие задачи);
ход
работы (условие задачи);
![]() результаты
работы (подробное решение задач);
результаты
работы (подробное решение задач);
![]() вывод
вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
4. Варианты заданий
Вариант 1
1.Найти общее решение дифференциального уравнения:
а) ![]() /-2x=0; б) х2у/-2ху=3;
в)
/-2x=0; б) х2у/-2ху=3;
в) ![]() .
.
2. Найти частное решение дифференциальных уравнений:
а) ![]() ; б) ydx-xdy=xdx, у(-1)=1;
; б) ydx-xdy=xdx, у(-1)=1;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 2
1.Найти общее решение дифференциального уравнения:
а) ![]() /=3/2(x2-1); б)
/=3/2(x2-1); б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б) (y2-3x2) dy+2xydx=0, у(1)=2;
; б) (y2-3x2) dy+2xydx=0, у(1)=2;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 3
1.Найти общее решение дифференциального уравнения:
а) ![]() -xy/=0; б) у/-
2y=e3x; в)
-xy/=0; б) у/-
2y=e3x; в) ![]() .
.
2. Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 4
1.Найти общее решение дифференциального уравнения:
а) x2dx=3y2dy; б) y’-2y-3=0; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б) dy=(3x2-2x)dx, у(2)=4;
; б) dy=(3x2-2x)dx, у(2)=4;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 5
1.Найти общее решение дифференциального уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() , у(1)=e;
, у(1)=e;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 6
1.Найти общее решение дифференциального уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 7
1.Найти общее решение дифференциального уравнения:
а) (1+x2)dy-xydx=0; б) х2у/-2ху=3;
в) ![]() .
.
2. Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() , у(-1)=1;
, у(-1)=1;
в) ![]()
3. Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 8
1.Найти общее решение дифференциального уравнения:
а) y/+ytgx=0; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 9
1.Найти общее решение дифференциального уравнения:
а) ![]() ; б) у/-
; б) у/- ![]() =x; в)
=x; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
3. Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 10
1.Найти общее решение дифференциального уравнения:
а) xydx=(1+x2)dy; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ;
;
б) ![]() , у(2)=1; в)
, у(2)=1; в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 11
1.Найти общее решение дифференциального уравнения:
а) x(1+y2)dx=ydy; б) ![]() ; в)
; в) ![]() .
.
2. Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() , у(0)=1;
, у(0)=1;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 12
1.Найти общее решение дифференциального уравнения:
а) ![]() /=3/2(x2-1); б)
/=3/2(x2-1); б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б) (y2-3x2) dy+2xydx=0, у(1)=2;
; б) (y2-3x2) dy+2xydx=0, у(1)=2;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 13
1.Найти общее решение дифференциального уравнения:
а) ![]() -xy/=0; б) у/-
2y=e3x; в)
-xy/=0; б) у/-
2y=e3x; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
3. Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 14
1.Найти общее решение дифференциального уравнения:
а) x2dx=3y2dy; б) y’-2y-3=0; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б) dy=(3x2-2x)dx, у(2)=4;
; б) dy=(3x2-2x)dx, у(2)=4;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 15
1.Найти общее решение дифференциального уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() , у(1)=e;
, у(1)=e;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 16
1.Найти общее решение дифференциального уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ;
;
б) ![]() ;
;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 17
1.Найти общее решение дифференциального уравнения:
а) (1+x2)dy-xydx=0; б) х2у/-2ху=3;
в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() , у(-1)=1;
, у(-1)=1;
в) ![]()
3.Проверить подстановкой, что данная функция является общим
![]()
Вариант 18
1.Найти общее решение дифференциального уравнения:
а) y/+ytgx=0; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ;
б)
;
б) ![]() ;
;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 19
1.Найти общее решение дифференциального уравнения:
а) ![]() ; б) у/-
; б) у/- ![]() =x; в)
=x; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
Вариант 20
1.Найти общее решение дифференциального уравнения:
а)xydx=(1+x2)dy; б) ![]() ; в)
; в) ![]() .
.
2.Найти частное решение дифференциальных уравнений:
а) ![]() ;
;
б) ![]() , у(2)=1;
, у(2)=1;
в) ![]()
3.Проверить подстановкой, что данная функция является общим решением данного дифференциального уравнения:
![]()
5. Приложение
Основные производные.
1.![]() , с- const;
, с- const;
2.![]() (где
(где ![]() );
в частности,
);
в частности, ![]() ;
;
3.![]() , а>0; в частности
, а>0; в частности ![]() ;
;
4.![]() , a>0, a≠1; в
частности ,
, a>0, a≠1; в
частности , ![]()
5.(sinx)’=cosx; 6. (cosx)’=-sinx;
7.![]() ; 8.
; 8. ![]()
9.![]() ; 10.
; 10. 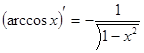
11.![]() ; 12.
; 12. ![]() ;
;
Таблица простейших интегралов.
1.![]() .
.
2.![]() .
.
В
частности, ![]() .
.
3.![]()
4.![]()
В
частности, ![]()
5.![]()
6.![]() .
.
7.![]()
8.![]()
9.![]()
В
частности, ![]()
10.![]()
В
частности, ![]()
11.![]()
12.![]()
13.![]()
14.![]()
15.![]()
16.![]()
Литература
1.Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2.Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений.-
М.: Высшая школа, 1997.-250 с.
3.Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4.Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5.Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
6.Циркунов А.Е. Справочник по математике. -С.-П.: Питер, 2000.- 160с.
7.Шнейдер В.Е. Краткий курс высшей математики. - М.: Просвещение, 1992.- 328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Элементы комбинаторики
Элементы теории вероятностей
учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть 1. Теоретическое обоснование
1.1 Элементы комбинаторики
1.1.1 Основные понятия
1.1.2 Размещения
1.1.3 Перестановки
1.1.4 Сочетания
1.1.5 Бином Ньютона
1.2 Элементы теории вероятностей
1.2.1 Введение
1.2.2 Основные термины и понятия теории вероятностей
1.2.3 Определение вероятности события
1.2.4 Теорема, сложения вероятностей
1.2.5 Теорема умножения вероятностей
1.2.7 Схема испытаний Бернулли.
Контрольные вопросы
Часть 2. Практическая работа
2.1. Цели работы
2.2. Порядок выполнения работы
2.3.Указания к оформлению
2.4. Варианты заданий
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой по дисциплине «Математика» для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Элементы комбинаторики.
Элементы теории вероятностей».
Основными целями данного пособия являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
-формирование представления о математике как форме описания и методе познания действительности.
Данное пособие начинается с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данного пособия, т. е. студенты, будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части данного пособия.
Критерием успешного усвоения материала является выполнение не менее 3 заданий практической части.
В результате изучения данной темы
студент должен
знать:
-основные понятия комбинаторики: факториал, размещения, сочетания, перестановки;
-понятие события;
-классическое определение вероятности;
-теоремы сложения, умножения вероятностей;
-формулу Бернулли;
уметь:
-находить перестановки, размещения, сочетания;
-подсчитывать вероятность события, пользуясь классическим определением вероятности и простейшими комбинаторными схемами;
-находить вероятность наступления события, используя теоремы сложения и умножения вероятностей;
-находить вероятность наступления события, используя формулу Бернулли.
Часть 1. Теоретическое обоснование
1.1 Элементы комбинаторики
1.1.1 Основные понятия
Комбинаторика–раздел дискретной математики, посвящённый решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными свойствами.
Дискретная математика – это область математики, в которой изучаются свойства структур конечного характера.
Группы, составленные из каких–либо элементов, называются соединениями.
Различают три вида соединений: размещения, перестановки и сочетания.
1.1.2 Размещения
Размещениями из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их следования.
Число размещений из n
элементов по m обозначается символом ![]() и вычисляется по формуле:
и вычисляется по формуле:
![]()
Пример 1.
Найти число размещений: 1) из 10 элементов по 4; 2) из n+4 элементов по n-2.
Решение.
По формуле размещений получим
1) ![]()
2) 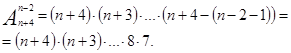
Пример 2.
Решить уравнение ![]()
Решение.
Перепишем уравнение в виде
![]()
Так как n≥6, разделим обе части на
![]()
![]()
Отсюда n=6; n=25.
1.1.3 Перестановки
Перестановками из n элементов называются такие соединения, которые отличаются друг от друга лишь порядком следования элементов.
Число перестановок из n элементов обозначается символом Pn.
Перестановки представляют собой частный случай размещения из n элементов по n в каждом, т.е.:
![]()
Таким образом, число всех перестановок из n элементов равно произведению последовательных натуральных чисел от 1 до n включительно.
Такое произведение обозначается n! и читается «n- факториал», причём 0!=1, 1!=1.
Поэтому Pn=n!
Используя обозначение факториала, формулу размещений можно переписать в следующем виде:
![]()
При решении задач удобно использовать равенство:
![]()
Пример 3
Составить все возможные перестановки из элементов:1)1;
2) 5,6;3) a,b,c
Решение.
1) P1=1;
2) (5;6), (6;5): P1=1∙2=2;
3) (a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a); P3=1∙2∙3=6.
1.1.4 Сочетания
Сочетаниями из n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n
элементов по m обозначается символом ![]()
и вычисляется по формуле:
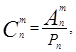
которую можно записать также в виде:
![]()
или
![]()
По определению полагают
![]()
Кроме того, при решении задач используются формулу, выражающие основные свойства сочетаний:
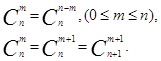
Пример 4.
Вычислить значения выражений: 1) 5!+6!; 2) ![]()
3)
![]()
Решение.
1) 5!+6!=5∙4∙3∙2∙1+6∙5∙4∙3∙2∙1=120+720=840;
2)
![]()
3)
![]()
![]()
1.1.5 Бином Ньютона
Из элементарной математики хорошо известны формулы сокращенного умножения:
![]()
![]()
Эти формулы можно записать так:
![]()
![]()
Имеет место и общая закономерность:
![]()
Это равенство и называется биномом Ньютона.
Пример 5.
Найти четвёртый член разложения (a+3)7.
Решение.
![]()

1.2 Элементы теории вероятностей
1.2.1 Введение
Теория вероятностей — это раздел математики изучающий закономерности массовых случайных событий.
Случайным называется событие, наступление которого нельзя гарантировать. Случайность того или иного события определяется множеством причин, которые существуют объективно, но учесть их все, а также степень их влияния на изучаемое событие, невозможно. К таким случайным событиям относятся: выпадение того или иного числа при бросании игральной кости, выигрыш в лотереи, количество больных записавшихся на прием к врачу и. т.п.
И хотя в каждом конкретном случае трудно предсказать исход испытания, при достаточно большом числе наблюдений можно установить наличие некоторой закономерности. Подбрасывая монету можно заметить, что число выпадения орла и решки примерно одинаково, а при бросании игральной кости, различные грани, также появляются, примерно одинаково. Это говорит, что случайным явлениям присущи свои закономерности, но они проявляются лишь при большом количестве испытаний. Правильность этого подтверждает закон больших чисел, который лежит в основе теории вероятностей.
1.2.2 Основные термины и понятия теории вероятностей
Испытанием называется совокупность условий, при котором может произойти данное случайное событие.
Событие - это факт, который при осуществлении определенных условий может произойти или нет. События обозначают большими буквами латинского алфавита А, В, С...
Например, событие А—рождение мальчика, событие В-выигрыш в лотерее, событие С-выпадение цифры 4 при бросании игральной кости.
События бывают достоверные, невозможные и случайные.
Достоверное событие-это событие, которое в результате испытания непременно должно произойти.
Например, если на игральной кости на всех 6 гранях нанести цифру 1, тогда выпадение цифры 1, при бросании кости, есть событие достоверное.
Невозможное событие — это событие, которое в результате испытания не может произойти.
Например, в ранее рассмотренном примере - это выпадение любой цифры, кроме 1.
Случайное событие - это событие, которое при испытаниях может произойти или не произойти. Те или иные события реализуются с различной возможностью.
Например, завтра днем ожидается дождь. В этом примере наступление дня является испытанием, а выпадение дождя - случайное событие.
События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого.
Например, при бросании монеты выпадение одновременно орла и решки есть события несовместные.
События называются совместными, если в результате данного испытания появление одного из них не исключает появление другого.
Например, при игре в карты появление валета и масти пик - события совместные
События называются равновозможными, если нет оснований считать, что одно из них происходит чаще, чем другое.
Например, выпадение, любой грани игрального кубика есть равновозможные события.
Два несовместных события А и ![]() (читается
«не А») называются
противоположными, если в результате испытания одно из них должно обязательно
произойти.
(читается
«не А») называются
противоположными, если в результате испытания одно из них должно обязательно
произойти.
Например, если стипендия начисляется только при получении на экзамене хороших и отличных оценок, то события «стипендия» и «неудовлетворительная или удовлетворительная оценка» - противоположные.
Событие А называется благоприятствующим событию В, если появление события А влечет за собой появление события В.
Например, при бросании игрального кубика - появлению нечетного числа благоприятствуют события, связанные с выпадением чисел - 1, 3 и 5.
1.2.3 Определение вероятности события
Случайные события реализуются с различной возможностью. Одни происходят чаще, другие реже. Для количественной оценки возможностей реализации события вводится понятие вероятности события.
Вероятность события - это число, характеризующее степень возможности появления событий при многократном повторении событий.
Вероятность обозначается буквой Р (probability (англ.) -вероятность). Вероятность является одним из основных понятий теории вероятностей.
Классическое определение вероятности заключается в следующем. Если известны все возможные исходы испытания и нет оснований считать, что одно случайное событие появлялось бы чаще других, т.е. события равновозможны и несовместны, то имеется возможность аналитического определения вероятности события.
Вероятностью Р(А) события А называется отношение числа благоприятствующих исходов т к общему числу равновозможных несовместных исходов п .
Свойства вероятности:
1. Вероятность случайного события А находится между.
|
|
|
2. Вероятность достоверного события равна 1. |
|
|
|
3. Вероятность невозможного события равна 0. |
|
|
0и1.
Пример 6.
Найти вероятность выпадения числа кратного 3 при одном бросании игрального кубика.
Решение:
Событие А выпадение числа кратного 3. Этому событию благоприятствуют два исхода: числа 3 и 6, т.е. m=2.
Общее число исходов состоит в выпадении чисел: 1,2,3,4,5, 6,
т.е. п=6. Очевидно, что эти события равновозможны. Тогда искомая вероятность, по определению, равна отношению числа благоприятствующих исходов к числу всех исходов.
![]()
Пример 7.
В урне 10 белых, 5 красных и 5 зеленых шаров. Найти вероятность того, что вынутый наугад шар будет цветным (не белым).
Решение:
![]() Число исходов, благоприятствующих событию А, равно
сумме красных и зеленых шаров: т=10. Общее число равновозможных несовместных исходов равно общему числу шаров в
урне: п=20. Тогда:
Число исходов, благоприятствующих событию А, равно
сумме красных и зеленых шаров: т=10. Общее число равновозможных несовместных исходов равно общему числу шаров в
урне: п=20. Тогда:
1.2.4 Теорема, сложения вероятностей
Зная вероятности одних событий можно вычислить вероятности других событий, если они связаны между собой. Теорема сложения вероятностей позволяет определить вероятность появления одного из нескольких случайных событий.
Теорема.
Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий:
![]()
Следствие.
Сумма вероятностей противоположных событий равна единице.
Пример 8.
Найти вероятность выпадения цифры 2 или 3 при бросании игральной кости.
Решение:
Событие А-выпадение цифры 2, вероятность этого события Р(А)=1/6. Событие В-выпадение цифры 3, вероятность этого события Р(В =1/6. События несовместные, поэтому
![]()
Пример 9.
Получена партия одежды в количестве 40 штук.
Из них 20 комплектов мужской одежды, 6-женской и 14-детской. Найти вероятность того, что взятая наугад одежда окажется не женской.
Решение:
Событие А-одежда мужская,
![]() вероятность
вероятность
|
|
|
|
|
Событие С- одежда детская
|
![]()
![]()
|
Событие В-одежда женская, |
![]()
В том случае, если события А и В являются совместными, то справедлива следующая теорема.
Теорема.
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т. е.
![]()
Пример 10 .
Вероятность попадания в мишень одного стрелка равна 0,65, а второго 0,6. Определить вероятность поражения мишени при одновременных выстрелах двух стрелков.
Решение:
Так как при стрельбе возможно попадание в мишень двумя стрелками, то эти события совместные, следовательно,
![]()
1.2.5 Теорема умножения вероятностей
Событие А называется независимым от события В, если вероятность осуществления события А не зависит от того произошло событие В или нет
Например, при повторении бросания игральной кости вероятность выпадения цифры 1 (событие A) не зависит от появления или не появления цифры 1 при первом бросании кости (событие B).
Событие А называется зависимым от события В если его вероятность меняется в зависимости от того, произошло событие В или нет.
Например, если в урне находятся черные и белые шары, то вероятность повторного появления черного шара (событие А) будет зависеть от того, какой шар вынули первый раз.
В случае зависимых событий А и В вводится понятие условной вероятности, под которой понимается вероятность события А при условии, что событие В произошло. Обозначается Р(А/В).
Пример 11.
В урне находится 10 шаров: 3 белых и 7 черных. Первым был вынут черный шар, найти вероятность того, что второй шар будет черным.
Решение:
Вероятность появления черного шара первый раз (событие В) равно Р(В)=3/10; а вероятность появления его второй раз
(событие А), при условии, что событие В произошло, равно Р(А/В)=2/9, т.к. в урне осталось 9 шаров, из них 2 черных.
Рассмотрим закон умножения вероятностей для независимых событий.
Произведением двух событий А и В называют событие С, состоящее в совместном осуществлении этих событий.
Теорема.
Вероятность произведения 2 независимых событий А и В равна произведению вероятностей этих событий:
![]()
![]() Этот закон справедлив и для п независимых событий
Этот закон справедлив и для п независимых событий
|
|
Пример 12.
В билете 3 раздела. Из 40 вопросов первого раздела студент знает 30 вопросов, из 30 вопросов второго-15, из 30 вопросов третьего-10. Определить вероятность правильного ответа студента по билету.
Решение:
Учитывая, что ответ на каждые разделы есть независимые
события A1, A2, A3, а их вероятности соответственно равны:
![]()
Тогда вероятность правильного ответа на билет Р(В), можно найти по формуле
![]()
Теорема.
Вероятность произведения двух зависимых событий А и В
равна произведению одного из них на условную вероятность второго, вычисленную при условии, что первое событие осуществилось.
![]()
Пример 13.
В группе из 20 человек, 5 студентов не подготовили задание. Какова вероятность того, что два первых студента, вызванные наугад, будут не готовы к ответу.
Решение:
Вероятность того, что первый студент не готов к ответу Р(А)=5/20, вероятность того, что и второй студент также не подготовлен, как и первый, Р(В/А)=4/19,. тогда для ответа на вопрос воспользуемся формулой:
![]()
События А1,А2,...,Ап называются независимыми
в совокупности, если каждое из этих событий и событие,
равное произведению любого числа остальных событий,
независимы.
Теорема.
Вероятность появления хотя бы одного из событий А1,А2,...,Ап, независимых, в совокупности, равна разности между единицей и
произведением вероятностей противоположных событий
![]()
![]()
Пример 14.
В трех театральных кассах продаются билеты. Вероятность наличия билетов за час до начала спектакля в первом театре равна 0,7; в кассе второго-0,3; а в кассе третьего-0,5. Какова вероятность того, что за час до начала спектакля имеется возможность купить билет хотя бы в одной кассе.
Решение:
Событие А-возможность купить билеты хотя бы в одной кассе.
![]() Тогда событие противоположное обозначим
Тогда событие противоположное обозначим ![]() . Оно
наступит тогда, когда наступит событие
. Оно
наступит тогда, когда наступит событие ![]() . Тогда
. Тогда
Пример 15.
Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго-0,8.
Найти вероятность того, что при одном залпе в мишень попадает только один стрелок.
Решение:
Вероятность того, что в мишень попадает первый стрелок и не
попадает второй, равна:
![]()
Вероятность того, что попадет второй стрелок в мишень и не
![]() попадет первый, равна:
попадет первый, равна:
Вероятность того, что в мишень попадёт только один стрелок, равна сумме этих вероятностей:
![]()
1.2.6 Формула полной вероятности. Формула Байеса
Следствием основных законов сложения и умножения,
вероятностей является формула полной вероятности.
Пусть требуется найти вероятность некоторого события В, которое может произойти вместе с одним из событий А1, А2, ... Ап, образующих полную группу несовместных событий. Так как события А1,А2,...Ап образуют полную группу, то событие В может произойти только в комбинации с каким-либо из них:
![]()
Так как событие Аг, А7,... Ап, несовместны, то и комбинации A1B А2В, АnВ несовместны.
Согласно закона сложения несовместных событий, имеем:
каждое из слагаемых является вероятностью произведения двух зависимых событий.
![]()
Пример 16.
Имеются три урны: в первой из них 5 белых шаров и 4 черных; во второй — 3 белых и 6 черных; в третьей -2 белых и 7 черных. Из выбранной наугад урны вынимают шар. Он оказался черным. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.
Решение:
А1-выбор первой урны; А2-выбор второй урны; A3-выбор третьей урны. До опыта все гипотезы равновероятны:
![]()
Событие В-появление черного шара. Условные вероятности
![]()
![]()
![]()
Таким образом, наиболее вероятным был выбор третьей урны.
1.2.7 Схема испытаний Бернулли.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0<p<1), событие наступит ровно k раз (безразлично, в какой последовательности), есть
![]() ; (где q=1-p).
; (где q=1-p).
Вероятность того, что событие наступит:
а) менее к раз: Рn(0)+Pn(1)+…+Pn(k-1),
б) более к раз: Рn(к+1)+Pn(к+2)+…+Pn(n),
в) не менее к раз: Рn(к)+Pn(к+1)+…+Pn(n),
г) не более к раз: Рn(0)+Pn(1)+…+Pn(к).
Пример 17.
Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3–блондином, с вероятностью 0,4–шатеном и с вероятностью 0,1–рыжим. Какова вероятность того, что среди пяти случайно встреченных лиц: а) не менее четырёх блондинов; б) два блондина и три шатена; в) хотя бы один рыжий?
Решение:
а) ![]()
б) 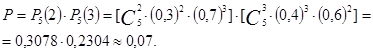
в)
![]()
Контрольные вопросы
1). Дать определение комбинаторики.
2). Что называется соединением?
3). Какие виды соединений бывают?
4). Дать определение размещения. Привести примеры.
5). Дать определение перестановки. Привести примеры.
6). Дать определение сочетания. Привести примеры.
7). Записать формулу бинома Ньютона.
8). Дать классическое определение вероятности.
9). Дать определение основных понятий теории вероятности.
10). Сформулируйте теорему сложения вероятностей совместных событий.
11). Чему равна сумма вероятностей двух противоположных событий?
12). Что называется условной вероятностью событий?
13). Какие события в совокупности называются независимыми?
14).Сформулируйте теорему умножения вероятностей независимых событий.
15). Сформулируйте теорему умножения вероятностей зависимых событий.
16). Запишите формулу Бернулли. Когда она используется?
Часть 2. Практическая работа
2.1. Цели работы
![]() научиться
применять формулы размещений сочетаний, перестановок для решения задач;
научиться
применять формулы размещений сочетаний, перестановок для решения задач;
![]() научиться
находить классическую вероятность события;
научиться
находить классическую вероятность события;
![]() научиться
применять теоремы сложения и умножения вероятностей для решения задач;
научиться
применять теоремы сложения и умножения вероятностей для решения задач;
2.2. Порядок выполнения работы
2.1. Проработать теоретический материал по теме.
2.2. Ответить на контрольные вопросы.
2.3. Получить вариант задания.
2.4. Выполнить задание.
2.5. Оформить отчёт о работе.
2.3.Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное
наименование работы;
точное
наименование работы;
![]() цель работы;
цель работы;
![]() ход работы
(условие задачи);
ход работы
(условие задачи);
![]() результаты
работы (подробное решение задач);
результаты
работы (подробное решение задач);
![]() вывод
вывод
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
2.4. Варианты заданий
Вариант 1
1. Найти значение выражения:
а) 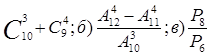
2. Решить уравнение:
![]()
3. Найти четвёртый член разложения (a+3)7
4. Случайным образом выбрали двузначное число. Найти вероятность того, что оно заканчивается нулём.
5. В урне находится 7 белых и 5 чёрных шаров. Найти вероятность того, что наудачу вынутый шар окажется чёрным.
Вариант 2
1. Найти значение выражения:
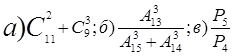
2. Решить уравнение:
![]()
3. Найти девятый член разложения:(a+√b)12
4. Случайным образом выбрали двузначное число. Найти вероятность того, что оно состоит из одинаковых цифр.
5. В урне находится 7 белых и 5 чёрных шаров. Найти вероятность того, что два наудачу вынутых шаров окажутся чёрными.
Вариант 3
1. Найти значение выражения:
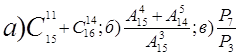
2. Решить уравнение:
![]()
3. Найти шестой член разложения: (a2+b3)13
4. Случайным образом выбрали двузначное число. Найти вероятность того, что оно больше27 и меньше 46.
5. В ящике находятся 4 одинаковых пары перчаток чёрного цвета и 7 пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлечённые перчатки образуют пару.
Вариант 4
1. Найти значение выражения:

2. Решить уравнение:
![]()
3. Найти средний член разложения: (√a-√b)8
4. Случайным образом выбрали двузначное число. Найти вероятность того, что оно не является квадратом целого числа.
5. В урне находится 3 белых и 6 чёрных шаров. Найти вероятность того, что среди трёх извлечённых шаров не менее двух белых.
Вариант 5
1. Найти значение выражения:
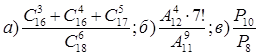
2. Решить уравнение:
![]()
3. Найти пятый член разложения: (x√x-1)14
4. Двузначное число составили из цифр 0,1,2,3,4. Какова вероятность того, что это число чётное.
5. В урне находится 4 белых и 5 чёрных шара. Три шара последовательно извлекаются без возвращения их в урну. Найти вероятность того, что третий по счёту шар окажется белым.
Вариант 6
1. Найти значение выражения:
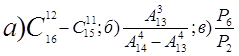
2. Решить уравнение:
![]()
3.
Найти
четвёртый член разложения: ![]()
4. Двузначное число составили из цифр 0,1,2,3,4. Какова вероятность того, что это число нечётное.
5. Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3–блондином, с вероятностью 0,4–шатеном и с вероятностью 0,1–рыжим. Какова вероятность того, что среди трёх случайно встреченных лиц: не менее двух брюнетов?
Вариант 7
1. Найти значение выражения:
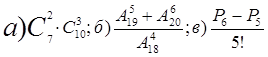
2. Решить уравнение:
![]()
3.
Найти
третий член разложения: ![]()
4. Двузначное число составили из цифр 0,1,2,3,4. Какова вероятность того, что это число делится на 5.
5. Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3–блондином, с вероятностью 0,4–шатеном и с вероятностью 0,1–рыжим. Какова вероятность того, что среди трёх случайно встреченных лиц один блондин и два шатена?
Вариант 8
1. Найти значение выражения:
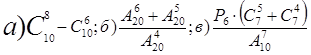
2. Решить уравнение:
![]()
3.
Найти
пятый член разложения: ![]()
4. Двузначное число составили из цифр 0,1,2,3,4. Какова вероятность того, что это число делится на 4.
5. Случайно встреченное лицо с вероятностью 0,2 может оказаться брюнетом, с вероятностью 0,3–блондином, с вероятностью 0,4–шатеном и с вероятностью 0,1–рыжим. Какова вероятность того, что среди трёх случайно встреченных лиц: хотя бы один рыжий?
Вариант 9
1. Найти значение выражения:
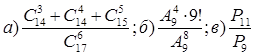
2. Решить уравнение:
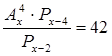
3. Найти член разложения (x+y)9, содержащий x7.
4. Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что обе они согласные.
5. Игральную кость подбрасывают 15 раз. Какова вероятность того, что цифра 1 при этом выпадет 8 раз?
Вариант 10
1. Найти значение выражения:
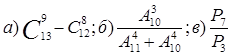
2. Решить уравнение:
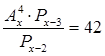
3. Найти член разложения (√a+b)9, содержащий a3.
4. Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что среди них есть «ъ».
5. Пусть вероятность того, что телевизор потребует ремонта в течении гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из трёх телевизоров не более одного потребует ремонта?
Вариант 11
1. Найти значение выражения:
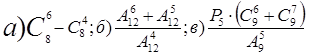
2. Решить уравнение:
![]()
3. Найти член разложения (√f+d)9, содержащий d4.
4. Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что среди них нет «ъ».
5. Вероятность наступления события в каждом из 10 независимых испытаний равна 0,2. Найти вероятность того, что событие произойдёт 7 раз?
Вариант 12
1. Найти значение выражения:
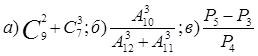
2. Решить уравнение:
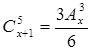
3. Вычислите коэффициент при x5 в разложении (1+x)7.
4. Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что одна из них гласная, а другая согласная.
5. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 18 новорождённых окажется 8 мальчиков?
Вариант 13
1. Найти значение выражения:
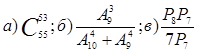
2. Решить уравнение:
![]()
3. Вычислите коэффициент при x17 в разложении (1+x5)7.
4. В группе 12 студентов, среди которых 8 отличников. По списку наудачу выбраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.
5. Слово «лотос» составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой три буквы. Какова вероятность того, что при этом появится слово «сто»?
Вариант 14
1. Найти значение выражения:
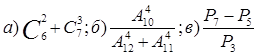
2. Решить уравнение:
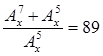
3. Вычислите коэффициент при x6 в разложении (1+x2)5.
4. Какова вероятность того, что наудачу выбранное целое число от 40 до 70 является кратным 6?
5. Монету бросают 5 раз. Найти вероятность того, что «герб » выпадет менее 2 раз?
Вариант 15
1. Найти значение выражения:
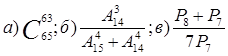
2. Решить уравнение:
![]()
3. Найти четвёртый член разложения:(8x-5y)6
4. В урне лежит 12 белых и 8 красных шаров. Вынули 8 шаров. Какова вероятность того, что три из них красные?
5. Вероятность выиграть по лотерейному билету равна 1/7. Найти вероятность выиграть не менее чем по двум билетам из шести?
Вариант 16
1. Найти значение выражения:
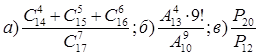
2. Решить уравнение:
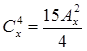
3. Найти пятый член разложения:(5a-2b)9
4. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 2 женщины и 3 мужчины?
5. Монету бросают 5 раз. Найти вероятность того, что «герб » выпадет не менее 2 раз?
Вариант 17
1. Найти значение выражения:
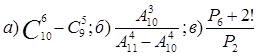
2. Решить уравнение:
![]()
3. Написать разложение (x+a)8
4. На пяти карточках написано по одной цифре из набора 1,2,3,4,5. Наугад выбирают одну за другой две карточки. Какова вероятность того, что число на второй карточке будет больше, чем на первой?
5. Пусть вероятность того, что наудачу взятая деталь нестандартная, равна 0,1. Найти вероятность того, что среди взятых наудачу 5 деталей не более 3 нестандартных?
Вариант 18
1. Найти значение выражения:
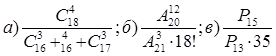
2. Решить уравнение:
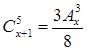
3. Найти третий член разложения:(2b-3c)9
4. Собрание, на котором присутствует 30 человек, в том числе 12 женщин, выбирает делегацию из 10 человек. Найти вероятность того, что в делегацию войдут 6 женщин и 4 мужчины?
5. Вероятность попадания при каждом выстреле равна 0,4. Найти вероятность разрушения объекта, если для этого необходимо не менее трёх попаданий, а сделано 15 выстрелов?
Вариант 19
1. Найти значение выражения:
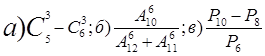
2. Решить уравнение:
![]()
3. Найти член разложения (y+y2)7, содержащий y10.
4. Собрание, на котором присутствует 20 человек, в том числе 8 женщин, выбирает делегацию из 6 человек. Найти вероятность того, что в делегацию войдут 4 женщины и 2 мужчины?
5. Найти вероятность того, что в семье, имеющей 6 детей, не более 2 девочек. Вероятности рождения девочек и мальчиков одинаковые.
Вариант 20
1. Найти значение выражения:
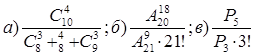
2. Решить уравнение:
![]()
3. Найти пятый от конца член разложения (2b-1,5c)7.
4. Брошены два одинаковых кубика. Найти вероятность того, что цифра 6 появится хотя бы на одной грани?
5. Слово «карета» составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают одну за другой буквы. Какова вероятность того, что при этом появится слово «ракета»?
Литература
1 Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений. М.: Высшая школа, 1997.-250 с.
3. Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4. Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5. Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
6. Циркунов А.Е. Справочник по математике.- С.-П.: Питер, 2000.-160с.
7. Шнейдер В.Е. Краткий курс высшей математики -М.: Просвещение, 1992.-328 c.
БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина»
И.В. Калинина
Определители и матрицы
учебно-методические материалы по дисциплине
«Математика» для студентов 2-го курса специальностей
отделения подготовки специалистов среднего звена
Оглавление
Введение
Часть 1. Теоретическое обоснование
1.1 Матрица
1.1.1 Основные понятия
1.1.2 Операции над матрицами
1.2. Определители
1.2.1 Определители n-го порядка
1.2.2 Методы вычисления определителей
1.3 Обратная матрица. Матричные уравнения
1.3.1 Обратная матрица
1.3.2 Матричные уравнения
1.4 Системы линейных уравнений
1.4.1 Исследование систем линейных уравнений
1.4.2 Различные способы решения систем линейных уравнений
Часть 2. Практическая работа
2.1 Цели работы
2.2 Порядок выполнения работы
2.3 Указания к оформлению
2.4 Варианты заданий
Литература
Введение
Данные материалы написаны в соответствии с действующей рабочей программой по дисциплине «Математика» для студентов БПОУ ВО «Череповецкий строительный колледж имени А. А. Лепехина».
Данные материалы предназначены для студентов II курса специальностей отделения подготовки специалистов среднего звена и содержат теоретическое обоснование и практическую работу по теме: «Определители и матрицы».
Основными целями данного пособия являются:
-прочное и сознательное овладение студентами математическими знаниями и умениями, необходимыми для успешного усвоения математики и использование её при изучении обще профессиональных и специальных дисциплин, в курсовом и дипломном проектировании;
-развитие логического и алгоритмического мышления;
-воспитание умений действовать по заданному алгоритму и конструировать новые;
- формирование представления о математике как форме описания и методе познания действительности.
Данное пособие начинается с необходимого минимума теоретического материала, изучение которого позволит более успешно выполнять контрольные задания, расположенные во второй части данного пособия, т. е. студенты, будут более прочно овладевать необходимыми умениями и навыками, которые потом они могут использовать на уроках спецдисциплин.
После теоретического изложения материала приведены контрольные вопросы по теме, ответы на которые являются обязательным условием начала выполнения студентами практической части данного пособия.
Критерием успешного усвоения материала является выполнение не менее 3 заданий практической части.
В результате изучения данной темы
Студент должен
знать:
-понятие о матрице;
-операции над матрицами;
-понятие определителя;
-свойства определителей;
-метод Гаусса;
-формулы Крамера;
уметь:
-выполнять операции над матрицами;
-вычислять определители;
-вычислять обратную матрицу;
-решать системы уравнений методом Гаусса, Крамера и матричным способом.
Часть 1. Теоретическое обоснование
1.1 Матрица
1.1.1 Основные понятия
Матрицей называется прямоугольная таблица из чисел, содержащая m строк и n столбцов:
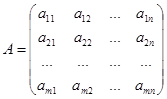
Её элементы–числа aij; i=1,…,m; j=1,…,n.
Первый индекс i указывает номер строки, в котором расположен элемент, а j-номер столбца.
Например
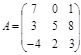
Квадратной матрицей называется матрица, в которой число строк совпадает с числом столбцов.
Диагональной матрицей называется квадратная матрица, у которой все элементы вне главной диагонали (т.е. с индексами i≠j) равны нулю.
Единичной (обозначается E) называется диагональная матрица с единицами на главной диагонали.
Нулевой называется матрица, все элементы которой равны нулю.
Примеры матриц:
а) 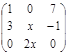 - квадратная; б)
- квадратная; б) ![]() - диагональная;
- диагональная;
в). 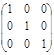 - единичная; г)
- единичная; г) ![]() - нулевая.
- нулевая.
1.1.2 Операции над матрицами
Суммой матриц A=(aij) и B=(bij) одинакового размера называется матрица C=(cij)того же размера, причём cij=aij+bij, для любых i,j.
Свойства операции сложения матриц:
1. A+B=B+A(коммутативность);
2. (A+B)+C=A+(B+C)=A+B+C (ассоциативность).
Произведением матрицы A=(aij) на число λ называется матрица B=(bij) того же размера, что и матрица A, причём bij=λ aij, для любых i,j.
Свойства операции умножения матриц на число:
1) λ∙(µ∙А)=(λ∙µ)∙А(ассоциативность);
2) λ∙(А+В)=λ∙А+λ∙В (дистрибутивность относительно сложения матриц);
3) (λ+µ)∙А=λ∙А+µ∙В(дистрибутивность относительно сложения чисел).
Пример 1.
Вычислить матрицу 2А+3В, где
![]()
Решение.
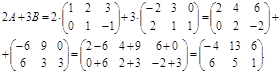
Произведением А∙В матриц А(размера m×n) и B(размера n×r) называется матрица С размера m×r, такая, что
Cij=ai1∙b1j+ai2∙b2j+…+ain∙bnj.
Таким образом, каждый элемент Cij, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицыА и j-го столбца матрицы В. Произведение А∙В существует, только если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц:
1) (A∙B)∙C=A∙(B∙C)=A∙B∙C (ассоциативность);
2) (А+В)∙С=А∙С+В∙С (дистрибутивность);
3) А∙(В+С)=А∙В+А∙С (дистрибутивность);
4) А∙В≠В∙А – отсутствует коммутативность.
Пример 2.
Найти произведение двух матриц:
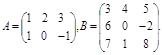
Решение.
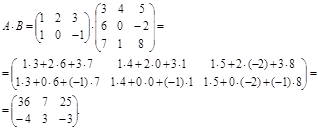
Произведение В∙А не существует, так как число столбцов матрицы В не совпадает с числом строк матрицы А (3≠2).
Транспонированной к матрице А=(aij) называется матрица АТ=(aji), все строки которой равны соответствующим столбцам матрицы А
(т.е. ajiТ=aij,для любых i,j).
Элемент строки матрицы называется крайним, если он отличен от нуля, а все элементы этой строки, находящиеся левее него, равны нулю.
Матрица называется ступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки.
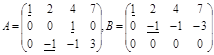
не ступенчатая ступенчатая
Элементарные преобразования матриц.
1. Перемена местами двух строк (столбцов).
2. Умножение строки (столбца) на число, отличное от нуля.
3. Прибавление к элементам одной строки (столбца) соответствующих элементов другой строки( столбца).
Пример 3.
Привести к ступенчатому виду матрицу А с помощью элементарных преобразований над строками:
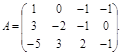
Решение.
1. Сделаем нулевыми все элементы матрицы под крайним элементом первой строки. Для этого вычтем из второй строки первую, умноженную на 3, и запишем результат во вторую строку. После этого к третьей строке прибавим первую, умноженную на 5, и запишем результат в третью строку. Получим матрицу А1.
2. Теперь сделаем равными нулю все элементы матрицы под крайним элементом второй строки. Для этого умножим вторую строку на 3, третью строку – на 2, получившиеся строки сложим и результат запишем в третью строку. Получим ступенчатую матрицу А2.
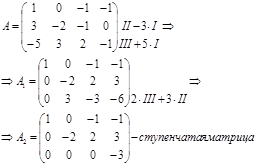
1.2. Определители
1.2.1 Определители n-го порядка
Любой квадратной матрице n –го порядка 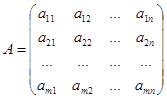
можно поставить в соответствие выражение, которое называется определителем (детерминантом) матрицы А и обозначается так:
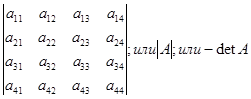
Определитель
2 порядка,
соответствующий квадратной матрице ![]() определяется равенством:
определяется равенством:
![]()
Определитель 3 порядка, задаётся равенством:
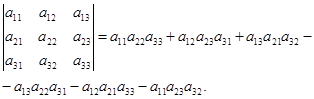
Определитель n-го порядка, задаётся равенством:
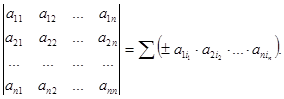
Свойства определителей
1. Если у определителя какая-либо строка (столбец) состоит только из нулей, то определитель равен 0.
2. Если какие-либо две строки (два столбца) определителя пропорциональны, то определитель равен нулю.
3. Если какую-либо строку (столбец) определителя умножить на произвольное число, то и весь определитель умножится на это число.
4. Если две строки (два столбца) определителя поменять местами, то определитель изменит знак.
5. Если к какой-либо строке (столбцу) определителя прибавить какую-либо другую строку (столбец), умноженное на произвольное число, то определитель не изменится.
6. Определитель произведения матриц равен произведению их определителей.
1.2.2 Методы вычисления определителей
1. Правило «треугольников» (правило Саррюса) вычисления определителей 3–го порядка.
Чтобы запомнить, какие произведения в правой части равенства с определителем 3-го-порядка берутся со знаком «+», а какие со знаком «-», полезно использовать следующее правило треугольников:
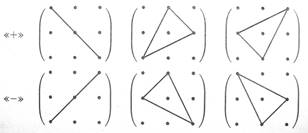
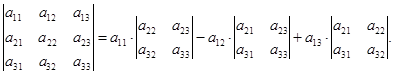
Таким образом, вычисление определителя 3-го порядка сводится к вычислению трёх определителей 2-го порядка.
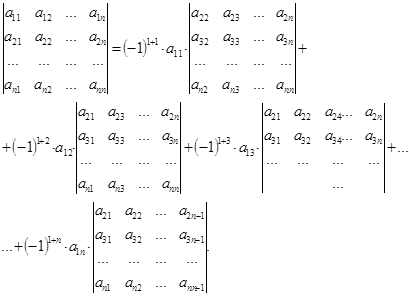
Аналогично задаются другие способы вычисления определителя n-го порядка – «разложение» по произвольной строке или произвольному столбцу.
Пример 4.
Вычислить определитель с помощью «правила треугольников» и разложением по первой строке:
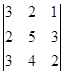 .
.
Решение.
1). 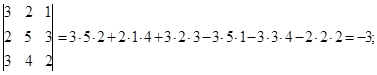
2). 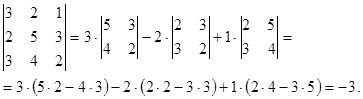
1.3 Обратная матрица. Матричные уравнения
1.3.1 Обратная матрица
Минором Мij к элементу аij квадратной матрицы А называется определитель, составленный из элементов А, оставшихся после вычёркивания i-й строки и j-го столбца.
Алгебраическим дополнением Аij к элементу аij квадратной матрицы А=( аij) называется произведение Аij=(-1)i+j∙Мij.
Например, в матрице
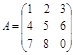 минором М21 является
определитель, составленный из элементов матрицы, оставшихся после вычёркивания
2-й строки и 1-го столбца:
минором М21 является
определитель, составленный из элементов матрицы, оставшихся после вычёркивания
2-й строки и 1-го столбца: ![]() соответственно алгебраическим дополнением
А21будет числоА21=(-1)2+1∙М21=(-1)3∙(-24)=24
соответственно алгебраическим дополнением
А21будет числоА21=(-1)2+1∙М21=(-1)3∙(-24)=24
Обратной матрицей к квадратной матрице А называется такая матрица А-1, что А-1∙А=А∙А-1=Е.
Замечание. Если матрица А-1 существует, то она единственная.
![]() Присоединённой матрицей к квадратной матрице Аij называется матрица ,
Присоединённой матрицей к квадратной матрице Аij называется матрица ,
полученная транспонированием из матрицы, составленной из алгебраических дополнений Аij к элементам аij.
Теорема.
Если квадратная матрица А - невырожденная (т.е. detA≠0), то
![]()
Пример 5.
Дана матрица 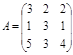 . Найти обратную матрицу.
. Найти обратную матрицу.
Решение.
Вычисляем определитель матрицы А:
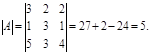
Находим алгебраические дополнения элементов этого определителя:
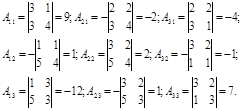
Составляем присоединённую матрицу:
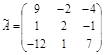 .
.
Находим обратную матрицу:
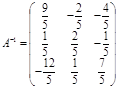 .
.
1.3.2 Матричные уравнения
Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом
1).АХ=В; 2).ХА=В; 3).АХС=В.
В этих уравнениях А,В,С,Х-матрицы таких размеров, что все используемые операции умножения возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.
Если в первом и втором уравнениях матрица - невырожденная, то их решения записываются следующим образом:
Х=А-1В,
Х=ВА-1.
Если в третьем уравнении матрицы А и С - невырожденные, то его решение записывается так:
Х=А-1ВС-1.
Пример 6.
Решить матричное уравнение:
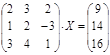
Решение.
Запишем данное матричное уравнение в виде: АХ=В. Его решением является матрица Х=А-1В (если существует обратная матрица А-1).
1). Найдём определитель матрицы А:
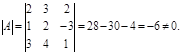
Значит, обратная матрица А-1 существует, и исходное уравнение имеет единственное решение.
2). Найдём обратную матрицу.
Вычислим алгебраические дополнения элементов этого определителя:
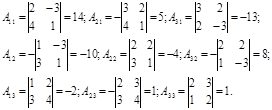
Таким образом,
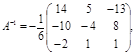
откуда
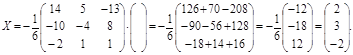
1.4 Системы линейных уравнений
1.4.1 Исследование систем линейных уравнений
Пусть задана система из m линейных уравнений с n неизвестными х1,х2,…,хn:
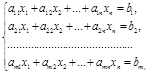
где числа аij (i=1,2,…,m; j=1,2,…,n) называется коэффициентами системы, а числа b1,…,bm-свободными членами.
Решением системы называется такой набор чисел (с1,с2,…,сn), что при его подстановке в систему вместо соответствующих неизвестных (с1 вместо х1, …, сn вместо хn) каждое из уравнений системы обращается в тождество.
Если данная система имеет хотя бы одно решение, она называется совместной; система не имеющая ни одного решения, называется несовместной. Система называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения.
Если b1=b2=…=bn=0, то система называется однородной, в противном случае она называется неоднородной.
1.4.2 Различные способы решения систем линейных уравнений
Будем рассматривать систему из n уравнений с n неизвестными:
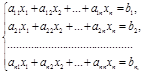
Составим определитель из коэффициентов данной системы:
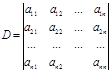 ,
,
Если D≠0, то данная система имеет единственное решение, которое находится по формуле:
![]() , n=1,2,…,n,
, n=1,2,…,n,
где Dk-определитель, получающийся из D заменой k-го столбца на столбец свободных членов.
Пусть система из n линейных уравнений с n неизвестными записана в матричной форме:
АХ=В,
где А=(aij)-матрица коэффициентов системы n×n,

Если D-определитель матрицы А-не равен нулю, то система совместна и определенна, её решение задаётся формулой:
Х=А-1∙В.
Пример 7.
Решить системы уравнений по формулам Крамера и с
помощью обратной матрицы: 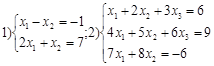
Решение.
1.а) Решим систему по формулам Крамера. Найдём определитель матрицы системы:
![]()
Так как D≠0, то решение системы существует и единственно
Найдём определитель D1 , подставляя в D вместо первого столбца столбец свободных членов:
![]()
Найдём определитель D2 , подставляя в D вместо второго столбца столбец свободных членов:
![]()
Отсюда получим решение системы уравнений:
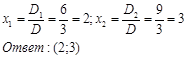
б) Решим систему с помощью обратной матрицы.
Найдём матрицу А-1, обратную к матрице системы ![]() .
.
Так как detA=3≠0, то обратная матрица существует, поэтому решение системы существует и единственно.
Найдём алгебраические дополнения к элементам матрицы А:
А11=1; А12=-2; А21=1; А22=1.
Составим матрицу из алгебраических дополнений:
![]()
Запишем матрицу
![]()
Найдём матрицу
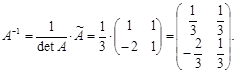
Найдём решение системы уравнений:
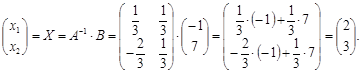
2.а) Решим систему по формулам Крамера. Найдём определитель матрицы системы:
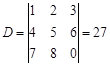
Так как D≠0, то решение системы существует и единственно
Найдём определители D1, D2, D3 подставляя столбец свободных членов вместо первого, второго и третьего столбцов определителя D соответственно:
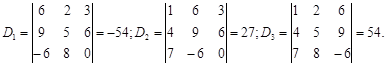
Отсюда получим решение системы уравнений:
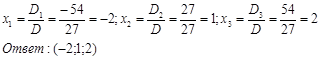
б) Решим систему с помощью обратной матрицы.
Найдём матрицу А-1, обратную к матрице системы 
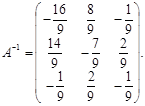
Найдём решение системы уравнений:
 Ответ: (-2;1;2)
Ответ: (-2;1;2)
3. Решение системы уравнений с помощью метода Гаусса.
Описанные выше способы решения системы уравнений неприменимы, если m≠n.
Однако существует универсальный метод, предложенный Гауссом и называемый ещё методом исключения переменных.
Для любой линейной системы уравнений он позволяет:
найти единственное решение, если оно существует;
указать способ нахождения любого числа решений, если их существует бесконечно много;
выяснить, что решений не существует, если их на самом деле нет.
Суть метода Гаусса.
1). Из первого уравнения системы выражаем одну переменную через остальные.
2). Подставляем эту переменную во все остальные равенства, которые образуют линейную систему с меньшим числом переменных. Для этой системы повторяем описанную выше процедуру, и т.д., сокращая на каждом шаге число переменных.
Ясно, что на каждом шаге может возникнуть противоречивое равенство. Тогда делаем вывод: система не имеет решения.
Может случиться, что на последнем шаге возникнет равенство вида схi=b, где с≠0, а хi-одна из переменных. Из него находим единственное значение хi. Затем находятся единственные решения каждой переменной. В этом случае исходная система имеет единственное решение.
Наконец, возможен случай, когда на последнем шаге возникло линейное уравнение, в котором есть несколько переменных с коэффициентами, отличными от нуля. Одну из этих переменных можно выразить через остальные (их называют свободными). Придавая последним любые фиксированные значения, мы можем найти все остальные неизвестные. У такой системы будет бесконечно много решений.
Пример 8.
Решить системы уравнений методом Гаусса:

Решение.
а). Подставляя выражение х через остальные переменные во второе и третье уравнения, запишем систему в виде
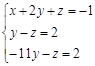
Находим y из второго уравнения и подставляем в третье:

т.е. z=-2 и тогда (из второго уравнения) y=0 и, наконец (из первого уравнения: х=1.
Ответ: (1;0;-2).
б). Подставляя выражение х во второе уравнение, получим:
-2=1. Возникло противоречивое равенство, т.е. система не имеет решений.
в). Рассуждая по прежней схеме, преобразуем систему к виду
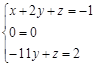
т.е. исходная система эквивалентна
![]()
Переменная y-свободная, придав ей любое значение (например, y=0), находим решение системы (y=0, z=2,x=-3). Исходная система имеет бесконечно много решений.
Контрольные вопросы
1). Дайте определение матрицы.
2). Дайте определение квадратной, диагональной, единичной, нулевой матриц.
3). При каком условии существует сумма двух матриц?
4). Перечислите свойства суммы матриц.
5). Как умножить матрицу на постоянный множитель?
6). Что называется произведением матриц?
7). При каком условии произведение матриц существует?
8). Перечислить свойства произведения матриц.
9). Какая матрица называется транспонированной, ступенчатой?
10). Перечислите элементарные преобразования матриц.
11). Что называется определителем?
12). Как вычислить определитель второго порядка?
13). Перечислите способы вычисления определителя n-го порядка.
14). Перечислите свойства определителя.
15). Дайте определение минора квадратной матрицы.
16). Дайте определение алгебраического дополнения квадратной матрицы.
17). Дайте определение обратной матрицы.
18). При каком условии существует обратная матрица?
19). Как вычислить обратную матрицу?
20). Что называется матричным уравнением?
21). При каком условии матричное уравнение имеет решение?
22). Что называется решением системы линейных уравнений?
23). Какая система называется совместной, несовместной?
24). Какая система называется определённой, неопределённой?
25). Какие способы решения систем линейных уравнений вы знаете? Перечислите.
26). Запишите формулы Крамера.
27). Как решить систему матричным способом?
28) В чём суть метода Гаусса?
Часть 2. Практическая работа
2.1 Цели работы
-научится выполнять действия над матрицами: сложение, произведение на число, умножение;
-научится вычислять определители различными способами;
-научится вычислять обратную матрицу;
-научится решать системы уравнений методом Гаусса, Крамера и матричным способом.
2.2 Порядок выполнения работы
2.1. Проработать теоретический материал по теме.
2.2. Ответить на контрольные вопросы.
2.3. Получить вариант задания.
2.4. Выполнить задание.
2.5. Оформить отчёт о работе.
2.3 Указания к оформлению
Отчёт по практической работе выполняется на листах А4 (210х297) и должен содержать:
![]() точное
наименование работы;
точное
наименование работы;
![]() цель работы;
цель работы;
![]() ход работы
(условие задачи);
ход работы
(условие задачи);
![]() результаты
работы (подробное решение задач);
результаты
работы (подробное решение задач);
![]() вывод.
вывод.
Отчёт должен быть сдан не позднее 3-х дней со дня проведения работы.
2.4 Варианты заданий
Вариант 1
1. Выполнить действия:
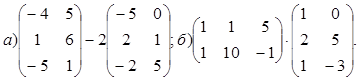
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
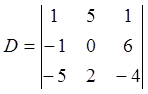
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
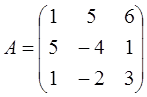
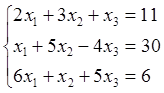
Вариант 2
1. Выполнить действия:
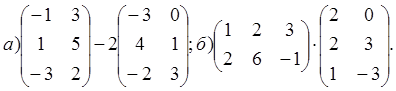
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
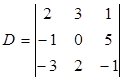
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
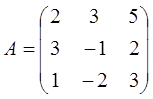
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
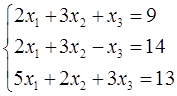
Вариант 3
1. Выполнить действия:
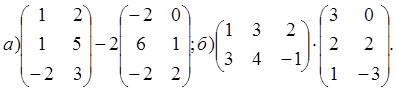
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
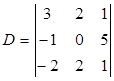
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
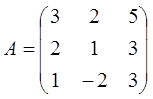
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
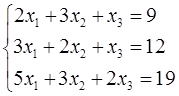
Вариант 4
1. Выполнить действия:
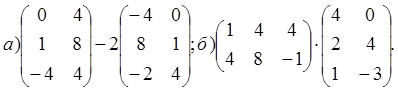
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
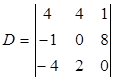
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
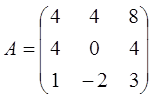
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
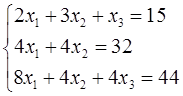
Вариант 5
1. Выполнить действия:

2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
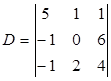
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
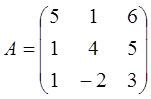
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
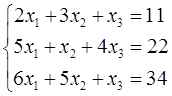
Вариант 6
1. Выполнить действия:
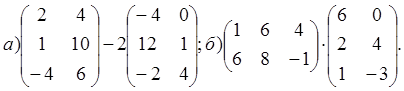
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
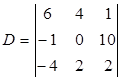
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
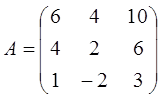
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
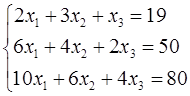
Вариант 7
1. Выполнить действия:
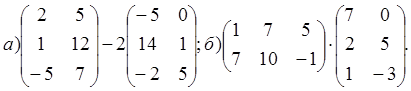
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
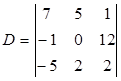
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
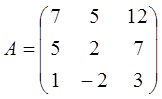
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
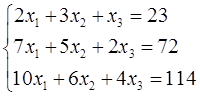
Вариант 8
1. Выполнить действия:

2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
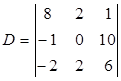
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
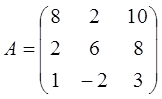
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:

Вариант 9
1. Выполнить действия:
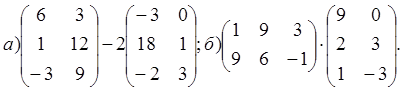
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
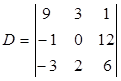
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
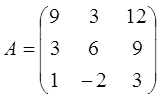
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
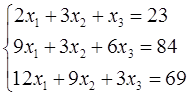
Вариант 10
1. Выполнить действия:
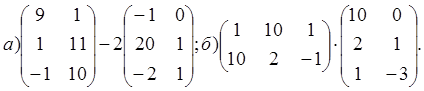
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
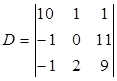
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
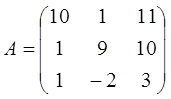
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
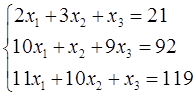
Вариант 11
1. Выполнить действия:
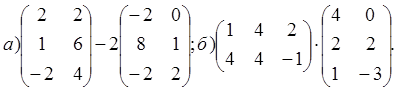
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
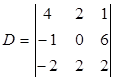
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
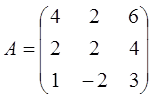
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:

Вариант 12
1. Выполнить действия:
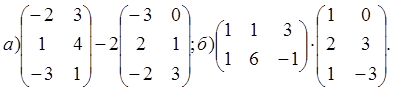
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
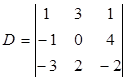
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
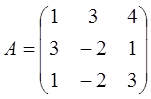
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
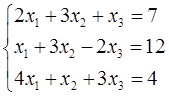
Вариант 13
1. Выполнить действия:
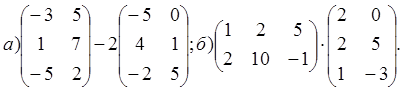
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
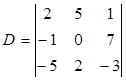
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
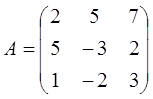
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
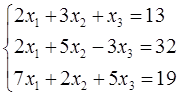
Вариант 14
1. Выполнить действия:
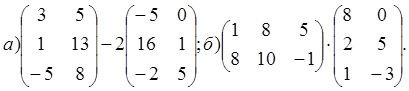
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
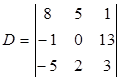
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
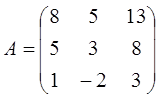
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
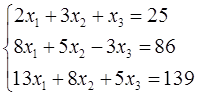
Вариант 15
1. Выполнить действия:
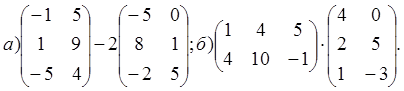
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
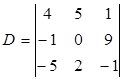
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
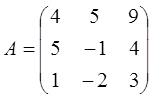
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
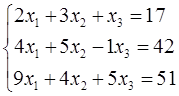
Вариант 16
1. Выполнить действия:
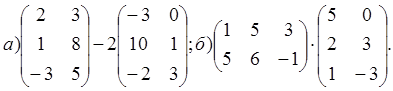
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
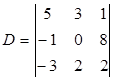
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
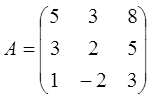
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
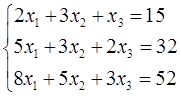
Вариант 17
1. Выполнить действия:
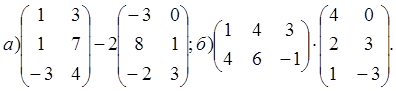
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
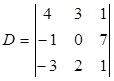
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
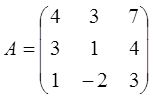
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
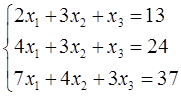
Вариант 18
1. Выполнить действия:
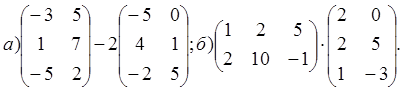
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
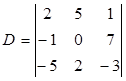
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
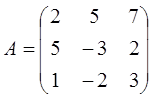
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
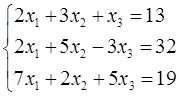
Вариант 19
1. Выполнить действия:
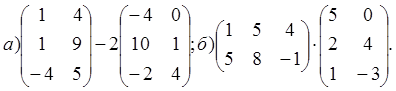
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
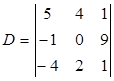
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
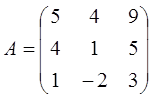
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:
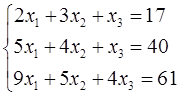
Вариант 20
1. Выполнить действия:
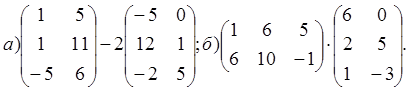
2. Вычислить определитель двумя способами:
а) по правилу «треугольников»; б) разложением по строке.
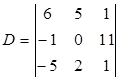
3. Найти обратную матрицу к матрице А и проверить выполнение равенства: А-1∙А=Е.
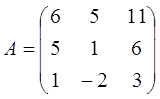
4. Решить систему уравнений тремя способами: а) по формулам Крамера; б) методом Гаусса; в) матричным способом:

Литература
1 Афанасьева О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов.- М.: Наука, 1991.- 420 с.
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений. М.: Высшая школа, 1997.-250 с.
3. Богомолов Н. В. Математика.- Москва: Дрофа, 2006.- 396 с.
4. Данко П. Е. Высшая математика в упражнениях и задачах, ч.1-М.: ОНИКС 21 век,2003.-304 с.
5. Лунгу К.Н. Сборник задач по высшей математике. 1 курс-М.: Айрис-пресс, 2007.-576 с.
6. Омельченко В. П. Математика.- Ростов н/Д: Феникс, 2007.-380 с.
7. Циркунов А.Е. Справочник по математике.- С.-П.: Питер, 2000.-160с.
8. Шнейдер В.Е. Краткий курс высшей математики -М.: Просвещение, 1992.-328 c.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.