Методическое пособие для самостоятельной работы студентов по теме: «Тригонометрические функции»

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ                                                                                                                                                                          «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»

МЕТОДИЧЕСКОЕ ПОСОБИЕ

Для самостоятельной работы студентов

По дисциплине: МАТЕМАТИКА (включая алгебру и начала математического анализа; геометрию)

Тема: «Тригонометрические функции»

Специальность: 34.02.01 Сестринское дело   Курс: 1

(базовой подготовки)

Купино

2020

Рассмотрено на заседании   предметной цикловой

Методической комиссии по общеобразовательным дисциплинам,

общему гуманитарному и социально-экономическому, математическому и

естественно-научному циклу

Протокол № _____ от «_____» _________20____г.                                             

Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.

Купино

2020 г

Пояснительная записка к методическому пособию

Методическое пособие предназначено для повторения теоретических и практических знаний по теме.

Цель пособия – повторить понятия тригонометрических функций, определять вид и строить графики функции, находить область определения и область значений и подготовится к занятию по теме «Тригонометрические функции».

Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения, свойства и формулы по теме: Тригонометрические функции, тест для самоконтроля и критерии оценки теста.

Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.

Тригонометрические функции

История тригонометрии, как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур, охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобились ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц. Историки полагают, что тригонометрию создали древние астрономы, немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, в наши дни она охватывает практически все естественные науки, технику и ряд других областей деятельности. Особенно полезными тригонометрические функции оказались при изучении колебательных процессов; на них основан также гармонический анализ функций и другие инструменты анализа. Томас Пейн в своей книге «Век Разума» (1794) назвал тригонометрию «душой науки».

Тригонометрические функции, их свойства и графики.

Все тригонометрические функции (синус, косинус, тангенс и котангенс) относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.

Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода , где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.

Теперь разберемся со всеми тригонометрическими функциями по-порядку.

Функция синус y = sin(x).

Изобразим график функции синус, его называют "синусоида".

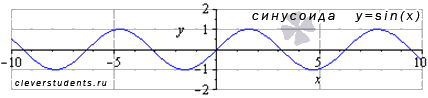
Свойства функции синус y = sinx.

1.Областью определения функции синус является все множество действительных чисел, то есть, функция y = sinx определена при

2.Наименьший положительный период функции синуса равен двум пи: .

3.Функция обращается в ноль при , где , Z – множество целых чисел.

4.Функция синус принимает значения из интервала от минус единицы до единицы включительно, то есть, ее область значений есть .

5.Функция синус - нечетная, так как .

6.Функция убывает при ,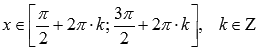

возрастает при .

7.Функция синус имеет локальные максимумы в точках ,
локальные минимумы в точках .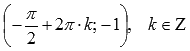

8.Функция y = sinx вогнутая при ,
выпуклая при .

9.Координаты точек перегиба .

10.Асимптот нет.

Функция косинус y = cos(x).

График функции косинус (его называют "косинусоида") имеет вид:

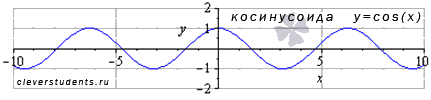
Свойства функции косинус y = cos x.

1.Область определения функции косинус: .

2.Наименьший положительный период функции y = cosx равен двум пи: .

3.Функция обращается в ноль при , где , Z – множество целых чисел.

4.Область значений функции косинус представляет интервал от минус единицы до единицы включительно: .

5.Функция косинус - четная, так как .

6.Функция убывает при ,
возрастает при .

7.Функция y = cosx имеет локальные максимумы в точках ,
локальные минимумы в точках .

8.Функция вогнутая при ,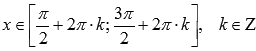
выпуклая при .

9.Координаты точек перегиба .

10.Асимптот нет.

Функция тангенс y = tg(x).

График функции тангенс (его называют "тангенсоида") имеет вид:

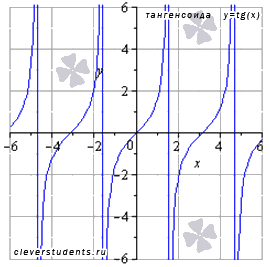
Свойства функции тангенс y = tgx.

1. Область определения функции тангенс: , где , Z – множество целых чисел.
2. Поведение функции y = tgx на границе области определения
   Следовательно, прямые , где , являются вертикальными асимптотами.
3. Наименьший положительный период функции тангенс .
4. Функция обращается в ноль при , где , Z – множество целых чисел.
5. Область значений функции y = tgx: .
6. Функция тангенс - нечетная, так как .
7. Функция возрастает при .
8. Функция вогнутая при ,
   
   выпуклая при .
9. Координаты точек перегиба .
10. Наклонных и горизонтальных асимптот нет.

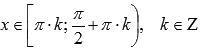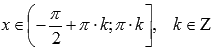Функция котангенс y = ctg(x).

Изобразим график функции котангенс (его называют "котангенсоида"):

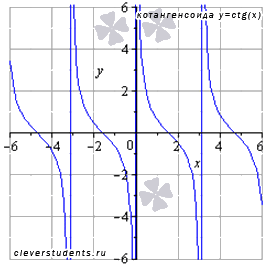
Свойства функции котангенс y = ctgx.

1. Область определения функции котангенс: , где , Z – множество целых чисел.
2. Поведение на границе области определения
   Следовательно, прямые , где являются вертикальными асимптотами.
3. Наименьший положительный период функции y = ctgx равен пи: .
4. Функция обращается в ноль при , где , Z – множество целых чисел.
5. Область значений функции котангенс: .
6. Функция нечетная, так как .
7. Функция y = ctgx убывает при .
8. Функция котангенс вогнутая при ,
   выпуклая при .
9. Координаты точек перегиба .
10. Наклонных и горизонтальных асимптот нет.

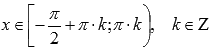Обратные тригонометрические функции, их свойства и графики.

Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.

Функция арксинус y = arcsin(x).

Изобразим график функции арксинус:

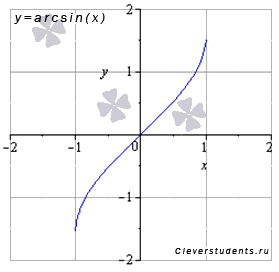
Свойства функции арксинус y = arcsin(x).

1.Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .

2.Область значений функции y = arcsin(x): .

3.Функция арксинус - нечетная, так как .

4.Функция y = arcsin(x) возрастает на всей области определения, то есть, при .

5.Функция вогнутая при , выпуклая при .

6.Точка перегиба (0; 0), она же ноль функции.  7.Асимптот нет.

 Функция арккосинус y = arccos(x).График функции арккосинус имеет вид: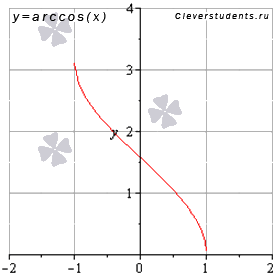

Свойства функции арккосинус y = arccos(x).

1.Область определения функции арккосинус: .

2.Область значений функции y = arccos(x): .

3.Функция не является ни четной ни нечетной, то есть, она общего вида.

4.Функция арккосинус убывает на всей области определения, то есть, при .

5.Функция вогнутая при , выпуклая при .

6.Точка перегиба .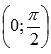

7.Асимптот нет.

Функция арктангенс y = arctg(x). График функции арктангенс имеет вид: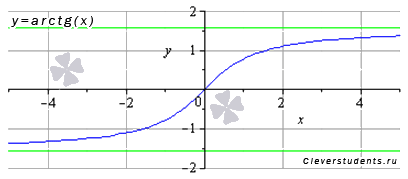

Свойства функции арктангенс y = arctg(x).

1. Область определения функции y = arctg(x): .
2. Область значений функции арктангенс: .
3. Функция арктангенс - нечетная, так как .
4. Функция возрастает на всей области определения, то есть, при .
5. Функция арктангенс вогнутая при , выпуклая при .
6. Точка перегиба (0; 0), она же ноль функции.
7. Горизонтальными асимптотами являются прямые при и при . На чертеже они показаны зеленым цветом.

Функция арккотангенс y = arcctg(x).

Изобразим график функции арккотангенс:

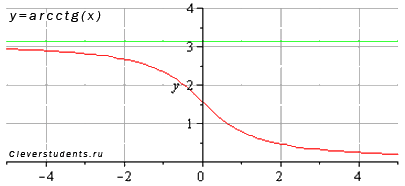
Свойства функции арккотангенс y = arcctg(x).

1. Областью определения функции арккотангенс является все множество действительных чисел: .
2. Область значений функции y = arcctg(x): .
3. Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.
4. Функция убывает на всей области определения, то есть, при .
5. Функция вогнутая при , выпуклая при .
6. Точка перегиба .

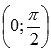Горизонтальными асимптотами являются прямые при  (на чертеже показана зеленым цветом) и y = 0

1. С помощью преобразования графика функции y=sinx построить

Решение. Приводим функцию к виду шаблона :

Имеем , причем перед коэффициентом стоит знак «минус», перед минуса нет. Таким образом, цепочка преобразований графика функции y=sinx примет вид:

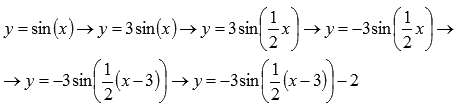
Поэтапное преобразование графика синусоиды.
График исходной синусоиды y=sin(x) . Наименьший положительный период равен . Максимумы находятся в точках , минимумы – в точках .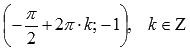

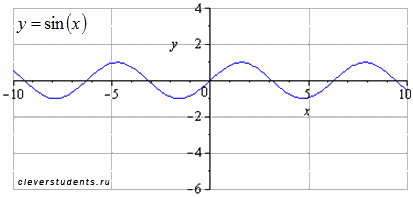
Растягиваем вдоль оси ординат втрое (амплитуда колебаний при этом возрастает в три раза). Наименьший положительный период равен . Максимумы переходят в точки , минимумы – в точки .

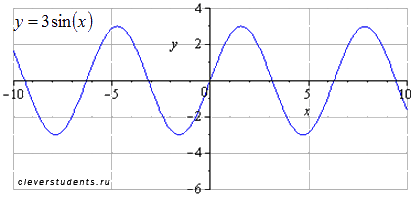
Растягиваем вдоль оси абсцисс вдвое. Наименьший положительный период при этом вдвое увеличивается . Максимумы переходят в точки , минимумы – в точки .

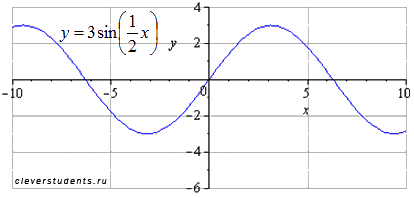
Симметрично отображаем относительно оси абсцисс. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .

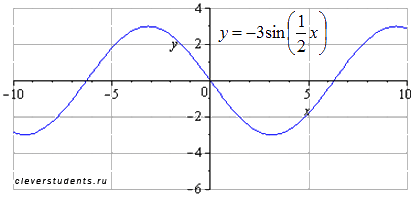
Сдвигаем график вправо на 3 единицы. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .

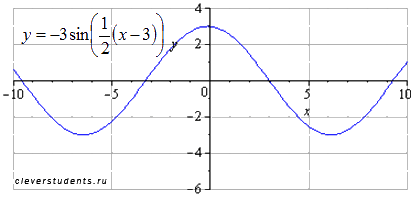
Сдвигаем график вниз на 2 единицы. Наименьший положительный период при этом не меняется . Максимумы переходят в точки , минимумы – в точки .

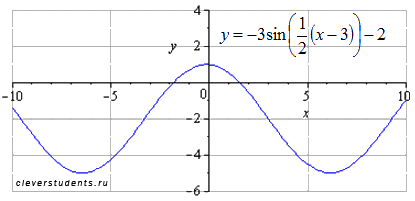
Этим этапом задача преобразования графика тригонометрической функции

Тест по теме: Тригонометрические функции Вариант 1

Работа состоит из 10 заданий. К каждому заданию А1 – А5 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ. К заданиям С1 – С2  - записать решение.

Часть А                                  

         1.  Найдите множество значений функции у = 3 – 2sinx

1)      [ 1; 5];       2)     [ - 1; 1];         3)      [ 3; 5 ];                  4)    [ 1; 3].

          2.  Вычислите  значение  sin2x, если  cosx =   и  

1)     –    ;          2)     ;                  3)     ;                          4) –     .

          3.  Найдите сумму всех целых чисел, которые входят в область значений функции     у = 4cos²x – 7

1)    – 25;               2)  25;                   3)      – 22;                       4)   0.

          4.   Упростите  выражение   5sin²x – 4 + 5cos²x

1)     1;                   2)   9;                     3)     – 9;                         4)  – 4.

           5.   Решите уравнение      cosx –  = 0

1)        2)    3) 

4)      

Часть В

          6.  Найдите значение выражения   при 

          7.  Упростите  выражение    

          8.  Определите, сколько корней уравнения   2сos²x + 7cosx – 4 = 0, принадлежит отрезку [ - 2

Часть С

           9.  Найдите наибольший отрицательный корень уравнения ( в градусах)   sin3x  cos5x – cos3x  sin5x = 0,5

           10.  Решите уравнение     sin²x +   – 2 = 0

Тест по теме: Тригонометрические функции Вариант 2

Работа состоит из 10 заданий. К каждому заданию А1 – А5 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ. К заданиям С1 – С2  - записать решение.

Часть А

           1.  Найдите множество значений функции  у = 3cosx – 2

1)     [ – 5; 1];           2)   [ – 1; 1];           3)   [ – 5; –2];           4) [ 1; 3].  

            2.     Вычислите  значение  cos2 ,  если sin = –      и 

1)    –  ;               2)    ;                     3)   – 0,5 ;                  4)  0,5.

            3.  Найдите произведение всех целых чисел, которые входят в область значений функции  у = 5 – 3sin²x

1)     120;                 2)    14;                     3)   – 15;                     4)     0.

           4.    Упростите  выражение   – 4sin²x + 5 – 4cos²x

1)    1;                       2)   9;                        3)  5;                             4)   4.

            5.   Решите уравнение    sinx  –   = 0

                   1)     2)     3)      4)      

  Часть В  

            6.  Найдите  значение выражения   при  cos =

            7.  Упростите  выражение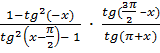    

            8.   Определите, сколько корней уравнения   2sin²x + 5sinx – 3 = 0, принадлежит отрезку [ - 2

Часть С

           9.  Найдите наименьший  положительный корень уравнения (в градусах)

                 cos3x  cosx – sinx  sin3x = 1

            10.  Решите  уравнение    cos²x +   – 2 = 0

Приложение №5

Эталоны ответов теста по теме: Тригонометрические функции

Критерии оценивания тестовых заданий

За каждое верно решенное задание части А обучающийся получает 1 балл, части В – 2 балла, части С – 3 балла.

       Таким образом, максимальное число баллов, которое можно получить за верное решение всех заданий, равно 17. 

Оценка «3» ставится, если ученик набрал от  4 до 8 баллов; 

оценка «4», если ученик набрал от 9 до 13 баллов; 

оценка «5», если ученик набрал от 14 до 17 баллов.

Литература

1.     Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М.: 2018

2. Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012

Интернет-ресурсы

1.     http://school-collection.edu.ru – Электронный учебник «Математика в

школе, XXI век».

2.     http://fcior.edu.ru - информационные, тренировочные и контрольные материалы.

3.     www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов