Муниципальное бюджетное общеобразовательное учреждение "Центр образования № 28 с углубленным изучением иностранных языков г. Владивостока" 

 

 

МЕТОДИЧЕСКОЕ  ПОСОБИЕ  ПО

ТЕМЕ  :

«Системы счисления: представление и использование в учебном процессе.»

 

 

Нечаева Ирина Владимировна,

учитель информатики

высшей категории

 

 

 

 

 

 

 

 

СОДЕРЖАНИЕ :

ТЕМА 1.Понятие  о  системах  счисления.                           Основные  определения. История вопроса……………….….…..2

ТЕМА 2.Представление чисел  в  позиционных  системах счисления. Недесятичные  системы  счисления. Развернутая  и  свернутая  формы  записи  чисел. Схема  Горнера……...…. ………….9

ТЕМА3.Двоичная система счисления.                                          

 3.1 Общие  сведения……….……………..………..…..………11                             3.2 Арифметические    операции     в    двоичной   системе счисления………………………...………………………………………19

ТЕМА  4.Связь  между  системами  счисления.                           4.1.Системы  счисления, родственные двоичной……………....15                       4.2.Геометрическое  представление  чисел………………...………….15     4.3. Перевод    десятичных     чисел    в    двоичную    систему счисления…………………………………………………….……………15                  4.3.1. Перевод  целых  чисел…………………………………………...15     4.3.2.Перевод  правильных  дробей………………………………...….16    4.3.3.Перевод  смешанных  чисел…………………………………...…16       4.3.4. Перевод  чисел  из  систем  счисдения  с  основанием  2ⁿ  в ситему  счисления  с  основанием  2  и  обратно ………………………16       

5.Системы счисления, используемые в ЭВМ……………….…………18  

Литература…………………………………………………………19

 

 

 

 

 

 

 

 

 

1.Понятие  о  системах  счисления

Основные определения. История вопроса.  

 

Кодирование  информации – это просто-напросто представление сведений в той  или иной  стандартной форме. Одни  и  те же сведения могут  быть представлены  , закодированы  в  нескольких  разных  формах. Совершенно  разные сведения могут  быть представлены  в похожей  форме.С  появлением  компьютеров  возникла  необходимость  кодирования ( т.е. представления  в  формальном, стандартизированном  виде)  всех  видов  информации,  с  которыми  имеют  дело  и  отдельный  человек,  и  человечество  в  целом. Но  решать задачу  кодирования  информации  человечество  начало  задолго  до  появления компьютеров.                                                                        Грандиозные  достижения  человечества – письменность  и  арифметика  -  есть  не  что  иное,  как  системы  кодирования  речи  и  числовой  информации.                                                                                           Дарвин  считал  , что  обезьяну  сделал  труд. Другие  ученые  считают, что человек стал  Человеком  благодаря  своим  успехам  в  кодировании  информации,  благодаря  изобретению  языка, письменности  и  способов  кодирования  и  записи  числовой  информации.                                                                                                             Считать  могут  не  только  люди. Установлено, что  считать  до  трех  могут  и  птицы  (  и  многие  другие  животные). Если  у  птицы  забрать  из  гнезда  одно  яйцо  из  пяти, то она  не  заметит  пропажи, а  вот  если  забрать  одно  из  трех, то  птица  начинает  проявлять  беспокойство. Но  от  такого  элементарного  счета  до  понятия  число  еще  очень  и  очень  далеко.                                                                                    Первобытные  люди  не  знали  чисел  и  использовали                        наглядное  представление  информации  для запоминания  того  или  иного  количества  предметов.  Например, чтобы  запомнить  ,  что на охоте  было  убито  пять  оленей  , пещерный «летописец»  просто  рисовал  их всех  на  стене  пещеры.                                                              Способы  кодирования  числовой  информации – способы  счета  и  представления  чисел – в  истории  человечества  последовательно  менялись. Следы  древних  систем  счета  и  представления  чисел  встречаются  и  сегодня в культуре  и  обычаях  многих  народов. К  Древнему  Вавилону  восходит  деления  часа  на  60  минут  и  угла  на  360  градусов. К  Древнему  Риму  восходит  традиция  записывать  в  римской  записи  небольшие  числа:   I , II , III , IV ,  V ,  VI ,  VII , VIII , IX , X , XI , XII , … . Нпример  , часто  пишут  « XIX   век» ,  «XX  век» вместо   «19-й век»  и  «20-й век» . к  англосаксам – жителям  Британских  островов – восходит  традиция  счета  дюжинами:  в  году  12  месяцев.  В  футе  12  дюймов,  сутки  делятся  на  два  периода  по  12  часов.                                                                                                             Много  информации  о  распространенных  в  прошлом  единицах  счета  до  сих  пор  сохранилось  в  современных  языках. Особую  роль  числа  40  при  счете  помнит  русский  язык:  сохранилось  выражение  «сорок  сороков», да  и само  слово  сорок  выбивается    из  основанного  на  десятке  ряда  числительных: двадцать, тридцать, пятьдесят, шестьдесят, семьдесят, восемьдесят. Во  французском  языке  сохранились  следы  счета  двадцатками: если  в русском  слово  восемьдесят  означает  «восемью десять» , то  форанцузское  числительное   quatre-vingts  может  быть переведено  как  «четырежды  двадцать».                                                                          «Все  есть число» ,- говорили  пифагорийцы, подчеркивая необычайно важную  роль чисел  в  практической  деятельности  . Известно  множество способов представления чисел. В любом  случае  число изображается группой символов (словом) некоторого алфавита. Будем называть такие символы цифрами, символические изображения чисел – кодами, а правила получения кодов – системами счисления (кодирования).                                                                                                       Историкам  не  известно, когда  появились  понятия  числа  и  количества, но  они  склонны  считать, то  это  произошло  на  самых  ранних  стадиях  развития  нашей  цивилизации. Началось  всё  с  подсчётов  одинаковых  конкретных  предметов: пять  ножей, пять  оленей  пять  деревьев. Затем  мало-помалу  понятие  количества  предметов-пять-стало  отделяться  от  того, какие  именно  предметы  считаются. Это  и  привело к  возникновению  понятия  число.                         Следы  того, как  люди  в  глубокой  древности  обходились  без  общего  понятия  число, можно  найти  в  языках  и  доныне  живущих  на  земле  примитивных  племён. У  них  в  языке  сохранились  различные  числительные  для  различных  предметов. Одни  числительные  используются  для  подсчёта  людей, другие - для  подсчёта  круглых  предметов, третьи-для  продолговатых  и  т. д. Например, в  языке  народа  чишмиенов ( Канада, провинция  Британская  Колумбия ) есть  целых  семь  видов  числительных  для  подсчёта  предметов  разной  природы. Да  и  в  русском  языке  для  счета  одушевленных  предметов  есть  особые  формы  числительных. Вспомните: “Один  с  сошкой,  семеро   с  ложкой” .                                        Чтобы  использовать  числа, нужно  их  как-то  называть  и записывать,  нужна  какая-то  система  записи  числа – нужна  система  нумерации.                                                                                                                 Разные  народы  в  разные  времена использовали  разные  системы  нумерации.                                                                                                Еще  недавно  существовали  племена,  в  языке  которых  было  всего  два  числительных : “один”  и  “два”. Это,  конечно,  не  означает,  что  представители  этих  племен  не  могли  сосчитать  три  предмета. Большие  числа  представлялись  комбинациями. Так,  например,  у  туземцев  островов,  расположенных    в  Торресовом  проливе,  было  всего  два  числительных:  урапан (один)  и  окоза (два).  Большие  числа  назывались  так : окоза-урапан  (три), окоза-окоза-урапан (пять)  и  т. д..  Правда,  эта  нумерация  не  успевала  стать  слишком  громоздкой.  Числа  начиная  с  семи  имели  единственное  обозначение  -  много.                                                               Наверное,  на  перых  порах  счета  до  семи  и  хватало  для  повседневных  нужд,  но  жизнь  не  стояла  на  месте.  Появлялись  новые  способы  охоты,  развивалось  земледелие,  и  такого  маленького  запаса  чисел  начинало  не  хватать.  Возникло  желание  увеличить  верхнюю  границу  счета.  Считать  стали  при  помощи  пальцев  рук,  ног  и  других  частей  тела.  Например,  те  же  островитяне  для  счета  употребляли  локти,  запястья,  плечи.                         Так  прокладывались  пути  к  счету  пятрками (пальцы  одной  руки),  двадцатками  (пальцы  рук  и  ног)  и  десятками -  счету  предметов  с  помощью  пальцев  двух  рук.  Из  счета  десятками  и выросла  современная  десятичная  система.                                   Определение 1. Система счисления – это совокупность  правил          для   обозначения  и  наименования  чисел.                                         Системы счисления делятся  на  следующие  виды:           1)непозиционные системы счисления;                                      2)позиционные системы счисления.                                      Простейшая  и  самая  древняя  - так называемая унарная система счисления. В  ней  для  записи  любых  чисел  используется  всего  один  символ – палочка, узелок, зарубка, камушек. Длина  записи  числа  при  таком  кодирвании пря  связана  с  его  величиной,  что роднит  это  способ  с  геометрическим  представлением  чисел  в  виде  отрезков.  Сами  того  не  осознавая , этим  кодом пользуются малыши, показывая на пальцах свой возраст. Именно унарная системы счисления до сих пор вводит  детей в мир счета.                                             Определение 2. Непозиционной называется такая система счисления, в которой количественный эквивалент каждой цифры не зависит  от ее положения (места, позиции) в коде числа.                             Непозиционные системы счисления возникли  раньше  позиционных. Вот  только некоторые примеры таких  систем.                                                            Пример 1. По  современным  данным,  развитые  системы  нумерации  впервые  появились  в  Древнем  Египте  и  Месопотамии.  Мы  многое  знаем  о  египетской  системе.  До  нас  дошли  надписи  внутри  пирамид,  на  плитах  и  обелисках.  Эти  надписи  сделаны  в  виде  картинок  иероглифов,  и  такой  способ  письма (кодирование  речи)  вообще  характерен  для  ранних  стадий  развития  человечества.  Многие надписи  сейчас  уже  прочитаны  и  расшифрованы.  Сохранились  также  два  математических  папируса,  позволяющих  узнать  об  арифметике  древних  египтян.                               Для  записи  чисел  египтяне  применяли  иероглифы  один,  десять,  сто, … ,  десять  миллионов.  Все  остальные  числа  записывались  с  помощью  этих  иероглифов  и операции сложения . Так  , что  в  египетской  записи  чисел  особую  важную  роль  играли  десятки  и  ее  степени. На  рисунке  изображены  цифры системы счисления  Древнего  Египта:

Делили  и  умножали  египтяне  совсем  не  так,  как  мы. Особую   роль  у  египтян  играло  число  два  и  его  степени:  2,4,8,16  и  т.д..  умножение  и  деление  проводилось  путем  последовательного  удвоения  чисел.                                                                                                       Пусть, например,  надо  умножить  19  на  94.  Египтяне  последовательно  удваивали  число  94 , причем  в  правом    столбце              записывали  результаты  удвоения,  а  в левом  -  соответствующие степени  двойки. (Разумеется,  записывали  они  это  по-своему, но  ниже  вычисления  показаны  в  современной  записи.  Суть  дела  от  этого  не  меняется.)       

                                       1          ï          94                                                                                            2            ï          188                                                                                          4          ï          376                                                                                          8          ï          752                                                                                          16        ï          1504   

   Удвоение  продолжалось  до  тех  пор,  пока  не  оказывалось,  что  из  чисел  левого  столбца  можно  составить  множитель  (в  нашем  случае  19=1+2+16).  Египтяне  отмечали  соответствующие  строки  вертикальными  черточками  и  складывали  те  числа,  которые  стоят  в  этих  же  строках  справа. В  приведенном  примере  сложение  трех  чисел  94+188+1504  дает  искомое  произведение  1786.                                                                                                                           Деление  египтяне  проводили  удвоением  делителя.  Пусть,  например,  требуется  разделить  1786  на  19.  В  этом  случае  египтяне  последовательно  удваивали  делитель  и  продолжали  до  тех  пор,  пока  числа  правого  столбца  оставались  меньше  делимого:                                       1          ï          19                                                                                            2          ï          38                                                                                            4          ï          76                                                                                            8          ï          152                                                                                          16        ï          304                                                                                          32        ï          608                                                                                          64        ï            1216                                        Затем    из  чисел  правого  столбца  они  пытались  составить  делимое,  и  если  это  удавалось, то  сумма  чисел  в  левом  столбце  давала  частное.  В  рассмотренном  случае  делимое  1786  можно  составить  как   1216+304+152+76+38,  значит,  частное  будет  64+16+8+4+2+=94.                                                                                                    Если  бы  делимое  не  делилось  без  остатка  на  делитель,  из  чисел  правого  столбца  удалось  бы  составить  лишь  число,  меньше  делимого.  Так  получились  бы  и  частное  ,  и остаток.                                Один  из  недостатков  египетской    системы  -  невозможность  записи  больших  чисел  без  придумывания  новых  иероглифов.  Иероглиф  для  десяти  миллионов  еще  есть,  а  вот  для  ста  миллионов  уже  нет.  Этот  недостаток  преодолен  в  позиционных  системах  счисления.                                                                                            Другой недостаток  египетской  системы – громоздкая  запись  чисел.  Для  записи  числа  девять  египтяне  девять  раз повторяли иероглиф  для  единицы.  Этого  недостатка  лишены  алфавитные  системы  записи  чисел,  принятые  в  свое  время  у  ионийцев,  древних  евреев,  финикийцев, армян,  грузин,  а  также  и  у славян.                     Пример  2. Славянская  алфавитная  нумерация  напоминала  современную  позиционную.  В  ней  числа  были  закодированы  буквами,  а  над  этими  буквами,  чтобы  избежать  путаницы ,  ставился  специальный  знак  -  титло: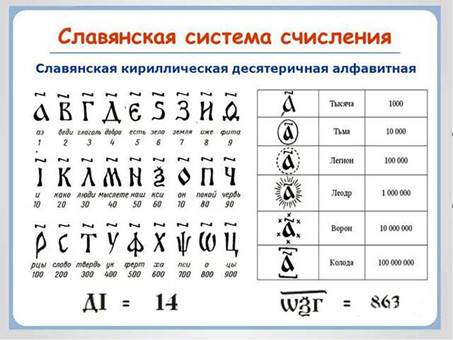              

Одной   буквой  кодировались  числа  от  1  до  9,  затем  10,20,…,90  и,  наконец,  100,200, …,900.  Для  больших  чисел  использовались  те  же  самые  буквы  с  добавленными  к  ним  специальными  значками,  например,  10 000  обозначалось  как                                                         ¹ a                                                      Пример 3. В  старину  на  Руси  широко  применялись системы счисления  , отдаленно  напоминающие  римскую. С  их  помощью  сборщики податей  заполняли  квитанцию  об  уплате  подати (яаска)  и делали записи  в  податной  тетради.                                             

Например, 1234 руб. 24 коп. изображается  так: 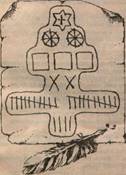 Вот текст   закона об этих так называемых ясачных знаках:  «Чтобы на каждой квитанции, выдаваемой Родовитому Старосте, от которого внесен бу­дет ясак, кроме изложения словами, было по­казано особыми знаками число внесенных руб­лей и копеек так, чтобы сдающие простым сче­том сего числа могли быть уверены в справед­ливости показания. Употребляемые в квитан­ции знаки означают:

звезда                         - тысяча рублей,

колесо                         - сто рублей,

квадрат                       - десять рублей,

х                                    -  один рубль,

1111111111      -  десять  копеек,
I                                             -  копейку.

 

Дабы неможно было сделать здесь никаких прибавлений, все таковые знаки очерчивать кругом прямыми линиями".

   Пример  4      . До наших  дней  дней сохранилась римская система счисления. В римской системе счисления цифры обозначаются буквами латинского алфавита: 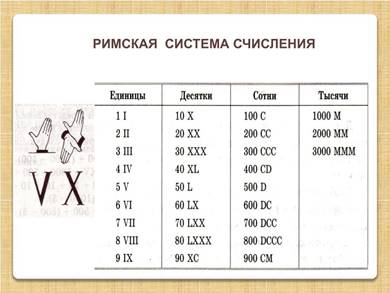                                                                    Для промежуточных  чисел  используется правило:                                             Меньшие знаки, поставленные  справа от большего прибавляются к его значению, а меньший знак , поставленный  слева от большего, вычитается из него.                                                                      Например, IX   обозначает  9, XI   обозначает   11. Десятичное число 28 представляется  следующим образом:                                                                             XXVIII =10+10+5+1+1+1  ,                                           а  десятичное  число  99  имеет  вот  такое представление                      IC = - 1+100               Римская система счисления  сегодня  используется  в  основном  для  обозначения  знаменательных  и  юбилейных  дат, разделов  и  глав  в  книгах.                                                         Если  складывать  и  вычитать  в  такой  системе  еще  можно  без  особого  труда  ,  то  умножать  очень  сложно,  а  деление   представляет  собой  почти  непосильную  задачу.                                               Вместе  с  тем    в римской  системе  счисления  есть  одна  важная  идея  :  вклад  буквы  в  число  зависит  не  только    от  самой  буквы  .  но  и  от  порядка  следования  ( позиции)  букв  в  записи  числа.   Так, например,  буква  I  дает  вклад  +1  в  число   VI     и  вклад  -1  в число  IV . развитие  этой  идеи  приводит  к  современным  позиционным  системам  нумерации.                                                                                                                                                          Непозиционные, системы счисления имеют ряд не­достатков:                     

1.   Для записи больших чисел приходится вводить новые
цифры. Например, пользуясь только цифрами I, V, X, число
"тысяча" записать неудобно. И всегда есть числа, которые
трудно изобразить даже вновь введенными цифрами.

2.   Невозможно записывать дробные и отрицательные
числа.

3.   Сложно выполнять арифметические операции.                                           Различные  системы  счета  и  записи  чисел  тысячелетиями   сосуществовали  и  соревновались  между  собой,  но  к  концу  «докомпьютерной  эпохи»  особую  роль  при  счете    стало  играть  число  десять,  а  самой  популярной  системой  кодирования  чисел  оказалась  так  называемая  позиционная  десятичная  система.                                                 

Определение 3. Система счисления называется позиционной, если количественный эквивалент (значение) цифры зависит от ее места (позиции) в коде числа.                                              

В привычной нам системе счисления для записи чи­сел используются десять различных знаков (цифры О, 1, 2, 3, 4, 5, 6, 7, 8 и 9). Поэтому ее называют десятичной.                                                             Десятичная  система  счисления  пришла  из  Индии,  где  она  появилась  не  позднее  VI   в.н.э.           

                                               Из двух написанных рядом цифр (55) левая выражает число, в десять раз большее, чем правая. Имеет значение не только сама цифра, но и ее место, позиция. Именно поэтому такую систему счисления называют позицион­ной (поместной).

Потребовалось много тысячелетий, чтобы люди научи­лись называть и записывать числа так, как это делаем мы с вами. Начало этому было положено в Древнем Египте и Вавилоне и было в основном завершено индийскими мате­матиками в V—VII вв. н.э. Арабы, познакомившись с этой нумерацией первыми, по достоинству ее оценили. Полу­чив название арабской, эта система в XII в. н.э. распрост­ранилась по всей Европе и, будучи проще и удобнее ос­тальных систем счисления, быстро их вытеснила. Произошло это еще и потому, что простейший счетный прибор, рабо­тающий в десятичной системе счисления, был всегда у человека под рукой — это его 10 пальцев. В XIII веке монах Беда Достопочтенный составил описание правил счета, со­гласно которым различные загибы фаланг пальцев позволя­ли изображать единицы, десятки, сотни и тысячи, а опре­деленные жесты рук — считать до миллиона. Правда, та­кой "инструмент" имел один весьма существенный недо­статок — неудобство хранения результатов даже в течение короткого времени. Но зато у него есть и ряд немаловажных достоинств, которыми современные ученые пытаются наделить современные счетные устройства. Это прежде всего простота и надежность, а также компактность и удобство "хранения и транспортировки".

Сегодня десятичными числами выражаются время, но­мера домов и телефонов, цены, бюджет, на них базируется метрическая система мер. Арифметические действия над десятичными числами производятся с помощью достаточ­но простых операций, в основе которых лежат известные каждому школьнику таблицы умножения и сложения, а также правило переноса: если в результате сложения двух цифр получается число, которое больше или равно 10, то оно записывается с помощью двух цифр, находящихся на соседних позициях.

Изучаемые в самом раннем возрасте, эти правила в результате повседневной практики усваиваются так проч­но, что мы оперируем ими уже подсознательно. По этой причине сегодня многие люди даже не догадываются о су­ществовании других систем счисления.

Кроме десятичной истории цивилизации известны многие другие позиционные системы счисления, в том числе двадцатеричная и шестидесятеричная системы счисления. Остатки пос­ледней мы находим в сохранившемся до наших дней обыкнове­нии делить один час на 60 минут, одну минуту — на 60 секунд.

Вавилонская  система  имела  основанием  60,  и  особую  роль  в  ней  играли  числа  60,  60 ²  =  3600  и т.д. Младший  знак  числа  означал  число  единиц,  следующий  знак  - число «шестидесятков» и т.д. Каждый знак был числом от 1 до 59. Поскольку основанием было число очень большое – 60, вавилоняне записывали числа от 1 до 59 в десятичной системе, применяя принцип сложения. При этом они пользовались всего двумя знаками: вертикальным клином для обозначения 1 и горизонтальным для 10.

Таким образом, цифры, т.е. все числа от 1 до 59, вавилоняне записывали в десятичной непозиционной системе, а число в целом – в позиционной системе с основанием 60. Например, число 92 записывалось так:

Вавилонская нумерация имела и еще одну особенность: сначала знака для нуля не было вовсе. И если был изображен один вертикальный клин, нельзя было без дополнительных комментариев определить, какое число изображено: 1, 60, 3600 или какая-нибудь другая степень 60. Впоследствии вавилоняне придумали знак для обозначения пропущенного разряда (два горизонтальных клина, один над другим). Но, увы, этот знак не ставился в конце чисел.

Наконец, из-за такого большого основания таблица умножения была просто огромной, ее никто не запоминал, а при вычислениях использовалась готовая таблица, как мы совсем недавно пользовались таблицами логарифмов. Все это и предопределило судьбу вавилонской системы: дав толчок к развитию позиционных систем, вавилонская система была забыта, хотя отголоски ее былой распространенности можно заметить сейчас в делении часа на 60 минут и круга на 360 градусов.

  В Китае долгое время пользовались пятеричной систе­мой счисления.

Широкое распространение до первой трети XX в. име­ли элементы двенадцатеричной системы счисления. При этом число двенадцать (дюжина) даже составляло конку­ренцию десятке в борьбе за почетный пост основания общеупотребительной системы счисления. Дело в том, что число 12 имеет больше делителей (2, 3, 4, 6), чем 10 (2 и 5). Поэтому в двенадцатеричной системе счисления го­раздо удобнее производить расчеты, нежели в десятич­ной. Неудивительно, что в    XIX в. среди математиков раз­давались голоса за полный переход на эту систему. И только возможность счета по пальцам рук склонила чашу весов. Тем не менее дюжина достаточно прочно вошла в нашу жизнь: в сутках две дюжины часов, час делится на пять дюжин минут, круг содержит тридцать дюжин градусов, фут делится на двенадцать дюймов. Влияние двенадцатеричной системы счисления ощущается сегодня хотя бы в том, что карандашей или фломастеров в наборе обычно бывает 6, 12, 24 и т.д.

А вот шведский король Карл XII в 1717 г. увлекался восьмеричной системой, считал ее более удобной, чем де­сятичная, и намеревался королевским указом ввести ее как общегосударственную. Только неожиданная смерть поме­шала осуществлению столь необычного намерения.

Основные достоинства любой позиционной системы счисления — простота выполнения арифметических опе­раций и ограниченное количество символов, необходимых для записи любого числа.

Французский математик Пьер Симон Лаплас (1749— 1827) такими словами оценил, "открытие" позицион­ной системы счисления: "Мысль выражать все числа не­многими знаками, придавая им, кроме значения по фор­ме, еще значение по месту, настолько проста, что имен­но из-за этой простоты трудно оценить, насколько она удивительна".

Позиционная система записи чисел удобна и экономич­на не только для записи чисел знаками на бумаге и для вы­полнения над ними арифметических действий. Она удобна и для механического представления чисел. Вспомним, напри­мер, счеты. Каждому разряду числа (единицам, десяткам, сотням, тысячам и т.д., а также десятым и сотым долям еди­ницы) на счетах соответствует своя проволока. Костяшки на этой проволоке могут занимать десять различных положений (одиннадцатое положение — когда все десять косточек нахо­дятся с левой стороны — допускается лишь в середине вычис­лений, а в конце их является запретным: все десять косточек должны быть переброшены направо, а на следующей по стар­шинству проволоке одна косточка переброшена справа нале­во) . На практике применяются и другие способы физическо­го представления десятичных чисел:

- с помощью нескольких колес, каждое из которых может фиксироваться в одном из десяти возможных поло­жений;

- перфокарт, в каждой из вертикальных колонок ко­торых может пробиваться отверстие на одном из десяти уровней по высоте, и т.п.

Общим для всех этих представлений является то, что не­который физический носитель состоит из некоторого числа п однородных элементов (проволок с костями, колес, верти­кальных колонок перфокарты или мест по отношению к пра­вому краю записи), каждый из которых может находиться в  одном из десяти состояний. Любая такая система пригодна для изображения или записи 10ⁿ различных чисел.

Определение 4. Основанием (базисом) позиционной системы счисления называется ко­личество знаков или символов, ис­пользуемых для изображения числа в заданной системе счисления.

Основание в любой системе записывается как 10, но в разных системах имеет разное количественное значе­ние. Оно показывает, во сколько раз изменяется количе­ственное значение цифры при перемещении ее на сосед­нюю позицию.

В десятичном числе

А = 255 = 2 х 10² + 5 х 10¹ + 5 х 10 ⁰ цифры 5, находящиеся на разных позициях, имеют  раз­личные количественные значения — 5 десятков и 5 еди­ниц. При перемещении цифры на соседнюю позицию ее вес (числовой эквивалент) изменяется в 10 раз.

Позиционных систем очень много, так как за основа­ние системы счисления можно принять любое число не меньше 2. Наименование системы счисления соответству­ет ее основанию (десятичная, двоичная, пятеричная и т.д.).

 

2. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ

 

Недесятичные системы счисления. Развернутая и свернутая формы записи чисел. Схема Горнера

В повседневной жизни наиболее употребительна деся­тичная система счисления. И тем не менее великий фран­цузский математик и естествоиспытатель ,Блез Паскаль пи­сал: "Десятичная система построена довольно неразумно, конечно — в соответствии с людскими обычаями, а вовсе не с требованиями естественной необходимости, как склонно думать большинство людей" . В ряде как теоретических, так ипрактических задач некоторые системы счисления, отлич­ные от десятичной, имеют определенные преимущества.

Наша десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу сле­дующего старшего разряда. Другими словами, единицы различных разрядов представляют собой различные степе­ни числа 10.

В системе счисления с основанием  q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q, иначе говоря,  q единиц какого-либо раз­ряда образуют единицу следующего разряда. Для записи чисел в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа О, 1, ...,q — 1. Запись числа q в q-ичной системе счисления имеет вид 10.

В позиционной системе счисления любое веществен­ное число может быть представлено в следующем виде:

A _q = + (a _n-1 q ^n-1 +a _n-2 q ^n-2 +…+a ₀ q ⁰ +a _-1 q ^-1 +

a _-2 q ^-2 +…+a _-m q ^-m )   

(1)

    A _q = + S a _i *q ⁱ                        (1)

 =

Здесь А_q   — само число,

q — основание системы счисления,

а _i — цифры данной системы счисления,

п — число разрядов целой части числа,

т — число разрядов дробной части числа.

Определение 5. Запись числа по формуле (1) на­зывается развернутой формой записи.

Иначе такую форму записи называют многочленной, или степенной.

Пример 1. Десятичное число А₁₀=4718,63 в виде (1) запишется так:

 

А₁₆=4 х10³+7 х10² + 1 х10¹+8 х10⁰+6 х10-¹+3 х10-²                                                                                                                                                                           

Пример 2. Восьмеричная система счисления.

Основание: q=8.

Алфавит: 0, 1, 2, 3, 4, 5, 6 и 7.

Формула (1) для восьмеричной системы счисления имеет вид:

 

A ₈ =(a _n-1 8 ^n-1 +…+a ₀ 8  ⁰+a _-1 8 ^-1 +…+a _-m 8 ^-m )

где а_i — цифры 0—7.

 

Восьмеричное число А ₈ =  7764.1 в виде (1) запишется так:

 

 

А₈ =7 х8³+7 х8²+6 х8¹+4 х8⁰ +1х8-¹

Пример 3. Пятеричная система счисления.

Основание: q=5.

Алфавит: 0, 1, 2, 3 и 4.

Пятеричное число А₅  = 2430,21 в виде (1) запишется так:

 

А₅ =2 х5³+4 х5²+3 х5'+0 х5°+2 х5^-1+1 х5-²

 

Вычислив это выражение, можно получить десятичный эквивалент указанного пятеричного числа: 365,44.

 

Пример 4. Шестнадцатеричная система счисления.

Основание: q=16.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е и F.

Здесь только десять цифр из шестнадцати имеют об­щепринятое обозначение 0—9. Для записи остальных цифр обычно используются первые пять букв латинского алфа­вита — А, В, С, D, Е и F, означающие соответственно 10, 11, 12, 13, 14 и 15.

Таким образом, запись ЗАF 16 означает:

 

ЗАF₁₆=Зх16²+10х16¹+15х16°=Зх256+160+15=943₁₀.

 

Из (1) легко получить формулу (2) для записи произ­вольного целого числа:

 

A _ц  =  + (a _n-1 q ^n-1 +a _n-2 q ^n-2 +…a ₀ q  ⁰ )            (2)    

                                                                   15                                        и формулу (3) для записи произвольного дробного числа:                                          

А _др = ± (а__-1 q-¹+а_-2  q ^-2 +...+а_-m q^-m  )                (3)

 

Рассмотрим несколько примеров.

 Пример 5. А₁₀=1996

 

А₁₀=1х10³+9х10²+9х10¹+6х10⁰=(1х10²+9х10+9)х10+6= =(((1х10+9) х10)+9) х10+6=

=(((1+0) х10+9)х 10+9) х10+6

 

 

Пример 6. А₁₀=0,2345

А₁₀= 2/10+3/100+4/1000+5/10000= =(2+3/10+4/100+5/1000)/10= =(2+(3+4/10+5/100)/10)/10= =(2+(3+(4+5/10)/10)/10)/10=

=(2+(3+(4+(5+0)/10)/10)/10)/10

Преобразования такого рода называются преобразо­ваниями по схеме Горнера.

Преобразуем степенные ряды для целой (2) и дроб­ной (3) частей по схеме Горнера:

 

А_ц= [А] = (...(a _n-1 +0) х q+ a _n-2 )хq + …+а₁ )х q + а₀ (2')

 

A_др=[A]=(…(a_-m+0)/q+a-_m-1)/q+…+a_-1)/q                    (3')

 

Определение 6.   Свернутой формой записи числа называется запись в виде

A = a _n-1 a _n-2 … a ₁ a ₀ a _-1 …  a _{–m                                                                        (4)}

Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной, или цифровой.                                                           

3.ДВОИЧНАЯ  СИСТЕМА  СЧИСЛЕНИЯ.

3.1.Общие  сведения.

 

Из   всех   позиционных систем  счисления особенна  проста  и  поэтому  интересна двоичная система  счисления  . В  ней  для  записи  чисел  ипользуются  всего  две  цифры : 0 и 1 . Запись  10  означает  число  2,  как  как  две  единицы  данного  разряда  составляют  единицу  старшего  разряда .

В  двоичной системе счисления   основание  q = 2 . В  этом  случае  формула  (1)  примет  вид:

 

A₂  = ( a_n-1  * 2 ^n-1 + … + a₀ * 2⁰ + a_-1 2^-1 + … + a _–m 2 ^–m) (5)

 

Здесь  a_i  -  возможные  цифры  ( 0  и  1 )

Выпишем  начало  натурального  ряда  чисел  в  десятичной  и  двоичной системах  счисления  :

 

А10	А2	А10	А2
0      1      2      3      4      5      6      7	0       1     10     11    100    101    110    111	8        9       10       11       12       13       14       15	1000       1001       1010       1011       1100       1101       1110       1111

   Вопреки  распространненому  заблуждению, двоичная  система  счисления  была  придумана  не  инженерами – конструкторами  электронно-вычислительных  машин, а  математиками  и  философами  задолго  до  появления  компьютеров, ещё                           в  XVII-XIX  в.в. Великий  немецкий  учёный  Лейбниц  считал:___ 

        “Вычисление  с  помощью  двоек… являетсядля  науки  основным  и  порождает  новые  открытия… При  сведении  чисел  к  простейшим  началам, каковы  0  и  1, везде  появляется  чудесный  порядок.”

        Позже  двоичная  система  была  забыта, и  только  в  1936-1938  г.г.  американский  инженер  и  математик  Клод Шеннон  нашёл  замечательные  применения  двоичной  системы  при  конструировании  электронных  схем.     

Стоит  отметить, что  двоичная система  счисления  издавна  была  предметом  пристального  внимания  многих  ученых. Вот  что  писал  П.С.Лаплас  об  отношении  к  двоичной  (бинарной) системе  счисления  великого  немецкого  математика  Г.Ф.Лейбница : « В  своей  бинарной  арифметике  Лейбниц  видел  прообраз  творения. Ему  представлялось,  что  единица  представляет  божественное  начало, а  едиица – небытие  и  что  высшее  существо  создает  все  сущее  из  небытия  точно  таким  же  образом  .  как  единица  и  нуль  в  его  системе  выражает  все  числа». Эти  слова  подчеркивают  удивительную  универсальность  алфавита,  состоящего  всего  из  двух  символов.

   Представим  десятичное  число  1579  в  двоичной системе счисления.

   Для  этого  составим  таблицу  степеней  числа  2.

 

Воспользуемся  так  называемым  методом  разностей  .

   Берем  степень  чила  2 , ближайшую  снизу  к  переводимому  числу,  и  составляем  разность: 1579 – 1024 = 555

Затем  находим  следующую  степень  числа  2, меньшую  555,  и  составляем  разность:  555 – 512 = 43.

Три  очередные  степени  числа 2 (256,128,64) больше  остатка  43  и  поэтому  пропускаются.

Последующие  разности: 43 – 32 = 11,

11 – 8 = 3,

3 –2 = 1.

В  итоге:  1579 = 1024 + 512 +  0 + 0 + 0 + 32 + 0 + 8 + 0 + 2 + 1 =

 

1 * 2¹⁰ + 1*2⁹ + 0*2⁸ + 0*2⁷ + 0*2⁶ + 1*2⁵ + 0*2⁴ + 1*2³ + 0*2² +

 

+ 1*2¹ + 1*2⁰.

 

Это  число  в  свернутой  форме  записи  будет  иметь  вид:

 

11000101011.

 

Итак, двоичное  число  представляет  собой  цепочку  из  нулей  и  единиц. Обычно  у  него  достаточно  большое  число  разрядов.                   Быстрый  рост  числа  разрядов – самый  существенный  недостаток  двоичной системы  счисления.

 

3.2. Арифметические  операции  в  двоичной системе  счисления.

 

Для  того  чтобы  лучше  освоить  двоичную систему  счисления, изложим  вкратце  правила  выполнения  арифметических  операций  над  числами  ,  представленными  в  двоичной  записи.

   Арифметика  двоичной системы  счисления

 

	+ 0         1 0   1 0                  1   1       10		- 0          1 0   1 0                 11   1         0		*   0       1 0   1   1 0                0   0      1

 

 

 

 

означает  заем  из  старшего  разряда.

 

Рассмотрим  подробно  каждую  операцию.

 

СЛОЖЕНИЕ.

 

  

ВЫЧИТАНИЕ           .

 

                                              УМНОЖЕНИЕ.

 

ДЕЛЕНИЕ.

 

  

 

 

4.СВЯЗЬ  МЕЖДУ  СИСТЕМАМИ  СЧИСЛЕНИЯ.

4.1. Системы   счисления, родственные  двоичной.

 

При  работе  с  компьютерами  иногда  приходится  иметь  дело  с  двоичными числами,  поскольку  двоичные  числа  заложены  в конструкцию  компьютера.  Двоичная  система  удобна  для  компьютера, но  неудобна  для  человека – числа  получаются  очень  длинными  и  их  трудно  записывать  и  запоминать.  Конечно,  можно  перевести  двоичное  число  в  десятичную  систему  и  записать  его  в  таком  виде,  а  потом,  когда  оно  понадобится,  перевести  его  обратно,  но  все  эти  переводы  очень  трудоемки.  На  помощь  приходят  системы,  родственные  двоичной, -  восьмеричная  и  шестнадцатеричная.  Перевод  из  родственной  системы  в  двоичную  и  обратно  может  быть  мгновенно  выполнен  в  уме.

   Начнем  с  восьмеричной  системы.  В  этой  системе  8  цифр:  0, 1, 2, 3,4, 5, 6, 7.  Цифра1,  записанная  в  самом  младшем  разряде,  означает,  как и  в  десятичном  числе, просто  единицу.  Та  же  цифра  1  в  следующем  разряде  означает  8,  в  следующем  -  64  и  т.д. число  100₈    есть  не  что  иное,  как  64₁₀   ,  а  число  611₈  равно  6  ´   64₁₀   +  1  ´  8₁₀   +  1   =  393₁₀  .

 

4.2. Геометрическое  представление  чисел.

 

   Числа  могут  быть  представлены  не  только  алгебраически  специальными  знаками  на  бумаге,  папирусе  или  бересте,  но  и  геометрически.  Такое  представление  чисел  широко  используется  в  различных  механических  устройствах ,  например  в спидометре.

   Спидометр  кодирует  числовое  значение  скорости  геометрически,  как положение  стрелки  на  круговой  или  линейной  шкале.  И  это  геометрическое  представление  ничуть  не  хуже  представления  цифрами,  а  в  чем-то  даже  и  лучше.  Летчик,  посмотрев  на  число,  может  ошибочно  принять  600  км/ч  за  900км/ч,  начать  снижать  скорость,  и  из-за   нехватки  скорости  самолет  войдет в  штопор.  Со  стрелочным  спидометром  вероятность  такой  ошибки  значительно  меньше.  Поэтому  даже  на самых  современных  самолетах  часть  приборов  выводит  данные  не  в  виде  символов,  а  в виде  положения  стрелки  на  циферблате,  шкале  и  т.п.

   Геометрическое  представление  экономических  данных,  результатов  выборов,  опросов  общественного  мнения  широко  используется  в  газетах,  журналах,  книгах.  Такое  представление  называется  диаграммой.     

4.3. Перевод чисел из одной системы счисления в другую.

4.3.1. Перевод  целых  чисел.

 

 

4.3.2. Перевод  правильных  дробей.

 

4.3.3. Перевод смешанных чисел

 

 

 

4.3.4. Перевод чисел из систем счисления с основанием 2ⁿ в систему счисления с основанием 2 и обратно

 

 

 

5. СИСТЕМЫ СЧИСЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В ЭВМ

 

От того, какая система счисления будет использована в ЭВМ, зависят скорость вычислений, емкость памяти, слож­ность алгоритмов выполнения арифметических операций.

Дело в том, что для физического представления (изобра­жения) чисел необходимы элементы, способные находиться в одном из нескольких

               устойчивых состояний. Число этих состояний должно быть равно основанию принятой системы счисления. Тогда каждое состояние будет представлять соот­ветствующую цифру из алфавита данной системы счисления.

Десятичная система счисления, привычная для нас, не является наилучшей для использования в ЭВМ. Для изобра­жения любого числа в десятичной системе счисления требу­ется десять различных символов. При реализации в ЭВМ этой системы счисления необходимы функциональные эле­менты, имеющие ровно десять устойчивых состояний. Так, в арифмометрах используются вращающиеся шестеренки, в которых фиксируется десять устойчивых положений. Но арифмометр и другие подобные механические устройства имеют серьезный недостаток — низкое быстродействие.

Создание электронных элементов, имеющих много ус­тойчивых состояний, затруднено. Наиболее простыми с точки зрения технической реализации являются так назы­ваемые двухпозиционные элементы, способные находить­ся в одном из двух устойчивых состояний, например:

-    электромагнитное реле замкнуто или разомкнуто;

-    ферромагнитная поверхность намагничена или раз­магничена;

—магнитный сердечник намагничен в одном направлении или в противоположном;

—транзисторный ключ находится в проводящем состоянии или запертом и т.д.

Одно из этих устойчивых состояний может представляться цифрой 0, другое — цифрой 1. С двоичной системой связаны и другие существенные преимущества. Она обеспечивает мак­симальную помехоустойчивость в процессе передачи инфор­мации как между отдельными узлами автоматического уст­ройства, так и на большие расстояния. В ней предельно прос­то выполняются арифметические действия и возможно при­менение аппарата булевой алгебры для выполнения логичес­ких преобразований.

Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.

Большое применение в ЭВМ нашли также восьме­ричная и шестнадцатеричная системы счисления. Об­мен информацией между устройствами большинства ЭВМ осуществляется путем передачи двоичных чисел. Пользо­ваться такими числами из-за их большой длины и зри­тельной однородности человеку неудобно. Поэтому спе­циалисты (программисты, инженеры) как на этапах со­ставления программ для ЭВМ, их отладки, ручного ввода/вывода данных, так и на этапах разработки, создания, настройки вычислительных систем заменяют коды машин­ных команд, адреса и операнды на эквивалентные

им ве­личины в восьмеричной или шестнадцатеричной систе­мах счисления. В результате длина исходного слова сокра­щается в три, четыре раза соответственно. Это делает ин­формацию более удобной для рассмотрения и анализа. Таким образом, восьмеричная и шестнадцатеричная сис­темы счисления выступают в качестве простейшего языка общения человека с ЭВМ, достаточно близкого как к при­вычной для человека десятичной системе счисления, так и к двоичному "языку" машины.

Как правило, пользователь ЭВМ вводит исходную ин­формацию и получает результат решения задачи в десятич­ной системе счисления.

При вводе информации в ЭВМ каждая десятичная цифра заменяется ее двоичным эквивалентом в виде тет­рады (четыре двоичных разряда). Десятичное число тре­бует для своего изображения стольких тетрад, сколько имеется десятичных разрядов в числе. Таким образом, де­сятичные цифры представляются в двоичной системе счис­ления, а все разряды без изменения — в десятичной сис­теме счисления. Это позволяет выполнять арифметичес­кие операции в десятичной системе счисления, используя двоичные элементы для хранения и переработки число­вой информации. Такая форма представления данных на­зывается двоично-десятичной. Говорят о двоично- десятич­ном коде (ДДК) или смешанной двоично-десятичной системе счисления.

 

Пример 1. Число 38 в смешанной двоично- десятичной системе будет иметь вид:

0011   1000

Обратите внимание на то, что приведенная запись не соответствует двоичному представлению десятичного числа 38 и

38₁₀=100110₂

Для преобразования двоично-десятично кода в двоич­ное число в ЭВМ используется схема Горнера.

 

Пример 2. Найдем двоичное представление числа, за­писанного в двоично- десятичном коде:

А_2-10_=001 1 1000_2-10_=0011₂х 1010₂+1000₂=1001

 

1010                                                  11110

·                                                     +

11                                                            1000

1010                                             100110 

         +

           1010

           11110                                                                                          36

При выводе информации из ЭВМ производится обрат­ное преобразование: двоичное число переводится в ДДК и затем десятичное число выводится на печать.

 

 

 

 

 

 

X	-1	0	1
-1	1	0	-1
0	0	0	0
1	1	0	1

 

ЛИТЕРАТУРА :

 

 

1.Касаткин В.Н. Информация, алгоритмы, ЭВМ: Пособие  для  учителя. – М.:Просвещение, 1991.

 

2.Нестеренко А.В. ЭВМ и профессия  программиста:

Книга  для  учащихся  старших классов средней школы, -

М.: Просвещение, 1990.

 

3.Зотов В.В. Пособие оператора ЭВМ:Практическое пособие, - М.:Высшая школа, 1993.

 

4.Лавров С.С. Введение  в  программирование. – М.: Наука, 1977.

 

5.Перельман Я.Н. Занимательная  арифметика. – М.: Триада-Литера, 1994.

6.Симонович С Общая  информатика. – М.:АСТ-ПРЕСС КНИГА, 2002                                                                                          

7.Кушниренко   А.Г.  и  др.   Информационная  культура  . Кодирование  информации, класс 9. – М., «Дрофа», 1995.