Методика изучения теоремы о вписанной и описанной окружности

Методика изучения теоремы

Теорема «В любой треугольник можно вписать окружность».

«Около лебого треугольника можно описать окружность».

1. Подготовительный этап

1.1.               Мотивация изучения теоремы

Для того чтобы начать изучать нашу тему давайте подумаем, сможем ли мы решить нашу задачу, основываясь только на изученный материал?   Нет, как вы можете видеть из условия задачи №1 старых знаний о касательной и секущей к окружности  нам не достаточно, для этого мы с вами сегодня познакомимся с понятиям описанной окружности.

Задача 1

Жильцы трех домов решили совместными усилиями построить колодец. Какое место для колодца следует выбрать, чтобы все три расстояния от него до домов были одинаковыми? [5].

Ответ: Пусть А, В и С — точки расположения трех данных домов. Проведем серединные перпендикуляры к отрезкам АВ и ВС. Тогда точка О их пересечения будет единственной точкой, равноудаленной от точек А, В и С, поскольку для этой точки выполнены равенства АО=ОВ и ВО=ОС, а если точку О выбрать иначе, то для нее хотя бы одно из указанных равенств будет несправедливо. Заметим, что проведенные перпендикуляры могут и не пересечься, но только в случае, когда точки А, В и С лежат на одной прямой. Таким образом, искомое место для колодца — точку О — можно найти приведенным способом, но лишь при условии, что дома расположены не на одной прямой.

1.2. Актуализация знаний и умений учащихся, необходимых для сознательного усвоения теоремы

Для того чтобы ученик полностью освоил тему и владел определениями и понятиями необходимо повторить ряд определений представленных в Табл. 1.

Таблица 1

№	То, что необходимо повторить	Задания для повторения
11	Окружность	Начертите окружность с радиусом 2 см ( рис. 1)             Рис. 1
2	Диаметр	Определить на рис. 2 диаметр окружности, если известно, что радиус -  2 см.               Рис. 2
	Радиус	Определите из рис. 3 радиус окружности, если известно, что диаметр 16 см.                            Рис. 3
	Сфера	Из рис. 4 сформулировать понятия сферы. Рис. 4

1.3. Подведение учащихся к формулировке теоремы

Задача 2

 Как далеко видно с воздушного шара, поднявшегося на высоту км над Землей (радиус Земли примерно равен  км)? (рис. 5).

Решение: По теореме о касательной к окружности, касательная перпендикулярна радиусу, проведенному в точку касания, то есть 
.
Тогда по теореме Пифагора: ,

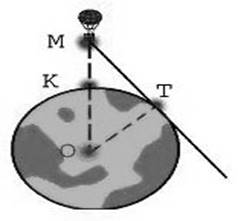
Рис.5

 (км.)

Ответ: км.

Сделать вывод.

В любой треугольник можно вписать окружность, центр вписанной окружности – точка пересечения биссектрис.

Около любого треугольника можно описать окружность, центр описанной окружности – точка пересечения серединных перпендикуляров.

2. Основной этап

2.1. Формулировка теоремы, овладение ее содержанием, структурой, назначением

Вписанная окружность

Определение: если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.                                                                                Рис. 6

Теорема: в любой треугольник можно вписать окружность, и притом только одну.

Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.

Свойство: в любом описанном четырехугольнике суммы противоположных сторон равны.

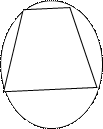Признак: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Описанная окружность

Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.                                                                       

   Рис. 7

Теорема: около любого треугольника можно описать окружность, и притом только одну.

Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.

Свойство: в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.

Признак: если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность

2.2. Формирование ориентировочной схемы доказательства. Проведение доказательства

Вписанная окружность

Описанная окружность

3. Заключительный этап

Вопросы для закрепления теоремы.

1.     Можно ли в параллелограмм вписать окружность? ( Не всегда, надо чтобы суммы противоположных сторон были равны)

2.     А описать около него окружность? ( Нет, не всегда, сумма противоположных углов должна быть 180)

Закончите предложение:

3.     Центр вписанной в треугольник окружности –точка пересечения его ...(биссектрис)

4.     Центр вписанной в треугольник окружности равноудален от его...(сторон)

5.     Многоугольник называется вписанным в окружность, если  все его ...(вершины лежат на окружности)

6.     Окружность вписана в многоугольник, если ...(все его  стороны касаются окружности)

7.     Вписанные углы равны, если они...(опираются на одну дугу)

8.     Центр описанной около треугольника окружности  равноудален от его ...(вершина)

Рассмотрение обратных, противоположных утверждений, связанных с теоремой.

В любой треугольник можно вписать окружность и притом только одну.

Если все стороны многоугольника являются касательными одной окружности, то такая окружность называется вписанной в многоугольник.

Около любого треугольника можно описать окружность и притом только одну.

Если на окружности лежат все вершины многоугольника, то окружность называется описанной около многоугольника.

 Задачи базового, основного и продвинутого уровня сложности (по 2 задачи каждого уровня).

В окружающем нас мире существует множества предметов которые имеют форму окружности или ее элементы и в связи с этим мы можем решить ряд практических задач.

Приведем примеры в табл. 2.

Таблица 2

Прикладные задачи с решениями.

Для закрепления теоретического материала необходимо решить ряд прикладных задач. Задачи такого типа, разбитые на уровни представлены в табл. 3.

Таблица 3

Включение теоремы в систему знаний

Решение задачи на нахождения радиуса вписанной и описанной окружности равнобедренного треугольника.

Задача1 .

Найдите радиус R описанной окружности  для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. (рис. 24).

 Сначала  выясним, где находится центр описанной окружности – от этого зависит рисунок к задаче. Здесь 10² меньше 13² + 13², значит, угол при вершине этого равнобедренного треугольника острый. Центр описанной окружности находится во внутренней области  равнобедренного треугольника.

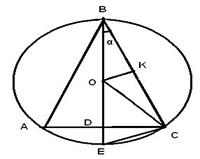
Рис. 24

Первый способ

Проведя серединный перпендикуляр  КО, получим точку  О – центр описанной окружности  (КО + ВС и ВК = КС = 6,5см). ОВ = ОС = R.   OD = BD – OB = 12 – R. Из ODC по теореме Пифагора  OD2  = ОС2 – DC2 = R2 – 52. R2  –  52   = (12 – R)2. Решив это уравнение, получим   R = 169/24  см.

Ответ: R = 169/24  см.

Второй способ

Из подобия треугольников  OBK  и  CBD  имеем ОВ/СВ = BK/BD, т.е. R/13 = 6,5/12 и  получаем.

 Ответ: R = 169/24 см

Третий способ

Продолжив BD до пересечения с описанной окружностью, получим прямоугольный треугольник ВСЕ, откуда ВС² = BD • BE, 132 = 12 • 2R, и

 R = 169/24см.

Четвёртый способ

По свойству хорд, пересекающихся внутри круга BD • DE = AD • DC; 12 • (2R –12) = 5 • 5.

Ответ: R = 169/24  см.

Пятый способ

По формуле  R = abc/(4S ),  где a,  b,  c – стороны треугольника, S – его площадь, которую мы вычислим без труда.

Шестой способ

И ещё один метод решения задачи – метод координат, который является универсальным методом геометрии.

Главное при решении задачи этим методом удачный выбор системы координат(основание треугольника лежит на оси абсцисс, а ось ординат проходит через высоту, проведённую к основанию .Вершины треугольника равноудалены от центра окружности).                                                

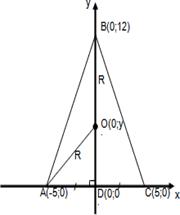ОА=ОВ

                     Рис. 25          

Задача2.

 Найдите радиус r вписанной окружности  для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см. (рис. 26)

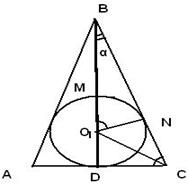
Рис. 26

Первый способ

Из BNO1  следует, что O1N = r = BO1 • sin, т.е. r = (12 – r) · 5/13   и 

 r = 10/3см.

Ответ: r = 10/3см 

Второй способ

О1 – центр вписанной окружности, O1N = r.  DC = CN = 5 см  по свойству касательных, проведённых из одной точки к одной  окружности.  

BN =13 – 5 = 8 (см).  ВО1 = 12 – r. Из BNO1 по теореме Пифагора

r2 = (12 – r)2 – 82,  откуда  r = 10/3см.

Третий способ

r = 2S/(a + b + c), r = 2 • 60/(13 + 10 + 13), тогда  r = 10/3см.

Четвёртый способ

Из подобия   O1NB и  CDB следует, что   ВО1/BC = BN/BD, 

(12 – r)/13 = 8/12  и   r = 10/3см.

Пятый способ

По свойству  биссектрисы  CBD,  имеем CD/CB = DO1/BO1, 

5/13 = r/(12 – r), а тогда из этой пропорции получим r = 10/3см.

Шестой способ.

 По свойству  касательной и секущей, проведёнными из одной точки к одной окружности, мы решили эту задачу так:

 BN2 = BD • BM, т.е. 82 = 12 • (12 – 2r), откуда r = 10/3см.