
7 МНОГОМЕРНАЯ ГЛОБАЛЬНАЯ УСЛОВНАЯ ОПТИМИЗАЦИЯ
7.1 Метод сведения к совокупности вложенных задач глобальной одномерной оптимизации
Рассматривается следующая многомерная задача глобальной условной оптимизации: найти минимум критерия оптимальности f(x), определенного во множестве D пространства Rn,
![]() (7.1)
(7.1)
где множество допустимых значений
![]() (7.2)
(7.2)
Положим, что множество допустимых значений D задается только с помощью ограничений типа неравенств и представляет собой гиперпараллелепипед
![]() (7.3)
(7.3)
Метод сведения к совокупности вложенных одномерных задач глобальной оптимизации состоит в решении вместо задачи (7.1), (7.3) следующей совокупности вложенных одномерных задач условной оптимизации
![]() (7.4)
(7.4)
где множества ![]() представляют собой соответствующие
сечения множества D (см. ниже).
представляют собой соответствующие
сечения множества D (см. ниже).
Поясним смысл метода с помощью примера.
Пример. Положим, что ![]() и
и ![]() , т.е. n = 2. Вложенные одномерные задачи глобальной оптимизации
(7.4) в этом случае можно представить в виде (рис. 7.1)
, т.е. n = 2. Вложенные одномерные задачи глобальной оптимизации
(7.4) в этом случае можно представить в виде (рис. 7.1)
![]() (7.5)
(7.5)
![]() (7.6)
(7.6)
где D(x1) – сечение
области D прямой, параллельной оси Ox. Задача (7.5) представляет собой одномерную задачу
глобальной оптимизации критерия оптимальности f(x1) по параметру ![]() ,
для вычисления значения которого при данном фиксированном x1
необходимо решить одномерную задачу глобальной оптимизации критерия оптимальности
f(x1, x2) по параметру
,
для вычисления значения которого при данном фиксированном x1
необходимо решить одномерную задачу глобальной оптимизации критерия оптимальности
f(x1, x2) по параметру ![]() .
.
Положим, что для решения всех вложенных одномерных задач глобальной
оптимизации (7.4) используется метод случайного поиска. Обозначим Nk число испытаний, необходимых для отыскания
методом перебора с заданной точностью глобального минимума функции ![]() по параметру
по параметру ![]() (когда параметры
(когда параметры ![]() фиксированы). Тогда общее
количество испытаний для решения задачи (7.1), (7.3) равно, очевидно,
фиксированы). Тогда общее
количество испытаний для решения задачи (7.1), (7.3) равно, очевидно,
![]() .
.
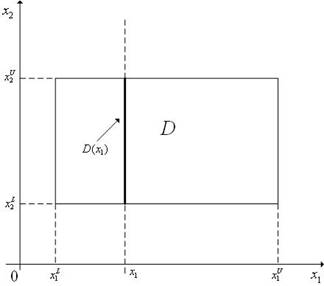 |
Рис. 7.1. При решении задачи (7.5) вычисление значения критерия оптимальности f(x) при некотором x = x1 требует решения задачи минимизации (7.6) на множестве D(x1)
Поэтому при n >
3 такой алгоритм становится неэффективным. При ![]() надежность
алгоритма достаточно высока, а затраты на поиск значительно меньше затрат на
полный перебор на той же сетке.
надежность
алгоритма достаточно высока, а затраты на поиск значительно меньше затрат на
полный перебор на той же сетке.
Метод решения многомерной задачи глобальной условной оптимизации путем сведения к совокупности вложенных одномерных задач глобальной оптимизации может быть скомбинирован со всеми рассмотренными в главе 4 методами решения одномерных задач глобальной оптимизации. Рассмотрим комбинацию этого метода с методом случайного поиска для двумерной задачи (7.1), (7.3).
Алгоритм комбинации метода с методом случайного поиска (n = 2)
Шаг 1. Задаем величины N1, N2 – количества испытаний при решении задач (7.5), (7.6), соответственно. Полагаем r = 1.
Шаг 2. Генерируем с помощью какого-либо программного генератора случайных
чисел, равномерно распределенных в интервале ![]() ,
случайное число
,
случайное число ![]() .
.
Шаг 3. Методом случайного поиска решаем задачу (7.6) при ![]() – находим точку
– находим точку ![]() и вычисляем значение критерия
оптимальности
и вычисляем значение критерия
оптимальности ![]()
Шаг 4. Аналогично шагу 2 генерируем случайное число ![]() .
.
Шаг 5. Методом случайного поиска решаем задачу (7.6) при ![]() – находим точку
– находим точку ![]() и вычисляем значение критерия
оптимальности
и вычисляем значение критерия
оптимальности ![]() .
.
Шаг 6. Если ![]() , то выполняем
присваивания
, то выполняем
присваивания ![]() .
.
Шаг 7. Если ![]() , то выполняем
присваивание
, то выполняем
присваивание ![]() и переходим к шагу 4. Иначе
принимаем точку
и переходим к шагу 4. Иначе
принимаем точку ![]() в качестве приближенного
значения точки глобального минимума функции f(x) в области D или
каким-либо из рассмотренных ранее методов организуем в окрестности указной
точки поиск локального минимума функции f(x) и заканчиваем вычисления.
в качестве приближенного
значения точки глобального минимума функции f(x) в области D или
каким-либо из рассмотренных ранее методов организуем в окрестности указной
точки поиск локального минимума функции f(x) и заканчиваем вычисления.
Отметим еще раз, что рассмотренный метод, как и любой другой метод глобальной оптимизации, при отсутствии априорной информации о свойствах минимизируемой функции не гарантирует нахождение глобального минимума.
Комбинацию рассматриваемого метода с методом случайного поиска для
двумерной задачи иллюстрирует рис. 7.2, на котором показан фрагмент линий
уровня функции Химмельблау (n =
2). Принято, что x* – точка минимума функции f(x) в области D
после (r – 1)-й итерации. Точки на прямой ![]() случайным
образом сгенерированы на r-й итерации. После завершения r-й
итерации очевидно
случайным
образом сгенерированы на r-й итерации. После завершения r-й
итерации очевидно ![]() .
.
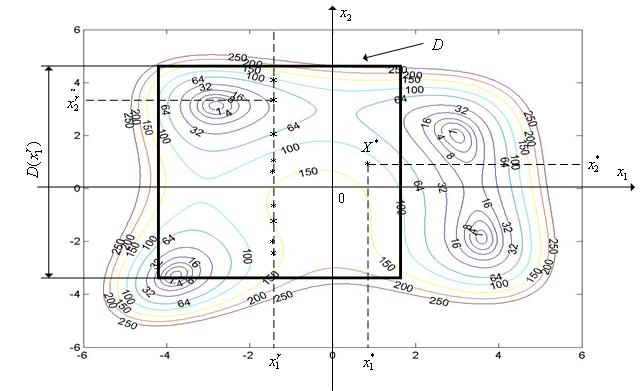 |
Рис. 7.2. Итерация номер r комбинации метода сведения с методом случайного поиска для двумерной задачи
7.2 Метод сведения к задаче одномерной глобальной оптимизации с помощью развертки Пеано
Рассмотрим многомерную задачу глобальной условной оптимизации
![]() (7.7)
(7.7)
где множество допустимых значений D задается только с помощью ограничений типа неравенств и представляет собой гиперкуб с длиной ребра, равной 1,
![]() .
(7.8)
.
(7.8)
Отметим, что произвольный гиперпараллелепипед с помощью линейного преобразования может быть сведен к гиперкубу (7.8), так что рассмотрение в качестве множества D гиперкуба (7.8), а не гиперпараллелепипеда, не сужает общности рассуждений.
Рассматриваемый метод основан на использовании непрерывного отображения гиперкуба D на отрезок вещественной оси.
Разбиение гиперкуба. Развертка Пеано
Шаг 1 (s = 1).
Координатными плоскостями гиперкуб D разбивается
на 2n гиперкубов первого разбиения с
длиной ребра, равной 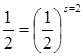 (рис. 7.3, а).
Пронумеруем их с помощью переменной
(рис. 7.3, а).
Пронумеруем их с помощью переменной ![]() таким образом,
чтобы гиперкубы с номерами, отличающимися на единицу, имели общую грань.
Соединим центры гиперкубов ломаной
таким образом,
чтобы гиперкубы с номерами, отличающимися на единицу, имели общую грань.
Соединим центры гиперкубов ломаной ![]() в порядке
введенной нумерации. Гиперкуб первого разбиения с номером z1
обозначим D(z1).
в порядке
введенной нумерации. Гиперкуб первого разбиения с номером z1
обозначим D(z1).
Шаг 2 (s = 2). По
рассмотренной схеме каждый гиперкуб первого разбиения разобьем плоскостями,
параллельными координатным плоскостям и проходящими через его центр, на 2n гиперкубов второго разбиения с длиной ребра,
равной 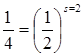 (рис. 7.3, б). Пронумеруем
полученные гиперкубы с помощью переменной
(рис. 7.3, б). Пронумеруем
полученные гиперкубы с помощью переменной ![]() по
тому же правилу, что и гиперкубы первого разбиения, с тем отличием, что нулевой
гиперкуб второго разбиения, входящий в гиперкуб D(z1), должен иметь общую грань с (2n – 1)-м гиперкубом
второго разбиения, входящим в гиперкуб D(z1 – 1). Соединим центры гиперкубов ломаной
по
тому же правилу, что и гиперкубы первого разбиения, с тем отличием, что нулевой
гиперкуб второго разбиения, входящий в гиперкуб D(z1), должен иметь общую грань с (2n – 1)-м гиперкубом
второго разбиения, входящим в гиперкуб D(z1 – 1). Соединим центры гиперкубов ломаной ![]() в порядке введенной нумерации.
Обозначим гиперкубы второго разбиения D(z1, z2).
в порядке введенной нумерации.
Обозначим гиперкубы второго разбиения D(z1, z2).
…
Шаг s. Аналогично шагу 2 разбиваем гиперкубы (s
– 1)-го разбиения на гиперкубы s-го разбиения с
длиной ребра, равной ![]() , нумеруем их с помощью
переменной
, нумеруем их с помощью
переменной ![]() , соединяем центры гиперкубов
ломаной
, соединяем центры гиперкубов
ломаной ![]() в порядке введенной нумерации и
обозначаем D(z1,z2,…,zs).
в порядке введенной нумерации и
обозначаем D(z1,z2,…,zs).
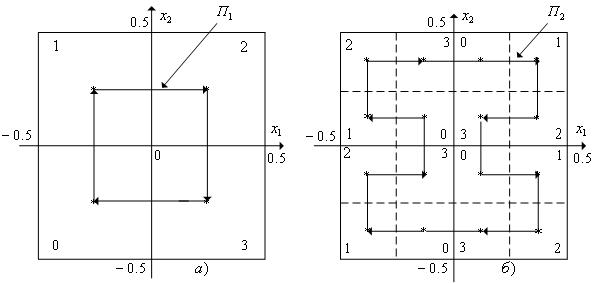
Рис. 7.3. К разбиению гиперкуба (n = 2). а) Первое разбиение. б) Второе разбиение. Стрелками показано направление нумерации гиперкубов
Ломаная ![]() называется разверткой
Пеано. В пределе при
называется разверткой
Пеано. В пределе при ![]() ломаная
ломаная ![]() называется кривой Пеано. Кривая
Пеано обладает тем свойством, что проходит через все точки гиперкуба и имеет в
каждой точке излом
называется кривой Пеано. Кривая
Пеано обладает тем свойством, что проходит через все точки гиперкуба и имеет в
каждой точке излом
Разбиение отрезка [0, 1]
Шаг 1 (s = 1).
Разобьем отрезок [0, 1] на 2n равных
частей длиной 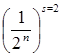 (рис. 7.4, а),
пронумеруем их слева направо с помощью переменной
(рис. 7.4, а),
пронумеруем их слева направо с помощью переменной ![]() и
обозначим
и
обозначим ![]() .
.
Шаг 2 (s = 2).
Каждый из отрезков ![]() ,
, ![]() разобьем на 2n равных частей длиной
разобьем на 2n равных частей длиной 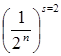 (рис.
7.4, б), пронумеруем их слева направо с помощью переменной
(рис.
7.4, б), пронумеруем их слева направо с помощью переменной ![]() и обозначим
и обозначим ![]() .
.
...
Шаг s. Аналогично шагу 2 каждый из
отрезков (s – 1)-го разбиения разобьем на 2n равных частей длиной ![]() ,
пронумеруем их слева направо с помощью переменной
,
пронумеруем их слева направо с помощью переменной ![]() и
обозначим
и
обозначим ![]() .
.
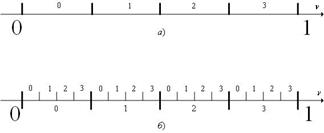 |
Рис. 7.4. К разбиению отрезка [0, 1]. а) Первое разбиение. б) Второе разбиение
Отображение отрезка [0, 1] на гиперкуб
Определим отображение точки ![]() отрезка
[0,1] на гиперкуб D следующим образом: если
точка
отрезка
[0,1] на гиперкуб D следующим образом: если
точка ![]() , то соответствующая точка
, то соответствующая точка ![]() является центром гиперкуба
является центром гиперкуба ![]() . Обозначим введенное отображение
. Обозначим введенное отображение ![]() . Таким образом, если
. Таким образом, если ![]() , то
, то ![]() =
=![]()
![]()
![]() (рис. 7.5).
(рис. 7.5).
На рис. 7.5 любая точка ![]() отображается в
центр гиперкуба D(0,2) – точку xD(0,2). Аналогично, любая точка
отображается в
центр гиперкуба D(0,2) – точку xD(0,2). Аналогично, любая точка ![]() отображается в точку xD(1,3) и любая точка
отображается в точку xD(1,3) и любая точка ![]() отображается в точку xD(2,1).
отображается в точку xD(2,1).
В пределе при ![]() введенное отображение
отображает отрезок [0,1] на кривую Пеано. Можно показать, что в пределе при
введенное отображение
отображает отрезок [0,1] на кривую Пеано. Можно показать, что в пределе при ![]() построенное отображение является
непрерывным и взаимнооднозначным.
построенное отображение является
непрерывным и взаимнооднозначным.
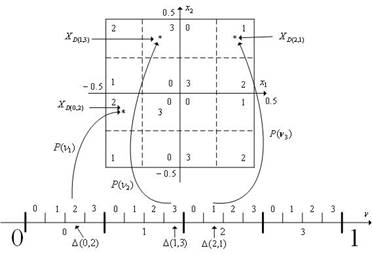 |
Рис. 7.5. К отображению отрезка [0, 1] на гиперкуб
Пусть ![]() – двоичное представление
числа
– двоичное представление
числа ![]() , т.е.
, т.е. ![]()
![]() .
.
Утверждение. Если ![]() , то первые sn двоичных цифр числа
, то первые sn двоичных цифр числа ![]()
![]() определяют разбиение
определяют разбиение ![]() отрезка [0,1]:
отрезка [0,1]:
![]()
![]()
...
![]()
Здесь ![]() – операция преобразования
двоичного числа в десятичное.
– операция преобразования
двоичного числа в десятичное.
Пример. Пусть область D
представляет собой квадрат (n =
2). На отрезке [0,1] рассмотрим точки ![]() –
рис. 7.6.
–
рис. 7.6.
Преобразуем ![]() в двоичную систему счисления:
в двоичную систему счисления:
0,26 · 2 = 0,52 – запоминаем целую часть 0;
0,52 · 2 = 1,04 – запоминаем целую часть 1;
0,04 · 2 = 0,08 – запоминаем целую часть 0;
0,08 · 2 = 0,16 – запоминаем целую часть 0;
0,16 · 2 = 0,32 – запоминаем целую часть 0;
0,32 · 2 = 0,64 – запоминаем целую часть 0;
0,64 · 2 = 1,28 – запоминаем целую часть 1.
Итого,![]() . Таким образом,
. Таким образом, ![]() .
.
Аналогично ![]() . Таким образом,
. Таким образом, ![]() .
.
И ![]() . Таким образом,
. Таким образом, ![]() .
.
 |
Рис. 7.6. К примеру
Определим на отрезке [0,1] функцию ![]() .
Отметим, что если функция f(x)
является непрерывной функцией, то функция
.
Отметим, что если функция f(x)
является непрерывной функцией, то функция ![]() также
непрерывна. Однако эта функция является негладкой и многоэкстремальной, даже
если исходная функция f(x)
гладкая и унимодальная.
также
непрерывна. Однако эта функция является негладкой и многоэкстремальной, даже
если исходная функция f(x)
гладкая и унимодальная.
Таким образом, с помощью развертки Пеано многомерная задача глобальной условной оптимизации (7.7), (7.8) сводится к одномерной задаче условной глобальной оптимизации
![]()
Решение задачи многомерной глобальной условной оптимизации с помощью развертки Пеано
Метод решения многомерной задачи глобальной условной оптимизации с использованием развертки Пеано называется методом развертки Пеано и может быть скомбинирован со всеми рассмотренными в главе 4 методами решения одномерных задач глобальной оптимизации. При этом тот факт, что фактически решается задача не одномерной, а многомерной оптимизации, вносит следующие особенности в указанные методы:
1 Должна быть задана требуемая точность ![]() решения
исходной задачи (7.7), (7.8) по x. Исходя из
этой точности, предварительно должно быть определено s – количество разбиений области D
(см. ниже).
решения
исходной задачи (7.7), (7.8) по x. Исходя из
этой точности, предварительно должно быть определено s – количество разбиений области D
(см. ниже).
2 Вычисления значений критерия оптимальности ![]() должны
производиться по следующей схеме:
должны
производиться по следующей схеме:
- для заданного ![]() находим sn цифр его двоичного представления
находим sn цифр его двоичного представления ![]() ;
;
- определяем числа ![]() ,
, ![]() ,…,
,…, ![]()
- в гиперкубе ![]() выбираем его центр x
выбираем его центр x![]() ;
;
- вычисляем значение критерия оптимальности f(x) в этой точке, которое и принимаем за значение ![]() .
.
При заданной точности ![]() решения задачи
(7.7), (7.8) по x необходимое количество s разбиений гиперкуба D
может быть найдено из следующих соображений. Гиперкуб s-го
разбиения
решения задачи
(7.7), (7.8) по x необходимое количество s разбиений гиперкуба D
может быть найдено из следующих соображений. Гиперкуб s-го
разбиения ![]() имеет длину ребра, равную
имеет длину ребра, равную ![]() . Максимальное расстояние точек
этого гиперкуба до его центра равно половине диагонали гиперкуба, которая,
очевидно, равна корню квадратному из суммы квадратов n ребер гиперкуба,
т.е.
. Максимальное расстояние точек
этого гиперкуба до его центра равно половине диагонали гиперкуба, которая,
очевидно, равна корню квадратному из суммы квадратов n ребер гиперкуба,
т.е. 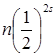 . Таким образом, s может быть найдено из условия
. Таким образом, s может быть найдено из условия
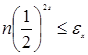 .
.
Отметим еще раз, что рассмотренный метод, как и любой другой метод глобальной оптимизации, при отсутствии априорной информации о свойствах минимизируемой функции не гарантирует нахождение глобального минимума.
7.3 Метод Монте-Карло
Рассмотрим многомерную задачу глобальной условной оптимизации
![]() (7.9)
(7.9)
где множество допустимых значений
![]() (7.10)
(7.10)
Метод Монте-Карло относится к классу прямых методов случайного поиска.
Алгоритм метода Монте-Карло
Шаг 1. Задаем общее количество испытаний N и полагаем счетчик числа итераций r = 1.
Шаг 2. С помощью какого-либо программного генератора случайных чисел
генерируем n компонент вектора ![]() .
.
Шаг 3. Вычисляем f(x1)
и полагаем ![]() .
.
Шаг 4. Аналогично шагу 2 генерируем случайную точку ![]() . Вычисляем соответствующее
значение критерия оптимальности
. Вычисляем соответствующее
значение критерия оптимальности ![]() .
.
Шаг 5. Выполняем следующие присваивания:
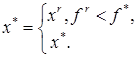
Шаг 6. Если r < N, полагаем r = r + 1 и переходим к шагу 4, иначе принимаем x*, f* в качестве приближенного решения задачи и заканчиваем вычисления.
Отметим, что в простейшем случае точки ![]() генерируются
равномерно распределенными в области D. С целью
сокращения вычислительных затрат и при наличии априорной информации о положении
точки глобального минимума целесообразно использовать законы распределения, в
которых вероятность генерации точки в окрестности предполагаемого глобального
минимума выше, чем вне этой окрестности.
генерируются
равномерно распределенными в области D. С целью
сокращения вычислительных затрат и при наличии априорной информации о положении
точки глобального минимума целесообразно использовать законы распределения, в
которых вероятность генерации точки в окрестности предполагаемого глобального
минимума выше, чем вне этой окрестности.
Для локализации с помощью метода Монте-Карло глобального минимума с высокой вероятностью и точностью требуется очень большое количество испытаний N. Поэтому метод Монте-Карло обычно комбинируют с каким-либо детерминированным методом локальной оптимизации.
Комбинация метода Монте-Карло с детерминированным методом локальной оптимизации
Шаг 1. Задаем общее количество исходных случайных точек N.
Шаг 2. С помощью какого-либо программного генератора случайных чисел
генерируем N случайных точек ![]() , принадлежащие множеству D.
, принадлежащие множеству D.
Шаг 3. Полагаем r = 1.
Шаг 4. Исходя из точки xr, каким-либо многомерным методом условной оптимизации (см. главу 6) находим локальный минимум (x*)r функции f(x) в окрестности этой точки и вычисляем f((x*)r) = (f*)r.
Шаг 5. Если r < N, полагаем r = r + 1 и переходим к шагу 4, иначе – переходим к следующему шагу.
Шаг 6. Находим минимальное из чисел (f*)r. Пусть
![]()
Принимаем в качестве приближенного решения задачи (x*)k, (f*)r и заканчиваем вычисления.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.