
МБУ ДОД города Ростова-на-Дону «Дворец творчества детей и молодежи»
Донская академия наук юных исследователей им. Ю. А. Жданова
Математика/Общая математика
Тема: «Несколько сюжетов вокруг красивой формулы»
Автор работы:
Кряквина Лилия Низамитдиновна,
учитель математики,
МБОУ «Школа № 31»,
Ростов-на-Дону
г. Ростов-на-Дону
2019 год
Оглавление
стр.
2.1 О высоте, проведённой из вершины прямого угла к гипотенузе 4
2.2 Об одной из высот треугольной пирамиды 6
2.3 Практическое применение полученных результатов 8
1. Введение
Актуальность темы состоит в том, что прямые углы мы встречаем часто в повседневной жизни: в строительстве, архитектуре, на местности. Во многих задачах геометрии расчёты связаны с высотами, проведёнными из вершин прямых углов к противоположной стороне или грани. Целью данной исследовательской работы является вывод некоторых интересных формул геометрии и их практическое применение. Показаны соотношения между катетами прямоугольного треугольника и высотой, проведенной из вершины прямого угла к гипотенузе, а также между высотой, проведённой из вершины прямого трёхгранного угла пирамиды и ребрами, исходящими из него. Эти формулы временами очень эффективны и позволяют достаточно быстро находить результат в поставленных задачах. При выводе выше названных соотношений применяются известные из школьного курса формула нахождения площади треугольника, теорема Пифагора, формула Герона, а также формула нахождения объёма пирамиды. В работе рассматриваются несколько задач, в которых показано применение выведенной формулы. Кроме того, делается вывод о целесообразности её применения.
2. Результаты исследования.
2.1 О высоте, проведённой из вершины прямого угла к гипотенузе.
Задача № 1
Рассмотрим
прямоугольный треугольник ABC с прямым углом С. Проведем из вершины
прямого угла С высоту СН к гипотенузе АВ. Введём следующие обозначения: CH=h, BC=a, AC=b, AB=c. Докажем, что ![]()
![]()
Доказательство.
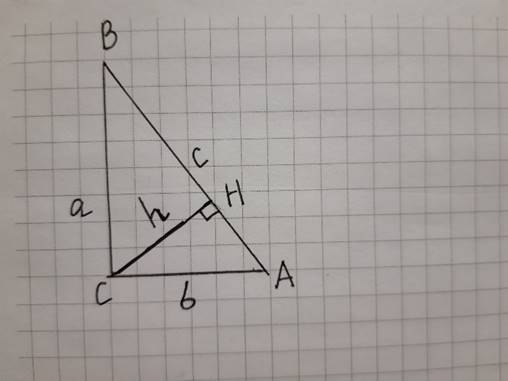
Площадь треугольника можно вычислить по
формуле S=![]() , с другой стороны, S=
, с другой стороны, S=![]() . Таким образом, получим равенства
. Таким образом, получим равенства ![]() , ab=c h,
, ab=c h, ![]() .
. ![]() . По теореме Пифагора
. По теореме Пифагора ![]() . Таким образом, имеем
. Таким образом, имеем ![]() или
или ![]() , что и требовалось доказать.
, что и требовалось доказать.
Равенство
![]() можно также представить в виде
можно также представить в виде ![]() . Следовательно, утверждение доказано.
. Следовательно, утверждение доказано.
Тема «Пропорциональные отрезки в прямоугольном треугольнике» всегда актуальна и имеет большой практический смысл. Решив задачу № 1, мы увидели ещё одну интересную формулу.
2.2. Об одной из высот треугольной пирамиды
В стереометрии решение задач, связанных с нахождением объёмов многогранников, и их неизвестных элементов, вызывает живой интерес. Известны формулы нахождения объёма пирамиды (см. приложение). Также временами полезно найти какую-либо из высот пирамиды, например, высоту треугольной пирамиды, проведённую из вершины прямого трёхгранного угла, к противоположному основанию. Рассмотрим задачу, связанную с данной высотой, и получим ещё одну красивую формулу.
Задача № 2
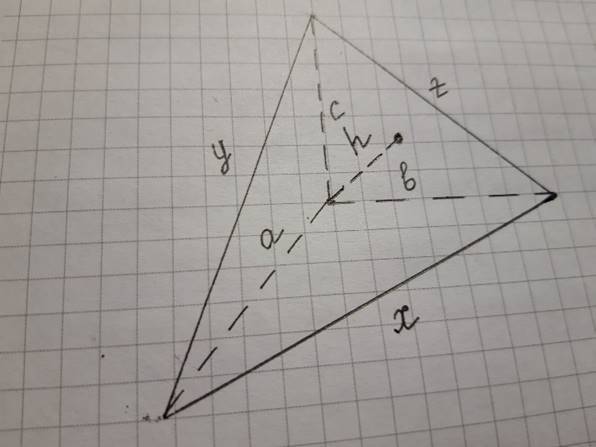
Дана
пирамида, у которой рёбра a, b, и c попарно
перпендикулярны. Найдём высоту h, проведённую из вершины угла,
заключённого между рёбрами a, b, c, к
противоположной грани пирамиды. Пусть x, y, z – стороны этой
грани, где x – гипотенуза
треугольника с катетами a и b, y – гипотенуза
треугольника с катетами a и c, z – гипотенуза
треугольника с катетами b и с. Примем за высоту пирамиды ребро c, тогда основанием
будет прямоугольный треугольник с катетами a и b. Объём такой
пирамиды вычисляется по формуле ![]() Если за основание мы примем грань с
ребрами x,y,z, тогда тот же
объём вычисляется следующим образом: V=
Если за основание мы примем грань с
ребрами x,y,z, тогда тот же
объём вычисляется следующим образом: V= ![]() , где
, где ![]() – площадь грани с рёбрами x,y,z. Найдём площадь
– площадь грани с рёбрами x,y,z. Найдём площадь ![]() по формуле Герона (см. приложение),
предварительно заметив, что
по формуле Герона (см. приложение),
предварительно заметив, что ![]() . Тогда
. Тогда ![]() и легко увидеть, что выполняется
равенство:
и легко увидеть, что выполняется
равенство:
![]() Преобразуем его:
Преобразуем его:
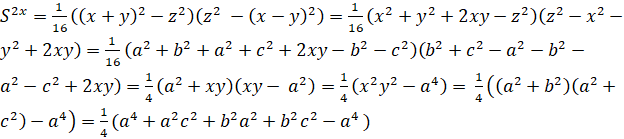 =
=![]() ) Таким образом, получаем
) Таким образом, получаем
![]() . В итоге имеем
. В итоге имеем ![]() (2).
(2).
2.3 Практическое применение полученных результатов
Рассмотрим применение выведенных формул при решении некоторых задач.
Задача № 3
Дан прямоугольный
треугольник с катетами a=![]() ; b=
; b=![]() . Необходимо найти высоту h, проведённую из
вершины прямого угла к гипотенузе.
. Необходимо найти высоту h, проведённую из
вершины прямого угла к гипотенузе.
Решение.
Для нахождения
высоты h используем
формулу ![]() . В результате имеем
. В результате имеем ![]() .
.
В этом примере очевидно преимущество выше показанной формулы, так при работе с иррациональными числами расчёты становятся достаточно простыми.
Задача № 4
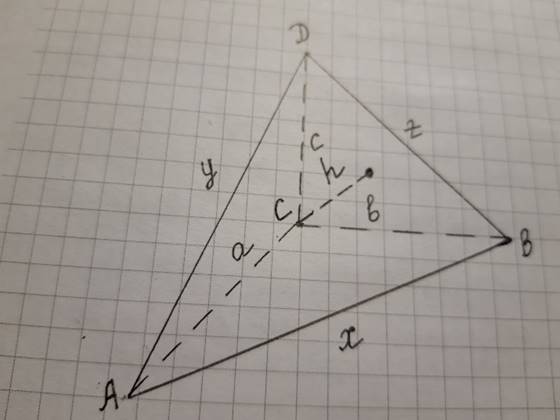
Дана пирамида DABC, в которой рёбра AC, BC, DC попарно перпендикулярны. Найдите высоту пирамиды, проведённую из вершины угла С к плоскости грани ABD, если известно, что AC=9 см, BC=12 см, DC= 8 см.
Решение.
Пусть BC=a, AC=b, DC=c. Для нахождения высоты h применим формулу (2).
В итоге имеем ![]() , h=
, h=![]() .
.
Очевидно, что использование данной формулы существенно упрощает вычислительную работу, связанную с нахождением неизвестного элемента треугольной пирамиды.
Задача № 5
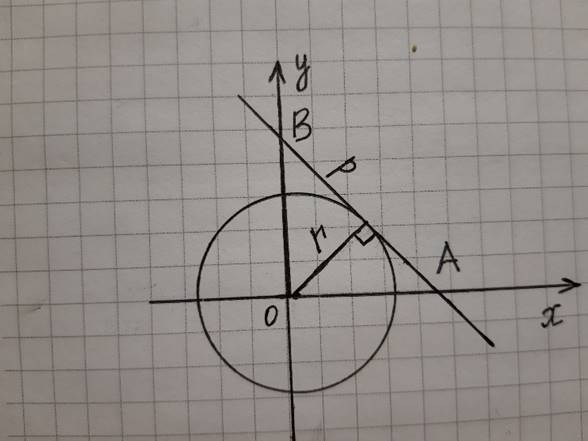
К окружности радиуса r, центр которой совпадает с началом прямоугольной системы координат, проведена касательная p. Известно, что A(x;0) – точка пересечения касательной с осью абсцисс. Найдите координаты точки пересечения этой касательной с осью ординат.
Решение.
Пусть B(0;y) – точка
пересечения данной касательной с осью ординат. Найдём y. Если рассмотреть
прямоугольный треугольник OAB, то радиус окружности, проведённой к
касательной, будет перпендикулярен ей, и, следовательно, будет являться высотой
этого треугольника, проведённой к гипотенузе AB. Воспользуемся
формулой (1). В данном случае h=r, a=x, b=y. Тогда (1) примет
вид: ![]()
![]() . Преобразуя эту формулу, получим
. Преобразуя эту формулу, получим ![]() , откуда
, откуда ![]() и y=
и y=![]() , y=
, y=![]() . Таким образом, точка B имеет координаты
(0;
. Таким образом, точка B имеет координаты
(0; ![]() ).
).
А теперь будем перемещать касательную к окружности вдоль дуги первой четверти окружности и посмотрим, на какой кривой будет находится точка с координатами (x; y). Рассмотрим предельные положения касательной, проходящей через точки с координатами (0; y) параллельно оси ox и (x;0) параллельно оси oy, и получим асимптоты для кривой, на которой будут лежать точки с координатами (x; y) – пересечения касательных с координатными осями.
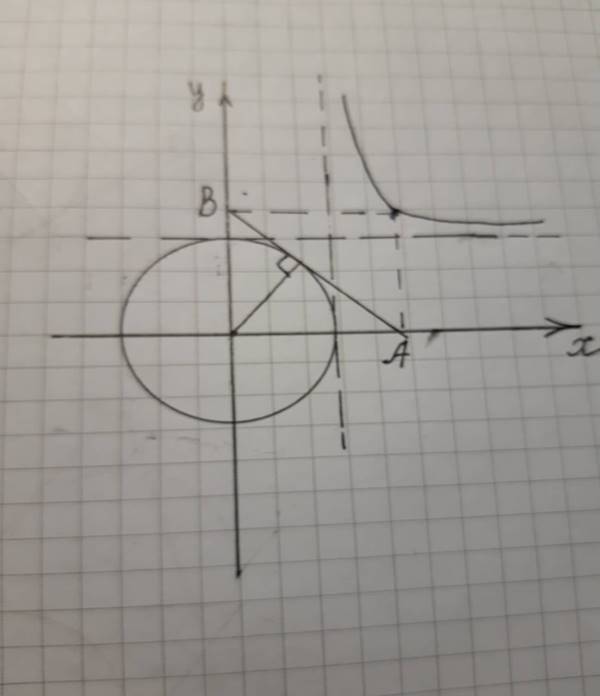
Построим кривую,
соответствующую уравнению ![]() , так как понятно, что величины x, y и r связаны формулой
(1). Получим крестообразную кривую 4-го порядка
, так как понятно, что величины x, y и r связаны формулой
(1). Получим крестообразную кривую 4-го порядка ![]() , где a=r. Этот факт хорошо
известен в книге [3].
, где a=r. Этот факт хорошо
известен в книге [3].
В приведённом примере мы увидели практическое применение формулы (1) в задачах, решаемых методом координат.
Задача № 6
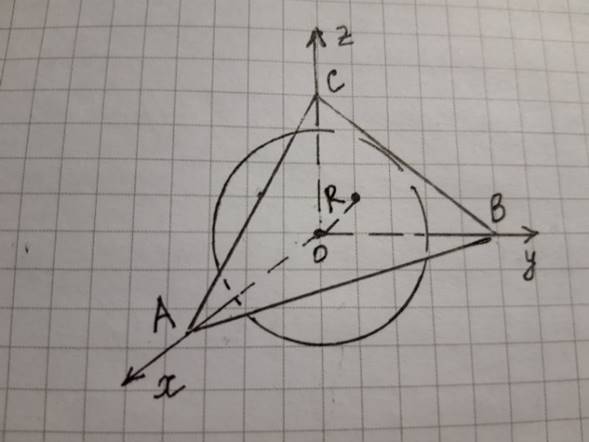
А сейчас ещё раз вернёмся к стереометрии. Метод координат в пространстве и шар – популярные темы этой области. Рассмотрим задачу, связанную с ними.
Шар неизвестного радиуса помещён в прямоугольную систему координат так, что его центр совпадает с началом координат O. К шару проведена касательная плоскость ABC, и известны координаты её точек пересечения с координатными осями: A(x;0;0) – точка пересечения с осью абсцисс, B(0;y;0) – с осью ординат, C(0;0;z) -–с осью аппликат. Найдём радиус шара.
Решение.
Обозначим радиус шара через R. Радиус шара перпендикулярен касательной плоскости, проведённой в точку касания. Мы получим треугольную пирамиду OABC, в которой данный радиус будет являться высотой, проведённой из вершины трёхгранного прямого угла, к противоположной грани ABC. Применим формулу (2) для нахождения радиуса шара. В этом случае h=R, a=x, b=y, c=z. В итоге получим
![]() , R=
, R= ![]() .
.
Таким образом, искомый радиус находится достаточно легко с помощью формулы (2).
Формула (1) при решении некоторых задач более эффективна по сравнению с использованием стандартных методов, а иногда нет. Рассмотрим следующие примеры, показывающие этот факт.
Задача № 7.
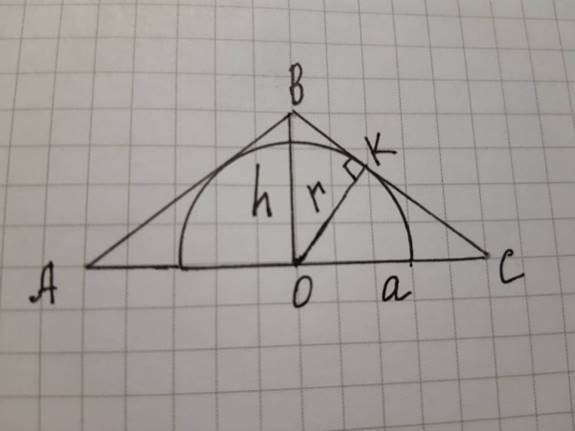
В равнобедренный треугольник ABC с основанием AC вписана полуокружность известного радиуса OK=r так, что её диаметр лежит на основании. Точка О является её центром, AC = 2a. Найти высоту BO треугольника ABC.
Решение.
1-й способ.
Обозначим BO через h. Тогда, применяя
формулу (1), имеем: ![]() , где OC=a. Очевидно, что
, где OC=a. Очевидно, что ![]() ,
, ![]() .
.
2-й способ.
С другой стороны,
из подобия треугольников OBK и OBC имеем равенство ![]() или
или ![]() , возведя обе части этого равенства в
квадрат, имеем
, возведя обе части этого равенства в
квадрат, имеем ![]() ,
,![]() ,
, ![]() . Откуда получаем
. Откуда получаем
![]() .
.
Мы использовали два способа для нахождения неизвестной высоты треугольника и увидели здесь преимущество формулы (1), позволяющей получить результат быстрее по сравнению со стандартным методом.
Задача № 8.

В равнобедренный треугольник ABC с основанием AC вписана окружность неизвестного радиуса OK=r. Точка О является её центром, AC = 2a. Известна высота BH=h, проведённая к основанию. Найдём радиус окружности.
Решение.
1-й способ.
Через точку O проведём отрезок OM, параллельный
основанию AC. OK=OH=r, BH=h, BO= h-r, HC=a. Обозначим OM через x. Применяя формулу
(1), имеем ![]() (3). Чтобы найти радиус из этого
равенства, необходимо воспользоваться соотношением
(3). Чтобы найти радиус из этого
равенства, необходимо воспользоваться соотношением ![]() (4), полученным из подобия треугольников BOM и BHC. Из соотношения
(4) выразим x =
(4), полученным из подобия треугольников BOM и BHC. Из соотношения
(4) выразим x = ![]() (5). Подставив (5) в (3) получим
достаточно сложное уравнение для нахождения радиуса r:
(5). Подставив (5) в (3) получим
достаточно сложное уравнение для нахождения радиуса r: ![]() .
.
2-й способ
Из подобия
треугольников BOK и BHC следует равенство
![]() или
или
![]() ,
, ![]() ,
,![]() , r (
, r (![]() +a) = a h, r =
+a) = a h, r = ![]() . Наблюдаем здесь преимущество
использования стандартного метода.
. Наблюдаем здесь преимущество
использования стандартного метода.
Рассмотрев данный пример, убеждаемся в том, что не всегда полученная красивая формула эффективна. Здесь удобнее решить задачу, рассмотрев пропорцию, следующую из подобия треугольников.
3. Выводы.
Представленный в работе материал нетривиален и полезен для практического применения, поскольку знакомит с интересными формулами планиметрии и стереометрии, позволяющими достаточно просто и быстро находить некоторые важные элементы в прямоугольных треугольниках и пирамидах, избегая сложных вычислений. Одна из них даёт возможность находить высоту прямоугольного треугольника, проведённую из вершины прямого угла, по его катетам. В трёхмерном случае, если все плоские углы при вершине треугольной пирамиды прямые, выражает высоту, проведённую из этой вершины через рёбра, исходящие из неё. На доступных примерах показана целесообразность применения этих формул. Очевидно, когда стороны выражены иррациональными числами, вычисления становятся гораздо проще при применении выведенных формул. А в некоторых случаях найденное соотношение позволяет быстро добиться искомого результата. Показанная формула известна, но красива, так как даёт возможность рассмотрения возникающих параллельно задач. Результаты этой исследовательской работы могут использоваться как справочный материал школьниками при решении геометрических задач. Естественно, что любая удобная для практического использования формула даёт хороший опыт работы с заданиями творческого характера и это интересно.
4. Литература.
1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7-9 классы: учеб. для общеобразовательных учреждений. 20-е изд. – М.: Просвещение, 2010. – 384 с.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия 10-11 классы: учеб. для общеобразовательных учреждений. 20-е изд. – М.: Просвещение, 2011. – 255 с.
3. Савелов А. А. Плоские кривые. Систематика, свойства, применение. (Справочное руководство). -М.: Физматгиз, 1960. – 295 с.
4. http://joselorlop.blogspot.com
5. Приложение
Формула Герона позволяет вычислить площадь треугольника (S) по его сторонам a, b, c:
![]()
где p — полупериметр
треугольника: p=![]() .
.
Объём пирамиды можно вычислить по следующей формуле:
V=![]() ,
,
Где S – площадь основания пирамиды, h – её высота.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.