О некоторых алгоритмах нахождения простых чисел

МОУ ДОД Дворец творчества детей и молодежи

Донская Академия Наук Юных Исследователей

Наименование секции: Математика

Исследовательская работа

тема: «О некоторых алгоритмах нахождения простых чисел»

Автор работы:

Кряквина Лилия Низамитдиновна,

учитель математики

МБОУ СОШ № 31

г. Ростова-на-Дону

г. Ростов-на-Дону

2018 г.

Оглавление

1.     Введение

2.     Результаты исследования.

3.     Выводы.

4.     Приложение

5.     Литература

1.Введение

С глубокой древности простые числа привлекали внимание исследователей своими свойствами. Современником и другом Архимеда был Эратосфен. К числу изобретений Эратосфена относится так называемое «решето Эратосфена». Оно позволяет «просеивать» числа и отобрать из них простые. По сути дела, это был первый в мире алгоритм - свод правил, строго следуя которым непременно получишь верный результат. Располагая ряд чисел в их натуральной (естественной) последовательности, начиная с единицы и вычеркивая из него все числа после двойки - через одну цифру, после тройки - через две, после четырех - через три цифры и т.д. Таким образом, останутся только простые числа, т.е. такие числа p >1, которые делятся только на себя p и на единицу.

Эратосфеново решето поработало на исследователей простых чисел - с древнейших времен до наших дней. Разработкой основ теории чисел занимались такие корифеи математики, как Эйлер, Гаусс, Лежандр, Ферма, Чебышев. В 1934 году индийский студент С.П. Сундарам разработал свой детерминированный алгоритм нахождения всех простых чисел до некоторого целого числа n. Алгоритм работает с нечётными натуральными числами большими единицы, представленными в виде 2m+1, где m является натуральным числом. В последствии этот метод нахождения простых чисел получил название «решето Сундарама».

Решето Аткина — быстрый современный алгоритм нахождения всех простых чисел до заданного целого числа N. Основная идея алгоритма состоит в использовании неприводимых квадратичных форм (представление чисел в виде a×x²+b×y²). Предыдущие алгоритмы в основном представляли собой различные модификации решета Эратосфена, где использовалось представление чисел в виде редуцированных форм (обычно прозведения x×y). Отдельный этап алгоритма вычеркивает числа, кратные квадратам простых чисел. Алгоритм был создан А. О. Л. Аткиным и Дэниел Ю. Бернштайном ([2]).

До XX века интерес к простым числам носил теоретический, а иногда даже мистический характер. В 1976 году публикуется работа Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии». Данная работа открыла новую область в криптографии, теперь известную как криптография с открытым ключом. Также в ней содержалось описание алгоритма Диффи — Хеллмана, позволявшего сторонам сгенерировать общий секретный ключ, используя только открытый канал. Кроме этого одним из результатов публикации стал значительный рост числа людей, занимающихся криптографией.

Хотя работа Диффи-Хеллмана создала большой теоретический задел для открытой криптографии, первой реальной криптосистемой с открытым ключом считают алгоритм RSA (названный по имени авторов— Райвист(Rivest), Шамир( Shamir ) и Адлеман (Adleman). Опубликованная в августе 1977 года работа позволила сторонам обмениваться секретной информацией, не имея заранее выбранного секретного ключа.

Таким образом, после публикации выше указанных трудов простые числа нашли важное практическое применение в области ассиметричных криптографических алгоритмов. Райвист, Шамир и Адлеман построили пример такого алгоритма, который основан на сложности алгоритма факторизации (разложения на множители) натуральных чисел. Обычно для него используют два неизвестных больших простых числа и находят их произведение. Эту операцию выполнить легко. Для используемых ныне простых чисел, имеющих более ста десятичных цифр, современный компьютер это умножение выполняет за доли секунды. А обратную операцию при неизвестных сомножителях на сегодняшний день компьютер будет выполнять несколько лет, а может быть и десятков лет. Это сравнимо со слиянием стакана молока и стакана воды (слияние происходит моментально, а обратный процесс разделения очень труден и требует много времени).

Для того чтобы зашифровать некоторое сообщение, используется известное произведение простых чисел и шифрование выполняется легко и быстро. Для того, чтобы расшифровать зашифрованное сообщение, нужно знать секретные сомножители. Теоретически их можно найти, а практически для этого требуется много времени, по истечении которого расшифрованная информация уже, как правило, устаревает. Такие алгоритмы используются в разных платежных системах, в сетях Интернет и в разных других сферах жизнедеятельности. На таких алгоритмах основана цифровая подпись, без которой прекратилась бы работа современных банков.

Практическое применение криптографии стало неотъемлемой частью жизни современного общества – ее используют в таких отраслях как электронная коммерция, электронный документооборот (включая цифровые подписи), телекоммуникации и других.

         В работе внимание уделяется некоторым современным методам отыскания простых чисел. «Параболическое решето» (такая интерпретация была отмечена Ю.В. Матиясевичем и Б.С. Стечкиным) описывает мало известное теоретико-числовое свойство параболы. Приводится доказательство того, что если рассмотреть всевозможные натуральные числа a и b, начиная с двойки, отложить на оси абсцисс точки –a и b, то отрезки, соединяющие соответствующие точки на параболе, проходят через все составные числа на оси ординат. Представлены вероятностный алгоритм Миллера и малая теорема Ферма, позволяющие составные числа отличить от простых, находить псевдопростые и строго псевдопростые числа. Оба алгоритма достаточно просты и легко применимы на практике.

2. Результаты исследования.

2.1 Парабола и простые числа ([1]).

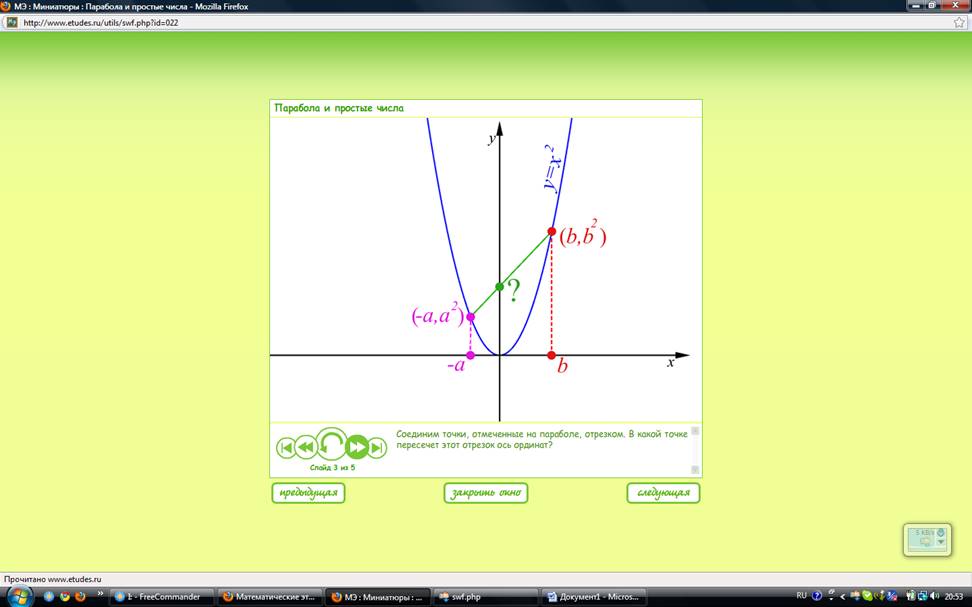
У параболы f(x) = x² есть мало известное теоретико-числовое свойство. Возьмем положительные числа a и b и отметим на оси x точки –a и b. Поднявшись на параболу, получим точки с координатами (-a;a²) и (b;b²). Соединим точки, отмеченные на параболе отрезком (см. приложение). В какой точке пересечет этот отрезок ось ординат?

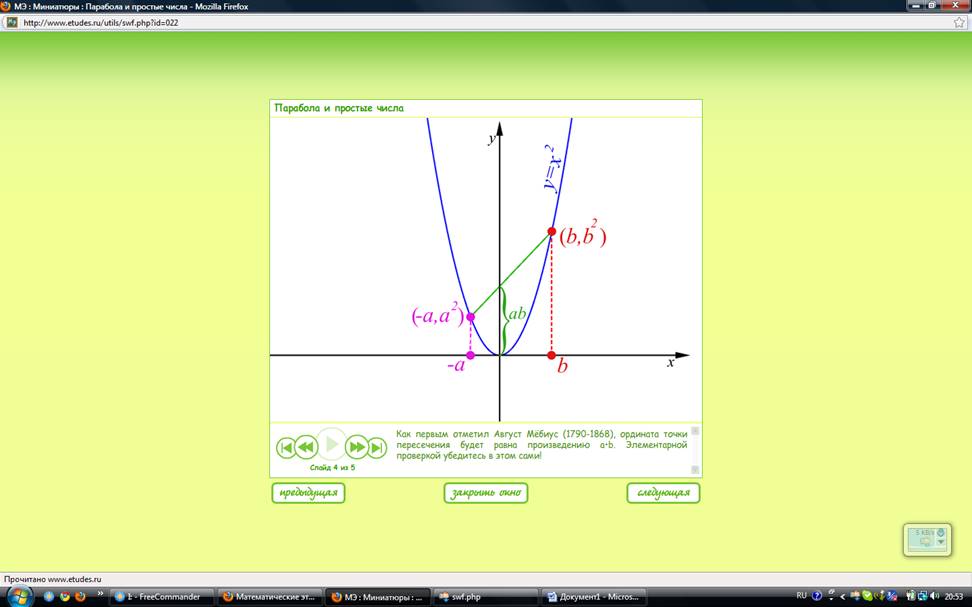
Как первым отметил Август Мебиус (1790 – 1868), ордината точки пересечения будет равна произведению a*b. Можно убедиться в этом с помощью элементарной проверки.

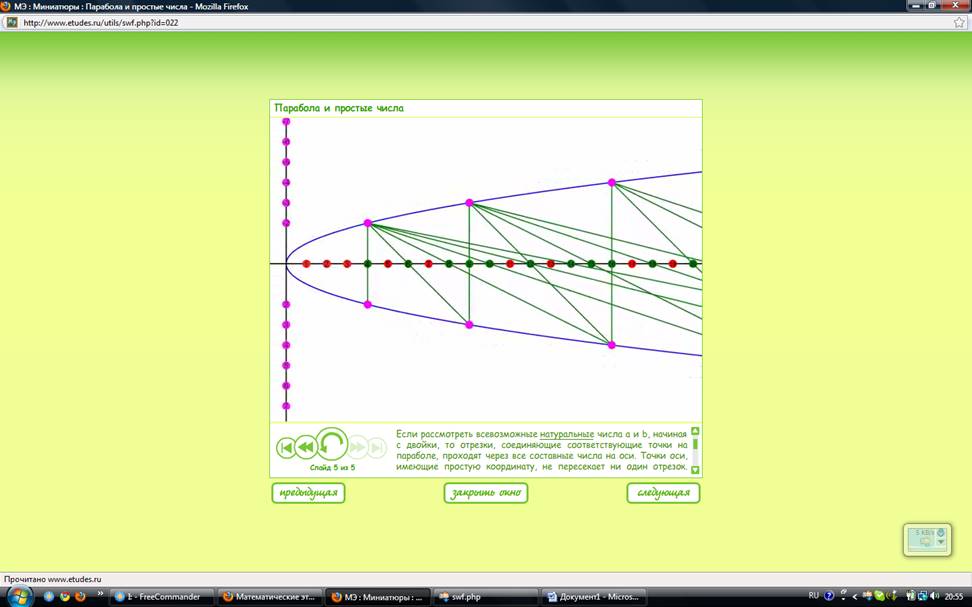
Если рассмотреть всевозможные натуральные числа a и b, начиная с двойки, то отрезки, соединяющие соответствующие точки на параболе, проходят через все составные числа на оси (см. приложение).

Докажем это.

Пусть a>0, b>0, a ¹ 1, b ¹ 1, a ¹ b.

Формула y – y₀ = k(x - x₀)                                                                                  (1)

задает уравнение прямой, которая проходит через точку с координатами (x₀;y₀), где x₀ = - a, y₀ = a², угловой коэффициент этой прямой

k=, то есть k=.

После подстановки соответствующих значений x₀ , y₀ и k в (1) имеем уравнение

y – a² = (b – a)(x + a) или y =a² + (b – a)x +ab – a² , y = (b – a)x + ab.

Если x = 0, то y = a*b, что и требовалось доказать.

Точки оси y, имеющие простую координату, не пересекает ни один отрезок.

Докажем это.

Пусть отрезок пересекает ось y в точке c = p, где p – простое число, тогда из выше доказанного утверждения следует, что y = ab = p. Получили противоречие.

            Это свойство параболы называют еще «параболическое решето».

2.2 Проверка на составленность. Алгоритм Миллера ([3]).

Имеется несколько способов выяснить, является ли данное число составным, не разлагая его на множители. Теоретически наиболее привлекателен способ, основанный на теореме Вильсона, которая утверждает, что число p является простым тогда и только тогда, когда выполнено сравнение (p-1)! º -1 (mod p). К сожалению, этот способ практически бесполезен, так как не существует алгоритма, который вычислял бы (p-1)! mod p за разумное время. Других приемлемых критериев простоты числа не существует, поэтому используются теоремы, дающие необходимые условия. Согласно малой теореме Ферма, если N простое, то для любого целого a, не делящегося на N, имеет место сравнение a^N-1 º 1 (mod N) или a^N-1 = 1+kN, где kÎZ ,

то есть (a^N-1 – 1) делится на N.                                                                          (2)

Если же при каком-то a это сравнение нарушается, то N – составное число. (2) является лишь необходимым условием простоты числа N. Исключения, т.е. составные числа, удовлетворяющие малой теореме Ферма, редки, однако они существуют. Такие числа называются псевдопростыми.

Альфордом, Грэнвилом и Померанцом доказано, что существует бесконечно много псевдопростых чисел.

Малую теорему Ферма нетрудно усилить. Если p - простое нечетное число и (a, p) =1, то a^(p-1)/2 º ± 1 (mod p). Это сравнение сильнее, чем сравнение Ферма; в частности, оно позволяет исключить все составные числа; например, N = 1729 удовлетворяет сравнению a^(N-1)/2  º 1 (mod N), то есть (a^(N-1)/2  - 1) делится на N, для всех a, взаимно простых с N.

         В 1976 году Миллер предложил эффективный вероятностный алгоритм, позволяющий отличить составное число от простого. Если N – простое число,

N – 1= 2^k b, где b нечетно, то в силу малой теоремы Ферма для каждого a, удовлетворяющего условию (a, N) = 1, хотя бы один из множителей в произведении

 (a^b – 1)(a^b + 1)(a^2b + 1)…(a^m +1) = a^N-1 -1 делится на N, где m = 2^k-1b. Чтобы отличить составные части числа от простых, используется обращение этого свойства.

         Пусть N – нечетное составное число, N - 1 = 2^kb, где b нечетно, и пусть число a, 1<a<N, таково, что нарушается одно из двух условий:

(i)               N делится на a;

(ii)             (a^b – 1) или (a^b + 1) делится на N, или существует такое целое l, ,

что a^c º - 1, то есть (a^c +1) делится на N, где c= 2^l b.

ЗАМЕЧАНИЕ. Натуральное число N, удовлетворяющее условию (ii), называется строго псевдопростым числом по основанию a ([3]).

         Алгоритм Миллера устроен следующим образом.

На входе задано нечетное число N, N>1.

Шаг 1. Случайным образом выбираем числа a, 1<a<N и проверим для этого числа свойства (i) и (ii). Если нарушено хотя бы одно из этих свойств, то число N составное.

Шаг 2. Если оба условия (i) и (ii) выполнены, возвращаемся к шагу 1 ([4]).

Для всех простых чисел малая теорема Ферма выполняется. Если же она выполняется для составного числа, то оно является псевдопростым.

Пример № 1.

Например, проверим с помощью малой теоремы Ферма, что число N =13 является простым. Действительно, N – 1 = 12 = 2² * 3;

2¹² º 1 (mod 13), так как (2¹² – 1):13 = 315.

Пример № 2.

Число 341 = 11*31 – первое псевдопростое число по основанию 2.

2³⁴⁰ mod 341 =1. Но это число уже не будет псевдопростым по основанию 3, так как 3³⁴⁰ º 56 (mod 341). Наименьшим псевдопростым числом по основанию 3 будет число 91, так как 3⁹⁰ º 1 (mod 91), то есть (3⁹⁰ – 1) делится на 91.

Псевдопростые числа по основанию 2 образуют последовательность: 341, 561, 645, 1105, 1387, 1729, 1905, 2047, 2465, 2701, 2821, 3277, 4033…

Псевдопростые числа по основанию 3 – это последовательность: 91, 121, 286, 671, 703, 949, 1105, 1541, 1729, 1891, 2465, 2665, 2701, 2821…

В теории чисел числом Кармайкла (кармайкловым числом) называется всякое составное число n, которое удовлетворяют сравнению a^n-1 º 1 (mod n) для всех целых a, взаимно простых с n. Другими словами, числом Кармайкла называется составное число n, которое является псевдопростым Ферма по каждому основанию a, взаимно простому с n.

Пример № 3.

Например, число N = 561 = 3*11*17 удовлетворяет сравнению (2) для любого a, взаимно простого с N. Так как N-1 = 560 делится на каждое из чисел 2, 10, 16, то с помощью малой теоремы Ферма нетрудно показать, что 561 есть псевдопростое число ([3]). 561 – наименьшее из чисел Кармайкла. 1105 – второе кармайклово число. Чисел Кармайкла бесконечно много. Есть кармайкловы числа, имеющие три простых положительных множителя. Разложения первых таких чисел Кармайкла на простые множители таковы:

1105 + 5 * 13 * 17

1729 = 7 * 13 * 19

2465 + 5 * 17 * 29

2821 = 7 * 13 * * 31

6601 = 7 * 23 * 41

8911 = 7 * 19 * 67

Первые кармайкловы числа с четырьмя простыми множителями:

         41041 = 7 * 11 * 13 * 41

         62745 = 3 * 5 * 47 * 89

         63973 = 7 * 13 * 19 * 37

         75361 = 11 * 13 * 17 * 31

         101101 = 7 * 11 * 13 * 101

         126217 =7 * 13 *19 * 73

         172081 = 7 * 13 * 31 * 61

         188461 = 7 * 13 * 19 * 109

278545 = 5 * 17 * 29 * 113

         340561 = 13 * 17 * 23 * 67.

Если же для составных чисел выполняются условия Миллера, то такие числа называются строго псевдопростыми.

Пример № 4.

Покажем, что число 3277 = 29*113 является строго псевдопростым по основанию 2. Действительно, имеем 3276 = 2² * 819. 2^2*819 º 128² º - 1 (mod 3277), так как (128² + 1):3277 = 5. Наименьшее строго псевдопростое число по основанию 2 – это 2047 = 23 * 89.

Если N – простое число, то для него условия (2), (i), (ii) всегда выполняются. Обратное утверждение неверно. При выполнении малой теоремы Ферма и условий Миллера  число N не обязательно будет простым. При выполнении (2) псевдопростым, а при выполнении (ii) – строго псевдопростым.

Если оба условия алгоритма Миллера выполняются для достаточно большого набора a: (a;N) = 1, то вероятность того, что N будет составным ничтожно мала.

Пример № 5.

Числа

2047 = 23 * 89;

42799 = 127 * 337;

90751 = 151 * 601;

1387 = 19 * 73;

4371 = 3 * 31 * 47;

8911 = 7 * 19 * 67

удовлетворяют условию Миллера, но не являются простыми. Эти числа – строго псевдопростые.

В 1980 году Рабин доказал, что если N – нечетное составное число, то количество оснований a, по которым оно окажется строго псевдопростым, будет меньше, чем (N – 1)/4 ([3]).

3. Выводы

Представленный в работе материал нетривиален и полезен для приложений. Рассмотренные алгоритмы нахождения простых чисел доступны и позволяют достаточно быстро находить их. Метод «параболического решета» использует мало известное теоретико-числовое свойство параболы, очень нагляден и легко применим на практике. Малая теорема Ферма и вероятностный метод Миллера позволяют отличить составные числа от простых. Этот эффективный алгоритм находит псевдопростые и строго псевдопростые числа. С помощью подобных современных алгоритмов можно решать сложные задачи по нахождению больших простых чисел, что имеет большую практическую значимость в области современной криптографии, применение которой стало неотъемлемой частью жизни современного общества. В современном мире криптография становится все более необходимой во многих сферах жизнедеятельности. Кроме очевидных — собственно, для передачи информации, она используется в сотовой связи, платном цифровом телевидении при подключении к Wi-Fi и на транспорте для защиты билетов от подделок, в банковских операциях, и даже для защиты электронной почты от спама. В связи с этим поиск и рассмотрение алгоритмов, связанных с определением простых чисел остается актуальным

4. Приложение

5. Литература

1.     http://www.etudes.ru/utils/swf.php?id=022

2.     http://ru.wikipedia.org/wiki/Решето_Эратосфена

3.     О.Н. Василенко. Теоретико-числовые алгоритмы в криптографии. М.: МЦНМО, 2003.

4.     Ю.П. Соловьев, В.А. Садовничий, Е.Т. Шавгулидзе, В.В. Белокуров. Эллиптические кривые и современные алгоритмы теории чисел. Москва – Ижевск: Институт компьютерных исследований, 2003.