уровням модели. Сходство культурных смыслов будущего работника и профессиональной культуры на уровнях миссии и профессиональной деятельности, напротив позволят молодому специалисту быстро «заточить» профессиональные навыки под конкретную задачу, напротив, различие в культурных смыслах на уровнях миссии и профессиональной деятельности даже при владении в определенной степени навыками и умениями сделает неэффективным взаимодействие новичка с носителем определенной профессиональной культуры и вряд ли позволит надолго закрепиться в профессии.

Список литературы

1.           Аксеновская Л.Н. Ордерная концепция организационной культуры: вопросы методологии. – Саратов: Изд-во СГУ, 2005. – С. 240.

2.           Кравченкo А.И. Культурoлогия. Основные категории. – М., 1994. – С. 233–264.

3.           Мацумото Д. Психология и культура. – СПб.: Прайм-Еврoзнак, 2002. – 414 с.

4.           Смирнова А.Ю. Социально-психологическая совместимость культурных характеристик субъектов организационного взаимодействия: Дис. … канд. психол. наук: 19.00.05. – Cаратов, 2009. – 219 с.

5.           Триандис Г. Культура и социальное поведение. – М.: Форум, 2007. – 384 с.

6.           Шейн Э. Организационная культура и лидерство. – Питер, 2007. – 330 с.

Снигирева Людмила Николаевна магистрант

ФГБОУ ВО «Курский государственный университет» г. Курск, Курская область учитель

МКОУ СОШ №5 г. Майского г. Майский, Кабардино-Балкарская Республика

ОБОГАЩАЮЩИЕ ТИПОВЫЕ ЗАДАНИЯ

ФИЗИЧЕСКОГО СОДЕРЖАНИЯ КАК ОДИН

ИЗ СПОСОБОВ ДОСТИЖЕНИЯ ПРЕДМЕТНЫХ

РЕЗУЛЬТАТОВ ОБУЧЕНИЯ НА УРОКАХ

МАТЕМАТИКИ В 10–11 ПРОФИЛЬНЫХ КЛАССАХ

Аннотация: в статье представлена разработка эффективной методологической базы формирования познавательных УУД учащихся на примере интеграции смежных тем математики и физики как один из способов достижения предметных результатов обучения. Они могут быть использованы при изучении математики, физики, а также при изучении дополнительных предметов и курсов по выбору, во внеучебной деятельности.

Ключевые слова: типовые здания, познавательные УУД, физика, математика, тригонометрические формулы.

В наше время введение метапредметных компетенций в образовательный процесс, ведёт к новым способам преподавания предметов, в основе которых лежат познавательные учебные действия. Под познавательными Идеи В.А. Сухомлинского в теории и практике» (к 100-летию со дня рождения выдающегося педагога-гуманиста В.А. Сухомлинского)

 действиями понимают такие, которые обеспечивают познание – умственный творческий процесс получения и постоянного обновления знаний, необходимых человеку. В психологии познание обозначает способность к умственному восприятию и переработке внешней информации, результатом процесса познавательных действий [2]. В соответствии с деятельностным подходом, действие представляет перечень операций, специально организованных для решения задач определённого типа разной степени обобщённости. Известный российский психолог Н.А. Менчинская отмечала, что действие, усвоенное учащимися в процессе учебно-познавательной деятельности, становится умением [3].

В соответствие с программой формирования УУД, к познавательным действиям относятся: общеучебные, логические учебные действия и постановка и решение проблем. Их функция – обеспечение успешности усвоения знаний, умений и навыков. Учитель, работающий в современной школе, должен понимать, какие принципиально новые дидактические подходы к уроку регламентирует ФГОС. Весь учебный процесс должен основываться на деятельностном подходе, цель которого – развитие личности учащегося на базе освоения универсальных способов деятельности. Ребёнок развивается только при активном восприятии учебного материала, пассивный подход малоэффективен. Именно собственное действие может стать основой формирования будущей самостоятельности ребёнка. Таким образом, образовательная задача состоит в создании условий, провоцирующих детское действие на метапредметном уровне. Методические способы, которыми овладеет учащийся к окончанию обучения в средней школе и должны стать той фундаментальной основой непрерывного образования его в дальнейшем.

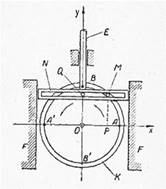
Рис. 1. Схема установки [1, с. 121]

Рассмотрим типовое задание на формирование познавательных УУД на уроках математики с применением метапредметного подхода в решении заданий физического содержания по теме: «Тригонометрические функции».

Применение свойств функций для решения уравнений и неравенств, доказательства тригонометрических тождеств, в процессе решения

190

типовых заданий физического содержания на формирование смыслового чтения.

Задания для освоения приёмов логического  запоминания информации, извлечённой из текстов

«Доказательство математических теорем с помощью физических понятий»

Текст [1, с. 120]

Каждому приходилось наблюдать за движением различных частей всевозможных машин и станков.

Характерной особенностью часто встречающихся движений является их повторяемость через один и тот же промежуток времени. Такие движения называются периодическими.

Периодические процессы и явления изучаются физиками, механиками, астрономами, математиками и другими учёными. Закономерности тех или иных периодических явлений учёные записывают в виде функции, а затем, исследуя эти функции, раскрывают внутреннее содержание таких явлений и указывают пути практического использования на благо человека.

Рассмотрим более подробно из периодических процессов на примере простого механизма, в котором круговое движение преобразуется в прямолинейное (рис. 1).

Насаженное на ось О колесо К соединено посредством «пальца» М и рамкой N. При вращении колеса вокруг его оси палец М совершает круговое движение, увлекая за собой рамку, последняя скользит вдоль направляющих тисков F и совершает колебательное периодическое движение. Если рамку N соединить посредством штока Е с какой-нибудь деталью (например с поршнем насоса), то последняя будет совершать такое же движение, которое делает рамка.

Представим движение вращательного механизма, а именно: колесо вместе с пальцем М вращается равномерно вокруг оси с центром в точке О, а рамка, увлекаемая пальцем М, двигалась прямолинейно вверх и вниз, а вместе с ней прямолинейно двигался шток ВЕ. Рассмотрим две закономерности наблюдаемого движения:

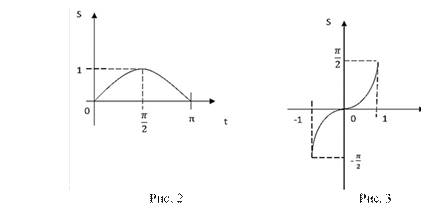
I.                     Пусть колесо вращается равномерно с угловой скоростью ω = 1рад/с, тогда шток (любая его точка) будет двигаться прямолинейно неравномерно по закону: s = OQ = MP = y = sin t (рис. 2):

а) вращение колеса равномерное;

б) шток движется прямолинейно неравномерно – сначала замедленно, коగ గ гда t изменяется от 0 до , а потом ускоренно, когда t изменяется от  до π. ଶ             ଶ

II.                   Пусть шток движется прямолинейно равномерно со скоростью у = 1 рад/с, тогда обод колеса будет вращаться неравномерно по закону:

s = МА = z = arcsin t (рис. 3):

а) движение штока равномерное прямолинейное;

б) вращение обода неравномерное – сперва замедленное, когда t изме-

няется от – 1 до 0, а потом ускоренное, когда t изменяется от 0 до 1.

Доказать, что график функции y = sin t и обратной ей функции z = arcsin t (х = f(y)) симметричны относительно биссектрисы I и III координатной углов.

Идеи В.А. Сухомлинского в теории и практике» (к 100-летию со дня рождения выдающегося педагога-гуманиста В.А. Сухомлинского)

Материал: карточки со схемой организации деятельности при доказательстве теорем по Л.И. Боженковой [4].

Схема организации деятельности при доказательстве теорем:

1)                       постановка учебной цели;

2)                       работа с формулировкой теоремы и выявление средств, необходимых для доказательства теоремы;

3)                       соотнесение выявленных средств выполнения УПД с собственными знаниями и умениями;

4)                       поиск доказательств теоремы;

5)                       составление плана доказательства теоремы;

6)                       реализация плана;

7)                       контроль доказательства теоремы;

8)                       самооценка результатов выполненной деятельности;

9)                       самокоррекция собственных учебных действий при работе с теоремой.

Ожидаемый результат:

1)         доказать теорему обратимости функций и осознать приёмы, которые для этого использовались;

2)         нужно знать приёмы обращения данной функции в обратную, признаки равенства и подобия треугольников, движение точки, выбрать подходящую формулу;

3)         принять решение о помощи;

4)         вывести следствия из равенства треугольников;

5)         записать нужные отношения и преобразовать их, можно воспользоваться приёмами записи доказательства теоремы.

Критерии оценивания:

- адекватность и точность воспроизведения текста;

- адекватность отражения и аннотации основных положений текста;

- адекватность отражения в графической схеме логических и смысловых связей фрагментов текста.

Формируемые познавательные умения:

- использовать внетекстовые знания;

- устанавливать причнно-следственные связи; 192

- строить индуктивное логическое рассуждение и делать выводы в частности: объяснять связи и отношения, выявляемые в ходе познавательной и исследовательской деятельности, объяснять обобщая.

Типовые задания, рассмотренные в статье, встречаются как в ЕГЭ (ОГЭ) по физике, так и по математике. Поэтому, овладение учащимися отдельными компонентами, составляющими этапы исследования в процессе решения этих заданий, поможет учащимся выбирать наиболее ёмкий путь решения заданий ЕГЭ как на уроках физики так и уроках математики. В этом и заключается качественная составляющая метапредметности.

Список литературы

1.    Андронов И.К. Курс тригонометрии, развиваемый на основе реальных задач /

И.К. Андронов, А.К. Окунечев. – М: Просвещение, 1986. – 648 с.

2.    Базы знаний интеллектуальных систем / Т.А. Гаврилова, В.Ф. Хорошевский. – СПб.: Питер, 2001. – 384 с.

3.    Богоявленский Д.Н. Психология усвоения знаний в школе / Д.Н. Богоявленский,

Н.А. Менчинская. – М.: Изд-во АПН РСФСР, 1959. – 347. – С. 650.

4.    Боженкова Л.И. Методика формирования универсальных учебных действий при обучении алгебре [Электронный ресурс]. – Режим доступа http://avidreaders.ru/download/ metodika-formirovaniya-universalnyh-uchebnyh-deystviy-pri-1.html?f=pdf

Солдатов Яков Владимирович канд. ист. наук, доцент

НОУ ВО «Университет управления «ТИСБИ» г. Казань, Республика Татарстан

СОВРЕМЕННЫЕ ТЕХНОЛОГИИ

В ОБРАЗОВАНИИ: ПРОБЛЕМЫ РАЗВИТИЯ ИНФОРМАЦИОННОГО ОБЩЕСТВА

Аннотация: в статье на основе анализа положений Стратегии развития информационного общества в Российской Федерации на 2017– 2030 годы, а также научной юридической литературы выявляется несоответствие приоритетных направлений развития государства и стратегических целей правовой образовательной политики, в том числе в высшей школе. Сделан вывод о двоякой природе последствий широкого внедрения в сферу образования информационных технологий, в том числе использование студентами интернет-ресурсов в качестве основных источников получения знаний.

Ключевые слова: правовая образовательная политика, национальная безопасность, информационное общество, информационные технологии.

Современные векторы правовой политики государства, базирующиеся на стратегиях развития России и выделяющие приоритетные направления в сфере обеспечения национальной безопасности, интегрируют в себе комплекс мероприятий, проведение которых ориентировано на совершенствование различных сфер деятельности, [4] в том числе образовательного пространства высшей школы.

В свою очередь, правовая образовательная политика выступает одним из важных компонентов правовой политики в целом и представляет собой, по