Тема: «Организация

самостоятельной

деятельности учащихся»

 

 

Выполнил:

 учитель математики МБОУ

Головинской основной школы

Николаевский район

Фролова Екатерина Викторовна

 

 

 

 

 

 

 

 

 

 

 

 

2023

 

 

 

СОДЕРЖАНИЕ:

 

1. Введение

1.1 Проблема формирования самостоятельной деятельности учащихся…3-7

2. Основная часть. Организация самостоятельной работы учащихся

2.1 Анализ подходов к определению понятия «самостоятельная работа»...8-11

2.2  Виды самостоятельных работ учащихся………………………………11-18

2.3 Цели, задачи и функции самостоятельной работы учащихся………   18-24

2.4 Технология организации самостоятельной работы учащихся………..24-27

 

3. Заключение

3.1 Необходимость  формирования самостоятельной деятельности

учащихся …………………………………………………………………….28-29

 

4. Приложения ……………………………………………………………..30-41

 

5. Литература ……………………………………………………………….42-43

 

 

 

 

 

 

 

 

 

 

 

 

1. ВВЕДЕНИЕ

1.1 Проблема формирования самостоятельной деятельности учащихся.

Современная педагогическая наука приоритетным направлением развития школы определяет гуманистический подход в организации процесса обучения. Эффективность методики обучения  в  школе напрямую зависит от оптимального решения проблемы формирования и развития самостоятельности учащихся.  Ведущим принципом гуманистической модели учебного процесса является развитие личности школьника. Степень развития ученика измеряется и оценивается его способностью самостоятельно приобретать новые знания и использовать их в учебной и практической деятельности. Существующая сегодня система общего образования не носит еще подлинно гуманистический характер. В связи с этим не в полной мере школа способствует развитию и саморазвитию учащихся, готовит к творческому выполнению всех функций в новом обществе.

Среди факторов, способствующих формированию творческой активности учащихся, одно из ведущих мест занимает самостоятельная работа. Только целенаправленная систематическая самостоятельная работа каждого школьника позволяет глубоко усвоить знания, выработать и закрепить умения, превратить их в соответствующие навыки умственного труда.

Актуальность исследования.

Ведущим принципом построения современной образовательной системы является дифференциация образования, ставшая средством решения задачи удовлетворения интересов, склонностей и потребностей учащихся, стимулом развития их творческой активности. В последнее время отмечается тенденция увеличения числа школ и классов гуманитарного направления. В этих условиях имеет место ослабление интереса учащихся к предметам математического цикла.

Поэтому главным принципом работы учителя математики является организация деятельности школьников, направленной на формирование не только предметных знаний и умений, но и на развитие самостоятельности и творческой активности учащихся.

Значительный вклад в развитие теории самостоятельности и творческой активности учащихся в процессе обучения внесли видные педагоги Бабанский Ю.К., Данилов М.А., Есипов Б.П., Лернер И.Я., Махмутов М.И., Огородников И.Т., Пидкасистый П.И., Скаткин М.Н. и др.; психологи Богоявленский Д.Н., Выготский Л.С., Гальперин П.Я., Давыдов В.В., Занков Л.В., Матюшкин А.М., Менчинская Н.А., Леонтьев А.Н., Рубинштейн С.Л., Эльконин Д.Б., Эсаулов А.Ф. и др. Эти исследования показали, что одним из эффективных средств развития самостоятельности и творческой активности учащихся является самостоятельная работа.

Дрозина В.В. сформулировала основные положения теории и практики организации творческой самостоятельной деятельности учащихся. Сущность понятия "самостоятельная работа", цели, задачи, дидактические принципы, функции самостоятельной работы, формы и методы ее организации в процессе обучения полно и глубоко проанализированы в исследованиях: Гарунова М.Г., Королькова Б.Е., Нильсона О.А., Орловского В.Г., Пидкасистого П.И., Цукаря А.Я., Чиканцевой Н.И. и др.

Актуальность данной проблемы бесспорна, так как знания, умения, убеждения, духовность нельзя передать от преподавателя к учащемуся, прибегая только к словам. Этот процесс включает в себя знакомство, восприятие, самостоятельную переработку, осознание и принятие этих умений и понятий. Данная проблема актуальна для современной школы, потому что она ещё не достаточно разработана, не изучена до конца.

Ребенок, в первый раз переступающий порог школы, не может еще самостоятельно ставить цель своей деятельности, не в силах еще планировать свои действия, корректировать их осуществление, соотносить полученный результат с поставленной целью, следовательно, эта проблема актуальна и для общества в целом.

В процессе обучения математике задача учителя состоит не только в том, чтобы обеспечивать прочные знания, предусмотренные программой, но и в том, чтобы развивать самостоятельность и активность мышления учащихся.

Самостоятельная работа - это такая познавательная учебная деятельность, когда последовательность мышления ученика, его умственные и практические операции и действия зависят и определяются самим учеником. Присутствие самостоятельной работы необходимо на уроках, в том числе и на уроках математики, так как они тренируют волю, воспитывают работоспособность, внимание, дисциплинируют учащихся. Учителю на уроках математики  необходимо опираться на самостоятельную работу учеников, самостоятельное рассуждение, умозаключение.

Самостоятельная работа - это метод, который очень помогает учителю для выяснения способностей учащихся. Работая самостоятельно, ученик должен постепенно овладеть такими общими приемами самостоятельной работы как представление цели работы ее выполнение, проверка, исправление ошибок.

Проблема исследования.

Проблема исследования обусловлена противоречиями:

- между обязательным уровнем математической подготовки, зафиксированным в программе по математике и не способностью учащегося достичь определенного достаточно высокого уровня самостоятельности, открывающего возможность справиться с разными заданиями, добывать новое в процессе решения математических задач.

- между отсутствием в методике математики обобщенного подхода и рекомендаций по организации системы самостоятельных работ и программой, предусмотренной для изучения математики;

- между минимальным уровнем обязательных требований к учащимся и стремлением к более полному раскрытию математических способностей школьников.

Тема исследования.

Организация самостоятельной деятельности у  учащихся 8 класса в процессе изучения геометрии на примере темы "Четырёхугольники».

Объект исследования.

Самостоятельная деятельность школьника на уроках математики.

Предмет исследования.

Условия реализации самостоятельной деятельности школьника на уроках математики.

Цель исследования.

Теоретически выявить и путем опытно-экспериментальной работы проверить комплекс условий формирующих самостоятельную познавательную деятельность учащихся на уроках математики.

Гипотеза исследования.

Реализация самостоятельной деятельности учащихся на уроках математики будет более эффективна при организации следующих педагогических условий:

 - прививать школьникам навыки выполнения самостоятельной работы;

 - использовать на уроках различные виды самостоятельной работы.

Тогда у детей вырабатывается самостоятельность и развивается мышление, они стремятся выполнять более трудные задания.

Задачи исследования.

1.                 Определить уровень сформированности навыков самостоятельной работы на уроках математики.

2.                 Определить систему упражнений по формированию навыков самостоятельной работы у учащихся при изучении математики.

3.                 Выявить развитость у учащихся самостоятельности в познавательной деятельности.

4.                 Исследовать степень самостоятельности учащихся в овладении знаниями, формировании своего мировоззрения.

5.                 Исследовать способность учащихся самостоятельно применять имеющиеся знания в учении и практической деятельности.

Методы исследования.

 - Наблюдение, интервьюирование учеников и учителя, анализ продуктов деятельности учащихся;

 - Сравнение, изучение документации;

- Теоретический анализ педагогической и психологической литературы по проблеме исследования.

Практическая значимость исследования заключается в том, что выводы и результаты  работы могут быть использованы в учебно-воспитательном процессе общеобразовательных учреждений.

2. Особенности организации самостоятельной работы учащихся

 

2.1 Анализ подходов к определению понятия «самостоятельная работа»

 

Изучение вопроса самостоятельности началось еще в древности. Аристосен, Сократ, Платон, Аристотель глубоко и всесторонне обосновали в своих трудах значимость добровольного, активного и самостоятельного овладения ребенком знаниями. При этом они исходили из того, что развитие мышления человека может успешно протекать только в процессе самостоятельной деятельности, а совершенствование личности и развитие ее способности - путем самопознания. Такая деятельность доставляет ребенку радость и удовлетворение и тем самым устраняет пассивность с его стороны в приобретении новых знаний. Свое дальнейшее развитие идея о самостоятельности в обучения получает в высказываниях Франсуа Рабле, Мишеля Монтеня, Томаса Мора, которые в эпоху мрачного средневековья в разгар процветания в практике работы школы схоластики, догматизма и зубрежки требуют обучать ребенка самостоятельности воспитывать в нем вдумчивого, критически мыслящего человека. Те же мысли развиваются на страницах педагогических трудов Я.А. Каменского, Ж.Ж. Руссо, И.Г. Песталоцци и др.

В педагогической же литературе самостоятельность учащихся как один из ведущих принципов обучения рассматривается с конца ХVIII века. Вопрос о развитии самостоятельности и активности учащихся – центральный в педагогической системе К. Д. Ушинского, который обосновал пути и средства организации самостоятельной работы учащихся с учетом возрастных периодов обучения.

В 20-х годах ХХ века определенную роль в развития теория самостоятельности учащихся сыграли комплексное обучение и другие формы индивидуализации обучения.

Один из ведущих педагогов Пидкасистый П. И. в своей работе «Самостоятельная познавательная деятельность школьников в обучении» он рассматривает следующее определение: «самостоятельная работа - это не форма организации учебных занятий и не метод обучения. Её правомерно рассматривать скорее как средство вовлечения учащихся в самостоятельную познавательную деятельность, средство ее логической и психологической организации».

В педагогическом же энциклопедическом словаре приводится следующая дефиниция: «Самостоятельная работа учащихся, индивидуальная или коллективная учебная деятельность, осуществляемая без непосредственного руководства учителя». На наш взгляд, данное определение не является достаточно полным. Оно не раскрывает сущностных характеристик данного понятия и требует значительных уточнений.
Педагог-психолог Зимняя И.А. определяет, что самостоятельная работа школьника есть следствие правильно организованной его учебной деятельности на уроке, что мотивирует самостоятельное её расширение, углубление и продолжение в свободное время. Для учителя это означает чёткое осознание не только своего плана учебных действий, но и осознанное его формирование у школьников как некоторой схемы освоения учебного предмета в ходе решения новых учебных задач. Но в целом это параллельно существующая занятость школьника по выбранной им из готовых программ или им самим выработанной программе усвоения какого-либо материала. При этом самостоятельная работа – это высшая форма учебной деятельности школьника, форма самообразования, связанная с его работой в классе.

Такие различные аспекты проблемы самостоятельной работы учащихся исследовались Б. П. Есиповым, М. А. Даниловым, М. Н. Скаткиным, И. Я. Лернером, Н. А. Полоеноковой, А. В. Усовой и др. Однако мнения ученых о сущности самостоятельной работы расходятся. Одни определяют её через понятие «метод обучения», другие - через систему приемов учения.

Так, самостоятельная работа – это такая работа, которая выполняется без непосредственного участия учителя, но по его заданию, в специально предоставленное для этого время, при этом учащиеся, сознательно стремятся достигнуть поставленные цели, употребляя свои усилия и выражая в той или иной форме результат умственных или физических (либо тех и других вместе) действий.

Именно самостоятельная работа вырабатывает высокую культуру умственного труда, которая предполагает не только технику чтения, изучение книги, ведение записей, а, прежде всего, потребность в самостоятельной деятельности, стремление вникнуть в сущность вопроса, идти в глубь ещё не решённых проблем. В процессе такого труда наиболее полно выявляются индивидуальные способности школьников, их наклонности и интересы, которые способствуют развитию умения анализировать факты и явления, учат самостоятельному мышлению, которое приводит к творческому развитию и созданию собственного мнения, своих взглядов, представлений, своей позиции.

Некоторые же ученые рассматривают самостоятельную работу как средство развития обобщенных умений, познавательной самостоятельности, творческой активности и социализации личности, связывают её со способностью к самоорганизации (Г.Н. Алова, З.А. Вологодская, А.А.Дикая, М.Е. Дуранов, В.М. Железяко, В.А. Козаков, В.Я. Ляудис, В.П. Чихачев и др.).

По нашему мнению, наиболее полное определение самостоятельной работы дается В. И. Андреевым. Его точка зрения обусловливается тем, что в процессе самостоятельной работы учащихся могут быть применены самые разнообразные методы и приемы обучения, и поэтому, по его мнению, подводить самостоятельную работу под понятие «метод» в качестве родового понятия некорректно. Также он считает, что понятие «средство» является не основным, а лишь вспомогательным, частным признаком и не может быть взято за родовое понятие.

Таким образом, самостоятельная работа учащихся - это форма организации их учебной деятельности, осуществляемая под прямым или косвенным руководством преподавателя, в ходе которой учащиеся преимущественно или полностью самостоятельно выполняют различного вида здания с целью развития знаний, умений, навыков и личных качеств.

 

 

§2. Виды самостоятельной работы учащихся

 

Все виды самостоятельной работы, применяемые в учебном процессе, можно классифицировать по различным признакам: по дидактической цели, по характеру учебной деятельности учащихся, по содержанию, по степени самостоятельности и элементу творчества учащихся и т. д.

В зависимости от целей самостоятельные работы можно разделить на следующие:

Ø Обучающие.

Ø Тренировочные.

Ø Закрепляющие.

Ø Повторительные.

Ø Развивающие.

Ø Творческие.

Ø Контрольные.

Рассмотрим более подробно каждый из видов.

1. Обучающие самостоятельные работы. Их смысл заключается в самостоятельном выполнении школьниками данных учителем заданий в ходе объяснения нового материала. Цель таких работ развитие интереса к изучаемому материалу, привлечение каждого ученика к работе на уроке. При выполнении данного вида работ школьник сразу видит, что ему непонятно, и он может попросить дополнительно объяснить эту часть материала. Учитель же составляет схему дальнейшего объяснения материала, в которой прописывает сложные для учеников моменты, на которые в дальнейшем необходимо будет обратить внимание. Также данный вид самостоятельных работ помогает выделить пробелы в знаниях прошлого материала у школьников. Самостоятельные работы по формированию знаний проводятся на этапе подготовки к введению нового содержания, также при непосредственном введении нового содержания, при первичном закреплении знаний, т.е. сразу после объяснения нового, когда знания учащихся еще не прочны.

Так как самостоятельные обучающие работы проводятся объяснения нового материала или сразу после объяснения, то, на наш взгляд, необходима их немедленная проверка. Она создает четкую картину того, что происходит на уроке, какова степень понимания учащимися нового материала, на самом раннем этапе его обучения. Цель этих работ – не контроль, а обучение, поэтому им следует отводить достаточно времени на уроке. К самостоятельным обучающим работам можно также отнести составление примеров на изученные свойства и правила.

Очевидно, что самостоятельная работа, организуемая при подготовке к усвоению новых знаний, для учащихся имеет важное значение. Нужно заметить, что данный вид деятельности можно организовать в следующих случаях:

Ø    в процессе установления связи нового материала с ранее усвоенными знаниями, умениями и навыками;

Ø    при создании поисковой ситуации и раскрытии перспективы предстоящей учебной работы;

Ø    в ходе переноса приобретенных приёмов познавательной деятельности при овладении новыми знаниями, умениями, навыками.

Если ученик в процессе самостоятельной работы продумывает факты, на основании которых излагается новый материал или решается задача, то значительно повышается продуктивность его дальнейшей работы.

Проведение самостоятельной работы надо организовывать так, чтобы она не только обеспечивала восприятие программного материала, но и способствовала бы всестороннему развитию учащихся.

2. Тренировочные самостоятельные работы. К ним относятся задания на распознавание различных объектов и свойств.

В тренировочных заданиях часто требуется воспроизвести или непосредственно применить теоремы, свойства тех или иных математических объектов и др.

Тренировочные самостоятельные работы в основном состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила. Такая работа позволяет выработать основные умения и навыки, тем самым создать базу для дальнейшего изучения материала. При выполнении тренировочных самостоятельных работ необходима помощь учителя. Также можно разрешить пользоваться учебником и записями в тетрадях, таблицами и т.п. Все это создает благоприятный климат для слабых учащихся. В таких условиях они легко включаются в работу и выполняют её. В тренировочные самостоятельные работы можно включить выполнение заданий по разноуровневым карточкам. Самостоятельная работа оказывает значительное влияние на глубину и прочность знаний учащихся по предмету, на развитие их познавательных способностей, на темп усвоения нового материала.

3. Закрепляющие самостоятельные работы. К ним можно отнести самостоятельные работы, которые способствуют развитию логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно усвоен учебный материал. По результатам проверки заданий данного типа учитель определяет количество времени, которое нужно посвятить повторению и закреплению данной темы. Примеры таких работ в изобилии встречаются в дидактическом материале.

4. Очень важны так называемые повторительные (обзорные или тематические) работы.

5. Самостоятельные работы развивающего характера. Это могут быть задания по составлению докладов на определенные темы, подготовка к олимпиадам, научно творческим конференциям, проведение в школе дней математики и др. На уроках это могут быть самостоятельные работы, в которые включены задания исследовательского характера.

6. Большой интерес вызывают у учащихся творческие самостоятельные работы, которые предполагают достаточно высокий уровень самостоятельности. Здесь учащиеся открывают для себя новые стороны уже имеющихся у них знаний, учатся применять эти знания в неожиданных, нестандартных ситуациях. В творческие самостоятельные работы можно включить задания, при выполнение которых необходимо найти несколько способов их решений.

7. Контрольные самостоятельные работы. Как понятно из названия, их главной функцией является функция контроля. Необходимо выделить условия, которые нужно учитывать при составлении заданий для самостоятельных контрольных работ. Во-первых, контрольные задания должны быть равноценными по содержанию и объему работы; во-вторых, они должны быть направлены на отработку основных навыков; в-третьих, обеспечивать достоверную проверку уровня знаний; в-четвертых, они должны стимулировать учащихся, позволять им продемонстрировать все их навыки и умения.

Эффективность самостоятельной работы, формирование навыков самостоятельной деятельности во многом зависит от своевременного анализа результатов работы, когда у ученика еще не окончен процесс корректировки собствен новых знаний, очевидно, что анализ самостоятельной работы должен носить обучающий характер, т.е. не просто констатировать количество ошибок, а производить их разбор, с тем, чтобы учащиеся смогли до конца понять вопросы, в которых сделали ошибки.

Существует еще одна классификация самостоятельной работы по дидактической цели, которая выделяет пять групп деятельности:

1) приобретение новых знаний, овладение умением самостоятельно приобретать знания;

2) закрепление и уточнение знаний;

3) выработка учения применять знания в решении учебных и практических задач;

4) формирование учений и навыков практического характера;

5) формирование умений и навыков творческого характера, умения применять знания в усложненной ситуации.

Каждая из перечисленных групп включает в себя несколько видов самостоятельной работы, поскольку решение одной и той же дидактической задачи может осуществляться различными способами. Указанные группы тесно связаны между собой. Эта связь обусловлена тем, что одни и те же виды работ могут быть использованы для решения различных дидактических задач.

К основным видам самостоятельных работ можно отнести следующие:

1.                 Работа с книгой.

2.                 Упражнения.

3.                 Выполнение практических и лабораторных работ.

4.                 Проверочные самостоятельные, контрольные работы, диктанты, сочинения.

5.                 Подготовка докладов, рефератов.

6.                 Домашние опыты, наблюдения.

7.                 Техническое моделирование и конструирование.

Говоря о типах самостоятельной работы, принято выделять в соответствии с уровнями самостоятельной деятельности воспроизводящие, реконструктивно-вариативные, эвристические, творческие.

К творческим самостоятельным работам можно отнести такие формы как:

Ø практические работы;

Ø контрольные работы;

Ø тематические зачеты;

Ø защита и написание рефератов;

Ø решение проблемных задач прикладного характера и другие.

С точки зрения организации самостоятельная работа может быть:
фронтальной (общеклассной) - учащиеся выполняют одно в то же задание; групповой - для выполнения задания учащиеся разбиваются на небольшие группы (по 3-б чел.); парной – например, при проведении опытов, выполнении различных построений, конструировании моделей; индивидуальной – каждый учащийся выполняет отдельное задание.

Организуя самостоятельную работу ученика, учитель ненавязчиво раскрывает конфликтную ситуацию при изучении материала. Нет необходимости придумывать противоречия, проблемы, конфликтные ситуации, они есть в каждой теме, они составляют суть процесса познания любого объекта или процесса.

Рассматривая самостоятельную деятельность в качестве познавательной, выделяют четыре ее разновидности в процессе обучения:

1. Цель и план работы ученик определяет с помощью учителя.

2. Цель учащийся определяет с помощью учителя, а план самостоятельно.

З. Цель и план учащийся определяет самостоятельно, но задание даёт учитель.

4. Без помощи учителя учащийся сам определяет содержание, цель, план работы и самостоятельно её выполняет.

Первая разновидность наиболее простая, и с неё учитель должен начинать подготовку ребят к более сложным этапам самостоятельной работы. Затем постепенно, переходя от этапа к этапу, ученик получает возможность полностью проявлять свои знания, инициативу, личные качества и индивидуальные особенности. Самостоятельная работа организуется с помощью индивидуальных форм обучения. Ученик работает самостоятельно дома при выполнении домашних заданий, написании рефератов и т. д. Индивидуальная форма предполагает деятельность ученика по выполнению общих для всего класса заданий без контакта с одноклассниками, в едином для всех темпе. Она преимущественно используется при закреплении знаний, формировании умений и навыков, контроле знаний. Индивидуальная работа на уроке требует от учителя тщательной подготовки, большой затраты сил и времени. Однако эта форма организации познавательной деятельности не всегда создаёт условия для полной самостоятельной деятельности учащихся. Она является хорошим средством организации деятельности сознательных учеников. Но нередко можно наблюдать на уроках картину, когда слабо успевающие учащиеся либо ничем не занимаются, т. к. не могут справиться самостоятельно с заданием, либо спрашивают у соседей по парте о способе решения, что ведет к списыванию и подсказкам. Для организации большей самостоятельности школьников используется индивидуализированная форма обучения. Эта форма предполагает такую организацию работы, при которой каждый ученик выполняет свое, отличное от других, задание, с учетом учебных возможностей. Практический опыт учителей многих школ показал, что:

1. Систематически проводимая самостоятельная работа (с учебником по решению задач, выполнению наблюдений и опытов) при правильной ее организации способствует получению учащимися более глубоких и прочных знаний по сравнению с теми, которые они приобретают при сообщении учителем готовых знаний.

2. Организация выполнения учащимися разнообразных по дидактической цели и содержанию самостоятельных работ способствует развитию их познавательных и творческих способностей, развитию мышления.

3. При тщательно продуманной методике проведения самостоятельных работ ускоряются темпы формирования у учащихся умений и навыков практического характера, а это в свою очередь оказывает положительное влияние на формирование познавательных умении и навыков.

С течением времени при систематической организации самостоятельной работы на уроках и сочетании ее с различными видами домашней работы по предмету у учащихся вырабатываются устойчивые навыки самостоятельной работы. В результате для выполнения примерно одинаковых по объему и степени трудности работ учащиеся затрачивают значительно меньше времени по сравнению с учащимися таких классов, в которых самостоятельная работа практически не организуется или проводится нерегулярно. Это позволяет постепенно наращивать темпы изучения программного материала, увеличить время на решение задач, выполнение экспериментальных работ и других видов работ творческого характера.

 

2.3  Цели, задачи и функции самостоятельной работы учащихся.

 

Весь процесс обучения направлен на достижение определенной цели - формирование и воспитание многогранной, творческой личности, с сложившимися приоритетами, правилами поведения, с системой ценностей и верными представлениями о мире в целом. Поэтому любая деятельность учителя должна носить целенаправленный характер. Очевидно, что педагог лишь организует и направляет познавательную деятельность обучаемых. Ее эффективность зависит от собственных усилий последних. При правильной организации самоподготовка имеет решающее значение для развития самостоятельности как одной из ведущих черт ученика и выступает средством, обеспечивающим для школьников:

Ø сознательное и прочное усвоение знаний по предмету;

Ø овладение способами и приемами самообразования;

Ø развитие потребности в самостоятельном пополнении знаний.

Самоподготовка способствует формированию высокой культуры умственного труда, приобретению приемов и навыков самостоятельной работы, умений разумно расходовать и распределять свое время, накапливать и усваивать необходимую для успешного обучения и профессионального становления информацию. Она развивает у учеников такие качества, как организованность, дисциплинированность, инициативность, волю; вырабатывает мыслительные умения и операции (анализ, синтез, сравнение, сопоставление и др.), учит самостоятельному мышлению, позволяет сформировать свой собственный стиль работы, наиболее полно соответствующий личным склонностям и познавательным навыкам школьника. В условиях же высокого уровня развития науки и техники особые требования предъявляются именно к подготовке учащихся в школе. Задача образования не может сводиться только к вооружению учащихся определенной суммой знаний. Необходимо сформировать у них умение оперировать приобретенными знаниями, применять их в новых ситуациях, делать самостоятельные выводы и обобщения, находить решения в нестандартных условиях. В настоящий период когда развитие науки и техники происходит чрезвычайно быстро, когда делаются всё новые и новые научные открытия, когда появляются неизвестные ранее отрасли науки, техники, экономики, исключительную значимость приобретает проблема подготовки учащихся к самостоятельному овладению новыми знаниями, к изучению научной и технической литературы. Для этого им необходимы такие умения как читать текст, насыщенный информацией, вычленять из него главное, ставить перед собой вопросы и находить в тексте ответы на них, определять, что осталось не выясненным до конца, четко формулировать, что именно надо выяснить, обращаться за справкой к другому разделу книги или другой литературе и т.п. Вместе с тем, для того чтобы подготовить учащихся к применению знаний в конкретных условиях, к решению сложных вопросов, выбору из имеющегося набора решений оптимального варианта и т.д., необходимо сформировать определенные умения в решении задач. Самостоятельная деятельность учащихся можно и нужно организовывать на различных уровнях, от воспроизведения действий по образцу и узнавание объектов путем их сравнения с известным образцом до составления модели и алгоритма действий в нестандартных ситуациях.

Это переориентирует самостоятельную работу с традиционной цели – простого усвоения знаний, приобретения умений и навыков, опыта творческой и научно-информационной деятельности – на развитие внутренней и внешней самоорганизации учащегося, активно преобразующего отношения к получаемой информации, способности выстраивать индивидуальную траекторию самообучения.

Данная особенность постановки целей имеет дидактическое значение для педагогической деятельности – преподаватель может ориентироваться на представленную номенклатуру при организации и самостоятельной работы учащихся. Вместе с тем важно научить школьника самого ставить перед собой цели. На разных занятиях в ходе анализа нового материала, при проверке заданий желательно вначале подводить учащегося к пониманию цели педагога, а затем к самостоятельной постановке своих, имеющих для него личностный смысл целей. Важное условие при этом – цели школьников должны быть реально достижимыми.

Общей же целью самостоятельной работы учеников при изучении математики является формирование математического мышления учеников.

Эта цель самостоятельной работы при изучении математики конкретизируется в задачах самостоятельной работы по каждой теме, среди которых выделяются приоритетные.

Для достижения поставленных целей большое значение имеют условия организации самостоятельной работы, которые позволяют значительно повысить ее эффективность. К ним можно отнести индивидуализацию, которая включает:

·       увеличение удельного веса интенсивной работы с более подготовленными учащимися;

·       деление занятия на обязательную и творческую части (для всех, пытающихся самостоятельно справиться с более трудными и, главное, - нестандартными задачами, дополнительными вопросами, учебно-проблемными ситуациями и т. д.);

·       регулярность консультаций с обучаемыми;

·       исчерпывающее и своевременное информирование о тематическом содержании самостоятельной работе, сроках выполнения, потребности во вспомогательных средствах, формах, способах контроля и оценке итоговых результатов с обязательным сравнением с ожидаемыми.

Данные условия определяют применение личностно-ориентированного подхода при обучении, который способствуют полноценному раскрытию способностей каждого из обучающихся и последующему творческому развитию.

При постановке целей и задач самостоятельной работы необходимо учитывать следующие дидактические требования:

1. Самостоятельная работа должна носить целенаправленный характер. Это достигается четкой формулировкой цели работы. Задача учителя заключается в том, чтобы найти такую формулировку задания, которая вызывала бы у школьников интерес к работе и стремление выполнить ее как можно лучше. Учащиеся должны ясно представлять, в чем заключается задача и каким образом будет проверяться ее выполнение. Это придает работе учащихся осмысленный, целенаправленный характер, и способствует более успешному ее выполнению.

Недооценка указанного требования приводит к тому, что учащиеся, не поняв цели работы, делают не то, что нужно, или вынуждены в процессе ее выполнения многократно обращаться за разъяснением к учителю. Все это приводит к нерациональной трате времени и снижению уровня самостоятельности учащихся в работе.

2. Самостоятельная работа должна быть действительно самостоятельной и побуждать ученика при ее выполнении работать напряженно. Однако здесь нельзя допускать крайностей: содержание и объем самостоятельной работы, предлагаемой на каждом этапе обучения, должны быть посильными для учащихся, а сами ученики – подготовлены к выполнению самостоятельной работы теоретически и практически.

3. На первых порах у учащихся нужно сформировать простейшие навыки самостоятельной работы. В этом случае самостоятельной работе учащихся должен предшествовать наглядный показ приемов работы с учителем, сопровождаемый четкими объяснениями, записям и на доске.

Самостоятельная работа, выполненная учащимися после показа приемов работы учителем, носит характер подражания. Она не развивает самостоятельности в подлинном смысле слова, но имеет важное значение для формирования более сложных навыков и умений, более высокой формы самостоятельности, при которой учащиеся оказываются способными разрабатывать и применять свои методы решения задач учебного или производственного характера.

4. Для самостоятельной работы в большинстве случаев нужно предлагать такие задания, выполнение которых не допускает действия по готовым рецептам и шаблону, а требует применения знаний в новой ситуации. Только в этом случае самостоятельная работа способствует формированию инициативы и познавательных способностей учащихся.

5. В организации самостоятельной работы необходимо учитывать, что для овладения знаниями, умениям и навыками различным учащимися требуется разное время. Осуществлять это можно путем дифференцированного подхода к учащимся.

Наблюдая за ходом работы класса в целом в отдельных учащихся, учитель должен вовремя переключать успешно справившихся с заданиями на выполнение более сложных.

6. Задания, предлагаемые для самостоятельной работы, должны вызывать интерес учащихся. Он достигается новизной выдвигаемых задач, необычностью их содержания, раскрытием перед учащимися практического значения предлагаемой задачи или метода, которым нужно овладеть.

7. Самостоятельные работы учащихся необходимо планомерно и систематически включать в учебный процесс. Только при этом условии у них будут вырабатываться твердые умения и навыки.

8. При организации самостоятельной работы необходимо осуществлять разумное сочетание и изложения материала учителем с самостоятельной работой учащихся по приобретению знаний, умений и навыков. В этом деле нельзя допускать крайностей: излишнее увлечение самостоятельной работой может замедлить темпы изучения программного материала, темпы продвижения учащихся вперед в познании нового.

9. При выполнении учащимися самостоятельных работ любого вида руководящая роль должна принадлежать учителю. Учитель продумывает систему самостоятельных работ, их планомерное включение в учебный процесс. Он определяет цель, содержание и объем каждой самостоятельной работы, ее место на уроке, методы обучения различным видам самостоятельной работы. Он обучает учащихся методами самоконтроля и осуществляет контроль за качеством ее выполнения, изучает индивидуальные особенности учащихся и учитывает их при организации самостоятельной работы.

Самостоятельная работа обладает большим потенциалом для развития различных умений школьников. Так, основными из них являются:

Ø    умения работать с книгой (учебником, математическим текстом, справочниками, таблицами и.др.), работа по плану, алгоритму, предписанию. Навыки работы учащихся по плану особенно успешно развиваются на уроках геометрии. Так, умение работать по образцу не приходит само собой, а требует специальных приемов работы учителя, на уроках математики можно применять карточки с пропусками;

Ø    классификация, систематизация учебного материала успех самостоятельной работы нередко зависит от умения систематизировать учебный материал;

Ø    навыки самоконтроля и самоанализа.

Организация самостоятельной работы, руководство ею – это ответственная и сложная работа каждого учителя. Воспитание активности и самостоятельности необходимо рассматривать как составную часть воспитания учащихся. Эта задача выступает перед каждым учителем в числе задач первостепенной важности.

 

2.4  Технология организации самостоятельной работы учащихся.

 

Говоря о технологической стороне, организация самостоятельной работы может включать в себя следующие компоненты:

Целевой компонент самостоятельной работы. Основаниями для отбора целей являются цели, определенные Государственным образовательным стандартом, и конкретизация целей по разделам дисциплины. Кроме того, пели самостоятельной работы должны соответствовать структуре готовности к дальнейшему самообразованию, включающей мотивационный, когнитивный, деятельностный компоненты.

Содержательный компонент самостоятельной роботы. Основаниями отбора содержания самостоятельной работы являются Государственный образовательный стандарт, источники самообразования (литература, опыт, самоанализ). Индивидуально-психологические особенности учеников (обучаемость, обученность, интеллект, мотивация, особенности учебной деятельности). При этом важную роль играет подборка учебного материала, т.к. с его помощью мы черпаем информацию содержания обучения. Однако сама по себе информация вне потребности ребенка не имеет для него никакого значения и не оказывает никакого воздействия. Если же информация созвучна потребностям учащегося к подвергается эмоциональной переработке, то он получает импульс к последующей деятельности. Для этого содержание учебного материала должно быть доступно ученику, должно исходить из имеющихся у него знаний и опираться на них и на жизненный опыт детей, но в то же время материал должен быть достаточно сложным и трудным.

Необходимо отметить тот факт, что содержание самостоятельной работы полностью направлено на реализацию её целей. Это является основополагающим при рассмотрении проблем эффективного применения самостоятельной работы учеников как при изучении математики в школе, так и при обучении всем другим дисциплинам. Рассмотрим различные аспекты данного вопроса.

При отборе содержания для самостоятельной работы необходимо учитывать следующие психолого-педагогические условия, способствующие повышению эффективности ее применения:

Ø    включение в образовательный процесс дидактических средств, оптимизирующих деятельность учителей и школьников;

Ø    усиление роли контрольно-диагностических процедур для повышения эффективности самостоятельной работы;

Ø    формирование активно-поискового уровня самостоятельности школьников через использование дидактических средств образовательного процесса;

Ø    учет индивидуальных стилей учебной деятельности.

Вообще говоря, к условиям отбора содержания самостоятельной работы можно отнести достаточно большой ряд различных факторов, но на наш взгляд, большую роль играют следующие:

1. Обеспечение правильного сочетания объема совместной с учителем
работы и самостоятельной.

2. Методически правильная организация работы учащегося в классе и вне его.

3. Обеспечение ученика необходимыми методическими материалами с целью превращения процесса самостоятельной работы в процесс творческий.

4. Контроль за ходом самостоятельной работы и меры, поощряющие
ученика за ее качественное выполнение.

При построении системы заданий самостоятельных работ каждый учитель должен руководствоваться следующими дидактическими требованиями:

·        Система самостоятельных работ должна способствовать решению основных дидактических задач – приобретению учащимися глубоких и прочных знаний, развитию у них познавательных способностей, формированию умения самостоятельно приобретать, расширять и углублять знания, применять их на практике.

·        Система должна удовлетворять основным принципам дидактики, и, прежде всего принципам доступности и систематичности, связи теории с практикой, сознательной и творческой активности, принципу обучения на высоком научном уровне.

·        Входящие в систему работы должны быть разнообразны по учебной цели и содержанию, чтобы обеспечить формирование у учащихся разнообразных умений и навыков.

·        Последовательность выполнения домашних и классных самостоятельных работ логически вытекало из предыдущих и готовило почву для выполнения последующих. В этом случае между отдельными работами обеспечиваются не только «ближние», но и «дальние» связи. Успех решения этой задачи зависит не только от педагогического мастерства учителя, но и от того, как он понимает значение и место каждой отдельной работы в системе работ, в развитии познавательных способностей учащихся, их мышления и других качеств.

Контрольно-корректировочный компонент самостоятельной работы. Включает тщательный отбор средств контроля, определение эталон, разработку индивидуальных форм контроля.

При самостоятельном обучении у школьников формируются прочные мотивы учения, постоянного совершенствования, самообучения, самовоспитания и самоорганизации в ходе урока. Такой урок обучает рациональной организации самостоятельной и учебно-тренировочной деятельности. Так как по форме и содержанию самостоятельные работы могут быть разнообразны, это позволяет значительно повышать интерес учащихся к предмету и влиять на совершенствование процесса обучения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3. Заключение

3.1 Необходимость  формирования самостоятельной деятельности

      Одним из важнейших средств систематического и прочного усвоения программного материала по математике, развития творческих сил и воспитания учащихся является самостоятельная работа.

Привитие учащимся навыков самостоятельной работы всегда являлось одной из главных задач на каждом этапе развития школы.

Практика показывает, что при обучении математике необходимо уделять значительное место самостоятельной работе учащихся, организации различных упражнений. Без этого не может быть усвоения программного материала по математике. Только в выполнении различных упражнений закрепляются математические понятия, вырабатываются вычислительные навыки, приобретается умение геометрических построений, развивается пространственное представление учащихся, умение практически применять знания, свой опыт при решении задач и т. д.

В процессе выполнения самостоятельной работы по математике у учащихся развивается внимание, память, стремление обосновывать высказываемое, инициатива. Сама же организация самостоятельной работы в условиях классно-урочной формы обучения воспитывает высоконравственные качества.

Самостоятельная работа была и остается важной неотъемлемой частью учебного процесса. Как известно, наибольший развивающий эффект учебно-познавательной деятельности достигается в том случае, когда она выполняется учеником с максимальной степенью самостоятельности. Лишь тогда, когда ученик сам, без какой-либо помощи со стороны учителя справляется с учебными заданиями, сам находит решение задачи, сам применяет приобретенные знания не только в стандартных, но и в измененных ситуациях, в новых сочетаниях и комбинациях, можно говорить о высокой эффективности учебного процесса. Еще К.Д. Ушинский отмечал, что школа должна так организовывать труд учителя и учеников, чтобы дети, по возможности, трудились самостоятельно, а учитель руководил этим самостоятельным трудом и давал для него материал. Именно самостоятельную учебную работу он считал «единственным прочным основанием всякого плодовитого учения».

Проблеме самостоятельной работы посвящено множество трудов педагогов, психологов и методистов. Результаты анализа психолого-педагогической литературы показал, что многочисленные попытки раскрытия сущности самостоятельной работы базируются, как правило, на определении наиболее значимых с точки зрения каждого конкретного автора признаков характеризуемого понятия.

В соответствии с тем, на каких именно признаках самостоятельной работы акцентируют свое внимание те или иные исследователи, меняется смысл, вкладываемый в содержание самого понятия.

В качестве методических рекомендаций по организации математических уроков можно выделить следующее:

Взаимосвязь в содержании, формах и методах организации учебной работы и занятий;

Обеспечивать взаимосвязь (по содержанию) уроков и факультативных занятий;

Единство в содержании занятий различных разделов математики;

Активизация самостоятельной работы учащихся;

Построение учебного процесса как совместная исследовательская деятельность учащихся;

Использование наглядных пособий; применение конспект-таблиц на лекциях;

Использование системы ключевых задач по темам на факультативных занятиях;

Использование историко-математического материала на уроках;

Принципы занимательности занятий;

Построение занятий проблемного изучения материала.

4. Приложения

Приложение 1.

Конспект урока геометрии (8 класс)

 

Тема урока: «Четырехугольники»

Тип урока: урок обобщения и систематизации знаний.

Цель урока: систематизация сведений о четырехугольниках.

Задачи:

1.     Повторение определений, свойств, признаков всех видов четырехугольников.

2.     Активизация поисково-познавательной деятельности в процессе решения задач на моделирование геометрических фигур, установление их вида и свойств.

3.     Воспитание исследовательских умений и навыков.

4.     Доказательство теоремы Вариньона.

Оборудование: плакат «Генеалогическое древо четырехугольников»; листы бумаги произвольной четырехугольной формы; наборы подвижных моделей для задач на моделирование (их можно сделать из трубочек от сока, скрепленных скрепками); бумажные заготовки параллелограммов, прямоугольников, ромбов, равнобедренных трапеций по количеству учащихся; плакаты с изображением дельтоида и произвольного четырехугольника, имеющего равные диагонали; чертежный треугольник; масштабная линейка; циркуль.

 

Ход урока

I.      Фронтальный опрос

1)    определения;

2)    свойства;

3)    признаки известных видов четырехугольников.

 

Вопросы к классу (эта часть урока в форме беседы):

1. Какие вы знаете четырехугольники, у которых диагонали равны?

2. А существует ли четырехугольник, у которого диагонали равны, но он не является ни одним из изученных видов? Изобразите его.

3. Назовите виды четырехугольников со взаимно перпендикулярными диагоналями.

4. Постарайтесь изобразить четырехугольник, у которого диагонали взаимно перпендикулярны, но он не является ни одним из изученных видов. (Показать дельтоид и немного рассказать о нем.)

5. В трапеции только два угла могут быть прямыми. Так ли это? Почему?

6. Нарисуйте четырехугольник, в котором:

а) каждая диагональ больше любой его стороны;

б) каждая диагональ меньше любой его стороны.

7. Вспомните, сколько элементов определяет треугольник? (три). Треугольник – жесткая фигура. Давайте выясним, достаточно ли 4-х элементов для определения четырехугольника? Возьмите, например:

1) 4 палочки, скрепки и составьте четырехугольник. (Класс убеждается, что у всех получились разные четырехугольники). Т.е. четыре стороны не определяют четырехугольник;

2) 3 стороны и угол;

3) 3 стороны и диагональ;

4) 2 диагонали и угол.

Что получается в каждом из случаев?

Вывод: Любой четырехугольник разбивается диагональю на 2 треугольника.

1)    один треугольник определяется тремя элементами;

2)    для того, чтобы второй треугольник был задан, нужно задать еще два элемента (т.к. один элемент у треугольников общий).

А сейчас составьте четырехугольник по четырем сторонам и диагонали.

Какими способами можно это сделать?

1 способ. Соединить 4 палочки скрепками в точках A, B, C, D, а затем поставьте еще одну палочку-распорку по диагонали AC.

2 способ (более надежный). Соединить 3 палочки в треугольник ABC. Затем присоединить еще две палочки CD и AD в точках A, C и D. (Рисунок 1)

 

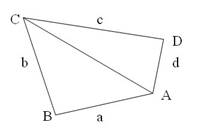
Всегда ли возможно выполнить такое построение? (если данный вопрос вызывает затруднения, тогда нужно подобрать палочки такой длины, чтобы построение было невыполнимо).

Вывод (делают учащиеся): AC < a + b и AC < c + d.

 

II.   Задачи на моделирование.

(в этих задачах все используемые палочки одинаковы по длине).

1. Из пяти палочек без наложения составить 2 треугольника и четырехугольник.

 

Рисунок 2

Определите: а) вид полученных фигур (ромб и равносторонние треугольники); б) углы четырехугольника ()

 

2. Из 7 палочек без наложения составить 3 треугольника и 3 четырехугольника.

 

Рисунок 3

Определите: а) вид полученных четырехугольников (2 ромба и 1 равнобедренная трапеция); б) углы трапеции.

      

       3. Из 9 палочек составить 4 треугольника, 3 ромба, 2 трапеции и параллелограмм, не являющийся ромбом.

Рисунок 4

Определите: а) периметр параллелограмма, если длина палочки равна а. (Р=6а)

 

       4. Из 9 палочек составить 5 треугольников, 3 ромба, 3 трапеции.

Рисунок 5

Определите: а) сравните периметр большого треугольника и периметр параллелограмма. (Ртреуг=6а,  Рпарал-ма= 4а)

 

       5. Из 8 палочек составить квадрат, 2 треугольника и выпуклый шестиугольник.

Рисунок 6

Определите: а) определите чисто всех диагоналей (9)

 

       Вывод: любой многоугольник можно составить из треугольников. Обратное утверждение тоже верно.

       Разбивать можно не только диагоналями, но и другими отрезками. Например, медианами, биссектрисами, средними линиями.

       Вопрос: На какие фигуры разобьют треугольник средние линии?

       Ответ на этот вопрос – теорема, которую вы докажете дома. (Средние линии разбивают треугольник на 4 равных треугольника).

 

III.     Проблемная задача.

       Как только с помощью перочинного ножика из куска линолеума произвольной четырехугольной формы вырезать заплату в форме параллелограмма?

       Для того, чтобы ответить на заданный вопрос, давайте предварительно решим следующую задачу.

       Задача. Показать, что середины сторон выпуклого четырехугольника являются вершинами параллелограмма.

Дано: ABCD – четырехугольник, F – середина AB, M – середина BC, N – середина CD, K – середина DA. Доказать: FMNK – параллелограмм.

Рисунок 7

Доказательство:

Проведем диагонали АС и BD,

тогда FM – средняя линия , следовательно FM || AC, ;

     KN – средняя линия , следовательно KN || AC, .

По свойству параллельных прямых KN|| FM и KN= FM по свойству транзитивности.

Значит FMNК – параллелограмм (по 1 признаку параллелограмма).

Задача решена.

 

Итак, решив данную задачу, мы с Вами доказали теорему, известную как теорема Вариньона. (Некоторые факты биографии французского математика Вариньона представлены на стенде. Желающие могут с ними ознакомиться).

Далее предлагается учащимся взять бумажную заготовку параллелограмма и с помощью сгибания убедиться в том, что получается параллелограмм.

Далее вопросы к классу (учащиеся отвечают на них, используя заготовки четырехугольников):

1.     Какая фигура получается, если соединить середины сторон прямоугольника? (Ответ: ромб, Рисунок 8).

2.     Какая фигура получается, если соединить середины сторон ромба? (Ответ: прямоугольник, Рисунок 9).

3.     Какая фигура получится, если соединить середины сторон равнобедренной трапеции? (Ответ: ромб, Рисунок 10).

4.     Постарайтесь нарисовать ещё какие-нибудь четырехугольники такие, что середины сторон являются вершинами:

                             а) прямоугольника (Рисунок 11);

                             б) ромба (Рисунок 12).

А  теперь попытайтесь проанализировать и ответьте на вопрос: «При каком условии четырехугольник, вершинами которого служат середины сторон данного четырехугольника является:

а) прямоугольником (ответ: если диагонали взаимно перпендикулярны);

б) ромбом (ответ: если диагонали равны);

в) квадратом (ответ: если диагонали перпендикулярны и равны)».

 

Задача (если есть время):

Доказать, что отрезки, соединяющие середины противоположных сторон выпуклого четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке.

Решение.

Рисунок 13.

 

MNPK – параллелограмм (ключевая задача);  O – середина NK (по свойству диагоналей параллелограмма).

LN – средняя линия , следовательно LN || AB, ,

KS – средняя линия , следовательно KS || AB, .

По свойству параллельных прямых LN || KS и LN = KS по свойству транзитивности.

Значит KLNS – параллелограмм (по 1 признаку параллелограмма).

 Пусть  X – середина NK, т.е. Х=О.

 

IV.      Итог урока.

В следующих предложениях заменить многоточие словами: «необходимо и достаточно», «необходимо, но не достаточно», «достаточно, но необходимо».

1) Для того, чтобы четырехугольник был прямоугольником … чтобы его диагонали были равны.

2) Для того, чтобы четырехугольник был параллелограммом … чтобы все его стороны были равны.

3) Для того, чтобы четырехугольник был ромбом … чтобы его диагонали были взаимно перпендикулярны и в точке пересечения делились пополам.

 

V.         Домашнее задание.

1)    Доказать теорему о разбиении треугольника средними линиями на 4 равных треугольника;

Составьте утверждение, обратное свойству параллелограмма о равенстве противоположных углов. Верно ли оно. Если да, доказать

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 2.

Урок геометрии  8 класс

Тема: « Четырехугольники »

Тип урока: обобщение.

Цели урока:

N образовательные: а) обобщение и систематизация знаний учащихся по теме «Четырехугольники»;

                                      б) закрепление навыков решения задач по данной теме;

N развивающие:  формирование и развитие мыслительных операций (сравнения, обобщения, систематизации );

N воспитательные: развитие чувства коллективизма, умения выслушивать ответы товарищей, привитие интереса к предмету.

Реквизит:

                   - карточки « Домино »;

                   - магнитные карточки с геометрическими фигурами;

                   - дифференцированные карточки - задачи;

Учащиеся разбиваются на 5 групп по 2-3  человека.

Ход урока.

I. Организационный момент. Объявление темы урока. Постановка целей.

II. Повторение основных понятий. Игра « Домино ».

У каждого ученика имеется карточка, содержащая вопрос и ответ. Начинает игру ученик с карточкой, в которой обозначены слова: « Старт » и « Финиш ». Он задает стартовый вопрос, и он же  заканчивает игру финишным ответом. Каждый ученик должен внимательно следить за ходом игры, чтобы не пропустить свой ответ. Ответив, ученик задает свой вопрос и т. д.

       III. Повторение свойств и признаков основных видов четырехугольников. Групповая работа.      

                Каждая группа получает задание:

1.     Начертить заданный четырехугольник.

2.     Указать его основные свойства и признаки.

    Виды четырехугольников: 1 группа - трапеция

                                                  2 группа - параллелограмм

                                                  3 группа - прямоугольник

                                                  4 группа - ромб

                                                  5 группа - квадрат

IV. Систематизация сведений о четырехугольниках и их свойствах.

       Выступления представителей от каждой группы, по ходу которых на магнитной доске постепенно выстраивается  классификационная таблица « Четырехугольники ».

V. Обобщение.

       Учащиеся делают выводы о том, что квадрат имеет свойства ромба и прямоугольника, прямоугольник и ромб имеют свойства и признаки параллелограмма, трапеция и параллелограмм - это разные виды четырехугольников.

VI. Самостоятельная работа.

       Ученики решают задачи по карточкам. В зависимости от уровня подготовленности ,решающий выбирает задачу N1, N2 или обе задачи. За две задачи оценка «5», за N2 - «4», за N1 - «3».

VI. Подведение итогов урока.

VIII. Домашнее задание. Составить задачу по теме « Четырехугольники » на построение.

 

      

       

  

                        В                                С                 

                                                                                             В                С                                    

                                         О

                   

                   А                                   D                                E                    F 

 

                                                                                          А                     D                         

 

 

AB||CD  AB=CD  ÐA=ÐC  AO=OC   BC||AD  BC=AD  ÐB=ÐD  BO=OD

BC||AD           BC+AD  EF =        2

   

                                                                                                 B

 B                                      C     B                    C

 

                      O                                                    A                                  C                                                                                 

                                                         O                                    O                                                     

 A                                      D

                                                A                      D                   D

                                                                                                

BD=AC                                                                        ÐA=ÐB=ÐC=ÐD=900

BD^AC   AB=BC=CD=AD

                                                         

                           Карточки  « Домино»

Финиш.

Ответ. Прямоугольник, у которого все стороны равны.

Старт.

Вопрос. Какая фигура называется многоугольником?

 

 

Ответ. Фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные не имеют общих точек.

Вопрос. Какие вершины многоугольника  называются соседними?

 

 

Ответ. Две вершины, принадлежащие одной стороне.

Вопрос. Что называется  диагональю многоугольника?

 

 

Ответ. Отрезок, соединяющий любые две не соседние вершины.

Вопрос. Какой многоугольник называется выпуклым?

 

 

Ответ. Многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.

Вопрос. Что такое n- угольник?

 

 

Ответ. Многоугольник, с n вершинами, имеющий n сторон.

Вопрос. Чему равна сумма углов выпуклого n- угольника?

 

 

Ответ. (n - 2) * 180 ⁰

Вопрос. Какая фигура называется четырехугольником?

 

 

Ответ. Многоугольник, который имеет 4 вершины, 4 стороны и 2 диагонали.

Вопрос. Как называются две несмежные стороны четырехугольника?

 

 

Ответ. Противоположные.

Вопрос. Какие вершины четырехугольника называются противоположными?

 

 

Ответ. Две вершины, не являющиеся соседними.

Вопрос. Чему равна сумма углов выпуклого четырехугольника?

 

 

Ответ. 360°

Вопрос. Что называется параллелограммом?

 

 

Ответ. Четырехугольник, у которого противоположные стороны попарно параллельны.

Вопрос. Является ли параллелограмм выпуклым четырехугольником?

 

 

Ответ. Является.

Вопрос. Что такое трапеция?

 

 

Ответ. Четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Вопрос. Что называется основаниями трапеции?

 

 

Ответ. Параллельные стороны трапеции.

Вопрос. Как называются непараллельные стороны трапеции?

 

 

Ответ.  Боковыми сторонами.

Вопрос. Какая трапеция называется равнобедренной?

 

 

Ответ. Трапеция, у которой боковые стороны равны.

Вопрос. Как называется трапеция, у которой  один из углов прямой?

 

 

Ответ. Прямоугольной.

Вопрос. Какая фигура называется прямоугольником?

 

 

Ответ. Параллелограмм, у которого все углы прямые.

Вопрос. Что такое ромб?

 

 

Ответ. Параллелограмм, у которого все стороны равны.

Вопрос. Что называется квадратом?

 

 

 

 

Карточки - задачи

 

 

I вариант

 

N1. В параллелограмме ABCD сторона СD равна 4 см, отрезок ВМ делит сторону АD на отрезки 4 и 3 см. Угол АВМ = 60 ⁰.Вычислите периметр параллелограмма и его углы.

 

N2. В трапеции ABCD (AB II СD) диагональ BD  делит среднюю линию трапеции на отрезки 6 см и 12 см. найдите основания этой трапеции.

 

 

II вариант

 

N1. Диагональ ромба образует с одной из его сторон угол 40 ⁰. Найдите углы ромба.

 

N2. Концы отрезка, расположенного по одну сторону от прямой, удалены от нее на расстояния 6 см и10 см. На каком расстоянии от этой прямой находится середина этого отрезка?

 

III вариант

 

N1. Биссектриса угла А прямоугольника ABCD делит сторону  ВС  на части 2 см и 6 см. Найдите периметр прямоугольника.

 

N2. В равнобокой трапеции диагональ образует с основанием угол 30 ⁰. Найдите углы трапеции, если известно, что меньшее основание трапеции равно ее боковой стороне.

 

 

IV вариант

 

N1. Меньшая сторона прямоугольника равна 4 см и образует  с диагональю угол   60⁰.

Найдите диагонали прямоугольника.

 

N2. В равнобокой трапеции диагональ перпендикулярна  к ее боковой стороне и образует с основанием угол 15 ⁰.Найдите углы трапеции.

 

 

5. Литература.

 

1.     Азевич Алексей. От Евклида до Петра. Страницы истории на уроках математики //Учительская газета. 1995 №10

2.     А.А. Окунев «Спасибо за урок, дети! О развитии творческих способностей учащихся» Книга для учителя: из опыта работы. -  М.: «Просвещение», 1988 г.

3.      Б.Г. Зив «Задачи в урокам геометрии 7-11 классы», НПО «Мир и семья 95», С-Пб, издательство «Акация», 1995 г.

4.      Б.Г. Зив, В.Б. Некрасов «Дидактические материалы по геометрии. 8 класс»; М: «Просвещение», 2001 г.

5.     В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович Практикум по элементарной математике. Геометрия. – М.: 2007.

6.     В.В. Прасолов «Задачи по планиметрии»; М: «Наука», главная редакция физико-математической литературы, 1986 г.

7.     В. Кармушина  Технология развивающего метода на уроках математики // Учитель. № 2. 2004.

8.     Л.С. Атанасян, В.Ф. Бутузов «Геометрия 7-9». – М.: Просвещение, 2008.

9.     С.Г. Манвелов Развитие самостоятельности учащихся через формирование навыков самоконтроля. самостоятельная работа учащихся в прцессе обучения математике. /Сост. Ю.Д. Кабалевский/. – М.: Просвещение, 1988.

10.  Ф.С. Мухаметзянова Компетентстно-ориентированные измерители образовательных достижений учащихся по математике.// Психолого-педагогические ресурсы современного урока  [Текст]: методические рекомендации/ под ред. Т.Ф. Есенковой, В.В. Зарубиной. – Ульяновск: УИПКПРО, 2009.

11.  С. Неделяева  Групповая работа на уроке. //Математика. - № 5/98. - 11 с.

12.  Н.Л. Стефанова, Н.С. Подходова, В.В. Орлов и др. «Методика и технология обучения математике»; М: «Дрофа», 2005 г.

13.  Н. Мельников Тематический контроль по геометрии. Особенности содержания и возможности использования. //Математика.- № 2/99.- 46-48с.

 

14.  Э.Г. Готман «Задачи по планиметрии и методы их решения», М: «Просвещение», АО «Учебная литература», 1996 г.Т. О. Митрофанова Технологии отбора задач на уроках. // Математика. – № 1 / 98. – 13 с.

 

15.  Ю. Выплов  Развитие мыслительной деятельности учащихся // Математика. №24, 2004.

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru