Отношение площадей треугольников, имеющих общую высоту (основание)

1) S_ABM - ?

2) S_MBС - ?

3) Если AM=MC, то сравните площади этих треугольников.

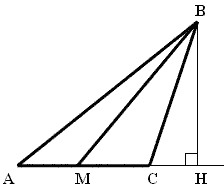
Записать вывод в тетрадь:

Медиана делит треугольник на два равновеликих (равных по площади) треугольника, и площадь каждого из которых равна половине площади данного треугольника.

4)

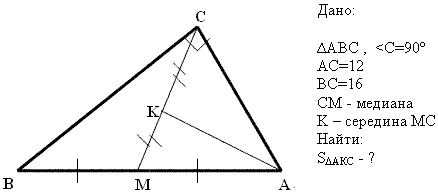
Дано:

ВМ – медиана АВC

ВК – медиана АВМ

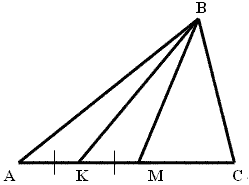
Найдите отношение площадей

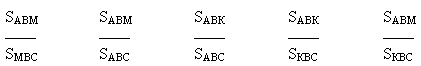
5) Известно, что S_ABС=20см² (по условию предыдущего задания)

Найти S_ABМ; S_МBС; S_ABК; S_КBС -?

6)

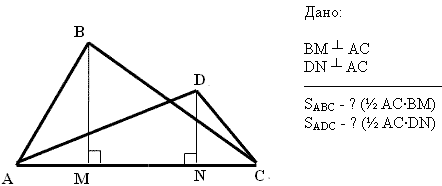
Чему равно отношение площадей двух треугольников, имеющих общее основание?

Записываем вывод в тетради:

S_ABС: S_ADС = BM : DN

Площади треугольников, имеющих общее основание, относятся как высоты, проведенные к основанию.

Далее заслушиваем и обсуждаем теоретические ответы учащихся по ДЗ.

3. Закрепление ранее изученного материала.

1. Выполняем задание №40 стр. 18-19 рабочей тетради по геометрии для 8 кл.

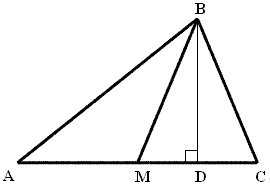
На рисунке точка М делит сторону АС АВС в отношении АМ : МС = 2 : 3

Площадь АВС равна 180 см². Найдите площадь треугольника АВМ.

2. Решаем задачу №475 учебника.

Начертите АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.

3.

Обсуждаем решение, используя слайды презентации

4. н/о (если позволяет время)

Данный параллелограмм разделите на три равновеликие части прямыми, выходящими из одной вершины.

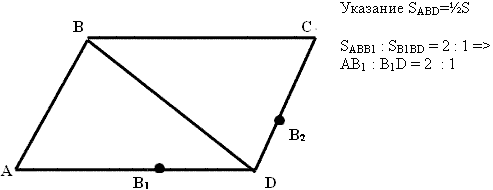
Аналогично, ВВ₂ делит DВС на треугольники, имеющие одну высоту, их площади относятся как основания DB₂ : B₂C = 1 : 2 => Алгоритм построения: разделить каждую из сторон AD и DC параллелограмма в отношении 2 :1, считая от вершин А и С.

4. Самостоятельная работа обучающего характера

Вариант -1

1) СК – медиана АВС

S_СКВ = 32 см². Найти S_ABС

2) S_КDM = 40 см²

На стороне КМ отмечена точка А так, что КА : АМ = 2 :3

Найти: S_КDА

Вариант - 2

1) АМ – медиана АВС, площадь которого 48 см²

Найти площадь АМС

2) S_DРК = 60 см²

На стороне DК отмечена точка А так, что DА : АK = 3 :1

Найти: S_APK -?

5. Постановка домашнего задания

Д.З. по учебнику стр. 124-125 № 473; 506; 511(а)