ОУД 04 Рабочая тетрадь для самостоятельной работы

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ РЕСПУБЛИКИ БАШКОРТОСТАН

«СТЕРЛИТАМАКСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»

(ГАПОУ РБ «СТЕРЛИТАМАКСКИЙ МЕДИЦИНСКИЙ КОЛЛЕДЖ»)

 

 

 

 

 

 

 

 

 

Рабочая тетрадь по дисциплине

 ОУД.04 Математика для студентов 1 курса

специальность 34.02.01 Сестринское дело

 

 

 

 

 

 

 

 

 

 

2020

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Методическое пособие для самостоятельной работы студентов по ОУД 04 Математика разработано на основе Федерального государственного стандарта и рабочей программы учебной дисциплины «Математика»  для специальностей 34.02.01 Сестринское дело

Данная тетрадь предназначена для организации аудиторной и самостоятельной работы обучающихся I курсов по теме «Координаты и векторы». Собран теоретический материал, подобраны примеры решения некоторых задач. По теме «Разложение вектора по трем некомпланарным векторам» практическая представлена работа. В конце изучения раздела имеются вопросы для самоконтроля и тест. В тетради присутствуют указания к решению примеров и ответы.

Составители :Громова Ю.В. преподаватель  первой  квалификационной категории

Фомина Светлана Владимировна, преподаватель

СОДЕРЖАНИЕ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА                                                                                                         2

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ                                                                                         4

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ САМОСТОЯТЕЛЬНОЙ РАБОТЫ                                  4

ТЕМА 1 ДЕКАРТОВЫ КООРДИНАТЫ. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ             5

ТЕМА 2 КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА. ПАРАЛЛЕЛЬНЫЙ                                         6

ПЕРЕНОС.                                                                                                                                           6

ТЕМА3 ВЕКТОРЫ В ПРОСТРАНСТВЕ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ                                  7

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ                                                                            8

ТЕМА4  СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.                                                                  9

ТЕМА5  РАЗЛОЖЕНИЕ ВЕКТОРА ПО ТРЕМ НЕКОМПЛАНАРНЫМ ВЕКТОРАМ.              10

ТЕМА6  УРАВНЕНИЕ ПЛОСКОСТИ                                                                                             15

ПРОВЕРЬ СЕБЯ                                                                                                                                17

ТЕСТ ДЛЯ САМОКОНТРОЛЯ                                                                                                        18

УКАЗАНИЯ К РЕШЕНИЮ                                                                                                              19

ЛИТЕРАТУРА                                                                                                                                   20

 

 

 

 

 

 

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

Методические указания по выполнению внеаудиторной самостоятельной  работы по  дисциплине Математика ставят своей целью оказать помощь студентам первого  курса в организации самостоятельной работы по овладению системой знаний, умений, навыков в объеме действующей программы.

Объем самостоятельной работы студентов определяется государственным   образовательным   стандартом среднего профессионального образования (ФГОС СПО).

 

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

 

№ п/п	Тема	Содержание самостоятельной работы	Кол-во часов
1.	Декартовы координаты. Расстояние между двумя точками	Решение вариативных задач и упражнений	2
2.	Координаты середины отрезка. Параллельный перенос.	Решение вариативных упражнений и задач	2
3.	Векторы в пространстве. Действия над векторами	Решение вариативных упражнений и задач	2
4.	Скалярное произведение векторов.	Решение вариативных упражнений и задач	2
5.	Разложение вектора по трем некомпланарным векторам.	Решение вариативных задач и упражнений	2
6.	Уравнение плоскости	Решение вариативных задач и упражнений	2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА 1.  ДЕКАРТОВЫ КООРДИНАТЫ. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ

Прямые х, у, z называются­__________________, точка их пересечения О ___________________________ а плоскости ху, yz и xz __________________________. Точка О разбивает каждую из осей координат на две полупрямые - полуоси, которые мы условимся называть положи­тельной и отрицательной.

_________________ точки А будем назы­вать число, равное по абсолютной величине длине отрезка ОА_х: _________________, если точка А_х лежит на положительной полуоси х, и _________________, ес­ли она лежит на отрицательной полуоси. Если точка А_х совпадает с точкой О, то полагаем _________

 Расстояние между точками А₁ (х₁‘, y₁; z₁) и А₂ (х₂; у₂; z₂) вычисляется по формуле. Запишите

 

 

 

 

 

ЗАДАЧИ ДЛЯ АУДИТОРНОЙ РАБОТЫ

1.            Где лежат те точки пространства, для которых координаты х и у равны нулю?

2.             Даны точки А (1; 2; 3), В (0; 1; 2), С (0; 0; 3), D (1; 2; 0). Какие из этих точек лежат: 1) в плоскости ху; 2) на оси z;3)в плоскости уz?

3.            Найдите расстояния от точки (1; 2; -3) до: 1) координатных плоскостей; 2) осей координат; 3) начала координат.

4.            В плоскости ху найдите точку D (х; у; 0), равноудаленную от трех данных точек: А (0; 1; -1), В (-1; 0; 1), С (0; -1; 0).

5.            Найдите точки, равноотстоящие от точек (0; 0; 1), (0; 1; 0), (1; 0; 0) и отстоящие от плоскости yz на расстояние 2.

6.            На оси х найдите точку С (x; 0; 0), равноудаленную от двух точек

А (1; 2; 3), В (-2; 1; 3).

7.            Составьте уравнение геометрического места точек пространства, равноудаленных от точки А (1; 2; 3) и начала координат.

8.            Постройте в координатном пространстве точки с заданными координатами: А (1,2,1) , В (-2,0,1), С (0,0,3), D(0,1,3)

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1.   Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2).

2.   Найти расстояние между точками A(0, -3, 3) и B(3, 1, 3).

3.   Задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем  точки  A (1, 2, 3)A (1, 2, 3) и B(−7, −2, 4)B-7, -2, 4 .Найти  .

4.   Постройте в координатном пространстве векторы с заданными координатами :а₁(1,2,-3) , а ₂ (0,3,1), а ₃ (-2,0,2).

 

ТЕМА 2. КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА. ПАРАЛЛЕЛЬНЫЙ

ПЕРЕНОС

Формула вычисления координат середины отрезка с концами A(x_a, y_a, z_a) и B(x_b, y_b, z_b) в пространстве:

xc =	xa + xb		yc =	ya + yb		zc =	za + zb
	2			2			2

Примеры вычисления координат середины отрезка в пространстве

Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).

Решение.

x_c = x_a + x_b2 => x_b = 2x_c - x_a = 2·1-(-1)=2+1=3 

y_c = y_a + y_b2 => y_b = 2y_c - y_a = 2·5-3=10-3=7 

z_c = z_a + z_b2 => z_b = 2z_c - z_a = 2·2-10=4-10=-6 

Ответ: B(3, 7, -6).

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (х; у, г) фигуры переходит в точку (х + а; у + b; z + с), где числа а, Ь, с одни и те же для всех точек (х; у,z). Параллельный перенос в пространстве задается формулами х^! = х + а, у' = у + Ь, z' = z + с, выражающими координаты х', у', z точки, в которую переходит точка (х; у, z) при параллельном переносе. Так же как и на плоскости, доказываются следующие свойства параллельного переноса:

1.     Параллельный перенос является движением

2.     При параллельном переносе любая прямая переходит в прямую, ей параллельную.

3.     При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.

4.     Каковы бы ни были точки А и А', существует единственный параллельный перенос, при котором точка А переходит в точку А'.

 

 

 

 

ЗАДАЧИ ДЛЯ АУДИТОРНОЙ РАБОТЫ

1.       В прямоугольной системе координат трехмерного пространства дан параллелепипед. Известно, что  , а   - середина диагонали  . Найдите координаты точки А.

2.       Докажите, что четырехугольник ABCD с вершинами в точках А (1; 3; 2), В (0; 2; 4), С (1; 1; 4), D (2; 2; 2) является параллелограммом.

3.        Докажите, что четырехугольник ABCD является паралле­лограммом, если: 1) А (0; 2; -3), В (-1; 1; 1), С (2; -2; -1), D (3; -1; -5); 2) А (2; 1; 3), В (1; 0; 7), С (-2; 1; 5), D (-1; 2; 1).

4.        Докажите, что четырехугольник ABCD является ромбом, если: 1) А (6; 7; 8), В (8; 2; 6), С (4; 3; 2), D (2; 8; 4);

5.       А (0; 2; 0), В (1; 0; 0), С (2; 0; 2), D (1; 2; 2).

6.        Дан один конец отрезка А (2; 3; -1) и его середина С (1; 1; 1). Найдите другой конец отрезка В (х; у; z).

7.        Найдите координаты вершины D параллелограмма ABCD, если координаты трех других его вершин известны: А (2; 3; 2), В (0; 2; 4), С (4; 1; 0); 2) А (1; -1; 0), В (0; 1; -1), С (-1; 0; 1); 3) А (4; 2; -1), В (1; -3; 2), С (-4; 2; 1).

8.                  

 

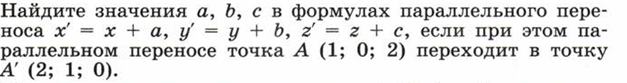
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1.                 Докажите, что середина отрезка с концами в точках А (а; с; -b) и В (-а; d; b) лежит на оси у.

2.                 Докажите, что середина отрезка с концами в точках С (а; b; с) и D (р; q; -с) лежит в плоскости ху.

3.   

 

ТЕМА3. ВЕКТОРЫ В ПРОСТРАНСТВЕ. ДЕЙСТВИЯ НАД ВЕКТОРАМИ

 

Суммой векторов ⃗a(a₁;a₂) и ⃗b(b₁;b₂) называется вектор ⃗c(a₁+b₁;a₂+b₂)
т.е. ⃗a(a₁;a₂)+⃗b(b₁;b₂)=⃗c(a₁+b₁;a₂+b₂)

Для любых векторов ⃗a(a₁;a₂) и ⃗b(b₁;b₂) справедливы равенства:

• переместительный закон: ⃗a+⃗b=⃗b+⃗a 
• сочетательный закон: ⃗a+(⃗b+⃗c)=(⃗a+⃗b)+⃗c 
• из переместительного и сочетательного законов следует, что, складывая любое число векторов, можно как угодно переставлять и группировать слагаемые.

Правило треугольника: Свойство дает следующий способ построения суммы произвольных векторов ⃗a и ⃗b Надо от конца вектора ⃗a отложить вектор равный вектору ⃗b. Тогда вектор, начало которого совпадает с началом вектора ⃗a, а конец - с концом вектора ⃗b, будет суммой векторов ⃗a и ⃗b

Правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.

Разностью векторов ⃗a(a₁;a₂) и ⃗b(b₁;b₂) называют такой вектор ⃗c(c₁c₂), который в сумме с вектором ⃗b(b₁;b₂) дает вектор ⃗a(a₁;a₂). Таким образом: ⃗c(c₁c₂) + ⃗b(b₁;b₂) = ⃗a(a₁;a₂), откуда c₁ = a₁ - b₁ и c₂ = a₂ - b_2.

Правило треугольника. Чтобы найти разность двух векторов, нужно: изобразить их исходящими из одной точки; дополнить чертеж отрезком так. чтобы получился треугольник; придать отрезку направление от вычитаемого к уменьшаемому; этот направленный отрезок и будет вектором разности.

Произведением вектора ⃗a(a₁;a₂)  на число λ называется вектор ⃗b(b₁;b₂)  такой что b₁ = λa₁ и b₂ = λa₂. т.е. λ⃗a(a₁;a₂)=⃗b(λa₁;λa₂)

Для любых векторов ⃗a(a₁;a₂), ⃗b(b₁;b₂) и чисел λ, μ справедливы два распределительных закона:

• (λ+μ)⃗a=λ⃗a+μ⃗a
• λ(⃗a+⃗b)=λ⃗a+λ⃗b

ЗАДАЧИ ДЛЯ АУДИТОРНОЙ РАБОТЫ

1.     Даны три точки А (1; 0; 1),      В (-1; 1; 2), С (0; 2; -1). Найдите точку D (х; у; г), если  векторы АВ и CD равны.

2.      Найдите точку D в задаче 51, если сумма векторов АВ и CD равна нулю.

3.      Даны векторы (2; n; 3) и (3; 2; m). При каких тип эти векторы коллинеарны?

4.      Дан вектор а (1; 2; 3). Найдите коллинеарный ему вектор с началом в точке А (1; 1; 1) и концом В на плоскости ху.

5.      При каком значении n данные векторы перпендикулярны:

1)      а (2; -1; 3), B (1; 3; n); 2) а_(n; -2; 1), B (n; -n; 1);

2)      а (n; -2; 1), b (n; 2n; 4); 4) а (4; 2n; -1), b (-1; 1; n)?

6.     Даны три точки А (1; 0; 1), В (-1; 1; 2), С (0; 2; -1). Найдите на оси z такую точку D  (0; 0; с), чтобы векторы АВ и CD были перпендикулярны.

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1.       Даны точки  и . Найти векторы  и .

2.       Даны точки  и . Найти векторы  и .

3.       Даны точки  и . Найти векторы  и .

4.        Даны точки . Найти векторы .

5.       Зная разложения вектора a¯по базисной системе векторов: a¯=3i¯−k¯, записать координаты этого вектора в пространстве.

6.       Вектор a¯ задан своими координатами: a¯=(2;−1;5)a¯=(2;−1;5). Записать разложение данного вектора по ортам осей координат.

ТЕМА 4.  СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

 

Скалярным произведением двух ненулевых векторов называют произведение длин этих векторов на косинус угла между ними:
S=⃗a⋅⃗b=|⃗a|⋅|⃗b|⋅cos  , если угол между векторами равен .

· Если хотя бы один из двух векторов нулевой, то их скалярное произведение равно 0: S=⃗a⋅⃗b=0

· Если векторы ⃗a и ⃗b равны, то S=(⃗a)² и говорят о скалярном квадрате вектора. В  этом случае cos =1, т.е. S=|⃗a|² .  Итак, скалярный квадрат вектора совпадает и квадратом его длины: (⃗a)²=|⃗a|².

· Если векторы ⃗a и ⃗b перпендикулярны, то S=⃗a⋅⃗b=0 Векторы ⃗a и ⃗b перпендикулярны в том и только в том случае, когда их скалярное произведение равно нулю.

Для любых векторов ⃗a, ⃗b, ⃗c и числа λ справедливы равенства:

• (λ⃗a⋅⃗b)=λ(⃗a⋅⃗b)
• ⃗a(⃗b+⃗c)=⃗a⋅⃗b+⃗a⋅⃗c

Аналогично рассматриваются вектора и в пространстве.

 

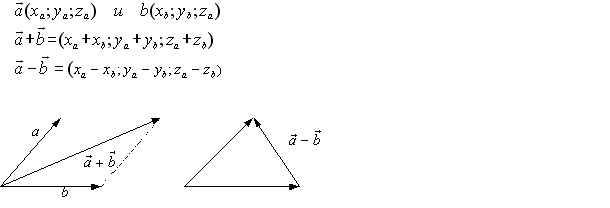
ЗАДАЧИ ДЛЯ АУДИТОРНОЙ РАБОТЫ

1.     Векторы а и b образуют угол  60°, а вектор с им перпендикулярен. Найдите абсолютную величину вектора а + b + с.

2.     Векторы а, b, с единичной длины образуют попарно углы 60° . Найдите угол ᵩ между векторами: 1) а и b + с; 2) а и b - с.

3.      Даны четыре точки А (0; 1; -1), В (1; -1; 2), С (3; 1; 0), D (2; -3; 1). Найдите косинус ᵩ угла  между векторами АВ и CD.

4.     Вычислить скалярное произведение векторов a¯ и b¯ , если их длины соответственно равны 2 и 3, а угол между ними 60°.

5.     Вычислить угол между прямыми АВ и CD, если А(1; 1; 0), B(3; -1; 0), С(4; -1; 2), D(0; 1; 0).

6.     Дано: ABCD - параллелограмм. А(-6; -4; 0), В(6; -6; 2), С(10; 0; 4). Найти координаты вершины D и угол между векторами

7.     Дано: МАВС - тетраэдр. М(2; 5; 7), А(1; -3; 2), B(2; 3; 7), С(3; 6; 2). Найти расстояние от точки М до точки О пересечения медиан ΔABC.

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

 

1.     Даны три точки А (0; 1; -1), В (1; -1; 2), С (3; 1; 0). Найдите косинус угла С треугольника ABC.

2.      Из вершины прямого угла А треугольника ABC восставлен перпендикуляр AD к плоскости треугольника. Найдите косинус угла  между векторами ВС и BD, если угол ABD равен а, а угол ABC равен.

3.      Наклонная образует угол 45° с плоскостью. Через основание наклонной проведена прямая в плоскости под углом 45° к проекции наклонной. Найдите угол между этой прямой и наклонной.

4.     Из точки вне плоскости проведены перпендикуляр и две равные наклонные, образующие углы  с перпендикуляром. Найдите угол  между проекциями наклонных, если угол между наклонными.

 

 

ТЕМА5.  РАЗЛОЖЕНИЕ ВЕКТОРА ПО ТРЕМ НЕКОМПЛАНАРНЫМ ВЕКТОРАМ

Пример1 дан куб  с ребром m. Точка К – середина ребра . Разложить вектор  по векторам  и найти его длину.

Решение: построим заданный куб (рис. 3).

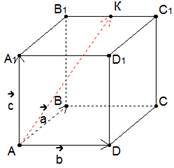
Рис. 3. Куб, задача 1

Векторами  и  задается плоскость квадрата . Третий вектор  не лежит в этой плоскости, отсюда заключаем, что три заданных вектора ,  и  некомпланарны, и мы можем выразить через них искомый вектор . Найдем вектор  по правилу многоугольника. Очевидно, что в данной задаче для этого есть множество способов, но мы выбираем самый короткий путь: . вектор  мы по условию обозначили как вектор . Вектор  согласно свойствам куба равен вектору , обозначенному за вектор .

вектор  составляет половину вектора , так как точка К – середина ребра  по условию: . Вектор  согласно свойствам куба, равен вектору , обозначенному как вектор . Имеем: 

Так, заданный вектор выражен через три некомпланарных вектора. Осталось найти его длину. Здесь нужно применить теорему Пифагора. Рассмотрим прямоугольный треугольник . Он прямоугольный потому, что ребро  перпендикулярно всей плоскости основания , значит и любой прямой в этой плоскости, значит прямой . Один из катетов  равен m как ребро куба. Катет  найдем из другого прямоугольного треугольника – , где он уже является гипотенузой. Здесь катет  равен m как ребро куба. Катет  равен , так как точка К – середина ребра . Имеем: 

Вернемся к первому треугольнику: 

Пример 2. Векторы ,  и  компланарны. Компланарны ли векторы ,  и ? Компланарны ли векторы ?

Решение: тот факт, что векторы ,  и  компланарны, означает, что, будучи отложенными от одной точки, они расположены в одной плоскости (рисунок 4.а). Это значит, что один из векторов, например, вектор , можно однозначно разложить по двум другим: . Очевидно, что векторы ,  и  тоже компланарны, т. к. умножение вектора на положительное число не меняет его направления, а меняет только длину, и векторы останутся в той же плоскости (рисунок 4.б).

Рис. 4. а

Рис. 4. б

Очевидно, что тройка векторов  также компланарна, потому что всякая линейная комбинация компланарных векторов есть вектор, им компланарный. Мы имеем три вектора, компланарных заданным векторам, очевидно, что они компланарны между собой.

 

 

ПРАКТИЧЕСКАЯ РАБОТА

Тема: «Разложение вектора по трем некомпланарным векторам»

 

Цель: уметь применять основные определения и теоремы по теме «Разложение вектора по трем некомпланарным векторам» при обосновании этапов решения задач; уметь выполнять чертежи по условию задачи, понимать чертежи, находить на чертежах векторы, уметь раскладывать вектор по данным векторам, используя правило параллелепипеда, параллелограмма, треугольника, знать определение коллинеарных и компланарных векторов.

 

Оборудование: тетрадь для практических работ, ручка, простой карандаш, линейка, методические рекомендации по выполнению работы.

 

Методические рекомендации по выполнению практической работы:

Задание №1. Дан куб  с реб­ром m. Точка К – се­ре­ди­на ребра . Раз­ло­жить век­тор  по век­то­рам .

Ре­ше­ние: по­стро­им за­дан­ный куб (рис. 1).

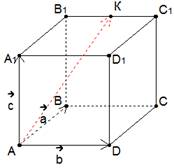
Рис. 1.

 

Век­то­ра­ми  и  за­да­ет­ся плос­кость квад­ра­та . Тре­тий век­тор  не лежит в этой плос­ко­сти, от­сю­да за­клю­ча­ем, что три за­дан­ных век­то­ра ,  и  неком­пла­нар­ны, и мы можем вы­ра­зить через них ис­ко­мый век­тор . Най­дем век­тор  по пра­ви­лу мно­го­уголь­ни­ка. . Век­тор  мы по усло­вию обо­зна­чи­ли как век­тор . Век­тор  со­глас­но свой­ствам куба равен век­то­ру , обо­зна­чен­но­му за век­тор .

Век­тор  со­став­ля­ет по­ло­ви­ну век­то­ра , так как точка К – се­ре­ди­на ребра  по усло­вию: . Век­тор  со­глас­но свой­ствам куба, равен век­то­ру , обо­зна­чен­но­му как век­тор . Имеем: 

Так, за­дан­ный век­тор вы­ра­жен через три неком­пла­нар­ных век­то­ра. Оста­лось найти его длину.

 

Задание №2.  Задан треугольник АВС. Точка М – точка пересечения медиан. Точка О – произвольная точка пространства. Разложить вектор  по векторам ,  и . (рис. 1)

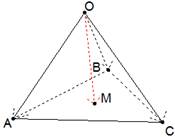
Рис. 2.

 

Согласно правилу треугольника .

Продлим отрезок АМ до пересечения со стороной ВС треугольника (рисунок 3), получим точку  – середину этой стороны (точка М по условию точка пересечения медиан треугольника). Кроме того, вспомним свойство медиан треугольника: медианы треугольника пересекаются в одной точке, которая рассекает их в отношении 2:1, считая от вершины. Так, имеем: 

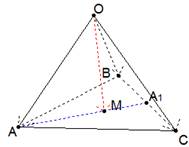
Рис. 3. Дополнительное построение к задаче 2

Снова применим правило треугольника:  

 

 

 

 

 

 

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:

 

Вариант №1   Задание №1. Дан  – параллелепипед. Точки К и Т – середины ребер ВС и  соответственно. Разложите векторы: а)  ; б)  в) ; д) ; е); ж) по векторам .   Задание №2. Дан АВСD – тетраэдр. Точка М – точка пересечения медиан треугольника АВС, причем =, =, =. Разложите векторы: а) ;  б) ; в) по векторам: .

Вариант №2   Задание №1. Дан  – параллелепипед. Причем АК:КВ=3:2, =1:4. Разложите векторы: а)  б)   в) ; г) ; д) ; е) ; ж) по векторам .   Задание №2. Дан АВСD – тетраэдр. Точка Т – середина ребра CB, H - точка пересечения медиан треугольника АВС. Разложите векторы: а) ;  б) ; в) по векторам: .

 

КОНТРОЛЬНЫЕ ВОПРОСЫ (ответьте письменно):

1.       Дайте определение вектора.

2.       Дайте определение нулевого вектора.

3.       Дайте определение длины вектора.

4.       Дайте определение коллинеарных векторов.

5.       Сформулируйте правило треугольника для сложения векторов.

6.       Сформулируйте правило параллелограмма для сложения векторов.

7.       Дайте определение разности векторов.

8.       Дайте определение умножения вектора на число.

9.       Дайте определение компланарных векторов.

10.   Сформулируйте признак компланарности трех векторов.

11.   Сформулируйте правило параллелепипеда.

12.    Сформулируйте теорему о разложении вектора по трем некомпланарным векторам.

 

ТЕМА 6.  УРАВНЕНИЕ ПЛОСКОСТИ

 

Теорема Всякая плоскость в прямоугольной системе координат Oxyz  в трехмерном пространстве может быть задана уравнением вида Ax+By+Cz+D=0 где А,В,С,D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид Ax+By+Cz+D=0, определяет плоскость в трехмерном пространстве

Пример 1.  Заданы точки M₀(1, -1, -3) и N₀(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение : Подставим координаты точки М₀ в исходной уравнение плоскости:

2·1+3·(-1)-(-3)-2=0⇔0=0

Мы видим, что получено верное равенство, значит точка M₀(1, -1, -3) принадлежит заданной плоскости.

 Аналогично проверим точку N₀. Подставим ее координаты в исходное уравнение:

2·0+3·2-(-8)-2=0⇔12=0 Равенство неверно. Таким, образом, точка N₀(0, 2, -8) не принадлежит заданной плоскости.

Ответ: точка М₀ принадлежит заданной плоскости; точка N₀ – не принадлежит.

Пример 2. В прямоугольной системе координат задана плоскость √2x+3y−z+5=0 Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение: Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор  исходной плоскости имеет координаты (√2, 3, −1) В свою очередь, множество нормальных векторов запишем так:

λ⋅=(λ⋅√2, λ⋅3, −λ), λ∈R, λ≠0

Ответ:  (λ⋅√2, λ⋅3, −λ), λ∈R, λ≠0

Пример 4. Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М₀(7, −2, 3) Необходимо составить общее уравнение заданной плоскости.

Решение: Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M₀(7, −2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости  x+DA=0, иначе говоря, должно быть верным равенство  7+DA =0 . Требуемое уравнение  имеет вид: x−7=0.

Пример 5. Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М₀(−3, 1, 2)М₀(-3, 1, 2).

Решение:  Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0) Условием задачи дано, что плоскость проходит через начало координат, тогда D=0и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0

Найдем значение BA. В исходных данных фигурирует точка М₀(−3, 1, 2) координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: −3+BA⋅1=0, откуда определяем BA=3

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0x+3y=0.

Ответ: x+3y=0x+3y=0.

ЗАДАЧИ ДЛЯ АУДИТОРНОЙ РАБОТЫ

1.                  Составьте уравнение плоскости, которая проходит через точку А и перпендикулярна прямой АВ, если:

1.                   А(-1; 1; 2), В(2; 0; 1);

2.                   А( 1; 0; -1), В(4; 6; -3);

3.                   А(3; -4; 5), В(2; 1; -3).

2.                   Найдите расстояние от точки С (6; -8; 10) до плоскостей из предыдущей задачи.

3.                   Найдите отрезки, которые плоскость ах + by + cz = d от­секает на осях координат, если коэффициенты а, Ь, с и d не равны нулю.

4.                   Докажите, что любая плоскость, параллельная плоскости ах + by + сz + d = 0, задается уравнением ах + by + cz +  d₁ = 0, d₁  d.

5.                   Докажите, что плоскости, заданные уравнениями х + у + + z = 1, 2х + у + 3z + 1 = 0, х + 2z + 1 = 0, не имеют ни одной общей точки.

6.                   Найдите точку пересечения трех плоскостей, задаваемых уравнениями:

1)                       x+y+z=1, x-2y=0, 2x+y+3z+1=0

2)                       x-y=3, y+z=2, x-z=4

3)                       x+z=0, 2x-y=3,3x+y+2z=8

4)                       x+2y+3z=1,3x+y+2z=2,2x+3y+z=3

7.                  При каком условии плоскость, заданная уравнением ах + by + cz + d = 0: 1) параллельна оси z; 2) проходит через ось г; 3) перпендикулярна плоскости xz?

 

ПРОВЕРЬ СЕБЯ

Контрольные вопросы

1.                   Объясните, как определяются координаты точки в прост­ранстве.

2.                   Выразите расстояние между двумя точками через коорди­наты этих точек.

3.                   Выведите формулы для координат середины отрезка через координаты его кондов.

4.                   Что такое преобразование симметрии относительно точки? Какая фигура называется центрально-симметричной?

5.                   Объясните, что такое преобразование симметрии относи­тельно плоскости. Что такое плоскость симметрии фигу­ры?

6.                   Какое преобразование фигуры называется движением?

7.                   Докажите, что движение в пространстве переводит плос­кость в плоскость.

8.                   Какие фигуры в пространстве называются равными?

9.                   Дайте определение параллельного переноса.

10.                Перечислите свойства параллельного переноса.

11.                Докажите, что при параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в парал­лельную плоскость.

12.                Что такое преобразование подобия? Перечислите его свой­ства.

13.                Какое преобразование называется гомотетией? Докажите, что преобразование гомотетии в пространстве переводит любую плоскость, не проходящую через центр гомотетии, в параллельную плоскость (или в себя).

14.                 Докажите, что площадь ортогональной проекции много­угольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и пло­скостью его проекции.

15.                Что такое абсолютная величина вектора? Какие векторы называются одинаково направленными?

 

ТЕСТ ДЛЯ САМОКОНТРОЛЯ

Тема: «Координаты и векторы»

 

Задание 1. (выберите один вариант ответа) Укажите координаты вектора .

Варианты ответов:

1) (0; 1; 3)                             2) (1; 0; 3)                               3) (1; 3; 0)

 

Задание 2. (выберите один вариант ответа) Укажите, при каких значениях n и p векторы  и  коллинеарные.

Варианты ответов:

1)                          2)                          3)

 

Задание 3. (выберите один вариант ответа) Укажите координаты вектора , если А(2; - 3; 4) и В(- 8; 4; 6).

Варианты ответов:

1) (1; 3,5; - 5)                        2) (- 5; 3,5; 1)                                   3) (5; - 3,5; - 1)

 

Задание 4. (выберите один вариант ответа) Укажите координаты суммы векторов , если  и .

Варианты ответов:

1)                                      2) (0; - 11; - 7)                         3) (0; - 11; - 5)

 

Задание 5. (выберите один вариант ответа) Укажите, чему равно скалярное произведение векторов, если и угол между векторами 30°.

Варианты ответов:

1)                                    2) 6                                         3)

 

Задание 6. (выберите один вариант ответа) Найдите  скалярное произведение векторов  и .

Варианты ответов:

1) - 2                                               2) (0; 0; - 2)                             3) – 4

 

Задание 7. (выберите один вариант ответа) Укажите, при каком значениях z векторы  и  перпендикулярные.

Варианты ответов:

1)                               2)                                   3)

 

Задание 8. (выберите один вариант ответа) Укажите длину вектора , если

А(5; 3; 1), В(4; 5; 1).

Варианты ответов:

1) 3                                       2)                                       3)

 

Задание 9. (выберите варианты ответов согласно тексту задания) Установите соответствие между векторами и их длинами.

А)                       Б)                       В)

Варианты ответов:

1)                                    2)                                      3)

 

Задание 10. (выберите один вариант ответа) Укажите середину отрезка АВ, заданного точками А(3; - 7; 11) и В(- 1; 3; - 3).

Варианты ответов:

1) (- 2; 5; - 7)                         2) (4; - 2; 1)                             3) (1; - 2; 4)

 

Задание 11. (выберите два варианта ответов) Установите, какие из точек принадлежат прямой .

Варианты ответов:

1) (2; 3)                                            2) (- 4; - 6)                                3) (- 2; 3)

 

Задание 12. (выберите один вариант ответа) Какой нормальный вектор имеет прямая, заданная уравнением у – 2х + 5 = 0?

Варианты ответов:

1) (- 2; 1)                                2) (- 2; - 1)                                3) (1; - 2)

 

Задание 13. (выберите один вариант ответа) Укажите уравнение окружности с центром в точке А(5; - 3) и радиусом R = 2.

Варианты ответов:

1) (х + 5)² + (у - 3)² = 4                   2) (х - 5)² + (у + 3)² = 2                      3) (х - 5)² + (у + 3)² = 4

 

УКАЗАНИЯ К РЕШЕНИЮ

 

Тема 1 №1на оси z №2 (1,0,0), (0,2,0),(0,0,3),(1,2,0),(1,0,3),(0,2,3) №3 Расстояние от плоскости xy равно 3,от плоскости xz равно 2, от плоскости yz равно1, расстояния от осей x,y,z соответственно равны   . №5 (2,2,2) и (-2,-2,-2) №6 С (0,0,0) №7 x+2y+3z=7

Тема 2 №1 (7,3,-8), №6 B (0,-1,3) №7D (6,2,-2) D(0,-2,2) D(-1,7,-2)

Тема 3 №1 D (-2,3,0) №2 D (2,1,-2) №3 n=, m= №5 1)n= 2)n=-1 3)n=2 4)n=4 №6 с=1

Тема 6 №13x-y-z+6=0 №2 1)2 2) 3) №5.Указание: Сложите почленно первое и третье уравнение.

Тест для самоконтроля

 

ЛИТЕРАТУРА

 

1.   Математика. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. – М.: Просвещение, 2018. – 366 с.

2.   Математика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. – М.: Просвещение, 2018. – 416 с.

3.   Погорелов А.В. Геометрия 10-11 классы: учеб для общеобразоват. учреждений: базовые и проф. уровни-М.: Просвещение, 2018-175стр.

Дополнительные источники:

4.   Дадаян А.А. Математика:Учебник-2-е издание-М.:Форум:ИНФРА-М.2006-552с.

5.   Математика. 11 кл. профильный уровень: учебник для общеобразоват. учебных заведений / В.А. Касьянов. – М.: Дрофа, 2013.

6.   Павленко Ю.Г. Математика. Избранные задачи. – М.: Издательство «Экзамен», 2013 г.

 

Скачано с www.znanio.ru