Пахта ва пиллани теримини чет эл таҳлили

Sinusoidal tok va uni tavsiflovchi asosiy kattaliklar

Davriy o‘zgaruvchan toklar ichida eng keng tarqalgani sinusoidal toklardir. Sanoatda va turmushda foydalaniladigan o‘zgaruvchan tok sinusoidal qonun bo‘yicha o‘zgaradigan o‘zgaruvchan tokdir. Bu tokni yuqori kuchlanish bilan uzoq masofalarga uzatish hamda o‘zgaruvchan tokda ishlovchi mashina va apparatlar (tranformatorlar, asinxron va sinxron dvigatellar) ni ishga tushirishda ishlatish mumkin. Nisbatan past chastotali sinusoidal toklar sinxron generatorlar yordamida olinsa yuqori chastotali sinusoidal tok va EYUK lar elektron generatorlar yordamida hosil qilinadi. Sinusodal tok va kuchlanishlarni grafik ravishda, trigonometrik funksiya ko‘rinishida, dekart yoki kompleks tekislikdagi aylanuvchi vektorlar ko‘rinishida ifodalash mumkin. Sinusoidal tok analitik ko‘rinishda quyidagicha ifodalanishi mumkin:

.            (11.1)

Grafik ifodasi 4.1-rasmda berilgan. Funksiyaning eng katta qiymati amplituda I_m deyiladi, T – davr to‘liq bir o‘zgarish uchun ketgan vaqt, chastota  - 1 sekunddagi tebranishlar soni, chastotaning birligi sek^-1 yoki Gs.

Burchak chastotasi , birligi rad/sek yoki sek^-1.

Funksiyaning argumenti, ya’ni (wt+y) – faza deb ataladi. Faza t vaqtning o‘sha moment uchun tebranishning holatini belgilaydi. y - boshlang‘ich faza. Grafikda boshlang‘ich faza burchagi  y ning qiymati sinusoidaning koordinata boshidagi holati bilan aniqlanadi. Sinusoidal o‘zgaruvchan funksiyaning nol qiymatlaridan musbat qiymatlariga o‘tish nuqtasi davrning boshlanish lahzasi hisoblanadi. Musbat boshlang‘ich faza koordinata boshidan chap tomonga, manfiysi o‘ng tomonga qo‘yiladi. 11.2-rasmda kuchlanish va tokning grafigi (vaqt diagrammasi) berilgan.

,                             (11.2)

.                              (11.3)

Bu sinusoidal kattaliklarning boshlang‘ich fazalari orasidagi burchak y faza siljish burchagi deyiladi.

.  (11.4)

j=0 bo‘lganda tok va kuchlanish faza bo‘yicha bir xil,  bo‘lganda kvadraturada - qarama–qarshi fazada bo‘ladi. Fazalar siljishi burchagidan foydalanib, (11.2) va (11.3) larni quyidagicha ifodalash mumkin:

, .

Bu munosabatlar shuni ko‘rsatadiki, sinusoidal tok, sinusoidal kuchlanishdan j burchakka orqada qolar ekan.

Sinusoidal kattaliklarning o‘rtacha va ta’sir etuvchi

qiymatlari

Sinusoidal tokning o‘rtacha qiymati musbat yarim davrdagi oniy toklar yig‘indisining o‘rtacha arifmetik qiymatiga teng. U holda tok  ning o‘rtacha qiymati

.      (11.5)

Xuddi shu yo‘l bilan EYUK va kuchlanishning o‘rtacha qiymatlarini topish mumkin:

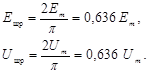
Umumiy holda o‘zgaruvchan tokning ta’sir etuvchi qiymati deb, mazkur tokning T davr ichida R qarshilikdan o‘tayotib, xuddi shu kattalikdagi o‘zgarmas tok ta’sirida ajralib chiqadigan issiqlik miqdoriga ekvivalent bo‘lgan qiymatga aytiladi.

O‘zgarmas tokning R qarshilikdan T davr ichida o‘tishida ajralib chiqqan issiqlik miqdori Q_-=I² RT.

SHu davrda R qarshilikdan o‘tgan sinusoidal tok i=I_m sinwt ta’siridan ajralib chiqqan issiqlik miqdori .                

Ikkala tok issiqlik ta’sirining ekvivalentlik sharti Q_=Q_~

   yoki          yoki    .

  Xuddi shunday:  

Sinusoidal kattaliklarni dekart va kompleks tekislikda

vektorlar bilan ifodalash

Sinusoidal EYUK, kuchlanish va toklarni dekart yoki kompleks tekislikda aylanuvchi vektorlar yordamida ifodalash mumkin. Koordinata boshidan uzunligi amplituda qiymatiga teng bo‘lgan radis vektorlar o‘tkaziladi. Bu vektorlar soat strelkasiga qarama – qarshi yo‘nalishda w burchak tezligida harakatga keltiriladi. Faza burchagi musbat absissa o‘qidan boshlab hisoblanadi. Vektorlarning ordinata o‘qiga proeksiyasi oniy qiymatlarni beradi. To‘g‘ri burchakli koordinatalar sistemasida bir–biriga nisbatan to‘g‘ri orintatsiyalarda qurilgan, turli amplituda va boshlang‘ich fazaga ega bo‘lgan bir xil chastotadagi sinusoidal miqdorlarni tavsiflovchi vektorlar yig‘indisiga vektor diagramma deyiladi. Kuchlanish (7.2) va tok (7.3) vektorlari  7.3-rasmda ko‘rsatilgan.

Agar umumiy tok ₃–tarmoqlar toklari ₁ va ₂ larning yig‘indisidan iborat bo‘lsa:

₃= ₁+ ₂

va agarda

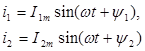
bo‘lsa, yig‘indi tok  i₃ ham sinusoidal bo‘ladi: i₃=I_3m sin (wt+y₃).

Ammo I_3m amplituda va boshlang‘ich faza y₃ ni analitik usul bilan aniqlash qiyin. Vektorlar diagrammasi yordamida aniqlash bir muncha qulay.

11.4-rasmda bu kattaliklarning vektor diagrammasi ko‘rsatilgan,  vektori  va  vektorlarini qo‘shish bilan aniqlangan. Bu vektorlarni bir xil burchak tezligi  w bilan aylantirilsa, ularning o‘zaro joylanishi va ular orasidagi fazalar farqi a=y₁-y₂ o‘zgarishsiz qoladi. Vektorlar diagrammasini masshtabda qursak, I_3m va y₃ larning qiymatlarini aniqlash imkoniyati tug‘iladi.

11.5-rasmda kompleks tekislik berilgan. Bu tekislikda kompleks sonlarni ifodalash mumkin. Kompleks son haqiqiy va mavhum qismdan iborat. Kompleks tekislikning absissa o‘qida haqiqiy qismi ordinata o‘qida mavhum qismi belgilanadi.

Matematika kursidan Eyler formulasi:

.                    (11.7)

 - kompleks soni kompleks tekislikda birga teng bo‘lgan vektor bilan ifodalanadi. a burchak +1 o‘qidan soat strelkasiga qarama – qarshi yo‘nalishda olinadi.  funksiyasining moduli birga teng:

.                        (11.8)

 funksiyasining +1 o‘qga proeksiyasi , +j  o‘qga proeksiyasi : Agar  funksiyasi o‘rniga I_m funksiyasini olsak,

.                      (11.9)

Kompleks tekislikda äbu funksiyaning vektori +1 o‘qiga nisbatan a burchak ostida olinib, vektorning uzunligi I_m marta katta bo‘ladi. Agar  bo‘lsa, sinusoidal funksiyalarni kompleks tekislikda ifolalashda wt = 0 deb qabul qilinadi.

.                         (11.10)

11.6-rasmda  - vektori berilgan.  vektori  bilan belgilanadi.  kompleks kattalik, uning moduli I_m ga teng, vektorning +1 o‘qga nisbatan og‘ish burchagi boshlang‘ich faza y ga teng.  tok i ning kompleks amplitudasi deyiladi.

Misol: Tok i=8sin(wt+20)A. SHu tokning kompleks amplitudasini ifodalang. Bu holatda I_m= 8 A  y=20⁰, demak =8e^j20° kompleks tokning kompleks ta’sir etuvchi qiymati:

.                    (11.11)

YAna ham tushunarli bo‘lishi uchun kompleks sonlar bilan quyidagi operatsiyalarni bajaramiz. 7.7-rasmda  kompleks soni ifodalangan. Bu erda

 - algebraik ko‘rinish.

 - ko‘rsatkichli ko‘rinish.

 - trigonometrik ifodasi.

 - modul.

 - burchak.

Ikki va undan ortiq kompleks sonlarning yig‘indisini olish algebraik ko‘rinishda amalga oshiriladi. Bunda haqiqiy qismi alohida mavhum qismi alohida qo‘shiladi.

.

Ko‘paytirish va bo‘lish amallarini kompleks sonning darajali ko‘rinishida amalga oshirish qulay. Agar kompleks sonni  kompleks songa bo‘lish talab qilinsa,

,

ko‘paytirishda esa

,

lekin, ko‘paytirish va bo‘lish amallarini algebraik ko‘rinishda ham amalga oshirish mumkin. Amaliyotda +j bilan – j ni ko‘paytirish kerak bo‘ladi. Masalan,  berilgan. j va (– j) vektorlarini  ko‘rsatkichli ko‘rinishda ifodalaymiz:

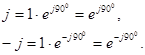
U holda

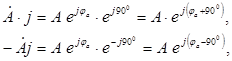
ya’ni vektorni j ga ko‘paytirilsa, u 90⁰ ga soat strelkasiga teskari tomonga buriladi, agarda (-j) ga ko‘paytirilsa (soat strelkasi bo‘ylab) 90⁰ ga buriladi. Modul o‘zgarishsiz qoladi.

Sinusoidal tok zanjirida aktiv qarshilik, induktivlik va kondensator

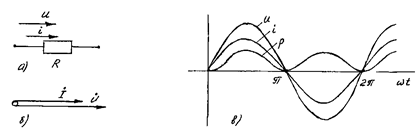
Elektr zanjirida aktiv qarshilik. Aktiv qarshilikli elektr zanjiri (11.8-rasm, a) bo‘ylab i=I_m sin w t, (y_I=0) tok o‘tayotgan bo‘lsa, Om qonuniga binoan kuchlanish

u= iR=RI_m sin wt,

yoki                                                                      (11.12)

u=U_m sin wt,

bu erda U_m=RI_m .

Vektor diagrammasida tok va kuchlanishning komplekslari berilgan. y=0 bo‘lgani uchun  va   ga teng bo‘ladi   (11.8-rasm, b).

11.8-rasm, v da tok, kuchlanish va quvvat oniy qiymatlarining grafigi berilgan.

.                 (11.13)

11.8 – rasm.

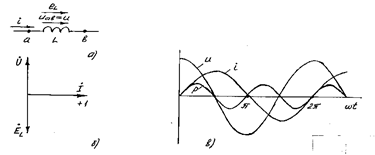
Sinusoidal tok zanjirida induktivlik. Ixtiyoriy cho‘lg‘am (g‘altak) induktivlik L va aktiv qarshilik R dan iborat. Sxemada g‘altakni ketma –ket ulangan induktivlik L bilan aktiv qarshilik R sifatida ifodalash mumkin. Tahlil uchun induktivlikni o‘zini ajratib olamiz.

11.9-rasm, a da induktivlik bo‘ylab, i=I_msinwt, y_I=0 tok o‘tayotgan bo‘lsin, u holatda g‘altakda o‘zinduksiya EYUK si vujudga keladi.

,                   (11.14)

u =- e_L ekanligi ma’lum, u holda (11.14) ni:

,         (11.15)

bunda wLI_m=U_m zanjirdagi kuchlanishning amplituda qiymati; wL-  induktiv g‘altakning reaktiv qarshilig yoki induktiv qarshilik deb atalib, X_L bilan belgilanadi. O‘lchov birligi Om,

.                          (11.16)

11.9 – rasm.

Induktivlikdagi kuchlanish tokdan 90⁰ ilgari yuradi j=y_u-y_i=90-0=90⁰, EYUK 90⁰ orqada qoladi. U holda  bo‘ladi. 11.9-rasm, b da  va kattaliklarning vektor diagrammasi ko‘rsatilgan. ,u,r oniy qiymatlarning grafigi 7.9-rasm, v da ko‘rsatilgan.

Oniy quvvat quyidagicha ifodalanadi:

                 (11.17)

bu qiymat yo tok, yo kuchlanish noldan o‘tganda noldan o‘tadi. R>0 bo‘lganda manbadan olingan energiya magnit maydon energiyasini hosil qilish uchun sarflanadi. R<0 bo‘lganda, magnit maydon energiyasi yana manbaga qaytarilib beriladi.

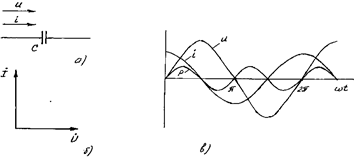
Sinusoidal tok zanjirida kondensator. Agar 11.10-rasm, a dagi zanjirga u=U_msinwt, y_u=0 kuchlanish berilsa, q=Su=CU_msinwt kondensator davriy ravishda zaryadlana boshlaydi. Buning natijasida kondensatordan zaryadlanish toki o‘ta boshlaydi.

,(4.18)

,                         (11.19)

bu erda  - sig‘im qarshiligi, u chastotaga teskari proporsional.

.                     (11.20)

(11.20) dagi munosabat shuni ko‘rsatadiki kondensatordan o‘tayotgan tok kuchlanishdan 90⁰ ilgari yuradi. 11.10-rasm, b da tok va kuchlanishning vektorlari  tasvirlangan. 11.10-rasm, v da oniy qiymatlar u, i, r larning grafiklari berilgan. Oniy quvvat

.                                  (11.21)

Yuqorida ko‘rilganlardan shunday xulosa qilish mumkinki, aktiv qarshilikda tok va kuchlanish bir xil fazada bo‘ladiInduktivlikda kuchlanish tokdan 90⁰ ilgari yuradi. Kondensatorda kuchlanish tokdan 90⁰ orqada qoladi.

11.10 – rasm

Nazorat savollari

1. Qarshiliklarni ketma-ket ulash.

2. Kirxgorfning birinchi qonuni.

3. Qarshiliklarni aralash ulash.

4. Ketma-ket ulangan o‘zgaruvchan induktiv va sig‘im qarshiliklari zanjirini chizing va taxlil kiling.

 5. Paralel ulangan o‘zgaruvchan tok zanjirini chizing va taxlil kiling.

6. Kuchlanishlar rezonansiga tushuncha bering.

7. Toklar rezonansiga tushuncha bering.

 8. Quvvat koeffitsienti nima va uni xalq xo‘jaligidagi axamiyati nimada.

Скачано с www.znanio.ru