Павутиноподібна модель ринку

Павутиноподібна модель ринку

У реальності визначення рівнозваженої ціни відбувається досвідченим шляхом. Ця процедура називається павутиноподібною моделлю ринку.

          Процес відшукання рівнозваженої ціни називається «намацуванням»  і є ітераційним (рис.5.1). Припустимо що в початковий момент на ринку спостерігалася нестача товарів, ціна товару дорівнювала р₀. У цих умовах виробник зацікавлений у  збільшенні обсягу товару й у наступний момент викине на ринок товар в більшому обсязі, але за ціною р_{1, .}  З огляду на знову сформовану ситуацію виробник товару в наступний момент викине на ринок товар у меншому обсязі. Ціна зміниться з  p до p, p< p_1. Тобто одержуємо безперервне коливання навколо рівнозваженої ціни.

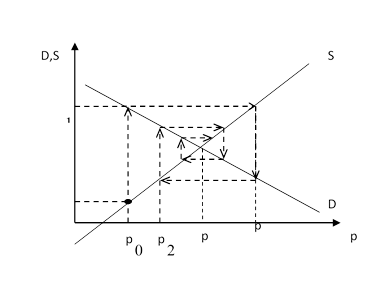
                                                      Рис. 5.1

Якщо  в деякому околу рівнозваженої ціни процес ітерацій сходиться до стану рівноваги при будь-якому початковому значенні ціни з цього околу, то стан рівноваги називається стійким. У противному випадку стан рівноваги називається нестійким.

На рис. 5.2 показана графічна модель, у якій стан рівноваги стійкий, а ціна змінюється від найменшої ціни (ціни покупя) до найбільшої ціни (ціни торговця). Для того, щоб стан рівноваги був стійким у цій моделі, необхідно виконання умови:

_,

де    - похідна функції пропозиції,  

- похідна функції попиту.

  Для аналітичного визначення рівнозваженої ціни зручно використати табл. 5.1.

Таблиця 5.1

В таблиці задається початкова ціна p₀ , _, а потім обчислюються D₀ , S₀

D₀ = a-bp₀,

S₀= -c+dp₀.

Із рис. 5.2 видно, що .  Звідси знаходимо нову ціну p₁

                          S₁= -c+dp_1,

_.

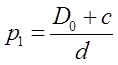Цю ціну наносимо в таблицю 5.1 і знаходимо D₁ . Аналогічно обчислюємо інші значення цін, попиту та пропозиції. Ітераційний процес вкючає чотири-пять ітерацій.

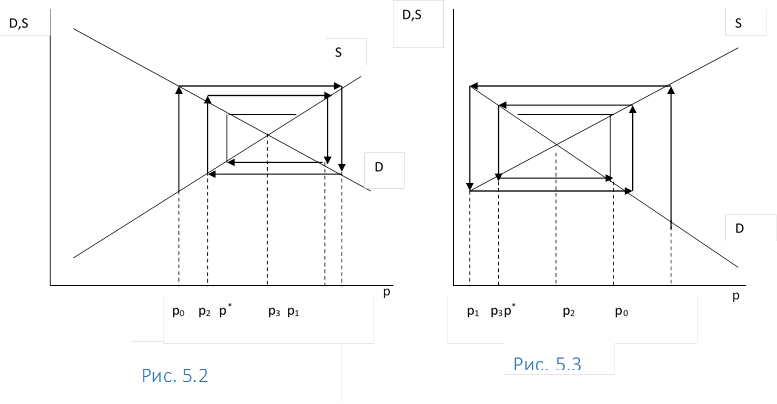
На рис. 5.3 показана графічна модель, у якій стан рівноваги стійкий, а ціна змінюється від найбільшої ціни (ціни торговця) до найменшої ціни (ціни покупця) Для того, щоб стан рівноваги був стійким у цій моделі, необхідно виконання умови:

_.

Для аналітичного визначення рівнозваженої ціни зручно використати табл. 5.2.

Таблиця 5.2

 В таблиці задається початкова ціна p₀ , _, а потім обчислюються D₀ , S₀

D₀ = a-bp₀,

S₀= -c+dp₀.

Із рис. 5.3 видно, що .  Звідси знаходимо нову ціну p₁

D₁ = a-bp₁,

_.

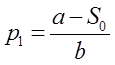Цю ціну наносимо в таблицю 5.2 і знаходимо S₁ . Аналогічно обчислюємо інші значення цін, попиту та пропозиції. Ітераційний процес вкючає чотири-пять ітерацій.

            При побудові моделі, у якій стан рівноваги нестійкий,  обчислення виконуються до одержання першого негативного значення ціни, попиту або пропозиції.