План-конспект урока по математике в 5 классе «Представление обыкновенных дробей в виде десятичных»

Государственное бюджетное профессиональное образовательное учреждение Московской области «Спортивное училище (техникум) № 5»

План-конспект  урока по математике
в 5 классе

«Представление обыкновенных дробей в виде десятичных»

подготовила

учитель математики

Калмыкова М.Е.

г. о. Егорьевск
 2025

Тип урока: изучение нового материала.

Ход урока

1. Организационный момент. Включение в деловой ритм. Настрой на урок.

2. Устная работа (фронтальная работа с классом).

Ребята, сегодня на уроке  вас ждут необычные задания.

Чтобы узнать, о чем мы будем сегодня говорить,  вам нужно выполнить задания. Обратите внимание на доску. Предлагаю устно решить задания:

1)      Для украшения актового зала к празднику купили 100 шаров. Среди них  красных. Какую часть составляют красные шары?  ()

2)      В магазин привезли 600 кг картофеля. До обеда продали  всего количества. Сколько картофеля продали до обеда? (180 кг)

3)      Замените число 7 дробью со знаменателями 10. (70 / 10)

4)      Коля прочитал  книги, что составляет 15 страниц. Сколько страниц в книге? (150 стр.)

5)      200 солдат построились в ряд.

     Все они дружно идут на парад.

      было усатых.

     Сколько было безусых солдат? (60 солдат)

6)      200  солдат построились в ряд.

Все они дружно идут на парад.

 было усатых.

Сколько же было усых солдат? (180 солдат )

7)      Выделите из неправильной дроби 37/10 целую часть. (3 7/10)  

8)      Представьте смешанное число в виде неправильной дроби  5 3/4= 23/4

3.  Сообщение темы урока.

С древних времен людям приходилось не только считать предметы, но и измерять длину, время, массу, вести расчет за купленные ими товары. Не всегда результат измерения или стоимость товара удавалось выразить натуральным числом. Приходилось учитывать и части. Так появились дроби: они были известны ещё древнем Египте примерно 3000 лет тому назад.  Дроби записывали в виде палочек – это были целая часть, а палочки в два раза меньше – означали дробные части.  Как вы думаете, удобно было это делать? У людей возникла необходимость ввести числа более удобные для расчета и вычислений.

А как вы думаете, можно ли по-другому записывать дробные числа?

Давайте посмотрим, что же это за числа?

Задание: Из чисел:  4  ;    ;  45 ; 5,7  ;  17  ;  6   ;  41,31 ; 

Назовите 1) натуральные числа,

                2) смешанные числа,

                3)обыкновенные дроби

Какие числа остались? Знакомы вам эти числа?

Ò Как называются?

Ò Как возникли эти числа?

Ò Как записываются?

Ò Как читаются?

(Десятичными дробями)  (Дети высказывают свои предположения).

Чтобы нам легче было ответить на все эти вопросы,  давайте выполним задание

Задание:  На доске записаны дроби:

,,,,,,,,,,

- Прочитайте дроби.
- Что интересного заметили? (У всех дробей в знаменателе единица и нули)
- На какие две группы их можно разделить? (Правильные и неправильные)

- В XVI веке (1585 г.) нидерландский математик Симон Стевин придумал для дробей  более короткую и удобную запись, например:

;      ;      ;      (Возникает проблема)

- Но не ко всем обыкновенным дробям можно применить новую запись.

 Кто догадался, к каким?                Эти дроби перед вами.
                                                           Полюбуйтесь ими сами.
                                                           В знаменателе, смотри – 
                                                           Единица и нули.

- Чему вы сегодня научитесь на уроке?

(Сегодня на уроке мы будем учиться записывать дробные числа по-новому)

 Запишите в тетради число  и оставьте место для написания темы урока.

 Запишите тему урока “Десятичная запись дробных чисел”.

4. Работа по новой теме.

- Как записать дробные числа по-другому?

Числа со знаменателями  10, 100, 1000,10 000 и т.д. условились записывать без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть  отделяют от дробной части запятой.

Например,       ;  ;  .

На ваших партах находятся таблицы с заданием. Давайте внимательно изучим эту таблицу (внимательно разбираем с учениками первые 4 задания).

В последнем задании на месте десятичной дроби стоит вопросительный знак, и я предлагаю вам объединиться в пары и подумать над этим вопросом.

Какую закономерность вы заметили? (количество нулей совпадает с количеством цифр после запятой)

- Как же вы запишите последние числа? (выберите верный вариант)

А. 0,037 
Б. 0,0037 
В. 0,37

А. 3,5216
Б. 0,035216
В. 0,35216

Итак, проблема была, как записать обыкновенные дроби, смешанные числа – по-новому.  Давайте рассмотрим алгоритм записи десятичных дробей:

1.     Записать целую часть (она может быть равна нулю).

2.     Поставить запятую, отделяющую целую часть от дробной.

3.     После запятой поставим столько точек, сколько нулей в знаменателе дробной части.

4.     С последней точки записываем числитель, начиная с последнего знака

5.     В пустые места записываем нули. 

Так как эти числа равны, то десятичную дробь читают аналогично.

5. Закрепление изученного материала.

1.  Представьте в виде десятичной дроби:

 Прочитайте получившиеся десятичные дроби

2.  Работа в тетради (самостоятельно).

- Выпишите в тетрадь правильные дроби (в столбик). Замените их десятичными дробями.

Проверка (слайд)

- Теперь выпишите неправильные дроби и замените их десятичными.

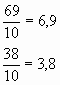
Проверка (слайд)

3. Упражнение, направленное на формирование умения читать десятичные дроби.

Инсценировка: Ученики примерно одинакового роста крепят на грудь бумажные плакаты с написанными на них цифрами. У того ученика, который ниже всех ростом, на плакате знак запятой. “Запятая” перебегает на различные места в ряду учеников - цифр, а сидящие в классе читают получившиеся числа.

Например,

4.     Знаки, стоящие в десятичной дроби после запятой, называют десятичными знаками. Любую десятичную дробь легко записать в виде обыкновенной дроби (простой или смешанной):

Замени десятичную дробь обыкновенной или смешанным числом.

        0,9 =                    7,1 =            

      0,03 =                 63,93 =                 

      7,093 =               0,0017 =                                                                               

Выполнение упражнения по учебнику.

5. Закрепление изученного материала.

 1. Работа в тетради  №1144 (самостоятельно парами).

Проверка (На слайде выписаны ответы)

2. Упражнение по учебнику, направленное на формирование умения читать десятичные дроби,  №1145.

6. Подведение итогов урока.

Наш урок заканчивается.  Чему вы сегодня научились? (Мы с вами сегодня разобрали,  как читать, записывать десятичные дроби). А наш урок достиг целей? Это мы сейчас проверим.

·       Какую обыкновенную дробь можно заменить десятичной?

·       Как называют число, записанное перед запятой?

·       Как называют число, записанное после запятой?

·       Как определить, сколько знаков должно быть после запятой?

7. Домашнее задание.

п. 30, с. 180, №1166(а), 1167.

Дополнительное задание

- В России впервые о десятичных дробях было сказано в русском учебнике математики – “Арифметике”. Мы сможем узнать его автора, если запишем дроби и смешанные числа десятичными дробями. (Смешанные числа записаны на доске, а десятичные дроби - на карточках, на обратной стороне которых – буква. В ходе выполнения задания учащиеся составляют слово.)

 (М)
 (А)
(Г)
 (Н)
 (И)
 (Ц)
 (К)
 (И)
 (Й)

МАГНИЦКИЙ

Магницкий Леонтий Филиппович - автор первого учебника математики в России "Арифметика" (1703 г.), по которому учился М.В.Ломоносов (слайд).

“Что есть арифметика? Арифметика - есть художество честное, независтное, и всем удобоятное, многополейзнейшее, и многопохвальнейшее от древних же и новейших, в разные времена явившихся изряднейших арифматиков”.

- Как вы понимаете эти слова?

Историческая справка.

- Правила вычислений с десятичными дробями описал знаменитый ученый средневековья Аль-Каши в начале XV веке. Он записывал десятичные дроби так же, как принято сейчас, но вместо запятой дробную часть записывал красными чернилами или отделял вертикальной чертой.

28 43 или

Скачано с www.znanio.ru