План-конспект урока по теме " Показательные уравнения"

Урок алгебры по теме «Показательные уравнения. Методы решения»

Учитель математики: Зюзина Татьяна Ивановна (высшая квалификационная категория).

г.Липецк НОУ Православная гимназия г.Липецка им.прп. Амвросия Оптинского

 

«Алгебра и начала анализа .11класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (профильный уровень) (А.Г. Мордкович и др.) под ред А.Г. Мордковича – М.: Мнемозина.

«Алгебра и начала анализа .11класс. В 2 ч. Ч. 2. Задачник для общеобразовательных учреждений (профильный уровень) (А.Г. Мордкович и др.) под ред А.Г. Мордковича – М.: Мнемозина

Тема урока: Показательные уравнения. Методы решения.

Тип урока: Урок систематизации и обобщения нового материала

Образовательные ресурсы: презентация, учебник, конспект в тетрадях

Цель урока (уроков): применение знаний для решения показательных уравнений с помощью различных методов, с опорой на логическое действие обобщение и классификацию

Задачи урока:

Предметные:

- повторить определение показательных уравнений, их характеристическое свойство, свойства степеней;

- систематизировать методы решения показательных уравнений;

- уметь применять изученные понятия, методы для решения задач.

 

Планируемые образовательные результаты:

Учащиеся научатся:

- определять зависимость между показательным уравнением и методом его решения;

- точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии;

Получат возможность научиться:

- адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность, контролировать процесс и результат учебной математической деятельности;

- формулировать, аргументировать и отстаивать своё мнение.

 

План урока

1. Организационный этап.

2. Постановка цели и задач урока. Мотивация учебной деятельности.

3. Актуализация знаний.

4. Закрепление материала.

5. Физкультминутка.

6. Творческое применение и добывание знаний в новой ситуации (проблемные задания).

7. Этап информации учащихся о домашнем задании и инструктаж по его выполнению.

8. Рефлексия

 

Ход урока

 

«Умная перемена»: слайды с цитатами известных ученых - математиков, их портретами, объединенные темой: уравнения. На перемене учитель обращает внимание на подготовку детей к уроку, отмечает отсутствующих. Предоставляет раздаточный материал, необходимый для работы на уроке: учебник, письменные принадлежности (пенал), дневник.

1.      Организационный этап

Звонок. На доске цитата: «Холодные числа, внешне сухие формулы математики полны внутренней красоты и жара сконцентрированной в них мысли.»

А.Д. Александров

2.      Постановка цели и задач урока. Мотивация учебной деятельности.

Здравствуйте, начнём урок. Я рада видеть вас на нашем занятии, которое мне бы хотелось начать словами гениального учёного Альберта Энштейна:

«Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно».

(слайд №1)

 

 

 

Как, по-вашему, связаны эти слова с темой нашего урока? О чём пойдёт сегодня речь? (Ученики формулируют тему урока)

 

 

 

 

(слайд №2)

 

 

 

 

На слайде появляется тема «Показательные уравнения. Методы решения»

Открываем тетради и записываем дату и тему урока. Эпиграфом к нашему занятию станут слова С.Коваля: «Уравнения – это ключ, открывающий все математические сезамы».

Т.е. другими словами можно сказать, что если вы будете уметь решать уравнения, то экзамена по математике вам не стоит бояться. Для того, чтобы урок прошёл с максимальной пользой для каждого и нас, мы должны знать: «А что нам нужно?»

Сформулируйте и запишите личную цель урока на полях.

Возможные варианты личной цели:

·         Узнать новое по теме

·         Доказать свою точку зрения

·         Научиться слушать и слышать

·         Найти выход из проблемной ситуации

·         Доказать истинность своего мнения

·         Уточнить, дополнить высказывание товарищей

·         Составить новую учебную задачу (тест, кроссворд, учебное задание, учебный вопрос)

·         Изучить материал учебника

·         Проявить и развивать свои способности (перечислить…)

·         Свой вариант цели. Кто хотел бы её озвучить?

Итак, цель наша сегодня: повторить применение свойств показательной функции при решении показательных уравнений, систематизировать методы решения показательных уравнений

3.      Актуализация знаний.

Для реализации целей урока нам потребуется некоторый теоретический материал.

Давайте приведём в готовность наши теоретические знания - вспомним основные положения, необходимые для решения уравнений.

(слайд №3)

Вопросы.

1.Функцию какого вида называют показательной?

2.Какова область определения показательной функции

3..Каково множество значений показательной функции?

4. Что можно сказать о монотонности показательной функции в зависимости от основания

5.Уравнения какого вида называются показательными?

(После ответа учащихся на интерактивной доске появляются верные ответы)

·         Назовите характерную особенность показательных уравнений. Что отличает их от других?

(Неизвестное содержится в показателе степени)

3.3.3 Осуществлять классификацию, т.е. делить род (класс) на виды (подклассы) на основе установления признаков объектов, составляющих род

Вспомним, что такое классификация. Классификация бывает естественная и искусственная.

Естественная классификация опирается на свойства рассматриваемых понятий, предметов.

Искусственная классификация не дает возможности судить о свойствах предметов (например, список фамилий, расположенных по алфавиту, алфавитный каталог книг), применяется для более легкого отыскания вещи, слова и т.д.

 

(слайд №4)

(интерактивное задание)

Задание. Проверим, сможем ли мы из приведенных здесь уравнений выбрать показательные?

 

 

При решении показательных уравнений главное – действие со степенями. Без знания этих действий ничего не получится!!!

(слайд № 5)

 

- Посмотрите на доску. Вашему вниманию предлагаются уравнения.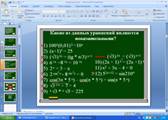 

 

Раскрывается доска, на которой записаны уравнения:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Учащимся предлагается следующее задание:

Учитель: Устно объедините эти уравнения в группы и попытайтесь объяснить, по какому признаку проведено распределение.

Ученики: Уравнения (1) и (11) можно объединить в одну группу, так как это иррациональные уравнения.

Уравнения (2) и (5) можно объединит в одну группу, так как это квадратные уравнения.

Уравнения (3), (4), (6), (9),(10) тоже можно объединить в одну группу, так как у этих уравнений есть общий признак: неизвестное у всех этих уравнений находится в показатели степени)

(8) трансцендентное уравнение

Учитель:

- Посмотрите на выписанные вами показательные уравнения. Какие из них являются простейшими уравнениями.

Ученики: Уравнение (3) 6 ^х = 36.

Учитель:

- Верно. Давайте его решим.

Учитель записывает решение уравнения на доске, ученики в тетради.

Учитель:

- Посмотрите на остальные показательные уравнения. Являются ли они простейшими?

Ученики: Нет.

Учитель: Как же мы будем их решать?

Итак, у нас возникла проблема: Как решать остальные показательные уравнения, которые не являются простейшими показательными уравнениями.

- Ребята, предложите метод решения уравнения (4).

( учащиеся предлагают свои варианты решения)

Таким образом, решаются уравнения 4,6,7.

Учитель:

- Ребята, а ваши предложения для решения уравнения (8). (функционально-графический)

Учитель: Решим уравнение (9). Скажите, сталкивались ли мы с таким видом показательного уравнения. Попробуйте предложить метод для решения этого уравнения.

(Учащиеся должны предложить метод введения новой переменной).

- А теперь последнее уравнение .

- Давайте вспомним, какой метод мы ещё использовали при решении тригонометрических уравнений.

- При решение однородных уравнений мы использовали почленное деление на выражение неравное нулю.

Учитель: Давайте теперь ребята обобщим наши знания и назовём все методы, которые будем использовать при решении показательных уравнений.

Учащиеся называют, на экране появляются названия методов

 

(слайд №6)

 

 

 

 

 

 

4.      Закрепление материала

На экране появляются номера из учебника, затем чистые листы для работы.

Деятельность учащихся – решение номеров

№12.19 (а);

№12.27 (а);

№12.29 (а);

№12.36 (а);

№12.41 (а).

(слайд 7)

 

Древнегреческий поэт Нивей утверждал, что «математику нельзя изучать, наблюдая, как это делает сосед». Поэтому будем сейчас работать самостоятельно.

 

Вариант 1.

1.Какой из графиков является графиком функции ?

1) 2) 3) 4)

 

 

 

 

 

 

2.Решите уравнение

1) х=1 2)х=-1 3)х=0 4)х=3

3.Решите уравнение

1)х=4 2)х=-4 3)х=2 4) х=-2

4.Найти сумму корней уравнения

1) -1 2) 1 3) 3 4) -3

 

5. Решите уравнение 3·10х -5·4х +2·25х =0

1) 0 и -1; 2) 1 и -2,5; 3) 0; 4) 1.

 

6.Решите уравнение

 

Вариант 2.

1.Какой из графиков является графиком функции ?

1) 2) 3) 4)

 

 

 

 

 

 

2.Найти промежуток, которому принадлежит корень уравнения

1) (-5;-2) 2) 3)(4;6) 4)

3. Найти промежуток, которому принадлежит корень уравнения

1) 2) 3) 4)

4.Найти сумму корней уравнения

1) 2 2) 0 3) 1 4) -1

5. Решите уравнение 5·25х -7·10х +2·4х=0

1) 1; 2) 1 и ; 3) 0; 4) 0 и -1

6.Решите уравнение

 

 

 

 

 

 

 

(слайды 17-20)

 

5.      Физкультминутка.

Мы при встрече улыбнемся,

Подмигнем слегка друг другу,

Вправо, влево повернемся

И кивнем, затем по кругу

Все идеи победили -

Вверх взметнулись наши руки.

Груз забот с себя стряхнули

И продолжим путь науки.

 

 

 

(слайд 10-14)

 

6.      Творческое применение и добывание знаний в новой ситуации (проблемные задания)

Решите уравнение:

4 ^x + (x-13) * 2 ^x – 2x + 22 = 0.

Решение:

Пусть 2 ^x = у, тогда у ² + (х – 13)у – (2х – 22) = 0

D = (x-9) ²

у1 = - х+11

у2 = 2

2 ^x = - х+11(2)

2 ^x = 2(1)

(1) х = 1

(2) у = 2 ^x - монотонно возрастающая функция, а у = -х + 11 – монотонно убывающая, поэтому по свойству монотонных функций уравнение (2) имеет не более одного корня. Легко угадать, что х = 3.

Ответ: 3.

(Учащиеся выполняют самопроверку, сверяя своё решение с решением на доске)

 

Информация о домашнем задании, инструктаж по его выполнению

Учитель:

- Какой из методов решения показательных уравнений вам понравился больше всего и почему?

- Достигнуты ли цели урока? В какой мере?

- Какие цели ставим перед собой на следующий урок?

 

- А закончить наш урок я хочу словами Лейбница «Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, - что, следуя этому методу, мы достигнем цели».

- Поэтому я вам желаю, чтобы при решении уравнений дома, вы всегда правильно бы находили метод, который приведет вас к нужному конечному результату.

Домашнее задание

 

Учитель: Запишите домашнюю работу.

п.12;

№12.19 (б);

№12.27 (б);

№12.29 (б);

№12.36 (б);

№12.41 (б).

 

 

8.      Рефлексия (подведение итогов)

 

Оценка личной цели, отношения к уроку.

Обращение к целям и задачам урока, оценка их выполнения.

Учитель обращает внимание детей на то, что оценки за урок они получат после проверки письменных работ.

 

 

 

активно

пассивно

·         Своей работой на уроке я

·         доволен

·         не доволен

·         Урок для меня показался

·         коротким

·         длинным

·         За урок я

·         не устал

·         устал

·         Моё настроение

·         стало лучше

·         стало хуже

·         Материал урока мне был

·         полезен

·         бесполезен

·         интересен

·         скучен

 

 

Давайте вернемся к эпиграфу нашего урока: «Уравнения – это ключ, открывающий все математические сезамы».

Мне хотелось бы вам пожелать, чтобы каждый из вас нашел в жизни свой «золотой ключик», с помощью которого перед вами открывались любые двери.

Спасибо за урок!