План-конспект урока по теме "Конус. Полная и боковая поверхность конуса."

План урока по теме «Тела вращения. Конус»

Дисциплина:_математика (геометрия)

Преподаватель:__Дареева С. Н.      

Тип занятия:_урок изучения нового материала

Вид занятия:__комбинированный урок

Цели занятия:

1.       Образовательная (дидактическая):

·     ознакомить с понятиями: конус, образующая конуса, высота конуса, основание и боковая поверхность конуса; с формулами для нахождения площади боковой и полной поверхности конуса.

·     научить применять формулы площади боковой и полной поверхности конуса при решении задач.

2.       Развивающая: 

·        развивать внимание, вычислительную и графическую культуру,

3. Воспитательная:

·     воспитывать аккуратность, точность;

·     прививать интерес к математике.

Межпредметные связи:__алгебра, физика, биология, химия, черчение.

Оснащение занятия:

Наглядные пособия, раздаточный материал по теме урока, презентация по теме конус, тестовые задания по теме «Цилиндр», мультимедийная презентация

ТСО:_интерактивная доска Smart Board, программа Notebook, ПК, экран, проектор для показа презентаций.
 

Структура занятия:

1.   Организационный момент.

2.   Повторение  пройденного материала (письменное тестирование по теме «Цилиндр»).

3.   Изучение нового материала (Просмотр мультимедийной презентации).

4.   Закрепление материала - решение задач практического характера.

5.   Итог урока.

6.   Домашнее задание.

Оборудование: компьютер,  раздаточный материал по теме урока, буклеты.

Ход урока:

1.     Здравствуйте, ребята. Вокруг нас очень много геометрических  тел, которые приносят пользу нам в нашей жизни. Например, остовы для мостов делают в форме цилиндров,  так как  такая форма очень устойчива и долговечна под длительным и большим давлением.

2.     Сейчас проверим ваши знания по теме «Цилиндр». Проведем тестирование по вариантам. (Листы с тестовыми заданиями лежат на столах у ребят, они вписывают ответы прямо в лист.)

3.      Сегодня мы ознакомимся с новым понятием,  это также тело вращения - конус. Запишите тему нашего занятия: Конус. Площадь боковой и полной поверхности конуса. На этом занятии вы узнаете, что такое конус, ознакомитесь с видами конуса и формулами нахождения площадей поверхности конуса.

(Смотрим презентацию).

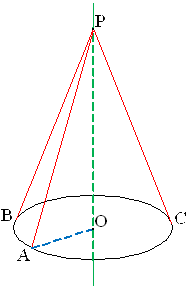
Итак, мы ознакомились с телом вращения - конус, узнали его основные элементы. Я буду показывать, а вы называйте элемент конуса. (слайд 24)

Элементы конуса: Боковая поверхность

(коническая поверхность)

Образующие (АР, ВР, РС )

Основание (круг)

Вершина (т. Р)

Ось – прямая ОР

Высота – отрезок ОР

                                           Радиус - АО

Задачи практического характера: (на слайдах  31-32)

Задача 1.  Какова площадь поверхности воронки, образовавшейся при взрыве 122-мм бомбы? 

Задача 2.  Сколько квадратных метров брезента потребуется для сооружения палатки конической формы?

Чтобы решить эти задачи, нам нужно знать формулы площади боковой и полной поверхности конуса.

Смотрим следующий слайд (слайд 33) и выпишем формулы в тетрадь:

Формулы для вычисления боковой поверхности и полной поверхности конуса: Sбок.= πRℓ, Sосн.= πR², Sп.п.к. =Sбок.+Sосн.= πR(R+ℓ)

4.     Теперь вернемся к задачам и решим их с помощью новых формул.

Задача 1 (слайд 34): Для решения задачи нада измерить длину окружности основания воронки: С= 12м  и глубину по склону: ℓ=1,5 м

     Найти: Sбок.=?     Решение: Sбок.= πRℓ,    С= 2πR ,   R=С/2π

Sбок.= πRℓ= πСℓ / 2π=С ℓ/ 2=12*1,5 / 2= 9 м²           Ответ: 9 м²

Задача 2 (слайд 36):  Дано: Н=4 м,  D=6 м  Найти: Sбок.=?

Решение:  Sбок.= πRℓ,     R=D:2 = 6:2 = 3(м),  ℓ= √ Н² +R² = √4² + 3² = 5 (м.)       Sбок.≈ 3,14* 3*5 ≈ 47,1(м²)                        Ответ: ≈ 47 м²

Задача 3(слайды 37-39): Фонарь установлен на высоте 8 м. Угол рассеивания фонаря 120°. Определите, какую поверхность освещает фонарь.

Решение: S= πR²

_ FАО= 180° - 120°/2=30°

   FA=8•2=16 (катет, лежащий против угла в 30°)

  АО= √ FA²-FO² = √16²-8² = 8√3 (по теореме Пифагора)

  S = π (8√3)² =192π ≈602,88 м²

  Ответ: ≈603 м²

(Проверяем решение)

5.   Подведение итогов (на мультимедийной доске,  слайды 40-42):

Задание 1: Какое из изображенных тел является конусом? Выбрать эти тела:

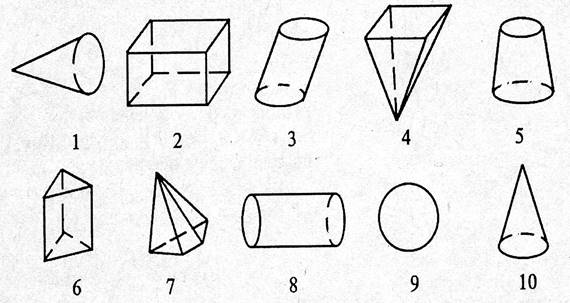
Задание 2: Ответьте на вопрос и запишите первую букву напротив вопроса.  Как называется:

1. Фигура, полученная при поперечном сечении конуса?

2. Отрезок, соединяющий вершину с окружностью основания?

3. Имеет ли конус центр симметрии?

4. Тело, полученное при пересечении конуса плоскостью, параллельной основанию?

5. Фигура, являющаяся боковой поверхностью конуса?

Какое слово получилось из первых букв? (КОНУС)

Задание 3: Домашнее задание (на слайде 43).

6.   Заключение: Итак, сегодня вы узнали, что такое конус, ознакомились с формулами вычисления площадей (боковой и полной конуса). Применили эти формулы при решении задач. До свидания.

Литература:

1.       Атанасян Л.С. и др.  Геометрия 10-11.Учебник для 10-11 классов средней школы. –М.:Просвещение, 2015.

2.       Pedsovet.ru

Приложение 1

Тестовая работа по теме «Цилиндр». Вариант 1.

Продолжение приложения 1

Тестовая работа по теме «Цилиндр». Вариант 2.

Скачано с www.znanio.ru