Уравнения в натуральных числах

 

   Пример 1. Решить в натуральных  числах  уравнение: 

                             ( x - 2y ) ( 2x – 1 – y ) = 11.

 

   Решение. Так как 11 - простое число, то существует ровно 4 варианта его разложения в произведение двух целых чисел:

   11=1∙11=11∙1=(-1)∙(-11)=(-11)∙(-1),

Достаточно рассмотреть следующие 4 системы уравнений:

                                    

                                 

    Однако, если подумать, то выписывать все разложения числа 11 на множители и соответствующие системы не обязательно: для натуральных чисел х и у второй множитель 2х – 1 + у больше или равен 2 – 1 + 1=2, а 11 имеет единственный такой множитель -11, так что

2х+у–1=11, х - 2у = 1,

и сложив удвоенное первое равенство со вторым, получим 5х–2=23, откуда х=5, и следовательно, у=2.

                                                                                 Ответ: (5; 2).

 

   Пример 2. Решить в натуральных  числах  уравнение:   

                           (11x + 6y – 8 )( 6 x+ 8y - 1) = 100.

 

   Решение. Первый сомножитель в левой части данного уравнения

 больше или равен 11+6–8=9,

 второй больше или равен 6+8–1=13, и поэтому их произведение не меньше 9∙13,

 т.е. больше 100, и значит, уравнение решений не имеет.

 

Задачи для самостоятельного решения

1. (3x+5y–7)(5x+4y+11)=20,                                   Ответы:  1) (1, 1),

2. (51–4x–7y)(31x+2y–6)=68,                                                   2) (2, 6),

3. (13x+3y–2)(2x–8y–13)=11.                                                   3) нет решений.

 

 

Уравнения в целых числах, решаемые с помощью разложения на множители

   Пример 1. Решить в целых числах  уравнение:   (х+у)(у–1)=4.

 

   Решение: Значения у–1 надо искать среди делителей числа 4=2∙2, то есть

у–1=-4; -2; -1; 1; 2; 4 или у=-3; -1; 0; 2; 3; 5.

   Соответственно, х=;-1; -4; 2; -1; -4.

                                                                Ответ: (2; -3); (-1; -1); (-4; 0); (2; 2); (-1; 3); (-4; 5).

 

 

 

 

 Пример 2. Решить в целых числах  уравнение:   х²+ху=10.  

 

   Решение: х(х+у)=10. Значения х надо искать среди делителей числа 10=2∙5, то есть

х=-10; -5; -2; -1; 1; 2; 5; 10.

    Соответственно, у=–х=9; 3; -3; -9; 9; 3; -3; -9.

                                     Ответ: (-10; 9); (-5; 3); (-2; -3); (-1; -9); (1; 9); (2; 3); (5; -3); (10; -9).

 

Задачи для самостоятельного решения

 

1. (х–у)(х–1)=4,                                         Ответ: 1) (-3; -2); (-1; 1); (0; 4); (2; -2); (3; 1); (5; 4),

2. (х–3)(ху+5)=5,                                                     2) (-2; 3); (2; -5); (4; 0),

3. (у+1)(ху–1)=3,                                                     3) (0; -4); (1; -2); (1; 2),

4. х²–3ху+2у²=3,                                                      4) (-5; -2); (1; 2); (-1; -2); (5; 2),

5. х²–2ху–3у²=5,                                                      5) (-4; -1); (-2; 1); (2; -1); (4; 1).

 

Уравнения в целых числах, решаемые с помощью замены

  

   Пример 1. Решить в целых числах  уравнение:  х²–47=у².

 

   Решение: Очевидно, что |x|>|y|.

Обозначим |x|=|y|+n, где n – положительное целое.

Тогда  х²=у²+2n|y|+n²=y²+47 или  n(n+2|y|).

Поскольку 47 – простое число, n и n+2|y| –положительные целые, делящие 47, и n≤ n+2|y|, то n=1; |y|=(47–1)/2=23; |x|=|y|+n=24.

                                                                    Ответ: (-24; 23); (-24; 23); (24; -23); (24; 23). 

 

Задачи для самостоятельного решения

 

1. х²–у²=4,                                                   Ответы: (-2; 0); (2; 0).

2. х²+23=у².                                                                 (-11; -12); (-11; 12); (11; -12); (11; 12).

 

Диофантовы уравнения первой степени.

  

    Пример 1. Решить в целых числах  уравнение:  147х–25у=14.

 

    Решение. Числа 147 и 25 взаимно просты. Выразим через них 1.

 

Алгоритм Евклида             Представление единицы

 147=25∙5+22,                        1=22-3∙7=22-(25-22)∙7=

  25=22∙1+3,          =>              =(147-25∙5)∙8-25∙7= 

  22=3∙7+1                                    =147∙8-25∙47.

 

   Полученное равенство 1=147∙8 - 25∙47 умножим на 14. Тогда

1=147∙-25∙,

т.е. пара чисел (112;658) – решение данного уравнения. Все решения в области целых  чисел имеют вид х=112+25∙t, у=658+147∙t, где t.

Ответ: х=112+25∙ t, у=658+147∙t, где t.

 

 

 

   Пример 2. Решить в целых числах  уравнение:  5х-8у-4=0.

 

   Решение. 1-й способ. НОД(5,8)=1. Найдём какое-нибудь решение (х₀, у₀) данного уравнения 5х-8у-4=0. Выразим переменную, коэффициент у которой по модулю меньше  Достаточно взять у₀=2, тогда х₀=4.

 Запишем ответ х=4-8t, у=2-5t (t) (*).

   Решение. 2-й способ. Выразим  Целые решения существуют, если 3у-1=5n(). Аналогично  т.е. 2n+1=3p(). Отсюда  Последнее равенство в целых числах возможно, если p=2t+1(). Выражая х и у через t, получим х=4+8t, у=2+5t(t). Отметим, что полученный ответ совпадает с ответом (*), так как .

 

Задачи для самостоятельного решения

 

1. Найти все целые решения уравнений:

 

    а) 6х+9у=2;                                                                  Ответы: а) нет решений;                                                          

    б) 5х+9у=2;                                                                                  б) х=4+9t, у=-2+5t();  

    в) 15х+78у=12;                                                                            в) х=-20+26t, у=4-5t();

    г) 13х+9у=-1;                                                                               г) х=2+9t, у=-3-13t();  

    д) 7х+17у=5.                                                                                д) х=25+17t, у=-10-7 t();

 

2*. Пусть А – множество целых чисел, имеющих при делении на 5 остаток 3, а В – множество целых чисел, имеющих при делении на 8 остаток 7. Найти все числа, которые входят одновременно в оба множества.

 

                                                                           Ответ: Числа вида 23+40t, .

                                                          Указание. Решить в целых числах уравнение 5х+3=8у+7.

 

3. Найти все целые решения систем уравнений:

    а)                        Ответы: а) х=-85-31t, у=72+26t, z=8+3t();

    б)                                        б) х=-140+43t, у=138-42t, z=-29+9t();

    в)                                        в) нет решений.

 

 

 

 

 

 

 

 

Уравнения в целых числах, решаемые как квадратный трёхчлен относительно одной переменной

 

   Пример 1. Решить в целых числах  уравнение:  х²–3ху+2у²=3.

 

   Решение. Выражение х²–3ху+2у² является квадратным трёхчленом относительно х, и его корни

   х_1,2=х=2у, х=у, так                                                                                                                          что х²–3ху+2у²=(х–2у²)(х–у). Поэтому мы можем переписать данное уравнение в виде

(х–2у²)(х–у)=3.

   Так как простое число 3 раскладывается в произведение целых множителей четырьмя способами:

3=3·1=1·3=(-3)·(-1)=(-1)·(-3),

то множество решений данного уравнения есть объединение множества решений систем:

            

 

   Вычитая в каждой системе первое уравнение из второго, из первой получаем у=-2, х=-1, из второй – у=2, х=5, из третьей – у=2, х=1, из четвёртой – у=-2, х=-5. Соответствующие пары и составляют множество решений данного уравнения.

                                                                                         Ответ: (-2; -1); (2; 5); (2; 1); (-2; -5).

 

   Пример 2. Решить в целых числах  уравнение:    х²–4ху+5у²+2х–8у+5=0.

 

   Решение. Рассмотрим левую часть данного уравнения как квадратный трёхчлен относительно х и запишем его в стандартном виде:

х²–(4у–2)х+5у²–8у+5=0

   Тогда

=(2у–1)²–(5у²–8у+5)=–у²+4у–4=–(у–2)²≤0, откуда следует, что уравнение может иметь решение только если у=2. Тогда х²–6х+9=0, х=3. Следовательно, данное уравнение имеет единственное решение.

                                                                                                            Ответ: (3, 2).

Задачи для самостоятельного решения

 

1) х²–4ху–5у²=7;                                           Ответы: 1) (6, 1), (2, -1), (-6, -1), (-2, 1);

2) 2х²+ху–6у²+3=0;                                                     2) (3, -1), (-7, 5), (-3, 1), (7, -5);                                                       

3) х²–ху+у²=1;                                                             3) (±1, 0), (0, ±1), (1, 1), (-1, -1);                                                       

4) 7х²+12ху–4у²=21;                                                   4) нет решений;

5) х²–2ху+2у²+4х–2у+5=0;                                         5) (1, 1), (5, 1), (5, 5), (9, 5);                                                        

6) х²+ху+у²–2х+2у+4=0;                                             6) (2, -2);                                                             

7) х²+2ху+у²–4х+2у+4=0.                                           7) х=6k²±6k+2, y=–6k² (k).     

 

 

 

                                                     

 

 

Уравнения в целых и натуральных числах, решаемые с помощью метода остатков

 

   Пример 1. Решите в целых числах

                             3^х=1+у²        (1)

 

   Решение. Видно, что (0;0) – решение данного уравнения. Докажем, что других решений нет.

   Рассмотрим случаи:

   1) х у

   Если х то 3^х делится на три без остатка, а у²+1 при делении на три даёт остаток либо 1, либо 2. Следовательно, равенство (1) при натуральных значениях х, у невозможно.

   2) Если х – целое отрицательное число, у, тогда 0<3^х<1, а 1+у²≥1 и равенство (1) также невозможно.

   Следовательно, (0;0) – единственное решение.

                                                                                                           Ответ: (0;0).

 

   Пример 2. Докажите, что уравнение

                                6^х=у²+у–2;

   не имеет решения в целых числах.

 

  Решение. Сначала заметим, что х≥0, так как, если х – целое отрицательное число, то 0·6^х<1, а у²+у–2 при у, тогда данное равенство невозможно. 

у²+у–2=у²+2·+––2=

6^х=, 4·6^х=4

                                                             (4·6^х)+9=(2у+1)².                                                             (*)                                                  

   Известно, что любая натуральная степень числа 6 оканчивается на 6, а значит, 4·6^х при любом натуральном х оканчивается на 4. Значит, (4·6^х)+9 при любом натуральном х оканчивается на 3. (2у+1)² – квадрат целого числа, и значит, на 3 оканчиваться не может.

   То есть левая часть уравнения (*) при  всегда оканчивается на 3, а правая представляет собой квадрат целого числа, а он не может оканчиваться на 3. Значит, уравнение (*) не имеет решений в целых числах.

                                                                                       Ответ: решений в целых числах нет.

 

  Пример 4. Решите в целых числах

                            х²+у²=4z–1.

 

   Решение. Запишем уравнение в виде

                            х²+у²+1=4z.          

   Рассмотрим, какие остатки могут давать при делении на 4 левая и правая части этого уравнения.

   При делении на 4 точные квадраты могут давать только два различных остатка 0 или 1. Тогда х²+у²+1 при делении на 4 может давать три возможных остатка 1, 2, 3, а 4z при  z делится на 4 без остатка.

   Следовательно, данное уравнение целых решений не имеет.

                                                                                Ответ: решений в целых числах нет.

 

 

 

   Пример 5.  Решите в целых числах

                             х²+у²+z²=8t–1.

 

   Решение. 1) Решение уравнения основано на утверждении, что точные квадраты при делении на 8 могут давать остатки 0, 1, 4(проверить самостоятельно).

   2) Запишем данное уравнение в виде

                            х²+у²+z²+1=8t.

   Правая часть данного уравнения делится на 8 без остатка, а левая часть при делении на 8 может давать следующие остатки: 1, 2, 3, 4, 5, 6, 7. Следовательно, данное равенство невозможно.

                                                                                    Ответ: решений в целых числах нет.

   Пример 6.  Решите в целых числах

                            х³+21у²+5=0.

      Решение. Так как , то х³. Значит, х³ при делении на 7 может давать три различных остатка: 0, 1, 6.

   Так как 21у² делится на 7 нацело при , то х³+21у²+5 при делении на 7 может давать три различных остатка: 4, 5, 6; а значит, не может быть равным нулю, т.е. данное уравнение целых решений не имеет.

                                                                                    Ответ: решений в целых числах нет. 

   Пример 7.  Решите в целых числах

                         1!+2!+3!+ … +х!=у².

   Решение. 1) Видно, что при

 а) х=1, 1!=1, тогда у²=1, у=±1;

 б) х=3, 1!+2!+3!=9, т. е. у²=9, у=±3.

   Получаем следующие решения: (1; 1), (1; -1), (3; 3), (3; -3).

   Заметим, что если х=2, 1!+2!+3!=3, у²=3, у=±, но у, значит, при х=2 целочисленных решений нет.

   При х=4 получаем у²=33, а так как у, то целочисленных решений при х=4 нет.

   2) Если х≥5, то 5!+6!+ … +х! можно представить в виде 10n, где n. Таким образом,

1!+2!+3!+4!+5!+ … +х!=33+10n

   – число, оканчивающееся цифрой 3, значит, оно не может быть квадратом целого числа. Следовательно, при х≥5 целых решений нет.

                                                                                    Ответ: (1; 1), (1; -1), (3; 3), (3; -3).

   Пример 8.  Докажите, что уравнение

                               х⁵ – у⁵=1993   не имеет решений в целых числах.  

   Решение. Предположим, что данное уравнение имеет решения в целых числах. Из того, что х⁵ – у⁵=1993 следует, что х⁵> у⁵ и х> у.

   Запишем данное уравнение в виде

(х–у)(х⁴+х³у+х²у²+ху³+у⁴)=1993.

   Так как 1993 – число простое, а х–у>0, то х–у равно либо 1, либо 1993.

   Если х–у=1, то

х⁵–у⁵=(у+1)⁵–у⁵=5(у⁴+2у³+2у²+у)+1;

   т.е. исходное уравнение примет вид

5(у⁴+2у³+2у²+у)+1=1993.

   Видно, что левая часть уравнения при делении на 5 даёт остаток 1, а правая, т.е. 1993, при делении на 5 даёт остаток 3. Значит, в данном случае решений нет.

   Если х–у=1993, то

х⁴+х³у+х²у²+ху³+у⁴=1,

   а это невозможно, так как

х⁴+х³у+х²у²+ху³+у⁴=х³(х+у)+у³(х+у)+х²у²=(х+у)( х³+у³)+ х²у²=(х+у)²(х²–ху+у²)+ х²у²≥ х²у²>1.

   Следовательно, данное уравнение не имеет решений в целых числах.

                                                                                 Ответ: решений в целых числах нет. 

Пример 9. Докажите, что система уравнений

                                                                                                                

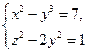
   не имеет решений в целых числах.

  Решение. Предположим, что система разрешима. Из второго уравнения , т. е. z² – нечётное число и z – нечётное, значит z=2m+1. Тогда у²=2m²+2m, значит, у² – чётное число и у – чётное, у=2n, .

   х=8n³+7, т. е. х² – нечётное число и х – нечётное число, х=2k+1, .

   Подставим значения х и у в первое уравнение, получаем

                                      2(k²+k–2n³)=3,

что невозможно, так как левая часть делится на 2, а правая нет.

   Значит, наше предположение неверно, т. е. система не имеет решений в целых числах.

                                                                                   Ответ: решений в целых числах нет. 

 

 

 

Задачи для самостоятельного решения.

 

  1)  2^х–1=у²;                                                     Ответы: 1) (0; 0), (1; 1), (1; -1);

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Уравнения в целых и натуральных числах, решаемые методом «бесконечного» спуска.

  

   Пример.  Решите в целых числах

                          4х³–2у³–z³=0.

 

   Решение. Здесь левая часть уравнения не разлагается на целые множители и вообще не поддаётся преобразованиям.

   Запишем данное уравнение в виде

                    z³=2(2х³–у³).                                                                                                              (1)

   Следовательно, z³ – чётное, значит и z должно делиться на два, т.е.

z=2z₁,. Тогда

4х³–2у³–8z₁³=0,

                                                                 2х³–у³–4z₁³=0.                                                              (*) 

   Из уравнения (*) видно, что у – чётное, т.е. у=2у₁, у₁.

2х³–8у₁³–4z₁³=0,

                                                                  х³–4у₁³–2z₁³=0.                                                          (**)

   Из уравнения (**) следует, что х – чётное, т. е. х=2х₁, х.

8х₁³–4у₁³–2z₁³=0, z₁³=2(2х₁³–у₁³).

   Получаем уравнение вида (1).

   Из всех проделанных рассуждений можно сделать следующие выводы. Во-первых, числа х, у, z должны быть чётными. Во-вторых, числа х₁, у₁, z₁, т. е. , , , удовлетворяющие этому уравнению, тоже чётные.

   Итак, оказалось, что числа, удовлетворяющие уравнению (1), чётные, и сколько раз мы не делили бы их на 2, получаем числа, которые также делятся на 2. Единственное число, обладающее этим свойством, есть нуль.

   Следовательно, данное уравнение имеет единственное решение х=0, у=0, z=0.

                                                                                                            Ответ: (0; 0; 0).

 

 

Задачи для самостоятельного решения.

 

   Докажите, что уравнения не имеют решений в натуральных числах:

1)      8х⁴+4у⁴+2z⁴=t⁴;

2)      х²+у²+z²=2хуz;

      3)   х²+у²+z²+u²=2xyzu.