Добавить материал

и получить 10 документов
и свидетельство СМИ

Громов Александр Викторович

Подготовка к успешной сдаче ЕГЭ по информатике

pdf
27.01.2025

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Подготовка к успешной сдаче ЕГЭ по информатике

Podgotovka_k_uspeshnoy_sdachi_EGE_informatika.pdf

Златопольский Д. М.

Подготовка к успешной сдаче ЕГЭ

по информатике

Москва, 2024

УДК 373.167.1:004+004(075.3)

ББК 32.97я72 З67

Златопольский Д. М.

З67 Подготовка к успешной сдаче ЕГЭ по информатике. – М.: ДМК Пресс,

2024. – 422 с.: ил.

ISBN 978-5-93700-236-5

Книга предназначена для самостоятельной подготовки учащихся к Единому государственному экзамену по информатике. В ней рассматриваются все 27 заданий ЕГЭ, их типовые варианты и особенности каждого из них, приводятся различные методы их выполнения, даются полезные советы и рекомендации, обеспечивающие ускорение выполнения заданий и уменьшающие вероятность ошибки. Предлагаются задания для самостоятельного выполнения.

Кроме учащихся 11-го класса, готовящихся к сдаче ЕГЭ, книгу могут использовать учителя и преподаватели информатики. Конечно, она будет полезна и учащимся 9–10-х классов, планирующим сдавать экзамен в будущем.

ISBN 978-5-93700-236-5 © Издание, оформление, ДМК Пресс, 2024

Содержание

Предисловие ................................................................................................................6 Глава 1. Задания 1 .......................................................................................................7

1.1. Общие вопросы. Теория ...............................................................................................7

1.2. Примеры заданий типа 1 и методика их выполнения ............................................10 1.3. Примеры заданий типа 2 и методика их выполнения ............................................18

1.4. Выводы и рекомендации ...........................................................................................25 1.5. Задания для самостоятельного выполнения ...........................................................25

Глава 2. Задания 2 ....................................................................................................31

2. 1. Общие вопросы. Теория ............................................................................................31

2.2. Примеры заданий и методика их выполнения ........................................................34

2.3. Выполнение заданий с использованием электронной таблицы или программы ...53

2.4. Полезные факты и рекомендации по выполнению задания ..................................60 2.5. Задания для самостоятельного выполнения ............................................................62

Глава 3. Задания 3 ....................................................................................................64

3.1. Общие вопросы ...........................................................................................................64

3.2. Примеры заданий и методика их выполнения ........................................................66

3.3. Рекомендации по выполнению задания ..................................................................76 3.4. Задания для самостоятельного выполнения ............................................................77

Глава 4. Задания 4 ....................................................................................................78

4.1. Общие вопросы. Теория .............................................................................................78

4.2. Примеры заданий и методика их выполнения ........................................................79 4.3. Задания для самостоятельного выполнения ............................................................86

Глава 5. Задания 5 ....................................................................................................89

5.1. Общие вопросы ...........................................................................................................89

5.2. Примеры заданий и методика их выполнения ........................................................90

5.3. Выполнение заданий в среде электронной таблицы ...............................................98 5.4. Выводы и рекомендации ...........................................................................................99

5.5. Другие возможные варианты задания .................................................................... 101 5.5. Задания для самостоятельного выполнения .......................................................... 107

Дополнение. Некоторые формулы для расчета значения результата

выполнения алгоритма .............................................................................................. 112 Глава 6. Задания 6 ..................................................................................................113

6.1. Общие вопросы ......................................................................................................... 113

6.2. Подготовка к выполнению заданий ........................................................................ 115

6.3. Примеры заданий и методика их выполнения ...................................................... 117 6.4. Задания для самостоятельного выполнения .......................................................... 125

Глава 7. Задания 7 ..................................................................................................127

7.1. Общие вопросы. Теория ........................................................................................... 127

7.2. Примеры задач на кодирование графики и методика их выполнения ................ 130

7.3. Примеры задач на кодирование звука и методика их выполнения ..................... 142

Глава 8. Задания 8 ..................................................................................................151

8.1. Общие вопросы ......................................................................................................... 151

8.2. Примеры заданий на подсчет количества слов и методика их выполнения ....... 152 8.3. Примеры заданий на подсчет количества чисел и методика их выполнения ..... 166

Глава 9. Задания 9 ..................................................................................................177

9.1. Общие вопросы. Используемые функции .............................................................. 177

9.2. Примеры заданий и методика их выполнения ...................................................... 180 9.3. Задания для самостоятельного выполнения .......................................................... 189

Глава 10. Задания 10 .............................................................................................190

10.1. Общие вопросы ....................................................................................................... 190

10.2. Примеры заданий и методики их выполнения .................................................... 191

10.3. Рекомендации по выполнению задания 10 .......................................................... 197

10.4. Задания для самостоятельного выполнения ........................................................ 198

Глава 11. Задания 11 .............................................................................................199

11.1. Общие вопросы. Теория ......................................................................................... 199

11.2. Примеры заданий и методика их выполнения .................................................... 201 11.3. Задания для самостоятельного выполнения ........................................................ 206

Глава 12. Задания 12 .............................................................................................208

12.1. Общие вопросы ....................................................................................................... 208

12.2. Примеры заданий и методика их выполнения .................................................... 209 12.3. Задания для самостоятельного выполнения ........................................................ 221

Глава 13. Задания 13 .............................................................................................224

13.1. Общие вопросы ....................................................................................................... 224

13.2. Примеры заданий и методика их выполнения .................................................... 226 13.3. Задания для самостоятельного выполнения ........................................................ 234

Глава 14. Задания 14 .............................................................................................236

14.1. Общие вопросы ....................................................................................................... 236

14.2. Примеры заданий типа 1 и методика их выполнения ......................................... 236

14.3. Примеры заданий типа 2 и методика их выполнения ......................................... 241

Глава 15. Задания 15 .............................................................................................252

15.1. Общие вопросы ....................................................................................................... 252

15.2. Примеры заданий, связанных с делимостью, и методика их выполнения ........ 253

15.3. Примеры заданий с отрезками числовой прямой и методика их выполнения ... 258 15.4. Примеры заданий с координатной плоскостью и методика их выполнения .... 264

Глава 16. Задания 16 .............................................................................................269

16.1. Общие вопросы. Подготовка к выполнению заданий ......................................... 269

16.2. Примеры заданий и методика их выполнения .................................................... 274 16.3. Задачи для самостоятельного решения ................................................................ 282

Глава 17. Задания 17 ..............................................................................................285

17.1. Общие вопросы ....................................................................................................... 285

17.2. Примеры заданий и методика их выполнения .................................................... 285 17.3. Задания для самостоятельного выполнения ........................................................ 292

Глава 18. Задания 18 .............................................................................................293

18.1. Общие вопросы. Подготовка к выполнению заданий ......................................... 293

18.2. Методика выполнения заданий из демонстрационных вариантов ЕГЭ ............ 298

18.3. Задания для самостоятельного выполнения ....................................................... 308

Глава 19. Задания 19, 20 и 21 ..............................................................................309

19.1. Общие вопросы ....................................................................................................... 309

19.2. Готовимся выполнять задания .............................................................................. 309

19.3. Примеры заданий с игрой с одной кучкой камней и методика

их выполнения ............................................................................................................ 311

19.4. Примеры заданий с игрой с двумя кучками камней и методика

их выполнения ............................................................................................................ 319 19.5. Задания для самостоятельного выполнения ........................................................ 323

Глава 20. Задания 22 .............................................................................................329

20.1. Общие вопросы ....................................................................................................... 329

20.2. Задание 22 из демонстрационного варианта ЕГЭ 2023 года и методика

его выполнения .......................................................................................................... 329

20.3. Задание 22 из демонстрационного варианта ЕГЭ 2024 года и методика

его выполнения .......................................................................................................... 339 Глава 21. Задания 23 .............................................................................................343

21.1. Общие вопросы ....................................................................................................... 343

23.2. «Базовая задача» и методы ее решения ................................................................ 344

23.3. Примеры заданий и методика их выполнения ................................................... 349 23.4. Задачи для самостоятельного решения ................................................................ 356

Глава 22. Задания 24 .............................................................................................358

22.1. Общие вопросы ....................................................................................................... 358

22.2. Примеры заданий и методика их выполнения ................................................... 358 22.3. Задание из демонстрационного варианта ЕГЭ по информатике 2024 года ....... 375

Глава 23. Задания 25 .............................................................................................380

23.1. Общие вопросы ....................................................................................................... 380

23.2. Первый вариант решения ...................................................................................... 381

23.3. Второй вариант решения ....................................................................................... 383 23.4. Задания для самостоятельного выполнения ........................................................ 384

Глава 24. Задания 26 .............................................................................................387

24.1. Общие вопросы ....................................................................................................... 387

24.2. Примеры заданий и методика их выполнения .................................................... 387 24.3. Выводы и рекомендации ....................................................................................... 401

Глава 25. Задания 27 .............................................................................................402

25.1. Общие вопросы ....................................................................................................... 402

25.2. Примеры заданий и методика их выполнения .................................................... 402 25.3. Задание для самостоятельного выполнения ........................................................ 420 Литература ..............................................................................................................421

Предисловие

Большинство книг, связанных с Единым государственным экзаменом по информатике, представляют собой сборники заданий для самопроверки или «решебники», в которых приводится решение заданий без подробных комментариев. Данная книга отличается от них тем, что в ней после соответствующей теоретической подготовки рассказывается о типовых вариантах всех 27 заданий ЕГЭ и особенностях каждого из них, приводятся различные методы их выполнения, даются полезные советы и рекомендации, обеспечивающие ускорение выполнения заданий и уменьшающие вероятность ошибки. После знакомства с этими вопросами читатель может проверить свои знания и умения, выполнив предлагаемые в книге задания для самостоятельной работы. В книге учтены задания из демонстрационных вариантов ЕГЭ по информатике нескольких последних лет до варианта 2024 года включительно.

При изложении методики выполнения заданий с помо щью собственных программ логика действий в них описывается на школьном алгоритмическом языке (система программирования КуМир). Русский синтаксис этого языка и большое число комментариев к программам делают приводимые методики и программы максимально понятными, и читатель сможет разработать аналогичные программы на языке программирования, которым владеет.

Методика выполнения заданий в среде электронной таблицы описывается применительно к программе Microsoft Excel. При использовании читателем другой программы, естественно, должны быть учтены ее особенности.

Глава 1

Задания 1

1.1. Общие вопросы. Теория

В Спецификации контрольных измерительных материалов для проведения в 2024 году Единого государственного экзамена по информатике [1]^{^[1]} в качестве проверяемого элемента содержания применительно к заданию 1 указывается «умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 1 двух типов.

Тип 1 (пример)

Условие

«На рисунке схема дорог N-ского района изображена в виде графа. В таблице содержатся сведения о протяженности каждой из этих дорог (в километрах).

Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе».

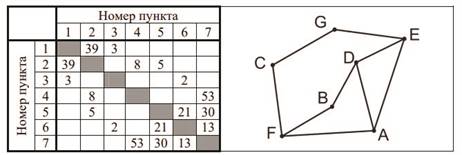
Далее излагался один из двух вариантов требований по выполнению задания:

1) «Определите длину дороги из пункта … в пункт …. В ответе запишите целое число»;

2) «Определите, какова сумма протяженностей дорог из пунк та … в пункт … и из пункта … в пункт …. В ответе запишите целое число».

Тип 2 (пример)

Условие

На рисунке изображена схема дорог N-ского района. В таб лице звездочкой обозначено наличие дороги из одного населенного пункта в другой. Отсутствие звездочки означает, что такой дороги нет.

	Номер пункта
	1	2	3	4	5	6	7
1			*	*			*
2			*		*	*
3	*	*		*	*	*	*
4	*		*
5		*	*
6		*	*				*
7	*		*			*

Каждому населенному пункту на схеме соответствует номер в таблице, но неизвестно, какой именно номер. Определите, какие номера в таблице могут соответствовать населенным пунктам Б и Е на схеме. В ответе запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.

***

Основные определения

Граф – это изображение в виде набора вершин и соединяющих их ребер. Например, на графе, представленном ниже, имеются пять вершин, некоторые из которых соединены ребрами.

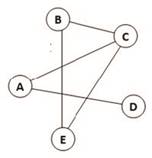
Чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес); оно может обозначать, например, расстояние между городами или стоимость перевозки. Вес ребра указывают рядом с ним:

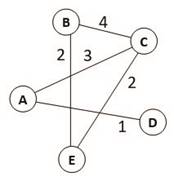
Количество ребер, с которыми связана каждая вершина, называют степенью вершины.

Граф описывается в виде таблицы, которую называют матрицей смежности (или применительно к взвешенному графу – весовой матрицей). В таблице по вертикали и по горизонтали перечислены номера вершин и на пересечении строк и столбцов с теми или иными номерами в весовой матрице указывается вес ребра графа, соединяющего эти вершины. Если клетка таблицы пустая, то это значит, что соответствующие ей вершины не связаны. Клетки на главной диагонали таблицы (они оттенены) не рассматриваются (почему – понятно).

Обратите внимание на то, что в примере 1 весовая матрица симметрична относительно главной диагонали. Это означает, например, что стоимости перевозки из пункта номер 5 в пункт номер 6 и из пункта номер 6 в пункт номер 5 равны. Такие матрицы будут представлены во всех заданиях, в которых фигурируют весовые матрицы. Таблицы, приводимые в заданиях типа 2, также симметричны относительно главной диагонали (что логично, учитывая смысл их содержания).

Прежде чем описывать методику выполнения заданий, предлагаем читателю ответить на следующие вопросы:

• как определить степень некоторой вершины по ее номеру в весовой матрице?

• как по весовой матрице или по таблице в примере задания типа 2 установить, с какими вершинами связана вершина с заданным но-

мером?

Знание ответов на них очень поможет успешно выполнять обсуждаемые задания.

1.2. Примеры заданий типа 1 и методика их выполнения

Во всех обсуждаемых заданиях мы будем приводить только граф и соответствующую весовую матрицу, а также искомое значение. Подробное условие приведено в разделе 1.1.

1.2.1. Пример 1

Условие

Определите длину дороги из пункта В в пункт Г.

	1	2	3	4	5	6	7
1		45		10
2	45			40		55
3					15	60
4	10	40				20	35
5			15			55
6		55	60	20	55		45
7				35		45

Решение

Для нахождения ответа в данном и других заданиях нужно определить, какие номера в таблице имеют вершины В и Г. Как?

На схеме вершина В – единственная, имеющая степень 5 (с пятью дорогами). В таблице таким пунктом является пункт номер 6. Сразу же заметим, что применительно к таблице (весовой матрице) с целью упрощения вместо фразы «пункт номер 6» мы будем говорить «номер 6» и т. п.

Вершина Г − единственная со степенью 3. Соответствующий номер в таблице – 2.

Согласно таблице, длина дороги из пункта 6 в пункт 2 равна 55.

Ответ: 55^{^[2]}.

1.2.2. Пример 2

Условие

Определите длину дороги из пункта А в пункт Д.

	1	2	3	4	5	6	7
1			30		25		18
2			17	12
3	30	17		23		34	15
4		12	23			46
5	25						37
6			34	46			18
7	18		15		37	18

Решение

По изображению графа находим, что обе интересующие нас вершины (А и Д) имеют степень 3. Такую же степень имеет еще одна вершина – Г. Как в таблице найти нужные и «отсеять» вершину Г?

Определим, какие номера в таблице имеют степень 3: – 1, 4 и 6. Какой из этих трех номеров «лишний», не нужный нам для расчетов?

Анализ показывает, что у вершин А и Д есть общее ребро, а вершина Г – отдельная, не связанная с А и Д. Значит, в таблице надо проверить связи номеров 1, 4 и 6.

Находим, что номера 4 и 6 связаны между собой, а номер 1 с ними не связан. Значит, искомые вершины А и Д – это вершины в номерами 4 и 6 (или 6 и 4).

По весовой матрице определяем длину дорог между ними – 46.

Ответ: 46.

1.2.3. Пример 3

Условие

Определите длину дороги из пункта А в пункт Г.

	1	2	3	4	5	6	7
1		57		20		25
2	57		22	42	8		21
3		22			23		8
4	20	42				7	33
5		8	23
6	25						9
7		21	8	33		9

Решение

Здесь номер одной из искомых вершин – Г – найти легко. Ее степень равна 5, а в таблице номер с такой степенью – единств енный (2). Степень второй искомой вершины (А) равна трем. Но такую же степень имеют вершины Е и К. Как их определить и не учесть? – Это вершины, которые связаны между собой!

По таблице определяем, что номера 1 и 6 между собой связаны, то есть вершина А имеет номер 3.

Итак, вершины Г и А в таблице имеют номера, соответственно, 2 и 3.

Длина дороги между ними – 22.

Ответ: 22.

1.2.4. Пример 4

Условие

Определите длину дороги из пункта Е в пункт К.

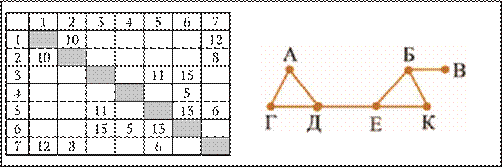
Решение

Здесь задача усложняется – у вершин Е и К (их степень, соответственно, 3 и 2) есть «конкуренты» с такими же степенями. Отличить вершину Е от вершины Д можно по такому признаку: вершина Е связана с двумя вершинами степени 3 (Д и Б), а вершина Д – только с одной. Определим степень каждого номера в весовой матрице:

	1	2	3	4	5	6	7
1		10					12	2
2	10						8	2
3					11	15		2
4						5		1
5			11			13	6	3
6			15	5	13			3
7	12	8			6			3

Примечание. При оформлении таблицы на бумаге можно в целях сокращения времени значения весов ребер не указывать, а делать в соответствующих клетках некоторую отметку:

	1	2	3	4	5	6	7
1		ü					ü	2
2	ü						ü	2
3					ü	ü		2
4						ü		1
5			ü			ü	ü	3
6			ü	ü	ü			3
7	ü	ü			ü			3

Видно, что степень 3 имеют номера 5, 6 и 7. Если начать проверку их связей с номера 5, то можно сразу установить, что он связан и с номером 6, и с номером 7. Значит, вершина Е имеет в таблице номер 5.

Осталось найти номер второй нужной нам вершины К. Ее признак – это единственная вершина степени 2, связанная с вершиной Е. По таблице можно определить, что таким номером является 3.

Итак, нужная нам дорога ведет из 3 в 5 (и наоборот); ее длина равна 11.

Ответ: 11.

1.2.5. Пример 5

Условие

Определите длину дороги из пункта Б в пункт Г.

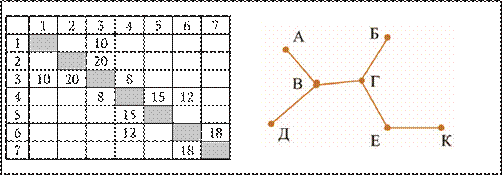
Решение

Находим вершину Г (ее степень – 3).

Отличие вершины Г от вершины В с той же степенью: у нее есть связь в двумя вершинами степени 1, 2 и 3 (у вершины В – 1, 1 и 3).

Проверка номера 3 (со степенью 3)

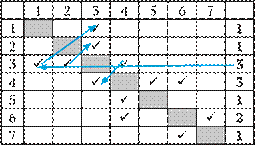
показывает, что этот номер не подходит. Значит, вершина Г имеет номер 4 (это также можно было установить, начав проверку с номера 4).

Обратите внимание на методику использования таблицы со степенями.

Вторая искомая вершина (Б) – это связанная с найденной вершиной Г (номер 4), имеющая степень 1.

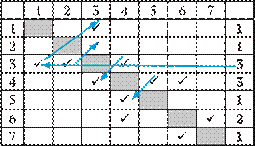
Такой номер – 5 (см. таблицу).

Искомое расстояние между найденными пунктами 4 и 5 равно 15.

Ответ: 15.

1.2.6. Пример 6

Условие

Определите длину дороги из пункта Б в пункт В.


	1	2	3	4	5	6
1		7			15	4
2	7				12
3				5
4			5		10	9
5	15	12		10		16
6	4			9	16

Решение

Вершина В в таблице имеет номер 5.

Как найти вершину Б? Ее степень – 3. Но такую же степень имеют вершины Г и Д. В чем их отличие от вершины Б?

У вершины Б связанные с ней вершины имеют степень 2, 3 и 4.

У вершины Г: 3, 3 и 4.

У вершины Д: 4, 3 и 1.

Проверим номера 1, 4 и 6 (их степень – 3) по описанной методике.

Проверка уже первого номера (1)

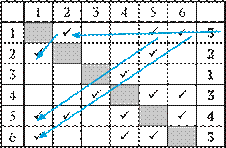
показывает, что он соответствует вершине Б.

По таблице находим расстояние между номерами 5 и 1 – оно равно 15.

Ответ: 15.

1.2.7. Пример 7 (задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Определите, какова сумма протяженностей дорог из пункта Б в пункт В и из пункта Г в пункт Д.

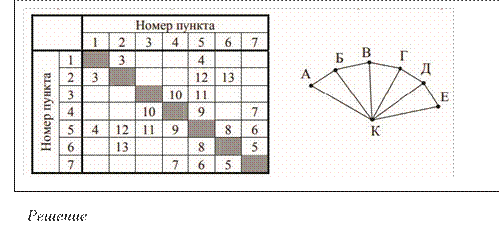
Для нахождения ответа нужно найти вес ребер Б–В и Г–Д. У всех перечисленных вершин степень равна 3. По таблице можно установить, что такую степень имеют номера 2, 4, 6, 7. Как определить, какой номер соответствует каждой из вершин? – Для этого надо установить отличие одной вершины от другой.

Вершины Б и Д – это те вершины, у которых есть «связь» с вершинами со степенью 2. Находим номера со степенью 2 – это 1 и 3. Что из группы номеров 2, 4, 6, 7 с ними связано? – Номера 2 и 4. Значит, вершинам Б и Д соответствуют номера 2 и 4, или наоборот.

Осталось найти вторую вершину для каждого из двух указанных в начале ребер. Это «оставшиеся» вершины со степенью 3 (с номерами 6 и 7). Как они связаны с найденными номерами 2 и 4? – По таблице находим:

• с номером 2 связан номер 6, • с номером 4 – номер 7.

Итак, интересующее нас ребро Б–В в весовой матрице – это ребро 2–6, а ребро Г–Д – это ребро 7–4. Вес этих ребер (протяженность дорог) указан, соответственно, 13 и 7, то есть искомая в задании сумма равна 20.

Ответ: 20.

1.2.8. Пример 8 (задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Определите, какова сумма протяженностей дорог из пункта D в пункт B и из пункта F в пункт A.

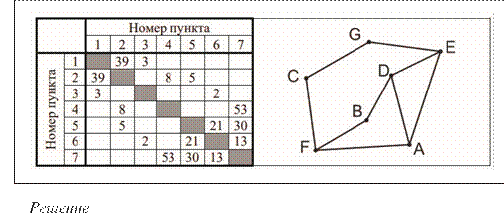
Обратим внимание на три вершины, фигурирующие в условии, – D, А и F. Это вершины со степенью 3. Есть еще одна вершина с такой же степенью (Е). Как их различить в таблице? – Вершина А – единственная, не имеющая связи с вершиной степени 2.

Итак, в таблице находим номера со степенью 3. Это 2, 5, 6, 7. Анализ показывает, что только номер 5 не имеет указанной чуть выше связи. Итак, А = 5.

Вершина В – единственная из имеющих степени 2 (В, С и G), не связанная с другой такой вершиной. По таблице определяем, что из номеров 1, 3 и 4 по этому признаку подходит номер 4, то есть В = 4.

Далее, D – вершина степени 3, связанная с уже найденными номерами 4 и 5. Из номеров 2, 6 и 7 подходит номер 2. D = 4.

Оставшаяся вершина F связана с В (4) и А (5). В таблице соответствующий номер – 7.

Итоги: ребро В–D – это 4–7, ребро A–F – это 5–2. В весовой матрице вес этих ребер (протяженность дорог) указан, соот ветственно, 53 и 5, то есть искомая в задании сумма равна 58.

Ответ: 58.

1.3. Примеры заданий типа 2 и методика их выполнения

Во всех обсуждаемых заданиях мы будем приводить только граф и соответствующую таблицу связей между пунктами, а также искомые значения. Подробное условие приведено в разделе 1.1.

1.3.1. Пример 1

Условие

Определите номера населенных пунктов А и G в таблице.

		Номер пункта
	1	2	3	4	5	6
1		*		*
2	*			*		*
3				*	*
4	*	*	*		*	*
5			*	*
6		*		*

Решение

Чем особенны вершины А и G? – Их степень – 2 (по схеме). Но такую же степень имеют и вершины C и E. Как отличить первые две от последних? – Вершины А и G связаны между собой, а вершины C и E – нет.

По таблице в условии определяем, что степень 2 имеют пункты с номерами 1, 3, 5 и 6.

Запишем эти номера в первом столбце таблицы, а связанные с ними – во втором:

Номер пункта	Связан c номерами
1	2 и 4
3	4 и 5
5	3 и 4
6	2 и 4

Какие из четырех номеров связаны друг с другом? – 3 и 5.

Ответ: 35.

1.3.2. Пример 2 (пример из демонстрационного варианта ЕГЭ 2024 года)

Условие

Определите номера населенных пунктов E и F в таблице.

Номер пункта
		1	2	3	4	5	6	7
	1		*	*	*	*	*	*
	2	*						*
	3	*				*		*
	4	*				*	*
	5	*		*	*
	6	*			*
	7	*	*	*

Решение

Чем особенны вершины E и F? – Их степень – 3. Но такую же степень имеют и вершины D и G. Как отличить первые две от последних? – E и F связаны только с вершинами, степень которых равна 3 и 6, а D и G – нет.

Номер вершины со степенью 6 очевиден – 1.

По таблице в условии определяем, что степень 3 имеют номера 3, 4,

5 и 7.

Запишем эти номера в первом столбце таблицы, а связанные с ними номера – во втором:

Номер пункта	Связан c номерами
3	1, 5 и 7
4	1, 5 и 6
5	1, 3 и 4
7	1, 2 и 3

Так как пункты с номерами 6 и 2 не входят в число имеющих степень 3, то варианты с ними не подходят:

Номер пункта	Связан c номерами
3	1, 5 и 7
4	~~1, 5 и 6~~
5	1, 3 и 4
7	~~1, 2 и 3~~

Остаются варианты с пунктами 3 и 5 в первом столбце. Это и есть искомые номера пунктов E и F.

Ответ: 35.

1.3.3. Пример 3

Условие

Определите номера населенных пунктов В и С в таблице.

		Номер пункта
	1	2	3	4	5	6	7
1					*	*
2			*	*			*
3		*			*		*
4		*				*
5	*		*			*
6	*			*	*
7		*	*

Решение

Здесь также имеются четыре вершины со степенью, равной 3 (В, С, F и G). Интересующие нас вершины В и С отличаются тем, что они не связаны друг с другом.

Определив по таблице в условии номера со степенью, равной 3, и связанные с ними, можем составить таблицу:

Номер пункта	Связан c номерами
2	3, 4 и 7
3	3, 5 и 7
5	1, 3 и 5
6	1, 4 и 5

Ее анализ показывает, что с друг другом связаны номера 3 и 5. Нас же интересуют не такие. Это номера 2 и 6. Ответ: 26.

1.3.4. Пример 4

Условие

Определите номера населенных пунктов F и G в таблице.

Номер пункта
		1	2	3	4	5	6	7
	1		*	*	*	*		*
	2	*		*	*
	3	*	*					*
	4	*	*			*
	5	*			*		*
	6					*		*
	7	*		*			*

Решение

Как и интересующие нас вершины F и G, степень 3 имеют также пункты D, E и A.

Вершины F и G отличаются тем, что они не связаны с вершиной С. Найдем все такие вершины.

Так как степень вершины С равна 2, то ее номер в таблице – 6.

Как и ранее, составим таблицу:

Номер пункта	Связан c номерами
2	1, 3 и 4
3	1, 2 и 7
4	1, 2 и 5
5	~~1, 4 и 6~~
7	~~1, 3 и 6~~

Видно, что пункты с номерами 5 и 7 с вершиной С (6) связаны. По схеме определяем, что это пункты D и Е. Значит, «наши» вершины, а также вершина А находятся среди трех оставшихся с номерами 2, 3 и 4. Как исключить вершину А? – На схеме она связана с «нашими», а «наши» вершины друг с другом не связаны.

В созданной таблице есть номер, связанный с двумя другими, – номер 2. Значит, искомые вершины F и G имеют номера 3 и 4.

Ответ: 34.

1.3.5. Пример 5

Условие

Определите номера населенных пунктов Б и В в таблице.

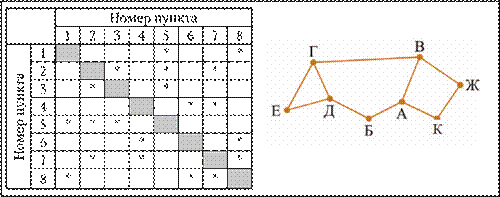
Решение

Так как вершина А – единственная, связанная с двумя вершинами степени 2, то по таблице можно установить, что ее номер – 8^{^[3]}.

Заметим, что после этого можно определить номер вершины В. Предлагая читателям сделать это, продолжим – попробуем «вычислить» вершину Б.

Степень 2, кроме нее, имеют также вершины Е, К и Ж, при этом вершины К и Ж связаны друг с другом. Найдем их. По таблице в условии отберем номера со степенью 2 и составим такую:

Номер пункта	Связан c номерами
1	5 и 8
3	2 и 5
4	6 и 7
6	4 и 8

Друг с другом связаны номера 4 и 6, то есть это и есть вершины К и Ж, а интересующая нас вершина Б имеет номер 1 или 3.

Итак, мы знаем, что А – это 8, а Б – 1 или 3. В таблице номер 8 с номером 3 не связан, а с номером 1 связан. Значит, номер вершины Б – 1.

Как определить номер вершины В, определите самостоятельно (если вы не сделали это раньше).

1.3.6. Пример 6

Условие

Выпишите последовательно, без пробелов и знаков препинания, указанные на схеме буквенные обозначения пунктов с номерами 1 до 7: сначала букву, соответствующую пункту 1, затем букву, соответствующую пункту 2, и т. д.

Номер пункта
		1	2	3	4	5	6	7
	1			*				*
	2				*	*		*
	3	*					*	*
	4		*			*	*	*
	5		*		*		*
	6			*	*	*		*
	7	*	*	*	*		*

Решение

На основе анализа схемы и таблицы в условии составим две таблицы:

Номер	Степень	Вершина	Степень	Номер
1	2	А	3
2	3	Б	4
3	3	В	3
4	4	Г	4
5	3	Д	5
6	4	Е	3
7	5	Ж	2

Их сопоставление позволяет определить номера двух вершин:

Вершина	Степень	Номер
А	3
Б	4
В	3
Г	4
Д	5	7
Е	3
Ж	2	1

Далее ищем на схеме другие «оригинальные» вершины. Вершина Е со степенью 3 отличается от других с такой же степенью тем, что она связана с известной вершиной Ж (1). В таб лице с номером 1 связаны номера 3 и 7. Значит, вершина Е имеет номер 3.

Вершина	Степень	Номер
А	3
Б	4
В	3
Г	4
Д	5	7
Е	3	3
Ж	2	1

Зная номер вершины Е (3), можно определить, какая из вершин со степенью 4 (Б или Г) с ней связана. По таблице в условии это пункт номер 6. Значит, вершина Б имеет номер 6, а оставшаяся вершина Г – 4:

Вершина	Степень	Номер
А	3
Б	4	6
В	3
Г	4	4
Д	5	7
Е	3	3
Ж	2	1

Номера остальных двух вершин установите самостоятельно.

1.4. Выводы и рекомендации

Анализ приведенных решений позволяет сделать вывод о том, что для успешного выполнения задания 1 ЕГЭ следует уметь:

1) применительно к графу:

• определять степень каждой вершины;

• устанавливать отличительные особенности вершин, соответствующие номера которых надо определить в весовой матрице (таблице), а при необходимости – и других вершин;

2) применительно к таблице:

• определять степень каждой вершины;

• устанавливать номера, связанные с данным номером;

• находить степень номеров, связанных с данным номером.

Можно также сформулировать следующие рекомендации:

• начинать анализ следует с поиска номеров вершин, являющихся «оригинальными» с точки зрения их степени, связей с другими вершинами и т. п., причем и с вершин, номера которых не являются искомыми по условию задания;

• в ходе рассуждений найденные номера вершин при необходимости записывать на схеме рядом с соответствующей вершиной.

1.5. Задания для самостоятельного выполнения

Во всех заданиях мы будем приводить только граф и соответствующую таблицу связей между пунктами.

1. Выполните задание примера 2 в разделе 1.1.

2. Определите номера населенных пунктов Б и В в таблице.

	Номер пункта
	1	2	3	4	5	6	7
1						*	*
2			*	*		*
3		*		*
4		*	*		*
5				*			*
6	*	*					*
7	*				*	*

3. Определите номера населенных пунктов С и F в таблице.

Номер пункта
		1	2	3	4	5	6	7
	1				*			*
	2			*		*		*
	3		*			*	*	*
	4	*					*
	5		*	*			*
	6			*	*	*
	7	*	*	*

4. Определите номера населенных пунктов Е и G в таблице.

Номер пункта
		1	2	3	4	5	6	7
	1			*			*
	2				*	*	*	*
	3	*						*
	4		*			*		*
	5		*		*		*
	6	*	*			*
	7		*	*	*

5. Определите номера населенных пунктов В и Е в таблице.

	Номер пункта
	1	2	3	4	5	6	7
1						*	*
2			*	*		*
3		*		*
4		*	*		*
5				*			*
6	*	*					*
7	*				*	*

6. Выпишите последовательно, без пробелов и знаков препинания, указанные на схеме буквенные обозначения пунктов с номерами 1 до 7: сначала букву, соответствующую пункту 1, затем букву, соответствующую пункту 2, и т. д.

Номер пункта
1		2	3	4	5	6	7
	1		*			*	*
	2	*		*	*		*	*
	3		*		*	*	*
	4		*	*				*
	5	*		*			*
	6	*	*	*		*
	7		*		*

7. Определите длину дороги из пункта В в пункт Е.

	1	2	3	4	5	6	7
1		45		10
2	45			40		55
3					15	60
4	10	40				20	35
5			15			55
6		55	60	20	55		45
7				35		45

8. Определите длину дороги из пункта Б в пункт Д.

	1	2	3	4	5	6	7
1		40		15
2	40			35		48
3					10	65	11
4	15	35				22	33
5			10			50
6		48	65	22	50		40
7			11	33		40

9. Определите длину дороги из пункта Б в пункт В.

	1	2	3	4	5	6
1		10			8	5
2	10			20	12
3				4
4		20	4		15
5	8	12		15		7
6	5				7

10. Определите длину дороги из пункта Б в пункт Г.

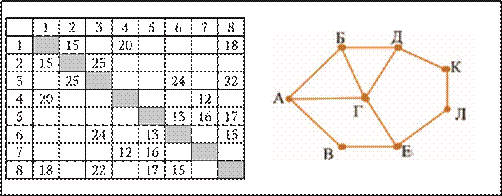
11. Определите длину дороги из пункта А в пункт Г.

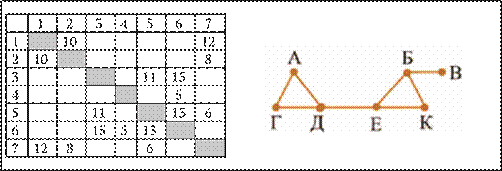
12. Определите длину дороги из пункта Г в пункт Е.

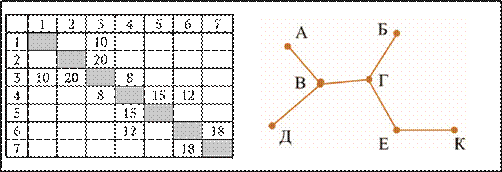
13. (Задание из демонстрационного варианта ЕГЭ 2021 года) Определите длину дороги из пункта Б в пункт В.

Номер пункта
	1	2	3	4	5	6	7
1				9			7
2				5		11
3						12
4	9	5			4	13	15
5				4		10	8
6		11	12	13	10
7	7			15	8

14. Определите, какова сумма протяженностей дорог из пункта Г в пункт Е и из пункта Д в пункт З.

Номер пункта
		1	2	3	4	5	6	7
	1						12	7
	2					10	11	9
	3				5	6	3
	4			5		15
	5		10	6	15
	6	12	11	3
	7	7	9

15. Определите, какова сумма протяженностей дорог из пункта А в пункт D и из пункта A в пункт G.

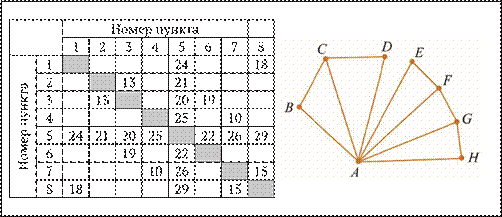
Глава 2 Задания 2

2. 1. Общие вопросы. Теория

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 2 указывается «умение строить таблицы истинности и логические схемы».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

***

Логические переменные – переменные величины, принимающие только два значения – ИСТИНА или ЛОЖЬ (или 0 или 1).

Логические выражения – записи, в которых представлено несколько^{^[4]} логических переменных, соединенных знаками логических операций. Логические операции и их знаки:

Операция	Знак операции	Примеры
Отрицание, инверсия, НЕ А	¬ или −	¬A, A
Дизъюнкция, логическое сложение, А ИЛИ В	∨ или +	A ∨ B, A + B
Конъюнкция, логическое умножение, А И В	∧ или	A ∧ B, А В
Импликация (следование)	→	A → B
Эквивалентность (равносильность)	≡	A ≡ B

Когда в выражении представлено несколько логических операций, то при определении общего значения выражения сначала выполняются все операции НЕ, затем – И, потом – ИЛИ, импликация и самая последняя – эквивалентность. Для нарушения указанного порядка используются скобки. Операции в скобках имеют самый большой приоритет (они выполняются в первую очередь).

Общий результат может иметь значение ИСТИНА (1) или ЛОЖЬ (0). В первом случае говорят, что «выражение истинно», во втором – «выражение ложно».

Введем понятия, которые будем использовать при описании методики выполнения заданий:

• переменная, представленная непосредственно: например, х, у, z и т. п.;

• переменная с отрицанием: ¬у, w;

• элемент логической операции – логические величины, представленные в операциях дизъюнкции, конъюнкции, следования и эквивалентности,

а также напомним правила, по которым определяются результаты логических выражений:

1) логическое выражение с одной или несколькими операциями конъюнкции истинно (имеет результат ИСТИНА, или 1), только когда все его элементы истинны;

2) логическое выражение с одной или несколькими операциями конъюнкции ложно (имеет результат ЛОЖЬ, или 0), когда хотя бы один его элемент ложен;

3) логическое выражение с одной или несколькими операциями дизъюнкции истинно, когда хотя бы один из его элементов является истинным;

4) логическое выражение с одной или несколькими операциями дизъюнкции ложно, когда все его элементы ложны;

5) отрицание истинного элемента является ложным и наоборот;

6) результат импликации (следования) А → В ложен (равен 0) тогда и только тогда, когда A (посылка) истинна, а B (следствие) – ложно;

7) результат эквивалентности (равносильности) А ≡ B истинен (равен 1) тогда и только тогда, когда оба значения А и В одновременно равны 0 или одновременно равны 1.

Таблица истинности логического выражения определяет его значения при всех возможных комбинациях входящих в него переменных.

Количество комбинаций зависит от числа переменных, представленных в выражении:

Число переменных	2	3	4
Количество комбинаций	4	8	16

При любом числе комбинаций в таблицах истинности не может быть двух одинаковых строк.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 2, общий вид которых следующий:

«Миша заполнял таблицу истинности функции F

<приводится логическое выражение>,

но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.

				F
1		1		1
0	1		0	1
	1	1	0	1

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно».

Задания такого типа можно выполнять методом рассуж дений, в сложных случаях – с использованием разработанной программы на языке программирования или с помощью электронной таблицы Microsoft Excel либо подобной программы. В электронной таблице Microsoft Excel имеются логические функции И, ИЛИ и НЕ, возвращающие результат по правилам логических операций конъюнкции, дизъюнкции и отрицания. В ячейках можно записывать формулы со знаками операций сравнения (отношения) «=», «<>», «>», «>=», «<», «<=», результатом которых являются значения ИСТИНА или ЛОЖЬ.

Пример:

	…	E	F	G	H
1
2		=B2=1	=A2<>D2	=C2<=A2	=И(E2;F2;G2)
…

Результат:

	…	E	F	G	H
1
2		ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ
…

2.2. Примеры заданий и методика их выполнения

2.2.1. Пример 1^{^[5]}

Условие

Ниже приведен фрагмент таблицы истинности функции

F = ¬x ∨ y ∨ (¬z ∧ w),

содержащий все наборы аргументов, при которых функция ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

				F
0	0	0	1	0
0	1	0	1	0
0	1	1	1	0

Решение

В логическом выражении используется операция дизъюнкции с тремя элементами:

• ¬x;

• y; • ¬z ∧ w.

Обратим внимание на запись переменных х и у в заданном выражении: х записана со знаком отрицания, а у – «непосредств енно». Представленные значения функции – 0 (ЛОЖЬ).

Результат операции дизъюнкции равен 0, только если все ее элементы ложны (см. правило 3 в разделе 2.1), поэтому исследуем указанные элементы.

Начнем с переменной у. Может ли она быть записана во втором, третьем или четвертом столбце? – Нет, не может, так как в этих столбцах имеются значения 1. Значит, переменная у представлена в первом столбце.

Запишем это в таблицу:

у				F
0	0	0	1	0
0	1	0	1	0
0	1	1	1	0

Исследуем переменную х. Может ли она быть записана во втором или третьем столбце? – Нет, не может, так как в этих столбцах имеются значения 0, которые при отрицании должны «превратиться» в 1. Значит, переменной х соответствует четвертый столбец:

у			х	F
0	0	0	1	0
0	1	0	1	0
0	1	1	1	0

Осталось разобраться с двумя средними столбцами и переменными z и w.

Составим таблицу истинности для выражения ¬z ∧ w:

z	w	¬z	¬z ∧ w
0	0	1	0
0	1	1	1
1	0	0	0
1	1	0	0

Вторая комбинация значений z и w не подходит (результат равен 1).

Сравним остальные три комбинации значений этих переменных (0 и 0, 1 и 0, 1 и 1) с таблицей истинности в условии:

z	w	у			х
0	0	0	0	0	1
1	0	0	1	0	1
1	1	0	1	1	1

Анализ показывает, что второй столбец правой таблицы соответствует переменной z, третий – переменной w.

Итак, ответ: уzwx.

2.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2021 года)

Условие

Миша заполнял таблицу истинности функции

(x ∧ y) ∧ ¬(y ≡ z) ∧ ¬w,

но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

				(x ∨ y) ∧ ¬(y ≡ z) ∧ ¬w
1		1		1
0	1		0	1
	1	1	0	1

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.

Решение

В заданном выражении используется операция конъюнкции с тремя элементами:

• ¬w;

• x ∨ y; • ¬(y ≡ z).

Обратим внимание на запись переменной w со знаком отрицания, а также на то, что в таблице представлены значения функции, равные 1 (ИСТИНА).

Итак.

Результат операции конъюнкции является истинным, если все ее элементы истинны (см. правило 1 в разделе 2.1). Исследуем элементы конъюнкции.

Чтобы элемент ¬w был истинным (1), значение переменной w должно быть равно 0.

Может ли переменная w быть записана в первых трех столбцах таблицы? – Нет, так как в этих столбцах есть значения, равные 1, которые с отрицанием «превратятся» в 0, что даст общий результат, равный 0. Значит, переменная w записана в четвертом столбце. Дополним таблицу:

			w
1		1	0
0	1		0
	1	1	0

Далее, элемент ¬(y ≡ z) будет истинным, если значение у не равно значению z.

Может ли переменная z быть записана в третьем столбце? – С учетом только что сформулированного условия – нет (в этом случае в третьем столбце будут одинаковые значения и с первым столбцом, и со вторым, то есть или со значением х, или с у). Значит, z – в первом или во втором столбце.

Допустим, в первом:

z			w
1		1	0
0	1		0
	1	1	0

Где при этом может быть переменная у? – Только во втором столбце (значения z и у должны быть разными, а для третьего столбца это условие не соблюдалось бы):

z	у	х	w
1		1	0
0	1		0
	1	1	0

Дополним таблицу разными значениями z и у:

z	у	х	w
1	0	1	0
0	1		0
0	1	1	0

Так как, записав в оставшуюся пустой клетку значение 0, мы получим вариант, при котором во втором и третьем столбцах соблюдается условие истинности элемента x ∨ y, то это значит, что допущение о «месте» переменной z возможно.

Ответ: zyxw.

Можно было в ситуации

			w
1		1	0
0	1		0
	1	1	0

попробовать найти место для переменных х и у (есть три их комбинации: 0 и 1; 1 и 0, 1 и 1).

Анализ показывает, что запись этих переменных в первом и втором столбцах и в первом и третьем не подходит (убедитесь в этом!). Значит, для них подходят второй и третий столбцы (как именно – пока не знаем), а переменная z записана в первом столбце:

z			w
1		1	0
0	1		0
	1	1	0

Так как значение у не должно быть равно значению z, то переменная у может быть записана только во втором столбце.

Результат, естественно, тот же.

2.2.3. Пример 3

Условие

Логическая функция F задается выражением (¬x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w.

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.

				F
0		0	1	0
	0		1	0
0	1	1		0

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.

Решение

В логическом выражении используется операция дизъюнкции с тремя элементами:

• ¬x ∧ ¬y;

• y ≡ z;

• ¬w.

Обратим внимание на то, что в таблице представлены значения функции 0 (ЛОЖЬ).

Результат операции дизъюнкции является ложным, если все ее элементы ложны. Вот условия ложности перечисленных элементов:

• x ∨ y;

• y ≠ z;

• w = 1.

«Место» для значений переменной w очевидно:

			w	F
0		0	1	0
	0		1	0
0	1	1	1	0

Где могут быть записаны переменные х и у с учетом результата операции дизъюнкции?

Возможны три варианта:

• в первом и втором столбцах (в любом порядке); • в первом и третьем столбцах (также в любом порядке); • во втором и третьем столбцах (тоже в любом порядке).

В первом случае невозможно получить комбинацию значений 1 и 1.

Во втором – в первой строке будет комбинация значений 0 и 0, невозможная при дизъюнкции.

Третий вариант возможен (переменной z «остается» первый столбец):

z			w	F
0	1	0	1	0
	0	1	1	0
0	1	1	1	0

Осталось распределить переменные х и у по столбцам.

Так как y ≠ z, то переменная у в третьем столбце не может быть представлена. Значит, значения у записаны во втором столбце, а х – в третьем.

Результат: zyxw.

2.2.4. Пример 4

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Миша заполнял таблицу истинности логической функции

F = ¬(y → x) ∨ (z → w) ∨ ¬z,

			F
	0		0
0	1		0
1		0	0

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Решение

Особенность данного задания – использование в логическом выражении операций импликации (следования). Поэтому прежде всего расскажем малоизвестные особенности этой операции:

Операция импликации A → B может быть заменена неравенством А ≤ В, а отрицание импликации (A → B) – неравенством А > В.

Итак.

В заданном логическом выражении используется операция дизъюнкции с тремя элементами и в таблице все значения функции равны 0 (ЛОЖЬ).

Результат дизъюнкции является ложным, если все ее элементы ложны. Ложность трех элементов заданного выражения обеспечивается при:

• y → x;

• ¬(z → w);

• z = 1.

Столбец со значениями переменной z может быть только третьим:

		z		F
	0	1		0
0	1	1		0
1		1	0	0

Обсудим ложность выражения ¬(z → w). Как отмечалось, отрицание такой импликации можно заменить неравенством z > w. Так как все значения z равны 1, то все значения w равны 0. Такие значения могут быть только в четвертом столбце:

		z	w	F
	0	1	0	0
0	1	1	0	0
1		1	0	0

Осталось распределить переменные х и у по двум первым столбцам. Для этого учтем, что импликация y → x может быть заменена условием у ≤ х. Анализ показывает, что для соблюдения этого условия значения х не могут быть представлены в первом столбце.

Значит, искомая последовательность обозначений переменных: ухzw.

2.2.5. Пример 5

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Миша заполнял таблицу истинности логической функции F

¬(y → (x ≡ w)) ∧ (z → x),

				F
	1	1		1
0			0	1
	0	1	0	1

Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.

Решение

Получим комбинации переменных x, y, z, w, при которых результат функции равен 1. Это возможно, когда оба элемента ¬(y → (x ≡ w)) и z → x истинны. В свою очередь, это означает, что импликация y → (x ≡ w) должна давать результат, равный 0.

Импликация ложна лишь тогда, когда посылка истинна, а следствие ложно (правило 6 в разделе 2.1). Значит, у = 1, а x ≠ w.

Учтем значение у = 1 в единственном «подходящем» столбце:

		у		F
	1	1		1
0		1	0	1
	0	1	0	1

Исследуем таблицу на соблюдение условия x ≠ w. Оно соблюдается, только если значения этих переменных записаны в двух первых столбцах (варианты первый столбец и третий столбец, а также второй столбец и третий столбец не подходят). Переменной z «остается» четвертый столбец:

		у	z	F
	1	1		1
0		1	0	1
	0	1	0	1

Учтем в двух первых столбцах условие x ≠ w и заполним пустые клетки в них:

		у	z	F
0	1	1		1
0	1	1	0	1
1	0	1	0	1

Осталось распределить столбцы между переменными х и w. Для этого надо заполнить пустую клетку. Тут надо вспомнить (см. раздел 2.1), что в таблице истинности не может быть двух одинаковых строк, то есть в пустой клетке должна быть записана единица:

		у	z	F
0	1	1	1	1
0	1	1	0	1
1	0	1	0	1

Вспомнив для второй импликации особенности, отмеченные при выполнении предыдущего задания, можно записать z ≤ x. Это условие соблюдается, только если значения х записаны во втором столбце. Ответ: wхуz.

Заметим следующее. Конечно, рассуждения, сделанные при выполнении задания, не простые и несколько «длительные». Вместо них для решения можно применить следующий метод – получить комбинации переменных w, x, y, z, при которых заданное логическое выражение является истинным, и сравнить их с таблицей из условия. Получить же нужные комбинации можно, перебрав все возможные комбинации и отобрав из них те, для которых значение истинно. Последнюю задачу удобно решать, разработав программу на одном из языков программирования или с помощью электронной таблицы.

Общая схема программ, решающих указанную задачу:

цикл для значений х 0 и 1 цикл для значений у 0 и 1 цикл для значений z 0 и 1 цикл для значений w 0 и 1 если значение функции равно требуемому (Истина) то вывод с новой строки значений x, y, z, w все конец цикла конец цикла конец цикла конец цикла

В данном случае условие для отбора нужных комбинаций:

если (y = 1) и (x <> w) и (z <= x) то вывод нс, x, y, z, w все

Обратим внимание на то, что в нем учтены:

• ложность импликации ¬(y → (x ≡ w)), что возможно только при у = 1 и x ≠ w;

• истинность импликации z → x, что возможно при z ≤ x.

Результаты выполнения программы будут следующими:

0101

1100

1110

Сопоставим таблицу с полученными комбинациями с таблицей в условии:

х	у	z	w
0	1	0	1		1	1
1	1	0	0	0			0
1	1	1	0		0	1	0

При анализе следует иметь в виду, что в обеих таблицах строки, соответствующие друг другу, и столбцы, соответствующие друг другу, могут быть сформированы в любом порядке и не совпадать. В то же время составы (количество единиц и количество нулей) столбцов в полной таблице истинности и в соответствующих столбцах неполной таблицы из условия должны быть одними и теми же. В правой таблице не может быть двух одинаковых строк и двух одинаковых столбцов.

«Место» для переменной у, равной 1, в правой таблице – третий столбец (в остальных столбцах есть нули). Учтем это:

х	у	z	w			у
0	1	0	1		1	1
1	1	0	0	0		1	0
1	1	1	0		0	1	0

В последнем столбце правой таблицы в пустой клетке может быть только 1 (в левой таблице нет столбцов с одними нулями:

х	у	z	w			у
0	1	0	1		1	1	1
1	1	0	0	0		1	0
1	1	1	0		0	1	0

После этого можно заполнить пустые клетки первого столбца (в левой таблице нет строк из одних нулей):

х	у	z	w			у
0	1	0	1	0	1	1	1
1	1	0	0	0		1	0
1	1	1	0		0	1	0

х	у	z	w			у
0	1	0	1	0	1	1	1
1	1	0	0	0		1	0
1	1	1	0	1	0	1	0

(В левой таблице нет столбцов с одними нулями.)

Записав в оставшуюся клетку 1 (почему 1 – установите самостоятельно), получим:

х	у	z	w			у
0	1	0	1	0	1	1	1
1	1	0	0	0	1	1	0
1	1	1	0	1	0	1	0

Далее. В левой таблице оригинальный столбец – первый, для переменной х (только в нем две единицы). В правой таблице такой столбец – второй:

х	у	z	w		х	у
0	1	0	1	0	1	1	1
1	1	0	0	0	1	1	0
1	1	1	0	1	0	1	0

Так как x ≠ w, то значения переменной w записаны в первом столбце, то есть ответ: wхуz.

При использовании электронной таблицы оформим лист следующим образом^{^[7]}:

	A	B	C	D	E	F	G	H
1	x	y	z	w	y=1	x<>w	z<=x	все
2	0	0	0	0	=B2 = 1	=A2 <> D2	=C2 <= A2	=И(E2; F2; G2)
3	0	0	0	1
4	0	0	1	0
	A	B	C	D	E	F	G	H
5	0	0	1	1
6	0	1	0	0	ИСТИНА	1	0	ИСТИНА
7	0	1	0	1	ИСТИНА	1	0	ИСТИНА
8	0	1	1	0	ИСТИНА	1	1	ИСТИНА
9	0	1	1	1	ИСТИНА	1	1	ИСТИНА
10	1	0	0	0	ЛОЖЬ	0	0	ЛОЖЬ
11	1	0	0	1	ЛОЖЬ	0	0	ЛОЖЬ
12	1	0	1	0	ЛОЖЬ	0	1	ИСТИНА
13	1	0	1	1	ЛОЖЬ	0	1	ИСТИНА
14	1	1	0	0	ЛОЖЬ	1	0	ИСТИНА
15	1	1	0	1	ЛОЖЬ	1	0	ИСТИНА
16	1	1	1	0	ЛОЖЬ	1	1	ИСТИНА
17	1	1	1	1	ЛОЖЬ	1	1	ИСТИНА

Результат расчетов по формулам будет таким:

	A	B	C	D	E	F	G	H
1	x	y	z	w	y=1	x<>w	z<=x	все
2	0	0	0	0	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ
3	0	0	0	1	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ
4	0	0	1	0	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ
5	0	0	1	1	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ЛОЖЬ
6	0	1	0	0	ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ
7	0	1	0	1	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
8	0	1	1	0	ИСТИНА	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ
…	…	…	…	…	…	…	…	…
13	1	0	1	1	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ
14	1	1	0	0	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
15	1	1	0	1	ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ
16	1	1	1	0	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
17	1	1	1	1	ИСТИНА	ЛОЖЬ	ИСТИНА	ЛОЖЬ

(Обратите внимание на совместное использование значений 0 и 1 и ЛОЖЬ и ИСТИНА.)

Нас интересуют комбинации переменных, при которых значение выражения равно 1. Чтобы получить их, отсортируем строки в порядке убывания значений в последнем столбце:

	А	B	C	D	E	F	G	H
1	х	y	z	w	y=1	x<>w	z<=x	все
2	0	1	0	1	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
3	1	1	0	0	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
4	1	1	1	0	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
5	0	0	0	0	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ
6	…	…	…	…	…	…	…	…

Выпишем найденные комбинации:

х	у	z	w
0	1	0	1
1	1	0	0
1	1	1	0

После этого также можно провести сопоставление этой таблицы с таблицей в условии и получить искомый результат, как это делалось при разработке программы.

Оформления листа и все расчеты значительно упрощаются, если учесть, что во всех комбинациях значение у равно 1. Поэтому можно рассматривать комбинации значений только трех переменных:

х	z	w	x<>w	z<=x	И
0	0	0	ЛОЖЬ	ИСТИНА	ЛОЖЬ
0	0	1	ИСТИНА	ИСТИНА	ИСТИНА
0	1	0	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ
0	1	1	ИСТИНА	ЛОЖЬ	ЛОЖЬ
1	0	0	ИСТИНА	ИСТИНА	ИСТИНА
1	0	1	ЛОЖЬ	ИСТИНА	ЛОЖЬ
1	1	0	ИСТИНА	ИСТИНА	ИСТИНА
1	1	1	ЛОЖЬ	ИСТИНА	ЛОЖЬ

После сортировки можно получить три комбинации:

х	z	w
0	0	1
1	0	0
1	1	0

дополнив которые столбцом для переменной у, можно провести сопоставление двух таблиц:

х	у	z	w
0	1	0	1		1	1
1	1	0	0	0			0
1	1	1	0		0	1	0

В заключение заметим, что предложенную методику (с разработкой программы или использованием электронной таблицы) можно использовать и при выполнении заданий, рассмотренных в пп. 2.2.2–2.2.4 (см. раздел 2.3).

2.2.6. Пример 6

Условие

Логическая функция F задается выражением

(¬x ∨ y ∨ z) ≡ (¬y ∨ z ∨ w).

На рисунке приведен частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

			F
1	1	1	1
0	0		1
1		1	1

Решение

Здесь выполнение задания метом рассуждений, как это делалось в пп. 2.2.2, 2.2.3 и 2.2.4, затруднено. Можно получить «полную» таблицу с комбинациями переменных, для которых значение выражения равно 1, и сопоставить ее с таблицей из условия.

При использовании электронной таблицы лист оформляется следующим образом:

	A	B	C	D	E	F	G	H	I
1	x	y	z	w	не х	или	не у	и	экв
2	0	0	0	0	=НЕ(A2)	=ИЛИ(E2; B2; C2)	=НЕ(B2)	=И(G2; C2; D2)	=F2 = H2
3	0	0	0	1	…	…	…	…	…

Результат расчетов и последующей сортировки будет таким:

	А	B	C	D	E	F	G	H	I
1	х	y	z	w	не х	или	не у	и	экв
2	0	0	1	1	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
3	1	0	0	0	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА
4	1	0	0	1	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА
5	1	0	1	1	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
6	0	0	0	0	ИСТИНА	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ
7	…	…	…	…	…	…	…	…	…

Выпишем найденные комбинации:

x	y	z	w
0	0	1	1
1	0	0	0
1	0	0	1
1	0	1	1

и сопоставим с ними таблицу из условия, дополнив ее четвертой строкой:

х	у	z	w
0	0	1	1	1	1	1
1	0	0	0	0	0
1	0	0	1	1		1
1	0	1	1

Последовательное заполнение свободных клеток правой таблицы (на каждом этапе новые значения оттенены; обоснование установите самостоятельно):

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

Осталось распределить переменные х и w – их состав один и тот же (три единицы и один ноль).

В данном случае, в отличие от рассмотренных ранее заданий, сравнение строк с этими переменными затруднено. Придется пробовать варианты.

Рассмотрим два варианта распределения:

х	у	z	w	у	х	z	w
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

х	у	z	w	у	w	z	x
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

Для каждого из них выпишем значения в правой таблице в порядке переменных x, y, z, w.

х	у	z	w	у	х	z	w
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

1011 0001 1001

1001 2)

х	у	z	w	у	w	z	x
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

1011 1000 1001

0011

В первом случае, во-первых, получились две одинаковые последовательности и, во-вторых, получилась последовательность (0001), которой нет в левой таблице.

Второй вариант подходит.

Итак, ответ: ywzx.

Можно использовать все ту же электронную таблицу.

Подставим в первые четыре строки значения переменных в двух только что рассмотренных вариантах, получим:

	А	B	C	D	E	F	G	H	I
1	x	y	z	w	не х	или	не у	и	экв
2	1	0	1	1	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
3	0	0	0	1	ИСТИНА	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ
4	1	0	0	1	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА
5	1	0	1	0	ЛОЖЬ	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ
	А	B	C	D	E	F	G	H	I
1	х	y	z	w	не х	или	не у	и	экв
2	1	0	1	1	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
3	1	0	0	0	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА
4	1	0	0	1	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА
5	0	0	1	1	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА

Подходит только второй вариант, столбцы из которого обеспечивают требуемое истинное значение. Значит, для переменной х столбец имеет значения 1, 1, 1, 0. В правой таблице такой столбец – последний. Результат – тот же (ywzx).

Читатели, хорошо знающие законы логики, могли на их основе определить, что значение переменной у равно 0 во всех случаях. Это позволит упростить отбор нужных комбинаций остальных переменных с помощью электронной таблицы. Для этого достаточно рассмотреть

8 вариантов:

	A	B	C	D	E	F	G
1	x	z	w	не х	или	и	экв
2	0	0	0	=НЕ(A2)	=ИЛИ(D2; B2)	=И(B2; C2)	=E2 = F2
3	0	0	1		ИСТИНА	0	0
4	0	1	0		ИСТИНА	0	1
5	0	1	1
6	1	0	0		ИСТИНА	0	1
7	1	0	1		ИСТИНА	1	0
8	1	1	0		ИСТИНА	1	0
9	1	1	1		ИСТИНА	1	1

Сортировка в порядке убывания определит нужные варианты:

	A	B	C	D	E	F	G
1	x	z	w	не х	или	и	экв
2	0	1	1	ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА
3	1	0	0	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА
4	1	0	1	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА
5	1	1	1	ЛОЖЬ	ИСТИНА	ИСТИНА	ИСТИНА
6	0	0	0	ИСТИНА	ИСТИНА	ЛОЖЬ	ЛОЖЬ
7	1	0	1		ИСТИНА	1	0

Сопоставим с ними таблицу из условия, дополнив ее четвертой строкой и учтя известные значения переменной у:

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0			0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

Дальнейшие действия по определению «мест» х и w дадут, естественно, тот же результат.

В программе для отбора нужных комбинаций значений переменных условие будет таким:

(не(x = 1) или (y = 1) или (z = 1)) = (не(y = 1) и (z = 1) и (w = 1))

2.3. Выполнение заданий с использованием электронной таблицы или программы

2.3.1. Задание примера из п. 2.2.2 Напомним таблицу из условия:

				(x ∨ y) /\ ¬(y ≡ z) ∧ ¬w
1		1		1
0	1		0	1
	1	1	0	1

а также что:

• известно, что w = 0 и значения записаны в последнем столбце.

Фрагмент листа электронной таблицы с «базовыми» для копирования формулами в строке 2 оформляется так:

	A	B	C	D	E	F	G
1	х	у	z	х или у	у = z	отрицание	все
2	0	0	0	=ИЛИ(A2; B2)	=B2 = C2	=НЕ(E2)	=И(D2; F2)
3	0	0	1

После заполнения формулами всех строк и сортировки данных по значениям в столбце G в порядке убывания можно получить таблицу истинности для трех переменных:

х	у	z
0	1	0
1	0	1
1	1	0

Сопоставим ее с приведенным в задании фрагментом таблицы истинности (учтя также переменную w):

х	у	z	w				w
0	1	0	0	1		1	0
1	0	1	0	0	1		0
1	1	0	0		1	1	0

Могут ли в пустых клетках второго и третьего столбцов правой таблицы быть записаны единицы? – Нет, не могут, так как в левой таблице нет столбцов с тремя единицами. Единица не может быть представлена и в пустой клетке первого столбца (в левой таблице нет строки с тремя единицами). Запишем в пустые клетки 0:

х	у	z	w				w
0	1	0	0	1	0	1	0
1	0	1	0	0	1	0	0
1	1	0	0	0	1	1	0

После этого в левой таблице ищем оригинальные по составу столбцы или строки.

Анализ показывает, что в левой таблице оригинальный столбец – третий, для переменной z (только в нем одна единица и два нуля).

Есть ли аналогичный по составу столбец в правой таблице? – Есть (первый). Значит, в этом столбце записана переменная z:

х	у	z	w	z			w
0	1	0	0	1	0	1	0
1	0	1	0	0	1	0	0
1	1	0	0	0	1	1	0

Как во втором и третьем столбцах распределены «оставшиеся» переменные х и у? Для ответа надо вспомнить, что значения переменных у и z не должны быть во всех случаях одними и теми же. Значит, переменная у может быть записана только во втором столбце. Итак, ответ: zyxw.

Можно было при сопоставлении таблиц

х	у	z	w				w
0	1	0	0	1	0	1	0
1	0	1	0	0	1	0	0
1	1	0	0	0	1	1	0

рассуждать и так.

В левой таблице оригинальная строка – первая, для переменной (только в ней одна единица).

Есть ли аналогичная по составу строка в правой таблице? – Есть (вторая). В ней единственная единица записана во втором столбце, то есть он соответствует переменной у:

х	у	z	w		у		w
0	1	0	0	1	0	1	0
1	0	1	0	0	1	0	0
1	1	0	0	0	1	1	0

Ищем «место» для оставшихся переменных х и z.

Так как значение z не должно быть равно значению у, то это значит, что переменная z представлена в первом столбце. Переменной х «остается» третий столбец (для контроля можно убедиться, что при этом для переменных у и х требования по их значениям соблюдаются). Общий результат – тот же: zyxw.

Программа, с помощью которой можно получить требуемые комбинации переменных, аналогична приведенной в п. 2.2.5. Отличие – в условии для отбора комбинаций:

если (x = 1 или y = 1) и не(y = z) и w = 0 то вывод нс, x, y, z, w все

Примечание. В программах на языке Python для логическ их операций дизъюнкции, конъюнкции и отрицания можно к величинам логического типа применить операторы or, and и not.

(x or y) and not(y == z) and not(w)

В дальнейшем мы также будем приводить только фрагмент с условием для отбора.

2.3.2. Задание примера из п. 2.2.3 Напомним таблицу из условия:

				F
0		0	1	0
	0		1	0
0	1	1		0

а также что:

• логическое выражение имеет вид: (¬x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w; • известно, что w = 1 и значения записаны в последнем столбце.

Фрагмент листа электронной таблицы с «базовыми» для копирования формулами в строке 2 оформляется так:

	A	B	C	D	E	F	G	H
1	х	у	z	не х	не у	и	у = z	все
2	0	0	0	=НЕ(A2)	=НЕ(В2)	=И(D2; E2)	=B2=C2	=ИЛИ(F2; G2)
3	0	0	1

После заполнения формулами всех строк и сортировки данных по значениям в столбце Н в порядке возрастания можно получить таблицу истинности для трех переменных:

х	у	z
0	1	0
1	0	1
1	1	0

которую затем сопоставить с приведенным в задании фрагментом таблицы истинности (с учетом известного столбца с переменной w):

х	у	z	w				w
0	1	0	1	0		0	1
1	0	1	1		0		1
1	1	0	1	0	1	1	1

В пустых клетках правой таблицы не могут быть записаны нули (убедитесь в этом!):

х	у	z	w				w
0	1	0	1	0	1	0	1
1	0	1	1	1	0	1	1
1	1	0	1	0	1	1	1

Требования по трем комбинациям переменных х и у соблюдаются только во втором и третьем столбцах, то есть переменной отведен первый z столбец:

х	у	z	w	z			w
0	1	0	1	0	1	0	1
1	0	1	1	1	0	1	1
1	1	0	1	0	1	1	1

Осталось распределить переменные по двум столбцам.

Так как значение y не должно быть равно значению z, то значение y записано во втором столбце.

Итак, ответ: zyxw.

Можно было при сопоставлении таблиц

х	у	z	w				w
0	1	0	1	0	1	0	1
1	0	1	1	1	0	1	1
1	1	0	1	0	1	1	1

рассуждать и так.

Значение y не должно быть равно значению z. Этому условию соответствуют первый и второй столбцы, то есть переменной х «остается» третий столбец:

х	у	z	w			х	w
0	1	0	1	0	1	0	1
1	0	1	1	1	0	1	1
1	1	0	1	0	1	1	1

Далее. Остались нераспределенными переменные у и z. Требования по трем комбинациям переменных х и у соблюдаются только во втором и третьем столбцах, то есть переменной у отведен второй столбец. Результат – тот же: zyxw.

В программе для отбора комбинаций переменных в данном случае следует учесть, что отбирать нужно комбинации, при которых значение выражения равно 0 (следует использовать общее отрицание):

если не(x = 0 и y = 0 или y = z или w = 0) то вывод нс, x, y, z, w все

Можно также, применив закон де Моргана, использовать следующее условие:

(x = 1 или y = 1) и y <> z и w = 1

2.3.3. Задание примера п. 2.2.4 Напомним таблицу из условия:

			F
	0		0
0	1		0
1		0	0

а также что:

• логическое выражение имеет вид: ¬(y → x) ∨ (z → w) ∨ ¬z; • известно, что z = 1 и значения записаны в третьем столбце.

Учтя это, а также особенности импликации, отмеченные в разделе 2.1, выражение без учета переменной z можно представить в виде:

(y > x) ∨ (1 ≤ w).

Соответствующее оформление листа электронной таблицы:

A	B	C	D	E	F	G
1	х	у	w	y > x	1 <= w	или
2	0	0	0	=B2 > A2	=1 <= C2	=ИЛИ(D2; E2)
3

Нужные для дальнейшего анализа значения:

х	у	w
0	0	0
1	0	0
1	1	0

Сопоставим полученную таблицу (с учетом столбца с переменной z) с приведенным в задании фрагментом таблицы:

х	у	z	w			z
0	0	1	0		0	1
1	0	1	0	0	1	1
1	1	1	0	1		1	0

«Места» записи переменной w в правой таблице очевидны. Три нуля (значения w) могут быть записаны только в четвертом столбце:

х	у	z	w			z	w
0	0	1	0		0	1	0
1	0	1	0	0	1	1	0
1	1	1	0	1		1	0

Далее в левой таблице обратим внимание на последнюю строку (с тремя единицами). В правой таблице такой состав может иметь только последняя строка. Запишем в ней 1:

х	у	z	w			z	w
0	0	1	0		0	1	0
1	0	1	0	0	1	1	0
1	1	1	0	1	1	1	0

В результате в правой таблице сформирован столбец со значениями 0, 1, 1, который в левой таблице относится к переменной х.

Оставшейся переменной у соответствует первый столбец, то есть искомая в задании последовательность имеет вид ухzw.

Ответ: ухzw.

В программе также следует учесть, что отбирать нужно комбинации, при которых значение выражения равно 0:

если не(не(y <= x) или (z <= w) или не(z = 1)) то вывод нс, x, y, z, w все

или

если (y <= x) и (z > w) и (z = 1) то вывод нс, x, y, z, w все

2.4. Полезные факты и рекомендации по выполнению задания

• Если в заданном фрагменте таблицы истинности логического выражения с одной или несколькими операциями конъюнкции все значения равны 1, то все элементы выражения истинны.

• Если в заданном фрагменте таблицы истинности логическ ого выражения с одной или несколькими операциями дизъюнкции все значения равны 0, то все элементы выражения ложны.

• Если значение логического выражения с операциями конъюнкции равно 1 (ИСТИНА), то переменная, представленная непосредственно, во всех строках таблицы истинности имеет значение 1, а переменная с отрицанием – значение 0.

• Если значение логического выражения с операциями дизъюнкции равно 0 (ЛОЖЬ), то переменная, представленная непосредственно, во всех строках таблицы истинности имеет значение 0, а переменная с отрицанием – значение 1.

• Если в логическом выражении с операциями дизъюнкции одним из элементов является операция импликации и значение выражения равно 0 (ЛОЖЬ), то следует учесть, что результат операции импликации ложен лишь тогда, когда в ней посылка истинна, а следствие ложно.

• Для элемента a ∨ b возможные варианты сочетания значений переменных a и b:

а	b
0	0
0	1
1	1

• Для элемента а → b возможные варианты сочетания значений переменных a и b:

а	b
0	0
0	1

• Для элемента ¬(а → b) возможные варианты сочетания значений переменных a и b:

а	b
1	0

• Возможны два метода выполнения задания:

1) на основе рассуждений;

2) на основе сравнения неполной таблицы из условия с «полной» таблицей со всеми комбинациями переменных, при которых обеспечивается требуемое значение логического выражения (1 или 0).

• В первом случае анализ следует начинать с переменных, представленных в заданном выражении «непосредственно» или с отрицанием. После нахождения их «места» в таблице нужно учитывать связи значений переменных, результаты логических операций и т. п.

• В втором случае получить «полную» таблицу со всеми комбинациями переменных можно, разработав программу или используя электронную таблицу.

• При анализе следует иметь в виду, что в обеих таблицах строки, соответствующие друг другу, и столбцы, соответствующие друг другу, могут быть сформированы в любом порядке и не совпадать. В то же время составы (количество единиц и количество нулей) столбцов в полной таб лице истинности и в соответствующих столбцах неполной таблицы из условия должны быть одними и теми же. В правой таблице не может быть двух одинаковых строк и двух одинаковых столбцов.

• При сопоставлении фрагментов таблиц истинности надо обращать внимание на:

§ отсутствие (или наличие) строк/столбцов со всеми нулями или всеми единицами;

§ оригинальные по составу значений столбцы/строки в полной таблице;

§ одинаковые по составу значений столбцы в обеих таб лицах.

2.5. Задания для самостоятельного выполнения

1. Логическая функция F задается выражением (x ∨ ¬y) ∧ ¬(w ≡ z) ∧ w.

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности этой функции:

				F
1		0	0	1
1	0	0	1	1
1	0			1

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

2. Логическая функция F задается выражением

(x ∧ ¬y) ∨ (y ≡ z) ∨ w.

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности этой функции:

				F
			1	0
1	0	0	0	0
1	1	0		0

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.

3. Логическая функция F задается выражением (x ∨ y) → (z ≡ x).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности этой функции:

		F
0	0	0
0		0

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.

4. Логическая функция F задается выражением (x ≡ y) ∨ ((y ∨ z) → x).

Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности этой функции:

		F
1	1	0
	1	0

Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.

5. Логическая функция F задается выражением (x ∨ y) ¬(y ≡ z) ∧ ¬w.

Дан частично заполненный фрагмент таблицы истинности этой функции, содержащий неповторяющиеся строки.

				F
1				1
0	0	1	0	1
	1	0	0	1

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

6. (Задание из демонстрационного варианта ЕГЭ 2024 года) Миша заполнял таблицу истинности логической функции

F = (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w,

но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответст вует каждая из переменных w, x, y, z.

				F
		0	0	0
1	0		0	0
1	0	1		0

Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Глава 3 Задания 3

3.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 3 указывается «знание о технологии хранения, поиска и сортировки информации в реляционных базах данных».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

Задание выполняется с использованием прилагаемого файла^{^[8]}.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 3, общий вид которых следующий:

В файле приведен фрагмент базы данных «Продукты» о поставках товаров в магазины районов города. База данных состоит из трех таблиц. Таблица «Движение товаров» содержит записи о поставках товаров в магазины в течение первой декады …, а также информацию о проданных товарах. Поле Тип операции содержит значение Поступление или Продажа, а в соответствующее поле Количество упаковок занесена информация о том, сколько упаковок товара поступило в магазин или было продано в течение дня. Заголовок таблицы имеет следующий вид:

Таблица «Товар» содержит информацию об основных характеристиках каждого товара. Заголовок таблицы имеет следующий вид:

Таблица «Магазин» содержит информацию о местонахождении магазинов. Заголовок таблицы имеет следующий вид:

На рисунке приведена схема указанной базы данных.

После этого указывается, что нужно определить.

Дополнение автора:

• Прилагаемый к заданию файл представляет собой файл электронной таблицы (предлагаются три типа файла: .ods, xls и .xlsx).

• В файле имеются три листа, имена которых совпадают с именами таблиц в условии:

Названия полей приведены в первой строке каждого листа.

Для выполнения заданий необходимо уметь использовать фильтры (один или несколько) для отбора значений разного типа в столбцах листа электронной таблицы, а также проводить сортировку данных по значениям в некотором столбце с автоматическим расширением выделенного диапазона ячеек. Понадобится использование функции СУММПРОИЗВ (см. пп. 3.2.3, 3.2.5, 3.2.6). С ее особенностями ознакомьтесь самостоятельно.

3.2. Примеры заданий и методика их выполнения

3.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Используя информацию из приведенной базы данных^{^[9]}, определите общий вес (в кг) крахмала картофельного, поступившего в магазины Заречного района за период с 1 по 8 июня включительно. В ответе запишите только число.

Решение

Для нахождения искомого значения нужно знать количество упаковок крахмала картофельного, поступивших в магазины Заречного района, и вес одной упаковки этого товара в килограммах.

Вес одной упаковки записан в поле Количество в упаковке в таблице Товар.

Количество упаковок того или иного товара, поступившего в тот или иной магазин, указано в таблице Движение товаров. Чтобы узнать нужное в данном случае количество, необходимо знать артикул товара «Крахмал картофельный» и какие магазины находятся в Заречном районе (их ID). Информация об артикулах записана в таблице Товар, а ID магазинов того или иного района – в таблице Магазины.

Итак, сначала^{^[10]} надо узнать артикул товара (а заодно и вес одной упаковки) и перечень магазинов Заречного района.

1. Для отбора магазинов следует:

• активировать лист «Магазин»;

• включить фильтр по столбцу «Район»;

• в окне для выбора параметров фильтра оставить «галочку» только на Заречный:

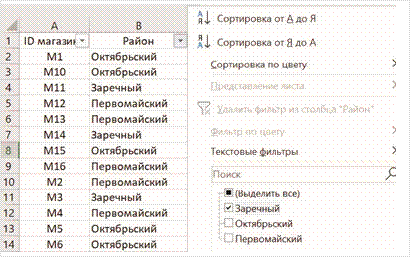
После применения фильтра будет показана информация:

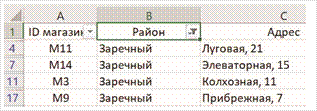
Надо выписать ID всех магазинов Заречного района (М11, М14, М3, М9).

Примечание. ID всех магазинов Заречного района в данном случае можно также определить, отсортировав данные по значению в столбце В («Район») в порядке возрастания – магазины Заречного района будут представлены в первых строках листа.

2. Для определения артикула товара «Крахмал картофельный» и веса одной его упаковки:

• активировать лист «Товар»;

• включить фильтр по столбцу «Наименование»;

• в окне для выбора параметров фильтра оставить «галочку» только на Крахмал картофельный:

Надо выписать (или запомнить) значения 42 (артикул) и 0,5 кг (вес одной упаковки).

Примечание. В данном случае есть единственный поставщик этого товара. Если бы их было несколько и было указано, что расчеты надо проводить для конкретного поставщика, то понадобилось бы использование фильтра по столбцу «Поставщик» («Производитель»).

3. Для нахождения количества упаковок, поступивших в магазины Заречного района:

• активировать лист «Движение товаров»;

• включить фильтры:

§ по столбцу «Артикул» (со значением 42);

§ по столбцу «ID магазина» (со значениями М11, М14, М3, М9); § по столбцу «Тип операции» (со значением Поступление).

Фильтр по столбцу «Дата» в данном случае включать не нужно, так как во всех отобранных значениях даты попадают в интервал, указанный в условии (с 1 по 8 июня включительно):

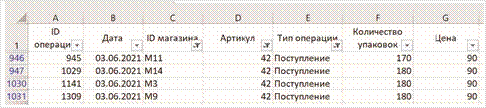
В результате будет отобрана информация о количестве упаковок крахмала картофельного, поступивших в тот или иной магазин Заречного района за период с 1 по 8 июня включительно.

Искомое значение общего веса всех упаковок равно общему числу упаковок, умноженному на вес одной упаковки (0,5 кг).

Для нахождения общего числа упаковок следует, установив указатель активной ячейке на свободную ячейку столбца F, щелкнуть на инструменте СУММА () – в ячейку будет введена формула с функцией ПРОМЕЖУТОЧНЫЕ.ИТОГИ, которая вернет результат, равный 710.

Это значит, что искомый результат равен 710 × 0,5 = 355 кг.

Ответ: 355 (без единицы измерения!).

Внимание! Общее число упаковок в столбце F определять по формуле =СУММ(F2:F5), вводимой вручную, нельзя. Причина в том, что поскольку данные отфильтрованы, часть строк скрыта, в функции СУММ будет использован весь диапазон ячеек, то есть она просуммирует не только видимые ячейки, но и скрытые.

Можно также для нахождения общего числа упаковок использовать так называемую «строку состояния» (самая нижняя полоса окна программы). Если выделить ячейки столбца «Количество упаковок, шт.», то в строке состояния можно прочитать: Сумма: 710^{^[11]}.

3.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2022 года)

(Файл к заданию – тот же, что и к предыдущему заданию^{^[12]}.)

Условие

Используя информацию из приведенной базы данных, определите, на сколько увеличилось количество упаковок яиц диетических, имеющихся в наличии в магазинах Заречного района, за период с 1 по 10 июня включительно.

В ответе запишите только число.

Решение

Чтобы определить то, что требуется в условии, надо знать общее количество упаковок этого товара, поступивших в магазины Заречного района в указанный период, и общее количество упаковок, проданных в них (искомое значение равно разности этих количеств). Эти количества представлены в таблице Движение товаров.

Значит, как и при выполнении задания в предыдущем пункте, надо предварительно определить:

• какие магазины находятся в Заречном районе (их ID); информация записана в таблице Магазины;

• артикул товара «Яйцо диетическое» (информация записана в таблице Товар).

Из условия надо выписать (или запомнить) период, за который следует провести расчеты.

В данном случае магазины Заречного района – те же.

Для определения артикула нужного товара надо на листе Товар отсортировать данные по значениям в столбце «Наименование товара», в данном случае – в порядке убывания (Сор тировка от Я до А). Соответствующий артикул – 15.

После этого в «основной» таблице на листе «Движение товаров»:

• в столбце «Артикул» включить фильтр для значения 15;

• в столбце «ID магазина» включить фильтр для значений М11, М14, М3, М9.

После применения всех фильтров будут отобраны 16 записей. Их надо отсортировать по значениям в столбце «Тип операции»:

Осталось определить две суммы в столбце Е: для поступивших упаковок и для проданных. Это можно сделать разными способами.

Проще всего использовать «строку состояния». Если выделить ячейки столбца «Количество упаковок, шт.» в тех строках, где тип операции – «Поступление», то в строке состояния можно прочитать: Сумма: 1420.

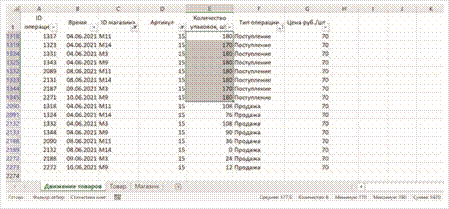
Аналогично для ячеек в строках, где операция – «Поступление», в строке состояния будет указана сумма 454.

Разность двух сумм составляет: 1420 – 454 = 966.

Ответ: 966.

Можно также скопировать отсортированные данные из столбца «Количество упаковок, шт.» на новый лист:

после чего в ячейку А9 ввести формулу с помощью инструмента СУММА ( ), которую затем распространить (скопировать) на ячейку В9, а в ячейке С9 рассчитать разность двух сумм.

3.2.3. Пример 3

Условие

Используя информацию из приведенной базы данных, определите, сколько рублей потребовалось магазинам Первомайского района для закупки яиц диетических за период с 1 по 10 июня включительно.

В ответе запишите только число.

Решение

Для нахождения искомой суммы надо знать, сколько упаковок указанного товара поступило в магазины Первомайского района в указанный период и стоимость одной упаковки. Эта информация указана в таблице «Движение товаров».

Предварительно следует определить ID магазинов Первомайского района и артикул товара. Эти значения определяются аналогично тому, как это делалось при выполнении предыдущих заданий:

• ID магазинов: M2, M4, M7, М8, М12, М13 и M16;

• артикул: 15.

После этого на листе применить фильтр по указанным значениям, а также по значению «Поступление» в столбце «Тип операции». Результат будет таким:

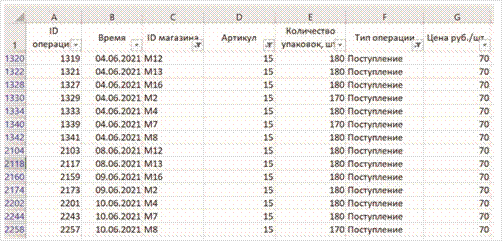
Для нахождения искомой суммы денег надо общее число поступивших упаковок умножить на стоимость (цену) одной упаковки.

Как и в предыдущем примере, нужно скопировать отобранные данные из столбцов Е, F и G на новый лист:

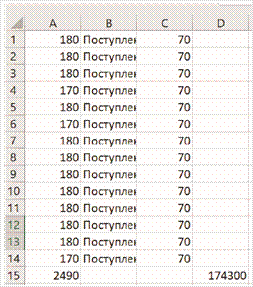
Так как товар закупался по одной и то же цене, то;

• в ячейке А15 определяем общее число упаковок с помощью инструмента СУММА ();

• в ячейке D15 – искомую сумму денег по формуле: =А15 * С14.

Ответ: 174 300.

Внимание! Если бы товар закупался по разным ценам (от разных поставщиков), то тогда искомое значение нужно было бы определять с помощью функции СУММПРОИЗВ по формуле:

=СУММПРОИЗВ(A1:A14; C1:C14).

3.2.4. Пример 4

Условие

Используя информацию из приведенной базы данных, определите, сколько рублей выручили магазины Заречного района от продажи соды пищевой за период с 1 по 10 июня включительно. В ответе запишите только число.

Комментарий к выполнению

Задание выполняется аналогично рассмотренному в предыдущем пункте, с той разницей, что нужно учесть упаковки указанного товара, проданные в указанный период.

Выполните задание самостоятельно.

3.2.5. Пример 5

Условие

Используя информацию из приведенной базы данных, определите, сколько рублей выручили магазины Октябрьского района от продажи риса (всех видов) за период с 1 по 10 июня включительно.

В ответе запишите целое число – найденную общую стоимость в рублях.

Решение

Отличие данного задания от предыдущего в том, что в общей стоимости надо учесть не один вид товара, а несколько.

На листе «Товар» можно найти три вида риса. Их артикулы 21, 22 и 23.

Внимание! Так как наименования товаров – видов риса такие: «Рис круглозерный», «Рис длиннозерный» и «Бурый рис», то при сортировке наименований и в списке наименований для выбора значений в фильтре эти наименования будут представлены не рядом, и можно не учесть некоторые виды товара. Чтобы отобрать все виды риса, следует в окне фильтра использовать окно поиска:

ID магазинов Октябрьского района: M1, M5, M6, М10 и M15.

Применив на листе «Движение товаров» фильтры для перечисленных артикулов и ID магазинов, а также для значения «Продажа» в столбце «Тип операции», получим:

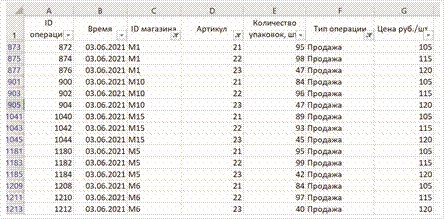
Осталось определить общую стоимость продуктов. Для этого нужно скопировать отобранные данные из столбцов Е, F и G на новый лист. Так как цены разных видов риса разные, то для определения общей выручки магазинов необходимо на этом листе использовать уже упоминавшуюся функцию

СУММПРОИЗВ: =СУММПРОИЗВ(A1:A15; C1:C15).

Результат будет равен 129 000. Ответ: 129 000.

3.2.6. Пример 6

Условие

Используя информацию из приведенной базы данных, определите общую стоимость продуктов, поставленных за указанный период с макаронной фабрики в магазины Первомайского района.

В ответе запишите целое число – найденную общую стоимость в рублях.

Решение

Здесь надо отобрать все продукты, поставленные поставщиком «Макаронная фабрика» в магазины указанного района. Для этого надо знать артикул каждого продукта. Соответствующие артикулы определяются на листе «Товар»:

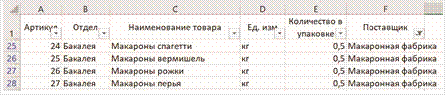
ID магазинов Первомайского района мы уже определяли: M2, M4, M7, М8, М12, М13 и M16.

Зная это, перейдем на лист «Движение товаров» и установим фильтры для перечисленных артикулов и ID магазинов, а также для значения «Поступление» в столбце «Тип операции»:

Осталось определить общую стоимость продуктов. Она также определяется на новом листе с помощью функции

СУММПРОИЗВ: =СУММПРОИЗВ(A1:A28; C1:C28).

Результат будет равен 241 080.

Ответ: 241 080.

3.2.7. Пример 7

Условие

Используя информацию из приведенной базы данных, определите общую сумму выручки, полученную от продаж продуктов мясной гастрономии в магазинах Центрального района с 1 по 7 июня.

В ответе запишите число – найденную сумму выручки в рублях.

Решение

Здесь особенность – в отборе артикулов товаров для расчета стоимости. Он проводится на листе «Товар» по значению «Мясная гастрономия».

Выполните задание самостоятельно.

3.3. Рекомендации по выполнению задания

Прежде всего определите, что надо знать для расчета требуемого значения.

Эти значения определяются на листах «Товар» и «Магазин» с использованием фильтрации данных.

Все найденные значения целесообразно записать (также целесообразно предварительно записать диапазон дат, указанный в условии).

При отборе нескольких товаров одного вида (рис, кофе и т. п.) следует учесть, что их наименования на листе могут быть записаны не рядом.

Итоговая информация формируется на листе «Движение товаров» (также с фильтрацией и при необходимости с сортировкой данных). Некоторые искомые значения можно определить с помощью инструмента СУММА () или по информации на строке состояния окна программы (при ее соответствующей настройке).

Если нужные расчеты с полученной информацией на указанном листе провести нельзя, то это надо сделать на отдельном (новом) листе с использованием функций СУММ или СУММПРОИЗВ.

3.4. Задания для самостоятельного выполнения

1. Определите, сколько килограммов паштета из куриной печени было продано в магазинах Октябрьского района за период с 1 по 3 июня включительно.

2. Определите, на сколько увеличилось количество упаковок соды пищевой, имеющихся в наличии в магазинах Октябрьского района, за период с 1 по 8 июня включительно.

3. Определите, сколько рублей потребовалось магазинам Октябрьского района для закупки чечевицы красной за период с 5 по 10 июня включительно.

4. Определите общую выручку от продажи всех видов кофе в магазинах Октябрьского района за период с 3 по 9 июня включительно.

5. Определите общую стоимость продуктов, поставленных с 1 по 10 июня включительно с мелькомбината в магазины Заречного района.

6. Определите среднюю стоимость, за которую 1 июня в магазинах Заречного района продавались товары, для которых единица измерения в базе данных указана «литр».

7. (Задание из демонстрационного варианта ЕГЭ 2024 года)

Используя информацию из приведенной базы данных^{^[13]}, определите общую массу (в кг) всех видов зефира, полученных магазинами на улице Металлургов за период с 4 по 13 июня включительно.

Глава 4 Задания 4

4.1. Общие вопросы. Теория

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 4 указывается «умение кодировать и декодировать информацию».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 2 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 4, связанные с кодированием сообщений методом, удовлетворяющим так называемому «условию Фано». Такое кодирование является одним из вариантов неравномерного кодирования, при котором более вероятным символам присваиваются более короткие кодовые слова.

Условие Фано формулируется так: «Никакое кодовое слово не может быть началом другого кодового слова». При нарушении этого условия при чтении закодированного сообщения будет иметь место неопределенность. Например, если буквы Б, И, Т закодировать двоичными цифрами (словами), соответственно, 01, 0101 и 11, то сообщение 01010111 может быть прочитано как БББТ, ИБТ или БИТ.

Проверку условия Фано для известных кодов и их выбор удобно проводить с помощью двоичного дерева. Напомним, что полное двоичное дерево имеет вид:

Места на дереве, обозначенные небольшими кружочками, называют «узлами» и обозначают последовательностью цифр, ведущих к ним из корня дерева: 0, 10, 011 и т. п. Отдельные отрезки дерева или ломаные из отрезков будем называть «ветвями» и также обозначать в соответствии с их узлами: 0, 10, 011 и т. п.

Обратим внимание на то, что если для кодирования использовать только кодовые слова на последнем уровне полного дерева, то такое кодирование будет равномерным (все кодовые слова имеют одинаковую длину). Поэтому при неравномерном кодировании двоичное дерево является неполным с ветвями разной «длины».

Пример двоичного дерева для неравномерного кодирования пяти букв, удовлетворяющего условию Фано:

На нем представлены кодовые слова 000, 001, 01, 10 и 11. Нетрудно убедиться, что для всех слов условие Фано соблюдается (при «продлении» дерева вниз для всех новых кодовых слов – также).

4.2. Примеры заданий и методика их выполнения

4.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение

В условии речь идет о кодировании последовательности букв «кодом Фано».

Построим двоичное дерево для заданных кодовых слов. Всего их три, все длиной в две цифры, поэтому дерево будет таким:

Расставим по соответствующим кодам известные буквы:

Для букв с известными кодами условие Фано, естественно, соблюдается. Остались две буквы, из которых, по условию, надо найти кодовое слово для буквы П. Причем это слово должно удовлетворять двум условиям:

• оно должно быть минимально возможной длины; • оно должно иметь наименьшее числовое значение.

Для удовлетворения первого условия надо учесть, что в узле 1 не использована одна из ветвей 10. Добавим ее:

Далее обсудим, можем ли мы выделить букве П новый код 10? – Нет, не можем, так как тогда не будет возможности назначить код пятой букве (которая тоже может передаваться в сообщении). В этом случае при продлении любой ветви (00, 01, 10, 11) новый код не будет соответствовать условию Фано (коды букв Л, М, П и Н будут началом нового кода, что недопустимо). Как быть? – Надо не выделять букве П код 10, а «продлить» ветку кодов 10. Будут получены два новых кодовых слова: 100 и 101, – из которых минимальное числовое значение – у первого.

Ответ: 100.

Сделаем важный вывод: нельзя выделять все возможные коды одной длины (одного «уровня» двоичного дерева), если нужно кодировать еще какие-то буквы. В рассмотренном примере нельзя было использовать код 10 в дополнение к известным кодам 00, 01 и 11.

4.2.2. Пример 2

Условие

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение

В данном случае среди известных кодовых слов есть два слова из трех цифр, поэтому дерево кодов будет таким:

Расставим соответствующие кодам известные буквы:

Остались две буквы, из которых, по условию, надо найти кодовое слово для буквы Д. Причем, как и в предыдущем примере, это слово должно удовлетворять двум условиям:

• оно должно быть минимально возможной длины; • оно должно иметь наименьшее числовое значение.

Эти условия соблюдаются, если к узлу 0 добавить вторую ветвь (01), после чего «продлить» ветку кодов 01. Будут получены два новых кодовых слова: 010 и 011, – из которых минимальное числовое значение – у первого.

Ответ: 010.

Сделаем еще один важный вывод: для получения двух новых кодовых слов надо достраивать двоичное дерево в узле самого высокого уровня с одной ветвью, после чего продлить новую ветвь и выбрать из двух новых кодовых слов требуемое (это может быть и слово с максимальным числовым значением). Учитывая это, целесообразно при изображении дерева сразу использовать в узлах ветвление (две ветви) и указывать два значения (0 и 1).

4.2.3. Пример 3

Условие

По каналу связи передаются сообщения, содержащие только 4 буквы П, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.

Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение

Построим дерево для заданных кодовых слов, учтя совет, данный в предыдущем пункте:

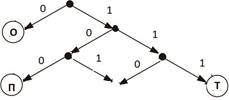
Достраивать дерево можно в узлах 10 или 11. Условие минимальности числового значения кода обеспечивается в первом случае – будет получен код 101.

Ответ: 101.

4.2.4. Пример 4

Условие

По каналу связи передаются сообщения, содержащие только буквы А, Б, В, Г, Д, Е. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано; для букв A, Б, В используются такие кодовые слова: А – 0, Б – 101, В – 110.

Какова наименьшая возможная суммарная длина всех кодовых слов?

Решение

Отличие данного задания от предыдущих – в новой искомой величине (наименьшая возможная суммарная длина всех кодовых слов). Ясно, что для ее определения надо знать длину всех кодовых слов. Три из них известны, следует найти еще две.

Перечислим возможные коды в порядке возрастания длины.

Можно сразу сказать, что любой код, начинающийся с 0, не подходит, так как код 0 (у буквы А), поэтому рассматриваем только те, которые начинаются с 1:

• 1 – нельзя, так как есть коды, начинающиеся с 1;

• 10 – нельзя, так как есть код, начинающийся с 10;

• 11 – нельзя, так как есть код, начинающийся с 11;

• 111 – можно использовать, пусть это будет одной из букв, для которых подбираем коды, например 4.

Исследуем оставшееся кодовое слово из трех цифр – 100. Если его использовать, то будет получено дерево, заканчивающееся «листьями» 0, 100, 101, 110 и 111, продлевать которое без нарушения условия Фано нельзя.

Это значит, что для оставшихся двух букв достаточно взять любые два допустимых кода длины 4. Например, 1100 и 1101.

В результате сумма длин кодовых слов составит:

1 + 3 + 3 + 3 + 4 + 4 = 18.

Ответ: 18.

4.2.5. Пример 5

Условие

По каналу связи передаются шифрованные сообщения, содержащие только пять букв: А, Б, В, Г, Д. Для передачи используется неравномерный двоичный код. Для букв А, Б, В и Д используются кодовые слова 00, 01, 10 и 111 соответственно.

Укажите длину самого короткого кода для слова БАГ, при котором код не будет удовлетворять условию Фано, при этом в записи этого слова используются кодовые слова для букв длиною более одного символа, а сами коды для символов не должны совпадать друг с другом. Если таких слов несколько, то укажите длину слова с минимальным числовым значением.

Решение

Здесь обратим внимание на то, что искомым является такой код слова БАГ, в котором не соблюдается условие Фано, причем этот код должен быть самым коротким из всех возможных.

Итак, буква Б кодируется кодовым словом 01, буква А – словом 00. Для буквы Г нельзя использовать кодовые слова 1 и 0, так как по условию кодовые слова должны быть длиннее одного символа. Также нельзя использовать кодовые слова 00, 01, 10, поскольку они «заняты» буквами А, Б и В. Для буквы Г можно использовать код 11, так как он длиннее одного символа и не используется для кодирования других букв, при этом не удовлетворяет условию Фано. Это значит, что двоичный код для слова БАГ будет таким: 010011. Его длина – 6 символов.

Ответ: 6.

При выполнении заданий такого типа необходимо определить самое короткое кодовое слово для буквы «без кода», при котором условие Фано не соблюдается (или самые короткие кодовые слова для букв «без кода», если таких букв больше одной).

4.2.6. Пример 6

Условие

По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 010, Б – 101, В – 1001, Г – 111, Д – 0110, Е – 110. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ЛИЛИЯ?

Решение

Здесь минимально коротким кодом следует в первую очередь по возможности закодировать повторяющиеся буквы.

Однозначные (0 и 1) и двузначные 01, 10 и 11 коды использовать нельзя, так эти коды являются началом уже использованных кодовых слов. Почему нельзя использовать кодовое слово 00, установите самостоятельно. Придется использовать кодовые слова длины 3. Для повторяющихся букв это будут коды 000 и 001. В результате будут использованы все кодовые слова длины 3:

• в виде полного кода – 000, 001, 010, 101, 110 и 111;

• как начало другого кодового слова – 011 и 100.

Значит, «оставшуюся» букву Я можно закодировать кодовым словом длины 4. Каким? – Только 0111 (кодовое слово 1001 уже использовано). Итак, искомое количество двоичных знаков составит – 3 × 4 + 4 = 16.

Ответ: 16.

Заметим, что остальные буквы можно будет закодировать кодами длины не менее 5, начинающимися с 1000.

4.2.7. Пример 7

Условие

По каналу связи передаются сообщения, содержащие только шесть букв: А, Б, Г, И, М, Я. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 010, Б – 011, Г – 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова МАГИЯ?

Решение

Построим дерево известных кодов, в том числе с новыми ветвями в узлах 0 и 1 (см. пример 2):

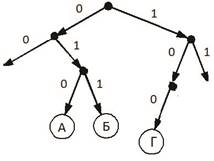
Видно, что коды для двух букв слова МАГИЯ (А и Г) есть. Остались незакодированными три буквы: М, И, Я.

В новых ветвях (в узлах 0 и 1) получены, соответственно, коды 00 и 11. Один из них, например 00, можно выделить для одной из трех букв, а «раздвоив» другой (110 и 111), получить еще два кода для двух букв.

Итак, общее количество двоичных знаков для кодирования слова МАГИЯ составит 3 + 3 (длина кодов букв А и Г) + 2 + 3 + 3 (длина кодов букв М, И, Я в любом сочетании) = 14.

Ответ: 14.

Внимание! Если бы в условии требовалось получить коды с минимальной суммой числовых значений, то нужно было бы для одной из букв принять код 11, а для еще двух – 000 и 001.

4.2.8. Пример 8

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

По каналу связи передаются сообщения, содержащие только буквы из набора: А, З, К, Н, Ч. Для передачи используется двоичный код, удовлетворяющий прямому условию Фано, согласно которому никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Кодовые слова для некоторых букв известны: Н – 1111, З – 110. Для трех оставшихся букв А, К и Ч кодовые слова неизвестны. Какое количество двоичных знаков потребуется для кодирования слова КАЗАЧКА, если известно, что оно закодировано минимально возможным количеством двоичных знаков?

Решение

Код для наиболее встречающейся в слове КАЗАЧКА буквы А очевиден (0). Осталось найти коды для букв К и Ч. Здесь имеется «подводный камень» 😊. Кажущееся очевидным продление ветви 1 до 10 и присваивание буквам К и Ч кодов 100 и 101 даст общее количество знаков для кодирования слова КАЗАЧКА, равное 3 + 1 + 3 + 1 + 3 + 3 + 1 = 15. Однако возможен вариант кодирования, при котором эта сумма равна 14. Найдите его.

4.3. Задания для самостоятельного выполнения

1. Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв К, Л, М, Н использовали соответственно кодовые слова 000, 001, 010, 11. Для двух оставшихся букв – П и Р – длины кодовых слов неизвестны.

Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

2. По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова. Для буквы А − 00, Е – 010, И – 011, К – 1111, Л – 1101, Р – 1010, С – 1110, Т – 1011, У – 100.

Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

3. По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В используются такие кодовые слова: А – 0; Б – 110; В – 101.

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наибольшим числовым значением.

4. По каналу связи передаются сообщения, содержащие только четыре буквы: А, Б, В, Г. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 0, Б – 1011. Укажите сумму длин кратчайших кодовых слов для букв В и Г, которые будут удовлетворять условию Фано.

5. Для кодирования некоторой последовательности, состоящей из букв А, Б, В и Г, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Для букв А, Б, В используются такие кодовые слова: А – 000, Б – 1, В – 011.

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

6. По каналу связи передаются сообщения, содержащие только буквы А, Б, В, Г, Д, Е. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано; для букв A, Б, В используются такие кодовые слова: А – 1, Б – 010, В – 001.

Какова наименьшая возможная суммарная длина всех кодовых слов?

7. По каналу связи передаются шифрованные сообщения, содержащие только шесть букв: А, Б, В, Г, Д, Е. Для передачи используется неравномерный двоичный код. Для букв А, Б, В и Г используются кодовые слова 00, 01, 10 и 11 соответственно.

Укажите длину самого короткого кода для слова БЕДА, при котором код не будет удовлетворять условию Фано, при этом в записи этого слова используются кодовые слова для букв длиною более одного символа, а сами коды для символов не должны совпадать друг с другом. Если таких слов несколько, то укажите длину слова с минимальным числовым значением.

8. По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 000, Б – 01, В – 1101, Г – 111, Д – 0010, Е – 100. Какое наименьшее количество двоичных знаков потребуется для кодирования слова КОКОС?

9. По каналу связи передаются сообщения, содержащие только шесть букв: А, Б, Ф, И, М, Р. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 010, Ф – 00, Б – 101. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ФИРМА?

10. (Задание из демонстрационного варианта ЕГЭ 2024 года)

По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, В, Г, Д, Е, Ж и З. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:

А	000
Б	001
В	0101
Г	0100
Д	011
Е	101

Какое наименьшее количество двоичных знаков потребуется для кодирования двух оставшихся букв?

В ответе запишите суммарную длину кодовых слов для букв: Ж, З.

Глава 5 Задания 5

5.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 5 указывается «формальное исполнение прос того алгоритма, записанного на естественном языке, или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд, или умение восстанавливать исходные данные линейного алгоритма по результатам его работы».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 4 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 5, общий вид которых следующий:

«На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. <Далее указывается, как меняется двоичная запись числа N>.

Полученная таким образом запись является двоичной записью искомого числа R.

Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа <указывается значение>».

или

«Укажите минимальное число R, которое превышает число <указывается значение> и может являться результатом работы данного алгоритма».

В обоих случаях в ответе соответствующее число следует записать в десятичной системе счисления.

5.2. Примеры заданий и методика их выполнения

5.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2020 года)

Условие

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа).

Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы ее цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает число 97 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

Решение

Задание может быть выполнено разными способами. Один из них – метод рассуждений и проб.

Проанализируем, что происходит с двоичной записью числа N в результате выполнения алгоритма. Рассмотрим варианты.

• Если сумма цифр (или, что то же самое, количество единиц) в ней нечетная, то к этой записи дописывается цифра 1. В результате сумма цифр станет четной и к записи справа еще добавится 0. Например, при исходной двоичной записи 111 будет получена запись 11110.

• Если сумма цифр в двоичной записи числа N четная, то к этой записи дописывается цифра 0. Четность суммы не изменится, и на втором этапе будет также добавлен 0. Например, при двоичной записи 101 будет получена запись 10100.

При приписывании к концу двоичного числа двух нулей соответствующее десятичное значение N увеличивается в 4 раза, а при приписывании двух цифр 10 становится равным N × 4 + 2.

Это значит, что первое возможное значение N равно 24. Исследуем его двоичную запись. Ее можно получить:

• «вручную», записав единицы в разрядах со степенями двойки: 11000₂ (24 = 16 + 8);

• с помощью стандартной программы Калькулятор операционной системы в режиме Программист:

Количество единиц в двоичной записи – четное. По только что установленному правилу результат R в этом случае будет равным 24 × 4 = 96, что не больше 97.

Проверим следующее число N = 25.

25₁₀ = 11001₂.

Количество единиц в двоичной записи – нечетное. Значит, результат R в этом случае будет равным 25 × 4 + 2 = 102, что больше 97.

Итак, ответ: 102.

Можно также разработать программу, моделирующую действия, которые мы проводили.

Пусть дано значение N. Как получить результат работы алгоритма R? – Это можно сделать следующим образом:

1) ввести в программу значение N;

2) определить количество единиц в его двоичной записи (к1);

3) если оно четное, то результат будет равен N × 4, в противном случае – N × 4 + 2;

4) вывести на экран значение R.

Значение к1 можно найти путем перевода десятичного значения N в двоичную систему методом последовательного деления на основание 2. В программе на школьном алгоритмическом языке соответствующий фрагмент имеет вид:

к1 := 0 нц пока N > 0 если mod(N, 2) = 1 то к1 := к1 + 1 все N := div(N, 2) кц

где mod – функция школьного алгоритмического языка, возвращающая остаток от деления своего первого аргумента на второй, div – функция, возвращающая целую часть частного от такого деления (в других языках программирования для расчета указанных значений используются не функции, а специальные операции).

Однако при этом исходное значение N изменится, что недопустимо, учитывая, что его нужно будет менять. Чтобы решить проблему, надо при определении количества единиц использовать «копию» значения N.

Далее нужно проверить четность значения к1 – и получаем результат по одной из двух возможных зависимостей:

если mod(к1, 2) = 0 то R := N * 4 иначе R := N * 4 + 2 все

Вся программа:

алг нач цел N, N2, R, к1 ввод N N2 := N | Используем "копию" числа N к1 := 0 нц пока N2 > 0

если mod(N2, 2) = 1 | Если последняя цифра - 1 то к1 := к1 + 1 все | Определяем целочисленное частное N2 := div(N2, 2) кц

| Меняем значение N

если mod(к1, 2) = 0 то R := N * 4 иначе R := N * 4 + 2 все вывод нс, R кон

Но так как проверять придется не одно значение числа N, то лучше использовать оператор цикла для проверки ряда значений N. Соответствующая программа:

алг нач цел N, N2, R, к1 нц для N от 1 до 30 | Определяем кол-во единиц в значении N N2 := N | используя его "копию" к1 := 0 нц пока N2 > 0 если mod(N2, 2) = 1 то к1 := к1 + 1 все N2 := div(N2, 2) кц если mod(к1, 2) = 0 то R := N * 4 иначе R := N * 4 + 2 все если R > 97 то | Искомый результат получен | Выводим его вывод нс, R | Выходим из оператора цикла выход все кц кон

5.2.2. Пример 2 (пример из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.)

Условие

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа еще два разряда по следующему правилу:

Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы ее цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.

Решение

Задача решается аналогично рассмотренной, с той разницей, что надо найти и вывести на экран не значение R, удовлетворяющее условию, а значение N, при котором получен этот результат.

В связи с этим в программе надо вместо значения 97 использовать значение 77 и при нахождении нужного результата вывести на экран значение N. Разработайте соответствующую программу самостоятельно. Рассуждения же при выполнении задания без программы также аналогичны.

Первое возможное значение N в данном случае равно 18.

18₁₀ = 10010₂.

Количество единиц в двоичной записи – четное. По только что установленному правилу результат R в этом случае будет равным 18 × 4 = 72, что не больше 77.

Следующее число N = 19.

19₁₀ = 10011₂.

Количество единиц в двоичной записи – нечетное. Значит, результат R в этом случае будет равным 19 × 4 + 2 = 78, что больше 77.

Итак, ответ: 19.

5.2.3. Пример 3

(пример из демонстрационного варианта ЕГЭ 2023 года)

Условие

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа еще два разряда по следующему правилу:

а) если сумма цифр в двоичной записи числа четная, то к этой записи справа дописывается 0, а затем два левых разряда заменяются на 10;

б) если сумма цифр в двоичной записи числа нечетная, то к этой записи справа дописывается 1, а затем два левых разряда заменяются на 11.

Полученная таким образом запись является двоичной записью искомого числа R. Например, для исходного числа 6₁₀= 110₂ результатом является число 1000₂ = 810, а для исходного числа 410 = 100₂результатом является число 1101₂^{= 13}₁₀.

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, большее 40. В ответе это число запишите в десятичной системе счисления.

Решение

Здесь решение задачи путем рассуждений и с помощью программы затруднено, так как трудно определить правила, по которым меняется значение N в двух случаях (хотя и возможно). Если вы сможете определить эти правила, то выполните задания описанными методами.

Мы считаем целесообразным для выполнения таких заданий использовать электронную таблицу. Методика следующая.

В обоих случаях (при четной сумме цифра в двоичной записи числа N и при нечетной) количество цифр в этой записи в результате выполнения алгоритма увеличивается на 1.

Определим количество цифр в двоичной записи «предельного» числа 40. Это можно сделать, как уже отмечалось вначале, разными способами.

40₁₀ = 101000₂.

Итак, в двоичной записи числа 40 – 6 цифр. Значит, в исходном числе двоичных цифр – 5.

Оформим лист следующим образом.

В строке 1 запишем минимальное пятизначное двоичное число (16₁₀):

	A	B	C	D	E	F	G
1	1	0	0	0	0		1
2

В ячейке G1 определим четность суммы цифр в нем. Для этого используем функции СУММ и ОСТАТ^{^[14]}:

=ОСТАТ(СУММ(A1:E1); 2)

Во второй строке получим цифры двоичного числа, которое будет результатом описанного в условии алгоритма:

• в ячейке F2 будет записана дополнительная цифра. Ее можно получить в зависимости от четности суммы цифр в диапазоне А1:Е1 по формуле =ЕСЛИ(G1 = 1; 1; 0) или, проще, =G1;

• в ячейке А2 в любом случае останется цифра 1;

• цифра в ячейке В2 также зависит от четности, то есть формула в ней – та же, что и в F2;

• цифры в ячейках С2, D2 и Е2 в общем случае будут такими же, как и в соответствующих ячейках в строке 1.

Приведем фрагмент таблицы с отображенными в строке 2 формулами:

	A	B	C	D	E	F	G
1	1	0	0	0	0		1
2	1	=ЕСЛИ(G1 = 1 ; 1; 0)	=С1	=D1	=E1	=G1

а также с результатами вычислений по ним:

	A	B	C	D	E	F	G
1	1	0	0	0	0		1
2	1	1	0	0	0	1

Осталось получить десятичный эквивалент полученного в строке 2 двоичного числа. Это можно сделать, сложив весомос ти двоичных разрядов, в которых записаны единицы:

1 + 16 + 32 = 49.

Итак, уже для минимально возможного пятизначного двоичного числа 10000 (16₁₀) преобразования дают десятичное число, превышающее «предельное» число 40, то есть в данном случае искомое десятичное число N равно 16.

Нетрудно увидеть, что описанные действия моделировали действия, проводимые в ходе выполнения алгоритма в условии задания.

А если бы полученное число не было больше 40?

Допустим, что «предельное» число равно 50. В таком случае нужно увеличивать число в первой строке на 1 до тех пор, пока в ячейке G3 не появится число, большее 50.

Так как в таких случаях придется многократно в уме определять сумму весомостей двоичных разрядов, в которых записаны единицы, то лучше в строке 3 указать весомости разрядов, а в ячейку G3 ввести формулу:

=СУММПРОИЗВ(A1:F6;A2:F2)

Вот последовательные результаты таких вычислений:

	A	B	C	D	E	F	G	H	I
1	1	0	0	0	0		1		16
2	1	1	0	0	0	1
3	32	16	8	4	2	1	49
	A	B	C	D	E	F	G	H	I
1	1	0	0	0	1		0		17
2	1	0	0	0	1	0
3	32	16	8	4	2	1	34
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	0		0		18
2	1	0	0	1	0	0
3	32	16	8	4	2	1	36
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	1		1		19
2	1	1	0	1	1	1
3	32	16	8	4	2	1	55

Примечание. В столбце I записаны значения проверяемого числа N.

Итак, искомое в данном случае значение N равно 16 + 3 = 19.

В заключение заметим, что описанная методика может быть использована и при выполнении заданий, рассмотренных в пп. 5.2.1 и 5.2.2 (см. следующий раздел).

Добавим также, что действия в описанном в условии алгоритме можно смоделировать также с помощью программы. Правда, удобно это делать на языках программирования, в которых предусмотрены стандартные функции для перевода десятичных значений в двоичные и обратно (например, в языке Python). Общая схема действий в таких программах приведена в п. 5.4.2.

5.3. Выполнение заданий в среде электронной таблицы

5.3.1. Задание из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.

(см. п. 5.2.2)

В данном случае двоичная запись числа N увеличивается на две цифры.

«Предельное» число 77 в двоичной системе записывается как 1001101. Значит, в исходном числе двоичных цифр – 5.

Учитывая все сказанное и особенности работы алгоритма, можем так оформить лист электронной таблицы:

	A	B	C	D	E	F	G	H
1	1	0	0	0	0			=ОСТАТ(СУММ(A1:E1); 2)
2	1	=В1	=С1	=D1	=E1	=H1	0
3	=B3 * 2	=C3 * 2	=D3 * 2	=E3 * 2	=F3 * 2	=G3 * 2	1

Результаты расчетов для нескольких последовательно увеличивающихся исходных чисел:

	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	0			1		16
2	1	0	0	0	0	1	0
3	64	32	16	8	4	2	1	66
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	1			0		17
2	1	0	0	0	1	0	0
3	64	32	16	8	4	2	1	68
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	0			0		18
2	1	0	0	1	0	0	0
3	64	32	16	8	4	2	1	72
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	1			1		19
2	1	0	0	1	1	1	0
3	64	32	16	8	4	2	1	78

Итак, ответ: 19.

5.3.2. Задание из демонстрационного варианта ЕГЭ 2020 года (см. п. 5.2.1)

Как уже отмечалось, отличие данного задания от рассмотренного в том, что нужно найти не минимальное входное число N, а минимальное значение результата выполнения алгоритма, которое превышает число 97. Так как при выполнении задания по описанной в предыдущем пункте методике значение результата выводится в столбце Н, то именно значение из этого столбца будет являться ответом (числа в столбце J в данном случае записывать не нужно). Выполните задание самостоятельно.

5.4. Выводы и рекомендации

Прежде всего заметим, что приведенные далее рекомендации относятся к выполнению заданий, аналогичных рассмотренным, в которых результат выполнения алгоритма зависит от четности суммы цифр двоичной записи «входного» числа N. Некоторые другие возможные задания рассмотрены в разделе 5.5.

5.4.1. Если можно установить формулы^{^[15]}, по которым определяется результат выполнения алгоритма в двух случаях (при четной сумме цифр двоичной записи числа N и при нечетной), то задание может быть выполнено с помощью программы или путем рассуждений и проб.

Общая схема действий в программе

В цикле с параметром рассматриваются возможные значения N (это может быть большой диапазон значений, начинающийся с 1). Для каждого значения N:

• определяется количество единиц в его двоичной записи (на основе перевода десятичного числа в двоичную систему счисления методом последовательного деления на основание с использованием переменной – копии переменной N);

• в зависимости от четности указанного количества по одной из двух формул рассчитывается значение результата выполнения алгоритма R.

Если значение R удовлетворяет условию задания, то:

• в качестве ответа выводится значение R или соответствующее значение N;

• проводится выход из цикла.

При поиске ответа методом рассуждений и проб:

• на основе установленных формул (см. выше) определяется минимальное значение N, с которого можно проводить проверку;

• это число переводится в двоичную систему счисления («вручную» или с помощью стандартной программы Калькулятор), и определяется количество единиц в его двоичной записи;

• в зависимости от четности указанного количества по одной из двух формул рассчитывается значение результата выполнения алгоритма R;

• если рассчитанное значение R удовлетворяет условию задания, то оно или соответствующее значение N является искомым ответом, в противном случае значение N увеличивается на 1 и все действия повторяются до получения нужного результата.

5.4.2. Если формулы, о которых шла речь в п. 5.4.1, установить сложно, то задание можно выполнить в среде электронной таблицы или с помощью разработанной программы.

В среде электронной таблицы задача решается по следующей методике.

1. «Предельное» значение R переводится в двоичную систему счисления («вручную» или с помощью стандартной программы Калькулятор), и определяется количество единиц в его двоичной записи.

2. На основе анализа алгоритма устанавливается, как меняется общее количество цифр в исходном и последующих числах в результате работы алгоритма (увеличивается или уменьшается и на сколько).

3. С учетом найденного на предыдущем этапе числа рассчитывается количество цифр k во входном числе N.

4. На листе электронной таблицы:

• в строке 1 записываются цифры минимального k-значного двоичного числа, а также рассчитывается остаток от деления их суммы на 2;

• в строке 2 записываются формулы, определяющие двоичные цифры результата выполнения алгоритма (с учетом особенностей его работы);

• с учетом весомости разрядов в строке 3 определяется его десятичный эквивалент^{^[16]};

• если полученное десятичное значение не больше «предельного» числа в условии, то двоичное число в первой строке последовательно увеличивается на 1 до появления в строке 3 требуемого числа.

Ответом может являться как найденное значение результата R, так и значение N, при котором этот результат получен.

Общая схема действий по решению задачи в программе (напомним, что это целесообразно делать не на всех языках программирования):

• оно переводится в двоичную систему счисления (с помощью стандартной функции);

• полученное число преобразовывается в строку символов-цифр;

• определяется количество единиц в строке;

• в зависимости от четности указанного количества значение строки символов изменяется согласно особенностям работы алгоритма (добавляются, удаляются или заменяются символы);

• новое значение строки преобразовывается в число (из двоичных цифр);

• полученное число переводится в десятичную систему.

Если последнее значение (это будет результат выполнения алгоритма R) удовлетворяет условию задания, то:

• в качестве ответа выводится значение R или соответствующее значение N;

• проводится выход из цикла.

5.5. Другие возможные варианты задания

5.5.1. Пример 1

Условие

Автомат обрабатывает натуральное число N по следующему алгоритму:

1. Строится двоичная запись числа N.

2. К этой записи дописываются справа еще два разряда по следующему правилу: если N четное, в конец числа (справа) дописывается 10, в противном случае справа дописывается 01. Например, двоичная запись 1001 числа 9 будет преобразована в 100101.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма.

Укажите максимальное число R, которое не превышает 102 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

Решение

Отличия данного задания:

1) результат работы автомата зависит не от четности суммы цифр в двоичной записи числа N, а от четности самого числа;

2) искомым значением является максимальное число из возможных (а не минимальное).

Прежде всего установим зависимость результата R от четности числа N (см. дополнение к данной главе):

если – четное число то R = N × 4 + 2 иначе R = N × 4 + 1

В программе решения задачи надо вывести на экран все значения R, меньшие либо равные 102:

алг нач цел N, R нц для N от 1 до 30 если mod(N, 2) = 0 то R := N * 4 + 2 иначе R := N * 4 + 1 все если R <= 102 то вывод нс, N все кц кон

а в качестве ответа – максимальное из них.

Ответ: 101.

Можно также провести анализ числа 102 и меньших. Он основан на том, что если результат R – четный, то он получен по формуле R = N × 4 + 2, в противном случае – по формуле R = N × 4 + 1.

Число 102 – четное, то есть оно могло быть получено так: R = N × 4 + 2, откуда N = 25. Но это невозможно, так как при четном результате 102 значение N должно быть четным.

Предшествующее число 101 – нечетное, оно могло быть получено следующим образом: R = N × 4 + 1, откуда N = 25, что допустимо.

Итак, ответ: 101.

5.5.2. Пример 2

Условие

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число следующим образом:

1) строится двоичная запись числа N;

2) к этой записи дописываются справа еще два разряда по следующему правилу: если N четное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Укажите максимальное число N, для которого результат работы алгоритма будет меньше 134. В ответе это число запишите в десятичной системе счисления.

Комментарий к решению

Здесь особенности алгоритма аналогичны приведенным в заданиях пп. 5.2.1 и 5.2.2. Отличие – в требовании определения максимального значения из возможных.

Выполните задание самостоятельно.

5.5.3. Пример 3

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. Далее эта запись обрабатывается по следующему правилу:

а) если число N делится на 3, то к этой записи дописываются три последние двоичные цифры;

б) если число N на 3 не делится, то остаток от деления умножается на 3, переводится в двоичную запись и допи сывается в конец числа. Полученная таким образом запись является двоичной запи сью искомого числа R.

3. Результат переводится в десятичную систему и выводится на экран.

Например, для исходного числа 12 = 1100₂ результатом является число 1100100₂ = 100, а для исходного числа 4 = 100₂ это число 10011₂ = 19.

Укажите минимальное число R, большее 151, которое может быть получено с помощью описанного алгоритма. В ответе запишите это число в десятичной системе счисления.

Решение

Проанализируем, как меняется входное число N в результате выполнения описанного алгоритма.

Если N кратно трем, то к его двоичной записи добавляются три цифры. Это значит, что значение N увеличивается как минимум в 8 раз и как максимум в 8 раз, после чего произведение увеличивается еще на 7 (убедитесь в этом!).

Если остаток от деления N на 3 равен 2 (10₂), то к двоичной записи числа N также добавляются три цифры (110₂). Это значит, что и в этом случае значение N увеличивается как минимум в 8 раз (если быть точным, то увеличивается в 8 раз, после чего произведение увеличивается еще на 6 – также убедитесь в этом).

Если остаток от деления N на 3 равен 1, то к двоичной записи числа N добавляются две цифры (11₂), то есть в этом случае значение N увеличивается в 4 раза, после чего к произведению добавляется 3.

Множество значений N для двух первых случаев будем называть множество «02», для третьего – множество «1».

С каких значений N можно начинать проверку работы алгоритма?

Рассмотрим множество «02». Первое большее 151 число – 152. Найдем целую часть частного от деления (152 – 7) на 8 – получим 18.

Проверку этого числа проведем с помощью таблицы:

N	18
N2	10010
Остаток	0
Новая запись N₂	10010010
R	18 × 8 + 2 = 146

Следующее число из множества «02» – 20:

N	18	20
N2	10010	10100
Остаток	0	2
Новая запись N₂	10010010	10100110
R	18 × 8 + 2 = 146	20 × 8 + 6 = 166

Получен результат R, больший числа 151. Означает ли это, что найденное значение является минимальным из чисел-результатов, больших 151? – Нет, так как есть еще входные числа N из множества «1». Надо проверить и их.

Найдем целую часть частного от деления (152 – 6) на 4 – получим 36. Но это число кратно трем, то есть не входит в множество «1». Поэтому проверим следующее число 37:

N	37
N2	100101
Остаток	1
Новая запись N₂	10010111
R	37 × 4 + 3 = 151

Следующее число из множества «1» – 40:

N	37	40
N2	100101	101000
Остаток	1	1
Новая запись N₂	10010111	10100011
R	37 × 4 + 3 = 151	40 × 4 + 3 = 163

Найденное число 163 является наименьшим из всех возможных результатов работы алгоритма, больших числа 151.

Ответ: 163.

Примечание. Если бы в задании требовалось найти минимальное значение входного числа N, при котором результат работы алгоритма превышает число 151, то ответ был бы 20.

5.5.4. Пример 4

Условие

На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1. Строится двоичная запись числа N.

2. Далее эта запись обрабатывается по следующему правилу:

а) если число N кратно 3, тогда в конец дописывается три младших разряда полученной двоичной записи;

б) если число N не кратно 3, тогда в конец дописывается двоичная последовательность, являющаяся результатом умножения 3 на остаток от деления числа N на 3.

Полученная таким образом запись является двоичной записью искомого числа R.

Например, для исходного числа 5₁₀ = 101₂ результатом является число 101110₂ = 46₁₀, а для исходного числа 9₁₀ = 1001₂ результатом является число 1001001₂ = 73₁₀.

Укажите наибольшее число N, после обработки которого с помощью этого алгоритма получается число R, меньшее 100. В ответе запишите это число в десятичной системе счисления.

Решение

Принципиальное отличие данного задания от предыдущего в том, что требуется найти наибольшее число N, при котором результат выполнения алгоритма меньше заданного (а не минимальный результат работы алгоритма R, больший заданного значения).

Итак. Здесь также надо рассмотреть два множества значений N.

Для входных чисел из множества «02» максимальное число, для которого надо проводить проверку, – целая часть частного от деления 99 на 8^{^[17]}, то есть 12:

N	12
N2	1100
Остаток	0
Новая запись N₂	1100100
R	12 × 8 + 4 = 100

Следовательно, число 12 не удовлетворяет условию. Проверим предыдущее число из множества «02» – 11.

N	12	11
N2	1100	1011
Остаток	0	2
Новая запись N₂	1100100	1011110
R	12 × 8 + 4 = 100	11 × 8 + 6 = 94

При N = 11 получен результат, меньший 100. Является ли 11 максимальным значением? – Нет, надо проверить также числа из множества «1».

В этом множестве проверку начинаем с числа, равного целой части частного от деления 99 на 4, то есть с 22. Его проверка:

N	22
N2	10110
Остаток	1
Новая запись N₂	1011011
R	22 × 4 + 3 = 91

Следовательно, 22 – наибольшее число из множества «1», при котором результат работы алгоритма будет меньше 100.

Из двух найденных чисел в каждом множестве (11 и 22) максимальным является второе.

Ответ: 22.

Анализ заданий, аналогичных рассмотренным в пп. 5.4.3–5.4.4, показывает, что на экзамене в аналогичных заданиях искомым может быть:

1) минимальное значение результата R выполнения алгоритма:

• большее заданного числа;

• не меньшее заданного числа;

2) минимальное значение входного числа N, при котором результат R выполнения алгоритма:

• больше заданного числа;

• не меньше заданного числа;

3) максимальное значение результата R выполнения алгоритма:

• меньшее заданного числа;

• не большее заданного числа;

4) минимальное значение входного числа N, при котором результат R выполнения алгоритма:

• меньше заданного числа;

• не больше заданного числа.

5.5. Задания для самостоятельного выполнения

1. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) к этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 137. В ответе это число запишите в десятичной системе.

2. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) к этой записи дописываются справа еще два разряда по следующему правилу:

Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы ее цифр на 2.

Укажите минимальное число R, которое превышает число 83 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

3. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) к этой записи дописываются справа еще два разряда по следующему правилу: складываются все цифры двоичной записи, если а) сумма нечетная, к числу дописывается 11, б сумма четная, дописывается 00.

Укажите такое наименьшее число R, которое превышает 114 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе счисления.

4. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) в конец записи (справа) добавляется (дублируется) последняя цифра;

3) складываются все цифры полученной двоичной записи. В конец записи (справа) дописывается остаток от деления суммы на 2;

4) результат переводится в десятичную систему и выводится на экран.

Пример.

Дано число N = 13. Алгоритм работает следующим образом:

1) двоичная запись числа N: 110;

2) дублируется последняя цифра, новая запись 11011;

3) сумма цифр полученной записи 4, остаток от деления на 2 равен 0, новая запись 110110; 4) на экран выводится число 54.

Какое наименьшее число, большее 105, может появиться на экране в результате работы алгоритма?

5. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) далее эта запись обрабатывается по следующему правилу:

а) если число четное, то к двоичной записи числа слева дописывается 1, а справа 0. Например, для исходного числа 100₂ результатом будет являться число 11000;

б) если число нечетное, то к двоичной записи числа слева дописывается 11 и справа дописывается 11.

Полученная таким образом запись является двоичной записью искомого числа R.

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число, большее, чем 52. В ответе запишите это число в десятичной системе счисления.

6. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число следующим образом:

1) строится двоичная запись числа N;

Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления.

7. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число следующим образом;

1) строится двоичная запись числа N;

2) к этой записи дописывается справа два нуля, если число четное, или две единицы в противном случае.

Укажите максимальное число N, после обработки которого с помощью этого алгоритма получается число менее 94. В ответе это число запишите в десятичной системе.

8. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) далее эта запись обрабатывается по следующему правилу:

а) если число N делится на 3, то в этой записи дописываются справа три последние двоичные цифры;

б) если число N на 3 не делится, то остаток от деления умножается на 3, переводится в двоичную запись и дописывается в конец числа.

Полученная таким образом запись является двоичной записью искомого числа R;

3) результат переводится в десятичную систему и выводится на экран.

Например, для исходного числа 12 = 1100₂ результатом является число 1100100₂ = 100, а для исходного числа 4 = 100₂ результатом является число 10011₂ = 19.

Укажите минимальное число N, после обработки которого с помощью этого алгоритма получается число R, не меньшее, чем 76.

9. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1) строится двоичная запись числа N;

2) далее эта запись обрабатывается по следующему правилу:

а) если число N делится на 3, то в этой записи дописываются справа три последние двоичные цифры;

Полученная таким образом запись является двоичной записью искомого числа R;

3) результат переводится в десятичную систему и выводится на экран.

Укажите максимальное число R, не превышающее 137, которое может быть получено с помощью описанного алгоритма. В ответе запишите это число в десятичной системе счисления.

Дополнение Некоторые формулы для расчета значения

результата выполнения алгоритма

Приписывание к двоичной записи числа N	Значение результата R
0	R = N × 2
1	R = N × 2 + 1
00	R = N × 4
01	R = N × 4 + 1
10	R = N × 4 + 2
11	R = N × 4 + 3
000	R = N × 8
001	R = N × 8 + 1
010	R = N × 8 + 2
011	R = N × 8 + 3
100	R = N × 8 + 4
101	R = N × 8 + 5
110	R = N × 8 + 6
111	R = N × 8 + 7

Глава 6 Задания 6

6.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 6 указывается «определение возможных результатов работы простейших алгоритмов управления исполнителями и вычислительных алгоритмов».

• Уровень сложности задания – Б (базовый).

• Макс. балл за выполнение задания – 1.

• Примерное время выполнения задания – 4 мин.

***

В демонстрационных вариантах ЕГЭ по информатике 2023 и 2024 гг. приводятся два варианта задания 6. В реальных вариантах экзаменационной работы будет предложен только один вариант задания. Приведем условие заданий 2023 года^{^[18]}.

Вариант 1

Исполнитель Черепаха действует на плоскости с декартовой системой координат. В начальный момент Черепаха находится в начале координат, ее голова направлена вдоль положительного направления оси ординат, хвост опущен. При опущенном хвосте Черепаха оставляет на поле след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды:

Вперед n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает ее голова, и

Направо m (где m – целое число),

вызывающая изменение направления движения на m градусов по часовой стрелке.

Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз.

Черепахе был дан для исполнения следующий алгоритм:

Повтори 7 [Вперед 10 Направо 120]

Определите, сколько точек с целочисленными координатами будет находиться внутри области, ограниченной линией, заданной данным алгоритмом. Точки на линии учитывать не следует.

Вариант 2

• Поднять хвост, означающая переход к перемещению без рисования; • Опустить хвост, означающая переход в режим рисования;

• Вперед n (где n – целое число), вызывающая передвижение Черепахи на n единиц в том направлении, куда указывает ее голова;

• Назад n (где n – целое число), вызывающая передвижение в противоположном голове направлении;

• Направо m (где m – целое число), вызывающая изменение направления движения на m градусов по часовой стрелке;

• Налево m (где m – целое число), вызывающая изменение направления движения на m градусов против часовой стрелки.

Запись Повтори k [Команда1 Команда2 … КомандаS] означает, что последовательность из S команд повторится k раз. Черепахе был дан для исполнения следующий алгоритм:

Повтори 2 [Вперед 10 Направо 90 Вперед 20 Направо 90]

Поднять хвост

Вперед 3 Направо 90 Вперед 5 Налево 90

Опустить хвост

Повтори 2 [Вперед 70 Направо 90 Вперед 80 Направо 90]

Определите, сколько точек с целочисленными координатами будет находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

6.2. Подготовка к выполнению заданий

Прежде чем описывать методику выполнения заданий, обсудим ряд вопросов, ответы на которые будут полезными при решении задач.

1. Результат выполнения ряда алгоритмов исполнителя Черепаха приведен в табл. 6.1.

Таблица 6.1

	Алгоритм	Что будет изображено
1	Повтори 4 [Вперед a Направо 90]	Квадрат со стороной а
2	Повтори 2 [Вперед a Направо 90 Вперед b Направо 90]	Прямоугольник со сторонами а и b
3	Повтори 3 [Вперед a Направо 120]	Правильный треугольник со стороной а
4	Повтори 3 [Направо 120 Вперед a]
5	Направо 30 Повтори 3 [Направо 120 Вперед a]
6	Повтори 6 [Вперед a Направо 60]	Правильный шестиу гольник со стороной а Начало координат выделено жирной точкой
7	Повтори 6 [Направо 60 Вперед a]
8	Направо 30 Повтори 6 [Вперед a Направо 60]

Во всех случаях после исполнения алгоритма Черепаха будет находиться в начале координат (на рисунках в последнем столбце оно отмечено жирной точкой).

2. Черепаха нарисовала параллельный или перпендикулярный оси абсцисс отрезок длиной n (n – целое число).

а) Сколько всего точек с целочисленными координатами имеется на отрезке? – Ответ: n + 1^{^[19]};

б) сколько точек с целочисленными координатами не принадлежит концам отрезка? – Ответ: n – 1.

3. На координатной плоскости имеется параллельный или перпендикулярный оси абсцисс отрезок длиной n (n – вещественное число). Один из концов отрезка имеет целочисленные координаты.

а) Сколько всего точек с целочисленными координатами имеется на отрезке? – Ответ: ⌊n⌋ + 1, где ⌊ ⌋ символы обозначают целую часть числа, записанного между ними;

б) сколько точек с такими координатами не принадлежит концам отрезка? – Ответ: ⌊n⌋;

в) сколько точек с такими координатами не принадлежит концам отрезка? – Ответ: ⌊n⌋.

4. Черепаха нарисовала прямоугольник размером а на b со сторонами, параллельными и перпендикулярными осям координат (а на b – целые числа). Одна из вершин прямоугольника имеет целочисленные координаты.

а) Сколько всего точек с целочисленными координатами имеется внутри прямоугольника (без учета точек, находящихся на его сторонах)? – Ответ: (а – 1) × (b – 1);

б) сколько всего точек с целочисленными координатами имеется внутри прямоугольника и на его сторонах? – Ответ: (а + 1) ×

(b + 1).

5. На координатной плоскости имеется участок, ограниченный нарисованным Черепахой равнобедренным прямоугольным треугольником с катетами, равными а (а – целое число). Катеты параллельны и перпендикулярны оси абсцисс. Вершина с прямым углом имеет целочисленные координаты.

а) Сколько всего точек с целочисленными координатами имеется внутри треугольника (без учета точек, находящихся на его сторонах)? – Ответ: 1 + 2 + … + (а – 1);

б) сколько всего точек с целочисленными координатами имеется внутри треугольника и на его сторонах? – Ответ: 1 + 2 + … +

(а + 1).

6. На координатной плоскости имеется участок, ограниченный нарисованной Черепахой равнобедренной трапецией с большим основанием а и меньшим основанием b. Углы при большем основании равны 45 градусов (то есть высота трапеции равна )). Основания трапеции параллельны и перпендикулярны оси абсцисс. Концы большего основания имеют целочисленные координаты.

а) Сколько всего точек с целочисленными координатами имеется внутри трапеции (без учета точек, находящихся на ее сторонах)? – Ответ: (b + 1) + (b + 3) + … + (а – 1);

б) сколько всего точек с целочисленными координатами имеется внутри трапеции и на ее сторонах? – Ответ: (b + 1) + (b + 3) + … + (а + 1).

Примечание. При необходимости указанные зависимости можно установить, рассмотрев простой пример, например такой (а = 4, b = 3):

6.3. Примеры заданий и методика их выполнения

6.3.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Напомним, что в первом варианте задания требовалось определить, сколько точек с целочисленными координатами будет находиться внутри области, ограниченной линией, заданной алгоритмом:

Повтори 7 [Вперед 10 Направо 120]

(Точки на линии учитывать не следует.)

Решение

Так как в результате выполнения алгоритма Повтори 3 [Вперед 10

Направо 120] будет изображен равносторонний треугольник со стороной 10 (см. алгоритм 3 в табл. 6.1) и Черепаха окажется в исходном положении, то после еще четырех повторений тех же двух команд ничего нового нарисовано не будет.

Изобразим полученный треугольник и еще ряд линий (см. рис. 6.1).

Рис. 6.1

Размер высоты треугольника, оформленной пунктирной линией, составляет ≈ 8,6. Сколько точек с целочисленными координатами будет находиться на этой высоте (без учета левой точки, расположенной на линии)? – 8 (см. воп рос 3б).

А как определить количество других точек?

Рассмотрим небольшую утолщенную горизонтальную линию. Ее размер можно определить с помощью пропорции:

× 8,6 ≈ 1,7.

Это значит, что количество учитываемых на ней точек с целочисленными координатами равно 1 (также согласно ответу на вопрос 3б).

Для других горизонтальных линий, расположенных ниже этой и выше пунктирной линии, соответствующие значения приведены в таблице:

Линия	Примерная длина	Количество учитываемых точек
2-я	3,4	3
3-я	5,1	5
4-я	6,8	6

Для линий ниже пунктирной все аналогично.

Итак, общее искомое число точек равно

(1 + 3 + 5 + 6) × 2 + 8 = 38.

Удобно провести расчеты с помощью электронной таблицы.

Оформим лист следующим образом:

	А	В	С
1	1	1,732051	1
2	2	3,464102	3
3	3	5,196152	5
4	4	6,928203	6
5	5	8,660254	8
6	4	6,928203	6
7	3	5,196152	5
8	2	3,464102	3
9	1	1,732051	1

В столбце В получим длины всех горизонтальных отрезков, расположенных в треугольнике. Для этого запишем формулы:

• в ячейку В5: =КОРЕНЬ(10 * 10 - 5 * 5), или =КОРЕНЬ(100 - 25), или =КОРЕНЬ(75);

• в ячейку В1: ==$B$5 / 5 * A1.

Последнюю формулу скопируем в остальные ячейки столбца В – получим следующее:

	А	В	С
1	1	1,732051	1
2	2	3,464102	3
3	3	5,196152	5
4	4	6,928203	6
5	5	8,660254	8
6	4	6,928203	6
7	3	5,196152	5
8	2	3,464102	3
9	1	1,732051	1

После этого в столбце С рассчитаем целую часть значений в столбце В (количество нужных нам точек с целочисленными координатами). Для этого в ячейку С1 надо ввести формулу =ЦЕЛОЕ(B1), которую затем распространить (скопировать) на другие ячейки:

	А	В	С
1	1	1,732051	1
2	2	3,464102	3
3	3	5,196152	5
4	4	6,928203	6
5	5	8,660254	8
6	4	6,928203	6
7	3	5,196152	5
8	2	3,464102	3
9	1	1,732051	1

Искомое по условию значение определяется как сумма чисел в столбце С. Можно также значение 8,660254 получить в первой строке:

	А	В	С
1	5	8,660254	8
2	1	1,732051	1
3	2	3,464102	3
4	3	5,196152	5
5	4	6,928203	6
6	4	6,928203	6
7	3	5,196152	5
8	2	3,464102	3
9	1	1,732051	1

В этом случае «базовая» для копирования формула в ячейке B2: =$B$1/5*A2.

Конечно, особенно удобно проводить расчеты в среде элект ронной таблицы при больших размерах фигур, изображенных Черепахой.

Рекомендации

На экзамене с целью экономии времени координатную сетку, учитываемые точки и т. п. можно не рисовать. Достаточно только изобразить эскиз с видом фигуры и несколькими линиями, а также учесть важный вывод: если значение высоты треугольника, на рис. 6.1 оформленной пунктиром, не является целым числом, то и все другие размеры отрезков горизонтальных линий, рассчитываемые по пропорциям, также не будут целочисленными, поэтому количество учитываемых на них точек равно целой части размера линии (см. выше). При этом в ряде случаев могут рассматриваться и линии, параллельные оси ординат.

Решение задачи варианта 2

Напомним, что Черепахе был дан для исполнения следующий алгоритм:

Повтори 2 [Вперед 10 Направо 90 Вперед 20 Направо 90]

Поднять хвост

Вперед 3 Направо 90 Вперед 5 Налево 90

Опустить хвост

Повтори 2 [Вперед 70 Направо 90 Вперед 80 Направо 90]

– и требовалось определить, сколько точек с целочисленными координатами будет находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, включая точки на границах этого пересечения.

Проанализировав результаты выполнения алгоритма (сделав эскиз рисуемого Черепахой изображения – см. рис. 6.3^{^[20]}) с учетом табл. 6.1 (см. алгоритм 2), можно установить, что будут изображены два прямоугольника с размерами 10×20 и 70×90. Пересечение этих фигур также является прямоугольником (на рис. 6.2 он оттенен), имеющим размеры 15 на 7. Согласно ответу на вопрос 4б искомое количество точек равно^{^[21]}

(15 + 1) (7 + 1) = 128.

Ответ: 128.

6.3.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2024 года)

Вариант 1 задания такой же, как в демоварианте экзамена 2023 года. Обсудим методику выполнения варианта 2 задания.

Условие (без описания команд Черепахе)

Черепахе был дан для исполнения следующий алгоритм:

Повтори 2 [Вперед 8 Направо 90 Вперед 18 Направо 90]

Поднять хвост

Вперед 4 Направо 90 Вперед 10 Налево 90

Опустить хвост

Повтори 2 [Вперед 17 Направо 90 Вперед 7 Направо 90]

Определите, сколько точек с целочисленными координатами будет находиться внутри объединения фигур, ограниченного заданными алгоритмом линиями, включая точки на линиях.

Решение

Здесь в условии надо обратить внимание на фразу «внутри объединения фигур».

Что будет изображено в результате выполнения приведенного алгоритма? По первой команде будет нарисован прямоугольник высотой 8 и шириной 18 (см. рис. 6.3).

После этого Черепаха без рисования переместится внутрь этого прямоугольника, после чего нарисует второй прямоугольник высотой 17 и шириной 7. Общий результат схематично представлен на рис. 6.3.

Рис. 6.3

Объединение двух прямоугольников оттенено. Сколько нужных по условию точек есть в этом объединении?

В первом (нижнем) прямоугольнике таких точек 19 × 9 = 171 (см. ответ на вопрос 4б в разделе 6.2).

Осталась еще часть второго прямоугольника размером 13×7. Можем ли аналогично подсчитать количество нужных точек в этой части? – Нет, не можем, так как ряд точек этой части мы уже учли. Без их учета можно сказать, что нам осталось определить количество нужных точек в прямоугольнике размером (13 – 1) × 7, то есть размером 12×7. Это количество равно 13 × 8 = 104, а общее искомое количество – 275.

Ответ: 275.

Анализ выполнения рассмотренного примера говорит о важности умения определять количество точек с целочисленными координатами в объединении двух прямоугольников. См. задание 6 для самостоятельной работы.

6.3.3. Пример 3

Условие

Дан алгоритм:

Направо 30 Повтори 6 [Направо 60 Вперед 8]

Определите, сколько точек с неотрицательными целочисленными координатами будет находиться внутри области, ограниченной линиями, которые будут изображены заданным алгоритмом, и линией, описываемой функцией х = 8.

Решение

Что будет изображено в результате выполнения приведенного алгоритма? Согласно табл. 6.1 (см. алгоритм 7), правильный шестиугольник со сторонами, равными 10. Учитывая расположение этой фигуры относительно начала координат, можно сделать вывод о том, что точки с неотрицательными целочисленными координатами расположены на оси абсцисс и выше. Нарисуем соответствующую часть фигуры:

Рис. 6.4

Рассмотрим прямоугольник, ограниченный одной из сторон шестиугольника, осью абсцисс и высотами трапеции, оформленных пунктиром. Его высота равна примерно 6,9. Согласно ответу на вопрос 3а, на этой высоте 6 + 1 = 7 точек с целочисленными координатами, на верхнем основании трапеции – 9 (см. ответ на вопрос 2а в разделе 6.2), то есть общее число таких точек во всем прямоугольнике – 63.

С точками в прямоугольных треугольниках сложнее. В них удобно рассматривать не горизонтальные линии, как при выполнении задания в п. 6.3.1, а вертикальные. Таких линий – 3. Зная размер 6,9, можно пропорционально определить длины отрезков этих линий внутри треугольников: 1/4 × 6,9 ≈ 1,72; 2/4 × 6,9 ≈ 3,4; 3/4 × 6,9 ≈ 5,2.

Соответствующее количество точек с целочисленными координатами 2, 4 и 6 (см. ответ на вопрос 3а в разделе 6.2). С учетом точки в начале координат общее количество точек в левом прямоугольном треугольнике равно 13^{^[22]}, а искомое в задании количество точек – 63 + 13 × 2 = 89. Итак, ответ: 89.

Рекомендация

Самостоятельно убедитесь в том, что использование при решении последней задачи пропорций для отрезков горизонтальных линий потребовало бы большего времени для расчетов.

А вот аналогичные расчеты с помощью электронной таблицы:

	А	В	С
1		6,928203
2	1	1,732051	2
3	2	3,464102	4
4	3	5,196152	6
5	3	5,196152	6
6	2	3,464102	4
7	1	1,732051	2
8			24

(Базовая для копирования формула в ячейке

B2: =$B$1 / 4 * A2.)

Учтя еще два значения, равных 1, получим искомое значение:

63 + 24 + 2 = 89.

6.4. Задания для самостоятельного выполнения

В заданиях 1–5 речь идет об алгоритмах, выполняемых исполнителем Черепаха, система команд которого включает 6 команд:

• Поднять хвост;

• Опустить хвост;

• Вперед n (где n – целое число);

• Назад n (где n – целое число); • Направо m (где m – целое число);

• Налево m (где m – целое число).

1. Дан алгоритм:

Поднять хвост Назад 400 Опустить хвост

Повтори 8 [Вперед 12 Налево 90]

2. Определите, сколько точек с целочисленными координатами будет находиться внутри области, ограниченной линиями, которые будут изображены заданным алгоритмом:

Налево 90 Вперед 12 Повтори 2 [Налево 120 Вперед 12] Точки на линиях также должны учитываться.

3. Дан алгоритм:

Направо 90 Поднять хвост Повтори 6 [Налево 120 Вперед 8] Вперед 18 Опустить хвост Повтори 5 [Вперед 10 Налево 120]

Определите, сколько точек с целочисленными координатами будет находиться внутри области, ограниченной линиями, которые будут изображены заданным алгоритмом. Точки на линиях не должны учитываться.

4. Определите, сколько точек с целочисленными координатами будет находиться внутри пересечения фигур, ограниченных заданными алгоритмом линиями, без учета точек на границах этого пересечения.

Налево 90 Повтори 2 [Вперед 15 Налево 90 Вперед 10 Налево 90]

Поднять хвост

Назад 2 Направо 180

Опустить хвост

Повтори 2 [Вперед 20 Направо 90 Вперед 13 Направо 90]

5. Дан алгоритм:

Поднять хвост

Направо 90 Вперед 5

Налево 90 Опустить хвост Вперед 10

Налево 135 Вперед 15

Определите, сколько точек с целочисленными координатами будет находиться внутри области, ограниченной линиями алгоритма и осью абсцисс. Точки на линиях также должны учитываться.

6. Определите, сколько точек с целочисленными координатами имеется в оттененной части изображения на рис. 6.5:

а) с учетом точек на границе изображения;

б) без учета этих точек.

Рис. 6.5

7. Исполнитель Чертежник перемещается на координатной плоскости, оставляя след в виде линии. Чертежник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертежника из точки с координатами (x, y) в точку с координатами (x + a; y + b). Например, если Чертежник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертежника в точку (6, −1).

Дан алгоритм:

сместиться на(12, 0) сместиться на(-4, 4) сместиться на(-4, 0) сместиться на(-4, -4)

Определите, сколько точек с целочисленными координатами будет находиться внутри области, ограниченной линиями алгоритма.

Точки на линиях учитываться не должны.

Глава 7 Задания 7

7.1. Общие вопросы. Теория

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 7 указывается «умение определять объем памяти, необходимый для хранения графической и звуковой информации».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 5 мин.

***

Кодирование растровых изображений

Растровое изображение – изображение, представляющее собой сетку пикселей (цветных или черных и белых точек) на мониторе и других отображающих устройствах.

При хранении информации о растровом изображении в памяти компьютера запоминается цвет каждого пикселя изображения. Если для хранения цвета каждого пикселя требуется ГЦ бит, то объем памяти ОП, необходимый для хранения изображения из КП пикселей, равен:

ОП = КП × ГЦ бит. (7.1)

Обозначение ГЦ использовано потому, что количество бит, необходимое для хранения цвета одного пикселя, называют глубина цвета (или разрядность кодирования). Глубина цвета ГЦ зависит от количества используемых в изображении цветов КЦ.

При заданном количестве цветов КЦ, используемых в изображении, количество бит ГЦ, требуемых для хранения информации о цвете одного пикселя, определяется следующим образом.

1. Если КЦ является степенью двойки, то ГЦ = log₂КЦ.

Приведем таблицу некоторых значений КЦ и ГЦ:

Таблица 7.1

КЦ	2	4	8	16	32	64	128	256	65536
ГЦ	1	2	3	4	5	6	7	8	16

2. Если КЦ не есть степень двойки, то ГЦ равно показателю степени ближайшей большей КЦ степени двойки. Например, при КЦ = 18 ближайшей большей степенью двойки является число 32 (2⁵), то есть соответствующая глубина цвета ГЦ равна 5.

Таблица для некоторых значений КЦ и ГЦ:

Таблица 7.2

КЦ	5–7	9–15	17–31	33–63	65–127	129–255	257–511	513–1023	1025–2047
ГЦ	3	4	5	6	7	8	9	10	11

При известном значении глубины цвета ГЦ количество возможных цветов КЦ определяется как 2^ГЦ.

Количество пикселей в изображении КП равно произведению его ширины Ш на высоту В (оба размера – в пикселях).

При выполнении заданий важно помнить зависимость между разными единицами измерения информации:

1 байт = 2³ (8) бит;

1 килобайт = 2¹⁰ (1024) байт = 2¹³ бит;

1 мегабайт = 1024 (2¹⁰) килобайт = 2²⁰ байт = 2²³ бит; 1 гигабайт = 2³³ бит.

В заданиях, связанных с кодированием растровых изображений, могут быть представлены задачи, в которых фигурирует так называемое разрешение сканирования.

Разрешение сканирования – это величина, определяющая, сколько точек (элементов растрового изображения, в котором будет представлен сканируемый документ) должен зафиксировать сканер на одной линии сканирования. Значение этой величины указывается в так называемых dpi (англ. dots per inch, например 300 dpi означает 300 точек на один дюйм).

Кодирование звуковых объектов

При сохранении звука в памяти компьютера (говорят – «при оцифровке звука») запоминаются только отдельные значения сигнала, которые нужно потом выдать на динамик или наушники.

Количество сигналов (отсчетов), запоминаемых за 1 секунду, называют частотой дискретизации. Она измеряется в герцах (Гц). 1 Гц (один герц) – это один отсчет в секунду. Возможны также производные единицы, как правило, это килогерц (кГц). 1 кГц – это 1000 отсчетов в секунду (не 1024!).

Количество битов, которые выделяются в памяти для хранения значения одного отсчета, называют глубиной кодирования (используется также понятие разрешение кодирования, или, короче, разрешение).

Сказанное означает, что для хранения информации о звуке длительностью С секунд, закодированном с частотой дискретизации ЧД герц и глубиной кодирования ГК бит, требуется:

ЧД × ГК × С бит памяти. (7.2)

При стереозаписи звука (двухканальной^{^[23]}) объем памяти, необходимый для хранения данных одного канала записи, умножается на 2, при четырехканальной звукозаписи (квадрозаписи) – на 4.

Как и при расчетах, связанных с кодированием растровых изображений, важно помнить зависимость между разными единицами измерения информации (см. выше). Целесообразно также по возможности использовать значения степеней двойки и принять, что 1000 ≈ 1024 = 2¹⁰. При этом для значений времени и количества информации можно использовать приближенные равенства:

1 мин = 60 сек ≈ 64 сек = 2⁶ сек;

1 килобайт ≈ 1000 байт;

1 мегабайт ≈ 1 000 000 байт.

Типы задач

В заданиях 7, представленных в демонстрационных вариантах ЕГЭ по информатике и в других публикациях, связанных с экзаменом, можно выделить четыре типа задач с условными названиями^{^[24]}:

1) «прямые задачи»;

2) «обратные задачи»;

3) «прямые задачи с изменением»;4) «обратные задачи с изменением».

Эти типы задач связаны как с кодированием графики, так и с кодированием звука.

7.2. Примеры задач на кодирование графики и методика их выполнения

7.2.1. «Прямые задачи»

В таких задачах известны значения размеров изображения – ширина Ш и высота В, глубина цвета ГЦ (или количество цветов КЦ), и нужно определить объем памяти, требуемой для хранения изображения. Два основных варианта таких задач решаются по формулам, приведенным в таблице:

Известны	Промежуточные вычисления	Объем памяти в битах
Размеры Ш и В, глубина цвета ГЦ		ОП = Ш × В × ГЦ
Размеры Ш и В, количество цветов КЦ	Глубина цвета ГЦ = log₂КЦ или (!) с учетом табл. 7.2	ОП = Ш × В × ГЦ

Пример 1

Какой минимальный объем памяти (в Кбайтах) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей, если известно, что цвет каждого пикселя кодируется восемью битами?

Прежде чем приводить решение, обратим внимание на то, что искомое значение должно быть выражено в килобайтах, а при расчете значения объема памяти по формуле, приведенной в таблице чуть выше, результат равен количеству битов. В таких случаях значения используемых величин удобно выражать в виде степеней двойки.

Решение

Учтем, что 128 = 2⁷, и определим общее количество пикселей в изображении: 2⁷ × 2⁷ = 2¹⁴.

Далее, так как глубина цвета составляет 8 (2³), то объем памяти, занимаемый изображением, равен 2¹⁴ × 2³ = 2¹⁷ бит.

Так как 1 Кбайт = 10¹³ бит (см. раздел 7.1), то искомое значение в килобайтах равно 2¹⁷: 10¹³ = 2⁴ = 16.

Ответ: 16.

Пример 2

Имеется растровое изображение размером 64×64 пикселей, в котором используются 256 различных цветов. Какой минимальный объем памяти (в Кбайтах) нужно зарезервировать для его хранения в памяти компьютера?

Решение

Рассчитываем количество пикселей КП в изображении, также учитывая сделанную чуть выше рекомендацию об использовании степеней двойки:

КП = 64 × 64 = 2⁶× 2⁶ = 2¹².

Определяем глубину цвета ГЦ. Так как количество цветов 256 есть степень двойки, то ГЦ = 8 бит.

Рассчитываем объем памяти, требуемый для хранения изображения:

212 × 23 = 215 бит.

Так как по условию требуется определить этот объем в килобайтах (1 килобайт = 2¹³ бит), то искомое значение равно

215 : 213 = 22 = 4.

Ответ: 4.

Возможны также задачи, в которых речь идет об изображениях, которые хранятся в памяти в сжатом виде.

Пример 3 ([4], автор задачи Е. Джобс)

Необходимо сохранить изображение размером 960×512 пикселей. Известно, что каждый пиксель может быть окрашен в один из 1200 цветов. Для кодирования цвета каждого пикселя используется одинаковое количество битов, коды пикселей записываются в файл один за другим без промежутков. После кодирования информации о цветах пикселей изображение сжимают. Исходный файл изображения больше, чем сжатый, на 35 %. Какое минимальное целое количество килобайтов необходимо выделить для хранения сжатого изображения?

Решение

Объем памяти для хранения исходного (несжатого) изображения: 960 × 512 × 11 бит, где 11 – глубина цвета при 1200 различных цветах (см. табл. 7.2).

Определим соответствующее значение в килобайтах, используя значения степеней двойки:

960 = 64 × 15 = 2⁶ × 15

512 = 2⁹

2⁶ × 15 × 2⁹× 11 = 165 × 2¹⁵ бит = 165 × 2² байт = 660 байт.

Далее следует учесть сжатие этого изображения. Так как по условию исходный файл изображения больше, чем сжатый, на 35 %, то его объем в 1,35 больше. Значит, объем сжатого файла будет в 1,35 меньше, чем 660 байт, то есть равен ≈ 489 байт.

По условию требуется найти минимальное целое количество килобайтов, которое в данном случае равно 1.

Ответ: 1.

Внимание! Для нахождения объема сжатого файла умножать объем исходного файла на 0,65 нельзя! Это замечание следует учитывать и при выполнении аналогичных заданий.

7.2.2. «Обратные задачи»

В таких задачах известен объем памяти ОП, выделяемой для хранения изображения, а также некоторые характеристики изображения, от которых он зависит, и требуется определить какую-то другую характеристику. Например, известны:

• объем памяти ОП,

• количество пикселей КП, и нужно определить глубину цвета ГЦ.

Формула для расчета глубины цвета: ГЦ = , при этом значение ОП должно быть выражено в битах.

Если требуется определить максимальное количество цветов, которое при этом можно использовать в изображении, то после определения глубины цвета ГЦ это количество рассчитывается по формуле 2^ГЦ.

Пример 1 (задание из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.)

Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 20 Кбайт памяти без учета размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество битов, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

Решение

Заданный объем файла переводим из килобайтов в биты:

20 Кбайт = 20× 2¹⁰ байт = 20 × 2¹³ бит.

При неизвестной глубине цвета ГЦ можем составить неравенство, определяющее максимальное значение ГЦ:

128 × 320 × ГЦ ≤ 20 × 2¹³.

Упростив его:

2⁷ × 2⁵ × 10 × ГЦ ≤ 20 × 2¹³

2¹³ × 5 × ГЦ ≤ 20 × 2¹³

– и решив, получим ГЦ ≤ 4.

Максимальная глубина цвета равна 4, а соответствующее количество цветов – 2⁴= 16.

Ответ: 16.

В задачах рассмотренного типа максимальное значение глубины цвета ГЦ может быть определено из неравенства:

Ш × В × ГЦ ≤ ОП_Кбайт × 2¹³,

где Ш и В – соответственно ширина и высота изображения (оба размера – в пикселях, значения по возможности представлены в виде степеней двойки), ОП_Кбайт – предельный размер памяти в килобайтах, а искомое количество цветов будет равно 2^ГЦ.

Если в условии предельный размер памяти задан в мегабайтах, то соответствующее неравенство имеет вид:

Ш × В × ГЦ ≤ ОП_Мбайт × 2²³.

Возможны также задачи, в которых искомые характеристики изображения определяются в зависимости не от всего объема выделяемой памяти, а от какой-то его части.

Пример 2

Для проведения эксперимента создаются изображения, содержащие случайные наборы цветных пикселей. Размер изображения – 320×240 пикселей, при сохранении изображения каждый пиксель кодируется одинаковым числом битов, все коды пикселей записываются подряд, методы сжатия не используются. Размер файла не должен превышать 100 Кбайт, при этом 20 Кбайт необходимо выделить для служебной информации. Какое максимальное количество различных цветов можно использовать в изображении?

Решение

Здесь надо учесть, что на изображение надо выделить не 100, а 100 – 20 = 80 Кбайт.

Остальные расчеты аналогичны:

• объем для изображения в битах: 80 Кбайт = 80 × 2¹³;

• неравенство, определяющее максимальное значение глубины цвета: 320 × 240 × ГЦ ≤ 80 × 2¹³, решение которого дает ГЦ ≤ 8,533. Значит, ГЦ = 8;

• соответствующее количество цветов: 2⁸= 256.

Ответ: 16.

Приведем еще один пример, в котором заданный объем памяти корректируется.

Пример 3

Для хранения сжатого произвольного растрового изображения размером 192×960 пикселей отведено 90 Кбайт памяти без учета размера заголовка файла. При сжатии объем файла уменьшается на 35 %. Для кодирования цвета каждого пикселя используется одинаковое количество битов, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

Решение

Здесь надо обратить внимание на то, что объем выделенной памяти указан для сжатого изображения. Поэтому сначала найдем объем несжатого изображения.

Рассуждения такие. Так как при сжатии объем исходного файла уменьшается на 35 %, то его объем стал составлять 65 % от исходного. Это значит, что при отведенных 90 килобайтах памяти в них можно сохранить 90 : 0,65 ≈ 138,5 Кбайт несжатого изображения. После этого можно записать неравенство:

192 × 960 × ГЦ < 138 × 2¹³ бит,

откуда глубина цвета ГЦ = 6. Значит, в изображении можно использовать не более 2⁶ = 64 цветов.

Ответ: 64.

Возможны также задачи, в которых речь идет не об одном, а о нескольких изображениях.

Пример 4

В информационной системе хранятся изображения размером 1024×768 пикселей. Методы сжатия изображений не используются. Каждое изображение дополняется служебной информацией, которая занимает 1280 Кбайт. Для хранения 2048 изображений потребовалось 4 Гбайта. Сколько цветов использовано в палитре каждого изображения?

Решение

Здесь фигурируют 2048 изображений, а также имеется дополнительная служебная информация об изображении. Для нахождения ответа следует определить объем, необходимый для хранения одного изображения без учета служебной информации.

Для хранения одного изображения, включая служебную информацию, потребуется

= 2048 Кбайт,

а без ее учета 2048 − 1280 = 768 Кбайт.

После этого можно составить неравенство:

1024 × 768 × ГЦ ≤ 768 × 2¹³,

откуда ГЦ = 8. Итак, в палитре используется 2⁸ = 256 цветов.

Ответ: 256.

Пример 5

Автоматическая фотокамера производит растровые изображения с палитрой из 256 цветов. При этом объем файла с изображением не может превышать 150 Кбайт, упаковка данных не производится. Какой максимальный размер изображения в битах может быть при этом?

Решение

Здесь искомым является размер изображения. Поскольку объем памяти для хранения растрового изображения равен произведению количества пикселей КП на глубину цвета КЦ, которая в данном случае равна 8, то для соблюдения требуемого условия должно соблюдаться неравенство:

КП × 8 ≤ 150 × 2¹³ бит.

Его решение дает максимальное значение КП, равное 153 600.

Ответ: 153 600.

В задачах рассмотренного типа максимальный размер изображения в пикселях КП может быть определен из неравенства:

КП × ГЦ ≤ ОП_Кбайт × 2¹³,

где ГЦ – глубина цвета изображения (определяемая заданной палитрой цветов и выраженная в виде степени двойки), ОП_Кбайт – предельный размер памяти в килобайтах.

Если в условии предельный размер файла задан в мегабайтах, то соответствующее неравенство имеет вид:

КП × Г ≤ ОП_Мбайт × 2²³.

7.2.3. «Прямые задачи с изменением»

Общая особенность таких задач:

• приводятся характеристики изображения, от которых зависит объем памяти для его хранения, и соответствующий объем. Далее говорится об изменении одной или более характеристик (например, количества цветов, используемых в изображении). Требуется определить новое значение объема памяти.

Пример 1

Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 2²⁴ = 16 777 216 цветов. Средний размер фотографии составляет 12 Мбайт. Для хранения в базе данных фотографии преобразуют в черно-белый формат с палитрой, содержащей 256 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?

Решение

Здесь изменилось количество цветов в фотографии. Так как на объем памяти непосредственно влияет глубина цвета, то нужно определить, как при этом изменилась эта характерис тика.

В исходной картинке глубина цвета была равна 24 бита, после преобразования она стала равной 8, то есть в три раза меньше. Значит, и средний размер изображения изменился пропорционально (в три раза) и станет равным 12 : 3 = 4 Мбайта.

Ответ: 4.

Можно так описать методику выполнения заданий рассмотренного типа:

• в зависимости от использованных палитр определить глубину цвета исходной фотографии ГЦ1 и измененной ГЦ2;

• если глубина цвета изменилась (увеличилась или уменьшилась) в k раз, то и размер изображения (общий или средний, как в рассмотренной задаче) также изменится в k раз.

Пример 2

Для хранения в информационной системе документы сканируются с разрешением^{^[25]} 300 dpi и цветовой системой, содержащей 2¹⁶ = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 18 Мбайт. В целях экономии было решено перейти на разрешение 200 dpi. Сколько Мбайт будет составлять средний размер документа, отсканированного с измененными параметрами?

Решение

Разрешение сканирования изменилось с 300 dpi на 200 dpi. Как изменится при этом общее количество точек в отсканированном документе?

Так как разрешение определяет количество точек, которые сканер должен зафиксировать на одной линии сканирования, то изменение этого параметра коснется всех линий (всего документа), то есть общее количество точек изменится пропорционально квадрату изменения разрешения:

Размер документа (в единицах измерения информации) прямо пропорционален количеству точек в нем, то есть также изменился в раза и стал равным 8 Мбайт.

Ответ: 8.

Общая методика выполнения заданий рассмотренного типа:

• по заданным значениям разрешения определить «коэффициент» изменения размера изображения в точках Кразм;

• новое значение размера документа изменится пропорционально квадрату изменения этого коэффициента.

Внимание! Величину изменения разрешения не следует представлять в десятичной форме в приближенном виде.

Пример 3

Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 2¹⁶ = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 16 Мбайт. В целях экономии было решено перейти на разрешение 150 dpi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с измененными параметрами?

Решение

Здесь изменились два исходных параметра сканирования.

Разрешение сканирования изменилось с 300 dpi на 150 dpi. Это значит, что количество точек в нем изменилось в

раза.

Первоначальная глубина цвета составляла 16, уменьшилась до 8, то есть изменилась в раза.

Следовательно, средний размер документа, отсканированного с измененными параметрами, станет равным

16 × = 2 Мбайта.

Ответ: 2.

Общая методика выполнения заданий рассмотренного типа:

• по заданным значениям разрешения определить «коэффициент» изменения размера изображения в точках Кразм;

• по заданным значениям количества цветов определить «коэффициент» изменения глубины цвета Кгц^;

• новое значение размера документа находится по формуле:

Рисх × Кразм × Кгц,

где Рисх – исходный размер.

Обратим внимание на то, что в задании может идти речь не об экономии памяти, а о повышении качества представления информации.

7.2.4. «Обратные задачи с изменением»

Общая особенность таких задач:

• приводятся характеристики изображения, от которых зависит объем памяти для его хранения, и соответствующий объем. Далее говорится о изменении объема памяти в результате изменения одной из характеристик. Требуется определить новое значение этой характеристики.

Пример

Автоматическая фотокамера с 400 Кбайт видеопамяти производит растровые изображения c фиксированным разрешением и 16-цветной палитрой. Сколько цветов можно будет использовать в палитре, если увеличить видеопамять до 800 Кбайт?

Решение

Как количество цветов в палитре влияет на объем памяти ОП? Мы знаем, как влияет глубина цвета ГЦ – прямо пропорционально (ОП = количество пикселей × ГЦ). Значит, если ОП увеличился в два раза, то в два раза увеличилась глубина цвета. При 16-цветной палитре она была равна 4, то есть стала равной 8. Следовательно, количество цветов, которые можно использовать в такой палитре, составляет 2⁸ = 256. Ответ: 256.

Можно так описать методику выполнения заданий рассмотренного типа:

1) определить глубину цвета в заданной палитре ГЦ1;

2) определить, как изменился объем памяти;

3) если он изменился в k раз (при k > 1 – увеличился, при k < 1 – уменьшился), то

• рассчитать глубину цвета в новой палитре ГЦ2 по формуле: ГЦ2 = ГЦ1 × k;

• искомое значение количества цветов в новой палитре будет равно 2^ГЦ².

7.2.5. Задачи для самостоятельного решения

1. Какой минимальный объем памяти (в Кбайтах) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 256×256 пикселей, если известно, что цвет каждого пикселя кодируется шестнадцатью битами?

2. Какой минимальный объем памяти (в Кбайтах) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512×512 пикселей, при условии что в изображении могут использоваться 256 различных цветов?

3. (Задание из демонстрационного варианта ЕГЭ 2024 года)

Прибор автоматической фиксации нарушений правил дорожного движения делает цветные фотографии размером 1024×768 пикселей, используя палитру из 4096 цветов. Для передачи снимки группируются в пакеты по 256 штук. Определите максимальный размер одного пакета фотографий в Мбайтах.

4. Необходимо сохранить изображение размером 1920×1024 пикселя. Известно, что каждый пиксель может быть окрашен в один из 600 цветов. Для кодирования цвета каждого пикселя используется одинаковое количество битов, коды пикселей записываются в файл один за другим без промежутков. После кодирования информации о цветах пикселей изображение сжимают. Исходный файл изображения больше, чем сжатый, на 40 %. Какое минимальное целое количество килобайтов необходимо выделить для хранения сжатого изображения?

5. Для хранения произвольного растрового изображения размером 128×320 пикселей отведено 40 Кбайт памяти без учета размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество битов, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

6. Автоматическая фотокамера производит растровые изображения размером 1600×1200 пикселей. При этом объем файла с изображением не может превышать 1 Мбайта, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?

7. Для проведения эксперимента создаются изображения, содержащие случайные наборы цветных пикселей. Размер изображения 640×480 пикселей, при сохранении изображения каждый пиксель кодируется одинаковым числом битов, все коды пикселей записываются подряд, методы сжатия не используются. Размер файла не должен превышать 280 Кбайт, при этом 40 Кбайт необходимо выделить для служебной информации. Какое максимальное количество различных цветов и оттенков можно использовать в изображении?

8. Для хранения сжатого произвольного растрового изображения размером 640×256 пикселей отведено 170 Кбайт памяти без учета размера заголовка файла. Исходный файл изображения больше, чем сжатый, на 35 % (считая размер сжатого файла за 100 %). Для кодирования цвета каждого пикселя используется одинаковое количество битов, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

9. В информационной системе хранятся изображения размером

2048×1536 пикселей. При кодировании используется алгоритм сжатия изображений, позволяющий уменьшить размер памяти для хранения одного изображения в среднем в 8 раз по сравнению с независимым кодированием каждого пикселя. Каждое изображение дополняется служебной информацией, которая занимает 128 Кбайт. Для хранения 32 изображений потребовалось 16 Мбайт. Сколько цветов использовано в палитре каждого изображения?

10. Автоматическая фотокамера производит растровые изображения с 16-цветной палитрой. При этом объем файла с изображением не может превышать 300 Кбайт, упаковка данных не производится. Какой максимальный размер изображения в битах может быть при этом?

11. Автоматическая фотокамера производит растровые изображения с 16-цветной палитрой. При этом объем файла с изображением не может превышать 1 Мбайта, упаковка данных не производится. Какой максимальный размер изображения в битах может быть при этом?

12. Автоматическая фотокамера делает фотографии высокого разрешения с палитрой, содержащей 2²⁴ = 16 777 216 цветов. Средний размер фотографии составляет 12 Мбайт. Для хранения в базе данных фотографии преобразуют в черно-белый формат с палитрой, содержащей 256 цветов. Другие преобразования и дополнительные методы сжатия не используются. Сколько Мбайт составляет средний размер преобразованной фотографии?

13. Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 2²⁴ = 16 777 216 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 18 Мбайт. В целях экономии было решено перейти на разрешение 150 dpi и цветовую систему, содержащую 2¹⁶ = 65 536 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с измененными параметрами?

14. Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 2¹⁶ = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 8 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 2²⁴ = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с измененными параметрами?

15. Автоматическая фотокамера с 200 Кбайт видеопамяти производит растровые изображения c фиксированным разрешением и 8-цвет-

ной палитрой. Сколько цветов можно будет использовать в палитре, если увеличить видеопамять до 400 Кбайт?

7.3. Примеры задач на кодирование звука и методика их выполнения

7.3.1. «Прямые задачи»

В таких задачах известны значения параметров дискретизации (частоты ЧД и глубины кодирования ГК), а также длительности записи С; нужно определить объем требуемой памяти для хранения звука.

Пример 1

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запис ь длится одну минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,2; 2) 2; 3) 3; 4) 4.

Решение

Переводим исходные данные в герцы, секунды и биты/байты:

• частота дискретизации: 16 кГц = 16 000 Гц;

• время записи: 1 минута = 60 секунд;

• глубина кодирования: 24 бита = 3 байта.

Размер полученного файла (формула (7.2)):

16 000 × 3 × 60 = 2 880 000 байт,

или (учитывая, что 1 Мбайт ≈ 1 000 000 байт) примерно 3 Мбайта.

Ответ: 3.

Возможны также задачи, в которых задана не глубина кодирования, а количество так называемых уровней дискретизации (или уровней квантования), то есть количество возможных значений отсчетов при дискретизации. Количество уровней дискретизации КУ связано с глубиной кодирования ГК следующим образом:

КУ = 2^ГК.

Зависимость значения ЧД от числа уровней дискретизации КУ:

ЧД = log₂КУ (см. также табл. 7.1–7.2).

Пример 2

Производится одноканальная (моно) звукозапись с частотой дискретизации 64 Гц. При записи используется 32 уровня дискретизации. Запи сь длится 4 минуты 16 секунд, ее результаты записываются в файл, причем каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в килобайтах?

1) 10; 2) 6; 3) 32; 4) 512.

Решение

При 32 уровнях дискретизации глубина кодирования составляет 5 бит. Время записи в секундах: 4 × 60 + 16 = 256, или 2⁸.

Выражая в виде степени двойки и частоту дискретизации (64 Гц), размер полученного файла можно определить следующим образом:

2⁶× 5 × 2⁸ = 5 × 2¹⁴бит.

Полученное значение выражаем в килобайтах:

5 × 2¹⁴бит = 5 × 2 × 2¹³бит = 10 Кбайт.

Ответ: 1.

Еще раз напомним, что при стереозаписи полученный объем памяти умножается на 2.

7.3.2. «Обратные задачи»

В таких задачах известен объем памяти ОП, выделяемой для хранения звукозаписи, а также некоторые характеристики дискретизации, от которых он зависит, и требуется определить какую-то другую характеристику.

Пример 1

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и глубиной кодирования 24. В результате был получен файл размером 120 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее ко времени записи целое число, кратное 5.

Решение

Время в минутах М должно удовлетворять равенству^{^[26]}:

64 000 × 24 бита × 2 канала × М (время в минутах) × 60 = = 120 Мбайт× 2²³.

Сокращаем 120 и переходим к степеням двойки:

64 000 ≈ 2⁶× 2¹⁰(1000 ≈ 1024 = 2¹⁰) 24 = 2³× 3. Новое равенство:

2⁶× 2¹⁰× 2³ × 3 × М = 2²³3 × М = 2⁴,

решая которое, получим М = 5.

Ответ: 5 минут.

Пример 2

Найдите используемую частоту дискретизации в килогерцах, если известно, что аудиофайл записывался в стереоформате при глубине кодирования 16 бит в течение одной минуты. Размер полученного файла составил 3750 Кбайт.

Решение

Здесь надо обратить внимание на то, что искомое значение частоты дискретизации должно быть выражено в килогерцах.

В герцах это значение ЧД должно обеспечивать равенство:

ЧД × 16 ×2 × 60 = 3750 × 2¹³,

откуда ЧД = 16 000.

Соответствующее значение в килогерцах – 16.

Ответ: 16.

Возможны также задания, в которых неизвестной характеристикой является:

• глубина кодирования;

• количество уровней дискретизации (уровней квантования).

Первая задача решается аналогично двум рассмотренным (с записью равенства).

Для определения количества уровней дискретизации сначала следует рассчитать глубину кодирования ГК, а затем – искомую величину как 2^ГК.

7.3.3. «Прямые задачи с изменением»

Общая особенность таких задач:

• приводится размер звукового файла и говорится об изменении одной или более характеристик звукозаписи (характеристик дискретизации) этого же файла. Требуется определить новое значение размера файла.

Пример 1 (задание из демонстрационного варианта ЕГЭ по информатике 2023 г.)

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранен в виде файла без использования сжатия данных. Размер полученного файла – 28 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 3,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер полученного при повторной записи файла в Мбайтах.

Решение

Так как размер звукового файла прямо пропорционален частоте дискретизации и разрешению кодирования, а также количеству каналов записи, то размер полученного файла можно определить следующим образом:

28 × = 98

(в числителе – увеличение разрешения и количества каналов, в знаменателе – уменьшение частоты дискретизации).

Ответ: 98.

Общая методика выполнения заданий рассмотренного типа:

• определяются коэффициенты изменения меняющихся характерис тик звукозаписи;

• размер исходного файла умножается на коэффициенты в случае увеличения характеристики или/и делится на коэффициенты в случае уменьшения характеристики.

Пример 2

Производится звукозапись музыкального фрагмента в формате стерео (двухканальная запись) с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записываются в файл, сжатие данных не производится; размер полученного файла – 64 Мбайт. Затем производится повторная запись этого же фрагмента в формате моно (одноканальная запись) с частотой дискретизации 16 кГц и 16-битным разрешением. Сжатие данных не производилось. Укажите размер файла в Мбайтах, полученного при повторной записи.

Решение

Здесь коэффициенты изменения характеристик звукозаписи не заданы – их надо определить:

• частота дискретизации уменьшилась в два раза;

• разрешение уменьшилось в два раза;

• количество каналов уменьшилось в два раза.

Это значит, что объем полученного файла будет в 8 раз меньше исходного.

Ответ: 8.

Возможны также задания, в которых речь идет о звуковом файле известного размера, в котором, кроме собственно звукового фрагмента, представлена и служебная информация о файле, размер которой задан и при изменении характеристик дискретизации не меняется. Нужно определить размер этого файла после изменения характеристик дискретизации.

Понятно, что при выполнении таких заданий следует:

• определить размер собственно звукового фрагмента;

• рассчитать новое значение этого размера в зависимости от изменений характеристик дискретизации;

• к найденному значению прибавить размер служебной информации о файле.

Пример 3

Для проведения эксперимента записывается звуковой фрагмент в формате квадро (четырехканальная запись) с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записываются в файл, сжатие данных не производится; дополнительно в файл записывается служебная информация, необходимая для эксперимента, размер полученного файла 97 Мбайт. Затем производится повторная запись этого же фрагмента в формате моно (одноканальная запись) с частотой дискретизации 16 кГц и 16-битным разрешением. Результаты тоже записываются в файл без сжатия и со служебной информацией, размер полученного файла 7 Мбайт. Объем служебной информации в обоих случаях одинаков. Укажите этот объем в мегабайтах.

Решение

Здесь объем служебной информации является искомым.

Итак, звуковой файл состоит из собственно звукового фрагмента и служебной информации. Объем первого меняется из-за изменения характеристик дискретизации, объем служебной информации не меняется.

Пусть объем служебной информации равен Х. Тогда объем собственно звукового фрагмента будет равен 97 – Х. После повторной записи он уменьшится в 2 × 2 × 4 = 16 раз. С учетом неизменившегося объема служебной информации новый размер файла станет равным 7:

+ X = 7,

откуда Х = 1. Ответ: 1.

7.3.4. «Обратные задачи с изменением»

Общая особенность таких задач:

• приводятся характеристики дискретизации, в результате которой был звуковой файл заданного размера. Далее говорится об изменении размера файла в результате изменения характеристик дискретизации. Требуется определить новое значение одной из характеристик.

Пример 1

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован с частотой дискретизации 44 кГц и разрешением 16 бит и сохранен без использования сжатия данных. Получился файл размером 120 Мбайт. Затем тот же фрагмент был записан в формате квадро (четырехканальная запись) с частотой дискретизации 88 кГц и тоже сохранен без сжатия, при этом получился файл размером 720 Мбайт. С каким разрешением проводилась вторая запись?

Решение

Обозначим искомое разрешение дискретизации второй записи Х.

Так как продолжительность записи не изменилась, то можем сравнить размер исходного файла (числитель) и полученного (знаменатель) в виде пропорции:

Сокращая, получим:

Можно рассуждать и так.

Новый файл стал больше исходного в 6 раз. За счет увеличения частоты дискретизации произошло увеличение в 2 раза, за счет увеличения количества каналов записи – также в 2 раза (всего в 4 раза). Остальное «пришлось» на изменение разрешения. Значит, «вклад» разрешения составил 6 : 4 = 1,5. Так как при первой записи разрешение было равно 16, то при второй записи – 16 × 1,5 = 24.

Ответ: 24.

Аналогично (записывая пропорцию или на основе рассуждений) решаются задачи определения других изменившихся характеристик дискретизации:

• частоты дискретизации; • количества каналов звукозаписи;

• продолжительности звучания.

7.3.5. Задачи для самостоятельного решения

1. Производится одноканальная (моно) звукозапись с частотой дискретизации 11 кГц и глубиной кодирования 24 бита. Запись длится семь минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 11; 2) 13; 3) 15; 4) 22.

2. В течение четырех минут производится двухканальная (стерео) звукозапись. Результаты записи записываются в файл, размер полученного файла – 40 Мбайт (c точностью до 10 Мбайт); сжатие данных не производилось. Среди перечисленных ниже режимов укажите тот, в котором проводилась звукозапись:

1) частота дискретизации 16 кГц и 24-битное разрешение;

2) частота дискретизации 16 кГц и 16-битное разрешение;

3) частота дискретизации 32 кГц и 24-битное разрешение; 4) частота дискретизации 32 кГц и 16-битное разрешение.

3. Когда Митя просматривал старые файлы, он нашел аудиозапись, которая занимала 661 500 байт на диске и была записана в течение 10 секунд в моноформате с количеством уровней квантования 4096. Сжатие данных не производилось. Какова была частота дискретизации в килогерцах?

4. Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 16-битной глубиной кодирования. В результате был получен файл размером 48 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее ко времени записи целое число.

5. Производится двухканальная (стерео) звукозапись с час тотой дискретизации 44 кГц. Запись длится 5 минут 25 секунд, ее результаты записываются в файл без сжатия данных, причем каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Информационный объем полученного файла без учета заголовка не превышает 82 Мбайт. Определите максимальную битовую глубину кодирования звука, которая могла быть использована в этой записи.

6. Производится двухканальная (стерео) звукозапись с час тотой дискретизации 48 кГц. Запись длится 4 минуты 5 секунд, ее результаты записываются в файл без сжатия данных, причем каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Информационный объем полученного файла без учета заголовка не превышает 46 Мбайт. Определите максимальное количество уровней дискретизации, которые могли быть использованы в этой записи.

7. Звукорежиссеру прислали аудиозапись с частотой дискретизации 32 кГц. Он отредактировал композицию, убрав некоторые фрагменты (время уменьшилось), и перезаписал данную аудиозапись, увеличив частоту дискретизации до 48 Гц. После данных изменений размер аудиофайла не изменился. На сколько секунд звукорежиссер сократил аудиозапись, если известно, что изначально она длилась 90 секунд^{^[27]}?

8. Музыкальный фрагмент был записан в формате квадро (четырехканальная запись), оцифрован и сохранен в виде файла без использования сжатия данных. Размер полученного файла без учета размера заголовка файла – 12 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер в Мбайтах файла, полученного при повторной записи.

9. Для проведения эксперимента записывается звуковой фрагмент в формате стерео (двухканальная запись) с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записываются в файл, сжатие данных не производится; дополнительно в файл записывается служебная информация, необходимая для эксперимента, размер полученного файла 42 Мбайт. Затем производится повторная запись этого же фрагмента в формате моно (одноканальная запись) с час тотой дискретизации 16 кГц и 16-битным разрешением. Результаты тоже записываются в файл без сжатия и со служебной информацией, размер полученного файла 7 Мбайт. Объем служебной информации в обоих случаях одинаков. Укажите этот объем в мегабайтах.

10. Музыкальный фрагмент был записан в формате моно (одноканальная запись), оцифрован с частотой дискретизации 42 кГц и разрешением 16 бит и сохранен без использования сжатия данных. Получился файл размером 45 Мбайт. Затем тот же фрагмент был записан в формате квадро (четырехканальная запись) с частотой дискретизации 84 кГц и тоже сохранен без сжатия, при этом получился файл размером 720 Мбайт. С каким разрешением проводилась вторая запись?

11. Музыкальный фрагмент был записан в формате квадро (четырехканальная запись), оцифрован с частотой дискретизации 22 кГц и разрешением 16 бит и сохранен без использования сжатия данных. Получился файл размером 150 Мбайт. Затем тот же фрагмент был записан с частотой дискретизации 88 кГц и разрешением 32 бита и тоже сохранен без сжатия, при этом получился файл размером 300 Мбайт. С каким количеством каналов проводилась вторая запись?

12. Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован с частотой дискретизации 25 кГц и разрешением 16 бит и сохранен без использования сжатия данных. Получился файл размером 30 Мбайт. Затем тот же фрагмент был записан в формате моно (одноканальная запись) с разрешением 64 бит и тоже сохранен без сжатия, при этом получился файл размером 120 Мбайт. С какой частотой дискретизации проводилась вторая запись?

13. Фрагмент песни был записан в формате моно (одноканальная запись), оцифрован с частотой дискретизации 42 кГц и разрешением 16 бит и сохранен без использования сжатия данных. Получился файл размером 45 Мбайт. Затем был записан фрагмент большей продолжительности в формате стерео (двухканальная запись) с частотой дискретизации 84 кГц и разрешением 32 бит и тоже сохранен без сжатия, при этом получился файл размером 720 Мбайт.

Во сколько раз увеличилась продолжительность записи?

Глава 8 Задания 8

8.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 8 указывается «знание основных понятий и методов, используемых при измерении количества информации».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 4 мин.

***

В демонстрационных вариантах ЕГЭ по информатике ряда последних лет и в других материалах, связанных с экзаменом, представлены задания 8, в которых речь идет об определении количества вариантов слов и чисел, удовлетворяющих некоторому условию. Такие задания могут быть выполнены различными методами – теоретически путем рассуждений и использования формул комбинаторики и с помощью разных вариантов компьютерных программ на языках программирования (см., например, [3–4]).

Для выполнения ряда заданий 8 подобного типа можно также использовать электронную таблицу Microsoft Excel или другую аналогичную программу. Примеры заданий и методика их выполнения приведены в разделах 8.2 и 8.3.

Здесь же напомним некоторые полезные формулы.

Если на первом месте некоторого набора может размещаться n объектов, на втором – (n – 1) объектов, на втором – (n – 2) … и на последнем, k-м, месте можно поставить любой из остальных n – k + 1 объектов, то общее количество вариантов размещения всех объектов равно n × (n – 1) × … × (n – k + 1). Например, четыре человека можно разместить на двух стульях 4 × 3 = 12 способами (на первом стуле может находиться любой из четырех человек, с каждым из них – любой из остальных трех людей).

Если k = n, то все варианты размещения называют «перестановками из n элементов». Их общее количество равно n× (n – 1) × … × 1. Например, из трех элементов а, b, c можно образовать 3 × 2 × 1 = 6 различных перестановок: abc, acb, bac, bca, cab и сba.

Если на первом месте может размещаться n₁ объектов, на втором – n₂, …, на k-м – n_k, то общее количество вариантов размещения равно n₁ × n₂ × … × n_k. Например, если первой буквой трехбуквенной последовательности могут быть латинские буквы A, C, L, второй – А, B, третьей – С и D, то возможны 12 вариантов такой последовательности:

1. ААС

2. ААD

3. АВС

4. АBD

5. САС

6. САD

7. СВС

8. СBD

9. LАС

10. LАD

11. LВС 12. LBD

8.2. Примеры заданий на подсчет количества слов и методика их выполнения

8.2.1. Пример 1

Условие

Митя составляет шестибуквенные слова, в которых есть только буквы П, Л, А, Н, причем буква А используется в каждом слове ровно один раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Митя?

Решение

В данном случае нам понадобится диапазон ячеек из шести строк и шести столбцов:

	A	B	C	D	E	F
1
2
3
4
5
6

В каждой ячейке одной строки будем указывать количество вариантов букв, которые могут быть записаны в той или иной позиции шестибуквенного слова (в столбце A – на первом месте слова и т. д.).

По условию буква А может быть записана только один раз в любом мес те. Отметим эти места, записав в соответствующих ячейках количество вариантов, равное 1:

	A	B	C	D	E	F
1	1
2		1
3			1
4				1
5					1
6						1

В других ячейках диапазона А1:F6 могут быть записаны любые из остальных букв слова ПЛАН, кроме буквы А. Таких букв – три. Запишем это в таблицу:

	A	B	C	D	E	F
1	1	3	3	3	3	3
2	3	1	3	3	3	3
3	3	3	1	3	3	3
4	3	3	3	1	3	3
5	3	3	3	3	1	3
6	3	3	3	3	3	1

Итак, когда буква А записана первой, всего можно получить 1 × 3 × 3 × 3 × 3 × 3 = 243 различных слова (см. начало статьи). Аналогично – и для остальных вариантов нахождения буквы А, то есть искомое количество слов, которые может написать Митя, равно 243 × 6 = 1458.

В данном случае все расчеты можно было провести в уме. Когда же в каждой строке количество чисел (множителей) или/и их значения большие, или/и значения множителей разные, для нахождения искомого числа удобно использовать формулы. Приведем применительно к рассмотренному примеру:

• в ячейку G1 вводится формула : =ПРОИЗВЕД(A1:F1);

• она распространяется (копируется) на другие ячейки столбца G;

• искомое количество определяется в ячейке G7 по формуле =СУММ(G1:G6) (удобно использовать так называемую «автосумму» – кнопку ).

8.2.2. Пример 2

Условие

Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует свое кодовое слово. В качестве кодовых слов Игорь использует шестибуквенные слова, в которых могут быть только буквы Ш, К, О, Л, А, причем буква К появляется ровно один раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь?

Решение

Задача решается аналогично, но с использованием формул:

	A	B	C	D	E	F	G	Н
1	1	4	4	4	4	4	1024	=ПРОИЗВЕД(A1:F1)
2	4	1	4	4	4	4	1024
3	4	4	1	4	4	4	1024
4	4	4	4	1	4	4	1024
5	4	4	4	4	1	4	1024
6	4	4	4	4	4	1	1024
7							6144	=СУММ(G1:G6)

Примечание

В столбце Н приведены формулы, по которым проводился расчет в столбце G.

Ответ: 6144.

Рекомендация

При выполнении заданий подобного типа с целью экономии времени целесообразно сначала заполнить все ячейки диапазона A1:G6 значениями, равными 4 (в данном случае), а затем изменить все числа 4 на диагонали на число 1.

8.2.3. Пример 3

Условие

Сколько существует различных символьных последовательностей длины 6 в четырехбуквенном алфавите {A, B, C, D}, если известно, что буква А должна встречаться в каждом слове ровно один раз и что «соседями» буквы A обязательно являются буквы D?

Решение

Решение показано на фрагменте листа электронной таблицы:

	A	B	C	D	E	F	G
1	1	1	3	3	3	3	81
2	1	1	1	3	3	3	27
3	3	1	1	1	3	3	27
4	3	3	1	1	1	3	27
5	3	3	3	1	1	1	27
6	3	3	3	3	1	1	81
7							270

Комментарии

Ячейки светло-серого цвета соответствуют количеству вариантов размещения буквы А, темно-серого – буквы D (обязательно рядом с буквой А). В остальных ячейках диапазона А1:F6 записано число вариантов размещения допустимых букв на соответствующих позициях (это могут быть любые буквы заданного алфавита, кроме А).

Ответ: 270.

8.2.4. Пример 4

Условие

Роман составляет семибуквенные слова, в которых есть только буквы Т, А, Н, Я, К, причем буква А используется в каждом слове ровно один раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. При этом рядом с буквой А не может находиться буква Я. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Роман?

Решение

Учтем возможные варианты записи буквы А:

	A	B	C	D	E	F	G
1	1
2		1
3			1
4				1
5					1
6						1
7							1

По условию рядом с ней не должно быть буквы Я. Поэтому справа и слева от числа 1 в диапазоне A1:G7 запишем число 3 (количество остальных букв, кроме А и Я):

	A	B	C	D	E	F	G
1	1	3
2	3	1
3		3	1	3
4			3	1	3
5				3	1	3
6					3	1	3
7						3	1

В остальных позициях семибуквенного слова может быть представлена любая буква, кроме А (таких букв – 4). Поэтому в остальных ячейках запишем число 4.

Введя в ячейки Н1:Н7 формулы с функцией ПРОИЗВЕД, а в ячейку Н8 – с функцией СУММ, получим:

	A	B	C	D	E	F	G	Н
1	1	4	4	4	4	4	4	4096
2	3	1	3	4	4	4	4	2304
3	4	3	1	3	4	4	4	2304
4	4	4	3	1	3	4	4	2304
5	4	4	4	3	1	3	4	2304
6	4	4	4	4	3	1	3	2304
7	4	4	4	4	4	4	1	4096
8								19712

Итак, ответ: 19 712.

8.2.5. Пример 5

Условие

Сколько существует различных символьных последовательностей длины 5 в четырехбуквенном алфавите {Ш, А, Р, М}, которые содержат ровно две буквы А?

Решение

В слове из пяти букв существует 10 различных вариантов размещения ровно двух букв А (это число сочетаний из 10 по 2). Отметим эти варианты^{^[28]} в таблице:

	A	B	C	D	Е
1	1	1
2	1		1
3	1			1
4	1				1
5		1	1
6		1		1
7		1			1
8			1	1
9			1		1
10				1	1

В остальных ячейках можно записать количество различных букв, которые могут быть представлены на соответствующих местах, – 3 (это остальные буквы Ш, Р и М).

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	3	1	1	3	3
6	3	1	3	1	3
7	3	1	3	3	1
8	3	3	1	1	3
9	3	3	1	3	1
10	3	3	3	1	1

Ответ: 270.

Комментарий. При достаточном опыте выполнения таких заданий можно не заполнять все 10 (в данном случае) строк, а, проведя расчеты для одной строки, умножить полученное произведение на количество вариантов размещения ровно двух букв А (также в данном случае).

8.2.6. Пример 6

Условие

Таня составляет трехбуквенные слова, в которых есть только буквы П, Е, К, Т, А, причем буква Е используется в каждом слове хотя бы один раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Таня? Решение

В слове из трех букв существует 7 вариантов размещения одной, двух или трех букв Е. Отметим эти варианты^{^[29]} в таблице:

	A	B	C
1	1
2		1
3			1
4	1	1
5	1		1
6		1	1
7	1	1	1

В остальных ячейках можно записать количество различных букв, которые могут быть представлены на соответствующих местах, – 4 (все допустимые буквы, кроме Е).

	A	B	C	D
1	1	4	4	16
2	4	1	4	16
3	4	4	1	16
4	1	1	4	4
5	1	4	1	4
6	4	1	1	4
7	1	1	1	1
8				61

Ответ: 61.

8.2.7. Пример 7

Условие

Петя составляет шестибуквенные слова, в которых есть только буквы Ф, О, Р, М, А. Каждая из букв может встречаться в слове любое количество раз или не встречаться совсем. При этом первой буквой слова должна быть согласная и в словах не должно быть никаких двух соседних одинаковых букв. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Петя?

Решение

Решение показано на фрагменте листа:

	A	B	C	D	E	F	G
1	3	4	4	4	4	4	3072
2	3	4	4	4	4	4	3072
3	3	4	4	4	4	4	3072
4							9216

Комментарий. Первой может быть одна из трех согласных букв. В каждом из трех случаев справа от любой буквы могут быть только остальные четыре допустимые буквы.

Ответ: 9276.

8.2.8. Пример 8

Условие

Митя составляет 10-буквенные слова, в которых есть только буквы М, А, К, Е, Т. Каждая из букв может встречаться в слове любое количество раз или не встречаться совсем. При этом слова должны начинаться с согласной буквы и согласные и гласные буквы должны чередоваться. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Митя?

Решение

Здесь для расчетов достаточно использовать одну строку лис та электронной таблицы:

	A	B	C	D	E	F	G	Н	I	J	K
1	3	2	3	2	3	2	3	2	3	2	7776

Ответ: 7776.

8.2.9. Пример 9

Условие

Сколько слов длины 5, начинающихся с согласной буквы и заканчивающихся гласной буквой, можно составить из русских букв? Каждая буква может входить в слово несколько раз или не встречаться совсем. Слова не обязательно должны быть осмысленными словами русского языка.

Решение

	A	B	C	D	E	F
1	23	33	33	33	10	8265510

Ответ: 8 275 510.

Комментарий. В русском алфавите 10 гласных букв и 23 согласных.

8.2.10. Пример 10

Условие

Сколько слов длины 6, начинающихся с гласной буквы, можно составить из русских букв, если:

• первой буквой должна быть согласная;

• в слове должно быть только одно буквосочетание НН;

• справа от этого буквосочетания не должно быть согласной буквы?

Каждая буква может входить в слово несколько раз или не входить совсем. Слова не обязательно должны быть осмысленными словами русского языка.

Решение

Решение показано на фрагменте листа:

	A	B	C	D	E	F	G
1	23	1	1	10	33	33	250470
2	23	33	1	1	10	33	250470
3	23	33	33	1	1	10	250470
4	23	33	33	33	1	1	826551
5							1577961

В его особенностях разберитесь самостоятельно.

Ответ: 1 577 961.

Полезно запомнить:

• в русском языке 33 буквы: 10 гласных букв (А, У, О, Ы, И, Э, Я, Ю, Е, Е), 21 согласная буква (Б, В, Г, Д, Ж, З, Й, К, Л, М, Н, П, Р, С, Т, Ф, Х, Ц, Ч, Ш,

Щ) и два знака (Ь, Ъ);

• алфавит английского языка по написанию совпадает с латинским алфавитом и состоит из 26 букв.

Возможны также задания, в которых дан список слов одинаковой длины в алфавитном порядке и нужно определить:

• слово, которое стоит на некотором заданном месте от начала списка;

• (или) на каком месте от начала списка стоит некоторое заданное слово.

Пример 1

Условие

Все пятибуквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:

1. ААААА

2. ААААО

3. ААААУ

4. АААОА

…

Запишите слово, которое стоит на 240-м месте от начала списка.

Решение

Подсчитаем, сколько всего пятибуквенных слов можно составить из трех букв.

Так как на каждом из пяти «мест» в словах может быть любая из трех букв, то, согласно формуле, приведенной в разделе 8.1, это количество равно 3 × 3 × 3× 3 × 3 = 243.

Последнее, 243-е, слово – это УУУУУ (см. третье слово в условии).

Далее идем назад: предпоследнее, 242-е, слово – УУУУО (см. второе слово в условии), затем идет 241-е слово УУУУА и, наконец, УУУОУ (240-е).

Ответ: УУУОУ.

В рассмотренном случае речь шла о слове, близком к концу списка. А если бы требовалось определить слово, стоящее на 120-м месте списка? В этом случае задачу можно решить так.

Посмотрите на таблицу:

1. ААААА

2. ААААО

3. ААААУ

4. АААОА

…

0. 00000 1. 00001 2. 00002

3. 00010

…

Что можно сказать о последовательности букв в левом столбце? – Это числа, записанные в системе счисления, в которой для цифры 0 используется буква А, для цифры 1 – буква О, для цифры 2 – буква У (то есть в троичной системе).

Рекомендация: целесообразно выписать буквы и цифры:

0 – А

1 – О

Как записаны числа-слова в левом столбце таблицы? – На первом мес те стоит число 0, на втором – 1 и т. д. Значит, на 120-м месте стоит число 119, записанное в троичной системе счисления.

Переведем 119 в троичную систему (например, методом последовательного деления на основание 3): 119₁₀ = 11102₃.

Осталось заменить цифры соответствующими буквами: ОООАУ.

Ответ: ОООАУ.

Общая методика выполнения заданий, аналогичных заданию примера 1:

Рассматривая приведенные в условии слова как числа, определить систему счисления, в которой они записаны, и соответствие использованных в ней букв цифрам (таблицу соответствия целесообразно выписать).

Заданный в условии номер слова, уменьшенный на 1, перевести в установленную систему счисления.

Заменить в полученном числе цифры соответствующими им буквами. Полученное слово будет искомым ответом.

Пример 2 ([4], автор задачи В. В. Путилов)

Условие

Все пятибуквенные слова, составленные из пяти букв А, К, Л, О, Ш, записаны в алфавитном порядке.

Вот начало списка:

ААААА ААААК ААААЛ

ААААО

ААААШ

АААКА

…

На каком месте от начала списка стоит слово ШКОЛА?

Решение

Здесь задача, так сказать, «обратная» по отношению к предыдущей.

Прежде всего можно увидеть, что приведенные слова соответствуют числам, записанным в пятеричной системе счисления с цифрами:

А – 0 К – 1 Л – 2

О – 3

Ш – 4

Значит, слово ШКОЛА будет записано как 41320_5.

Переведем это число в десятичную систему. Для этого удобно использовать электронную таблицу и следующую методику:

1) в строке 1 записать пятеричные цифры:

	A	B	C	D	E
1	4	1	3	2	0
2	625	125	25	5	1
3

2) в строке 2 записать весомости соответствующих разрядов:

	A	B	C	D	E
1	4	1	3	2	0
2	625	125	25	5	1
3

Примечание. Все весомости удобно (особенно при других основаниях системы счисления) получить следующим образом: в ячейку D3 ввести формулу =E3 * <основание>, которую затем распространить (скопировать) на остальные ячейки строки 3. См. также п. 14.2.1.

Искомое десятичное значение рассчитывается по формуле =СУММПРОИЗВ(А1:Е1; И1:Е1)^{^[30]} и равно 2710.

Поскольку нумерация слов в списке начинается с 1, а числа в пятеричной системе – с нуля (ААААА, или 00000), к полученному результату нужно прибавить 1.

Ответ: 2711.

Общая методика выполнения заданий, аналогичных заданию примера 2

Записать заданное слово с использованием цифр.

Полученное число перевести в десятичную систему счисления (с помощью электронной таблицы).

Ответ будет равен рассчитанному десятичному числу, увеличенному на 1.

8.2.11. Задания для самостоятельного выполнения

1. Павел составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует свое кодовое слово. В качестве кодовых слов Игорь использует пятибуквенные слова, в которых есть только буквы A, Б, B, Г, Д, Е, причем буква Д появляется ровно один раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Павел?

2. Оля составляет шестибуквенные слова, в которых есть только буквы Б, И, Н, О, М, причем буква Н используется в каждом слове ровно один раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. При этом рядом с буквой Н не может находиться гласная буква. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Оля?

3. Сколько существует различных символьных последовательностей длины 7 в четырехбуквенном алфавите {Б, А, Й, T}, которые содержат ровно две буквы Т?

4. Марина составляет четырехбуквенные слова, в которых есть только буквы Ф, О, Р, М, А, причем буква М используется в каждом слове хотя бы два раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.

Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Марина?

5. Сколько существует способов разместить на книжной полке семь книг, среди которых – четыре тома романа «Сага о Форсайтах», которые должны стоять рядом (но не обязательно по порядку)?

6. Сколько слов длины 6, начинающихся с согласной буквы, можно составить из букв М, И, Р, У? Каждая буква может входить в слово несколько раз или не встречаться совсем. Слова не обязательно должны быть осмысленными словами русского языка.

7. Сколько слов длины 6, начинающихся и заканчивающихся с гласной буквы, можно составить из букв латинского алфавита? Каждая буква может входить в слово несколько раз или не встречаться совсем. Слова не обязательно должны быть осмысленными словами.

8. Сколько слов длины 5, начинающихся с гласной буквы, можно составить из русских букв, если:

• первой буквой должна быть одна из гласных букв, кроме Е и Ы; • в слове должно быть только одно буквосочетание СС;

• справа от этого буквосочетания не должно быть гласной буквы?

9. Все пятибуквенные слова, составленные из букв К, М, Р, У, записаны в алфавитном порядке. Вот начало списка:

1. МММММ

2. ММММК

3. ММММР

4. ММММУ

5. МММКМ

…

Какое слово стоит на 91-м месте от начала списка?

10. Все пятибуквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:

1. ААААА

2. ААААО

3. ААААУ

4. АААОА

…

Укажите номер слова ОАОАО.

8.3. Примеры заданий на подсчет количества чисел и методика их выполнения

Особенности выполнения таких заданий в среде электронной таблицы по методике, аналогичной описанной в предыдущем разделе:

1) вместо гласных и согласных букв в заданиях могут фигурировать четные и нечетные цифры, цифры, кратные трем, и т. п.;

2) при определении количества цифр, с которых начинаются числа, следует учесть, что ноль не может быть первой цифрой числа.

И конечно, для недесятичных чисел необходимо рассматривать соответствующее количество цифр.

8.3.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Определите количество пятизначных чисел, записанных в восьмеричной системе счисления, в записи которых только одна цифра 6, при этом никакая нечетная цифра не стоит рядом с цифрой 6.

Решение

Прежде всего обратим внимание на то, что речь не идет об определении количества десятичных чисел, которые в восьмеричной системе счисления обладают указанными свойствами. Имеется в виду анализ только восьмеричных чисел.

Напомним также, что в восьмеричной системе счисления имеется четыре четные и четыре нечетные цифры.

Приведем решение в виде фрагмента листа электронной таб лицы:

	A	B	C	D	Е	F
1	1	3	7	7	7	1029
2	2	1	3	7	7	294
3	6	3	1	3	7	378
4	6	7	3	1	3	378
5	6	7	7	3	1	882
6						2961

Ответ: 2961.

Комментарии

1. Число 1 записано в разрядах, в которых может быть записана цифра 6.

2. Рядом с ней может быть записана только другая четная цифра. Таких цифр в восьмеричной системе – три. Но так как ноль (четная цифра!) не может быть первой цифрой, то в ячейке А2 записано число 2, а не 3.

3. В остальных разрядах могут быть представлены остальные семь восьмеричных цифр (в столбце А – шесть).

8.3.2. Пример 2

Условие

Определите количество пятизначных чисел, записанных в четверичной системе счисления, которые содержат ровно две цифры 3.

Решение

В пятизначном ряду чисел существует 10 различных вариантов размещения ровно двух цифр 3 (это число сочетаний из 10 по 2). Отметим эти варианты^{^[31]} в таблице:

	A	B	C	D	Е
1	1	1
2	1		1
3	1			1
4	1				1
5		1	1
6		1		1
7		1			1
8			1	1
9			1		1
10				1	1

В остальных ячейках можно записать количество различных цифр, которые могут быть представлены на соответствующих местах:

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	2	1	1	3	3
6	2	1	3	1	3
7	2	1	3	3	1
8	2	3	1	1	3
9	2	3	1	3	1
10	2	3	3	1	1

Примечание: 3 – это количество остальных цифр (0, 1, 2), 2 – …

(обоснование установите самостоятельно)

Ответ: 216.

8.3.3. Пример 3

Условие

Сколько существует шестизначных десятичных чисел, в которых все цифры различные и никакие две четные и две нечетные цифры не стоят рядом?

Решение

На первом месте может быть записана одна из цифр 1, 2, …, 9. В первых пяти строках будем рассматривать варианты с нечетными цифрами, в следующих четырех – с четными (см. столбец I):

	A	B	C	D	E	F	G	Н	I
1	1								1
2	1								3
3	1								5
4	1								7
5	1								9
6	1								2
7	1								4
8	1								6
9	1								8

На втором месте рядом с нечетными цифрами может быть записана одна из пяти четных цифр, и наоборот:

	A	B	C	D	E	F	G	Н	I
1	1	5							1
2	1	5							3
3	1	5							5
4	1	5							7
5	1	5							9
6	1	5							2
7	1	5							4
8	1	5							6
9	1	5							8

На третьем месте рядом с четными цифрами в столбце В может быть записана одна из четырех нечетных цифр (какая-то одна нечетная уже «использована» на первом месте), и наоборот:

	A	B	C	D	E	F	G	Н	I
1	1	5	4						1
2	1	5	4						3
3	1	5	4						5
4	1	5	4						7
5	1	5	4						9
6	1	5	4						2
7	1	5	4						4
8	1	5	4						6
9	1	5	4						8

На четвертом месте (в столбце D) рядом с нечетными цифрами в столбце С может быть записана одна из четырех четных цифр (какаято одна четная уже «использована» на втором месте), и наоборот:

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4					1
2	1	5	4	4					3
3	1	5	4	4					5
4	1	5	4	4					7
5	1	5	4	4					9
6	1	5	4	4					2
7	1	5	4	4					4
8	1	5	4	4					6
9	1	5	4	4					8

Аналогичными рассуждениями можно получить значения для пятой и шестой цифр:

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4	3	3			1
2	1	5	4	4	3	3			3
3	1	5	4	4	3	3			5
4	1	5	4	4	3	3			7
5	1	5	4	4	3	3			9
6	1	5	4	4	3	3			2
7	1	5	4	4	3	3			4
8	1	5	4	4	3	3			6
9	1	5	4	4	3	3			8

В каждой строке количество возможных вариантов, рассчитанное по формуле с функцией ПРОИЗВЕД, будет равно 720, а общее искомое шестизначных десятичных чисел – 6480.

Ответ: 6480.

Комментарий

Конечно, можно было не рассматривать 9 вариантов значений первой цифры, а рассуждать «в общем виде» следующим образом.

• Первой цифрой числа может быть одна из цифр 1, 2, …, 9 (9 вариантов).

• Второй может быть любая цифра, так сказать, «противоположной четности». Таких цифр для любой первой цифры – пять. В результате во всех случаях уже «использована» одна четная и одна нечетная цифра. Значит, в третьем и четвертом разрядах (при счете слева) могут быть записаны по четыре варианта цифр той или иной четности. Для остальных разрядов рассуждения аналогичные.

8.3.4. Пример 4

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

Сколько существует восьмеричных пятизначных чисел, не содержащих в своей записи цифру 1, в которых все цифры различны и никакие две четные или две нечетные цифры не стоят рядом?

Решение

Цифры 0 и 1 не могут быть первой цифрой числа. Выпишем остальные цифры восьмеричной системы счисления в столбце А листа и оформим его так^{^[32]}:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2
4	3
5	4
6	5
7	6
8	7

Примечание. Выделены (для наглядности) нечетные цифры.

Фраза в условии «никакие две четные или две нечетные цифры не стоят рядом» говорит о том, что четные и нечетные цифры в числе должны чередоваться.

Сколько вариантов второй цифры может быть в каждом из шести случаев? После четных цифр должны идти нечетные (без цифры 1 их три – 3, 5, 7), и наоборот (всего четных цифр четыре – 0, 2, 4, 6). Для удобства запишем возможные цифры в каждом случае:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2	3 5 7
4	3	0 2 4 6
5	4	3 5 7 9
6	5	0 2 4 6
7	6	3 5 7
8	7	0 2 4 6

После чего заменим перечень цифр на их количество:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2	3
4	3	4
5	4	3
6	5	4
7	6	3
8	7	4

Аналогично с количеством вариантов третьих цифр:

		A		B		C		D		E		F
1		1-я цифра		2-я		3-я		4-я		5-я
2				Кол-во вариантов								Всего
3		2		3		0 4 6
4		3		4		5 7
5		4		3		2 4 6
6		5		4		3 7
7		6		3		0 2 4
8		7		4		3 5
			A		B		C		D		E		F
	1		1-я цифра		2-я		3-я		4-я		5-я
	2				Кол-во вариантов								Всего
	3		2		3		3
	4		3		4		2
	5		4		3		3
	6		5		4		2
	7		6		3		3
	8		7		4		2

Обсудим количество вариантов четвертых цифр в каждом случае. В столбце D каждой строки записана цифра такой же четности, что и в столбце В (то есть там уже «использована» одна соответствующая цифра). Значит, количество возможных цифр в столбце D будет на 1 меньше, чем в столбце В:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2	3	3	2
4	3	4	2	3
5	4	3	3	2
6	5	4	2	3
7	6	3	3	2
8	7	4	2	3

Аналогичные рассуждения приведут к выводу о том, что количество возможных цифр в столбце Е будет на 1 меньше, чем в столбце С:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2	3	3	2	2
4	3	4	2	3	1
5	4	3	3	2	2
6	5	4	2	3	1
7	6	3	3	2	2
8	7	4	2	3	1

После этого можно определить общее число вариантов пятизначных чисел.

Когда первая цифра числа – 2, количество возможных вариантов в ячейке F3 можно рассчитать по формуле =ПРОИЗВЕД(B3:Е3). Распространив (скопировав) эту формулу на другие строки, получим количество возможных вариантов для других цифр, а просуммировав значения в столбце F, определим искомое общее количество чисел:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2	3	3	2	2	36
4	3	4	2	3	1	24
5	4	3	3	2	2	36
6	5	4	2	3	1	24
7	6	3	3	2	2	36
8	7	4	2	3	1	24
9						180

Ответ: 180.

При наличии опыта выполнения подобных заданий возможные цифры в столбцах В и С можно не выписывать, а сразу указывать соответствующее количество цифр.

Можно также в начале расчетов сгруппировать четные и нечетные цифры, что упростит запись нужных значений в столбцах В:Е:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2		Кол-во вариантов				Всего
3	2	3	3	2	2	36
4	4	3	3	2	2	36
5	6	3	3	2	2	36
6	3	4	2	3	1	24
7	5	4	2	3	1	24
8	7	4	2	3	1	24
9						180

Последний вариант позволяет оформить лист еще проще, записав в столбце А количество четных и нечетных цифр:

	A	B	C	D	E	F
1	1-я цифра	2-я	3-я	4-я	5-я
2	Кол-во вариантов					Всего
3	3	3	3	2	2	36
4	3	4	2	3	1	24
5						180

При этом формулы в ячейках F3 и F4 должны учитывать и количество в столбце А: =ПРОИЗВЕД(А3:Е3) и =ПРОИЗВЕД(А4:Е4).

8.3.5. Задания для самостоятельного выполнения

1. Определите количество шестизначных чисел, записанных в пятеричной системе счисления, в записи которых только одна цифра 3, при этом никакая четная цифра не стоит рядом с цифрой 3.

2. Сколько существует различных шестизначных чисел, записанных в пятеричной системе счисления, если известно, что цифра 2 должна встречаться в каждом слове ровно один раз и что «соседями» цифры 2 обязательно являются цифры 4 (эта цифра может быть записана и в других разрядах)? Каждая из других цифр может встречаться в слове любое количество раз или не встречаться совсем.

3. Сколько существует различных семизначных чисел, записанных в шестеричной системе счисления, если известно, что цифра 5 используется в каждом числе ровно один раз? Каждая из других цифр может встречаться в слове любое количество раз или не встречаться совсем. При этом рядом с цифрой 5 не может находиться цифра 0.

4. Сколько существует различных пятизначных чисел, записанных в четверичной системе счисления, если известно, что цифра 0 используется в каждом числе хотя бы один раз? Каждая из других цифр может встречаться в числе любое количество раз или не встречаться совсем.

5. Сколько существует различных шестизначных чисел, записанных в семеричной системе счисления, если:

• первой цифрой должна быть цифра, кратная трем;

• в числе должно быть только одно сочетание цифр 55;

• справа от этого сочетания не должно быть нечетной цифры?

Каждая цифра может входить в число несколько раз или не входить совсем.

6. Сколько существует восьмеричных пятизначных чисел, не содержащих в своей записи цифру 6, в которых все цифры различны и никакие две четные или две нечетные цифры не стоят рядом?

7. Сколько существует шестизначных девятеричных чисел, не содержащих в своей записи цифру 2, в которых все цифры различны и никакие две четные или две нечетные цифры не стоят рядом?

8. Сколько существует четырехзначных девятеричных чисел, не содержащих в своей записи цифры 1 и 2, в которых все цифры различны и никакие две четные или две нечетные цифры не стоят рядом?

9. Сколько существует пятизначных шестеричных чисел, которые начинаются с первой и последней четной цифры и у которых нет двух рядом расположенных четных цифр и двух рядом расположенных нечетных цифр?

Глава 9 Задания 9

9.1. Общие вопросы. Используемые функции

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 9 указывается «умение обрабатывать числовую информацию в электронных таблицах».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 6 мин.

Задание выполняется с использованием прилагаемого файла.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 9, в которых требуется в файле – документе электронной таблицы найти различные статистические показатели для приведенных в файле числовых данных (количество чисел или строк, удовлетворяющих некоторому условию, максимальное значение, среднее значение и т. п.).

При их выполнении используется ряд функций электронной таблицы. Применительно к программе Microsoft Excel это функции МАКС, МИН, СРЗНАЧ, ЦЕЛОЕ, ЕСЛИ, СЧЕТЕСЛИ^{^[33]}, СУММЕСЛИ и СРЗНАЧЕСЛИ.

Опишем особенности трех последних^{^[34]}.

Функция СЧЕТЕСЛИ

Она подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному критерию. Ее общий вид:

СЧЕТЕСЛИ(<диапазон>; <критерий>)

Аргумент <критерий> в форме числа, текста или адреса ячейки определяет, какие ячейки надо подсчитывать в указанном диапазоне. Например, критерий может быть выражен следующим образом: 10, "10", D6. Можно также использовать критерий со знаком сравнения и числом:

"=10"; ">10" и т. п.

Функция СУММЕСЛИ

Эта функция определяет сумму значений в некотором диапазоне, соответствующих заданному условию, проверяемому в другом диапазоне. Ее формат:

СУММЕСЛИ(<проверяемый_диапазон>; <критерий>; <диапазон_суммирования>),

где <критерий> – критерий (условие) для поиска значений в аргументе

<проверяемый_диапазон>; <диапазон_суммирования> – диапазон, в котором происходит суммирование подходящих значений.

Аргумент критерий может быть выражен в форме числа, текста или адреса ячейки, например как 32, "32", ">32", D6.

Работу функции проиллюстрируем на нескольких примерах:

проверяемый_диапазон

диапазон_суммирования

Значение функции =СУММЕСЛИ(B1:B5; "A"; D1:D5) будет равно 11

(3 + 8).

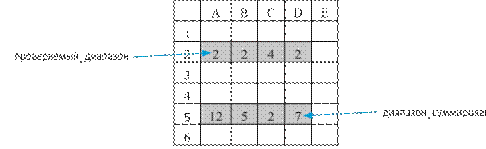
Значение функции =СУММЕСЛИ(A2:D2; 2; A5:D5) будет равно 24 (12 + 5 + 7).

проверяемый_диапазон

Значение функции =СУММЕСЛИ(A2:D2; А1; A5:D5) будет равно 14 (12 + 2).

проверяемый_диапазон диапазон_суммирования

Значение функции =СУММЕСЛИ(A2:D2; А1; F2:I2) будет равно 14 (12 + 2), а функции =СУММЕСЛИ(A2:D2; В1; F2:I2) будет равно 12 (5 + 7).

Функция СРЗНАЧЕСЛИ

Эта функция определяет среднее арифметическое значений в некотором диапазоне, соответствующих заданному условию, проверяемому в другом диапазоне. Ее формат:

СРЗНАЧЕСЛИ(<проверяемый_диапазон>; <критерий>; <диапазон_расчетов>),

где <критерий> – критерий (условие) для поиска значений в аргументе

<проверяемый_диапазон>; <диапазон_расчетов> – диапазон, в котором происходит расчет среднего арифметического подходящих значений.

При использовании этой функции в каждом из четырех примеров, рассмотренных применительно к функции СУММЕСЛИ, будет происходить:

• суммирование соответствующих значений;

• подсчет их количества;

• расчет среднего арифметического значения.

9.2. Примеры заданий и методика их выполнения

9.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2021 года)

Условие

Откройте файл электронной таблицы, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трех месяцев. Найдите разность между максимальным значением температуры и ее средним арифметическим значением.

В ответе запишите только целую часть получившегося числа.

Решение

В прилагаемом к заданию файле лист с исходными данными имеет вид:

	A	B	C	…	Y
1		0:00	1:00	…	23:00
2	01.04.2018	13,7	12,4	…
3	02.04.2018	11,8	12,1	…
…	…	…	…	…	…
92	31.09.2018			…

Следовательно, обработке подлежат данные в диапазоне B2:Y92.

Чтобы на экзамене узнать номер последней строки с данными, надо нажать комбинацию клавиш Ctrl+↓. Указатель активной ячейки перейдет к концу столбца с данными. Для возврата «наверх» – нажать комбинацию Ctrl+↑.

Чтобы определить букву последнего столбца с данными, используйте комбинацию клавиш Ctrl+→, для возврата на первый столбец – комбинацию Ctrl+←.

Для нахождения искомого в задании ответа надо знать максимальное и среднее арифметическое значения в указанном диапазоне, найти их разность и получить ее целую часть. Для этого используем функции МАКС, СРЗНАЧ и ЦЕЛОЕ, то есть формула для определения ответа^{^[35]} будет такой:

=ЦЕЛОЕ(МАКС(B2:Y92) - СРЗНАЧ(B2:Y92))

Эту формулу лучше всего ввести в ячейку А1.

Так как в приведенной формуле имеется два одинаковых диапазона, то второй можно записать, копируя первый.

9.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворять неравенству треугольника.

В ответе запишите только число.

Приведем несколько начальных строк из прилагаемого к заданию файла:

	A	B	C	D	E
1	73	43	11
2	43	93	36
3	33	87	31
4	16	89	42
5	…	…	…

Решение

Здесь для решения надо вспомнить, что «неравенство треугольника» – это следующее свойство треугольника: «Длина любой стороны треугольника меньше суммы длин двух других сторон».

Учитывая его, запишем в ячейку D1 формулу для вывода значений 1 и 0 в зависимости от особенностей трех чисел в столбцах А, В и С:

=ЕСЛИ(И(A2 < B2 + C2; B2 < A2 + C2; C2 < B2 + A2); 1; 0)

Распространив (скопировав) эту формулу на другие ячейки столбца D, получим:

	A	B	C	D	E
1	73	43	11	0
2	43	93	36	0
3	33	87	31	0
4	16	89	42	1
5	…	…	…

Быстрее всего скопировать формулу можно так:

• установить указатель активной ячейки на ячейку D1 и дважды щелкнуть мышью на темном квадратике в правом нижнем углу последней ячейки с формулой.

После этого искомое значение будет равно сумме всех чисел в столбце D. Соответствующую формулу удобно записать в ячейке Е1:

=СУММ(D1:D…)

где вместо многоточия должен быть указан номер последней строки с данными.

9.2.3. Пример 3

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

В файле электронной таблицы в каждой строке содержится шесть натуральных целых чисел. Определите количество строк таблицы, для которых выполнены оба условия:

• в строке только одно число повторяется дважды (ровно два раза), остальные числа не повторяются;

• среднее арифметическое неповторяющихся чисел строки не больше суммы повторяющихся чисел.

В ответе запишите только число.

Решение

Обсудим методику выполнения задания на простом примере:

	A	B	C	D	E	F
1	37	83	24	19	37	41
2	59	77	43	43	118	38
3	6	65	40	40	6	130
4	63	77	76	8	63	51
5	74	47	97	26	222	23

Как определить, что в некоторой строке соблюдается первое условие? Для этого надо знать, сколько раз каждое число встречается в строке.

Необходимые значения можно получить в столбцах G:L, записав в ячейке G1 формулу =СЧЕТЕСЛИ($A1:$F1; A1)^{^[36]} и распространив (скопировав) ее на остальные ячейки диапазона G1:L5:

	A	B	C	D	E	F	G	H	I	J	K	L
1	37	83	24	19	37	41	2	1	1	1	2	1
2	59	77	43	43	118	38	1	1	2	2	1	1
3	6	65	40	40	6	130	2	1	2	2	2	1
4	63	77	76	8	63	51	2	1	1	1	2	1
5	74	47	97	26	222	23	1	1	1	1	1	1

На первый взгляд, в строке первое условие соблюдается, если количество чисел 2 в диапазоне столбцов G:L равно 2. Для первой, второй и четвертой строк такое условие будет истинным, для третьей (есть две пары повторяющихся чисел) и пятой (нет повторяющихся чисел) – ложным.

Однако это не так! Дело в том, что возможен вариант, при котором наряду с числом, повторяющимся дважды, может быть записано число, повторяющееся трижды. Вот пример такой строки (она представлена в файле, прилагаемом к обсуждаемому заданию):

Предлагаем читателям еще раз прочитать условие и убедиться, что приведенная строка ему не удовлетворяет.

Правильное условие, при котором в строке только одно число повторяется дважды, а остальные числа не повторяются, такое: «Сумма количеств каждого из чисел в диапазоне G:L этой строки равна 8».

Получим только что упомянутую сумму в первой строке столбца M (с помощью функции СУММ), а в столбце N проверим, соблюдается ли наше условие (с помощью функции ЕСЛИ; если соблюдается, запишем 1, в противном случае – 0), после чего скопируем новые формулы:

	A	B	C	D	E	F	G	H	I	J	K	L	M	N
1	37	83	24	19	37	41	2	1	1	1	2	1	8	1
2	59	77	43	43	118	38	1	1	2	2	1	1	8	1
3	6	65	40	40	6	130	2	1	2	2	2	1	10	0
4	63	77	76	8	63	51	2	1	1	1	2	1	8	1
5	74	47	97	26	222	23	1	1	1	1	1	1	6	0

Видно, что четвертая и шестая строки не подходят.

Комментарий

«Базовые» для копирования формулы в ячейках M1 и N1:

=СУММ(G1:L1)

=ЕСЛИ(M1 = 8; 1; 0)

Теперь – о проверке строк на соблюдение второго условия. Для проверки надо знать:

• среднее арифметическое неповторяющихся чисел строки;

• сумму повторяющихся чисел.

Эти два значения получим в столбцах О и Р по «базовым» формулам:

=СРЗНАЧЕСЛИ(G1:L1; 1; A1:F1) =СУММЕСЛИ(G1:L1; 2; A1:F1)

а в столбце Q проверим, соблюдается ли в строке второе условие:

=ЕСЛИ(O2 <= P2; 1; 0) Результат будет следующим:

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	О	Р	Q
1	37	83	24	19	37	41	2	1	1	1	2	1	8	1	41,75	74	1
2	59	77	43	43	118	38	1	1	2	2	1	1	8	1	73	86	1
3	6	65	40	40	6	130	2	1	2	2	2	1	10	0	97,5	92	0
4	63	77	76	8	63	51	2	1	1	1	2	1	8	1	53	126	1
5	74	47	97	26	222	23	1	1	1	1	1	1	6	0	81,5	0	0

В каком случае в строке соблюдаются оба условия? – Если сумма значений в столбцах N и Q равна 2.

Рассчитав эту сумму для всех строк в столбце R, можно найти искомое в задании число как количество значений в этом столбце, равных 2 (используя функцию СЧЕТЕСЛИ). Соответствующую формулу можно ввести в одну из свободных ячеек в верхней части листа, например в S1:

	A	…	N	О	Р	Q	R	S
1	37	…	1	41,75	74	1	2	=СЧЕТЕСЛИ(R1:R…; 2)
2	59	…	1	73	86	1	2
3	6	…	0	97,5	92	0	0
4	63	…	1	53	126	1	2
5	74	…	0	81,5	0	0	0

В формуле в ячейке S1 вместо многоточия должен быть указан номер последней строки с данными (см. выше).

Можно упростить таблицу (то есть сократить время ее оформления, что важно на экзамене), если вместо двух формул в столбцах М и N записать в столбце N одну формулу:

=ЕСЛИ(СУММ(G2:L2) = 8; 1; 0)

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	О	Р	Q
1	37	83	24	19	37	41	2	1	1	1	2	1		1	41,75	74	1
2	59	77	43	43	118	38	1	1	2	2	1	1		1	73	86	1
3	6	65	40	40	6	130	2	1	2	2	2	1		0	97,5	92	0
4	63	77	76	8	63	51	2	1	1	1	2	1		1	53	126	1
5	74	47	97	26	222	23	1	1	1	1	1	1		0	81,5	0	0

Еще одно серьезное упрощение состоит в отказе от записи несколько сложной формулы с функцией ЕСЛИ в столбцах N и Q, в которых происходит проверка двух условий. Лучше использовать формулу, результатом которой является одна из логических констант ИСТИН или ЛОЖЬ. Соответствующая формула в ячейке N1:

=СУММ(G1:L1) = 8

а в ячейке Q1:

O2 <= P2 В результате лист примет вид:

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	О	Р	Q
1	37	83	24	19	37	41	2	1	1	1	2	1		ИСТИНА	41,75	74	ИСТИНА
2	59	77	43	43	118	38	1	1	2	2	1	1		ИСТИНА	73	86	ИСТИНА
3	6	65	40	40	6	130	2	1	2	2	2	1		ЛОЖЬ	97,5	92	ЛОЖЬ
4	63	77	76	8	63	51	2	1	1	1	2	1		ИСТИНА	53	126	ИСТИНА
5	74	47	97	26	222	23	1	1	1	1	1	1		ЛОЖЬ	81,5	0	ЛОЖЬ

При этом, как и ранее (когда находилось количество единиц в столбцах N и Q), нужно определить количество значений ИСТИНА в диапазоне столбцов N:Q, то есть «базовая» для копирования формула в ячейке R1 будет такой:

=СЧЕТЕСЛИ(N1:Q1; ИСТИНА)

Формула, определяющая искомый результат расчетов в ячейке S1, та же.

И еще об экономии времени. При описании методики выполнения задания мы каждую новую «базовую» формулу, записанную в первой строке, копировали в другие строки. При большом количестве строк (в файле, прилагаемом к данному заданию, содержится 6400 строк) целесообразно:

• сначала заполнить всю первую строку необходимыми формулами, в том числе и ячейку S1, указав в ней номер последней строки;

• а затем распространить (скопировать) формулы диапазона A1:Q1 на фактическое количество строк в обрабатываемом файле.

(Быстрее всего это сделать, если после выделения всех ячеек первой строки с формулами дважды щелкнуть мышью на темном квадратике в правом нижнем углу последней ячейки с формулой.)

В заключение заметим, что в ряде источников, связанных с ЕГЭ по информатике, предлагается после заполнения столбцов A:Q определять искомое значение с использованием фильтров. Это позволяет не вводить формулы в ячейки R1 и S1. Но для этого следует:

• вставить пустую первую строку^{^[37]};

• в ячейки N1 и Q1 ввести заголовки столбцов (можно условные);

• подключить к столбцам числовые фильтры, используя контекстное меню или с помощью инструмента Сортировка и фильтр ;

• в фильтрах столбцов N и Q оставить «галочки» только на значениях 1 или/и ИСТИНА:

В результате на листе будут отображены только те строки, для которых соблюдаются оба требуемых условия. Искомое в задании количество этих строк будет отражено на так называемой «строке состояния» (самая нижняя полоса окна программы). Но для этого, возможно, вам придется настроить эту строку таким образом, чтобы на ней отображалось количество отобранных строк.

Целесообразность такого решения предлагаем определить читателям.

9.2.4. Пример 4

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

Откройте файл электронной таблицы, содержащей в каждой строке семь натуральных чисел. Определите количество строк таблицы, для чисел которых выполнены оба условия:

• в строке есть два числа, каждое из которых повторяется дважды, остальные три числа различны;

• среднее арифметическое всех повторяющихся чисел строки меньше среднего арифметического всех ее чисел.

В ответе запишите только число.

Решение

Отличие данного задания от предыдущего:

• в каждой строке семь чисел, а не шесть;

• учитываться должны строки с двумя числами, каждое из которых повторяется дважды, а остальные три числа различны (а не строки, в которых есть только одно повторяющееся дважды число).

Первые две строки листа с данными прилагаемого к заданию файла имеют вид:

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	О	Р	Q	R	S	T	U
1	12	102	26	102	21	12	73
2	15	66	47	86	29	85	83

Приведем только «базовые» формулы в строке 1:

• формула в ячейке Н1 для определения количества каждого из чисел в столбцах А-G: =СЧЕТЕСЛИ($A1:$G1; A1);

• формула в ячейке О1 для расчета суммы указанных количеств: =СУММ(H1:N1);

• формула в ячейке Р1 для проверки соблюдения в строке первого условия: =ЕСЛИ(O1=11; 1; 0);

• формула в ячейке Q1 для расчета среднего значения всех чисел строки в столбцах А-G: =СРЗНАЧ(A1:G1);

• формула в ячейке R1 для расчета среднего значения повторяющихся чисел строки в столбцах А-G: =СРЗНАЧЕСЛИ(H1:L1; 2; A1:G1);

• формула в ячейке S1 для проверки соблюдения в строке второго условия: =ЕСЛИ(R1<Q1; 1; 0);

• формула в ячейке Т1 для проверки соблюдения в строке обоих условий: =P1 + S1.

Все формулы из диапазона Н1:Т1 распространяются (копируются) на остальные строки с данными (всего их – 16 000).

Внимание! После заполнения всех строк в рассматриваемом случае появляется множество сообщений об ошибке типа #ДЕЛ/0! (почему – проанализируйте самостоятельно). Их (сообщения) учитывать не нужно.

И конечно, в ячейку U1 следует ввести формулу для определения искомого значения: =СЧЕТЕСЛИ(T1:T16000; 2).

Приведем также короткие формулы, возвращающие значения ИСТИНА или ЛОЖЬ:

• в ячейке Р1: =СУММ(H2:N2) = 11;

• в ячейке S1: =R2 < Q2;

• в ячейке T1: =СЧЕТЕСЛИ(P1:S1; ИСТИНА).

9.2.5. Дополнение

Идея использования логических констант ИСТИНА и ЛОЖЬ вместо сложной формулы с функцией ЕСЛИ может быть реализована при выполнении и других подобных заданий, в частности задания 9 из демонстрационного варианта ЕГЭ по информатике 2022 года (см. п. 9.2.2).

Без использования функции ЕСЛИ формула в ячейке D1, учитывающая свойство треугольника («неравенство треугольника»), становится гораздо компактнее:

=И(A2 < B2+C2; B2 < A2+C2; C2 < B2+A2)

После ее копирования в столбце D будут выведены значения ИСТИНА и ЛОЖЬ. Как определить искомое значение в этом случае, установите самостоятельно.

9.3. Задания для самостоятельного выполнения

1. Выполните все задания, рассмотренные в данной главе.

2. С использованием файла, приложенного к заданию, рассмотренному в п. 9.2.3, определите:

а) число строк, в которых количество четных чисел не больше количества нечетных чисел;

б) разность максимального и минимального чисел всех тех строк, в которых каждое число встречается только один раз.

3. С использованием файла, приложенного к заданию, рассмотренному в п. 9.2.3, определите:

а) число строк, в которых количество четных чисел больше количества нечетных чисел в два и более раз;

б) разность максимального и минимального чисел всех тех строк, в которых каждое число встречается только один раз;

в) число строк таблицы, для чисел которых выполнены оба условия:

• в строке есть два числа, каждое из которых повторяется дважды, остальные три числа различны;

• среднее арифметическое всех повторяющихся чисел строки больше среднего арифметического неповторяющихся чисел.

Все задания 2 и 3 выполните двумя способами: без использования формул, возвращающих значения ИСТИНА или ЛОЖЬ, и с такими формулами – и сравните их.

4. Сформулируйте критерий для проверки условия:

• «В строке из пяти чисел только одно число повторяется дважды (ровно два раза), остальные числа не повторяются»;

• «В строке из шести чисел только одно число повторяется трижды (ровно три раза), остальные числа не повторяются».

Глава 10

Задания 10

10.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 10 указывается «информационный поиск средствами операционной системы или текстового процессора».

• Уровень сложности задания – Б (базовый).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

Задание выполняется с использованием прилагаемого файла. Возможные типы файла:

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 10, в которых требуется определить, сколько раз в прилагаемом файле (как правило, это файл с литературным произведением) встречается некоторое слово.

Пример: с помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «сад» или «Сад» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «сад», такие как «сады», «садик»и т. д., учитывать не следует. В ответе укажите только число.

***

В современных программах для работы с текстовыми документами имеются возможности поиска некоторого текста.

По умолчанию ищутся все формы заданного текста. Например, при поиске слова «сад» будут найдены и другие слова, в которых есть последовательность букв сад.

Для отбора только нужных форм слова в разных программах предусмотрены разные возможности. Далее будут рассмотрены методики выполнения заданий с помощью программы «Блокнот» и редактора Microsoft Word (или подобной). Возможности программ, которые вы используете, в части поиска текста исследуйте самостоятельно.

10.2. Примеры заданий и методики их выполнения

10.2.1. Пример 1 (задание из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.)

Условие

С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т. д., учитывать не следует.

Решение

Прежде всего обратим внимание на то, что:

• учитываться должны как слова «долг», так и «Долг» (в таких случаях говорят – «регистр не учитывать»);

• указанные слова в сносках учитываться не должны.

При выполнении задания с использованием программы «Блокнот» следует:

1) вызвать окно Навигация (с помощью комбинации клавиш Ctrl+F

Обратите внимание: поскольку в данном случае нас интересуют как слова «долг», так и «Долг», то не нужно включать флажок «С учетом регистра»;

2) щелкнуть по кнопке Найти далее (можно также щелкнуть мышью на тексте и нажимать функциональную клавишу F3).

Программа «Блокнот» и другие аналогичные программы ищут только заданную цепочку символов и не умеют искать слово в одной заданной форме (то есть будут найдены и другие слова, в которые входит последовательность букв долг). Поэтому приходится, неоднократно нажимая кнопку Найти далее, просматривать все найденные слова и подсчитывать количество только нужных слов. Слова в сносках не должны учитываться.

Ответ: 1.

При использовании программы Microsoft Word:

1) вызвать окно Навигация (аналогично тому, как это делалось в программе «Блокнот») и в поле для ввода ввести нужное слово:

В нижней части окна появятся фрагменты текста со всеми вхождениями букв долг. Среди них следует отобрать нужные слова. В данном случае такое слово – одно.

При большом количестве отобранных фрагментов можно вызвать окно Найти и заменить. Для этого в окне Навигация справа

от поля ввода щелкнуть на стрелке рядом с изображением лупы () и появившемся списке:

2) выбрать Расширенный поиск. Появится окно Найти и заменить, в котором надо поставить флажок в параметре Только слово целиком, в поле ввода ввести нужное слово и нажать клавишу Enter. После этого программа будет искать только то, что нужно, причем в современных версиях Microsoft Word в окне Навигация слева от документа будет отражаться информация о том, сколько слов найдено и в каких фразах.

Окно Найти и заменить с параметрами для поиска можно также вызвать, нажав комбинацию клавиш Ctrl+H или щелкнув на инструменте Заменить:

В появившемся окне надо выбрать вкладку Найти (первую):

и в ней провести поиск только нужных слов.

Обратим внимание на то, что хотя в условии говорилось о том, что слова в сносках не должны учитываться, мы это в расчет не принимали. Дело в том, что в литературных произведениях сноски отсутствуют. Об учете требования в условии, связанного со сносками (при их наличии в исследуемом тексте), будет рассказано в п. 10.3.2.

10.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается в тексте отдельное слово «теперь» со строчной буквы. Другие формы этого слова учитывать не следует.

Решение

Отличие данного задания от предыдущего в том, что должны учитываться только слова «теперь», а слова «Теперь» – нет.

В программе «Блокнот» окно Найти должно быть оформлено следующим образом:

а окно Найти и заменить в программе Microsoft Word:

Выполните это задание и установите, какой вариант использования окна Найти и заменить лучше – «через» окно Навигация и расширенный поиск или непосредственно (Ctrl+Н).

10.2.3. Пример 3

Условие

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов^{^[38]} и определите, сколько раз встречается слово «пристани» в конце предложения.

Решение

В конце предложения после слова «пристани» может быть точка, вопросительный или восклицательный знак. Проверив эти три варианта, можно найти ответ.

Выполните задание самостоятельно.

10.2.4. Пример 4

Условие

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз встречается сочетание букв народ только в составе других слов, но не как отдельное слово.

Решение

Здесь для нахождения ответа надо определить два значения: общее количество слов, в составе которых есть последовательность букв народ, и количество отдельных слов «народ». Первое количество равно 15, второе – 4. Искомое значение 15 – 4 = 11.

Ответ: 11.

10.2.5. Пример 5

Условие

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз слово «Севастополь» встречается в названии книги и глав.

Решение

После поиска всех слов «Севастополь» (именно в такой форме) необходимо подсчитать количество вхождений, представленных прописными буквами. Их – 3.

Ответ: 3.

10.2.6. Пример 6

Условие

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз в тексте встречается существительное «немец» в любой форме.

Решение

Здесь надо обратить внимание на то, что нужно учесть только существительные.

Если ввести в поле ввода слово немец, то всего будут найдены три слова – одно существительное (немец) и два прилагательных (немецкой и немецкими). Если ввести слово немц, то будут найдены два вхождения (немцы и немцами). Всего существительных с вхождением «немец» в любой форме – три.

Ответ: 3.

10.2.7. Пример 7

Условие

Текст произведения Льва Николаевича Толстого «Севастопольские рассказы» представлен в виде файлов различных форматов. Откройте один из файлов и определите, сколько раз в тексте встречаются слова, начинающиеся на осад или Осад.

Решение

Можно ли определять искомое значение по поиску вхождений осад? – Можно, но будут найдены 19 слов, среди которых будут слова досадно, посадка и т. п., после чего найти и подсчитать нужные будет не просто. Лучше провести поиск по образцу пробелосад. Таких слов – 5. Но при этом не будут найдены вхождения с прописной буквы. Чтобы учесть и их, следует провести поиск по слову Осад с учетом регистра. Такое слово – одно. Общее число искомых вхождений – 6.

Ответ: 6.

10.3. Рекомендации по выполнению задания 10

10.3.1. При выполнении задания обратите внимание в условии на особенности слов (слова), количество которых следует определить:

• на форму слов; если нужно учесть только одну форму, следует провести поиск с параметром Только слово целиком;

• на их регистр; если указано слово только в одном варианте (начинающиеся только со строчной или только с заглавной буквы), то при выполнении следует провести поиск с учетом регистра;

• на место указанной последовательности букв в словах (в начале слов или в конце);

• на место указанной последовательности букв в предложении (в начале или в конце);

• на место указанной последовательности букв в тексте (в заголовках или т. п.);

• на части речи, которой является заданное слово (существительное, прилагательное и т. п.);

• на место указанной последовательности букв в документе (в его основной части и в сносках или только в основной части).

10.3.2. При наличии в документе сносок, в случае когда указанные в условии слова в сносках учитываться не должны, при использовании для поиска редактора Microsoft Word следует ограничить так называемую «область поиска». Она указывается в окне Найти и заменить:

10.4. Задания для самостоятельного выполнения

1. С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «был» или «Был» в тексте романа в стихах А. С. Пушкина «Евгений Онегин»^{^[39]}. Другие формы слова «был», такие как «было», «были» и т. д., учитывать не следует.

2. С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «Онегин» в тексте романа в стихах А. С. Пушкина «Евгений Онегин». Другие формы слова «Онегин», такие как «Онегина», «Онегиным» и т. д., учитывать не следует.

3. С помощью текстового редактора определите, сколько раз в тексте романа в стихах А. С. Пушкина «Евгений Онегин», не считая сносок, последовательность букв ого встречается в конце слова.

4. (Задание из демонстрационного варианта ЕГЭ 2024 года)

Глава 11 Задания 11

11.1. Общие вопросы. Теория

В Спецификации контрольных измерительных материалов для проведения в 2023 году единого государственного экзамена по информатике [1] в качестве проверяемого элемента содержания применительно к заданию 11 указывается «умение подсчитывать информационный объем сообщения».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

***

Информационный объем сообщения – это размер памяти компьютера, требуемый для хранения этого сообщения.

Речь идет о сообщении, представляющем собой последовательность символов (букв, цифр, нот, специальных символов и т. д.).

Все возможные символы, которые могут быть в сообщении, составляют алфавит. Количество символов в некотором алфавите называют мощностю алфавита (M).

Информационный объем I сообщения равен произведению количества символов в нем S на число битов К, которое требуется для хранения одного символа:

I = S × K. (11.1)

Сколько битов требуется для хранения одного символа, зависит от мощности используемого алфавита M. Когда М есть степень двойки, то требуемое число битов К равно показателю этой степени:

Таблица 11.1

М	2	4	8	16	32	64	128	256	512	1024
K, бит	1	2	3	4	5	6	7	8	9	10

Можно сказать, что при этом К = log₂М.

А если М не является степенью двойки? В таких случаях количество битов К равно показателю этой степени для числа – степени двойки, ближайшего большего к М, например при М = 26 таким числом является 32 (2⁵), то есть К = 5; при М = 1200: К = 11.

если М есть степень двойки то

К = log₂М (11.2) иначе

К = ⌊log₂М⌋ + 1

где символы ⌊ ⌋ обозначают целую часть числа, записанного между ними.

Итак, зная количество символов в сообщении и число битов, требуемых для хранения одного символа, можно определить информационный объем сообщения I в битах.

Внимание! Если речь идет о хранении сообщения в памяти компьютера, то необходимый объем памяти измеряется в целом количестве байтов. Это значит, что если, например, I = 150 бит, то в памяти компьютера такое сообщение будет занимать 20 байт (160 бит).

В общем случае количество байтов Б определяется следующим образом:

если I есть степень двойки то

I Б = 8

иначе (11.3)

Б = ⌊ ₈^I⌋ + 1

11.2. Примеры заданий и методика их выполнения

11.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 250 символов и содержащий только десятичные цифры и символы из 1650-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байтов. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством битов. Определите объем памяти (в Кбайтах), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество байтов.

Решение

Здесь под сообщением подразумевается отдельный идентификатор объекта (в памяти компьютера будет храниться несколько идентификаторов/сообщений).

Определим информационный объем сообщения, особенности которого указаны в условии.

Мощность алфавита, используемого для записи идентификатора, равна 10 (количество цифр) + 1650 (количество специальных символов) = 1660.

Это значит, что согласно формуле 11.2 значение К = 11 бит.

Так как количество символов в идентификаторе равно 250, то его информационный объем согласно формуле 11.1 составляет:

250 × 11 = 2750 бит.

Поскольку в условии говорится: «В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байтов», то для определения числа байтов, необходимого для хранения одного идентификатора, следует использовать формулу 11.3:

Б = + 1 = 344 байта.

Всего идентификаторов – 65 536, то есть для их хранения потребуется 65 536 × 344 = 22 544 384 байта, или 22 544 384 : 1024 = 22 016 килобайт.

Ответ: 22 016.

11.2.2. Пример 2

(задание из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.)

Условие

При регистрации в компьютерной системе каждому объекту сопоставляется идентификатор, состоящий из 15 символов и содержащий только символы из 8-символьного набора: А, В, C, D, Е, F, G, H. В базе данных для хранения сведений о каждом объекте отведено одинаковое и минимально возможное целое число байтов. При этом используют посимвольное кодирование идентификаторов, все символы кодируют одинаковым и минимально возможным количеством битов. Кроме собственно идентификатора, для каждого объекта в системе хранятся дополнительные сведения, для чего отведено 24 байта на один объект. Определите объем памяти (в байтах), необходимый для хранения сведений о 20 объектах. В ответе запишите только целое число – количество байтов.

Решение

Отличие условия данного задания:

• кроме идентификатора объекта, в памяти компьютерной системы хранятся также дополнительные сведения о каждом из них;

• искомый объем памяти должен быть выражен в байтах.

Без учета дополнительных сведений число байтов, необходимых для хранения одного идентификатора, определяется аналогично ранее рассмотренной задаче.

Мощность используемого алфавита – 8.

Количество битов, требуемых для хранения одного символа согласно табл. 11.1, – 3.

Информационный объем собственно идентификатора согласно формуле 11.1 составляет:

15 × 3 = 45 бит.

Для его хранения в памяти системы потребуется 6 байт (см. формулу

11.3).

Так как дополнительные сведения о каждом идентификаторе занимают 24 байта, то общий объем памяти, необходимый для хранения сведений о 20 объектах, равен

(6 + 24) × 20 = 600 байт.

Ответ: 200.

В рассмотренных заданиях исходными данными были:

• количество символов, используемых для записи идентификатора (мощность алфавита);

• объем памяти, требуемый для хранения дополнительных сведений (условно будем считать, что в задании в п. 11.2.1 объем равен нулю);

• количество объектов, сведения о которых будут храниться в памяти,

– и требовалось определить общий объем памяти, необходимый для хранения сведений о всех объектах.

Возможны также различные варианты, так сказать, «обратных» задач, в которых общий объем памяти известен, а требуется определить одно неизвестное значение из трех других параметров кодирования.

11.2.3. Пример 3

Условие

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 64 символов. Для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байтов. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством битов. Для хранения 131 072 идентификаторов потребовалось 8 Мбайт. Определите максимально возможную мощность алфавита, используемого для записи идентификаторов. В ответе запишите только целое число.

Решение

Начинаем, так сказать, «с конца».

Для хранения одного из 131 072 идентификаторов потребовалось

8 × 1024 × 1024 : 131 072 = 64 байта.

Так как в идентификаторе 64 символа, то один символ кодируется одним байтом, или восемью битами. Это значит, что искомая максимально возможная мощность алфавита равна 256 (см. табл. 11.1).

Ответ: 256.

Дополнительный (важный!) вопрос:

«Каким может быть минимальное количество символов в используемом алфавите?»

Ответ: 129 (для кодирования 128 символов достаточно 7 бит).

11.2.4. Пример 4

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 11 символов. В базе данных для хранения сведений о каждом объекте отведено одинаковое и минимально возможное целое число байтов. При этом используют посимвольное кодирование идентификаторов, все символы кодируют одинаковым и минимально возможным количеством битов; это число одно и то же для всех объектов. Кроме собственно идентификатора, для каждого объекта в системе хранятся дополнительные сведения. Для хранения сведений о 30 объектах потребовалось 900 байт. Сколько байтов выделено для хранения дополнительных сведений об одном объекте? В ответе запишите только целое число – количество байтов.

Решение

Для кодирования каждого из 11 символов идентификатора требуется 4 бита (согласно формуле 11.2), а всех 11 символов (информационный объем собственно идентификатора) – 44 бита. Размер памяти в байтах согласно формуле 11.3 в этом случае будет равен 6 байт.

С другой стороны, можно определить общий размер памяти, требуемый для хранения одного из 30 объектов, он составляет 900 : 30 = 30 байт.

Это означает, что для хранения дополнительных сведений выделено

30 – 6 = 24 байта.

Ответ: 24.

Возможны также задания, в которых мощность алфавита в явном виде не задана, а представлена другая информация, требующаяся для его расчета.

11.2.5. Пример 5

Условие

Информационная панель может отображать сообщения, состоящие из семи цифр, причем каждая цифра может быть трех цветов. Цифры и цвета могут повторяться. Контроллер панели выделяет под каждое сообщение одинаковое и минимальное возможное целое число байтов. При этом используется посимвольное кодирование, все символы сообщения кодируются одинаковым минимально возможным количеством битов.

Укажите объем памяти в байтах для хранения 150 сообщений.

Решение

Здесь роль символов сообщения играют цифры, которые могут быть трех цветов. Значит, можно сказать, что мощность используемого алфавита равна

10 (количество возможных цифр) × 3 (количество возможных цветов) = 30.

Согласно формуле 11.2, для кодирования 30 вариантов требуется 5 бит.

Следовательно, информационный объем одного сообщения на панели 7 × 5 = 35 бит. Для его хранения потребуется 5 байт (согласно формуле 11.3), а для хранения всех 150 сообщений – 750 байт.

Ответ: 750.

11.2.6. Пример 6

Условие

В автомобильном номере используются буквы A, B, C, E, H, K, M, O и десятичные цифры. Каждый номер начинается с двух букв, затем идут три цифры, две буквы и три цифры, например АА799ЕН005. В компьютерной системе каждый такой номер кодируется посимвольно, при этом каждая буква кодируется одинаковым минимально возможным количеством битов и каждая цифра кодируется одинаковым минимально возможным количеством битов. Для каждого номера выделяется одинаковое и минимально возможное целое число байтов. Укажите объем памяти в байтах для хранения 130 номеров.

Решение

Особенность данной задачи в том, что цифры и буквы кодируются по-разному – в каждой группе мощность алфавита разная. Для букв она равна 8, для цифр – 10. Соответствующее количество битов для кодирования отдельного символа – 3 и 4. Это значит, что информационный объем сообщения (номера) равен сумме информационных объемов букв и цифр:

4 (количество букв) × 3 + 6 (количество цифр) × 4 = 36 бит.

Итак, целое количество байтов для хранения одного номера составляет 5, а для хранения всех 130 номеров – 650.

Ответ: 650.

11.3. Задания для самостоятельного выполнения

1. (Задание из демонстрационного варианта ЕГЭ 2024 года)

При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 60 символов и содержащий только десятичные цифры и символы из 250-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байтов. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством битов.

Определите объем памяти (в Кбайтах), необходимый для хранения 65 536 идентификаторов. В ответе запишите только целое число – количество Кбайтов.

2. При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 252 символов и содержащий только десятичные цифры и символы из 1700-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байтов. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством битов. Определите объем памяти (в Кбайтах), необходимый для хранения 4096 идентификаторов. В ответе запишите только целое число – количество Кбайтов.

3. При регистрации в компьютерной системе каждому объекту присваивается идентификатор, состоящий из 294 символов и содержащий только десятичные цифры и символы из 4550-символьного специального алфавита. В базе данных для хранения каждого идентификатора отведено одинаковое и минимально возможное целое число байтов. При этом используется посимвольное кодирование идентификаторов, все символы кодируются одинаковым и минимально возможным количеством битов. Определите объем памяти (в Кбайтах), необходимый для хранения 131 072 идентификаторов. В ответе запишите только целое число – количество

Кбайтов.

4. При регистрации в компьютерной системе, используемой при проведении командной олимпиады, каждому ученику выдается уникальный идентификатор – целое число от 1 до 1000. Для хранения каждого идентификатора используется одинаковое и минимально возможное количество битов. Идентификатор команды состоит из последовательно записанных идентификаторов учеников и вось-

ми дополнительных битов. Для записи каждого идентификатора команды система использует одинаковое и минимально возможное количество байтов. Во всех командах равное количество участников. Сколько участников в каждой команде, если для хранения идентификаторов 20 команд-участниц потребовалось 180 байт?

5. При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из шести символов и содержащий только символы из B, G, О, Р, Z, У. В базе данных для хранения сведений о каждом пользователе отведено одинаковое целое число байтов, при этом для хранения сведений о 200 пользователях используется 8000 байт. Для каждого пользователя хранятся пароль и дополнительные сведения. Для хранения паролей используют посимвольное кодирование, все символы кодируются одинаковым и минимально возможным количеством битов. Сколько битов отведено для хранения дополнительных сведений о каждом пользователе?

6. Информационная панель может отображать сообщения, состоящие из пяти цифр, причем каждая цифра может быть четырех цветов. Цифры и цвета могут повторяться. Контроллер панели выделяет под каждое сообщение одинаковое и минимально возможное целое число байтов. При этом используется посимвольное кодирование, все символы сообщения кодируются одинаковым минимально возможным количеством битов. Для хранения всех сообщений потребовался 1 килобайт памяти. Определите число сообщений.

7. Выполните задание примера 6 (п. 11.2.6), при условии что каждая буква и каждая цифра кодируются одинаковым минимально возможным количеством битов.

Глава 12 Задания 12

12.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 12 указывается «умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 6 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет приведены задания 12, в которых идет речь о выполнении программы исполнителем Редактор, который получает на вход строку цифр или строку букв и преобразовывает ее.

Общий вид задания

«Исполнитель Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

1) заменить(v, w)

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить(111, 27) преобразует строку 05111150 в строку 0527150.

Если в строке нет вхождений цепочки v, то выполнение команды заменить(v, w) не меняет эту строку.

2) нашлось(v)

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «Истина», в противном случае возвращает значение «Ложь». Строка исполнителя при этом не изменяется.

Цикл

ПОКА условие

последовательность команд КОНЕЦ ПОКА выполняется, пока условие истинно. В конструкции

ЕСЛИ условие

ТО команда1

ИНАЧЕ команда2

КОНЕЦ ЕСЛИ выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Приводится программа для указанного исполнителя, после чего указывается строка, которая подается на вход этой программе. В ответе следует записать полученную строку или число, удовлетворяющее некоторому условию.

***

От себя добавим, что возможна также конструкция:

ЕСЛИ условие

ТО команда

КОНЕЦ ЕСЛИ в которой команда выполняется, только если условие истинно. В противном случае ничего не выполняется.

12.2. Примеры заданий и методика их выполнения

12.2.1. Пример 1

(задание из демонстрационных вариантов ЕГЭ 2020 и 2022 гг.)

Условие (кроме описания команд и программных конструкций^{^[40]})

Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 70 идущих подряд цифр 8? В ответе запишите полученную строку.

НАЧАЛО

ПОКА нашлось(2222) ИЛИ нашлось(8888)

ЕСЛИ нашлось(2222)

ТО заменить(2222, 88)

ИНАЧЕ заменить(8888, 22)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Проще всего выполнить задание путем разработки несложной программы. В ней можно выделить три основных этапа:

1) формирование исходной строки;

2) моделирование действий программы в условии;3) вывод на экран измененной строки.

На этапе 2 определить, встречается ли заданная цепочка в строке исполнителя, можно с помощью функции, возвращающей позицию (номер символа), с которой в строке начинается цепочка: если функция возвращает значение, равное 0 (в языках программирования, в которых нумерация символов начинается с нуля, – равное –1), то заданная цепочка в строке отсутствует. В школьном алгоритмическом языке соответствующая функция – поз.

Для замены в строке одной цепочки символов на другую в языках программирования также предусмотрены процедуры (функции). Соответствующая процедура школьного алгоритмического языка – заменить:

алг нач лит с, цел i | Здесь и далее c – обрабатываемая строка | Этап 1 с := "" нц для i от 1 до 70 с := с + "8" кц | Этап 2 нц пока поз("2222", с) <> 0 или поз("8888", с) <> 0 если поз("2222", с) <> 0 то заменить(с, "2222", "88", нет) иначе заменить(с, "8888", "22", нет) все кц | Этап 3 вывод с кон

Примечание. Параметр нет в процедуре заменить говорит о том, что заменяться должно только первое вхождение цепочки.

12.2.2. Пример 2

Условие

Дана программа:

НАЧАЛО

ПОКА нашлось(49) ИЛИ нашлось(97) ИЛИ нашлось(47)

ЕСЛИ нашлось(47)

ТО заменить(47, 74)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(97)

ТО заменить(97, 79)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(49)

ТО заменить(49, 94)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

На вход приведенной ниже программы поступает строка, содержащая 40 цифр 7, 40 цифр 9 и 50 цифр 4, расположенных в произвольном порядке. Запишите без разделителей символы, которые имеют порядковые номера 25, 71 и 105 в получившейся строке.

Комментарии к решению

Напомним, что в программах величина строкового типа рассматривается как массив, элементами которого являются отдельные символы. Это значит, что для того чтобы использовать в программе значение отдельного символа строки, нужно указать имя строковой величины и в скобках (круглых или квадратных, в зависимости от языка программирования) – номер символа в памяти компьютера^{^[41]}. Следовательно, в программе после формирования строки-результата нужно вывести на экран символы с соответствующими номерами.

Всю программу разработайте самостоятельно.

При описании действий согласно программе в условии следует учесть, что, в отличие от предыдущего задания, когда на каждой итерации^{^[42]} выполнялась только одна из двух возможных команд заменить, в данном случае возможно выполнение и двух, и трех таких команд.

12.2.3. Пример 3

Условие

Найдите сумму цифр в строке, которая получится в результате применения приведенной ниже программы к строке, состоящей из 65 цифр 9.

НАЧАЛО

ПОКА нашлось(999) ИЛИ нашлось(222)

ЕСЛИ нашлось(222)

ТО заменить(222, 9)

ИНАЧЕ заменить(999, 2)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Комментарии к решению

Здесь после формирования строки-результата следует определить сумму ее цифр. Как использовать отдельный символ строки, рассказывалось при выполнении предыдущего задания.

Соответствующий фрагмент программы:

сум := 0 | Начальное значение искомой величины нц для i от 1 до длин(с) | Для всех символов строки с | Каждый символ-цифра преобразовывается в число | и учитывается в сумме сум := сум + лит_в_цел(с[i], успех) кц

где длин – функция школьного алгоритмического языка, возвращающая общее количество символов в строке, лит_в_цел – функция, преобразовывающая величину строкового типа в число; аргумент функции успех логического типа возвращает истинное или ложное значение в зависимости от того, можно ли провести указанное преобразование (строка символов может не представлять из себя число).

Всю программу разработайте самостоятельно.

12.2.4. Пример 4

Условие

Определите количество нулей в строке, получившейся в результате применения приведенной ниже программы к входной строке, состоящей из единицы, за которой следуют 80 нулей подряд. В ответе запишите только количество нулей в получившейся строке.

НАЧАЛО

ПОКА нашлось(10) ИЛИ нашлось(1)

ЕСЛИ нашлось(10)

ТО заменить(10, 001)

ИНАЧЕ

ЕСЛИ нашлось(1)

ТО заменить(1, 000)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Комментарии к решению

Количество цифр 0 в строке-результате можно определить с помощью стандартных функций (методов) используемого языка программирования, возвращающих количество вхождений заданного символа в заданную строку.

Всю программу разработайте самостоятельно.

12.2.5. Пример 5

Условие

Дана программа:

НАЧАЛО

ПОКА нашлось(11)

ЕСЛИ нашлось(112)

ТО заменить(112, 6)

ИНАЧЕ заменить(11, 3)

КОНЕЦ ПОКА

КОНЕЦ

Исходная строка содержит десять единиц и три двойки, других цифр нет, точный порядок расположения единиц и двоек неизвестен. Какую наибольшую сумму цифр может иметь строка, которая получится после выполнения программы?

Решение

Так как точный порядок расположения цифр в исходной строке неизвестен, то ее сформировать нельзя. Поэтому решим задачу методом рассуждений.

Сравним команды с точки зрения увеличения суммы цифр в строке в результате их выполнения.

По команде заменить(112, 6) сумма цифр увеличится на 2, по команде заменить(11, 3) – на 1. Значит, для получения наибольшей суммы цифр строка должна быть такой, чтобы все цепочки цифр вхождения цифр 112 (всего их может быть три) могли быть заменены. Достаточно очевидный вариант такой строки: 1121121121111. Результат ее обработки будет следующим: 66633. Сумма цифр строки-результата равна 24.

Ответ: 24.

12.2.6. Пример 6

Условие

Дана программа:

НАЧАЛО ПОКА нашлось (111) заменить(111, 2) заменить(222, 11) КОНЕЦ ПОКА

КОНЕЦ

К исходной строке, содержащей более 60 единиц и не содержащей других символов, применили приведенную выше программу. В результате получилась строка «2211». Какое наименьшее количество единиц могло быть в исходной строке?

Решение

Программа для нахождения искомого количества:

алг нач лит с, цел n, i | Рассматриваем значения n нц для n от 61 до 1000 | Формируем соответствующую исходную строку с := "" нц для i от 1 до n с := с + "1" кц | Моделируем работу программы в условии нц пока поз("111", с) <> 0 заменить(с, "111", "2", нет) заменить(с, "222", "11", нет) кц

| Проверяем полученную строку

если с = "2211" | Встретилась нужная строка то | Выводим на экран соответствующее значение n вывод n | Прекращаем рассмотрение значений n выход | Из программы все кц кон

12.2.7. Пример 7

Условие

Дана программа:

НАЧАЛО

ПОКА нашлось(25) ИЛИ нашлось(355) ИЛИ нашлось(555)

ЕСЛИ нашлось(25)

ТО заменить(25, 5)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(355)

ТО заменить(355, 52)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(555)

ТО заменить(555, 3)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

На вход приведенной выше программы поступает строка, начинающаяся с цифры 2, а затем содержащая n цифр 5 (n > 3).

Определите наименьшее значение n, при котором сумма цифр в строке, получившейся в результате выполнения программы, равна 17.

Комментарии к решению

Программа решения задачи аналогична предыдущей. Отличие в том, что прекратить рассмотрение значений n нужно в случае, когда сумма цифр сформированной строки станет равной 17 (о расчете суммы см. п. 12.2.3).

Всю программу разработайте самостоятельно.

12.2.8. Пример 8

(задание из демонстрационного варианта ЕГЭ 2024 г.)

Условие

Дана программа:

НАЧАЛО

ПОКА нашлось(52) ИЛИ нашлось(2222) ИЛИ нашлось(1122)

ЕСЛИ нашлось(52)

ТО заменить(52, 11)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(2222)

ТО заменить(2222, 5)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(1122)

ТО заменить(1122, 25)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

На вход приведенной выше программы поступает строка, начинающаяся с цифры 5, а затем содержащая n цифр 2 (3 < n < 10 000).

Определите наибольшее значение n, при котором сумма цифр в строке, получившейся в результате выполнения программы, равна 64.

Решение

Достаточно очевидный вариант действий в программе такой:

Перебрать все возможные значения n (от 10000 до 3) и для каждого значения: - сформировать соответствующую входную строку;

- над ней провести действия согласно программе в условии;

- определить сумму цифр полученной строки; - если она равна 64, то вывести соответствующее значение n; прекратить перебор значений n

Соответствующая программа:

алг нач лит с, цел n, сум, i, лог успех нц для n от 10000 до 3 шаг -1 | Формирование исходной строки с := "5"

нц для i от 1 до n с := с + "2" кц | Действия согласно программе нц пока поз("52", с) <> 0 или поз("2222", с) <> 0 или поз("1122", с) <> 0 если поз("52", с) <> 0 то заменить(с, "52", "11", нет) все если поз("2222", с) <> 0 то заменить(с, "2222", "5", нет) все если поз("1122", с) <> 0 то заменить(с, "1122", "25", нет) все кц | Определение суммы цифр сумма := 0 нц для i от 1 до длин(с) сум := сум + лит_в_цел(с[i], успех) кц | Проверка если сум = 64 то вывод n выход все кц кон

Недостатком приведенной программы является то, что в ней для большого числа значений n (несколько тысяч) многократно (тоже несколько тысяч раз) рассчитывается сумма цифр в сформированной строке, которая имеет значительное количество цифр (в начале – несколько тысяч). Конечно, на экзамене это потребует значительного времени на получение искомого результата.

Быстрее ответ можно получить, если перебор чисел проводить от меньшего к большему:

алг нач лит с, цел n, сум, i, лог успех нц для n от 3 до … | Формирование исходной строки с := "5" нц для i от 1 до n с := с + "2" кц | Действия согласно программе

…

| Определение суммы цифр

… | Выводим значения n и сумма вывод нс, n, " ", сум | Если сумма равна 64, выведем, например, восклицательный знак вывод " !" кц кон

Каким принять конечное значение параметра цикла n при переборе? В первом приближении – 100. Запустив программу, можно убедиться, что во втором столбце среди выводимых значений числа 64 нет.

Рассмотрим при переборе значения от 101 до 200. Фрагмент результата приведен ниже.

… …

150 65

151 62

152 64 !

153 67

154 64 !

155 67

156 64 !

157 66

158 69

159 66

160 69

… …

(При всех бóльших значениях n сумма больше 64.) Видно, что наибольшее значение n равно 156.

Ответ: 156.

Понятно, что при необходимости начальное и конечное значения n придется увеличивать до нахождения нужного результата. В рассмотренном примере можно было также, задав небольшой интервал «в районе» значения 500 (490–510) и увидев, что все результаты больше 64 и возрастают, уменьшить его до 240–260 и т. д.

12.2.9. Пример 9

(задание из демонстрационного варианта ЕГЭ 2023 г.)

Условие

НАЧАЛО

ПОКА нашлось(>1) ИЛИ нашлось(>2) ИЛИ нашлось(>0)

ЕСЛИ нашлось(>1)

ТО заменить(>1, 22>)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(>2)

ТО заменить(>2, 2>)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(>0)

ТО заменить(>0, 1>)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

На вход приведенной выше программы поступает строка, начинающаяся с символа «>», а затем содержащая 39 цифр 0, n цифр 1 и 39 цифр 2, расположенных в произвольном порядке. Определите наименьшее значение n, при котором сумма числовых значений цифр строки, получившейся в результате выполнения программы, является простым числом.

Решение

Особенностью задания является то, что во входной строке цифры 0, 1 и 2 расположены в произвольном порядке (то есть конкретный вид строки неизвестен). Поэтому данное задание выполняется методом рассуждений.

Кроме того, при работе программы на каждой итерации цикла ПОКА проверяются и при необходимости выполняются все три конструкции

ЕСЛИ.

Обсудим, что происходит в заданной строке после выполнения исполнителем каждой из конструкций ЕСЛИ.

Если встретится цепочка символов «>1», то единица будет заменена на две двойки, после которых будет записан символ «>» (такой же символ перед цифрой 1 удалится). Это значит, что:

• количество единиц уменьшится на 1;

• количество двоек увеличится на 2;

• символ «>» будет находиться после новых двоек.

Из этого, в свою очередь, следует, что новые двойки уже в дальнейшем не изменятся.

Если встретится цепочка символов «>2», то она будет заменена на «2>», то есть:

• количество двоек не изменится;

• символ «>» сместится вправо;

• «обработанная» при этом двойка уже измениться не может.

Если встретится цепочка символов «>0», то она будет заменена на «1>». В результате:

• количество нулей уменьшится на 1;

• количество единиц увеличится на 1;

• символ «>» сместится вправо и будет находиться после новых единиц (они уже не изменятся).

Обратим внимание на то, что во всех случаях символ «>» перемещается в строке вправо (к концу строки). После того как он станет последним символом строки, условие в цикле ПОКА станет ложным и все действия прекратятся. Как изменится количество тех или иных цифр в строке?

Ответ приведен в таблице:

Цифра	Было в исходной строке	Как изменится количество	Комментарий
0	39	Станет равно 0	Все 39 нулей будут заменены 39 единицами
2	39	Увеличится на 2n	Каждая из n исходных единиц будет заменена двумя двойками
1	n	Станет равно 39	См. выше два комментария

Итак, в полученной в результате приведенной программы строке будут записаны 39 единиц и 39 + 2n двоек. Сумма числовых значений всех этих цифр равна: 39 + (39 + 2n) × 2 = 117 + 4n. Осталось определить наименьшее значение n, при котором указанная сумма является простым числом. Это можно сделать, перебрав и рассмотрев значения n, равные 1, 2, …. Соответствующий анализ приведен в таблице:

n	Сумма	Анализ
1	121	Число, кратное 11
2	125	Число, кратное 5
3	129	Число, кратное 3
4	133	Число, кратное 19
5	137	Простое число

Ответ: 5.

12.3. Задания для самостоятельного выполнения

1. Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 68 идущих подряд цифр 8? В ответе запишите полученную строку.

НАЧАЛО

ПОКА нашлось(222) ИЛИ нашлось(888)

ЕСЛИ нашлось(222)

ТО заменить(222, 8)

ИНАЧЕ заменить(888, 2)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

2. Найдите сумму цифр в строке, которая получится в результате применения приведенной ниже программы к строке, состоящей из 65 цифр 9.

НАЧАЛО

ПОКА нашлось(999) ИЛИ нашлось(222)

ЕСЛИ нашлось(222)

ТО заменить(222, 9)

ИНАЧЕ заменить(999, 2)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

3. Дана программа:

НАЧАЛО

ПОКА нашлось(01) ИЛИ нашлось(02) ИЛИ нашлось (03)

заменить(01, 20) заменить(02, 120) заменить(03, 302) КОНЕЦ ПОКА

КОНЕЦ

Известно, что исходная строка начинается с цифры 0, а далее содержит 12 цифр 1, 15 цифр 2 и 17 цифр 3, расположенных в произвольном порядке. Сколько цифр 1 будет в строке, которая получится после выполнения данной программы?

4. Дана программа:

НАЧАЛО

ПОКА нашлось(11)

ЕСЛИ нашлось(112)

ТО заменить(112, 6)

ИНАЧЕ заменить(11, 3)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Исходная строка содержит десять единиц и четыре двойки, других цифр нет, точный порядок расположения единиц и двоек неизвестен. Какую наибольшую сумму цифр может иметь строка, которая получится после выполнения программы?

5. Дана программа:

НАЧАЛО ПОКА нашлось(111) заменить(111, 2) заменить(222, 11) КОНЕЦ ПОКА

КОНЕЦ

К исходной строке, содержащей более 60 единиц и не содержащей других символов, применили приведенную выше программу. В результате получилась строка 221. Какое наименьшее количество единиц могло быть в исходной строке?

6. Дана программа:

НАЧАЛО

ПОКА нашлось(72) ИЛИ нашлось(522) ИЛИ нашлось(2222)

ЕСЛИ нашлось(72)

ТО заменить(72, 2)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(522)

ТО заменить(522, 27)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(2222)

ТО заменить(2222, 5)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Определите наименьшее значение n, при котором сумма цифр в строке, получившейся в результате выполнения программы, равна 63.

7. Дана программа:

НАЧАЛО

ПОКА нашлось(73) ИЛИ нашлось(3333) ИЛИ нашлось(1133)

ЕСЛИ нашлось(73)

ТО заменить(73, 11)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(3333)

ТО заменить(3333, 7)

КОНЕЦ ЕСЛИ

ЕСЛИ нашлось(1133)

ТО заменить(1133, 37)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

На вход приведенной выше программы поступает строка, начинающаяся с цифры 7, а затем содержащая n цифр 3 (3 < n < 10 000).

Определите наибольшее значение n, при котором сумма цифр в строке, получившейся в результате выполнения программы, равна: а) 120;

б) 3995;

в) 200.

Глава 13 Задания 13

13.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 13 указывается «умение использовать маску подсети»^{^[43]}.

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

***

Напомним определения ряда терминов.

Узел компьютерной сети – устройство, соединенное с другими устройствами этой сети (узлами могут быть компьютеры, мобильные телефоны, а также специальные сетевые устройства, такие как маршрутизатор, коммутатор или концентратор).

IP-адрес узла (от англ. Internet Protocol) – уникальный числовой идентификатор устройства в компьютерной сети, работающей по протоколу IP.

Чаще всего IP-адрес узла – это четыре десятичных числа, которые разделены между собой точкой (такой формат поддерживается в протоколе IPv4). Пример: 192.168.1.49. В каждой части могут быть числа от 0 до 255.

IP-адрес узла состоит из двух частей: адреса сети, в которую входит данный узел, и номера узла в этой сети.

Чтобы определить, какая часть IP-адреса узла сети относится к адресу сети, а какая – к номеру самого узла в этой сети, используется так называемая «маска сети».

Маска подсети состоит из тех же четырех чисел и похожа на IP-адрес, например 255.255.0.0.

Напомним также о том, что такое «поразрядная конъюнкция».

Поразрядная конъюнкция – это операция над двумя десятичными числами, результат которой определяется следующим образом:

1) оба числа-операнда переводятся в двоичную систему счисления;

2) в каждом разряде двоичных представлений операндов происходит сложение цифр согласно такой таблице сложения:

Цифры

в разряде

Результат

Внимание! При поразрядной конъюнкции двух цифр 1 и 1 перенос в старший разряд не происходит;

3) полученный двоичный результат переводится в десятичную систему.

Например, при поразрядной конъюнкции чисел 23 и 13:

23₁₀ = 10111₂

13₁₀ = 1101₂

1 0 1 1 1

результат равен 1012 = 510.

Возможны три основных типа заданий на использование масок сетей:

• связанные с определением адреса сети;

• связанные с узлами сети (нахождение их количества, порядкового номера узла и др.);

• связанные с определением маски сети или ее части.

Примеры заданий и методика их выполнения приведены в следующем разделе.

13.2. Примеры заданий и методика их выполнения

13.2.1. Пример 1

Условие

Сеть задана IP-адресом 182.110.32.111 и маской сети 255.255.255.240. Определите адрес сети:

а) как последовательность двоичных цифр;

б) в десятичном виде;

в) как последовательность шестнадцатеричных цифр.

Решение

Переведем все десятичные числа в IP-адресе и маске сети в двоичную систему счисления. На экзамене это можно сделать с помощью стандартной программы Калькулятор в режиме Программист (см. главу 5)^{^[44]}:

10110110.01101110.00100000.01101111

11111111.11111111.11111111.11110000

(Обратите внимание на добавленные оттененные нули!)

Проведем поразрядную конъюнкцию над каждой частью IP-адреса и маски:

10110110. 01101110. 00100000. 01101111

(Для наглядности части адреса и маски отделены.)

Полученный результат и будет искомым адресом сети.

Другие требуемые виды адреса можно также получить из двоичного вида с помощью программы Калькулятор:

182.110.32.96 B6.6E.20.60

Обратим внимание на то, что если некоторая часть маски равна 255, то соответствующая часть адреса сети будет такой же, как аналогичная часть IP-адреса.

Добавим также, что в ряде языков программирования предусмотрена операция поразрядной конъюнкции десятичных значений, то есть нужные десятичные значения адреса сети можно получить с помощью несложной программы на таком языке.

Адрес сети в двоичном виде определяется в результате поразрядной конъюнкции IP-адреса узла этой сети и ее маски.

13.2.2. Пример 2

Условие

Сеть задана IP-адресом 180.125.32.166 и маской сети 255.255.255.240. Сколько узлов возможно в этой сети?

Решение

Как и в предыдущем задании, выделим из заданного IP-адреса адрес сети:

10110100. 01111101. 00100000. 10100110

Но вопрос в условии связан с узлами этой сети. Как выделить их?

Обсудим вопрос: сколько последних разрядов маски могут быть использованы для обозначения узлов в найденной сети? Ответ: только последние четыре цифры (если в пятом справа разряде записать 1, то тогда изменится адрес сети – убедитесь в этом!). Значит, для обозначения узлов в данном случае могут быть использованы только четыре последних разряда. Всего возможны 2⁴ = 16 вариантов номеров (от 0000 до 1111).

Ответ: 16.

Последние рассуждения позволяют сделать важный вывод: для обозначения узлов сети, заданной некоторой маской, в общем случае могут быть использованы только двоичные разряды после последней единицы двоичного представления маски.

Так как все возможные маски сети представляют собой (слева направо) последовательность единиц, после которой идет последовательность нулей, то можно сказать, что для обозначения узлов сети, заданной некоторой маской, в общем случае могут быть использованы ее разряды, в которых записаны нули.

Расскажем, какие IP-адреса будут у узлов рассмотренной в задании сети.

У первого узла IP-адрес совпадает с адресом сети: 0110100.01111101 00100000.10100000.

У второго – четвертая часть будет на 1 больше: 0110100. 01111101. 00100000. 10100001.

…

У последнего узла сети: 0110100.01111101.00100000.10101111 (это так называемый «широковещательный адрес»).

Общее количество узлов сети равно 2n, где n – число нулей в маске этой сети.

13.2.3. Пример 3

Условие

Для некоторой сети используется маска 255.255.254.0. Сколько различных IP-адресов узлов, доступных для пользователей, допускает эта маска?

Решение

Здесь надо обратить внимание на фразу «доступных для пользователей». Дело в том, что из всех возможных адресов узлов сети два IPадреса не используют. Это адрес, совпадающий с адресом самой сети, и широковещательный адрес (см. чуть выше).

Поэтому искомое в задании количество на два меньше общего числа узлов, возможных в данной сети.

Как отмечалось при выполнении предыдущего задания, за номера узлов в маске сети «отвечают» разряды, содержащие нули. Определим их количество.

В маске 255.255.254.0 первые два числа состоят полностью из единиц. Двоичное значение числа в третьей части маски: 11111110. Четвертое число маски в двоичном представлении состоит из восьми нулей. Значит, общее количество нулей в маске равно 9.

В девяти разрядах можно записать 2⁹ = 512 двоичных чисел. Из них для IP-адресов узлов, доступных для пользователей, – 510 чисел.

Ответ: 510.

13.2.4. Пример 4

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

В терминологии сетей TCP/IP маской сети называют двоичное число, которое показывает, какая часть IP-адреса узла сети относится к адресу сети, а какая – к адресу узла в этой сети. Адрес сети получается в результате применения поразрядной конъюнкции к заданному адресу узла и маске сети. Сеть задана IP-адресом 192.168.32.160 и маской сети 255.255.255.240. Сколько в этой сети IP-адресов, для которых сумма единиц в двоичной записи IP-адреса четна?

Решение

Сначала надо определить общее количество разрядов для обозначения номеров узлов в сети. Хотя это можно сделать только на основе анализа двоичного представления маски, найдем, как ранее, и адрес сети:

11000000. 10101000. 00100000. 10100000

Согласно сделанному в п. 13.2.2 выводу, для номеров узлов указанной сети можно выделить четыре разряда. Так как, в отличие от предыдущего задания, речь не идет об адресах, доступных для пользователей, общее количество узлов в этой сети равно 2⁴ = 16.

Но в данном случае нас интересуют не все 16 адресов, а только те, у которых сумма единиц в двоичной записи IP-адреса четна.

Исследуем вопрос, связанный с четностью суммы единиц в двоичной записи всего IP-адреса узла данной сети.

В его «сетевой» части 8 единиц. Значит, в адресах узлов этой сети также должно быть четное число единиц. В четырех разрядах это:

1) все нули (такое число одно – 0000);

2) все единицы (такое число тоже одно – 1111);

3) две единицы (количество таких чисел равно числу сочетаний из 4 по 2, то есть 6).

Общее число искомых адресов – 8.

Ответ: 8.

13.2.5. Пример 5

Условие

Если маска сети равна 255.255.255.240, а IP-адрес узла – 58.68.0.44, то чему равен порядковый номер этого узла в этой сети?

Решение

Заданные IP-адрес узла и маска сети, а также соответствующий адрес сети:

00111010.01000100.00000000.00101100

11111111.11111111.11111111.11110000

00111010.01000100.00000000.00100000

Как уже говорилось (см. п. 13.2.2), адрес узла, совпадающий с адресом самой сети (который, напомним, для пользователей недоступен), имеет порядковый номер – 1. IP-адреса узлов с остальными порядковыми номерами (всего их в данном случае 16) приведены в таблице:

Номер узла	IP-адрес узла
1	00111010.01000100.00000000.00100000
2	00111010.01000100.00000000.00100001
3	00111010.01000100.00000000.00100010
4	00111010.01000100.00000000.00100011
5	00111010.01000100.00000000.00100100
6	00111010.01000100.00000000.00100101
7	00111010.01000100.00000000.00100110
8	00111010.01000100.00000000.00100111
9	00111010.01000100.00000000.00101000
10	00111010.01000100.00000000.00101001
11	00111010.01000100.00000000.00101010
12	00111010.01000100.00000000.00101011
13	00111010.01000100.00000000.00101100
14	00111010.01000100.00000000.00101101
15	00111010.01000100.00000000.00101110
16	00111010.01000100.00000000.00101111

Какой номер у узла в условии

(00111010.01000100.00000000.0010110)? – 12.

Но как получить его, не оформляя таблицу? – Анализ чисел в таблице показывает, что это можно сделать так:

1) определить количество цифр в цепочке цифр адреса сети, начинающейся с последней единицы (100000), – оно равно 6, и запомнить соответствующее шестизначное число;

2) выделить число, состоящее из этого количества последних цифр IP-адреса (101100);

3) вычесть из второго двоичного числа первое: 101100 – 10000 = 1100 (разность можно получить, отбросив во втором числе начальную единицу);

4) полученную разность представить в десятичной системе:

1100₂ = 12₁₀.

Можно также поступить следующим образом:

1) инвертировать двоичное представление маски, то есть заменить все единицы на нули и наоборот: 00000000.00000000.00000000.000 01111;

2) провести поразрядную конъюнкцию этого представления маски и IP-адреса узла:

Начальные нули можно не выписывать 1111 00111010.01000100.00000000.00101100

Начальные нули можно не выписывать 1100 3) результат перевести в десятичную систему.

Описанные действия можно провести быстрее: выписать только единицы маски и такое же количество последних цифр IP-адреса узла, после чего провести поразрядную конъюнкцию выписанных чисел.

13.2.6. Пример 6

Условие

Если маска сети 255.255.224.0, а IP-адрес компьютера– 206.158.124.67, то чему равен порядковый номер узла в этой сети?

Решение

В двоичном виде заданный IP-адрес:

11001110.10011110.01111100.01000011,

а определенный с помощью маски адрес сети:

11001110.10011110.01100000.00000000.

Согласно методике, описанной при выполнении предыдущего примера:

1) цепочка цифр адреса сети, начинающаяся с последней единицы: 10000000000000; в ней – 14 цифр (1 + 5 + 8);

2) число из последних 14 двоичных цифр IP-адреса: 11110001000011;

3) их разность 1110001000011 (в данном случае также второе число без начальной единицы);

4) соответствующее десятичное число: 7235.

Ответ: 7235.

Решение с инвертированием маски:

11111.11111111

13.2.7. Пример 7

Условие

Для узла с IP-адресом 153.209.23.240 адрес сети равен 153.209.20.0. Чему равна третья слева часть маски? Ответ запишите в виде десятичного числа.

Решение

Прежде чем приводить решение, зададим вопрос: «Чему равны первые две части маски?» – и ответим на него.

Обратим внимание на то, что первые две части IP-адреса узла и адреса сети совпадают. В каком случае после проведения поразрядной конъюнкции IP-адреса узла и маски это может быть? – Если в двоичных представлениях этих частей маски записаны только единицы (убедитесь в этом, вспомнив таблицу сложения при поразрядной конъюнкции!), то есть десятичные значения этих частей – 255.

Почему третьи части IP-адреса узла и адреса сети разные? – Потому что в этой части маски представлены и нули. Начиная с какого разряда слева?

Методика поиска такого разряда следующая.

Представим третьи части IP-адреса и адреса сети в виде восьмиразрядных двоичных чисел и выпишем их одно под другим:

23₁₀ = 00010111₂

20₁₀ = 00010100₂

Ищем первое слева сочетание цифр «1 в IP-адресе и 0 в адресе сети». Оно – в седьмом разряде (втором справа).

В каком случае может быть такое сочетание цифр? – Когда в этом же разряде маски записан 0.

Является ли этот ноль первым в цепочке цифр маски? – В данном случае (!) является, так как слева от него в маске записана единица (убедитесь в этом).

Так как это первый ноль в маске, то двоичный вид третьей части маски: 11111100. Переведя это число в десятичную систему счисления, получим 252^{^[45]}.

Ответ: 252.

Дополнительный вопрос: «Какое десятичное значение у четвертой части маски?» Ответьте на него.

13.2.8. Пример 8

Условие

Для узла с IP-адресом 111.81.208.27 адрес сети равен 111.81.192.0. Чему равно наименьшее возможное значение третьей слева части маски? Ответ запишите в виде десятичного числа.

Решение

Здесь также первые две части маски в десятичном виде имеют значения 255. Исследуем третью часть.

Запишем третьи части IP-адреса и адреса сети в виде 8-разрядных двоичных чисел и выпишем их одно под другим:

208₁₀ = 11010000₂

192₁₀ = 11000000₂

Здесь первое слева сочетание цифр «1 в IP-адресе и 0 в адресе сети» находится в четвертом разряде. Является ли этот ноль этого разряда маски первым в цепочке ее цифр? – Необязательно, так ноль может быть и слева от него (в третьем разряде). Значит, возможны два варианта (два числа с различными третьими слева цифрами) – 11000000 или 11100000. По условию задачи требуется найти наименьшее значение – это 11000000. Переведя его в десятичную систему, получим

11000000₂ = 192₁₀.

Ответ: 192.

Обобщая два последних примера, общую методику определения положения первого нуля в маске можно описать следующим образом:

• определяются отличающиеся части IP-адреса и адреса сети;

• эти части записываются в виде восьмиразрядных двоичных чисел; • ищется первое слева сочетание цифр «1 в IP-адресе и 0 в адресе сети»;

• возможны два варианта, которые схематически можно оформить так:

IP-адрес							1
Адрес сети						1	0
Маска	1	1	1	…	1	1	0	0	…	0

IP-адрес							1
Адрес сети		1				0	0
Маска	1	1	?	?	?	?	0	0	…	0

В первом случае маска определяется однозначно, во втором – возможны варианты, из которых надо выбрать минимальное или максимальное значение данной части маски;

• найденное двоичное значение части маски переводится в десятичную систему.

Можно было при выполнении примера 8 рассуждать и так.

С каким числом нужно произвести поразрядную конъюнкцию числа 11010000₂, чтобы получить 11000000₂? – Очевидно, что первые две цифры этого числа должны быть единицами, а четвертая – нулем. Такими числами могут быть два числа с различными третьими слева цифрами – 11000000 или 11100000. Из них минимальное – первое.

13.3. Задания для самостоятельного выполнения

1. Сеть задана IP-адресом 10.50.128.6 и маской сети 255.255.255.0. Определите адрес сети.

2. Сеть задана IP-адресом 206.158.124.67 и маской сети 255.255.224.0. Сколько узлов возможно в этой сети?

3. Для некоторой сети используется маска 255.255.248.0. Сколько различных IP-адресов узлов, доступных для пользователей, допускает эта маска?

4. Сеть задана IP-адресом 11.53.128.33 и маской сети 255.255.255.248. Сколько в этой сети IP-адресов, для которых сумма единиц в двоичной записи IP-адреса кратна пяти?

5. Сеть задана IP-адресом 181.53.128.45 и маской сети 255.255.255.248. Сколько в этой сети IP-адресов, для которых сумма единиц в двоичной записи IP-адреса нечетная?

6. Если маска сети равна 255.255.240.0, а IP-адрес узла в сети – 162.198.75.44, то чему равен порядковый номер этого узла в этой сети?

7. Для узла с IP-адресом 224.128.112.142 адрес сети равен 224.128.64.0. Чему равна третья слева часть маски? Ответ запишите в виде десятичного числа.

8. Для узла с IP-адресом 158.198.228.220 адрес сети равен 158.198.128.0. Чему равна третья слева часть маски? Ответ запишите в виде десятичного числа.

9. Для узла с IP-адресом 225.209.23.200 адрес сети равен 225.209.23.192. Чему равно наибольшее возможное значение последней части маски? Ответ запишите в виде десятичного числа.

Глава 14 Задания 14

14.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 14 указывается «знание позиционных систем счисления».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 14 двух типов:

1) которые связаны с кратностью чисел в недесятичных системах счисления; такие задания будем называть «задания типа 1»;

2) в которых требуется определить количество тех или иных цифр в недесятичных числах; такие задания будем называть «задания типа 2».

14.2. Примеры заданий типа 1 и методика их выполнения

14.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Операнды арифметического выражения записаны в системе счисления с основанием 15.

123x5₁₅ + 1x233₁₅

В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления.

Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 14. Для найденного значения x вычислите частное от деления значения арифметического выражения на 14 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

Решение

Решение данной задачи^{^[46]} облегчается тем, что в условии использована 15-ричная система счисления и речь идет о кратности числу 14. Дело в том, что в любой системе с основанием q признак делимости числа на q – 1 аналогичен признаку делимости десятичных чисел на 9 (вспомните его!), то есть q-ричное число кратно числу q – 1, если сумма его цифр кратна q – 1.

В нашем случае q = 15. Сумма цифр операндов заданного арифметического выражения равна 20 + 2х. Наименьшее значение x, при котором эта сумма кратна 14, – 4.

Это значит, что операнды равны 12 345 и 14 233, а их пятнадцатеричная сумма – 26 578. Переведя ее в десятичную систему (удобно использовать электронную таблицу – см. главу 8), получим 122 738. Частное от деления этого числа на 14 равно 8767.

Ответ: 8767.

14.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

Операнды арифметического выражения записаны в системе счисления с основанием 19.

98897x21₁₉ + 2x923₁₉

В записи чисел переменной x обозначена неизвестная цифра из алфавита 19-ричной системы счисления.

Определите наибольшее значение x, при котором значение данного арифметического выражения кратно 18. Для найденного значения x вычислите частное от деления значения арифметического выражения на 18 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

Решение

Здесь также в условии идет речь о кратности числу 18, а операнды заданы в системе счисления, основание которой на 1 больше (19). То есть и в данном случае можно использовать признак делимости на 18.

Сумма цифр операндов заданного арифметического выражения равна

9 + 8 + 8 + 9 + 7 + x + 2 + 1 + 2 + x + 9 + 2 + 3 = 60 + 2x.

Далее задача усложняется (по сравнению с предыдущей) в связи с тем, что нужно найти наибольшее значение цифры х. Расчеты по его поиску удобно провести с помощью электронной таблицы.

Оформим лист следующим образом. В столбце А запишем возможные значения цифры х (это удобно сделать, используя так называемое «автозаполнение ячеек»), в столбце В – значение выражения 60 + 2x, в столбце С – частное от деления числа в столбце В на 18.

	А	В	С
1	x	60 + 2x	Частное^{^[47]}
2	1
3	2
4	3
…
19	18

Расчеты проведем, естественно, по формулам, введенным в ячейки В2 и С2, которые затем распространим (скопируем) на остальные ячейки диапазона В2:С19. В результате получим следующую картину:

	А	В	С
1	x	60 + 2x	Частное
2	1	62	3,444444
…	…	…	…
6	5	70	3,888889
7	6	72	4
8	7	74	4,111111
…	…	…	…
15	14	88	4,888889
16	15	90	5
17	16	92	5,111111
18	17	94	5,222222
19	18	96	5,333333

Видно, что наибольшее значение x, при котором эта сумма кратна 18, – 15.

Это значит, что операнды равны 98897(15)21 и 2(15)923. В данном случае находить их 19-ричную сумму нецелесообразно (убедитесь в этом!). Переведя каждый из них в десятичную систему (также см. главу 8) и сложив десятичные значения, получим 8442614664. Частное от деления этого числа на 18 равно 469034148.

Ответ: 469034148.

14.2.3. Другие возможные варианты задания

Возможны также варианты задания, в котором при системе счисления с основанием q речь может идти о делимости не на число q – 1.

Пример

Операнды арифметического выражения записаны в системе счисления с основанием 12.

5x361₁₂ + 133x5₁₂

В записи чисел переменной x обозначена неизвестная цифра из алфавита 12-ричной системы счисления.

Решение

В данном случае описанная в пп. 14.2.1 и 14.2.2 методика выполнения задания неприменима. Проще всего находить искомое значение путем разработки программы.

Программа основана на переборе всех возможных значений цифры х, расчете десятичных значений операндов заданного выражения по развернутой форме числа и их суммы:

алг нач цел х, сум нц для х от 0 до 11 | Для всех возможных значений цифры х | Рассчитываем сумму произведений цифр на весомость разряда сум := 5 * 12 ** 4 + х * 12 ** 3 + 3 * 12 ** 2 + 6 * 12 + 1 + 1 * 12 ** 4 + 3 * 12 ** 3 + 3 * 12 ** 2 + х * 12 + 5 | Выводим цифру х и частное от деления суммы на 18 вывод нс, х, " ", сум/18 кц кон где знак ** соответствует операции возведения в степень.

Выполнив программу, можно получить ряд значений, максимальное из которых – 8219.

Ответ: 8219.

Примечания

1. С целью уменьшения вероятности ошибки целесообразно сначала записать каждый операнд на отдельной строке (одни и те же разряды – один под другим), как это сделано в приведенной программе, а потом объединить эти две строки. Конечно, удобно вторую строку получить на основе копирования первой.

2. Можно также цифры с одинаковой весомостью разрядов суммировать:

сум := (5 + 1) * 12 ** 4 + (х + 3) * 12 ** 3 + (3 + 3) * 12 ** 2 + (6 + х) * 12 + 6

3. Можно переменную сум не использовать, а рассчитывать и выводить на экран частное от деления «большого» выражения на 18.

14.2.4. Задания для самостоятельного выполнения

1. Операнды арифметического выражения записаны в системе счисления с основанием 22:

63х59685₂₂ + 12х53₂₂ + 36х5₂₂

В записи чисел переменной x обозначена неизвестная цифра из алфавита 22-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 21. Для найденного значения x вычислите частное от деления значения арифметического выражения на 21 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.

2. Операнды арифметического выражения записаны в системе счисления с основанием 8:

25x63₈ + 143x5₈

В записи чисел переменной x обозначена неизвестная цифра из алфавита восьмеричной системы счисления.

Определите наибольшее значение x, при котором значение данного арифметического выражения кратно 16. Для найденного значения x вычислите частное от деления значения арифметического выражения на 16 и укажите его в ответе в десятичной системе счисления.

3. Операнды арифметического выражения записаны в системе счисления с основанием 11:

982x8₁₁ + 194x7₁₁

В записи чисел переменной x обозначена неизвестная цифра из алфавита 11-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 58. Для найденного значения x вычислите частное от деления значения арифметического выражения на 58 и укажите его в ответе в десятичной системе счисления.

14.3. Примеры заданий типа 2 и методика их выполнения

Прежде чем обсуждать задания, исследуем вид ряда десятичных чисел в двоичной системе счисления.

2-1^{^[48]}) число 2^с.

Рассмотрим несколько значений показателя степени с:

с	1	2	3
2с	2	4	8
Двоичная запись	10	100	1000
Количество нулей	1	3	3

Итак, число 2^с в двоичной системе состоит из (с + 1) цифр, из которых одна единица и с нулей.

2-2) число 2^c + 2^c равно 2^{c +}¹, то есть в двоичном виде состоит из единицы и (c + 1) нулей;

2-3) число 2^б + 2^м при б > м (обозначения б и м связаны со словами «большее» и «меньшее»).

Учитывая вид каждого слагаемого (см. выше), можно составить таб лицу:

…

Номер разряда

б + 1

м +1

Вывод: в числе 2^б + 2^м при б > м, записанном в двоичной системе счисления:

• общее количество цифр: б + 1;

• количество единиц: 2 (начальная и (м + 1)-я справа); • количество нулей: (б + 1) – 2, из которых: в конце записи: м нулей; в «середине» записи: (б + 1) – 2 – м = б – м – 1 нулей.

В частном случае, когда б – м = 1:

…

Номер разряда б + 1 м + 1

результат будет состоять из двух начальных единиц и м нулей;

2-4) число 2^с – 2^в (обозначение в связано со словом «вычитаемое»).

Рассмотрим вычитание при нескольких значениях показателя степени в:

• при в = 0:

1 0 … 0 0 0

–

1 … 1 1

Номер разряда с + 1 • при в = 1:

…

–

…

1 … 1

Номер разряда с + 1 с … 3 2 1

Можно сделать вывод: в числе 3^с – 3^в, записанном в троичной системе счисления:

• общее количество цифр: с;

• количество нулей: в;

• количество единиц: с – в.

Вывод: двоичная запись числа 2^c – 2^в состоит из (с – в) единиц и в нулей, записанных в общем случае в произвольном порядке.

2-5) число 3^б + 3^м – 3^в при б > м (обозначения б, м и в связаны со словами «большее», «меньшее» и «вычитаемое»).

Рассуждения такие.

Результат сложения будет следующим (см. пример 2-3):

1 0 …

1 0

…

Номер разряда б + 1 б

Далее рассмотрим два случая.

• при в < м:

м + 1 м

1 0 …

–

1 0

…

1 0 … 0 0 1 1 …

Номер разряда б + 1 б м + 1 м 2 1

Видно, что изменилась (по правилам, описанным для варианта

2-4) часть уменьшаемого, связанная с его «правой» единицей;

• при б > в > м:

–

…

1 0

0 0

…

1 0

…

Номер разряда б + 1

м + 1 м

Видно, что изменилась (по правилам, описанным для варианта 2-4) часть уменьшаемого, связанная с его «левой» единицей.

Обсудим несколько примеров заданий.

14.3.1. Пример 1

Условие

Сколько единиц содержится в двоичной записи значения выражения:

4⁸ + 2⁸ – 8?

Решение

Представим все числа в заданном в условии выражении в виде степеней двойки:

2¹⁶ + 2⁸ – 2³

При принятых выше условных обозначениях: б = 16, м = 8, у = 3.

Согласно правилам, приведенным применительно к варианту 2-3, в двоичном представлении числа-суммы будет две единицы (начальная и 9-я справа).

Теперь – вычитание. Так как в (3) меньше, чем м (8), то с учетом вывода, сделанного при рассмотрении варианта 2-5-1, в уменьшаемом изменится часть, связанная с его «правой» единицей. Как? – Согласно выводу, оттененному чуть выше, количество единиц в этой части станет равно 8 – 3 = 5. С учетом начальной единицы общее их количество будет равно 6.

Можно было оформить таблицу:

1 0 … 0 1 0 0 0 0 0 0 0 0

–

1 0 … 0 0 1 1 1 1

9 1

Ответ: 6.

Искомое значение можно также определить с помощью программы, основанной на переводе заданного выражения в двоичную систему счисления методом последовательного деления на основание 2 и подсчете определяемых при этом цифр (остатков), равных 1.

Соответствующая программа:

алг нач цел n, цифра, кол1 ¶ n := 4 ** 8 + 2 ** 8 - 8 ¶ кол1 := 0 ¶ нц пока n > 0 ¶ | Определяем цифру двоичного представления числа n цифра := mod(n, 2) ¶ если цифра = 1 ¶ то | Учитываем цифру, равную 1¶ кол1 := кол1 + 1 ¶ все ¶ | Меняем число n n := div(n, 2) ¶

кц ¶ вывод кол1 кон

Примечание. Можно также переменную цифра не использовать, а при подсчете количества единиц записать в программе:

если mod(n, 2) = 1 то кол1 := кол1 + 1 все

14.3.2. Пример 2

Условие

Сколько единиц содержится в двоичной записи значения выражения:

42014 + 22015 − 8?

Решение

Представим все числа в заданном в условии выражении в виде степеней двойки:

24028 + 22015 − 23

Рассуждения, аналогичные сделанным при выполнении предыдущего задания, приведут нас к выводу о том, что после сложения при вычитании также изменится часть, связанная с «правой» единицей двоичной суммы. При принятых обозначениях с и у этой части с = 2015, у = 3. После вычитания в ней будет 2015 – 3 = 2012 нулей, а во всей двоичной разности – 2013.

Ответ: 2013.

Внимание! Программа, аналогичная по сути приведенной в предыдущем пункте, может быть использована для поиска ответа только на языке Python, в котором возможна работа с очень большими числами. В программах на других языках программирования из-за особенностей операций возведения в степень потребуется использование специальных типов данных (см. [4]).

14.3.3. Пример 3

Условие

Сколько единиц содержится в двоичной записи значения выражения:

4²⁵⁵ + 2²⁵⁵ − 255?

Решение

Здесь в выражении есть число 255, не являющееся степенью двойки. Но вместо него можно записать 2⁸ − 2⁰.

С использованием степеней двойки заданное выражение станет таким: 2⁵¹⁰ + 2²⁵⁵ − 2⁸ + 1.

В двоичной записи суммы будет три единицы. При вычитании изменится часть суммы между «средней» и последней единицами. Согласно «оттененному выводу», без учета последней единицы количество единиц в этой части равно 255 – 8 = 247, а с ее учетом и учетом первой единицы всей суммы: 249.

Ответ: 249.

Исследуем также вид ряда десятичных чисел в троичной системе счисления:

3-1) число 2^с.

Рассмотрим несколько значений показателя степени с:

с	1	2	3
2с	3	9	27
Троичная запись	10	100	1000
Количество нулей	1	3	3

Итак, число 3^с в троичной системе состоит из (с + 1) цифр, из которых одна единица и с нулей;

3-2) число 3^c + 3^c равно 2 ×3^c, то есть в троичном виде состоит из начальной двойки и последующих c нулей;

3-3) число 3^б + 3^м при б > м (обозначения б и м связаны со словами «большее» и «меньшее»).

Учитывая вид каждого слагаемого (см. выше), можно составить таб лицу:

1 +

…

Номер разряда б + 1

м +1

Вывод: в числе 3^б + 3^м при б > м, записанном в троичной системе счисления:

• общее количество цифр: б + 1;

• количество единиц: 2 (начальная и (м + 1)-я справа);

• количество нулей: (б + 1) – 2, из которых: в конце записи: м нулей; в «середине» записи: (б + 1) – 2 – м = б – м – 1 нулей;

3-4) число 3^с – 3^в (обозначение в связано со словом «вычитаемое»).

Рассмотрим вычитание при нескольких значениях показателя степени в:

• при в = 0:

1 0 … 0 0 0

–

2 … 2 2

Номер разряда с + 1 • при в = 1:

…

–

…

2 … 2

Номер разряда с + 1 с … 3 2 1

Можно сделать вывод: в числе 3^с – 3^в, записанном в троичной системе счисления:

• общее количество цифр: с;

• количество нулей: в;

• количество двоек: с – в;

3-5) число 3^б + 3^м – 3^в при б > м (обозначения б, м и в связаны со словами «большее», «меньшее» и «вычитаемое»).

Рассуждения такие.

Результат сложения будет следующим (см. пример 2-3):

1 0 … 0 1 0 0 … 0 0

Номер разряда б + 1 б м + 1 м 2 1

Далее рассмотрим случай, когда в < м:

1 0 … 0 1 0 0 … 0 0

–

1 0 … 0 0 2 2 …

Номер разряда б + 1 б м + 1 м 2 1

Видно, что изменилась (по правилам, описанным для варианта 3-4) часть уменьшаемого, связанная с его «правой» единицей.

Вариант, когда б > в > м, исследуйте самостоятельно.

14.3.4. Пример 4

Условие

Значение арифметического выражения 9⁷ + 3²¹ – 9 записали в системе счисления с основанием 3. Сколько цифр 2 содержится в этой записи?

Решение

Представим все числа в заданном в условии выражении в виде степеней двойки:

3¹⁴ + 3²¹ – 3².

При принятых выше условных обозначениях: б = 21, м = 14, у = 2. Результат сложения первых двух чисел:

1 0 … 0 1 0 0 … 0 0

Номер разряда 22 21 15 14 2 1

Так как 2 (в) < 14 (м), то при вычитании изменится часть суммы после второй единицы. В ней появится м – у = 14 – 2 = 12 двоек.

Ответ: 12.

Анализ показывает, что выводы, сделанные применительно к числам, являющимся степенями тройки (и к троичной системе счисления), применимы и к другим числам, являющимся степенями некоторого числа (и к соответствующей системе счисления). Отличие в том, что в записи чисел в той или иной системе счисления вместо цифры 2 будет использоваться цифра, на 1 меньшая, чем основание системы.

14.3.5. Пример 5

(задание из демонстрационного варианта ЕГЭ 2021 года)

Условие

Значение арифметического выражения 49⁷ + 7²¹ – 7 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?

Решение

Представим все числа в заданном в условии выражении в виде степеней числа 7. Так как 49 = 7², то 49⁷ + 7²¹ – 7 = 7¹⁴ + 7²¹ – 7.

При принятых выше условных обозначениях: б = 21, м = 14, у = 1. Сумма 7¹⁴ + 7²¹ в семеричной системе счисления будет такой:

1 0 … 0 1 0 0 0 0

22 21 15 14 … 2 1

Так как у < м, то вычитание изменит в этой сумме конечную часть. Количество шестерок в ней будет равно м – у = 14 – 1 = 13. Можно было также провести вычитание:

1 0 … 0 1 0 0 0 0

–

1 0 … 0 0 6 …

22 21 15 14 … 2 1

Ответ: 13.

14.3.6. Пример 6

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Значение арифметического выражения

3 · 4³⁸ + 2 · 4²³ + 4²⁰ + 3 · 4⁵ + 2 · 4⁴ + 1

записали в системе счисления с основанием 16. Сколько значащих нулей содержится в этой записи?

Решение

Прежде чем описывать решение, заметим, что при решении всех предыдущих задач в условии была представлена сумма двух чисел. А как изменилась бы двоичная, троичная или семеричная сумма при сложении трех и более чисел? – В сумме были бы записаны три и более единиц, остальные цифры – нули.

Еще. В двух последних заданиях в условии фигурировали числа, являющиеся степенями некоторого числа, – основания использованной системы счисления (3 и 7). Например, в последнем задании выражение в условии свелось к такому:

7¹⁴ + 7²¹ – 7.

А как изменилась бы семеричная сумма двух первых чисел, например, в таком случае: 3 · 7¹⁴ + 6 · 7²¹? – По сути – ничего: в сумме вместо единиц в соответствующих разрядах были бы представлены цифры семеричной системы 3 и 6.

Итак, как и ранее, представим все числа в заданном в условии выражении в виде степеней числа 16 (возможно, с «коэффициентами»).

Так как

4³⁸= 16¹⁹, 2 · 4²³ = 8 · 16²², 4²⁰= 16¹⁰,

3 · 4⁵ = 12 · 4⁴= 12 ·16², 4⁴= 16², 1 = 16⁰,

то выражение можно записать в виде:

= 3 · 16¹⁹ + 8 · 16¹¹ + 16¹⁰ + 12 · 16² + 2 · 16² + 16⁰ = = 3 · 16¹⁹ + 8 · 16¹¹ + 16¹⁰ + 14 · 16² + 16⁰.

Согласно сделанным чуть выше выводам, можно сказать, что в шестнадцатеричной сумме всех слагаемых, кроме нулей, будут записаны цифры 3, 8, 1, Е (14) и 1. Так как общее число цифр в сумме – 20, то искомое число нулей равно 20 – 5 = 15.

Ответ: 15.

Можно было после представления заданного в условии выражения в виде

3 · 16¹⁹ + 8 · 16¹¹ + 16¹⁰ + 14 · 16² + 16⁰

сказать, что это так называемая «развернутая форма» записи некоторого шестнадцатеричного числа (в выражении есть только суммы произведений степеней числа 16 на цифры этого числа). Всего слагаемых – 5, то есть в развернутой форме записи представлено 5 цифр (цифры 0 не представляются). Так как наибольшая степень числа 16 в полученном выражении – 19, то общее количество цифр в шестнадцатеричной записи – 20. Значит, количество нулей в ней: 20 – 5 = 15.

14.3.7. Пример 7

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

Значение арифметического выражения

3 · 3125⁸ + 2 · 625⁷ – 4 · 625⁶ + 3 · 125⁵ – 2 · 25⁴ – 2024

записали в системе счисления с основанием 25. Сколько значащих нулей содержится в этой записи?

Решение

Представим операнды выражения в виде степеней числа 25:

3 · 31258 = 3 · (51 · 54)8 = 3 · (55)8 = 3 · 540 = 3 · 2520

2 · 6257 = 2 · 2514 4 · 6256 = 4 · 2512

3 · 1255 = 3 · (53)5 = 3 · 515 = 15 · 514 = = 15 · 257 2 · 254 = 2 · 254

Сложнее с числом 2024. Его перевести в 25-ричную систему счисления можно методом последовательного деления на основание 25:

2024₁₀ = 35(24)_25.

Далее представим результат сложения операндов со знаком «+»:

	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1
+	3	0	0	0	0	0	2	0	0	0	0	0	0	15	0	0	0	0	0	0	0

Добавив строку для операндов со знаком «–» и проведя вычитание, получим:

	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1
+	3	0	0	0	0	0	2	0	0	0	0	0	0	15	0	0	0	0	0	0	0
–									4	0	0	0	0	0	0	0	2	0	3	5	24
	3	0	0	0	0	0	1	24	21	0	0	0	0	14	24	24	22	24	21	19	1

В полученной разности имеется 9 нулей.

Ответ: 9.

14.3.7. Задачи для самостоятельного решения

1. Сколько единиц содержится в двоичной записи числа, являющегося результатом следующего выражения: 4¹⁴ + 2³² – 4?

2. Сколько единиц содержится в двоичной записи значения выражения 4⁵¹¹ + 2⁵¹¹ − 511?

3. Сколько единиц содержится в двоичной записи значения выражения 16⁴ + 8⁴ + 4⁶ − 64?

4. Значение арифметического выражения 9¹⁸ + 3⁵⁴ – 9 записали в системе счисления с основанием 3. Сколько цифр 2 содержится в этой записи?

5. Значение арифметического выражения 49¹⁰ + 7³⁰ – 49 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?

6. Значение выражения 4³⁶ + 3 · 4²⁰ + 4¹⁵ + 2 · 4⁷ + 49 записали в системе счисления с основанием 16. Сколько разных цифр встречается в этой записи?

Глава 15 Задания 15

15.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 15 указывается «знание основных понятий и законов математической логики».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 3 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет можно выделить три группы заданий:

1) задания, связанные с делимостью;

2) задания, связанные с отрезками числовой прямой; 3) задания, связанные с координатной плоскостью.

Прежде чем переходить к рассмотрению примеров заданий каждого типа и методики их выполнения, предлагаем читателям еще раз ознакомиться с содержанием раздела 2.1.

Ответьте также на вопросы, приведенные в конце данного раздела. Ответы на них будут полезными при выполнении заданий.

В данной главе мы еще будем использовать понятие элемент логической операции – логические величины, представленные в логических операциях.

Напомним также, что вместо операции посылка П → следствие С можно записать ¬П ∨ С^{^[49]}.

Вопросы

1. Чем отличаются промежутки (области) числовой оси, которые называют «отрезок», «интервал» и «полуинтервал»? Как их отличают при записи?

2. На числовой прямой даны два отрезка: P = [15, 30] и Q = [18, 25]. Какой промежуток (какие промежутки) удовлетворяет условиям:

а) (x P) ∨ (x Q)?

б) (x P) ∧ (x Q)?

в) (x P) ∧ ¬(x Q)?

Какой тип промежутка (какие типы промежутков) будет в каждом случае?

3. На числовой прямой даны два отрезка: P = [5, 20] и Q = [11, 27]. Какой промежуток удовлетворяет условиям:

а) (x P) ∨ (x Q)?

б) (x P) ∧ (x Q)?

в) (x P) ∧ ¬(x Q)?

г) ¬(x P) ∧ (x Q)?

Какой тип промежутка будет в каждом случае?

15.2. Примеры заданий, связанных с делимостью, и методика их выполнения

15.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 2) → ¬ДЕЛ(x, 3)) ∨ (x + A ≥ 100)

тождественно истинна (т. е. принимает значение 1) при любом натуральном значении переменной х?

Решение

Задачу можно решить, разработав программу. Она основана на переборе возможных значений А (от 1 до 100). Для каждого значения А, рассмотрев большое число значений х, например 1000, можно определить истинность приведенного в условии логического выражения. Если для всех значений х выражение будет истинно, то текущее значение А является одним из тех, среди которых есть искомое.

При этом так как в заданном выражении имеется операция импликации, то ее нужно заменить (см. выше). В результате выражение примет вид: ¬ДЕЛ(x, 2) ∨ ¬ДЕЛ(x, 3) ∨ (x + A ≥ 100). Программа, учитывающая все сказанное:

алг нач цел А, х, к | к – переменная-счетчик нц для А от 1 до 100 к := 0 нц для х от 1 до 1000 если mod(х, 2) <> 0 или mod(х, 3) <> 0 или х + А >=100 то к := к + 1 все кц если к = 1000 | При всех значениях х выражение истинно то | Выводим текущее значение А вывод нс, А все кц кон

Выполнив программу, получим:

100

Минимальное из найденных значений – 94.

Ответ: 94.

Так как в данном случае надо найти минимальное значение А, то после «встречи» первого подходящего значения дальнейшее рассмотрение других значений переменной А можно не проводить, завершив программу:

… если к = 1000 то вывод А выход^{^[50]} все

Приведем также решение методом рассуждений, которые будут полезны при выполнении других заданий.

Полученное ранее выражение

¬ДЕЛ(x, 2) ∨ ¬ДЕЛ(x, 3) ∨ (x + A ≥ 100)

истинно, если истинно хотя бы одно из трех элементов (простых выражений), соединенных знаками дизъюнкции, то есть для чисел х, которые:

• не кратны двум (например, 1, 3, 5 и т. п.);

• не кратны трем (например, 2, 4, 8 и т. п.);

• не кратны ни двум, ни трем (например, 7, 11 и т. п.).

Но это значит, что на любом подмножестве натуральных чисел, состоящих из более чем одного числа, указанное выражение будет истинным независимо от искомого значения А! Как же быть? Чтобы учесть влияние только переменной А, надо исключить влияние на общий результат двух первых простых выражений (¬ДЕЛ(x, 2) и ¬ДЕЛ(x, 3). Для этого надо исследовать случаи, когда оба этих выражения ложны.

Применив отрицание для дизъюнкции (закон де Моргана), получим: ¬(¬ДЕЛ(x, 2) ∨ ¬ДЕЛ(x, 3) = ДЕЛ(x, 2) ∧ ДЕЛ(x, 3)

Последнее выражение истинно, когда х кратно и двум, и трем. Наименьшее из таких чисел – 6. При таком х искомое наименьшее число А, при котором истинно выражение x + A ≥ 100, равно 94.

Ответ: 94.

Прежде чем идти дальше, дадим полезный совет. При выполнении задания методом рассуждений с целью сокращения записи используемых при анализе формул (а значит, и уменьшения времени выполнения задания на экзамене) нужно ввести короткие обозначения утверждений. В данном случае они, например, такие:

ДЕЛ(x, 2) = Д₂

ДЕЛ(x, 3) = Д₃

(x + A ≥ 100) = (х + А)

В результате приведенные выражения примут вид:

¬Д₂ ∨ ¬Д₃ ∨ (х + А)

¬(¬Д₂ ∨ ¬Д₃) = Д₂ ∧ Д₃

15.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2021 года)

Условие

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 9))

тождественно истинна (то есть принимает значение 1 при любом значении переменной х)?

Решение

Как при использовании программы, так и при решении задачи методом рассуждений надо отказаться от операций импликации в заданной формуле. При этом при преобразованиях учтем совет, данный при выполнении предыдущего задания. Введем обозначения:

ДЕЛ(x, А) = Д_А

ДЕЛ(x, 6) = Д₆

ДЕЛ(x, 9) = Д₉

и перепишем заданную формулу в виде → (Д₆ → ). Далее заменим первую импликацию:

Д_А ∨ (^Д₆→ )

и вторую:

Д_А ∨ .

Полученное логическое выражение и используем в программе. Прежде чем представлять ее, заметим, что так как по условию требуется найти наибольшее подходящее число, то перебор значений А лучше проводить от большего к меньшему.

Итак, программа:

алг нач цел А, х, к нц для А от 100 до 1 шаг -1 к := 0 нц для х от 1 до 1000 если mod(х, А) = 0 или mod(х, 6) <> 0 или mod(х,9) <> 0 то к := к + 1 все кц если к = 1000 то вывод нс, А выход все кц кон

Внимание! В некоторых случаях диапазона, который используется при переборе значений A и x, может не хватить для правильного решения задачи. Поэтому лучше увеличивать диапазон перебора до 10 000–50 000, по крайней мере для переменной x [4].

При поиске ответа методом рассуждений, как и в предыдущем задании, надо исключить влияние элементов дизъюнкции, не зависящих от значения А, исследовав ложность выражения ∨ . Применив к нему закон де Моргана, получим:

Д6 ∧ Д9

Это выражение истинно, когда х кратно как 6, так и 9. Какие это числа? – 18, 36, 54, … На какие числа делятся они (возможные значения А)? Вот делители каждого из них: 1, 2, 3, 6, 9, 18. Наибольшее значение 18 и является искомым значением А.

Ответ: 18.

Сделаем важный вывод.

Если в результате преобразований получено выражение с одной или несколькими операциями дизъюнкции, в которых имеются элементы, не включающие в себя переменную, значение которой нужно определить (А), то для решения задачи методом рассуждений следует:

• проанализировать ложность таких выражений и определить соответствующее значение (соответствующие значения) х;

• исследовать «влияние» найденных значений х на переменную А и найти соответствующее значение А.

15.2. 3. Задания для самостоятельного выполнения

1. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

¬ДЕЛ(x, А) → (ДЕЛ(x, 6) → ¬ДЕЛ(x, 4))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

2. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наибольшего натурального числа А формула

(A < 50) ∧ (¬ДЕЛ(x, А) → (ДЕЛ(x, 10) → ¬ДЕЛ(x, 12)))

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

3. Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».

Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 3) → ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 90)

тождественно истинна (т. е. принимает значение 1) при любом натуральном значении переменной x?

15.3. Примеры заданий с отрезками числовой прямой и методика их выполнения

15.3.1. Пример 1

Условие

На числовой прямой даны два отрезка: P = [4, 15] и Q = [12, 20].

Укажите наименьшую возможную длину отрезка A, для которого выражение

((x ∈ P) ∧ (x ∈ Q)) → (x ∈ A)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

Решение

Здесь тоже при анализе удобно использовать короткие обозначения элементов логических выражений.

Введем их: x А) ≡ A; (x P) ≡ P; (x Q) ≡ Q.

Заданное выражение примет вид: (P ∧ Q) → A.

Заменив в нем импликацию, получим: ¬P ∨ ¬Q ∨ A.

Последнее выражение должно быть истинным при любом значении переменной х. Так как оно включает дизъюнкции, то, как и ранее, надо исключить влияние на результат всего выражения элементов дизъюнкции, не зависящих от отрезка А (то есть выражения ¬P ∨ ¬Q).

Определим, когда ложно выражение ¬P ∨ ¬Q. Для этого применим закон де Моргана:

¬(¬P ∨ ¬Q) = P ∧ Q.

По схеме (см. рис. 15.1) можно установить, что условие P ∧ Q соблюдается на отрезке [12, 15]. Значит, A должно быть истинно именно на этом отрезке. Его длина равна 3 (это минимальный размер!).

		12	Q	20	х
4	Р		15

Рис. 15.1

Ответ: 3.

15.3.2. Пример 2

На числовой прямой даны два отрезка: P = [17, 54] и Q = [37, 83]. Какова наименьшая возможная длина интервала A, что формула

(x P) → (((x Q) ∧ ¬(x A)) → ¬(x P))

тождественно истинна, то есть принимает значение 1 при любом значении переменной х?

Решение

При тех же обозначениях, что и введенных в предыдущем пункте, и после замены двух операций импликации можно получить: ¬P ∨ ¬Q ∨ A. Две первые логические величины в последнем выражении c дизъюнкцией не зависят от А. Исключим их «влияние» на общий результат, для чего исследуем ложность выражения ¬P ∨ ¬Q.

Оно ложно при P ∧ Q. По схеме можно определить, что этому условию соответствует отрезок [37, 54]. Его длина – 17. Значит, чтобы заданное в условии выражение принимало значение 1 при любом значении переменной х, отрезок А должен «закрыть» найденный. Таким образом, минимальная длина отрезка А равна 54 – 37 = 17.

Ответ: 17.

15.3.3. Пример 3

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

На числовой прямой даны два отрезка: D = [17; 58] и C = [29; 80]. Укажите наименьшую возможную длину такого отрезка A, для которого логическое выражение

(x D) → ((¬(x C) ∧ ¬(x A)) → ¬(x D))

истинно, то есть принимает значение 1 при любом значении переменной х.

Решение

Введем обозначения:

(x D) = D;

(x C) = C;

(x A) = A,

при которых заданное логическое выражение примет вид:

D → (C ∧ A → D).

Заменим импликацию в скобках:

D → (С ∨ А ∨ D)

и полученную импликацию:

D ∨ С ∨ А ∨ D.

Так как D ∨ D = D, то запишем короче:

D ∨ С ∨ А.

Полученное выражение и является базовым для анализа. Нарисуем отрезки D и С на числовой оси:

	29		С	80	х
17		D	58

Рис. 15.2

Две первые логические величины в последнем выражении не зависят от А. Поэтому и здесь надо исключить их влияние на результат операции дизъюнкции. Можем утверждать, что выражение в условии будет равно 1 на той части числовой прямой, на которой А истинно, а

D ∨ С – ложно.

Итак, надо определить, когда ложно D ∨ С. Применив к последнему выражению закон де Моргана, получим:

D ∧ C.

Отрезок, удовлетворяющий полученному условию, на рис. 15.2 выделен черным цветом:

		29		С	80	х
	17		D	58

Рис. 15.2

Только на этом участке числовой оси все логическое выражение в условии задания истинно независимо от длины отрезка А. Значит, чтобы оно было истинным при любом значении переменной х, отрезок А должен «перекрывать» этот участок. Минимальная длина такого отрезка равна 29 – 17 = 12.

Ответ: 12.

15.3.4. Пример 4

Условие

На числовой прямой даны два отрезка: P = [10, 29] и Q = [13, 18].

Укажите наибольшую возможную длину отрезка A, для которого выражение

((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

Решение

Введем обозначения:

(x ∈ А) ≡ A;

(x ∈ P) ≡ P; (x ∈ Q) ≡ Q.

Заданное выражение примет вид: (А → P) ∨ Q.

Заменив в нем импликацию, получим:

¬A ∨ P ∨ Q.

Для этого исследуем ложность выражения P ∨ Q. Оно истинно на отрезке [10, 29] (убедитесь в этом!) и ложно вне его. Значит, именно вне отрезка [10, 29] должно быть истинно ¬A. Следовательно, A должно быть истинно на отрезке [10, 29]. Его длина 19 (это наибольшая длина!).

Ответ: 19.

15.3.5. Пример 5

Условие

На числовой прямой даны два отрезка: P = [5, 30] и Q = [14, 23]. Укажите наибольшую возможную длину промежутка A, для которого формула

((x ∈ P) ≡ (x ∈ Q)) → ¬(x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Решение

При тех же обозначениях, что и введенных в предыдущем пункте, и пос ле замены операции импликации можно получить:

¬(P ≡ Q) ∨ ¬A

или

(Р ≠ Q) ∨ ¬A.

Первый элемент дизъюнкции не зависит от А. Значит, чтобы это выражение было равно 1, ¬A должно быть истинным везде, где ложно Р ≠ Q. Так как А записано с отрицанием и Р ≠ Q – ложно, то последнее утверждение можно сформулировать так: «А может быть истинным только там, где истинно Р ≠ Q».

Нарисуем участок числовой оси:

Рис. 15.3

Где истинно выражение Р ≠ Q? – На двух полуинтервалах: [5, 14) и (23, 30], которые входят в Р и не входят в Q.

Значение А может быть истинным только внутри этих полуинтервалов, но поскольку А – это отрезок, то его наибольшая длина – это длина наибольшего из этих полуинтервалов, то есть 14 – 5 = 9 (длина второго полуинтервала равна 30 – 23 = 7).

Ответ: 9.

Общая методика выполнения заданий рассмотренного типа

Преобразовать заданное в условии логическое выражение в выражение с дизъюнкцией, заменив в нем операцию импликации.

Определить область (области) числовой оси, в которой (в которых) ложно выражение с элементами дизъюнкции, не зависящими от отрезка А.

Искомый отрезок А должен перекрыть эту область (при двух таких областях выбирается область максимальной или минимальной, в зависимости от условия задания, длины). При этом надо иметь в виду, что в элементе дизъюнкции, содержащем А, А может быть с отрицанием.

15.3.6. Задания для самостоятельного выполнения

1. На числовой прямой даны два отрезка: P = [5, 30] и Q = [14, 23]. Укажите наибольшую возможную длину промежутка A, для которого формула

((x ∈ P) ≡ (x ∈ Q)) → ¬(x ∈ A)

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

2. На числовой прямой даны два отрезка: P = [10, 29] и Q = [13, 18].

Укажите наибольшую возможную длину отрезка A, для которого выражение

((x ∈ A) → (x ∈ P)) ∨ (x ∈ Q)

тождественно истинно, то есть принимает значение 1 при любом значении переменной х.

3. На числовой прямой даны два отрезка: P = [20, 50] и Q = [30, 65].

Отрезок A таков, что формула

¬(x ∈ A) → ((x ∈ P) → ¬(x ∈ Q))

истинна при любом значении переменной x. Какова наименьшая возможная длина отрезка A?

4. На числовой прямой даны два отрезка: P = [130, 171] и Q = [150, 185]. Укажите наименьшую возможную длину такого отрезка A, что формула

(x P) → (((x Q) ∧ ¬(x A)) → ¬(x P))

истинна при любом значении переменной х, то есть принимает значение 1 при любом значении переменной х.

15.4. Примеры заданий с координатной плоскостью и методика их выполнения

15.4.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2020 года)

Условие

Для какого наименьшего целого неотрицательного числа А выражение (x + 2y < A) ∨ (y > x) ∨ (x > 30) тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?

Решение

Прежде всего обратим внимание на то, что так как в условии фигурируют две переменные х и у, то надо будет исследовать множество точек на координатной плоскости.

Задачу можно решить, разработав программу. Она также (см. п. 15.2.1) основана на переборе возможных значений А (например, от 0 до 199). Для каждого значения А, рассмотрев значения х и у, например, из того же диапазона, определить истинность приведенного в условии логического выражения. Если для всех сочетаний значений х и у выражение будет истинно, то текущее значение А является одним из тех, среди которых есть искомое. Так как найти нужно минимальное значение, то после «встречи» первого подходящего значения его надо вывести на экран и прекратить дальнейший перебор:

алг нач цел х, у, А, к нц для А от 0 до 199 к := 0

нц для х от 0 до 199 нц для у от 0 до 199 если х + 2 * у < А или у > х или х > 30 то к := к + 1 все кц кц если к = 40000 то

вывод нс, А выход все кц кон

Решим также задачу графически.

Анализ приведенного в условии выражения показывает, что в нем имеются только дизъюнкции, то есть его можно исследовать согласно уже неоднократно примененной методике без преобразований.

«Особый» участок координатной плоскости описывается неравенствами, не зависящими от значения А: y ≤ x и х ≤ 30. Изобразим его на плоскости с учетом того, что х и у неотрицательны (на рис. 15.4 такой участок выделен серым цветом).

Осталось «связать» неравенство x + 2y < A с этим участком.

Неравенство x + 2y < A можно записать в виде y < . График функции y = представляет собой прямую линию с убывающими значениями функции. Чтобы заданное в условии логическое выражение было истинным при любых целых неотрицательных значениях x и y, эта линия должна пройти выше самой высокой точки «особого» участка. Координаты этой точки (30; 30). Значит, должно соблюдаться неравенство > 30, откуда А > 90. Так как по условию А должно быть целым числом, то наименьшее подходящее значение А равно 91.

Ответ: 91.

15.4.2. Пример 2

Условие

Для какого наибольшего целого неотрицательного числа А выражение

(x · y < 121) ∨ (y > A) ∨ (x ≥ A)

тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?

Решение

Программа для поиска ответа аналогична приведенной в предыдущем пункте:

алг нач цел х, у, А, к нц для А от 199 до 0 шаг -1 к := 0 нц для х от 0 до 199 нц для у от 0 до 199 если х * у < 121 или у > А или х >= А то к := к + 1 все кц кц если к = 40000 то вывод нс, А выход все кц кон

Ее особенность (кроме оригинального условия для поиска значений А) в том, что так как искомым является максимальное значение А, то перебор значений этой переменной величины проводится от большего к меньшему.

Решим задачу графически.

Участок координатной плоскости, который описывается неравенством, не зависящим от значения А (x · y < 121), на рис. 15.5 закрашен.

Чтобы исходное выражение было тождественно истинно для любых целых и неотрицательных x и y, зависящее от А выражение

(y > A) ∨ (x ≥ A)

должно быть истинным вне этого участка. При каком значении А это возможно?

Рассуждения такие. Прямые х = А и у = А обязательно должны проходить через точку (11; 11). Значит, наибольшее целое неотрицательное А, удовлетворяющее условию задачи, – это A, равное 11.

Рис. 15.5

15.4.3. Пример 3

Условие

Укажите наименьшее целое значение А, при котором выражение

(y + 2x < A) ∨ (x > 20) ∨ (y > 30)

истинно для любых целых положительных значений x и y.

Решение

Приведем графическое решение (ответ с помощью программы найдите самостоятельно).

Второй и третий элементы выражения с дизъюнкцией не зависят от значения A. Значит, нам нужно выбрать значение A таким, чтобы условие (y + 2x < A) выполнялось при всех x и y, для которых ложно (x > 20) ∨ (y > 30), то есть при (x ≤ 20) ∧ (y ≤ 30).

Поскольку по условию значения x и y должны быть положительными, добавляем еще два условия (x > 0) ∧ (y > 0):

(x ≤ 20) ∧ (y ≤ 30) ∧ (x > 0) ∧ (y > 0).

Изобразим на координатной плоскости область, удовлетворяющую приведенному условию (на рис. 15.6 она заштрихована).

Рис. 15.6

Как уже отмечалось, для всех точек этой области должно соблюдаться условие y + 2x < A. Запишем его в виде уравнения: y < –2x + A.

Значит, вся область должна лежать ниже линии y = –2x + A (одна такая подходящая линия показана на рис. 15.6).

Очевидно, что минимальное значение A соответствует ситуации, когда при параллельном переносе показанной линии вниз, соответствующем изменению A, она коснется правого верхнего угла заштрихованного прямоугольника, то есть пройдет через точку (x = 20, y = 30). Значит, допустимые значения A определяются условием:

–2 ⋅ 20 + A > 30,

откуда следует, что A > 70, то есть искомое минимальное значение А равно 71.

Ответ: 71.

15.4.5. Задания для самостоятельного выполнения

1. (Задание из демонстрационного варианта ЕГЭ 2024 года.)

Для какого наименьшего целого неотрицательного числа A выражение

(x + 2y < A) ∨ (y > x) ∨ (x > 60)

тождественно истинно, т. е. принимает значение 1 при любых целых неотрицательных x и y?

2. Для какого наибольшего целого неотрицательного числа А выражение

(x · y < 140) ∨ (y > A) ∨ (x > A)

тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?

3. Для какого наименьшего целого неотрицательного числа А выражение

(y + 2x < A) ∨ (x > 30) ∨ (y > 20)

тождественно истинно, то есть принимает значение 1 при любых целых неотрицательных x и y?

Глава 16 Задания 16

16.1. Общие вопросы. Подготовка к выполнению заданий

В Спецификации [1] применительно к заданию 16 в качестве проверяемого элемента содержания указано «вычисление рекуррентных выражений».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 5 мин.

***

Рекуррентными выражениями (или рекуррентными соотношениями) называют формулы, выражающие очередной член числовой последовательности через один или несколько предыдущих членов. Например, в арифметической и геометрической последовательностях каждый член, начиная со второго, равен предыдущему, увеличенному на разность прогрессии: a_i = a_i_{– 1} + d – или умноженному на знаменатель прогрессии: ai = ai – 1 × k.

Как вычислить n-й член последовательности, заданной рекуррентным соотношением? Иногда для расчета n-го члена есть простая формула. Например, для арифметической прогрессии: a_n= a₁+ d(n – 1). Чаще, однако, такой простой формулы нет или она неизвестна. В этом случае члены последовательности вычисляют по рекуррентному соотношению один за другим от i = 1 до i = n.

Возможны два способа таких вычислений с помощью программы:

1) с использованием массива; 2) без использования массива.

Первый способ проиллюстрируем на примере следующей последовательности: 2, 3, 5, 9, 17, …, задаваемой рекуррентным соотношением a_i= 2 × a_i_{– 1}– 1, a₁= 2. Пусть требуется найти 30-й член последовательности.

Будем вычислять члены последовательности один за другим от i = 1 до i = 30, запоминая значение i-го члена такой последовательности в элементе м[i] массива м:

алг нач цел таб м[1:30], цел i м[1] := 2 | Первый член последовательности нц для i от 2 до n м[i] := 2 * м[i - 1] – 1 | Очередные члены последовательности кц вывод м[30] кон

Несколько отвлекаясь, заметим, что аналогом расчетов с использованием массива является расчет искомого значения с помощью электронной таблицы.

Оформим лист следующим образом (значения в столбце А можно получить, используя так называемое «автозаполнение»):

	А	В
1	n	F(n)
2	1
3	2
4	3
…	…	…
31	30

Учитывая особенности функции F, в ячейкe В2 запишем значение 2, а в ячейкe В3 – формулу =2 * B2 – 1:

	А	В
1	n	F(n)
2	1	2
3	2	3
4	3
…	…	…
31	30

Распространив (скопировав) формулу на другие ячейки диапазона В3:В31, получим:

	А	В
1	n	F(n)
2	1	2
3	2	3
4	3
…	…	…
31	30	536870913

Итак, ответ: 536870913.

Недостатком такого способа является то, что хотя нас интересует лишь 30-й член последовательности, в процессе выполнения программы компьютер вычисляет и хранит в памяти все члены последовательности от первого до 30-го. В программе надо описывать массив, а в электронной таблице – заполнять большое число ячеек.

Перечисленных недостатков лишен второй метод вычислений – без использования массива. Действительно, если для вычисления следующего члена последовательности нужно знать только значение предыдущего, то можно не запоминать все члены последовательности в массиве, а иметь одну величину а и при увеличении номера i изменять ее значение; для рассмотренного примера: a := 2 × a – 1. Другими словами, рекуррентное соотношение a_i= 2 × a_i_{– 1}– 1 можно заменить соотношением a_новое= 2 × a_старое– 1, которое записывается в виде оператора присваивания a := 2 × a – 1. Соответствующая программа:

алг нач цел a, i a := 2 нц для i от 2 до n a: = 2 * a – 1 кц вывод a кон

Можно также в программе использовать так называемые «рекурсивные функции». Рекурсивными называют функции или процедуры, которые используют (вызывают) как вспомогательную саму себя.

В качестве примера приведем функцию для расчета факториала натурального числа n (факториал числа n, обозначаемый n!, равен 1 × 2 × 3 × … × n). Такую функцию можно создать, имея в виду, что n! = (n – 1)! × n. На школьном алгоритмическом языке соответствующая функция имеет вид:

алг цел Факториал(арг цел n) нач знач := Факториал(n - 1) * n | Рекурсивный вызов функции Факториал | Служебное слово знач означает "значение функции" кон

На самом деле эта функция оформлена не по правилам, и при выполнении программы появится сообщение об ошибке. Дело в том, что при каждом вызове вспомогательной функции (или процедуры) для нее отводится место в оперативной памяти, которое «освобождается» после завершения ее (функции/процедуры) работы. Но если во вспомогательной функции имеется рекурсия, то вызовы продолжатся до тех пор, когда место в памяти будет исчерпано. Чтобы устранить этот недостаток, необходимо так оформлять функции (процедуры), чтобы рекурсивные вызовы осуществлялись по условию, которое когда-то станет ложным. Например, для приведенной функции это условие записывается так:

алг цел Факториал(арг цел n) нач если n > 1 то | Рекурсивный вызов функции Факториал знач := Факториал(n - 1) * n иначе | Известное значение знач := 1 все кон

или

алг цел Факториал(арг цел n) нач если n = 1 то знач := 1 иначе

знач := Факториал(n - 1) * n все кон

Чтобы найти факториал конкретного значения n, нужно в основной программе (в основной части программы) вызвать созданную функцию с известным аргументом:

вывод F(10)

Алгоритм вычисления значения рекурсивной функции F(n) может быть описан по-другому – с указанием двух или более вариантов значения, например в виде:

F(1) = 10

F(n) = F(n – 1) + 3 при n > 1, или

F(1) = 10

F(n) = F(n – 1) + 3 при n > 1

F(n) = 0 при n < 1, или

F(12) = 5

F(n) = F(n + 1) – 1 при n < 12, или

F(n) = 25 при n > 12

F(12) = 5

F(n) = F(n + 1) – 1 при n < 12 и т. п.

Видно, что в двух первых случаях рекурсивные вызовы осуществляются с меньшими значениями аргумента, в остальных – с большими. Во всех случаях когда-то рекурсивные вызовы прекратятся (убедитесь в этом!) и начнется передача результатов в «вызывающую» функцию.

Пример работы программы при вычислении значения факториала числа 4 показан на рис. 16.1–16.2.

Рис. 16.1

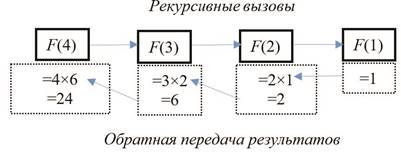
F(n)	F(4)	F(3)	F(2)	F(1)
Значение функции	24 ← 4 × 6	6 ← 3 × 2	2 ← 2 × 1	1
n	4	3	2	1

Рис. 16.2

Ответ: 24.

16.2. Примеры заданий и методика их выполнения

16.2.1. Пример 1

Условие

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1;

F(n) = F(n – 1) + n при n > 1.

Чему равно значение функции F(6)?

Решение

Видно, что функция F – рекурсивная (см. раздел 16.1). Она может быть оформлена в виде:

алг цел F(арг цел n) нач если n = 1 то знач := 1 иначе знач := F(n - 1) + n все кон

Основная программа:

алг нач вывод F(30) кон

Выполнив ее, можно получить ответ, равный 465.

Ответ: 465.

Можно также провести расчеты с помощью электронной таблицы. Оформим лист следующим образом:

	А	В
1	n	F(n)
2	1
3	2
4	3
…	…	…
31	30

Учитывая особенности функции F, в ячейкe В2 запишем значение 1, а в ячейкe В3 – формулу =B2 + A3:

	А	В
1	n	F(n)
2	1	1
3	2	3
4	3
…	…	…
31	30

Распространив (скопировав) формулу на другие ячейки диапазона В3:В31, получим:

	А	В
1	n	F(n)
2	1	1
3	2	3
4	3	6
…	…	…
31	30	465

16.2.2. Пример 2

Условие

Последовательность чисел задается рекуррентным соотношением:

F(1) = 1;

F(2) = 1;

F(3) = 1;

F(n) = F(n – 3) + F(n – 2) при n > 3, где n – натуральное число.

Чему равно двенадцатое число последовательности?

Решение

Здесь при рекурсивном вызове функция F использует два предыдущих значения. Соответствующая функция:

алг цел F(арг цел n) нач если n = 1 или n = 2 или n = 3 то знач := 1 иначе знач := F(n - 3) + F(n - 2) все кон

При использовании для решения электронной таблицы лист оформляется следующим образом:

	А	В
1	n	F(n)
2	1	1
3	2	1
4	3	1
5	4	=B2 + B3
…	…	…
13	12	=B10 + B11

Примечание. В столбце B приведены известные значения и формулы.

Ответ: 16.

16.2.3. Пример 3

(задание из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.)

Условие

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 1 при n = 1;

F(n) = n + F(n − 1), если n четно,

F(n) = 2 × F(n − 2), если n > 1 и при этом n нечетно. Чему равно значение функции F(26)?

Решение

Особенность приведенной функции в том, что в ней возможны три варианта расчета значения, из них два – рекурсивные. Поэтому в программе надо использовать так называемый «вложенный условный оператор»:

алг цел F(арг цел n) нач если n = 1 то знач := 1 иначе | Возможны два варианта если mod(n, 2) = 0 то знач := n + F(n - 1) иначе знач := 2 * F(n - 2) все все кон

Обратим внимание на то, что третий вариант, когда n > 1 и при этом n нечетно, с записью такого условия в функции рассматривать не нужно (этот вариант войдет в последнюю «ветвь» со служебным словом иначе).

Ответ: 4122.

Можно также провести расчеты с помощью электронной таблицы. Оформление листа электронной таблицы:

	А	В
1	n	F(n)
2	1
3	2
4	3
…
27	26

Учитывая особенности функции F, в ячейку В2 запишем значение 1, а в ячейки В3 и В4 – формулы:

	А	В
1	n	F(n)
2	1	1
3	2	=A3 + B2
4	3	=2 * B2
…	…	…
27	26

Так как далее две записанные формулы повторяются, то можно, выделив их, «протянуть» (распространить) их на другие ячейки:

	А	В
1	n	F(n)
2	1	1
3	2	3
4	3	2
…	…	…
26	25	4096
27	26	4122

16.2.4. Пример 4

Условие

Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1; G(1) = 1;

F(n) = F(n – 1) – G(n – 1) при n ≥ 2; G(n) = F(n–1) + G(n – 1) при n ≥ 2.

Чему равно значение F(15)?

Решение

Здесь имеет место так называемая «косвенная» рекурсия, при которой рекурсивная функция вызывает саму себя не непосредственно, а «через» другую, также рекурсивную функцию.

Соответствующая программа:

алг нач вывод F(15) кон

алг цел F(арг цел n) нач если n = 1 то знач := 1 иначе знач := F(n - 1) - G(n - 1) все кон

алг цел G(арг цел n) нач если n = 1 то знач := 1 иначе знач := F(n - 1) + G(n - 1) все кон

Ответ: 128.

В программе на языке Паскаль при использовании косвенной рекурсии возникает проблема, связанная с тем, что в этом языке программирования вспомогательная функция должна быть описана до основной функции или основной части программы, в то время как в данном случае обе функции являются вспомогательными. Решением проблемы является так называемое «опережающее» описание.

При использовании для решения электронной таблицы следует для значений каждой функции выделить отдельный столбец:

	A	B	C	D
1	n	F(n)		G(n)
2	1	1		1
3	2	=B2 - D2		=D2 + B2

16	15

16.2.5. Пример 5

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 1 при n = 1;

F(n) = n × F(n − 1) при n > 1.

Чему равно значение выражения F(2023)/F(2020)?

Решение

Внимательный читатель, конечно, обнаружил, что функция в условии определяет значение факториала числа n (см. раздел 16.1). Как известно, факториал является чрезвычайно быстро растущей функцией. Например, факториал числа 10 является семизначным числом, а

1000! ≈ 4,023872601 × 10²⁵⁶⁷.

Это значит, что определение значения выражения F(2023)/F(2020) путем расчетов значений F(2023) и F(2020) с помощью программы невозможно.

Можно рассуждать так.

Так как F(2021) = 2021 × F(2020), а F(2022) = 2022 × F(2021), то, заменив в последнем равенстве F(2021), получим

F(2022) = 2022 × 2021 × F(2020).

Аналогично для F(2023) = 2023 × F(2022), заменив F(2022), можно получить:

F(2023) = 2023 × 2022 × 2021 × F(2020).

Тогда значение дроби, указанной в условии, будет равно 2023 × 2022 × 2021. Результат умножения можно определить, разработав программу или с помощью электронной таблицы:

А	В
1	2023
2	2022
3	2021
4	8266912626

Ответ: 8266912626.

16.2.6. Пример 6

Условие

Алгоритм вычисления значения функции F(n), где n − натуральное число, задан следующими соотношениями:

F(0) = 0;

F(n) = F(n/2), если n > 0 и при этом четно; F(n) = 1 + F(n − 1), если n нечетно.

Сколько существует таких чисел n, что 1 ≤ n ≤ 500 и F(n) = 3?

Решение

Рекурсивная функция согласно условию:

алг цел F(арг цел n) нач если n = 0 то знач := 0 иначе если mod(n, 2) = 0 то знач := F(div(n, 2)) иначе знач := 1 + F(n - 1) все все кон

Обратите внимание на то, что даже для четных значений n при рекурсивном вызове функции используется операция целочисленного деления, поскольку тип аргумента функции F – целый.

Для нахождения искомого количества надо, используя переменную – счетчик к, перебрать в цикле значения n:

алг нач цел n, к к := 0

нц для n от 1 до 500 если F(n) = 3 то к := к + 1 все n := n + 1

кц вывод к кон

Ответ: 84.

16.2.7. Пример 7

Алгоритм вычисления значения функции F(n), где n − натуральное число, задан следующими соотношениями:

F(0) = 0;

F(n) = F(n/2), если n > 0 и при этом n четно; F(n) = 1 + F(n − 1), если n нечетно.

Найдите минимальное значение n, для которого F(n) = 12.

Решение

Рекурсивная функция в данном случае такая же, как и в предыдущем примере. С ее использованием надо найти минимальное значение n, для которого F(n) = 12. Так как в данном случае диапазон возможных значений n неизвестен, то это можно сделать с помощью оператора цикла с условием:

алг нач цел n n := 1 нц пока F(n) <> 12 n := n + 1 кц вывод n кон

Ответ: 4095.

16.3. Задачи для самостоятельного решения

1. Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 2;

F(n) = 2 × F(n – 1) + n – 1 при n > 1. Чему равно значение функции F(8)?

2. Последовательность чисел задается следующим рекуррентным соотношением:

F(1) = 2;

F(2) = 1;

F(n) = 2 × F(n – 2) + F(n – 1) при n > 2, где n – натуральное число. Чему равно десятое число этой последовательности?

3. Обозначим через a mod b остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n − натуральное число, задан следующими соотношениями:

F(0) = 0;

F(n) = n + F(n − 3), если n mod 3 = 0 и n > 0; F(n) = n + F(n − (n mod 3)), есл n mod 3 > 0.

Чему равно значение функции F(12)?

4. Алгоритм вычисления значений функций F(n) и G(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 20 при n < 10;

F(n) = F(n – 1) + G(n – 1) при n ≥ 10;

G(n) = 15 при n < 8;

G(n) = F(n – 1) + G(n – 1) при n ≥ 8.

Чему равно значение F(12)?

5. (Задание из демонстрационного варианта ЕГЭ 2024 года)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = n при n > 2024;

F(n) = n × F(n + 1), если n ≤ 2024.

Чему равно значение выражения F(2022)/F(2024)?

6. Алгоритм вычисления значения функции F(n), где n − натуральное число, задан следующими соотношениями:

F(0)= 0;

F(n) = F(n/2), если n > 0 и при этом четно; F(n) = 1 + F(n − 1), если n нечетно.

Сколько существует таких чисел n, что 1 ≤ n ≤ 900 и F(n) = 9?

7. Алгоритм вычисления значения функции F(n), где n − натуральное число, задан следующими соотношениями:

F(n) = 0;

F(n) = F(n/2), если n > 0 и при этом n четно; F(n) = 1 + F(n − 1), если n нечетно.

Найдите минимальное значение n, для которого F(n) = 11.

Глава 17 Задания 17

17.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 17 указывается «умение создавать собственные программы (20–40 строк) для обработки целочисленной информации».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 14 мин.

Задание выполняется с использованием прилагаемого файла.

***

В демонстрационных вариантах ЕГЭ по информатике 2022–2024 гг. представлены задания 17, в которых речь идет об определении количества и других характеристик пар или троек чисел, содержащихся в последовательности целых чисел, записанных в файле.

При выполнении таких заданий в программе нужно уметь работать с файлами – открывать их на чтение, считывать данные из них и закрывать. Обратим также внимание на то, что прилагаемый к заданиям файл – текстовый, то есть при чтении данных из него должно проводиться преобразование текстового представления чисел в числовое.

17.2. Примеры заданий и методика их выполнения

17.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых хотя бы одно число делится на 3, а сумма элементов пары – не более максимального элемента последовательности, кратного 3. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

Решение

Опишем сначала логику действий в программе.

Будем считать, что все числа из файла уже записаны в массив м из n элементов.

Для обработки пар чисел и нахождения искомых значений надо знать значение максимального числа, оканчивающегося на 3. Это значит, что предварительно должна быть решена задача нахождения такого максимума. Назовем эту задачу М3.

После ее решения можно проводить обработку (проверку) всех пар. При ее описании будем использовать следующие основные переменные величины^{^[51]}:

• макс3 – максимум чисел, оканчивающихся на 3;

• кол_пар – количество пар, удовлетворяющих условию (первое искомое значение);

• макс_сумма – максимальная из сумм квадратов элементов таких пар (второе искомое значение).

Фрагмент программы, в котором решается задача М3:

макс3 := -10001 | Начальное значение искомой величины нц для i от 1 до n если mod(м[i], 10) = 3 | Встретился элемент, оканчивающийся на 3 то | Сравниваем его со «старым» значением макс3 если м[i] > макс3 то | Встретился новый максимум | Запоминаем его макс3 := м[i] все все кц

Можно также использовать сложное условие:

макс3 := -10001 нц для i от 1 до n если mod(м[i], 10) = 3 и м[i] > макс3 то макс3 := м[i] все кц

Внимание! В ряде языков программирования остаток от деления отрицательных чисел на 10 не равен последней цифре делимого. Предлагаем читателям проверить это в используемом языке программирования. Если последняя цифра рассчитывается неправильно, то следует при определении остатка использовать абсолютную величину делимого.

Прежде чем приводить фрагмент программы, связанный с действиями по определению искомых величин, расскажем, как перебрать все возможные пары чисел. Для этого можно рассмотреть все элементы массива от первого до предпоследнего и для каждого из них вместе с «правым» от него элементом проверить соблюдение следующего условия: в паре элементов хотя бы одно число должно делиться на 3, а сумма элементов пары должна быть не более максимального элемента последовательности, кратного 3.

Итак, соответствующий фрагмент программы:

кол_пар := 0 | Начальные значения макс_сумма := 0^{^[52]} | искомых величин нц для i от 1 до n - 1 если mod(м[i], 10) = 3 и mod(м[i + 1], 10) <> 3 или mod(м[i], 10) <> 3 и mod(м[i + 1], 10) = 3 то | Встретилась пара чисел, только одно из которых

| оканчивается на 3 | Проверяем эту пару если м[i] * м[i] + м[i + 1] * м[i + ] >= макс3 * макс3 то | Встретилась пара чисел, | полностью удовлетворяющих условию | Увеличиваем количество таких пар кол_пар := кол_пар + 1 | Проверяем сумму квадратов элементов этой пары если м[i] * м[i] + м[i + 1] * м[i + 1] > макс_сумма то | Встретилась пара с новой | максимальной суммой квадратов

| Запоминаем эту сумму макс_сумма := м[i] * м[i] + м[i + 1] * м[i + 1] все все все кц

Конечно, после этого надо вывести на экран найденные значения кол_пар и макс_сумма.

Примечание. При необходимости надо учесть отмеченную выше особенность определения последней цифры отрицательного числа.

Теперь – о том, как заполнить массив числами из файла.

В программах на языках программирования, в которых имеется возможность записи всех чисел из файла в массив (например, в языке Python), для заполнения массива следует использовать соответствующую возможность. Размер полученного массива возвращает стандартная функция языка (в языке Python – функция len()).

В программах на остальных языках программирования заполнять массив надо, читая каждое число из файла и сразу записывая его в массив (с преобразованием типа данных). При этом возникает вопрос о размере используемого массива.

Так как в данном случае количество чисел в файле не указывается, то это количество можно узнать следующим образом:

• открыть прилагаемый к заданию файл;

• выделить все его строки (нажав комбинацию клавиш Ctrl+A);

• скопировать их;

• вставить скопированные строки в предварительно открытую программу – электронную таблицу.

Номер последней строки листа таблицы укажет количество чисел (о том, как узнать номер последней строки с данными, рассказывалось в разделе 9.2). Это количество n использовалось в приведенных выше фрагментах программы.

Можно также не определять количество чисел описанным методом, а сделать это в программе, описав массив, так сказать, «с запасом размера», а фактическое количество чисел определить, используя оператор цикла с условием и переменную-счетчик n:

Файл с исходными данными открывается на чтение n := 0

Пока не конец файла

| Значение переменной-счетчика увеличивается n := n + 1 Читается очередное число файла и записывается в n-й элемент массива, c преобразованием текстового значения в число Конец цикла

Файл закрывается

Всю программу для определения двух искомых значений соберите самостоятельно.

17.2.2. Задание из демонстрационного варианта ЕГЭ 2023 года

Условие

В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар последовательности, в которых только одно число оканчивается на 3, а сумма квадратов элементов пары не меньше квадрата максимального элемента последовательности, оканчивающегося на 3. В ответе запишите два числа: сначала количество найденных пар, затем максимальную из сумм квадратов элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

Комментарий к решению

Задание выполняется аналогично рассмотренному. Отличие – в условии для отбора необходимых пар чисел. Программу решения задачи разработайте самостоятельно.

17.2.3. Задание из демонстрационного варианта ЕГЭ 2024 года

Условие

В файле содержится последовательность натуральных чисел, каждое из которых не превышает 100 000. Определите количество троек элементов последовательности, в которых ровно два из трех элементов являются трехзначными числами, а сумма элементов тройки не больше максимального элемента последовательности, оканчивающегося на 13. Гарантируется, что в последовательности есть хотя бы одно число, оканчивающееся на 13. В ответе запишите количество найденных троек чисел, затем максимальную из сумм элементов таких троек. В данной задаче под тройкой подразумевается три идущих подряд элемента последовательности.

Решение

Отличия условия задания от рассмотренных:

• в файле записаны натуральные числа;

• речь идет не о парах чисел, а о тройках.

И конечно, условие для отбора необходимых троек чисел – другое.

Используем в программе следующие основные переменные величины (кроме массива м):

ф – файловая переменная; а – очередное число из файла в виде текста; n – количество чисел в файле; макс13 – максимальное из чисел, оканчивающихся на 13; кол3зн – количество трехзначных чисел в каждой тройке рассматриваемых элементов;

кол_троек – количество подходящих троек чисел (первое искомое значение);

макс_сумма – максимальная сумма чисел в таких тройках (второе искомое значение).

Итак. Заполним массив числами из файла:

ф := открыть на чтение("17.txt") n := 0 нц пока не конец файла(ф) ввод ф, а n := n + 1 м[n] := лит_в_цел(а, успех) кц закрыть(ф)

Здесь для решения тоже надо знать значение максимального числа, оканчивающегося на 13. Эта задача решается во многом аналогично решению задачи М3 в п. 17.2.1:

макс13 := 0 нц для i от 1 до n

если mod(м[i], 100) = 13 и м[i] > макс13 то макс13 := м[i] все кц

После определения значения макс13 можно перебирать и исследовать все возможные тройки элементов массива (i-й, (i + 1)-й и (i + 2)-й). При этом возникнет необходимость определить, сколько трехзначных чисел в тройке. Проще всего это сделать следующим образом:

кол3зн := 0 если м[i] >= 100 и м[i] <= 999 то кол3зн := кол3зн + 1 все если м[i + 1] >= 100 и м[i + 1] <= 999 то кол3зн := кол3зн + 1 все если м[i + 2] >= 100 и м[i + 2] <= 999 то кол3зн := кол3зн + 1 все

Перебор и проверка всех возможных троек элементов проводятся так:

кол_троек := 0 | Начальные значения макс_сумма := 0 | искомых величин нц для i от 1 до n - 2 | Определяем количество трехзначных чисел в текущей тройке … если кол3зн = 2 и м[i] + м[i + 1] + м[i + 2] <= макс13 то | Встретилась тройка чисел, полностью удовлетворяющих условию | Увеличиваем количество таких троек кол_троек := кол_троек + 1 | Проверяем сумму элементов этой тройки если м[i] + м[i + 1] + м[i + 2] > макс_сумма то | Встретилась тройка с новой максимальной суммой | Запоминаем эту сумму макс_сумма := м[i] + м[i + 1] + м[i + 2] все все кц

Так как выражение м[i] + м[i + 1] + м[i + 2] пришлось записать трижды, его можно копировать.

И еще. Если бы в задании требовалось определить минимальную из сумм подходящих троек элементов, то начальное значение минимальной суммы можно было бы принять равным 300001.

17.3. Задания для самостоятельного выполнения

1. Файл^{^[53]} содержит последовательность неотрицательных целых чисел, не превышающих 10 000. Назовем парой два идущих подряд элемента последовательности. Определите количество пар, в которых хотя бы один из двух элементов делится на 3 и хотя бы один из двух элементов меньше среднего арифметического всех четных элементов последовательности.

В ответе запишите два числа: сначала количество найденных пар, а затеммаксимальную сумму элементов таких пар.

Например, в последовательности (3 8 9 4) есть две подходящие пары: (3 8) и (9 4), в ответе для этой последовательности надо записать числа 2 и 13.

2. В файле содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество непересекающихся пар последовательности, в которых только одно число оканчивается на 3, а сумма квадратов элементов пары больше квадрата максимального элемента последовательности, оканчивающегося на 3.

В ответе запишите два числа: сначала количество найденных пар, затем минимальную из сумм квадратов элементов таких пар. В данной задаче под непересекающимися парами подразумевается: первая пара – 1-й и 2-й элементы, вторая пара – 3-й и 4-й элементы и т. д.

3. В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, для которых произведение элементов делится без остатка на 16, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.

4. Выполните задание, рассмотренное в п. 17.2.3 применительно к непересекающимся тройкам последовательности. В данной задаче под непересекающимися тройками подразумевается: первая тройка – 1-й, 2-й и 3-й элементы, вторая тройка – 4-й, 5-й и 6-й элементы и т. д. Так как в приложенном к заданию файле общее количество чисел не кратно трем, то удалите из файла необходимое количество чисел.

Глава 18 Задания 18

18.1. Общие вопросы. Подготовка к выполнению заданий

В Спецификации [1] применительно к заданию 18 в качестве проверяемого элемента содержания указано «умение использовать электронные таблицы для обработки целочисленных данных».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 8 мин.

Задание выполняется с использованием прилагаемого файла.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 18, общий вид которых следующий:

«Квадрат разлинован на N×N клеток (1 < N < …). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз^{^[54]}. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до …. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата».

Дополнение автора

В квадрате между клетками могут быть стены.

Указанная задача является типичной задачей, решаемой методом так называемого «динамического программирования» – особого метода поиска оптимальных решений, специально приспособленного к так называемым «многошаговым», или «многоэтапным», операциям.

Опишем, как методом динамического программирования решается рассматриваемая задача применительно к поиску максимальной суммы.

Пусть квадрат, по которому перемещается Робот, состоит из 36 клеток, между которыми нет стен. Квадрат будем моделировать в виде диапазона A1:F6 электронной таблицы, в ячейках которого записаны достоинства монет (см. рис. 18.1).

	A	B	C	D	E	F
1	13	8	20	9	20	7
2	18	9	3	10	17	14
3	8	10	16	5	2	19
4	11	9	10	4	2	5
5	15	13	13	2	7	6
6	7	4	13	5	2	3

Рис. 18.1

Итак. Понятно, из ячейки F5 к цели (в ячейку F6) можно попасть единственным способом – по команде вниз. При этом общая сумма, собранная Роботом, составит 6 + 3 = 9. Конечно, расчеты удобнее проводить с помощью электронной таблицы в диапазоне A8:F13 (рис. 18.2).

	A	B	C	D	E	F
1	13	8	20	9	20	7
…
6	7	4	13	5	2	3
7
8
9
10
11
12
13

Рис. 18.2

Запишем в ячейку F13 значение 3 (или, для общего случая, формулу =F6), а в ячейку F12 – формулу =F5 + F13. При этом, естественно, на листе появятся результаты расчета по формулам (см. рис. 18.3).

	A	B	C	D	E	F
…	…	…	…	…	…	…
8						54
9						47
10						33
11						14
12						9
13	34	27	23	10	5	3

Рис. 18.3

Аналогично из всех остальных клеток крайнего правого столбца квадрата имеется только один вариант перемещения. Это значит, что мы можем формулу в ячейке F12 распространить (скопировать) на остальные ячейки столбца F.

Для клеток последней строки квадрата также возможен единственный вариант движения Робота (вправо). Это означает, что в ячейку E13 можно ввести формулу =E6 + F13, которую затем распространить (скопировать) на ячейки А13:D13.

Итак, мы знаем, какая сумма может собрана Роботом при движении из клеток, моделируемых на рис. 18.3 ячейками с уже рассчитанными значениями. В дальнейшем для удобства будем говорить об условном перемещении исполнителя по ячейкам электронной таблицы.

Сложнее с выбором решения о направлении перемещения из ячейки E12. Здесь возможны два варианта: вправо (в ячейку F12) и вниз (в ячейку E13). Какой из них лучше? – Так как мы уже знаем, что из ячейки F12 до конца маршрута Робот может собрать 9, а из ячейки E13 – 5, то понятно, что следует идти вправо. В результате сумма при движении из E12 в F13 будет равна 16. В общем случае формула для определения максимальной суммы для ячейки E12 будет такой:

=ЕСЛИ(F12 > E13; F12 + E5; E13 + E5)

Можно использовать более короткую формулу с функцией МАКС:

=МАКС(F12 + E5; E13 + E5)

Эта формула может быть скопирована в остальные ячейки диапазона А8:Е12. В результате фрагмент листа А8:F13 примет вид:

	A	B	C	D	E	F
…	…	…	…	…	…	…
8	134	121	113	93	84	54
9	104	86	77	74	64	47
10	83	72	62	40	35	33
11	75	58	46	22	18	14
12	64	49	36	18	16	9
13	34	27	23	10	5	3

Рис. 18.4

Это значит, что искомая максимальная сумма равна 134.

Можно также проводить анализ с начала маршрута Робота. Для удобства повторим исходные данные:

	A	B	C	D	E	F
1	13	8	20	9	20	7
2	18	9	3	10	17	14
3	8	10	16	5	2	19
4	11	9	10	4	2	5
5	15	13	13	2	7	6
6	7	4	13	5	2	3

Рис. 18.5

Расчеты также будем проводить в диапазоне ячеек А8:F13.

В стартовой ячейке А1 имеется 13 монет, и Робот их соберет. Запишем это (формулой =А1) в ячейку А8.

В ячейку В1 Робот может попасть только из А1. Запишем в ячейку В8 формулу =A8 + B1 (в ней появится значение 21). Эту формулу можно распространить (скопировать) на остальные ячейки строки 8, в которые можно попасть единственным путем (из ячейки левее).

Аналогично можно заполнить ячейки диапазона А9:А13.

Обсудим, как Роботу лучше попасть в ячейку В9. Возможны два варианта – через ячейку В8 и через ячейку А9. Так как в ячейке А9 набранная им сумма больше, то идти надо через нее. В результате, находясь в ячейке В9 и взяв имеющиеся там 9 монет, Робот соберет 40 монет. В общем случае запишем в ячейку В9 формулу =МАКС(A9 + B2; B8 + B2). Для остальных оттененных на рис. 18.6 ячеек рассуждения аналогичны, то есть приведенную формулу можно скопировать в них. Результат показан на рис. 18.7.

	A	B	C	D	E	F
1	13	8	20	9	20	7
2	18	9	3	10	17	14
…	…	…	…	…	…	…
6	7	4	13	5	2	3
7
8	13	21	41	50	70	77
9	31
10	39
11	50
12	65
13	72

Рис. 18.6

	A	B	C	D	E	F
1	13	8	20	9	20	7
2	18	9	3	10	17	14
…	…	…	…	…	…	…
6	7	4	13	5	2	3
7
8	13	21	41	50	70	77
9	31	40	44	60	87	101
10	39	50	66	71	89	120
11	50	59	76	80	91	125
12	65	78	91	93	100	131
13	72	82	104	109	111	134

Рис. 18. 7

Ответ, естественно, тот же (134).

В дальнейшем мы при выполнении заданий будем проводить анализ с конца маршрута Робота.

Применительно к поиску минимальной суммы задача решается аналогично (конечно, с измененными формулами в ячейках диапазона В9:F13).

18.2. Методика выполнения заданий из демонстрационных вариантов ЕГЭ

18.2.1. Задание из демонстрационного варианта ЕГЭ 2021 года

Условие

Квадрат разлинован на N×N клеток (1 < N < 17). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.

Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Пример входных данных:

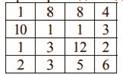
Для указанных входных данных ответом должна быть пара чисел:

Решение

В файле, приложенном к заданию, исходные данные представляют собой электронную таблицу размером 10×10, каждая ячейка которой соответствует клетке квадрата, в ячейках которого записаны достоинства монет (см. рис. 18.8). Стены между ячейками отсутствуют.

Методика выполнения задания аналогична описанной в разделе 18.1. Если расчеты по нахождению максимального значения провести в диапазоне ячеек A12:J21 и проводить анализ с конца маршрута, то «ключевые» для копирования формулы будут такими, как на рис. 18.9, а результаты расчетов – как на рис. 18.10.

	A	B	C	D	E	F	G	H	I	J
1	51	21	93	48	45	100	67	39	18	29
2	57	43	97	51	92	10	93	32	19	58
3	63	16	31	16	78	88	90	72	37	67
4	10	57	64	25	96	50	81	65	91	69
5	99	43	95	7	40	76	18	34	5	65
6	35	19	71	77	64	38	62	56	10	2
7	100	57	27	26	51	33	100	11	53	1
8	11	79	49	46	37	69	80	31	25	39
9	22	71	20	23	11	12	39	16	64	34
10	4	25	87	84	30	48	77	13	40	33

Рис. 18.8

	A	B	C	D	E	F	G	H	I	J
…	…	…	…	…	…	…	…	…	…	…
12
13
19
20									=МАКС(I9+J20;I9+I21)	=J21+J9
21									=J21+I10	=J10

Рис. 18.9

	A	B	C	D	E	F	G	H	I	J
…	…	…	…	…	…	…	…	…	…	…
12	1204	1153	1132	990	938	893	793	542	415	397
13	1139	1082	1039	942	891	736	726	503	390	368
14	1004	926	884	815	799	721	633	471	371	310
15	941	910	853	729	704	608	543	399	334	243
16	931	832	789	630	598	558	462	316	230	174
17	779	713	694	623	546	482	444	282	225	109
18	744	644	519	492	466	415	382	226	215	107
19	598	587	483	434	388	351	282	193	162	106
20	530	508	432	348	252	223	202	153	137	67
21	441	437	412	325	241	211	163	86	73	33

Рис. 18.10

Ответ (максимальное значение): 1204.

Для определения минимального значения можно использовать тот же диапазон ячеек, изменив формулу в ячейке I20 (см. рис. 18.12) и скопировав ее на остальные ячейки диапазона A12:I20:

	A	B	C	D	E	F	G	H	I	J
12
13
19
20									=МИН(I9+J20;I9+I21)	=J21+J9
21									=J21+I10	=J10

Рис. 18.12

Ответ (минимальное значение): 502.

18.2.2. Задание из демонстрационного варианта ЕГЭ 2022 года

Условие

Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние стены. Сквозь стену Робот пройти не может. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота. Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную.

Исходные данные представляют собой электронную таблицу размером N×N, каждая ячейка которой соответствует клетке квадрата. Внутренние и внешние стены обозначены утолщенными линиями.

Пример входных данных:

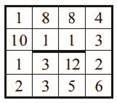
Решение

Здесь надо учесть, что в квадрате, в котором перемещается Робот, имеются стены.

В файле, приложенном к заданию, исходные данные представляют собой электронную таблицу размером 20×20, каждая ячейка которой соответствует клетке квадрата, в ячейках которого записаны достоинства монет (см. рис. 18.13^{^[55]}).

Рис. 18.13

Расчеты проведем в диапазоне ячеек А22:Т41. Чтобы в этом диапазоне были показаны и внутренние стены, скопируем в него ячейки диапазона А1:Т20, удалим все значения, кроме значений в правой нижней ячейке.

На рис. 18.14 показаны рассчитанные, как и ранее, значения в последней строке и в последнем столбце.

В отличие от предыдущих заданий, в данном случае в остальных ячейках формулы не будут однотипными. Целесообразно поступить так:

1) сначала заполнить их однотипными формулами (скопировав формулу в ячейке S40);

2) потом изменить формулы в ячейках над горизонтальной стеной и слева от вертикальной стены.

После первого этапа картина будет следующая (см. рис. 18.15):

Рис. 18.14

Рис. 18.15

Обсудим, как рассчитывать значения в ячейках у внутренних стен.

Слева от вертикальной стены в ячейках F25:F36 Робот может перемещаться только вниз. Формулы для этих ячеек можно скопировать (изменив имеющиеся) из любой ячейки последнего столбца, кроме правой нижней.

Аналогично для ячеек L38:R3 (над горизонтальной стеной) формулы можно скопировать из любой ячейки 41-й строки, кроме правой нижней.

Измененный результат показан на рис. 18.16.

Рис. 18.16

Итак, максимальная сумма равна 721.

Второе искомое значение (минимальная сумма) определяется аналогично.

18.2.3. Задание из демонстрационного варианта ЕГЭ 2023 года

Задание отличается от предыдущего содержанием прилагаемого файла (см. рис. 18.17).

Выполните его самостоятельно.

18.2.4. Задание из демонстрационного варианта ЕГЭ 2024 года

Условие

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	R	Q	S	T
1	27	29	25	26	27	28	30	30	27	26	27	30	28	25	29	30	26	25	27	28
2	27	29	25	27	30	26	25	26	25	30	25	25	30	25	30	28	28	29	27	27
3	30	30	26	26	30	28	27	25	29	30	26	27	27	26	30	30	25	26	29	29
4	25	30	27	29	27	26	29	28	29	25	27	29	29	29	27	29	29	27	30	26
5	27	30	27	28	28	26	26	28	27	25	28	30	28	27	28	28	28	29	30	28
6	28	30	28	25	25	25	29	25	30	25	27	29	27	26	30	29	25	29	27	28
7	29	25	25	28	30	26	27	26	30	26	27	25	25	29	26	29	29	28	30	30
8	26	28	28	29	26	30	29	29	25	29	26	26	30	25	29	28	25	27	30	28
9	29	26	30	29	27	28	28	25	28	25	25	27	29	29	27	26	29	27	28	26
10	26	28	28	25	26	27	30	27	27	27	30	26	30	25	25	26	29	25	26	28
11	30	30	27	29	26	26	30	25	25	30	26	27	27	25	25	25	30	28	26	25
12	27	26	29	25	29	25	30	27	25	29	29	26	25	30	29	25	28	30	26	26
13	25	29	27	27	29	25	30	27	25	29	25	26	30	27	26	27	30	26	27	28
14	27	30	30	26	28	27	25	29	26	27	30	26	28	28	28	30	26	29	27	30
15	26	27	28	27	26	28	26	26	26	28	29	27	26	28	29	30	30	29	27	29
16	27	27	26	30	26	29	27	28	30	27	28	30	26	29	29	28	28	26	26	25
17	29	30	30	29	30	26	28	26	28	30	25	29	25	27	26	25	25	29	27	28
18	29	30	26	28	26	26	29	28	29	29	25	27	25	29	27	29	25	29	29	28
19	30	30	28	27	30	27	28	26	27	25	26	25	28	26	28	26	27	27	27	25
20	25	27	30	26	29	28	25	29	27	27	27	27	27	29	25	25	30	26	29	25

Рис. 18.17

В «угловых» клетках поля – тех, которые справа и снизу ограничены стенами, Робот не может продолжать движение, поэтому накопленная сумма считается итоговой. Таких конечных точек может быть несколько, включая правую нижнюю клетку поля. При разных запусках итоговые накопленные суммы могут различаться.

Пример входных данных:

Решение

В файле, приложенном к заданию, исходные данные представляют собой электронную таблицу размером 20×20 (см. рис. 18.18).

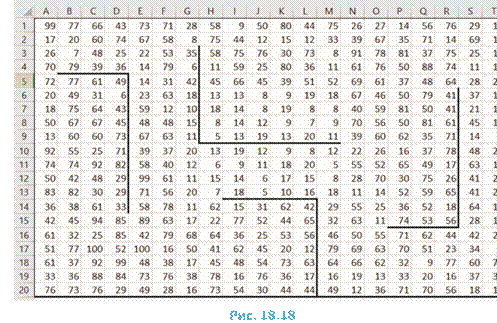
Прежде всего видно, что на поле, по которому перемещается Робот, в данном случае имеется не одна, а несколько клеток с двумя стенами – справа и снизу (в условии задания они названы «угловыми»). Понятно, что из них Робот перемещаться дальше не может.

Расчеты по нахождению максимального значения проведем в диапазоне ячеек A22:Т41.

Скопируем в указанный диапазон ячейки диапазона А1:Т20, удалим все значения, кроме чисел в «угловых» ячейках, и выделим цветом «особые» ячейки – над горизонтальными стенами и слева от вертикальных стен:

Дальнейшие действия аналогичны описанным при выполнении предыдущих заданий.

1. Формула в ячейке S41: =T41 + S20 копируется на все выделенные горизонтальные ячейки (кроме «угловых»). Результат показан на рис. 18.20.

Рис. 18.20

2. Формула в ячейке Т40: =T41 + T19 копируется на все выделенные вертикальные ячейки (кроме «угловых»):

3. Формула в ячейке S40: =МАКС(S19 + S41; S19 + T40) копируется на все остальные ячейки:

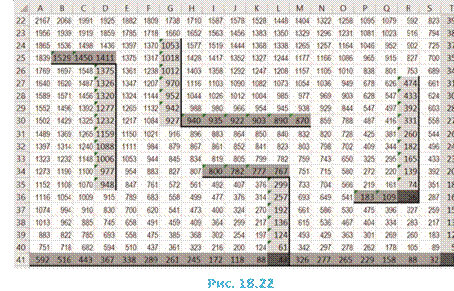
Искомая максимальная сумма указана в ячейке А22. Она равна 2167.

Минимальная сумма определяется аналогично.

В заключение объясним, почему при выполнении рассмотренного задания нецелесообразно применить анализ с начала маршрута. Дело в том, что в этом случае Робот остановится в одной из трех «угловых» клеток, и для поиска максимального и минимального значений общей суммы понадобится находить в отдельных ячейках максимум и минимум среди значений в этих трех клетках, на что понадобится дополнительное время.

18.3. Задания для самостоятельного выполнения

1. Выполните все рассмотренные задания применительно к нахождению минимальной суммы, собранной Роботом.

2. Квадрат разлинован на 6×6 клеток. Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вверх. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вверх – в соседнюю верхнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством, указанным на рис. 18.1. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.

Определите максимальную денежную сумму, которую может собрать Робот, пройдя из левой нижней клетки в правую верхнюю».

3. Квадрат разлинован на 6×6 клеток. Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из трех команд: вправо, вниз или вправовниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю, по команде вправовниз – по диагонали в соседнюю нижнюю правую. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством как на рис. 18.1. Посетив клетку, Робот забирает монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.

Определите минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю.

Глава 19 Задания 19, 20 и 21

19.1. Общие вопросы

В Спецификации [1] применительно к заданиям 19, 20 и 21 указаны следующие характеристики:

	Задание 19	Задание 20	Задание 21
Проверяемый элемент содержания	Умение анализировать алгоритм логической игры	Умение найти выигрышную стратегию игры	Умение построить дерево игры по заданному алгоритму и найти выигрышную стратегию
Уровень сложности задания	Б (базовый)	П (повышенный)	В (высокий)
Максимальный балл за выполнение задания	1	1	1
Примерное время выпол- нения задания, минут	6	8	11

В заданиях 19, 20 и 21, представленных в демонстрационных вариантах ЕГЭ по информатике нескольких последних лет, речь идет об игре двух участников, по очереди берущих камни по определенным правилам из одной или двух кучек камней. Игра заканчивается при наступлении некоторого заданного условия.

19.2. Готовимся выполнять задания

Прежде чем обсуждать методику выполнения указанных заданий, введем ряд понятий, важных для выполнения. Для этого обсудим более простую игру: «Два игрока играют в следующую игру. Они ходят по очереди, выкладывая на стол один, два или три предмета (монеты, спички или т. п.). В начальный момент на столе предметов нет. Игра завершается в тот момент, когда общее количество предметов на столе становится не менее 15».

В каком случае делающий очередной ход игрок А побеждает в игре? – Если на столе уже есть 14, 13 или 12 предметов. Каждую такую позицию в игре назовем «выигрышной» (для делающего очередной ход).

Следующий вопрос: «При каком количестве предметов на столе его соперник Б обязательно оставит ему одну из таких позиций, то есть любой его ход переведет ситуацию в игре в выигрышную позицию?» – При 11 предметах^{^[56]}. Позицию с 11 предметами назовем «проигрышной».

Получается, чтобы выиграть, А должен оставить после своего предпоследнего хода 11 предметов. Как это можно сделать? – Из позиций с 10, 9 или 8 предметами. Понятно, что эти позиции тоже выигрышные для А.

А как «заставить» Б оставить одну из этих позиций? Если до этого А оставит 7 предметов (проигрышную позицию).

Рассуждая аналогично, определим, что выигрышными для А являются позиции с 6, 5 или 4 предметами, а позиция с тремя предметами является проигрышной.

Итак, можно сделать такой вывод: «Чтобы выиграть, начинающий игру А должен оставить после своего хода проигрышную позицию с тремя камнями, после чего его соперник Б будет вынужден оставлять после своего хода выигрышную позицию, которую А переведет в проигрышную, и т. д. до окончания игры, в которой А станет победителем. В таких случаях, когда игрок может выиграть при любых ходах соперника, говорят, что «он имеет выигрышную стратегию». Эта стратегия заключается в том, что он должен все время переводить ситуацию в игре в проигрышную позицию.

Всегда ли у начинающего игру есть выигрышная стратегия? Анализ варианта игры, в которой условием для окончания игры является «Общее количество предметов на столе становится не менее 16», показывает, что начальной проигрышной позицией является позиция «4», которую начинающий игру оставить сопернику не может. В этом случае победителем станет игрок, делающий ход вторым (конечно, если он знает выигрышную стратегию).

Итак, можно дать такие определения:

• выигрышная позиция – в которой игрок, делающий очередной ход, может:

§ перевести ситуацию в игре в следующую такую же позицию независимо от того, какой ход сделает другой игрок,

§ или одним ходом победить в игре;

• проигрышная позиция – в которой игрок, делающий очередной ход, при любом своем ходе переведет ситуацию в игре в выигрышную для соперника позицию.

Вопросы для самоконтроля^{^[57]}

1. Если в аналогичной игре выкладывать можно один, два, три предмета или четыре предмета и игра завершается в тот момент, когда общее количество предметов на столе становится не менее 25, то какая последняя позиция является проигрышной?

2. Если в начале игры на столе уже находится S предметов, то кто выиграет – начинающий игру или делающий второй ход? Имеется в виду, что оба участника игры знают выигрышную стратегию.

И еще. Возможен также вариант рассмотренной игры, в котором в начальный момент на столе уже находится S предметов, а участники по очереди могут взять 1, 2, …, n предметов. Побеждает тот, кто своим ходом взял все оставшиеся предметы (или когда количество предметов на столе становится меньше некоторого значения. Что меняется в стратегии участников игры? По сути, ничего. Выигрышные и проигрышные позиции определяются по приведенным чуть выше особенностям.

Например, при S = 15 возможности взятия за один ход одного, двух или трех предметов и при окончании игры в момент, когда все предметы разобраны, позиции 1, 2 и 3 являются выигрышными, позиция 4 – проигрышная, позиции 5, 6 и 7 – выигрышные, позиция 8 – проигрышная и т. д.

Итак, задания из демонстрационных вариантов экзамена. Будем обсуждать группу из трех заданий (19, 20 и 21) каждого года.

19.3. Примеры заданий с игрой с одной кучкой камней и методика их выполнения

19.3.1. Пример 1

(задание 19 из демонстрационных вариантов ЕГЭ 2023 и 2024 гг.)

Условие

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя.

За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза^{^[58]}. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 129 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 128.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.

Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

Решение

Обратим внимание на то, что в условии идет речь о выигрыше Вани за один ход, а начинает игру Петя.

Так как говорится о выигрыше за один ход, то начинать анализ надо, так сказать, «с конца». Какие позиции являются выигрышными (см. выше) за один ход? Первая очевидная выигрышная позиция для Вани – если после хода Пети в куче окажется 128 камней. А если камней будет меньше? При 127 камнях тоже побеждает Ваня (он удвоит имеющееся количество камней). Анализ показывает, что выигрышная позиция у делающего последний ход Вани будет при количестве камней в куче от 65 до 128. При каком количестве камней его соперник Петя обязательно оставит ему одну из таких позиций? – При 64 (при таком количестве Петя выиграть не может, он может увеличить число камней либо до 65, либо до 128; в обоих случаях Ваня побеждает одним ходом).

Ответ: 64.

Запомним, что позиция (64) является проигрышной^{^[59]}.

19.3.2. Пример 2

(задание 20 из демонстрационных вариантов ЕГЭ 2023 и 2024 гг.)

Условие

Для игры, описанной в задании 19, найдите два наименьших значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Решение

Здесь речь идет о выигрыше Пети за два хода.

При выполнении предыдущего задания было установлено, что при 64 камнях делающий очередной ход проигрывает в любом случае. Значит, в данном случае Петя, чтобы выиграть, должен свести ситуацию в игре к 64 камням в куче. Когда он может это сделать? – Если при первом ходе Пети (в начале игры) в куче находится 63 или 32 камня.

Ответ: 32 63 (в порядке возрастания!).

19.3.3. Пример 3

(задание 21 из демонстрационных вариантов ЕГЭ 2023 и 2024 гг.)

Условие

Для игры, описанной в задании 19, найдите минимальное значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

• у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Если найдено несколько значений S, в ответе запишите минимальное из них.

Решение

Конечно, условия изложены «замысловато», поэтому прокомментируем их.

Обратим внимание на то, что начинает Петя, а речь идет о вариантах исхода игры для Вани, а также на слово «гарантированно».

Итак, в задании идет речь о поиске такой позиции, которая для Пети является проигрышной. Причем не исключено несколько таких позиций и надо найти минимальное значение S. Так как позиции диапазона (65)– (128) являются выигрышными за один ход, то минимальное значение S, при котором Петя создаст для Вани одну из выигрышных позиций, равно 33. Но является ли такой выигрыш Вани гарантированным? – Нет, так как у Пети есть и другие варианты хода (в данном случае – другой вариант: «+1», при котором Ваня вообще не выиграет).

Рассмотрим заведомо проигрышную позицию (уже известную) S = 64. В этом случае Ване гарантирована победа за один ход, что не соответствует второму условию задания.

Предыдущее значение S – 63. В этой позиции Петя тоже может перевести ситуацию в проигрышную для Вани позицию (64), то есть в этом случае Ваня не выигрывает.

А вот значение S = 62 удовлетворяет обоим условиям, приведенным в задании:

• если Петя переведет ее в позицию (63), то Ваня своим первым ходом «+1» сведет ее к проигрышной для Пети позиции (64), после чего выиграет вторым ходом;

• если Петя удвоит количество камней до 124, то тогда Ваня побеждает за один ход.

Ответ: 62.

Внимание! Анализ позволяет сделать важные выводы.

1. В заданиях 21, аналогичных рассмотренному (с ходами в игре «×n» при любом n и «+1»), искомым является значение, на 2 меньшее количества камней, чем в проигрышной позиции, найденной при решении задания 19 при тех же условиях игры. В рассмотренном случае мы имели 62 = 64 – 2.

2. В заданиях 21 с играми с командами «×n» (при любом n) и «+m» (при любом m) для определения искомого значения S следует вычитать 2m.

19.3.4. Пример 4

(задание 19 из демонстрационного варианта ЕГЭ 2022 года)

Условие

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 29. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу, в которой будет 29 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 28.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.

Решение

Здесь все рассуждения аналогичны сделанным в п. 19.3.1:

• выигрышные позиции: 28, 27, …, 15 камней; • проигрышная позиция перед ними: 14 камней.

Ответ: 14.

19.3.5. Пример 5

(задание 20 из демонстрационного варианта ЕГЭ 2022 года)

Условие

Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Решение

При выполнении задания 19 было установлено, что проигрышная позиция для делающего ход Вани – 14 камней.

Петя может достичь ее с позиций, когда на столе находится 7 или 13 камней.

Ответ: 7 13.

19.3.6. Пример 6

(задание 21 из демонстрационного варианта ЕГЭ 2022 года)

Условие

Для игры, описанной в задании 19, найдите значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

• у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Если найдено несколько значений S, в ответе запишите минимальное из них.

Решение

Согласно выводу 1, сделанному в п. 19.3.3, искомое значение равно 14 – 2 = 12.

(14 – проигрышная позиция.) Ответ: 12.

19.3.7. Обобщения

Обсудим другой возможный вариант задания 19 – в котором, кроме добавления в кучу одного камня, за один ход игрок может увеличить количество камней в куче в три раза. Пусть, например, игра завершается в тот момент, когда количество камней в куче становится не менее некоторого заданного значения предел. Надо указать такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

Рассмотрев три варианта значения предел, одно из которых кратно трем, заполним таблицы выигрышными (В) и проигрышной (П) позициями:

50	51	…	151	152	153 и более
П	В	В	В	В	Конец игры

50	51	…	150	151	152 и более
П	В	В	В	В	Конец игры

50	51	…	149	150	151 и более
П	В	В	В	В	Конец игры

Анализ показывает, что искомое значение в заданиях, аналогичных рассмотренным, определяется по формуле: , где символы ⌊ ⌋ означают целую часть частного от деления выражения, записанного между ними.

Обобщим также два рассмотренных задания 20.

Как уже говорилось, в них речь идет о выигрыше Пети за два хода, и искомые в них значения – это позиции, с которых он может создать проигрышную позицию для Вани.

Нетрудно увидеть, что искомые в них значения зависят от соответствующего искомого значения в задании 19:

• значения 32 и 63 зависят от 64;

• значения 7 и 13 зависят от 14.

В чем особенность расчетов каждой пары искомых значений, установите самостоятельно.

Понятно, что если найденные при выполнении задания 19 значения нечетные (см. выше), то в соответствующем задании 20 речь может идти о поиске одного значения:

• для 63 – это значение 62;

• для 13 – это значение 12.

Для заданий, аналогичных заданию 20, но с возможностью увеличения количества камней в куче в три раза логика расчетов та же. Если значение, найденное при выполнении задания 19 с теми же условиями игры, кратно трем, то в задании 20 искомыми являются два значения, в противном случае – одно:

• для 51 – это значения 17 и 50;

• для 50 – это значение 49.

19.3.8. Другие возможные варианты задания 19

Как уже отмечалось в пп. 19.3.1 и 19.3.4, в заданиях 19 из демонстрационных вариантов ЕГЭ 2022 и 2024 гг. искомым значением является количество камней в проигрышной позиции в игре.

Возможна также такая формулировка задания 19 при тех же правилах игры: «Известно, что Ваня выиграл своим первым ходом пос ле неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна». Далее задания подобного типа будем называть «задания типа Б».

Решение

Здесь под словом «неудачный» ход имеется в виду, что Петя во время первого хода не применил возможную выигрышную стратегию, а перевел игру в выигрышную для Вани позицию, в результате чего тот выиграл своим первым ходом.

Выпишем последние выигрышные позиции: 128, 127, …, 66, 65. С каких позиций к ним могли привести неудачные ходы Пети? – С позиций 64, 62, …, 33. Минимальное значение – 33.

Ответ: 33.

Для аналогичных заданий в играх с возможностью увеличения количества камней в куче более чем в два раза решение аналогично.

Приведем его применительно к предельному количеству камней (29) и с возможностью увеличения количества камней в три раза.

Последние выигрышные позиции: 28, 27, …, 12, 11, 10. К ним могли привести неудачные ходы Пети с позиций 27, 26, …, 9, 8, 7, 6, 5, 4.

Ответ: 4 (частное от деления на 3 минимального числа камней в выигрышных позициях, кратного трем, то есть числа 12).

Можно так сформулировать методику выполнения заданий типа Б в общем случае, когда наряду с возможностью добавления в кучу одного камня игроки могут увеличивать количество камней в куче в N раз.

1) выписать количество камней в последних выигрышных позициях в порядке убывания (одно максимальное значение и N минимальных);

2) в конце полученного списка найти минимальное число, кратное N; 3) ответом будет частное от деления этого числа на N.

В заключение рассмотрим такую задачу: «Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или пять камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 41. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 41 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 40.

Решение

Видно, что в отличие от рассмотренных ранее заданий 19 указанная игра отличается ходами, которые могут делать участники игры. Но решается задача аналогично.

Последние выигрышные позиции: 40, 39, …, 36.

Позиция, в которой при любом ходе Пети Ваня может выиграть своим первым ходом, – 35 камней.

Ответ: 35.

Другой вариант рассмотренной задачи (аналогичен заданиям типа Б): «Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна».

Решение

При какой позиции, сделав свой первый, ошибочный ход, Петя оставит Ване выигрышную позицию? Возможны две такие позиции:

• с 35 камнями (любой ход Пети переведет ситуацию в выигрышную позицию);

• с 31 камнем (ход Пети «+5» переведет ситуацию в выигрышную позицию с 36 камнями).

Комментарий.

Ход Пети «+1» при 31 камне не является ошибочным.

Ответ: 31.

Внимание! В задачах последнего типа, в которых могут быть три и более вариантов возможных ходов с добавлением камней, следует использовать максимальное «приращение». Например, если за один ход игрок может добавить в кучу один, четыре или восемь камней, то при решении должно использоваться число 8.

И конечно, возможен «комбинированный» вариант игры, в котором возможны два хода с добавлением камней и ход с увеличением камней в два или более раз. Рассуждения при решении всех таких задач аналогичны приведенным.

19.4. Примеры заданий с игрой с двумя кучками камней и методика их выполнения

19.4.1. Пример 1

(задание 19 из демонстрационного варианта ЕГЭ 2021 года)

Условие

Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 77 или больше камней.

В начальный момент в первой куче было семь камней, во второй куче – S камней; 1 ≤ S ≤ 69.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. В описание выигрышной стратегии не следует включать ходы играющего по этой стратегии игрока, не являющиеся для него безусловно выигрышными, т. е. не являющиеся выигрышными независимо от игры противника.

Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

Решение

Прежде всего обсудим, может ли вторая куча быть меньше первой (S < 7)? – Нет, потому что в этом случае даже четырехкратное (за два хода) увеличение большей кучи (с семью камнями) позволит «набрать» только 7 × 4 + 6 = 34, что меньше 77. Значит, в начальной ситуации большей была вторая куча с S камнями.

Далее. Анализ показывает, что есть несколько позиций (7, S), в которых после неудачного хода Пети Ваня выиграет (об этом же говорит тот факт, что в условии фигурирует слово «минимальное»). Одной из таких позиций является, например, (7, 34), то есть S = 34, которую Петя переведет в (7, 35), после чего Ваня выиграет, увеличив вдвое число камней во второй куче (7,70).

Минимальное значение S будет в том случае, если и Петя своим первым ходом, и Ваня будут удваивать число камней в большей (второй) группе. В этом случае для выигрыша Вани должно соблюдаться условие 7 + 4S > 76, откуда S > 69. Последнему неравенству соответствует минимальное целое значение S, равное 18.

Ответ: 18.

19.4.2. Пример 2

(задание 20 из демонстрационного варианта ЕГЭ 2021 года)

Условие

Для игры, описанной в предыдущем задании, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.

Решение

Так как Петя не может выиграть за один ход, то он должен этим ходом перевести ситуацию к проигрышной для Вани позиции. Как найти такую позицию или несколько таких позиций?

Точно можно сказать, что Ваня не выиграет в позициях, в которых удвоение им большей кучи даст общее число камней, равное 76. Так как бóльшая куча – вторая, то этому условию соответствуют следующие:

(8, 34), (10, 33), (12, 32), (14, 31), (16, 30), (18, 29), ….

Но позиции без количества камней в первой куче 8 и 14 созданы быть не могут. Значит, остаются две позиции: (8, 34) и (14, 31).

Как они могут быть получены из начальной позиции (7, S), достаточно очевидно – при изменении Петей количества камней в первой куче (ходами «+1» и «×2» соответственно).

Итак, получены два значения S (34 и 31), при которых Ваня не сможет выиграть. Но, может быть, в указанных случаях и Петя не сможет выиграть своим вторым ходом, если Ваня не будет вдвое увеличивать бóльшую кучу, а сделает один из трех других возможных ходов? Проверим значение 34:

Ход Вани	Получится позиция
«+1» в первую кучу	9, 34	Во всех случаях Петя также выигрывает, увеличив вдвое вторую кучу
«×2» в первой куче	18, 34
«+1» во вторую кучу	8, 35

Аналогично можно убедиться в том, что и позиция (14, 31) является проигрышной для Вани (Петя выигрывает вторым ходом).

Значит, значения S = 34 и S = 31 обеспечивают Пете выигрыш в соответствии с условиями задания.

Ответ: 31 34 (в порядке возрастания!).

19.4.3. Пример 3

(задание 21 из демонстрационного варианта ЕГЭ 2021 года)

Условие

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

• у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Решение

Логика решения данной задачи аналогична выполнению задания 21 с одной кучей камней (конечно, с учетом того, что в игре используются две кучи).

Еще раз обратим внимание на то, что начинает Петя, а речь идет о вариантах исхода игры для Вани.

Как и при выполнении задания с одной кучей камней, в данном случае искомое значение S должно быть таким, чтобы при любом ходе Пети Ваня выиграл игру одним или двумя ходами. Как найти такое значение (или несколько таких значений)?

Мы уже знаем, что Петя побеждал в позициях (7, 31) и (7, 34). Теперь в них должен оказаться Ваня. После каких ходов Пети?

Начнем с (7, 31). Эту позицию Петя может создать с позиции (7, 30). Ваня переведет в (14, 31), после чего выиграет своим вторым ходом.

Но у Пети есть и три других варианта хода. Какие исходы для них?

Явно неудачный ход Пети по увеличению второй кучи в два раза приведет к выигрышу Вани за один ход.

Анализ еще двух вариантов ходов Пети в позиции (7,30) приведен в таблице:

Ход Пети	Получится позиция	Петя переводит ее в позицию	Из которой
«+1» в первую кучу	(8, 30)	(16, 30)	он выигрывает своим вторым ходом
«×2» в первой куче	(14, 30)	(14, 31)	то же

Следовательно, для исходной позиции (7, 30) требуемые условия соблюдаются.

Проверим позицию (7, 34). Ее Петя может создать своим ходом с позиции (7, 33), после чего Ваня побеждает за два хода. Анализ трех других вариантов хода Пети с позиции (7, 34), который мы предлагаем провести читателям, показывает, что позиция (7, 33) также подходит.

Минимальное из двух найденных значений S – 30.

Ответ: 30.

Обратим внимание на то, что если бы в задании требовалось найти максимально возможное значение S, то ответ был бы равен 33.

19.5. Задания для самостоятельного выполнения

1. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда количество камней в куче становится не менее 43. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 43 или больше камней. В начальный момент в куче было S камней, 1 ≤ S ≤ 42.

А. Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом.

Б. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

В. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Г. Найдите значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

2. Выполните предыдущие задания для случая, в котором игра завершается в тот момент, когда количество камней в куче окажется больше 19.

3. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в 3 раза. Игра завершается в тот момент, когда количество камней в куче становится не менее 129. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 129 или больше камней^{^[60]}. В начальный момент в куче было S камней, 1 ≤ S ≤ 128.

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Г. Найдите значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

4. Такое же задание, как и предыдущее, но игра завершается в тот момент, когда количество камней в куче становится более 100.

5. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один, четыре или 10 камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 85. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 41 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 84.

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Г. Найдите значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

6. Такое же задание, как и предыдущее, но игра завершается в тот момент, когда количество камней в куче становится более 100.

7. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу два, четыре или пять камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 85. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 85 или больше камней^{^[61]}.

В начальный момент в куче было S камней, 1 ≤ S ≤ 84.

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Г. Найдите значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

8. Такое же задание, как и предыдущее, но игра завершается в тот момент, когда количество камней в куче становится более 100.

9. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один или два камня или увеличить количество камней в куче в два раза. Игра завершается в тот момент, когда количество камней в куче становится не менее 45. Победителем считается игрок, сделавший последний ход, т. е. первым получивший кучу из 45 или больше камней.

В начальный момент в куче было S камней, 1 ≤ S ≤ 44.

• Петя не может выиграть за один ход;

• Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня.

Найденные значения запишите в ответе в порядке возрастания.

Г. Найдите значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

10. Такое же задание, как и предыдущее, но игра завершается в тот момент, когда количество камней в куче становится более 101.

11. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 86. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 86 или больше камней.

В начальный момент в первой куче было семь камней, во второй куче – S камней; 1 ≤ S ≤ 79.

А. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Укажите минимальное значение S, когда такая ситуация возможна.

Б. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

• Петя не может выиграть за один ход;

В. Найдите минимальное значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

• у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

12. Два игрока, Петя и Ваня, играют в игру с двумя кучками, правила которой – выше.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 62. Победителем считается игрок, сделавший последний ход, т. е. первым получивший такую позицию, при которой в кучах будет 62 или больше камней.

В начальный момент в первой куче было 10 камней, во второй куче – S камней; 1 ≤ S ≤ 51.

В. Найдите максимальное значение S, при котором одновременно выполняются два условия:

• у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

• у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Глава 20 Задания 22

20.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 22 указывается «построение математических моделей для решения практических задач. Архитектура современных компьютеров. Многопроцессорные системы».

• Уровень сложности задания – П (повышенный).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 7 мин.

Задание выполняется с использованием прилагаемого файла.

Задания рассмотренного далее типа впервые появились в демонстрационном варианте ЕГЭ по информатике 2023 года.

20.2. Задание 22 из демонстрационного варианта ЕГЭ 2023 года и методика его выполнения

Условие

В файле содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.

Типовой пример организации данных в файле:

Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии что все независимые друг от друга процессы могут выполняться параллельно. Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.

***

Дополнение автора

Прилагаемый файл – электронная таблица с данными, представленными на рис. 20.1.

Комментарий

Из приведенного примера следует, что:

1) процесс с ID, равным 3, может выполняться только после выполнения процессов с ID, равными 1 и 2;

2) процесс с ID, равным 4, может выполняться только после выполнения процесса с ID, равным 3 (а значит, и после процессов с ID, равными 1 и 2);

3) процессы с ID, равным 1 и 2, могут выполняться параллельно, независимо друг от друга, но до процесса с ID, равным 3.

	A	B	C
1	ID процесса В	Время выполнения процесса В (мс)	ID процесса (процессов) А
2	1	4	0
3	2	3	0
4	3	1	1;2
5	4	7	3
6	5	6	3
7	6	3	5
8	7	1	4;6
9	8	2	7
10	9	7	0
11	10	8	0
12	11	6	9
13	12	6	10

Рис. 20.1

Комментарий: Самостоятельно определите взаимозависимость всех 12 процессов.

Решение

Так как прилагаемый к заданию файл представляет собой файл электронной таблицы, то и определять искомое значение целесообразно в среде указанной программы. Прежде чем описывать методику выполнения задания, обсудим поиск ответа без использования компьютера. Представим, что имеется таблица следующего вида:

ID процесса									Время, мс
ID процесса	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1
2
…
12

Рис. 20.2

Строку с числами 1, 2, … будем рассматривать как некую шкалу времени в миллисекундах. В остальных строках будем отмечать клетки, соответствующие периоду выполнения каждого из процессов (с помощью символа «х» – см. ниже).

Так как по условию требуется определить минимальное время, через которое завершится выполнение всей совокупности процессов, то каждый из процессов следует начинать сразу же, когда это возможно.

Процессы, которые являются независимыми, могут (и должны) выполняться с начала. Такими процессами являются процессы с ID, равными 1, 2, 10 и 11 (в дальнейшем понятие ID мы указывать не будем, а будем оперировать только числами-номерами). Отметим их продолжительность в таблице (см. рис. 20.3):

								Время, мс
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
9	х	х	х	х	х	х	х
10	х	х	х	х	х	х	х	х
11
12

Рис. 20.3

Обсудим особенности выполнения процесса 3. Он зависит от процессов 1 и 2. Когда он может начаться? – После завершения того, как будут выполнены все процессы, от которых он зависит. В данном случае – после окончания процесса 1. Отметим продолжительность этого процесса в таблице:

							Время, мс
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	х	х	х	х
2	х	х	х
3					х
4
…
9	х	х	х	х	х	х	х
10	х	х	х	х	х	х	х	х
11
12

Рис. 20.4

Процессы 4 и 5 начнутся после окончания процесса 3 (рис. 20.5):

Время, мс

…

Рис. 20.5

В таблице на рис. 20.5 отмечена также продолжительность процесса 6 (он начнется после завершения процесса 5).

Далее, процесс 7 зависит от процессов 4 и 6. Из них позже завершится процесс 6. Отметим продолжительность процесса 7 (она равна 1 мс):

								Время, мс
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	х	х	х	х
2	х	х	х
3					х
4						х	х	х	х	х	х	х
5						х	х	х	х	х	х
6												х	х	х
7															х
8																х	х
9	х	х	х	х	х	х	х
10	х	х	х	х	х	х	х	х
11
12

Рис. 20.6

В таблице выше записана также продолжительность процесса 8 (он начнется после завершения процесса 7) длительностью 2 мс. Осталось отметить время процессов 11 и 12:

Время, мс

Рис. 20.7

Итак, вся совокупность процессов может завершиться не ранее, чем через 17 мс.

Ответ: 17.

Опишем теперь методику выполнения задания 22 с использованием электронной таблицы Microsoft Excel.

1. Представим данные, записанные в столбце C «ID процесса(ов) A», через точку с запятой (см. рис. 20.1), в нескольких столбцах:

	А	В	С	D
1	ID процесса В	Время выполнения процесса В (мс)	ID процесса (процессов) А
2	1	4	0
3	2	3	0
4	3	1	1	2
5	4	7	3
6	5	6	3
7	6	3	5
8	7	1	4	6
9	8	2	7
10	9	7	0
11	10	8	0
12	11	6	9
13	12	6	10

Рис. 20.8

Это можно сделать вручную. После этого данные в столбцах С и D можно обработать по отдельности.

2. Назовем следующие свободные столбцы E, F и G, соответственно, «Время окончания процесса A1», «Время окончания процесса A2», «Время окончания процесса B». В столбцах «Время окончания процесса A1», «Время окончания процесса A2» будет записано время окончания работы тех процессов, от которых зависит процесс B, указанный в той или иной строке (см. рис. 20.9). Сразу же скажем, что эти заголовки столбцов нужны только для понимания логики расчетов, а на экзамене их с целью экономии времени можно не записывать.

Рис. 20.9

Количество столбцов «Время окончания процесса A*» зависит от максимального количества чисел, записанных через точку с запятой в столбце C «ID процесса(ов) A» задания, в рассматриваемом случае – два.

Отвлечемся на время от электронной таблицы. Как мы определяли начало и окончание тех процессов В, которые зависят от других процессов? Были возможны три случая:

1) если процесс В зависел от одного процесса А1, то он начинался сразу после его окончания и длился в течение времени, указанного в столбце В;

2) если процесс В зависел от двух процессов (А1 и А2), то он начинался сразу после окончания «самого позднего» из А1 и А2 (и также длился в течение времени, указанного в столбце В);

3) процессы, не зависящие от других, должны выполняться с самого начала.

Так как в первом случае можно условно рассматривать наличие второго процесса А2 со временем окончания, равным 0, а в третьем случае – наличие двух условных процессов А1 и А2 со временем окончания, равным 0, то можем объединить все три случая в один и определять время окончания любого процесса В так:

максимальное значение времени окончания процессов А1 и А2 + длительность процесса В.

Это значит, что в ячейку G2 можно записать формулу

=МАКС(E2; F2) + B2

и распространить (скопировать) ее на другие ячейки диапазона G2:G13.

Результат будет таким:

Рис. 20.10

Функция МАКС возвращает максимальное значение из всех значений ее аргументов (их может быть и больше двух).

Внимание! Полученные значения в столбце G не являются окончательными, так как пока не определены моменты окончания процессов А1 и А2 в столбцах Е и F. Здесь начинается самое трудное. Как определить эти моменты? – Они записаны в столбце G. Чтобы найти их, можно использовать ряд функций Excel.

Лучше всего использовать функцию ПРОСМОТР. Она позволяет определить значение, соответствующее некоторому заданному значению, в любом столбце. Ее общий вид:

ПРОСМОТР(заданное_значение; просматриваемый_диапазон; диапазон_результатов), где:

• заданное_значение^{^[62]} – значение, которое ищется;

• просматриваемый_диапазон – диапазон, в котором ищется заданное_значение; этот диапазон должен содержать только одну строку или только один столбец. Значения в нем обязательно (!) должны быть расположены в порядке возрастания, в противном случае функция ПРОСМОТР может вернуть неверный результат;

• диапазон_результатов – диапазон, из которого возвращается значение функции. Он должен содержать только одну строку или только один столбец и быть того же размера, что и просматриваемый_диапазон.

Когда указанные диапазоны расположены в столбцах, то эта функция работает следующим образом: в просматриваемом диапазоне находится заданное значение, а значение в той же строке диапазона результатов возвращается в качестве искомого значения функции:

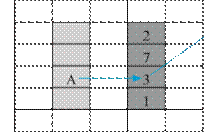Значение функции

Рис. 20.11

На рис. 20.11 светло-серым цветом выделен просматриваемый диапазон, темно-серым – диапазон результатов, А – заданное значение.

Например, для нахождения значения в ячейке Е4 (время окончания процесса 1) формула в ней должна быть такой:

=ПРОСМОТР(C4; $A$2:$A$13; $G$2:$G$13)^{^[63]}.

Смысл формулы: в диапазоне A2:A13 (номера ID процессов) нужно найти значение, соответствующее значению C4 (процессу 1), и в качестве результата вернуть значение из той же строки диапазона G2:G13 (время окончания процесса).

Введя эту формулу, получим в ячейке Е4 правильный результат (он будет равен 4). Но если распространить (скопировать) приведенную формулу на другие ячейки диапазона Е2:F13, то появятся сообщения об ошибках (убедитесь в этом!). Это связано с тем, что в столбце А нет значения 0 (условный номер ID процессов, используемый в пустых ячейках столбца С). Решить проблему легко – надо вставить строку перед сущест вующей строкой 2 и в новую ячейку А2 ввести номер 0. Но при этом в формулах с функцией ПРОСМОТР должны быть уточнены просматриваемый диапазон и диапазон результатов (в них добавилась одна строка).

Итак, для получения искомого результата следует в ячейку Е3 ввести формулу

=ПРОСМОТР(C3; $A$2:$A$14; $G$2:$G$14) и распространить (скопировать) приведенную формулу на другие ячейки диапазона Е2:F14. Результат показан на рис. 20.12.

При большом количестве процессов ответ из столбца G целесообразно получать следующим образом:

• выделить весь столбец, щелкнув левой кнопкой мыши на его заголовке;

• нажать правую кнопку мыши на так называемой «строке состояния» (самая нижняя полоса окна программы) – появится контекстное меню Настройка строки состояния:

Примечание. На рис. 20.13 показана часть меню.

• прокрутить колесо мыши до появления пункта Максимум:

Рис. 20.14

• поставить «галочку» в этом пункте – в меню будет показано искомое значение:

Рис. 20.15

Итак, кратко алгоритм решения рассмотренной задачи и других аналогичных задач можно сформулировать следующим образом:

1) в заданный файл вставить пустую строку 2;

2) записать в ячейку А2 число 0;

3) два числа (или больше), записанные в столбце С через точку запятой, «разбросать» в отдельные столбцы С и D (или в С, D и Е);

4) в ячейку Е3 записать формулу =ПРОСМОТР(C3; $A$2:$A$14; $G$2:$G$14); 5) распространить (скопировать) ее на все ячейки столбцов Е и F;

6) в ячейку G3 записать формулу =МАКС(E3; F3) + B3;

7) распространить (скопировать) ее на остальные ячейки столбца G.

Найти максимальное число в последнем столбце (просмотром или как в методике выше).

Что следует уточнить в описанном алгоритме, если в столбце С через точку с запятой записаны три числа, определите самостоятельно.

20.3. Задание 22 из демонстрационного варианта ЕГЭ 2024 года и методика его выполнения

Условие (только фрагмент с указанием искомого значения)

Определите максимальную продолжительность отрезка времени (в мс), в течение которого возможно одновременное выполнение четырех процессов, при условии что все независимые друг от друга процессы могут выполняться параллельно.

Дополнение автора

Прилагаемый файл – электронная таблица с данными, представленными на рис. 20.16.

Решение

Сразу же скажем, что в задании требуется в таблице, аналогичной приведенной на рис. 20.7, определить общее количество столбцов, в которых стоят четыре отметки «х».

Значит, прежде всего надо получить соответствующую таблицу. В данном случае в качестве отметок будем ставить цифру 1 (почему – станет ясно далее). Причем оформим таблицу на том же листе электронной таблицы, что и исходные данные.

Уменьшим ширину столбцов и отсортируем данные по столбцу С (кроме его заголовка), а также заполним первую строку, начиная со столбца Е, порядковыми номерами от 1 до 25 (это удобно сделать, используя так называемое «автозаполнение ячеек») – см. рис. 20.17.

Рис. 20.17

В результате независимые процессы будут представлены первыми. Запишем для них количество единиц согласно времени их выполнения (в столбце В):

После этого можно отметить процессы, зависящие от независимых

(с ID 11, 12 и 3)^{^[64]}:

а затем процессы, зависящие от процесса с ID 3 (рис. 20.20):

Далее отмечаем процесс с ID 6 (рис. 20.21):

и с ID 8 (рис. 20.22):

После этого осталось определить количество столбцов, в которых имеется ровно четыре отметки в виде единицы. Удобнее всего это сделать, подсчитав в каждом столбце диапазона Е:АВ, в строке 14, сумму значений в столбце (без учета порядкового номера в первой строке), а затем определить количество чисел 4 в диапазоне Е14:АВ14. Соответствующие расчеты предлагаем провести читателю.

***

Задания для самостоятельного выполнения – см. [3], раздел 22 «Многопроцессорные системы».

Для выбранных заданий определите также максимальную продолжительность отрезка времени (в мс), в течение которого возможно одновременное выполнение трех процессов, при условии что все независимые друг от друга процессы могут выполняться параллельно.

Глава 21 Задания 23

21.1. Общие вопросы

В Спецификации [1] применительно к заданию 23 в качестве проверяемого элемента содержания указано «умение анализировать ход исполнения алгоритма».

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 8 мин.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания, общий вид которых таков:

«Исполнитель преобразует число на экране.

У исполнителя есть <2 или 3> команды: <перечисляются команды> Программа для исполнителя – это последовательность команд».

Далее задается вопрос, который может быть в одном из трех вариантов:

1) «Сколько существует программ, для которых при исходном числе <…> результатом является число <…>, при этом траектория вычислений содержит число <…>?»

Можно сказать, что в таких заданиях речь идет о решении задачи, которую с точки зрения содержания можно назвать «задача “начальное – обязательное – конечное”»;

2) «Сколько существует программ, для которых при исходном числе <…> результатом является число <…>, при этом траектория вычислений не содержит <…>?»

Здесь решаемую задачу можно назвать «задача “начальное – конечное – кроме”»;

3) «Сколько существует программ, для которых при исходном числе <…> результатом является число <…>, при этом траектория вычислений содержит число <…> и не содержит <…>?»

Содержание задачи, решаемой в заданиях такого типа, можно назвать «задача “начальное – обязательное – конечное – кроме”».

Анализ показывает, что для решения указанных задач следует решить более простую задачу, которую назовем «базовой». Различные методы ее решения описаны в следующем разделе.

23.2. «Базовая задача» и методы ее решения

23.2.1. Условие

Исполнитель преобразует число на экране.

У исполнителя есть две команды, которые обозначены латинскими буквами:

A. Прибавить 1

B. Умножить на 2

Программа для исполнителя – это последовательность команд.

Сколько существует программ, для которых при исходном числе 1 результатом является число <указывается значение>?

Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы AВА при исходном числе 7 траектория будет состоять из чисел 8, 16 и 17.

23.2.2. Методы решения задачи

Прежде всего заметим, что полный перебор всех возможных вариантов, начиная с исходного числа, и последующий отбор нужных вариантов, при которых результат равен заданному числу, является нерациональным. Нерациональным с точки зрения выполнения задания является также использование графов.

Задание может быть выполнено различными методами.

Один из методов – с помощью таблицы. Рассуждения следующие.

Если нужно получить число 2 (обозначим такую задачу 1 → 2), то возможны два варианта программы:

1) команда А; 2) команда В.

Пусть нужно получить 3. Так как 3 – нечетное число, то оно может быть получено только из числа 2 одним способом. Общее количество вариантов для задачи 1 → 2 мы знаем (2). Значит, и для задачи 1 → 3 ответ равен 2.

Задача 1 → 4. Число 4 – четное, то есть оно может быть получено двумя способами – «через» 2 и «через» 3. Количество вариантов для каждого случая мы уже знаем (2 и 2, соответственно), то есть для задачи 1 → 4 ответ равен 2 + 2 = 4.

Искомые значения для бóльших результатов (и логика их получения) приведены в таблице:

Число	Может быть получено «через»	Общее количество вариантов
2	1	2
3	2	2
4	2 и 3	2 + 2 = 4
5	4	4
6	3 и 5	2 + 4 = 6
7	6	6

Конечно, описанный метод удобно применять, когда число, которое нужно получить, – небольшое.

Универсальные методы выполнения задания заключаются в использовании компьютерных программ. По нашему мнению, лучшим является решение с помощью программы, использующей рекурсию (см. главу 16).

Рекурсивная функция Кол(n), рассчитывающая количество программ, которыми можно получить число n, основана на следующих рассуждениях.

Если к – нечетное число, то значение функции совпадает с аналогичным значением для числа к – 1, в противном случае оно равно сумме двух значений Кол(к – 1) и Кол(к // 2), где // – знак операции целочисленного деления.

Как принято в рекурсивных функциях (см. раздел 16.1), вызовы (обращения) к этой же функции с другими аргументами должны проводиться по условию, которое когда-то станет ложным. Таким условием является следующее: к > 2 (при к = 2 значение функции известно – оно равно 2).

Соответствующая функция:

алг цел Кол(арг цел к) нач если к > 2 то | Рекурсивные вызовы функции если mod(к, 2) = 1 то знач := Кол(к - 1) | Значение функции иначе знач := Кол(к - 1) + Кол(div(к, 2)) все иначе | Известное значение функции знач := 2 все кон

Возможен также рекурсивный вариант, в котором рекурсивные вызовы происходят не с меньшими, а с большими значениями аргументов функции^{^[65]}. Рассуждения в данном случае такие. От некоторого начального значения н можно перейти либо к числу н + 1, либо к числу н × 2. Для двух указанных чисел дальнейшие действия аналогичны. Это значит, что рекурсивные вызовы для определения количества программ должны быть такими:

алг цел Кол(арг цел н, к) | Два аргумента функции!

… знач := Кол(н + 1, к) + Кол(н * 2, к)

Но при приведенной записи рекурсивные вызовы будут происходить «бесконечно», и их надо ограничить. Можно сказать, что эти вызовы должны происходить, если н < к:

алг цел Кол(арг цел н, к) нач если н < к то знач := Кол(н + 1, к) + Кол(н * 2, к)

А что должно быть в противном случае?

Когда первый аргумент функции станет равным или больше второго, то рекурсивные вызовы надо прекратить. Какие значения в вызывающую функцию должна вернуть текущая функция в таких случаях? Когда н стало равно к, то это значит, что получился еще один вариант программы (с последней командой А или В). Когда же очередное значение н превысило значение к, то и тогда вызовы надо, естественно, прекратить, а значение функции принять равным 0.

Вся соответствующая функция имеет вид:

алг цел Кол(арг цел н, к) нач

если н < к то | Рекурсивный вызов функции знач := Кол(н + 1, к) + Кол(н * 2, к) иначе если н > к то знач := 0 иначе | н = к знач := 1 все все кон

При вызове этой функции в основной части программы надо указать требуемое значение конечного числа: вывод Кол(1, …)

Можно также использовать в функции три неполных условных оператора (три команды если):

алг цел Кол(арг цел н, к) нач если н < к то знач := Кол(н + 1, к) + Кол(н * 2, к) все если н > к знач := 0 все если н = к то знач := 1 все кон

Несколько сократить оформление можно, если после проверки условий рекурсивный вызов функции провести «безусловно»:

алг цел Кол(арг цел н, к) нач если н > к знач := 0 все если н = к то

знач := 1 все знач := Кол(н + 1, к) + Кол(н * 2, к) кон

23.2.3. Универсальная функция

Преимуществом функции, в которой рекурсивные вызовы происходят с большими значениями аргументов (во всех вариантах ее оформления), заключается в том, что не нужно проводить проверку чисел на четность и использовать операцию целочисленного деления.

Еще одним важным преимуществом функции является универсальность – сделанные при ее разработке рассуждения позволяют прийти к выводу, что она применима и для нахождения искомых значений, когда начальное число – любое натуральное. В этом случае при вызове функции указываются два фактических значения ее аргументов: вывод Кол(…, …)

Более того, функция применима при любой другой системе команд исполнителя. В таких случаях должна быть уточнена команда если (неполный условный оператор), в которой происходят рекурсивные вызовы. Например, при системе команд

A. Прибавить 2

B. Умножить на 3 в этой команде должно быть записано: знач := Кол(н + 2, к) + Кол(н * 3, к)

Еще большую универсальность функции придает тот факт, что она может быть использована и при трех командах в системе команд исполнителя. В таких случаях в команде если, в которой происходят рекурсивные вызовы, должны быть учтены все команды.

Именно такую функцию мы будем использовать далее.

23.2.4. Задачи для самостоятельного решения

1. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1 2. Возвести в квадрат

Первая команда увеличивает число на экране на 1, вторая – возводит его в квадрат.

Сколько существует программ, которые преобразуют исходное число 3 в число 56?

2. У исполнителя есть три команды, которым присвоены латинские буквы:

А. Прибавить 1

В. Умножить на 2

С. Умножить на 3

Первая команда увеличивает число на экране на 1, вторая – умножает его на 2, третья – умножает его на 3.

Сколько существует программ, которые преобразуют исходное число 2 в число 44?

23.3. Примеры заданий и методика их выполнения

23.3.1. Пример 1

(задание из демонстрационных вариантов ЕГЭ 2020 и 2022 гг.)

Условие

Исполнитель преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Программа для исполнителя – это последовательность команд.

Сколько существует программ, для которых при исходном числе 1 результатом является число 20, при этом траектория вычислений содержит число 10?

Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8,

16, 17^{^[66]}.

Решение

Анализ условия показывает, что в нем идет речь о задаче, которая в разделе 23.1 названа «задача “начальное – обязательное – конечное”».

Рассуждения при ее решении такие.

Все программы обязательно должны обеспечивать расчет числа 10. Количество таких программ можно определить с помощью функции Кол, описанной в конце раздела 23.2.

Вторая часть задачи – определение количества программ для получения числа 20 при начальном числе 10. Учитывая универсальность функции Кол, ее можно применить и в этом случае, а общее искомое значение может быть определено как произведение двух частных результатов: вывод Кол(1, 10) * Кол(10, 20)

Заметим, что вторая задача может быть решена без использования программ. Так как 20 в два раза больше числа 10, то оно может быть получено двумя способами:

1) при умножении на 2 (в каждую из программ с траекторией, включающей число 10, добавится команда 2);

2) при 10-кратном увеличении на 1 (в каждую из программ с траекторией, включающей число 10, добавится десять команд 1).

Это значит, что общее искомое количество программ можно определить так:

Кол(1, 10) * 2 Ответ: 28.

23.3.2. Пример 2

Условие

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Сколько существует программ, для которых при исходном числе 1 результатом является число 45, при этом траектория вычислений содержит число 10?

Комментарии к решению

Отличие решения данной задачи от рассмотренной в предыдущем пункте – в поиске количества программ для получения из числа 10 числа 45. В этом случае без программы это количество определить сложно. Лучше использовать ту же рекурсивную функцию.

Решите задачу самостоятельно.

23.3.3. Пример 3

Условие

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1 2. Умножить на 2

Сколько существует программ, для которых при исходном числе 6 результатом является число 60, при этом траектория вычислений содержит число 10?

Комментарии к решению: здесь отличие – в значении начального числа.

Решите задачу самостоятельно.

23.3.4. Пример 4

Условие

У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

3. Умножить на 3

Сколько существует программ, которые преобразуют исходное число 2 в число 44 и при этом траектория вычислений содержит число 13?

Комментарии к решению

Отличие решения в том, что в функции Кол должна учитываться приведенная в условии система команд исполнителя.

Решите задачу самостоятельно.

Сделанные рассуждения позволяют сделать вывод о том, что для решения задачи вида «Сколько существует программ, для которых при исходном числе н результатом является число к, при этом траектория вычислений содержит число обяз» должна использоваться функция Кол, а искомое значение определяется по формуле:

Кол(н, обяз) * Кол(обяз, к)

При двух «обязательных» промежуточных числах искомый результат определяется как произведение трех соответствующих количеств.

23.3.5. Пример 5

Условие

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1 2. Умножить на 2

Сколько существует программ, для которых при исходном числе 1 результатом является число 45, при этом траектория вычислений не содержит число 12?

Решение

Анализ условия показывает, что в нем идет речь о задаче, которая в разделе 23.1 названа «задача “начальное – конечное – кроме”».

В условии задания есть требование о том, что траектория вычислений не должна содержать число 12. Как учесть это требование? Можно для решения задачи использовать уже упоминавшуюся рекурсивную функцию Кол, внеся в нее следующие изменения:

1) в описании функции использовать еще один аргумент – значение кроме (число, которого не должно быть в траектории выполнения программ);

2) нужно рассмотреть также вариант, при котором текущее значение аргумента н равно значению кроме (функция должна не учитывать этот вариант и возвращать нулевое значение).

Соответствующая измененная функция:

алг цел Кол2(арг цел н, к, кроме) нач если н = кроме то знач := 0 все если н > к то знач := 0 все если н = к то знач := 1 все знач := Кол2(н + 1, к, кроме) + Кол2(н * 2, к, кроме) кон

Варианты, возвращающие нулевое значение функции, можно объединить:

алг цел Кол2(арг цел н, к, кроме) нач

если н = кроме или н > к то знач := 0 все если н = к то

знач := 1 все знач := Кол2(н + 1, к, кроме) + Кол2(н * 2, к, кроме) кон

При вызове этой функции надо указать три фактических значения аргумента:

вывод Кол2(1, 45, 12)

23.3.6. Пример 6

Условие

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Сколько существует программ, для которых при исходном числе 5 результатом является число 45, при этом траектория вычислений не содержит числа 13 и 33?

Решение

Здесь в условии фигурируют два «недопустимых» числа. Что должно измениться в разработанной чуть выше функции Кол2? – Ответ:

1) в описании функции использовать два аргумента – кроме1 и кроме2;

2) в первом неполном условном операторе указать значения кроме1 и кроме2.

Соответствующая измененная функция:

алг цел Кол2(арг цел н, к, кроме1, кроме2) нач если н = кроме1 или н = кроме2 или н > к то …

Решите задачу самостоятельно.

23.3.7. Пример 7

(задание из демонстрационных вариантов ЕГЭ 2021 и 2023 гг.)

Условие

У исполнителя есть две команды, которые обозначены латинскими буквами:

А. Прибавить 1

В. Умножить на 2

Сколько существует программ, для которых при исходном числе 1 результатом является число 35, при этом траектория вычислений содержит число 10 и не содержит 17?

Решение

Это задача, которую в разделе 23.1 мы назвали «задача “начальное – конечное – кроме”». Ее можно разделить на две подзадачи:

1) определить количество программ для получения из числа 1 числа 10;

2) определить количество программ для получения из числа 10 числа 35, траектория вычислений которых не содержит число 17,

– после чего найти произведение найденных количеств.

Первую подзадачу можно решить с помощью функции Кол:

Кол 5(1, 10) а вторую – с использованием функции Кол2, приняв в качестве начального значения «обязательное» число 10:

Ко 5л2(10, 35, 17)

23.3.8. Пример 8

Условие

У исполнителя есть две команды, которые обозначены латинскими буквами:

А. Прибавить 1

В. Умножить на 2

Сколько существует программ, для которых при исходном числе 1 результатом является число 45, при этом траектория вычислений содержит число 20 и не содержит число 8?

Решение

Здесь также надо решить две подзадачи:

1) определение количества программ для получения из числа 1 числа 20 без учета программ, траектория вычислений которых содержит число 8;

2) определение количества программ для получения из числа 20 числа 45.

Эти подзадачи решаются с использованием, соответственно, функций

Кол2 и Кол.

Вывод: для решения задачи вида «Сколько существует программ, для которых при исходном числе н результатом является число к, при этом траектория вычислений содержит число обяз и не содержит число кроме» должно использоваться одно из двух выражений:

Кол(н, обяз) * Кол2(обяз, к, кроме)

или

Кол2(н, обяз, кроме) * Кол(обяз, к)

(В каком случае какое выражение – установите самостоятельно.)

Конечно, вместо обозначений чисел должны указываться фактические значения аргументов функций.

Чтобы не разрабатывать две функции (Кол и Кол2), можно для решения обеих подзадач использовать функции Кол2, а при определении количества программ, в которых число кроме не требуется не учитывать, указывать в качестве фактического значения аргумента кроме какое-то условное значение (0, 1000 или т. п.):

Кол2(н, обяз, 0) * Кол2(обяз, к, кроме)

или

Кол2(н, обяз, кроме) * Кол2(обяз, к, 0)

23.3.9. Пример 9

(задание из демонстрационного варианта ЕГЭ 2024 г.)

Условие

У исполнителя есть три команды, которые обозначены латинскими буквами:

A. Прибавить 1

B. Умножить на 2

C. Возвести в квадрат

Сколько существует программ, для которых при исходном числе 2 результатом является число 20, при этом траектория вычислений не содержит числа 11?

Комментарии к решению

Анализ показывает, что по условию требуется решить задачу, которая в разделе 23.1 названа «задача “начальное – конечное – кроме”». Такую задачу мы решали в п. 23.3.5. Естественно, в данном случае надо учесть другую систему команд исполнителя.

Решите задачу самостоятельно.

23.4. Задачи для самостоятельного решения

1. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Первая команда увеличивает число на экране на 1, вторая – умножает его на 2.

Сколько существует программ, которые преобразуют исходное число 1 в число 32 и при этом траектория вычислений содержит число 12?

2. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1 2. Умножить на 2

3. Прибавить 5

Первая команда увеличивает число на экране на 1, вторая – умножает его на 2, третья – увеличивает на 5.

Сколько существует программ, которые преобразуют исходное число 1 в число 28 и при этом траектория вычислений содержит число 9?

3. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1 2. Умножить на 3

3. Прибавить 3

Первая команда увеличивает число на экране на 1, вторая – умножает его на 3, третья – увеличивает на 3.

Сколько существует программ, которые преобразуют исходное число 1 в число 49 и при этом траектория вычислений содержит числа 10 и 15?

4. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 2

2. Прибавить 3

3. Умножить на 3

Первая команда увеличивает число на экране на 2, вторая – увеличивает на 3, третья – умножает его на 3.

Сколько существует программ, для которых при исходном числе 3 результатом является число 35 и при этом траектория вычислений не содержит числа 9 и 16?

5. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1 2. Умножить на 2

Первая команда увеличивает число на экране на 1, вторая – умножает его на 2.

Сколько существует программ, которые преобразуют исходное число 1 в число 38 и при этом траектория вычислений содержит число 11 и не содержит число 18?

6. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1

2. Прибавить 2

3. Умножить на 3

Первая команда увеличивает число на 1, вторая – на 2, третья – втрое.

Сколько существует таких программ, которые исходное число 2 преобразуют в число 29 и при этом траектория вычислений содержит число 9 и не содержит число 12?

Глава 22 Задания 24

22.1. Общие вопросы

В Спецификации [1] применительно к заданию 24 в качестве проверяемого элемента содержания указывается «умение создавать собственные программы (10–20 строк) для обработки символьной информации».

• Уровень сложности задания: – В (высокий).

• Максимальный балл за выполнение задания: – 1.

• Примерное время выполнения задания: – 18 мин.

Задание выполняется с использованием прилагаемого файла.

***

В демонстрационных вариантах ЕГЭ по информатике нескольких последних лет представлены задания 24, общий вид которых следующий:

«Текстовый файл состоит из символов <…>. Определите в прилагаемом файле максимальное количество идущих подряд символов (длину непрерывной подпоследовательности) …» (далее указывается, какими свойствами обладает подпоследовательность и что для выполнения этого задания следует написать программу).

При описании методики выполнения заданий наряду с термином «подпоследовательность» будем использовать термин «подстрока» и фразу «цепочка символов».

22.2. Примеры заданий и методика их выполнения

22.2.1. Пример 1

Условие

Текстовый файл состоит не более чем из 10⁶ латинских букв A, B и C, в которых есть несколько подпоследовательностей строк (цепочек символов) из букв А. Определите количество букв в самой длинной из них.

Решение

Начнем с варианта этого задания, в котором примем, что все символы файла записаны в заданной строке.

Для решения задачи надо определить максимальное из чисел – длин каждой подстроки (цепочек) букв А. Пусть заданная строка имеет вид:

ААВВАААСВССАААААААВВСВСССААСАААВВССААА

Как решает аналогичную задачу человек? – Его действия можно описать такой схемой:

1. Он просматривает каждую отдельную букву (слева направо). если это буква А то (цепочка букв А началась или продолжается) увеличивает длину текущей цепочки на 1

иначе (текущая цепочка букв А закончилась или не начиналась^{^[67]}) Сравнивает длину закончившейся цепочки со «старым» значением максимальной длины если длина закончившейся цепочки больше «старого» значения максимальной длины то в качестве значения максимальной длины запоминает длину закончившейся цепочки все

Готовится в будущем определять длину новой цепочки

(пока ее длина равна 0) все

2. Если в конце строки также оказалась цепочка из букв А, то он сравнивает её длину с максимальной длиной и при необходимости запоминает эту длину в качестве искомой максимальной^{^[68]}.

Разработаем соответствующую программу.

Используем в ней следующие переменные величины:

ст – обрабатываемая строка;

н – порядковый номер символа строки в памяти компьютера; тек_длина^{^[69]} – длина текущей цепочки букв А; макс_длина – искомая максимальная длина.

Итак, программа:

алг нач лит ст, цел тек_длина, макс_длина, н ввод ст тек_длина := 0 | Начальные макс_длина := 0 | значения нц для н от 1 до длин(ст) если ст[н] = "А" то | Цепочка началась или продолжается | Увеличиваем ее длину тек_длина := тек_длина + 1 иначе | Цепочка закончилась или не начиналась | Сравниваем ее длину со значением макс_длина если тек_длина > макс_длина то | Запоминаем новое значение макс_длина := тек_длина все | Готовимся к определению длины очередной цепочки тек_длина := 0 все кц | В любом случае проверяем длину последней цепочки букв А

| (если в конце строки нет цепочки букв А, то будет сравнение | значения макс_длина с нулем) если тек_длина > макс_длина^{^[70]} то макс_длина := тек_длина все | Выводим ответ вывод макс_длина кон

(О функции длин см. главу 12.)

Заметим, что в [4] приведен несколько более компактный вариант алгоритма решения задач, аналогичных обсуждаемой:

1. Начальные значения длины текущей цепочки

и искомой максимальной длины принимаются равными нулю

2. Цикл для каждого символа строки если он совпадает с заданным символом то

Длина текущей цепочки соответствующих символов увеличивается на 1

Полученная длина текущей цепочки сравнивается со «старой» максимальной длиной если полученная длина больше максимальной то

Длина текущей цепочки принимается в качестве максимальной все

иначе (очередной символ не совпадает с заданным символом) Начальное значение текущей длины очередной цепочки принимается равным нулю все конец цикла

Соответствующая программа (применительно к задаче, связанной с буквой А) оформляется так:

алг нач лит ст, цел тек_длина, макс_длина, н ввод ст тек_длина := 0 макс_длина := 0 нц для н от 1 до длин(ст) если ст[н] = "А" то | Цепочка букв А началась или продолжается | Увеличиваем ее длину тек_длина := тек_длина + 1 | Сравниваем если тек_длина > макс_длина то | Запоминаем новое значение макс_длина := тек_длина все иначе | Цепочка букв А закончилась или не начиналась | Готовимся к определению длины очередной цепочки букв А тек_длина := 0 все

кц вывод макс_длина кон

Особенность приведенного алгоритма в том, что проверка на максимум и при необходимости его изменение проводятся после «встречи» каждого требуемого символа, а не только после окончания цепочки нужных символов.

И еще важное замечание. Если на экзамене будет предложена задача нахождения порядкового номера цепочки максимальной длины, то решать её на основе «компактного» варианта, предложенного в [4], нельзя.

Обсудим выполнение задания в случае записи последовательности символов в текстовом файле.

Если применяемый используемый язык программирования допускает использование величин строкового типа размером до 1 млн и более символов (как, например, язык Python), то целесообразно сначала записать все символы из файла в строковую переменную, после чего обработать ее согласно описанной методике.

Если же язык программирования этого не допускает, то обработку последовательности символов следует проводить сразу после чтения каждого из них из файла. Опишем этот вариант.

В приведенной ниже программе переменная с – очередной прочитанный из файла символ.

алг нач файл ф, сим с, цел тек_длина, макс_длина тек_длина := 0 макс_длина := 0 ф := открыть на чтение("…") нц пока не конец файла(ф) | Читаем очередной символ с файла ввод ф, с | и исследуем его если с = "А" то тек_длина := тек_длина + 1 иначе если тек_длина > макс_длина то

макс_длина := тек_длина все тек_длина := 0 все

все кц если тек_длина > макс_длина то макс_длина := тек_длина все закрыть(ф) вывод макс_длина кон

Программу, основанную на «компактном» алгоритме из [4], разработайте самостоятельно.

22.2.2. Пример 2

Условие

Текстовый файл состоит из не более чем из 10⁶ латинских букв A, C и D. Определите максимальное количество идущих подряд символов, среди которых нет символов D. В качестве исходных данных используйте файл, приложенный к заданию 24 в демонстрационном варианте ЕГЭ 2023 года.

Решение

Здесь логика действий аналогична описанной применительно к предыдущему заданию. Отличие в условии, определяющем продолжение учитываемых цепочек символов, – очередной символ не является буквой D.

22.2.3. Пример 3

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Текстовый файл состоит из символов P, Q, R и S. Определите максимальное количество идущих подряд символов в прилагаемом файле, среди которых нет идущих подряд символов P.

Решение

Здесь надо обратить внимание на слово «подряд» в условии. Это означает, что если встретятся идущие подряд два символа Р, то учитываемая цепочка закончилась. Можно также сказать, что учитываемая цепочка продолжается, если очередной символ не является буквой Р или предшествующий ему не является этим символом (вспомните законы логики). В свою очередь, это значит, что в программе должны сравниваться два соседних символа.

Еще одна особенность: любой первый символ строки или файла (даже если это буква Р) должен учитываться в нужной цепочке.

Фрагмент программы, в котором находится искомое значение в строке символов ст, прочитанной из заданного файла и который основан на «компактном» алгоритме:

тек_длина := 1 | Начальные значения макс_длина := 0 | переменных нц для н от 2 до длин(ст) | Начинаем со 2-го символа если ст[н - 1] <> "P" или ст[н] <> "P" то | "Правильная" цепочка букв продолжается | Увеличиваем ее длину тек_длина := тек_длина + 1 | Сравниваем если тек_длина > макс_длина то | Запоминаем новое значение макс_длина := тек_длина все иначе | Встретилась такая же буква Р | "Правильная" цепочка букв кончилась

| Встретившаяся буква Р может быть | началом очередной "правильной" цепочки! тек_длина := 1 все кц

В варианте программы, обрабатывающей символы файла по одному, используем две новые переменные величины:

очер – очередной прочитанный символ; пред – символ, прочитанный перед ним.

По мере прочтения символов из файла значение переменной очер «передается» переменной пред, после чего переменная очер получает новое (прочитанное) значение.

Итак, программа:

алг

нач файл ф, сим очер, пред, цел тек_длина, макс_длина макс_длина := 0 ф := открыть на чтение("24.txt") | Читаем 1-й символ ввод пред

| Учитываем его в цепочке тек_длина := 1 | Остальные символы нц пока не конец файла(ф) | Читаем очередной символ очер файла ввод ф, очер | и исследуем его если очер <> "Р" или пред <> "Р" то тек_длина := тек_длина + 1 иначе если тек_длина > макс_длина то макс_длина := тек_длина все тек_длина := 1 | 2-й (очер) символ все все | "Передаем" значение пред := очер кц если тек_длина > макс_длина то макс_длина := тек_длина все закрыть(ф) вывод макс_длина кон

22.2.4. Пример 4

Условие

Текстовый файл состоит не более чем из 1 200 000 символов X, Y, и Z. Определите максимальное количество идущих подряд символов, среди которых нет подстроки XYZ. В качестве исходных данных используйте файл, приложенный к заданию 24 в демонстрационном варианте ЕГЭ 2021 года.

Решение

Здесь условие, при котором исследуемая цепочка символов продолжается (или началась), можно установить по аналогии с предыдущей задачей^{^[71]}.

Оно такое: не (стр[ном - 2] = "X" и стр[ном - 1] = "Y" и стр[ном] = "Y")

или

стр[ном - 2] <> "X" или стр[ном - 1] <> "Y" или стр[ном] <> "Z"

При обработке символов из файла следует:

• использовать три переменные величины, аналогичные переменным очер и пред (см. предыдущий пример);

• перед обработкой символов в цикле прочитать первые три символа файла и присвоить их значения указанным переменным;

• после проверки каждой очередной группы из трех символов читать следующие три символа или читать один очередной символ и менять значения трех используемых переменных.

22.2.5. Пример 5

Условие

Текстовый файл состоит из латинских букв. Найдите длину самой длинной цепочки, состоящей из одинаковых символов. В качестве исходных данных используйте файл, приложенный к заданию в демонстрационном варианте ЕГЭ 2022 года.

Решение

Вспомним решение примера 1. Там, когда заканчивалась нужная цепочка (символов А), мы «ждали» новую такую же цепочку. В данной задаче цепочка, следующая за какой-то окончившейся цепочкой, тоже может быть подходящей. Это значит, что нужно по окончании каждой цепочки запоминать символ следующей цепочки и учитывать именно его.

В приведенном ниже фрагменте программы, в котором находится искомое значение максимальной длины цепочки в строке символов ст, имя меняющегося учитываемого символа – с.

с := ст[1] тек_длина := 1 макс_длина := 0 нц для н от 2 до длин(ст) если ст[н] = ст[н - 1] то

тек_длина := тек_длина + 1 иначе

если тек_длина > макс_длина то макс_длина := тек_длина все тек_длина := 1 | Началась новая подстрока | возможных одинаковых соседних символов с := ст[н] все кц если тек_длина > макс_длина то макс_длина := тек_длина все

22.2.6. Пример 6

Условие

Текстовый файл состоит из латинских букв. Выведите символ, из которого строится цепочка максимальной длины. Если в файле есть несколько цепочек самой большой длины, то найти следует символ последней из таких цепочек. В качестве исходных данных используйте файл, приложенный к заданию в демонстрационном варианте ЕГЭ 2022 года.

Решение

Все действия аналогичны описанным применительно к предыдущему заданию. Отличия:

• после «встречи» очередной цепочки максимальной длины нужно запомнить также символ из этой цепочки (его имя в программе с_макс);

• чтобы был учтен символ последней цепочки максимальной длины, условие при проверке длин цепочек должно быть таким: тек_длина >= макс_длина

Соответствующий измененный фрагмент программы:

если тек_длина >= макс_длина то макс_длина := тек_длина | Запоминаем также символ текущей цепочки с_макс := с все

22.2.7. Пример 7

(задание из демонстрационного варианта ЕГЭ 2021 года)

Условие

Текстовый файл состоит не более чем из 10⁶ символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых каждые два соседних различны.

Решение

Отличие данного задания от задания примера 5 в том, что искомая цепочка состоит не из одинаковых соседних символов, а из разных. Соответственно, условие для учета очередного символа в цепочке будет таким:

ст[н] <> ст[н - 1].

22.2.8. Пример 8

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов вида согласная + гласная в прилагаемом файле. Для выполнения этого задания следует написать программу.

Решение

Здесь также надо определить максимальное из чисел – длин цепочек пар символов вида «согласная + гласная». Что меняется в таком случае в приведенных выше алгоритмах и программах?

Для случая обработки предварительно прочитанной из файла строки символов меняется характер «прохода» по строке. Остановимся на этом подробно.

После прочтения двух подряд идущих символов строки (н-го и (н + 1)-го) возможны четыре варианта их сочетания:

1) согласная + согласная (например, DD);

2) согласная + гласная (DA); 3) гласная + согласная (AD); 4) гласная + гласная (AA).

Второй вариант подходит – его надо учесть и пропустить два символа, после чего продолжить обработку строки.

В четвертом варианте нужно просто пропустить два «неподходящих» символа.

В остальных вариантах пропускать два символа нельзя (вторая буква D может быть частью подходящей пары). В этом случае надо пропустить один символ.

Чтобы не усложнять программу (не рассматривать все варианты), можно так определить особенности «прохода» по строке:

• если встретилась пара символов вида «согласная + гласная», то надо пропустить оба этих символа;

• в противном случае – пропустить только один символ и снова рассматривать очередную пару.

Это значит, что обработка строки должна проводиться с использованием не оператора цикла с параметром, а с помощью оператора цикла с условием.

Так как последние два символа могут составлять подходящую пару, то это условие такое:

н < длин(ст)

где н – номер «левого» символа в паре сравниваемых, ст – обрабатываемая строка символов.

И конечно, надо учесть особенности изменения переменной н (своеобразного указателя на очередной символ строки), которые отмечались чуть выше.

Другие используемые в программе переменные величины:

• кол_пар – количество пар, удовлетворяющих условию; • макс – искомое значение максимального количества пар.

В комментариях программы будем использовать термин «цепочка пар» (группа идущих подряд пар символов, соответствующих заданному условию).

Итак, программа:

алг

нач файл ф, лит ст, цел н, тек_длина, макс_длина ф := открыть на чтение("24.txt") ввод ф, ст закрыть(ф) макс := 0 кол_пар := 0 н := 1 нц пока н < длин(с) если (cт[н] = "C" или cт[н] = "D" или cт[н]= "F") и (cт[н +1] = "A" или cт[н + 1]= "O")^{^[72]} то | Встретилась еще одна пара подходящих символов кол_пар := кол_пар + 1 | Смещаем "указатель" на 2 символа н := н + 2 иначе | Цепочка подходящих пар кончилась (или не начиналась) | Проверяем ее длину если кол_пар > макс то макс := кол_пар все кол_пар := 0 | Смещаем "указатель" на 1 символ н := н + 1 все кц | Проверяем возможную последнюю цепочку если кол_пар > макс то макс := кол_пар все | Выводим ответ вывод нс, макс кон

В целях сокращения записи условия проверки типа пары «согласная + гласная» целесообразно разработать и использовать две вспомогательные функции логического типа, проверяющие, является ли некоторая буква, соответственно, согласной и гласной. В приведенных ниже функциях на школьном алгоритмическом языке их результат определяется с помощью оператора логического присваивания:

алг лог Согласная(арг сим буква) нач | Значение функции:

знач := буква = "C" или буква = "D" или буква = "F" кон алг лог Гласная(арг сим буква) нач знач := буква = "A" или буква = "O" кон

В программах на языках программирования, в которых величины логического типа не предусмотрены, результат функции (например, 1 или 0) определяется с помощью полного условного оператора следующего вида:

если буква = "C" или буква = "D" или буква = "F" то значение функции равно 1 иначе

значение функции равно 0

если буква = "A" или буква = "O" то значение функции равно 1 иначе значение функции равно 0 все

С использованием этих функций команда если в основной программе записывается короче:

если Согласная(ст[н]) и Гласная(ст[н + 1]) то …

Мы рассмотрели выполнение задания для случая обработки предварительно прочитанной из файла строки. При обработке символов файла по одному будем использовать в программе две новые переменные:

лев – «левый» элемент в паре сравниваемых; прав – то же, «правый».

Другие особенности программы приведены в комментариях.

алг нач файл ф, сим лев, прав, цел кол_пар, макс ф := открыть на чтение("24 txt") макс := 0 кол_пар := 0 | Читаем два первых символа файла ввод ф, лев ввод ф, прав нц пока не конец файла(ф) если Согласная(лев) и Гласная(прав) то кол_пар := кол_пар + 1

| Читаем два следующих символа

ввод ф, лев ввод ф, прав иначе если кол_пар > макс то макс := кол_пар все кол_пар := 0 | В следующей проверяемой паре бывший "правый" символ | станет "левым" лев := прав | Новый "правый" символ читаем из файла ввод ф, прав все кц закрыть(ф) если кол_пар > макс то макс := кол_пар все вывод нс, макс кон

Внимание! При выполнении приведенного варианта программы может возникнуть ошибка, связанная с выходом за пределы файла. Например, если последние три символа файла СОF^{^[73]}, то после чтения и учета «подходящей» пары СО прочитать два символа нельзя. Это означает, что чтение «правого» элемента очередной пары должно проходить не всегда, а только при условии, что не достигнут конец читаемого файла:

… нц пока не конец файла(ф) если Согласная(лев) и Гласная(прав) то кол_пар := кол_пар + 1 | Читаем два следующих символа ввод ф, лев если не конец файла(ф) то ввод ф, прав все

иначе …

22.2.9. Пример 9

Условие

Текстовый файл состоит из символов A, C, D, F и O. Определите максимальное количество идущих подряд пар символов, среди которых не более одной буквы D. В качестве исходных данных используйте файл, приложенный к заданию в демонстрационном варианте ЕГЭ 2023 года.

Решение

Это задание отличается тем, что некоторые буквы D надо учитывать в текущей длине цепочки, а другие – нет. Какие не следует? – Которые в текущей цепочке не первые. Значит, нужно использовать переменнуюсчетчик количества встретивших букв D в некоторой цепочке (колD).

Итак, возможны следующие варианты:

1) если очередной символ – не D, то цепочка продолжается или началась;

2) если очередной символ – буква D, то:

если это первая такая буква в текущей цепочке, то

цепочка продолжается или началась, иначе цепочка закончилась.

Остальные особенности действий в каждом из этих вариантов описаны в комментариях к приведенной ниже программе.

алг нач файл ф, сим с, цел тек_длина, макс_длина,колD ф := открыть на чтение("24.txt") макс_длина := 0 тек_длина := 0 колD := 0 нц пока не конец файла(ф) ввод ф, с если с <> "D" то

тек_длина := тек_длина + 1 все если с = "D" то

колD := колD + 1 если колD = 1 то тек_длина := тек_длина + 1 иначе | 2-я буква D если тек_длина > макс_длина то макс_длина := тек_длина все тек_длина := 1 | 2-я буква будет началом | следующей цепочки колD := 1 все все кц закрыть( ф) если тек_длина > макс_длина то макс_длина := тек_длина все вывод нс, макс_длина кон

22.2.10. Задания для самостоятельного выполнения

1. Текстовый файл состоит из символов латинского алфавита A, C, D, F и O. Определите:

а) длину самой длинной цепочки, состоящей из символов A, D или C (в произвольном порядке);

б) наибольшую длину цепочки, не содержащей символы D и F;

в) наибольшую длину цепочки символов, среди которых нет символов С и F, стоящих рядом;

г) максимальное количество идущих подряд пар символов вида

«согласная + согласная + гласная»;

д) наибольшую длину цепочки символов, среди которых не более двух букв F.

Во всех случаях в качестве исходных данных используйте файл, приложенный к заданию в демонстрационном варианте ЕГЭ 2023 года.

2. Дана строка символов, среди которых есть цифры. Определите длину самой длинной цепочки, состоящей из цифр.

3. Дана строка символов из одних цифр. Определите длину самой длинной цепочки, цифры которой образуют неубывающую последовательность.

Выполните также все задания, рассмотренные выше, разработав программу на языке программирования, которым владеете.

22.3. Задание из демонстрационного варианта ЕГЭ по информатике 2024 года

Мы выделили методику выполнения указанного задания, поскольку она принципиально отличается от приведенных в предыдущем разделе.

22.3.1. Условие

Текстовый файл состоит из символов T, U, V, W, X, Y и Z. Определите в прилагаемом файле максимальное количество идущих подряд символов (длину непрерывной подпоследовательности), среди которых символ T встречается ровно 100 раз. Для выполнения этого задания следует написать программу.

22.3.2. Подготовка к выполнению задания

Прежде всего покажем, о каких подпоследовательностях идет речь в условии. Сделаем это на простом примере – когда вместо числа 100 надо учитывать число 3.

Пусть начало последовательности символов в файле такое, как в таблице:

…

Рис. 22.1

Ряд подходящих по условию подпоследовательностей показан на рис. 22.2:

…

Рис. 22.2

Один из возможных вариантов решения задачи состоит в следующем:

1) записать все символы файла в строковую переменную;

2) для каждого i-го символа строки определить позицию 101-го по счету символа Т, расположенного после i-го (то есть определить, когда закончится подходящая подпоследовательность). Сравнив длины всех таких подпоследовательностей, можно найти длину самой большой из них.

Соответствующая программа по сути будет основана на двойном (полном и неполном) переборе всех возможных подпоследовательностей. Учитывая, что в файле, приложенном к обсуждаемому заданию, общее количество символов составляет более 9 млн, а также число 100 в условии, поиск результата потребует значительного времени.

Лучшим является вариант программы, основанный на следующих рассуждениях, которые сделаем применительно к рис. 22.1–22.2.

Первая подпоследовательность начинается с начала и заканчивается «до» четвертой по счету буквы Т.

Остальные несколько подпоследовательностей опишем с помощью таблицы:

Подпоследовательность	Начинается	Заканчивается
2-я	С первого символа после 1-й буквы Т	Символом «до» 5-й по счету буквы Т
3-я	С первого символа после 2-й буквы Т	Символом «до» 6-й по счету буквы Т
4-я	С первого символа после 3-й буквы Т	Символом «до» 7-й по счету буквы Т
…	…	…

Сравнив длины всех таких подпоследовательностей, можно найти длину самой большой из них.

22.3.3. Решение

Разработаем программу, работающую на основе сделанных рассуждений.

Итак, для нахождения искомого значения надо знать порядковый номер каждого символа Т в файле. Для хранения этих номеров в программе будем использовать массив с именем мас_ном. Размер этого массива должен быть принят достаточно большим (см. выше о размере файла), а для определения фактического количества символов Т в программе будем использовать переменную с именем колТ. Фрагмент программы, в котором происходит заполнение массива мас_ном, имеет вид^{^[74]}:

колТ := 0 ном := 0 ф := открыть на чтение("24.txt") нц пока не конец файла(ф) ном := ном + 1 | Номер очередного символа файла ввод ф, с если с = "T" то колТ := колТ + 1 мас_ном[колТ] := ном все кц закрыть(ф)

Дальше логика такая. Первая интересующая нас подпоследовательность из 100 символов Т начинается с первого символа файла и закончится символом, расположенным «до» 101-й по счету буквы Т. Ее длина составит мас_ном[101] – 1. Это значение можно принять в качестве начального значения искомой максимальной длины макс_длина.

Затем рассматриваем второй, третий и остальные символы Т, для каждого из них определяем длину подпоследовательности, в которой символ T встречается ровно 100 раз, и определяем максимальное значение длины.

Как найти длину подпоследовательности для некоторого i-го по счету символа T? Вспомнив рассуждения, сделанные для простого случая (см. таблицу выше), можем сказать, что эта подпоследовательность начинается с символа с номером в файле мас_ном[i – 1] + 1 и заканчивается символом номер мас_ном[i + 100] – 1. Длина такой последовательности равна:

(мас_ном[i + 100] – 1) – (мас_ном[i – 1] + 1) + 1

или

мас_ном[i + 100] – мас_ном[i – 1] – 1.

Фрагмент программы для нахождения искомого значения максимальной длины интересующей нас подпоследовательности может быть оформлен так:

нц для i от 2 до кол_Т – 101 | Определяем длину подпоследовательности | для i-го по счету символа Т длина := мас_ном[i + 100] – мас_ном[i – 1] – 1 | Сравниваем ее с текущим значением максимальной длины если длина > макс_длина то макс_длина := длина все кц

Внимание! В приведенном фрагменте не была рассмотрена подпоследовательность, включающая последний по счету символ Т (убедитесь в этом!). Эта последовательность может оказаться самой длинной. И хотя в файле, приложенном к обсуждаемому заданию, она такой не является, в общем случае надо учесть и ее.

Рассмотрев, как и в начале, простой вариант последовательности символов файла:

Последний символ

можем сказать, что в общем случае последняя последовательность начинается с символа с номером мас_ном[колТ – 100] + 1 и заканчивается последним символом файла (его номер равен значению переменной ном). Длина такой последовательности равна:

ном – (мас_ном[колТ – 100] + 1) + 1 = ном – мас_ном[колТ – 100] – 1.

Эту длину после окончания оператора цикла следует также сравнить с текущим значением максимальной длины и при необходимости уточнить последнее значение.

22.3.4. Обобщение

Описанная методика выполнения задания, естественно, может быть применена и для нахождения минимальной длины соответствующей подпоследовательности.

Кроме того, ее можно использовать и для выполнения таких заданий^{^[75]}:

«Текстовый файл состоит из символов T, U, V, W, X, Y и Z. Определите в прилагаемом файле максимальное количество идущих подряд символов (длину непрерывной подпоследовательности), среди которых символ Т встречается не более N раз» (вместо N указывается конкретное число).

Анализ рис. 22.1–22.2 показывает, что подпоследовательности, в которых буква Т встречается три раза, включают в себя подпоследовательности с двумя и одной буквой Т. Так как числа 1, 2, 3 удовлетворяют условию «не более трех», то максимальную длину будет иметь одна из подпоследовательностей с тремя буквами Т.

Распространяя рассуждения на указанное чуть выше задание, можем сказать, что искомое в нем количество равно длине самой большой подпоследовательности, в которой символ Т встречается ровно N раз. Задачу нахождения длины такой подпоследовательности мы решали в начале статьи.

Отдельно рассмотрим также такую задачу:

Ее можно решить с помощью приведенной программы, заменив все числа 100 в ней на 0. Но проще использовать решения, описанные в предыдущем разделе.

22.3.5. Задания для самостоятельного выполнения

Разработайте программу для выполнения обсуждаемого задания на языке программирования, которым владеете.

Найдите также минимальное количество идущих подряд символов (длину непрерывной подпоследовательности), среди которых символ Т встречается 50 раз.

Глава 23 Задания 25

23.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 25 указывается «умение создавать собственные программы (10–20 строк) для обработки целочисленной информации».

• Уровень сложности задания – В (высокий).

• Максимальный балл за выполнение задания – 1.

• Примерное время выполнения задания – 20 мин.

***

В демонстрационном варианте ЕГЭ по информатике 2023 года^{^[76]} было представлено следующее задание: «Назовем маской числа последовательность цифр, в которой также могут встречаться следующие символы:

• символ ? означает ровно одну произвольную цифру;

• символ * означает любую последовательность цифр произвольной длины; в том числе * может задавать и пустую последовательность.

Например, маске 123*4?5 соответствуют числа 123405 и 12300405.

Среди натуральных чисел, не превышающих 10¹⁰, найдите все числа, соответствующие маске 1?2139*4, делящиеся на 2023 без остатка.

В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 2023.


…	…

Ответ:

Количество строк в таблице для ответа избыточно».

Это задание может быть выполнено двумя способами.

23.2. Первый вариант решения

Определим диапазон чисел для поиска искомых значений.

Так как символ «*» может соответствовать и пустой последовательности, а минимальная цифра, соответствующая символу «?», равна 0, то минимальное число для анализа – 1 021 394.

О максимально возможном числе.

Число 10¹⁰ выглядит так: 10 000 000 000. Перебор всех чисел от 1 021 394 до 10 000 000 000 и проверка каждого из них на соответствие условию задания потребуют значительного времени. Попробуем уменьшить количество проверяемых чисел.

Число 10 000 000 000 не соответствует маске, то есть его можно не учитывать. Без него следующее максимальное число – десятизначное, 9 999 999 999. Оно тоже не подходит. Какое максимальное десятизначное число подходит?

Вот его «обязательные» цифры:

Значит, максимальное число для поиска равно 1 921 399 994.

Но и все числа от 1 021 394 до 1 921 399 994 проверять на соответствие условию задания также нецелесообразно. Лучше проверять только те числа из указанного диапазона, которые кратны 2023. С какого числа начинать проверку?

Рекомендуем это начальное число определять так.

С помощью программы Калькулятор рассчитать частное от деления 1 021 394 на 2023. Оно будет нецелым числом (504,9), поэтому начальное значение для проверки можно принять равным 504 · 2023.

Если бы частное было целым числом, то тогда число 1 021 394 можно было бы принять в качестве начального (оно кратно 2023).

Чтобы не использовать программу Калькулятор, а в разрабатываемой программе не рассматривать два варианта, можно с некоторым «запасом» в качестве начального числа для проверки принять произведение целой части указанного частного на 2023.

Внимание! Начинать проверку с числа 2023 нельзя (почему – установите самостоятельно).

Итак, мы определили, с какого числа надо начинать проверку и что проверять надо все числа, на 2023 большие, пока проверяемое число не превышает 1 921 399 994.

К соответствующей программе мы вернемся чуть ниже, а пока обсудим, как узнать, соответствует ли некоторое не более чем десятизначное число заданной маске 1?2139*4.

Прежде всего определим, сколько цифр может быть в последовательности, в маске, обозначенной символом «*». Так как в искомых числах обязательно должны быть 7 цифр, то в этой последовательности может быть не более трех цифр или их вообще может не быть. Поэтому соответствие числа маске будет, если:

• первая цифра числа равна 1;

• третья, четвертая, пятая и шестая цифры образовывают число 2139

(вторая цифра может быть любой; ее не контролируем);

• последняя цифра числа равна 4.

(Остальные цифры, кроме перечисленных, могут быть любыми и в любом количестве, не большем трех, или их вообще может не быть.)

Чтобы проводить указанную проверку на соответствие числа маске, надо выделять его отдельные цифры (первую и последнюю) и число, образованные его третьей–шестой цифрами. Если последнюю цифру выделить достаточно легко (последняя цифра числа любой «значности» равна остатку от деления этого числа на 10), то определение первой цифры числа неизвестной «значности» и числа, образованного третьей– шестой цифрами, затруднено (хотя и возможно). Поэтому целесообразно рассматривать проверяемые числа как строку из символов-цифр.

В соответствующей программе будем использовать две переменные величины:

пров_цел – проверяемые целые числа; пров_стр – соответствующие величины строкового типа.

К первой цифре величины пров_стр можно обратиться по ее индексу: пров_стр[1].

Последнюю цифру можно получить так:

пров_стр[длин(пров_стр)]

Для выделения подстроки из третьего–шестого символов используется так называемая «вырезка из строки» (или «срез строки»), в которой указываются номера начального и конечного символов для выделения: пров_стр[3:6]

Приводя программу решения обсуждаемой задачи, заметим, что в ней для преобразования числа пров_цел в соответствующую строку символов используется функция цел_в_лит:

алг нач цел пров_цел, лит пров_стр пров_цел := div(1021394, 2023) * 2023 | Первое | проверяемое число нц пока пров_цел <= 1921399994 | Преобразуем число в строку пров_стр := цел_в_лит(пров_цел) если пров_стр[1] = "1" и пров_стр[3:6]= "2139" и пров_стр[длин(пров_стр)] = "4" то | Встретилось число, соответствующее маске

| Выводим его | и целочисленное частное от деления на 2023 вывод нс, пров_цел, " ", div(пров_цел, 2023) все | Следующее проверяемое число пров_цел := пров_цел + 2023 кц кон

• определить минимально возможное min и максимально возможное max числа, соответствующие маске;

• определить минимальное число, кратное N (согласно сделанной выше рекомендации);

• в программе в цикле с условием рассмотреть все числа, кратные N, не превышающие значение max, и каждое из них проверить на соответствие маске; при соответствии – вывести на экран текущее проверяемое число и целочисленное частное от его деления на N.

23.3. Второй вариант решения

Этот вариант основан на переборе цифр, которые могут быть представлены в проверяемом числе вместо символов «?» и «*». Как уже говорилось, вместо первого символа может быть записана любая цифра от 0 до 9, а вместо символа «*» – любое число от 0 до 999.

В программе перебрать все варианты можно с помощью вложенного цикла:

нц для цифра от 0 до 9 нц для число от 0 до 999 … кц кц

Для каждого сочетания значений переменных цифра и число нужно:

• сформировать общее число в виде строки (имя переменной, как и ранее, – пров_стр);

• преобразовать ее в число (пров_цел);

• проверить кратность полученного числа числу 2023. Если оно кратно, то вывести это число и целочисленное частное от деления этого числа на 2023.

Соответствующая программа имеет вид:

алг нач цел цифра, число, пров_цел, лит пров_стр, лог успех нц для цифра от 0 до 9 нц для число от 0 до 999 | Формируем очередное число в виде строки пров_стр := "1" + цел_в_лит(цифра) + "2139" + + цел_в_лит(число) + "4" | Преобразовываем ее в число пров_цел := лит_в_цел(пров_стр, успех) | Проверяем кратность числу 2023 если mod(пров_цел, 2023) = 0 то вывод нс, пров_цел, " ", div(пров_цел, 2023) все кц кц кон

Примечание. О функции лит_в_цел см. главу 12.

23.4. Задания для самостоятельного выполнения

Прежде чем предлагать задания, обсудим еще два типа задач, аналогичных рассмотренной, которые могут быть предложены на экзамене.

Задача 1

Среди натуральных чисел, не превышающих 10⁸, найдите все числа, соответствующие маске 18?352?9 и делящиеся на 131 без остатка.

В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им частные от деления на 131.

Комментарии к решению

Здесь задача облегчается тем, что в указанной маске отсутствует символ «*».

Диапазон чисел для поиска искомых значений: минимальное число для анализа получится, если вместо символов «?» использовать цифру 0, – 18 035 209, максимальное – при записи цифры 9: 18 935 299.

Задача 2

Среди натуральных чисел, не превышающих 10⁷, найдите все числа, соответствующие маске 7*24*5 и делящиеся на число 473 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им частные от деления на 473.

Комментарии к решению

Особенность данной задачи – в отсутствии в маске символа «?».

Минимально возможное число для анализа определяется легко (найдите его).

Каким будет максимальное число?

Указанное в условии число 10⁷ выглядит так: 10 000 000. Так как оно не соответствует маске, то его можно не учитывать. Без него следующее максимальное число – семизначное, 9 999 999. Оно тоже не подходит.

Далее рассуждаем так. Поскольку четыре цифры являются «обязательными», то на две последовательности вместо символов «*» остается 7 – 4 = 3 цифры. Поэтому для ответа на заданный вопрос рассмотрим возможные варианты количества цифр в последовательностях вместо символов «*»:

Первый символ «*»	Второй символ «*»
0	1
0	2
0	3
1	0
2	0
3	0
Первый символ «*»	Второй символ «*»
1	1
1	2
2	1

Какой вариант обеспечивает максимальное значение всего числа, установите самостоятельно.

Задания

1. Выполните задание, условие которого приведено в начале данной главы. На языке программирования, которым владеете, разработайте два варианта программы по описанным методам решения и сравните эти методы по общему времени написания и выполнения программ.

2^{^[77]}. Среди натуральных чисел, не превышающих 10⁹, найдите все числа, соответствующие маске 1?34567?9 и делящиеся на 17 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им частные от деления на 17.

3. Среди натуральных чисел, не превышающих 10⁹, найдите все числа, соответствующие маске 123*567? и делящиеся на 169 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им частные от деления на 169.

4. Среди натуральных чисел, не превышающих 10⁶, найдите все числа, соответствующие маске 12*45* и делящиеся на число 51 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им частные от деления на 51.

5. Среди натуральных чисел, не превышающих 1010, найдите все числа, соответствующие маске 1?2157*4, делящиеся на 2024 без остатка. В ответе запишите в первом столбце таблицы все найденные числа в порядке возрастания, а во втором столбце – соответствующие им результаты деления этих чисел на 2024.

Глава 24 Задания 26

24.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 26 указывается «умение обрабатывать целочисленную информацию с использованием сортировки».

• Уровень сложности задания – В (высокий).

• Максимальный балл за выполнение задания – 2.

• Примерное время выполнения задания – 35 мин.

Задание выполняется с использованием прилагаемого файла.

24.2. Примеры заданий и методика их выполнения^{^[78]}

24.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрешки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т. д. Одну коробку можно поместить в другую, если длина ее стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.

Входные данные

В первой строке входного файла находится число N – количество коробок в магазине (натуральное число, не превышающее 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое – в отдельной строке. Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.

Типовой пример организации данных во входном файле:

40 32

Пример входного файла приведен для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих для упаковки «матрешкой», составляет 3 единицы. При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т. е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.

Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемого файла.

Решение

Как решает задачи такого типа человек? Предположим, что исходные числа с размерами коробок такие:

43 29 40 20 22 44 50 51 28 45 49

Прежде всего удобно записать все числа в порядке невозрастания:

51 50 49 45 44 43 40 29 28 22 20

Далее человек смотрит на первое число (50) и запоминает (выписывает) его. После этого он рассматривает остальные числа и ищет ближайшее число, меньшее записанного на 3 или больше. Таким числом является 45. Запоминается (выписывается) это число, после чего продолжается просмотр до конца последовательности и отбираются в набор другие числа, меньшие последнего записанного числа на 3 или больше. Количество чисел в полученном наборе будет первым искомым значением, последнее число набора – вторым.

Прежде чем переходить к программной реализации описанной методики решения задачи, заметим, что в программе числа из подходящего набора запоминать не обязательно, достаточно запомнить количество чисел в нем и последнее из подходящих чисел.

И еще. Так как в программе понадобится сортировать числа из заданного файла, то следует предварительно записать числа из файла в массив (в программе на языке Python – в список), а затем обрабатывать элементы этого массива (списка).

Здесь, как и при выполнении заданий 24 (см. главу 22), возникает вопрос о размере массива и количестве чисел для обработки. В данном случае общее количество чисел в файле записано в его первой строке. Целесообразно до написания всей программы прочитать и вывести на экран только данные в первой строке файла, а затем учесть найденное значение в программе.

Учитывая все сказанное, можно описать общую схему алгоритма решения задачи следующим образом:

1. Прочитать в файле первое число (значение N) и запомнить его.

2. Записать все остальные числа из файла в массив.

3. Отсортировать элементы массива в порядке невозрастания.4. Запомнить его первое число.

5. Количество элементов в искомом наборе принять равным 1.

6. Цикл (рассматривать второй, третий, …, последний элементы массива) Если его значение меньше запомненного числа на 3 или больше то Запомнить значение рассматриваемого элемента Количество элементов в наборе увеличить на 1 все Конец цикла 7. Вывести результаты.

Для сортировки (этап 3) целесообразно использовать соответствующие стандартные функции используемых языков программирования, работающие быстрее разработанных пользователем.

Опишем действия этапов 4–7.

Будем использовать в программе следующие основные переменные величины:

м – массив для хранения чисел (размеров коробок из файла); к – количество чисел в наборе, удовлетворяющих упаковке подарка по принципу «матрешки» (первое искомое значение);

п – последнее (минимальное) число в подходящем наборе (второе искомое значение).

Итак, действия в программе, связанные с выполнением этапов 4–7 описанного выше алгоритма решения задачи, такие:

24.2.2. Пример 2

(задание из демонстрационных вариантов ЕГЭ 2021 и 2022 гг.)

Условие

Системный администратор раз в неделю создает архив пользовательских файлов. Однако объем диска, куда он помещает архив, может быть меньше, чем суммарный объем архивируемых файлов. Известно, какой объем занимает файл каждого пользователя.

По заданной информации об объеме файлов пользователей и свободном объеме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранен в архиве, при условии что сохранены файлы максимально возможного числа пользователей.

Входные данные

В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объемов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.

Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранен в архиве, при условии что сохранены файлы максимально возможного числа пользователей.

Пример входного файла:

100 4

При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объемы этих двух файлов: 30 и 40, 30 и 50 или 40 и 50. Наибольший объем файла из перечисленных пар – 50, поэтому ответ для приведенного примера:

2 50

Решение

Сначала допустим, что все числа из файла уже переписаны в массив.

Отсортируем массив в порядке возрастания.

Чтобы проиллюстрировать логику дальнейших действий, рассмотрим простой вариант – пусть при S = 11 начальные элементы массива такие:

1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 5.

Складывая значения начальных элементов и сравнивая получающуюся сумму с S, получим максимальный набор значений, сумма которых не превышает S. Это будет набор из пяти элементов, сумма значений которых равна 9. Значение 5 будет первым искомым значением по условию.

Максимальное число в наборе – 3. Означает ли это, что оно является вторым искомым значением? – Нет, так как имеется «запас» до набора суммы, равной 11. Можно попробовать найти такое число, большее 3, которым можно заменить число 3 в наборе, если получающаяся при этом сумма не превысит 11. Таким числом будет 4, сумма станет равной 10, максимальное значение в наборе – 4. Следующая проба найдет еще одно число (5), которым в наборе можно заменить число 4. После этого сумма всех чисел набора станет равной 11 и дальнейшие действия можно прекратить.

Реализуем эту логику в программе. В ней будем использовать следующие основные переменные величины:

м – массив для хранения размеров файлов пользователей из N элементов;

сумма – меняющаяся сумма значений элементов массива (размеров отбираемых для хранения файлов);

кол – первое искомое значение; макс_число – второе искомое значение.

Предположим, нам уже известны значения S и N. Тогда фрагмент программы, в котором находится значение кол, следующий:

сумма := 0 нц для i от 1 до N | Цикл для всех элементов массива если сумма + м[i] <= S то сумма := сумма + м[i] кол := i | Обратите внимание на этот оператор иначе | Прекращаем проход по массиву выход все кц | Последнее найденное число запоминаем макс_число := м[кол]

Далее проверяем остальные элементы массива – могут ли они заменить максимальное число в найденном наборе:

нц для i от кол + 1 до N если сумма - макс_число + м[i] <= S то | i-м элементом можно заменить значение макс_число | Новое значение суммы:

сумма := сумма - макс_число + м[i] | Запоминаем новое найденное максимальное число макс_число := м[i] иначе | Необходимая сумма набрана | Прекращаем поиск выход все кц | Выводим ответы вывод кол, " ", макс_число

Обсудим теперь, как узнать значения S и N и заполнить массив числами из файла.

Указанные два значения записаны в первой строке заданного файла. Самый простой способ узнать их – прочитать с помощью программы только эту строку и вывести ее на экран.

После этого надо дополнить программу двумя операторами:

S :=

N :=

а затем прочитать из файла остальные N значений, записать их в массив и обработать его согласно описанной логике действий.

Прежде чем представлять начало программы, заметим, что, как и при выполнении предыдущего задания, для сортировки массива целесообразно использовать соответствующие стандартные функции языков программирования:

алг нач файл ф, цел таб м[1 : 970] цел S, N, сумма, кол, макс_число, i лит число, лог успех лит первая_строка ф := открыть на чтение("26.txt") ввод ф, первая_строка вывод нс, первая_строка S := 8200

N := 970 | Читаем N чисел из файла и записываем их в массив нц для i от 1 до N ввод ф, число м[i] := лит_в_цел(число, успех) кц закрыть(ф) | Сортируем массив

… | Обрабатываем его сумма := 0 нц для i от 1 до N если сумма + м[i] <= S … (см. выше)

24.2.3. Пример 3

Условие

Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъемность ограничена, поэтому перевезти сразу все грузы не удастся. Грузоподъемность автомобиля и масса каждого груза известны. Грузы массой 10 кг грузят в первую очередь (гарантируется, что все такие грузы поместятся).

Определите максимальное число грузов, которые можно погрузить в автомобиль, а также максимальную массу груза, который может быть перевезен, при условии что будет перевезено максимально возможное число грузов.

Первая строка входного файла содержит два целых числа: G – грузоподъемность грузовика в кг и N – общее количество грузов. Каждая из следующих N строк содержит одно целое число – массу груза в кг.

Решение

Данное задание по сути аналогично рассмотренному в предыдущем пункте (роль отдельных файлов, размещаемых на диске, играют грузы, загружаемые в автомобиль). Отличие в том, что есть грузы, которые обязательно должны быть загружены.

Если найти общую массу этих грузов и вычесть ее из грузоподъемности автомобиля, то будет получено значение, по смыслу аналогичное значению S в предыдущем задании. Это значит, что и решение будет аналогичным.

Обсудим, как определить общую массу «обязательных» грузов (ее имя – масса10). Лучше всего это сделать при записи чисел из файла в массив. Так как эти грузы потом учитываться не будут, то можно после учета их массы в общей массе считать, что их масса стала равна нулю. Конечно, следует определить и количество таких грузов кол10. Соответствующий фрагмент программы:

алг нач файл ф, цел таб м[1 : 970] цел G, N, сумма10, кол10, сумма, кол, макс_число, i лит число, лог успех лит первая_строка ф := открыть на чтение("26.txt") ввод ф, первая_строка вывод нс, первая_строка G := 2000

N := 970 | Читаем N чисел из файла и записываем их в массив нц для i от 1 до N ввод ф, число м[i] := лит_в_цел(число, успех) | Числа, равные 10, обрабатываем если м[i] = 10 то

сумма10 := сумма10 + м[i] кол10 := кол10 + 1 м[i] := 0 все кц закрыть(ф)

| Сортируем массив

… | Выводим ответы

вывод кол10 + кол, " ", макс_число

Примечание. Переменную кол10 можно не использовать. Зная значение переменной сумма10, соответствующее количество можно определить как сумма10/10.

Разработайте всю программу на изучаемом языке программирования самостоятельно и, используя файл, приложенный к предыдущему заданию, найдите искомые значения. Грузоподъемность автомобиля G примите равной 2000 кг (см. приведенный фрагмент программы).

24.2.4. Пример 4

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

Входной файл содержит сведения о заявках на проведение мероприятий в конференц-зале. В каждой заявке указаны время начала и время окончания мероприятия (в минутах от начала суток). Если время начала одного мероприятия меньше времени окончания другого, то провести можно только одно из них. Если время окончания одного мероприятия совпадает со временем начала другого, то провести можно оба. Определите, какое максимальное количество мероприятий можно провести в конференц-зале и каков при этом максимально возможный перерыв между двумя последними мероприятиями.

Входные данные

В первой строке входного файла находится число N (N ≤ 1000) – количество заявок на проведение мероприятий. Следующие N строк содержат пары чисел, обозначающих время начала и время окончания мероприятий. Каждое из чисел натуральное, не превосходящее 1440.

Запишите в ответе два числа: максимальное количество мероприятий и самый длинный перерыв между двумя последними мероприятиями (в минутах).

Пример входного файла:

10 150

100 120

131 170

150 180

120 130

При таких исходных данных можно провести максимум три мероприятия, например мероприятия по заявкам 2, 3 и 5. Максимальный перерыв между двумя последними мероприятиями составит 20 мин, если состоятся мероприятия по заявкам 2, 4 и 5.

Решение

Прежде всего прокомментируем выполнение задания для приведенного примера.

Максимальное число мероприятий (3) можно провести двумя способами:

1) начать их с мероприятия по заявке 2, затем провести мероприятия по заявкам 5 и 3;

2) начать их с мероприятия по заявке 2, затем провести мероприятия по заявкам 5 и 4.

В первом случае перерыв между двумя последними мероприятиями составит 131 – 130 = 1 мин, во втором – 150 – 130 = 120 мин.

Теперь – об основном задании.

Сначала обсудим методику определения максимального количества мероприятий.

Представим информацию об отдельной заявке (время начала и время окончания) в виде восьмисимвольной строковой величины, в первых четырех символах которой будет записано время начала, а во вторых – время окончания (в обоих случаях – с возможными начальными нулями). Для приведенного примера эти величины выглядели бы так:

00100150

01000120

01310170

01500180

01200130

Далее отсортируем их в порядке возрастания (величины строкового типа также можно сравнивать между собой):

00100150

01000120

01200130

01310170

01500180

Примечание. Для наглядности время окончания оттенено.

После этого рассуждения такие.

Прежде всего заметим, что начало всех мероприятий в списке записано в порядке возрастания.

Допустим, что мы рассмотрели некоторую заявку из отсортированного списка и ее мероприятие включили в план проведения, то есть знаем время окончания (оконч) этого мероприятия. Рассматриваем следующую за ней заявку. Здесь возможны два случая.

Если время окончания очередной заявки меньше, чем значение оконч, то лучше вместо последней учтенной заявки учесть в плане очередную заявку (ее мероприятие закончится раньше, что даст возможность включить в план больше мероприятий). В этом случае количество включенных в план заявок не изменится.

А если это не так (время окончания мероприятия очередной заявки больше, чем значение оконч)? В каком случае ее можно учесть в плане мероприятий? – Ответ: если в очередной заявке время начала мероприятия больше значения оконч. При этом количество включенных в план заявок увеличится на 1.

(Убедитесь в справедливости всех сделанных выводов.)

Разработаем фрагмент программы, работающей на основе сделанных рассуждений. В нем примем, что отсортированная информация обо всех заявках записана в массиве с именем мас, и используем в нем следующие основные переменные величины:

кол – искомое максимальное количество включенных в план заявок; заявка – восьмисимвольная строка с информацией о некоторой заявке;

оконч – время окончания мероприятия в предыдущей заявке.

Итак, соответствующий фрагмент программы:

| Учитываем в плане первую заявку (потом это решение может измениться)

| Определяем время окончания ее мероприятия

| Чтобы была возможность выделить его из значения элемента массива, | используем переменную заявка заявка := мас[1] | Выделяем время окончания, используя "вырезку" ("срез") оконч := заявка[5:8] | Учитываем первую заявку кол := 1 | Рассматриваем остальные заявки отсортированного массива нц для i от 2 до N заявка := мас[i]

если заявка[5:8] < оконч то | Запоминаем время окончания мероприятия по текущей заявке оконч := заявка[5:8] иначе | Сравниваем время начала мероприятия и значение оконч если заявка[1:4] >= оконч то | Включаем в план мероприятие по текущей заявке кол := кол + 1 | Запоминаем время окончания мероприятия оконч := заявка[5:8] все все кц

Можно отдельно первую заявку не рассматривать, а начинать в цикле рассмотрение всех заявок с нее, приняв в качестве начальных значений переменных оконч и кол нулевые значения:

оконч := "0" кол := 0 | Рассматриваем все заявки отсортированного массива нц для i от 1 до N …

Теперь о том, как определить максимально возможный перерыв между двумя последними мероприятиями.

Итак, по приведенному фрагменту программы мы определили максимальное количество мероприятий кол, которые можно провести. Последней была учтена некоторая заявка.

Но вместо последнего (кол-го) учтенного мероприятия в план можно включить и другие мероприятия, которые начнутся после него. В таких случаях значение кол не изменится, а увеличится время перерыва. Наибольший перерыв будет, если включить в план мероприятие с максимально поздним временем начала (это будет мероприятие по заявке, информация о которой в массиве мас записана в его последнем элементе).

При определении величины перерыва в примере в условии использовалось значение 130. Это время окончания предпоследнего мероприятия. Чтобы при выполнении основного задания узнать это время, надо знать номер последней заявки, включенной в план мероприятий. Обозначим этот номер посл. Его можно запоминать в ходе рассмотрения всех заявок:

нц для i от 1 до N заявка := мас[i] если заявка[5:8] < оконч то | Запоминаем время окончания мероприятия по текущей заявке оконч := заявка[5:8] | и ее номер посл := i иначе если заявка[1:4] >= оконч то | Включаем в план текущую заявку кол := кол + 1 | Запоминаем время окончания мероприятия оконч := заявка[5:8] | и номер текущей заявки посл := i все все кц

Зная значение посл, можно определить время окончания предпоследнего учтенного мероприятия. Обозначим это время – предпосл_оконч:

| Информация о предпоследней заявке заявка := мас[посл - 1] | Время окончания в ней предпосл_оконч := заявка[5:8]

Осталось учесть время начала мероприятия по последней заявке в массиве мас и вычесть из него время предпосл_оконч:

заявка := мас[N] макс_пер := лит_в_цел(заявка[1:4], успех) - лит_в_цел(предпосл_оконч, успех)

(Переменная макс_пер – искомое значение максимального перерыва.)

Пришло время рассказать, как заполнить массив мас с информацией обо всех заявках.

Напомним, что эта информация записана в файле, причем не в виде нужных нам восьмисимвольных значений. Придется преобразовывать значения из файла в нужную нам форму, добавляя при необходимости один, два или три нуля ко времени начала и конца мероприятия.

Приведем фрагмент программы, в котором проводится такое преобразование для строки ст, прочитанной из файла:

| Позиция пробела поз_пр := поз(" ", ст)

| Значение времени начала мероприятия

н := ст[1 : поз_пр - 1] | Добавляем к нему начальные нули выбор при длин(н) = 1: н := "000" + н при длин(н) = 2: н := "00" + н при длин(н) = 3: н := "0" + н все | Значение времени конца мероприятия к := ст[поз_пр + 1 : длин(ст)] выбор при длин(к) = 1: к := "000" + к при длин(к) = 2: к := "00" + к при длин(к) = 3: к := "0" + к все | Значение ст для записи в массив мас ст := н + к

Итак, основные этапы программы для поиска двух искомых значений:

1. Чтение информации о заявках, преобразование ее в нужную форму и запись в массив: ф := открыть на чтение("26_2024 txt") ввод ф, N нц для i от 1 до N ввод ф, ст | Преобразование значения ст

… | Запись в массив нового значения ст мас[i] := ст кц закрыть(ф)

2. Сортировка массива мас.

3. Определение значений кол и посл.

4. Расчет значения макс_пер.

5. Вывод результатов (кол и макс_пер).

Всю программу соберите самостоятельно.

В заключение заметим, что вместо массива мас с восьмисимвольными значениями можно использовать два одномерных числовых массива или один двумерный. Однако при этом упорядочивание таких массивов по значению времени начала мероприятия (этап 2) будет усложнено.

24.3. Выводы и рекомендации

1. При выполнении заданий 26 следует учесть, что при решении должна проводиться сортировка данных в файле.

2. Во всех заданиях:

• необходимо найти две характеристики некоторого набора значений;

• числа для обработки следует записать из прилагаемого файла в массив (список).

3. Возможны три типа задания 26:

1) в котором искомый набор формируется по мере обработке сразу всего массива;

2) в котором искомый набор формируется по мере обработке начальных элементов массива, а затем уточняется при обработке остальных элементов;

3) в котором сначала уточняется одно из исходных данных, а затем проводится обработка массива, как в задании предыдущего типа.

4. По мере обработки массива все числа из подходящего набора запоминать не обязательно, достаточно запомнить только значения переменных, являющихся искомыми в задании.

***

Задания для самостоятельного выполнения – см. [3–4].

Глава 25 Задания 27

25.1. Общие вопросы

В Спецификации [1] в качестве проверяемого элемента содержания применительно к заданию 27 указывается «умение создавать собственные программы (20–40 строк) для анализа числовых последовательнос тей».

• Уровень сложности задания – В (высокий).

• Максимальный балл за выполнение задания – 2.

• Примерное время выполнения задания – 40 мин.

Задание выполняется с использованием прилагаемого файла.

25.2. Примеры заданий и методика их выполнения^{^[79]}

25.2.1. Пример 1

(задание из демонстрационного варианта ЕГЭ 2023 года)

Условие

У медицинской компании есть N пунктов приема биоматериалов на анализ. Все пункты расположены вдоль автомагистрали и имеют номера, соответствующие расстоянию от нулевой отметки до конкретного пункта. Известно количество пробирок, которое ежедневно принимают в каждом из пунктов. Пробирки перевозят в специальных транспортировочных контейнерах вместимостью не более 36 штук. Каждый транспортировочный контейнер упаковывается в пункте приема и вскрывается только в лаборатории.

Стоимость перевозки биоматериалов равна произведению расстояния от пункта до лаборатории на количество контейнеров с пробирками. Общая стоимость перевозки за день равна сумме стоимостей перевозок из каждого пункта в лабораторию. Лабораторию расположили в одном из пунктов приема биоматериалов таким образом, что общая стоимость доставки биоматериалов из всех пунктов минимальна.

Определите минимальную общую стоимость доставки биоматериалов из всех пунктов приема в лабораторию.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число N (1 ≤ N ≤ 10 000 000) – количество пунктов приема биоматериалов. В каждой из следующих N строк находится два числа: номер пункта и количество пробирок в этом пункте (все числа натуральные, количество пробирок в каждом пункте не превышает 1000). Пункты перечислены в порядке их расположения вдоль дороги, начиная от нулевой отметки. В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B. Типовой пример организации данных во входном файле:

1 100

2 200

5 4

7 3

8 2

10 190

При таких исходных данных и вместимости транспортировочного контейнера, составляющей 96 пробирок, компании выгодно открыть лабораторию в пункте 2. В этом случае сумма транспортных затрат составит: 1 × 2 + 3 × 1 + 5 × 1 + 6 × 1 + 8 × 2.

Решение

Обсудим сначала решение приведенного примера.

Предположим, что у нас есть два массива, каждый из шести элементов, заполненный данными из примера:

1) массив номер:

1	2	5	7	8	10
1	2	3	4	5	6

2) массив кол_проб:

100	200	4	3	2	190
1	2	3	4	5	6

Так как стоимость перевозки равна произведению расстояния от пунк та приема до лаборатории на количество контейнеров с пробирками в этом пункте, то нужно будет при расчетах оперировать не количеством пробирок в том или ином пункте, а числом контейнеров, в которых они будут перевозиться. Как определить количество контейнеров, необходимых для перевозки заданного числа пробирок?

Ответ: если число пробирок кратно 96 то

количество контейнеров равно частному от деления числа пробирок на 96 иначе количество контейнеров равно целой части частного от деления числа пробирок на 96, увеличенной на 1

Учитывая это, заполним еще один массив кол_конт с количеством контейнеров для каждого пункта:

2	3	1	1	1	2
1	2	3	4	5	6

После этого можно определять общую стоимость перевозки из всех пунктов приема в пункт, в котором будет находиться лаборатория. Она будет равна сумме произведений числа контейнеров в каждом пункте приема на соответствующее расстояние перевозки. С целью упрощения можно не рассматривать пункты, находящиеся на автомагистрали до лаборатории, и пункты после нее, а учитывать все пункты, в том числе пункт с лабораторией (для него указанное произведение будет равно нулю).

Заметим также, что предварительно определять расстояние между тем или иным пунктом приема не обязательно – оно равно абсолютной величине разности номеров пунктов.

Так как в рассматриваемом примере количество пунктов небольшое, то можно использовать перебор всех возможных вариантов размещения лаборатории.

Соответствующий фрагмент программы определения минимальной общей стоимости доставки оформляется так:

мин_стоим := 100000 | Условное начальное значение искомой величины нц для i от 1 до N | Рассматриваем все пункты размещения лаборатории стоим[i] := 0 нц для j от 1 до N | Рассматриваем все пункты приема стоим[i] := стоим[i] + кол_конт[j] * iabs(номер[i] - номер[j]) кц

| Сравниваем рассчитанную общую стоимость с минимальной если стоим[i] < мин_стоим то | Меняем значение переменной мин_стоим мин_стоим := стоим[i] все кц

вывод нс, мин_стоим

Примечание. Функция iabs, возвращающая абсолютное значение своего аргумента, используется потому, что разность номеров пунк тов может быть отрицательной.

Конечно, при большом количестве пунктов (а для файла В оно составляет более 1 000 000) полный перебор вариантов будет длительным, и его применять нельзя. Решение для такого случая обсудим чуть ниже, а здесь рассмотрим случай, когда в файле значение N не очень большое (это значение можно определить, открыв прилагаемый к заданию файл с помощью программы Блокнот^{^[80]}).

Фрагмент программы решения задачи для такого случая будет аналогичным приведенному. Необходимо только предварительно заполнить массивы номер и кол_проб. Как это сделать, учитывая, что в файле в каждой строке записаны пары значений? – В разных языках программирования задача выделения из строки, прочитанной из файла, двух чисел решается по-разному. Разработайте всю программу самостоятельно и выполните обсуждаемое задание применительно к файлу А.

Теперь – о том, как решать задачу без полного перебора большого числа вариантов (как это должно быть применительно к файлу В).

Предположим, что мы уже знаем общую стоимость перевозки, когда лаборатория находится в некотором пункте А:

1 … А l В … N

…

При ее определении учитывалось количество контейнеров, доставляемых в лабораторию из пунктов приема, расположенных до нее, и из пунктов, расположенных после.

Как изменится эта стоимость, если лаборатория будет находиться в следующем пункте В?

Все контейнеры из пунктов приема, расположенных до пункта А, теперь будут перевозиться на l км дальше. Кроме того, на это же расстояние перевезутся также не учитывавшиеся ранее контейнеры из пункта А. Можно сказать, что к общей стоимости добавится произведение общего числа контейнеров до пункта В на расстояние l.

С другой стороны, все контейнеры из пунктов, расположенных после пункта А, теперь будут перевозиться на l км ближе.

Именно эти особенности позволяют определить общую стоимость для каждого возможного места размещения лаборатории и найти минимальную из них.

Итак, основные этапы определения искомого минимального значения общей стоимости перевозки следующие:

1. Прочитать все N пар значений из файла и записать их в два массива номер и кол_проб.

2. Для каждого пункта приема рассчитать количество контейнеров для перевозки пробирок из него и сохранить значения в массиве кол_конт.

3. Для каждого пункта приема рассчитать количество контейнеров, находящихся в пунктах, расположенных до него, и количество контейнеров, находящихся в пунктах, расположенных после него, и сохранить значения в массивах кол_конт_до и кол_конт_после соответственно.

4. Определить стоимость перевозки в лабораторию, расположенную в первом пункте приема, и принять ее в качестве начального значения искомой величины мин_стоим.

5. Для второго, третьего, …, N-го пунктов рассчитать стоимость стоим перевозки в него, зная стоимость для перевозки в предыдущий пункт (и учитывая описанные особенности изменения стоимости перевозки). Рассчитанное значение стоим сравнить с текущим значением переменной мин_стоим и при необходимости изменить последнее:

если стоим < мин_стоим то мин_стоим := стоим все

6. Вывести результат.

Первые два этапа выполняются аналогично описанным ранее.

Заполнение массивов кол_конт_до и кол_конт_после проводится по рекуррентным зависимостям^{^[81]}:

нц для i от 1 до N кол_конт_до[i] := 0 нц для j от 1 до i - 1 кол_конт_до[i] := кол_конт_до[i] + кол_конт[j] кц кц

нц для i от 1 до N - 1 кол_конт_после[i] := 0 нц для j от i + 1 до N кол_конт_после[i] := кол_конт_после[i] + кол_конт[j] кц кц

Фрагмент, описывающий этап 4:

стоим := 0 нц для i от 1 до N стоим := стоим + кол_конт[i] * (номер[i] - номер[1]) | Обратите внимание на разность в скобках кц

мин_стоим := стоим

а этап 5:

нц для i от 2 до N | Значение стоим рассчитывается в зависимости от значения

| в предыдущем пункте с учетом особенностей изменения | (какие-то произведения добавляются, какие-то – вычитаются) стоим := стоим + кол_конт_до[i] * (номер[i] - номер[i - 1]) – кол_конт_после[i - 1] * (номер[i] - номер[i - 1])^{^[82]}

| Сравнение если стоим < мин_стоим то мин_стоим := стоим все кц

25.2.2. Пример 2

(задание из демонстрационного варианта ЕГЭ 2022 года)

Условие

Дана последовательность из N натуральных чисел. Рассматриваются все ее непрерывные подпоследовательности, такие что сумма элементов каждой из них кратна k = 43. Найдите среди них подпоследовательность с максимальной суммой, определите ее длину. Если таких подпоследовательностей найдено несколько, в ответе укажите количество элементов самой короткой из них.

Входные данные

Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 ≤ N ≤ 10⁸). Каждая из следующих N строк содержит одно натуральное число, не превышающие

10 000.

Пример организации исходных данных во входном файле:

В этом наборе можно выбрать последовательности 21 + 13 + 9 (сумма 43) и 17 + 26 (сумма 43). Самая короткая из них, 17 + 26, имеет длину 2. Для указанных программа должна вывести число 2.

В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Решение

Прежде всего предложим читателям самостоятельно разработать несложную программу, основанную на переборе всех возможных подпоследовательностей, которую можно использовать для выполнения задания применительно к файлу А. В ней:

• используйте массив для хранения всех чисел из файла (его размер зависит от значения N, которое можно определить так, как и при выполнении предыдущего задания);

• заполните его, прочитав числа из файла;

• с помощью вложенного оператора цикла

нц для i от 1 до N - 1 … нц для j от i + 1 до N … кц кц

рассмотрите все варианты подпоследовательностей из двух чисел, исследуйте их свойства и найдите требуемую по условию.

А мы далее разработаем более сложную программу, которую следует использовать для выполнения задания применительно к файлу В (и, конечно, к файлу А).

Идею решения обсудим на более простом примере – при k = 7.

Допустим, мы обработали некоторое количество (5) первых чисел:

1 8 1 2 5

Как узнать, что среди них есть нужная нам подпоследовательность (а она – есть)?

Можно рассуждать так. Сумма всех чисел (общ_сумма) равна 17. Остаток от ее деления на 7 (ост) равен 3. Если в начале всей последовательности есть числа, остаток от деления суммы которых равен 3, то, найдя и исключив их, мы выделим нужную нам подпоследовательность. Сами числа этой подпоследовательности нам запоминать не нужно, достаточно знать их сумму и количество. Чтобы определить сумму чисел, надо из общей суммы общ_сумма вычесть сумму «исключаемых» чисел (17 – 10 = 7), а для нахождения количества вычесть из 5 количество «исключаемых» чисел (3).

В дальнейшем при рассуждениях и в программе будем использовать следующие основные переменные величины (кроме общ_сумма и ост):

нач_сумма – сумма «исключаемых» чисел; сумма – сумма чисел в очередной найденной подходящей подпоследовательности;

длина – количество чисел в ней; мин_длина – искомое по условию значение (количество элементов самой короткой подходящей подпоследовательности);

макс_сумма – максимальная сумма элементов в подходящих подпоследовательностях.

Схема действий по определению искомого значения:

1. Читаем очередное i-е число.

2. Находим сумму всех чисел (общ_сумма).

3. Определяем остаток от ее деления на k.

4. Если k <> 0 то

4.1. Начиная с начала последовательности определяем сумму нач_сумма и количество чисел, остаток от деления суммы которых на k равен нулю.

4.2. Если это количество меньше i (то есть в начале последовательности есть числа, которые можно «исключить» из общей суммы (общ_сумма) то (встретилась очередная подпоследовательность, сумма элементов которой кратна k)

4.2.1. Определяем ее характеристики:

– сумму сумма = общ_сумма – нач_сумма;

– количество чисел в ней длина (см. комментарии к программе ниже)

4.2.2. Сравниваем эти значения со значениями макс_сумма и мин_длина

Если сумма больше или при той же сумме длина меньше то запоминаем новые значения макс_сумма и мин_длина все все (конец этапа 4.2. Если «исключаемые» числа не найдены, как для последовательностей 1, 1 8, 1 8 1,

1 8 1 2, то рассматривается следующее число) иначе (k = 0)

Встретилась очередная подходящая подпоследовательность

– ее сумма общ_сумма является максимальной среди таких подпоследовательностей – ее длина равна i все (конец этапа 4)

5. Выводится ответ (значение мин_длина)

Перейдем к программной реализации описанных действий. Приведем сначала программу, в которой все числе из файла предварительно переписываются в массив м из N чисел. Хотя такой вариант не подходит для работы с файлом В (см. условие задания), поскольку количество чисел в нем превышает 4 млн, такая программа полезна для разработки программы для выполнения задания применительно к файлу В.

Итак, фрагмент программы, связанный с обработкой чисел, предварительно записанных в массив:

| Начальные значения переменных макс_сумма := 0 мин_длина := 5000000 общ_сумма := 0 нц для i от 1 до N общ_сумма := общ_сумма + м[i] ост := mod(общ_сумма, 43) если ост <> 0 то | Ищем числа, которые можно удалить | (используем оператор цикла с условием) j := 0 нач_сумма := 0 нц пока mod(нач_сумма, 43) <> ост j := j + 1 нач_сумма := нач_сумма + м[j] кц если j < i то | Встретилась очередная подпоследовательность | Ее сумма сумма := общ_сумма - нач_сумма | Ее длина длина := i - j | Сравниваем если сумма > макс_сумма или (сумма = макс_сумма и длина < мин_длина) то | Запоминаем новые значения макс_сумма := сумма мин_длина := длина все все иначе | ост = 0 | Встретилась очередная подходящая последовательность | Ее характеристики макс_сумма := общ_сумма длина := i все кц вывод нс, мин_длина

Анализ показывает, что рассматривать два случая (k <> 0 и k = 0) необязательно. При k = 0 будет: нач_сумма = 0, j = 0). Соответствующий фрагмент программы:

макс_сумма := 0 мин_длина := 5000000 общ_сумма := 0 нц для i от 1 до N общ_сумма := общ_сумма + м[i] ост := mod(общ_сумма, 43) | Ищем числа, которые можно удалить j := 0 нач_сумма := 0 нц пока mod(нач_сумма, 43) <> ост j := j + 1 нач_сумма := нач_сумма + м[j] кц если j < i то | Встретилась очередная подпоследовательность | Ее сумма сумма := общ_сумма - нач_сумма | Ее длина длина := i - j | Сравниваем если сумма > макс_сумма или (сумма = макс_сумма и длина < мин_длина) то | Запоминаем новые значения макс_сумма := сумма мин_длина := длина все все кц

вывод нс, мин_длина

Теперь – о выполнении задания без использования массива.

В рассмотренном варианте программы если по мере обработки элементов массива многократно встречалась сумма общ_сумма, остаток деления которой равен 3, то мы каждый раз исследовали числа в начале массива и находили числа «для удаления» (в примере, приведенном в начале раздела, это были три числа 1, 8, 1 с суммой нач_сумма, равной 10). При однократной обработке чисел сразу по мере считывания их из файла такие действия провести нельзя. Как быть? – Надо при первой встрече суммы общ_сумма с остатком 3 количество найденных чисел и их сумму запомнить в двух массивах, а потом при встрече очередной суммы с остатком 3 обращаться к уже известным соответствующим значениям. Размер этих массивов – 42, с индексами от 0 до 41 (значениями возможных остатков от деления на 42). Имена массивов:

мас_длин – для хранения количества «удаляемых» чисел; мас_сумм – для хранения их суммы.

Для приведенного выше примера фрагменты этих массивов будут такими:

0			3
0	1	2	3	…

0			10
0	1	2	3	…

А как заполняются элементы с индексами 1 и 2? Это происходит при обработке первого числа (1) и двух первых чисел (1 и 8). Для них:

• сумма общ_сумма равна, соответственно, 1 и 9;

• остаток от этой суммы на 7 – соответственно, 1 и 2;

• чисел для «удаления» в этих случаях нет, поэтому указанные значения и записываются в массивы^{^[83]}:

0	1	2	3
0	1	2	3	…

0	1	9	10
0	1	2	3	…

Прежде чем представлять всю программу, заметим, что в ней перед обработкой чисел из файла массивы мас_длин и мас_сумм заполняются нулевыми значениями.

Итак, программа:

алг нач файл ф, лит а, цел N, очер, i цел таб мас_длин[0:41], мас_сумм[0:41]

цел общ_сумма, ост, сумма, длина, макс_сумма, мин_длина

лог успех макс_сумма := 0 мин_длина := 100000 общ_сумма := 0 нц для i от 0 до 41 мас_длин[i] := 0 мас_сумм[i] := 0 кц ф := открыть на чтение("27_В txt") | Чтение количества чисел в последовательности N ввод ф, а N := лит_в_цел(а, успех) | Чтение и обработка остальных чисел из файла нц для i от 1 до N ввод ф, а | а - число как текст в файле очер := лит_в_цел(а, успех) | очер - очередное число | последовательности общ_сумма := общ_сумма + очер ост := mod(общ_сумма, 43) если мас_длин[ост] <> 0 то | Числа, которые надо удалить, раньше встречались | Удалив их, получим нужную подпоследовательность | Ее сумма сумма := общ_сумма - мас_сумм[ост] | Ее длина

длина := i - мас_длин[ост] | Сравнимаем если сумма > макс_сумма или (сумма = макс_сумма и длина < мин_длина) то | Запоминаем новые значения макс_сумма := сумма мин_длина := длина все

иначе Раньше числа, которые надо удалить, не встречались | Значения общ_сумма и i записываем в массивы | для дальнейшего использования мас_сумм[ост] := общ_сумма мас_длин[ост] := i все кц закрыть(ф) вывод нс, мин_длина кон

25.2.3. Пример 3

(задание из демонстрационного варианта ЕГЭ 2024 года)

Условие

По каналу связи передается последовательность целых чисел – показания прибора. В течение N минут (N – натуральное число) прибор ежеминутно регистрирует значение напряжения (в условных единицах) в электрической сети и передает его на сервер.

Определите три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K минут, а сумма этих трех чисел была максимально возможной. Запишите в ответе найденную сумму.

Входные данные

Дано два входных файла (файл A и файл B), каждый из которых в первой строке содержит число K – минимальное количество минут, которое должно пройти между моментами передачи показаний, а во второй – количество переданных показаний N. В каждой из следующих N строк находится одно целое число, по модулю не превышающее 10 000 000, которое обозначает значение напряжения в соответствующую минуту.

В ответе укажите два числа: сначала значение искомой величины для файла А, затем – для файла B.

Пример организации исходных данных во входном файле:

150

–150 20

–200

–300

При таких исходных данных искомая величина равна 170 – это сумма значений, зафиксированных на первой, третьей и шестой минутах измерений.

Предупреждение: для обработки файла B не следует использовать переборный алгоритм, вычисляющий сумму для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.

Прежде чем описывать методику выполнения задания, обсудим решение двух более простых задач.

Задача 1

Условие

Метеорологическая станция ведет наблюдение за количеством выпавших осадков. Показания записываются каждую минуту в течение N минут (N – натуральное число).

Определите два таких показания, чтобы между моментами их измерения прошло не менее K минут, а сумма этих двух показаний была максимально возможной. Запишите в ответе найденную сумму.

Решение

Предположим, что все изменения записаны в массиве м из N элементов, и пусть К = 2.

Рассмотрим начало массива (все значения – условные):

…

Первая подходящая пара чисел – 2 и 8 (число 1 не рассматриваем). Их сумма равна 10. Выделим обработанный диапазон чисел:

…

Рассмотрим очередное число (13).

Какая пара чисел дает максимальную сумму с его учетом?

13 и 8? – Нет, так как «расстояние» между числами 13 и 8 меньше двух.

13 и 1? – Нет, так как есть большее, чем 1, число. Здесь же заметим, что число 1 рассматривается впервые.

Число 2 подходит. Пара 13 и 2 дает сумму 15, что больше 10. Значит, после обработки числа 13 максимальная сумма пар стала равна 15.

Следующее число – 2. Для него максимальное значение среди отстоящих на два и более элементов – 8. Сумма чисел 2 и 8 равна 10, что меньше 15. Значение максимальной суммы не изменилось.

Итак, при рассмотрении некоторого очередного числа для выбора подходящей пары надо знать максимальное число среди «отстоящих от него на расстояние 2 и более».

Проиллюстрируем этот вывод на следующем числе 12. Для него впервые рассматриваемое число – 8. Его можно выбрать, так как оно больше, чем максимальное число среди рассматривавшихся до этого.

Значит, для нахождения искомой максимальной суммы при рассмотрении некоторого i-го элемента массива следует:

1) определить максимум среди двух чисел – значения (i – 2)-го элемента и максимального числа среди рассмотренных до этого;

2) сравнить сумму этого максимума и i-го элемента с максимальной суммой подходящих пар, найденной до этого, и при необходимости изменить максимальную сумму.

Разработаем соответствующий фрагмент программы. Используем в нем следующие переменные величины (кроме массива м и переменной N):

макс_сумма – искомая сумма двух чисел; макс – максимум из двух чисел, о которых шла речь чуть выше.

Вот соответствующий фрагмент:

| Начальные значения переменных макс_сумма := м[1] + м[3] макс := м[1] | Значение м[3] не может быть принято | в качестве максимального | Рассматриваем остальные элементы массива нц для i от 4 до N | от 1 + K + 1 макс := imax(макс, м[i - 2]) | Сравниваем если м[i] + макс > макс_сумма то макс_сумма := м[i] + макс все кц

вывод макс_сумма

где imax – функция школьного алгоритмического языка, возвращающая максимум из двух целых чисел – ее аргументов.

Можно не рассматривать два первых подходящих элемента (первый и третий), а принять в качестве начальных значений переменных макс_ сумма и макс нули:

| Начальные значения переменных макс_сумма := 0 макс := 0 | Рассматриваем остальные элементы массива

нц для i от 3 до N | В этом случае начинаем обработку | с третьего элемента (1 + 2)

…

Задача 2

Условие

Определите три таких записанных числа, чтобы между моментами записи любых двух из них прошло не менее K минут, а сумма этих трех чисел была максимально возможной. Запишите в ответе найденную сумму.

Решение

Здесь в условии речь идет о трех числах.

Как и ранее, рассмотрим массив, заполненный показаниями прибора:

…

Индекс i – 2k i – k i

С какими числами надо рассматривать возможность включения в тройку чисел некоторого i -го элемента?

Одно из таких чисел, как и ранее, – максимум между значением (i – 2K)-го элемента и максимальным числом среди рассмотренных до этого: макс := imax(макс, м[i – 2 * K])

В данной задаче есть также еще одно возможное значение – значение (i – K)-го элемента массива. Можно его включить в тройку, если сумма его значения и значения макс больше такой же суммы для выбранной тройки среди уже рассмотренных ранее чисел. Обозначим такую сумму – сумма2: сумма2 = imax(сумма2, макс + м[i - K])

После этого можно учесть и i-й элемент, сравнить результат со «старой» максимальной суммой и при необходимости изменить ее значение:

| Сравниваем если м[i] + сумма2 > макс_сумма то макс_сумма := м[i] + сумма2 все

Весь фрагмент программы, учитывающий сделанные рассуждения:

| Начальные значения переменных макс := 0 сумма2 := 0 макс_сумма := 0 нц для i от 1 + 2 * K до N макс := imax(макс, м[i - 2 * K]) сумма2 := imax(сумма2, макс + м[i - K]) если м[i] + сумма2 > макс_сумма то макс_сумма := м[i] + сумма2 все кц

вывод макс_сумма

Как и в первом варианте программы решения предыдущей задачи, можно в качестве начальных значений использовать реальные значения из массива:

макс := imax(м[1], м[1 + K]) | Значение элемента м[1 + 2 * K] | не может рассматриваться сумма2 := м[1] + м[1 + K]

макс_сумма := м[1] + м[1 + K] + м[1 + 2 * K]

При этом обработка остальных элементов массива должна начаться с (1 + 2K + 1)-го элемента:

нц для i от 1 + 2 * K + 1 до N макс := imax(макс, м[i - 2 * K]) …

Обратите внимание на последние фрагменты программы. Они будут использоваться при решении аналогичных задач при обработке файлов (см. ниже).

После всех разъяснений приведем программу для выполнению основного задания.

алг нач файл ф, лит а, цел K, N, очер, макс, макс_сумма, сумма2, i цел таб м[1:317] | Об определении размера массива см. выше лог успех

ф := открыть на чтение("27_A_2024 txt") ввод ф, а K := лит_в_цел(а, успех) ввод ф, а

N := лит_в_цел(а, успех)

| Чтение 1 + 2 * K чисел из файла и запись их в массив нц для i от 1 до 1 + 2 * K ввод ф, а м[i] := лит_в_цел(а, успех) кц

| Начальные значения переменных макс := imax(м[1], м[1 + K]) сумма2 := м[1] + м[1 + K] макс_сумма := м[1] + м[1 + K] + м[1 + 2 * K]

| Остальные числа из файла нц пока не конец файла(ф)

ввод ф, а очер := лит_в_цел(а, успех) макс := imax(макс, м[1]) сумма2 := imax(сумма2, макс + м[1 + K]) если очер + сумма2 > макс_сумма то макс_сумма := очер + сумма2

все

| Меняем массив

| Смещаем все элементы, начиная со 2-го, влево на 1 элемент нц для i от 1 до 2 * K

м[i] := м[i + 1] кц

| На последнее место в массиве записываем число очер м[1 + 2 * K] := очер кц закрыть(ф) вывод нс, макс_сумма кон

В заключение заметим, что если бы в задании требовалось определить три таких переданных числа, чтобы между моментами передачи любых двух из них прошло не менее K минут, а сумма этих трех чисел была бы минимально возможной, то по существу ничего не изменилось бы (начальное значение минимальной суммы должно быть принято достаточно большим, например 10¹⁰).

25.3. Задание для самостоятельного выполнения

Выполните все рассмотренные задания применительно к файлу В, разработав программы на языке программирования, которым владеете.

См. также соответствующие задания в [3–4].

Литература

1. Спецификация контрольных измерительных материалов для проведения в 2024 году единого государственного экзамена по информатике // https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/ tab/151883967-5. (Демоверсии, спецификации, кодификаторы 2023. Информатика.)

2. Демонстрационные варианты контрольных измерительных материалов единого государственного экзамена по информатике // https://fipi.ru/ege/demoversii-specifikacii-kodifikatory#!/tab/151883967-5 (Демоверсии, спецификации, кодификаторы. Информатика.)

3. Сайт «Сдам ГИА: шу ЕГЭ» (Образовательный портал для подготовки к экзаменам) // https://inf-ege.sdamgia.ru/.

4. Сайт К. Ю. Полякова // https://kpolyakov.spb.ru/school/ege.htm.

5. Златопольский Д. М. Подготовка к ЕГЭ по информатике в 2020 году. Решение задач по программированию. – М.: ДМКПресс, 2020.

6. Златопольский Д. М. Подготовка к ЕГЭ по информатике в компьютерной форме. – М.: ДМКПресс, 2021.

Книги издательства «ДМК ПРЕСС» можно купить оптом и в розницу в книготорговой компании «Галактика»

(представляет интересы издательств «ДМК ПРЕСС», «СОЛОН ПРЕСС», «КТК Галактика»).

Адрес: г. Москва, пр. Андропова, 38;

Тел.: +7(499) 782-38-89. Электронная почта: books@alians-kniga.ru.

При оформлении заказа следует указать адрес (полностью), по которому должны быть высланы книги; фамилию, имя и отчество получателя.

Желательно также указать свой телефон и электронный адрес.

Эти книги вы можете заказать и в интернет-магазине: www.galaktika-dmk.com.

Златопольский Дмитрий Михайлович

Подготовка к успешной сдаче ЕГЭ по информатике

Главный редактор Мовчан Д. А.

dmkpress@gmail.com

Зам. главного редактора Сенченкова Е. А.

Корректор Синяева Г. И.

Верстка Паранская Н. В. Дизайн обложки Мовчан А. Г.

Формат 70×100 1/16. Усл. печ. л. 14,13. Тираж 200 экз.

Веб-сайт издательства: www.dmkpress.com

[1] В дальнейшем этот документ будет упоминаться как «Спецификация».

[2] В качестве ответа следует вводить только число (без единицы измерения). Это замечание касается всех заданий экзамена.

[3] Методика определения степеней вершин, связанных с некоторой данной вершиной, описана в пп. 1.2.4–1.2.5.

[4] Или одна логическая переменная со знаком отрицания.

[5] Данный пример отличается от приведенных в демонстрационных вариантах нескольких последних лет, но методика его выполнения будет полезна и при выполнении заданий, представленных в демовариантах.

[6] Это требование относится ко всем рассмотренным далее заданиям и заданиям для самостоятельной работы, поэтому в дельнейшем мы будем его приводить в сокращенном виде.

[7] Обратите внимание на порядок формирования комбинаций переменных. Он обеспечивает быстрое и правильное формирование всех комбинаций. Можно использовать копирование одинаковых фрагментов. Показанные формулы во второй строке могут быть скопированы на остальные строки. Заметим также, что в формулах пробелы сделаны для наглядности. Так же мы будем оформлять формулы в электронной таблице и в дальнейшем в книге.

[8] Файл с заданием будет представлен на компьютере экзаменуемого.

[9] Файл представлен на сайте [2].

[10] До этого из условия надо выписать (или запомнить) период, за который надо провести расчеты.

[11] Если вывод суммы в строке состояния отключен, нужно настроить строку состояния так, чтобы этот параметр выводился. Как это сделать, установите самостоятельно.

[12] Это замечание относится ко всем заданиям, рассмотренным далее, в том числе к заданиям для самостоятельной работы (кроме задания 7).

[13] Файл представлен на сайте [2].

[14] С особенностями оформления этой функции ознакомьтесь самостоятельно.

[15] Некоторые формулы приведены в дополнении к данной главе.

[16] По методике, описанной в п. 5.2.3.

[17] Обратите внимание на то, что из числа 99 ничего не вычиталось. Это связано с тем, что ищется максимальное значение N.

[18] В демонстрационном варианте экзамена 2024 года вариант 1 задания 6 такой же, условие задания варианта 2 приведено в п. 6.3.2.

[19] Убедитесь в справедливости всех приведенных ответов.

[20] Координатная сетка приведена для наглядности.

[21] Напомним, что в условии идет речь о точках и на границах полученного пересечения.

[22] Точки на пунктирной линии уже учтены.

[23] Одноканальная запись называется «монозапись».

[24] Все названия предложены автором.

[25] О разрешении сканирования см. раздел 7.1.

[26] Для большей ясности оно записано с комментариями к значениям.

[27] Источник: https://informatika.shkolkovo.net/catalog/peredacha-dannyh-razmery-fajlov/zvukozapis/page-6.

[28] Обратите внимание на порядок записи вариантов.

[29] Также обратите внимание на порядок записи вариантов.

[30] С особенностями оформления этой функции ознакомьтесь самостоятельно.

[31] Обратите внимание на порядок записи вариантов.

[32] На экзамене с целью сокращения времени выполнения задания все тексты можно сократить.

[33] Можно именно так, а не СЧЕТЕСЛИ.

[34] С особенностями оформления остальных функций ознакомьтесь самостоятельно.

[35] Его определите самостоятельно.

[36] Обратите внимание на наличие в формуле так называемых «смешанных» (или «комбинированных») адресов (ссылок). Они позволяют копировать формулу как в ячейки справа от G1, так и в ячейки ниже G1. Напомним, что с целью экономии времени сразу символы «$» можно в формулу не записывать, а после записи формулы в виде =СЧЕТЕСЛИ(A1:F1; A1) разместить курсор внутри каждого относительного адреса в диапазоне ячеек (A1 и F1) и нажимать функциональную клавишу F4 до появления ссылки нужного типа. В втором аргументе функции (A1) тип ссылки менять не следует.

[37] Если этого не сделать, то верхние ячейки столбцов будут определены как заголовки и в фильтрации данных участия принимать не будут.

[38] Файл к этому и следующим заданиям представлен в демонстрационном варианте ЕГЭ по информатике 2022 года.

[39] Файл с текстом из романа представлен в демонстрационном варианте ЕГЭ по информатике 2023 года.

[40] Это уточнение касается всех заданий, рассмотренных далее.

[41] В языках программирования Python, С и ряде других нумерация символов в памяти компьютера начинается с нуля.

[42] Итерация – каждое отдельное повторение тела оператора цикла.

[43] Такой проверяемый элемент содержания после некоторого перерыва вновь появился в демонстрационном варианте ЕГЭ 2024 года.

[44] Двоичное представление числа 255 должно быть читателю известно.

[45] Такой результат можно получить, вычтя из 255 число 3.

[46] О других возможных вариантах задания 14 см. далее.

[47] На экзамене с целью экономии времени текст в строке 1 можно не записывать.

[48] Нумерация вариантов здесь и далее – условная, в данном случае связана с двоичной системой счисления.

[49] В главе 2 приводился другой вариант преобразования.

[50] В школьном алгоритмическом языке команда выход обеспечивает в данном случае не выход из программы, а выход из оператора цикла, в теле которого она записана.

[51] Мы приводим здесь и далее в книге «длинные» имена величин с целью лучшего понимания их назначения; на экзамене с целью экономии времени можно использовать короткие имена.

[52] Нулевое значение может быть присвоено, так как для чисел из файла искомая максимальная сумма не может быть отрицательной (используется сумма квадратов чисел).

[53] Файл, приложенный к заданию 17 демонстрационного варианта ЕГЭ по информатике 2023 года. Этот же файл используйте для выполнения заданий 2–3, предложенных ниже.

[54] Можно допустить, что не исключены и другие команды.

[55] Ширина столбцов по сравнению с представленными в файле уменьшена, что дает возможность видеть заголовки всех столбцов. Рекомендуем читателям на экзамене поступить так же.

[56] Убедитесь в этом!

[57] Ответы на эти вопросы будут полезными при выполнении заданий ЕГЭ.

[58] Для краткости такой ход иногда будем обозначать, соответственно, «+1» и «×2».

[59] О понятии «проигрышная позиция» см. раздел 19.2.

[60] Обратите внимание на то, что используется команда «×3».

[61] Обратите внимание на то, что минимальное приращение количества камней не равно 1.

[62] В справочных системах электронных таблиц этот аргумент, как правило, называется искомое_значение. По нашему мнению, использование термина заданное_значение делает особенности применения функции более понятными.

[63] Обратите внимание на использование в формуле так называемых «абсолютных» ссылок (адресов). Это позволит распространить (скопировать) формулы в другие ячейки. Напомним, что с целью экономии времени сразу символы «$» можно в формулу не записывать, а после записи формулы в виде =ПРОСМОТР(C4; A2:A13; G2:G13) разместить курсор внутри каждого относительного адреса (A2 и др.) и нажать функциональную клавишу F4.

[64] На рис. 20.19 выделены все учтенные процессы.

[65] Автор идеи метода – А. Сидоров [4].

[66] В дальнейшем в условиях заданий фразу «Исполнитель преобразует число на экране» и определения понятий «программа для исполнителя» и «траектория выполнения программ» мы приводить не будем.

[67] Далее с целью упрощения программы будем считать, что если текущая цепочка букв не начиналась, то действия будут такими же, как и при окончании цепочки.

[68] Также с целью упрощения программы такое сравнение будем проводить в любом случае.

[69] Еще раз напомним, что на экзамене для экономии времени можно использовать более короткие имена.

[70] Обратим внимание на то, что выделенный фрагмент можно скопировать с уже написанного текста программы.

[71] Так же можно определить нужное условие и в других аналогичных задачах.

[72] Обратите внимание на использование скобок в логическом выражении.

[73] Именно такими символами заканчивается файл, приложенный к обсуждаемому заданию.

[74] В программе на языке Python заполнение массива можно провести с использованием метода append().

[75] Такие задания представлены в ряде источников, связанных с ЕГЭ по информатике, например в [3].

[76] Аналогичное задание приведено в демонстрационном варианте ЕГЭ 2024 года (см.

задание 5 для самостоятельного выполнения).

[77] Задания 2–4 предложил А. Кабанов [4].

[78] Ряд примеров и методика их выполнения приведены также в книгах автора [5–6].

[79] Ряд примеров и методика их выполнения приведены также в книгах автора [5–6].

[80] Так же можно предварительно узнавать все необходимые для оформления программы значения при выполнении других аналогичных заданий.

[81] В их особенностях разберитесь самостоятельно.

[82] Выражение в правой части оператора присваивания можно упростить.

[83] Совпадение в первом массиве приведенных значений элементов и их индексов – случайное.

Златопольский Д. М. Подготовка к успешной сдаче

Примеры заданий типа 2 и методика их выполнения

Методика выполнения заданий в среде электронной таблицы описывается применительно к программе

Тип 1 (пример) Условие «На рисунке схема дорог

Далее излагался один из двух вариантов требований по выполнению задания: 1) «Определите длину дороги из пункта … в пункт …

Каждому населенному пункту на схеме соответствует номер в таблице, но неизвестно, какой именно номер

Клетки на главной диагонали таблицы (они оттенены) не рассматриваются (почему – понятно)

Решение Для нахождения ответа в данном и других заданиях нужно определить, какие номера в таблице имеют вершины

Решение По изображению графа находим, что обе интересующие нас вершины (А и

А) равна трем. Но такую же степень имеют вершины

Примечание . При оформлении таблицы на бумаге можно в целях сокращения времени значения весов ребер не указывать, а делать в соответствующих клетках некоторую отметку: 1…

Решение Находим вершину Г (ее степень – 3)

У вершины Б связанные с ней вершины имеют степень 2, 3 и 4

Как определить, какой номер соответствует каждой из вершин? –

Вершина В – единственная из имеющих степени 2 (В,

Чем особенны вершины А и G? – Их степень – 2 (по схеме)

Чем особенны вершины E и F? – Их степень – 3

Решение Здесь также имеются четыре вершины со степенью, равной 3 (В,

Решение Так как вершина А – единственная, связанная с двумя вершинами степени 2, то по таблице можно установить, что ее номер – 8 [1]

Выпишите последовательно, без пробелов и знаков препинания, указанные на схеме буквенные обозначения пунктов с номерами 1 до 7: сначала букву, соответствующую пункту 1, затем букву,…

Определите, какова сумма протяженностей дорог из пункта

Введем понятия, которые будем использовать при описании методики выполнения заданий: • переменная, представленная непосредственно : например, х , у , z и т

Миша заполнял таблицу истинности функции

Результат операции дизъюнкции равен 0, только если все ее элементы ложны (см

Анализ показывает, что второй столбец правой таблицы соответствует переменной z , третий – переменной w

Значит, переменная w записана в четвертом столбце

Так как, записав в оставшуюся пустой клетку значение 0, мы получим вариант, при котором во втором и третьем столбцах соблюдается условие истинности элемента x ∨…

В первом случае невозможно получить комбинацию значений 1 и 1

Операция импликации A → B может быть заменена неравенством

ЕГЭ 2022 года) Условие Миша заполнял таблицу истинности логической функции

Учтем в двух первых столбцах условие x ≠ w и заполним пустые клетки в них: у z

В данном случае условие для отбора нужных комбинаций: если (y = 1) и (x <> w) и (z <= x) то вывод нс , x,…

В последнем столбце правой таблицы в пустой клетке может быть только 1 (в левой таблице нет столбцов с одними нулями: х у z w у…

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0			0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

	A	B	C	D	E	F	G	H	I
1	1	0	0	0	0		1		16
2	1	1	0	0	0	1
3	32	16	8	4	2	1	49
	A	B	C	D	E	F	G	H	I
1	1	0	0	0	1		0		17
2	1	0	0	0	1	0
3	32	16	8	4	2	1	34
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	0		0		18
2	1	0	0	1	0	0
3	32	16	8	4	2	1	36
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	1		1		19
2	1	1	0	1	1	1
3	32	16	8	4	2	1	55

	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	0			1		16
2	1	0	0	0	0	1	0
3	64	32	16	8	4	2	1	66
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	1			0		17
2	1	0	0	0	1	0	0
3	64	32	16	8	4	2	1	68
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	0			0		18
2	1	0	0	1	0	0	0
3	64	32	16	8	4	2	1	72
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	1			1		19
2	1	0	0	1	1	1	0
3	64	32	16	8	4	2	1	78

	A	B	C	D	E	F	G
1	1	1	3	3	3	3	81
2	1	1	1	3	3	3	27
3	3	1	1	1	3	3	27
4	3	3	1	1	1	3	27
5	3	3	3	1	1	1	27
6	3	3	3	3	1	1	81
7							270

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	3	1	1	3	3
6	3	1	3	1	3
7	3	1	3	3	1
8	3	3	1	1	3
9	3	3	1	3	1
10	3	3	3	1	1

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	2	1	1	3	3
6	2	1	3	1	3
7	2	1	3	3	1
8	2	3	1	1	3
9	2	3	1	3	1
10	2	3	3	1	1

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4					1
2	1	5	4	4					3
3	1	5	4	4					5
4	1	5	4	4					7
5	1	5	4	4					9
6	1	5	4	4					2
7	1	5	4	4					4
8	1	5	4	4					6
9	1	5	4	4					8

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4	3	3			1
2	1	5	4	4	3	3			3
3	1	5	4	4	3	3			5
4	1	5	4	4	3	3			7
5	1	5	4	4	3	3			9
6	1	5	4	4	3	3			2
7	1	5	4	4	3	3			4
8	1	5	4	4	3	3			6
9	1	5	4	4	3	3			8

	A	B	C	D	E	F
1	37	83	24	19	37	41
2	59	77	43	43	118	38
3	6	65	40	40	6	130
4	63	77	76	8	63	51
5	74	47	97	26	222	23

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0			0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

	A	B	C	D	E	F	G	H	I
1	1	0	0	0	0		1		16
2	1	1	0	0	0	1
3	32	16	8	4	2	1	49
	A	B	C	D	E	F	G	H	I
1	1	0	0	0	1		0		17
2	1	0	0	0	1	0
3	32	16	8	4	2	1	34
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	0		0		18
2	1	0	0	1	0	0
3	32	16	8	4	2	1	36
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	1		1		19
2	1	1	0	1	1	1
3	32	16	8	4	2	1	55

	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	0			1		16
2	1	0	0	0	0	1	0
3	64	32	16	8	4	2	1	66
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	1			0		17
2	1	0	0	0	1	0	0
3	64	32	16	8	4	2	1	68
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	0			0		18
2	1	0	0	1	0	0	0
3	64	32	16	8	4	2	1	72
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	1			1		19
2	1	0	0	1	1	1	0
3	64	32	16	8	4	2	1	78

	A	B	C	D	E	F	G
1	1	1	3	3	3	3	81
2	1	1	1	3	3	3	27
3	3	1	1	1	3	3	27
4	3	3	1	1	1	3	27
5	3	3	3	1	1	1	27
6	3	3	3	3	1	1	81
7							270

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	3	1	1	3	3
6	3	1	3	1	3
7	3	1	3	3	1
8	3	3	1	1	3
9	3	3	1	3	1
10	3	3	3	1	1

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	2	1	1	3	3
6	2	1	3	1	3
7	2	1	3	3	1
8	2	3	1	1	3
9	2	3	1	3	1
10	2	3	3	1	1

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4					1
2	1	5	4	4					3
3	1	5	4	4					5
4	1	5	4	4					7
5	1	5	4	4					9
6	1	5	4	4					2
7	1	5	4	4					4
8	1	5	4	4					6
9	1	5	4	4					8

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4	3	3			1
2	1	5	4	4	3	3			3
3	1	5	4	4	3	3			5
4	1	5	4	4	3	3			7
5	1	5	4	4	3	3			9
6	1	5	4	4	3	3			2
7	1	5	4	4	3	3			4
8	1	5	4	4	3	3			6
9	1	5	4	4	3	3			8

	A	B	C	D	E	F
1	37	83	24	19	37	41
2	59	77	43	43	118	38
3	6	65	40	40	6	130
4	63	77	76	8	63	51
5	74	47	97	26	222	23

Подготовка к успешной сдаче ЕГЭ по информатике

Содержание

Предисловие ................................................................................................................6 Глава 1. Задания 1 .......................................................................................................7

Глава 2. Задания 2 ....................................................................................................31

Глава 3. Задания 3 ....................................................................................................64

Глава 4. Задания 4 ....................................................................................................78

Глава 5. Задания 5 ....................................................................................................89

выполнения алгоритма .............................................................................................. 112 Глава 6. Задания 6 ..................................................................................................113

Глава 7. Задания 7 ..................................................................................................127

Глава 8. Задания 8 ..................................................................................................151

Глава 9. Задания 9 ..................................................................................................177

Глава 10. Задания 10 .............................................................................................190

Глава 11. Задания 11 .............................................................................................199

Глава 12. Задания 12 .............................................................................................208

Глава 13. Задания 13 .............................................................................................224

Глава 14. Задания 14 .............................................................................................236

Глава 15. Задания 15 .............................................................................................252

Глава 16. Задания 16 .............................................................................................269

Глава 17. Задания 17 ..............................................................................................285

Глава 18. Задания 18 .............................................................................................293

Глава 19. Задания 19, 20 и 21 ..............................................................................309

Глава 20. Задания 22 .............................................................................................329

Глава 22. Задания 24 .............................................................................................358

Глава 23. Задания 25 .............................................................................................380

Глава 24. Задания 26 .............................................................................................387

Глава 25. Задания 27 .............................................................................................402

Предисловие

1.1. Общие вопросы. Теория

Тип 1 (пример)

Тип 2 (пример)

Основные определения

1.2. Примеры заданий типа 1 и методика их выполнения

1.2.1. Пример 1

1.2.2. Пример 2

1.2.3. Пример 3

1.2.4. Пример 4

1.2.5. Пример 5

1.2.6. Пример 6

1.2.7. Пример 7 (задание из демонстрационного варианта ЕГЭ 2022 года)

1.2.8. Пример 8 (задание из демонстрационного варианта ЕГЭ 2023 года)

1.3. Примеры заданий типа 2 и методика их выполнения

1.3.1. Пример 1

1.3.2. Пример 2 (пример из демонстрационного варианта ЕГЭ 2024 года)

1.3.3. Пример 3

1.3.4. Пример 4

1.3.5. Пример 5

1.3.6. Пример 6

1.4. Выводы и рекомендации

1.5. Задания для самостоятельного выполнения

2. 1. Общие вопросы. Теория

2.2. Примеры заданий и методика их выполнения

2.2.1. Пример 1[5]

(задание из демонстрационного варианта ЕГЭ 2021 года)

2.2.3. Пример 3

(задание из демонстрационного варианта ЕГЭ 2023 года)

(задание из демонстрационного варианта ЕГЭ 2022 года)

2.2.6. Пример 6

2.3. Выполнение заданий с использованием электронной таблицы или программы

2.4. Полезные факты и рекомендации по выполнению задания

2.5. Задания для самостоятельного выполнения

Глава 3 Задания 3

3.1. Общие вопросы

3.2. Примеры заданий и методика их выполнения

(задание из демонстрационного варианта ЕГЭ 2023 года)

(задание из демонстрационного варианта ЕГЭ 2022 года)

3.2.3. Пример 3

3.2.4. Пример 4

3.2.5. Пример 5

3.2.6. Пример 6

3.2.7. Пример 7

3.3. Рекомендации по выполнению задания

3.4. Задания для самостоятельного выполнения

4.1. Общие вопросы. Теория

4.2. Примеры заданий и методика их выполнения

(задание из демонстрационного варианта ЕГЭ 2022 года)

4.2.2. Пример 2

4.2.3. Пример 3

4.2.4. Пример 4

4.2.5. Пример 5

4.2.6. Пример 6

2.2.1. Пример 1^{^[5]}

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1		1
1	0	1	1	0			0
х	у	z	w	у
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0			0
х	у	z	w	у	?	z	?
0	0	1	1	0	1	1	1
1	0	0	0	0	0	0	1
1	0	0	1	0	1	0	1
1	0	1	1	0	1	1	0

	A	B	C	D	E	F	G	H	I
1	1	0	0	0	0		1		16
2	1	1	0	0	0	1
3	32	16	8	4	2	1	49
	A	B	C	D	E	F	G	H	I
1	1	0	0	0	1		0		17
2	1	0	0	0	1	0
3	32	16	8	4	2	1	34
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	0		0		18
2	1	0	0	1	0	0
3	32	16	8	4	2	1	36
	A	B	C	D	E	F	G	H	I
1	1	0	0	1	1		1		19
2	1	1	0	1	1	1
3	32	16	8	4	2	1	55

	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	0			1		16
2	1	0	0	0	0	1	0
3	64	32	16	8	4	2	1	66
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	0	1			0		17
2	1	0	0	0	1	0	0
3	64	32	16	8	4	2	1	68
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	0			0		18
2	1	0	0	1	0	0	0
3	64	32	16	8	4	2	1	72
	A	B	C	D	E	F	G	Н	I	J
1	1	0	0	1	1			1		19
2	1	0	0	1	1	1	0
3	64	32	16	8	4	2	1	78

	A	B	C	D	E	F	G
1	1	1	3	3	3	3	81
2	1	1	1	3	3	3	27
3	3	1	1	1	3	3	27
4	3	3	1	1	1	3	27
5	3	3	3	1	1	1	27
6	3	3	3	3	1	1	81
7							270

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	3	1	1	3	3
6	3	1	3	1	3
7	3	1	3	3	1
8	3	3	1	1	3
9	3	3	1	3	1
10	3	3	3	1	1

	A	B	C	D	Е
1	1	1	3	3	3
2	1	3	1	3	3
3	1	3	3	1	3
4	1	3	3	3	1
5	2	1	1	3	3
6	2	1	3	1	3
7	2	1	3	3	1
8	2	3	1	1	3
9	2	3	1	3	1
10	2	3	3	1	1

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4					1
2	1	5	4	4					3
3	1	5	4	4					5
4	1	5	4	4					7
5	1	5	4	4					9
6	1	5	4	4					2
7	1	5	4	4					4
8	1	5	4	4					6
9	1	5	4	4					8

	A	B	C	D	E	F	G	Н	I
1	1	5	4	4	3	3			1
2	1	5	4	4	3	3			3
3	1	5	4	4	3	3			5
4	1	5	4	4	3	3			7
5	1	5	4	4	3	3			9
6	1	5	4	4	3	3			2
7	1	5	4	4	3	3			4
8	1	5	4	4	3	3			6
9	1	5	4	4	3	3			8

	A	B	C	D	E	F
1	37	83	24	19	37	41
2	59	77	43	43	118	38
3	6	65	40	40	6	130
4	63	77	76	8	63	51
5	74	47	97	26	222	23