Поэтапное формирование математических понятий

РЦМО ГБПОУ «СОМК»

 

 

 

 

ПОЭТАПНОЕ ФОРМИРОВАНИЕ

МАТЕМАТИЧЕСКИХ ПОНЯТИЙ

 

 

 

 

                                                         Кондрикова Любовь Юрьевна

                                                         преподаватель математики

                                                          высшей категории

 

 

 

 

 

 

 

 

 

 

 

 

Ревда

2021

 

Введение

Образование – целенаправленный процесс воспитания и обучения в интересах человека, общества, государства, сопровождающийся констатацией достижения гражданином (обучающимся) установленных государственных уровней (образовательных цензов).

 Основной целью образования является – формирование готовности старшеклассников к профессиональному самоопределению, воспитание профессионально важных качеств личности, необходимых для принятия решений о выборе профессии, профессиональной мобильности, обеспечивающей ей успешную адаптацию в социокультурной среде региона. Исходя из вышесказанного, одной из важнейших задач, которые призвано решать общеобразовательное заведение, - обеспечение усвоения обучающимися системы знаний основ наук.

В систему научных знаний входят следующие элементы:

- научные факты;

- понятия;

- законы;

- теории.

Все они находятся в тесной связи, между ними трудно установить резко очерченные границы. Тем не менее, в содержании любой науки, можно выделить указанные элементы, как относительно самостоятельные единицы знаний.

В содержании общеобразовательных дисциплин, как в любой системе знаний, важнейшую роль играют понятия. Они образуют в результате анализа вновь открытых научных фактов. Через системы научных понятий формируются законы. Каждый закон выражает связь между понятиями. Изучение теории также требует усвоения понятий.

Таким образом, без усвоения понятий не может быть ни усвоения законов, ни усвоения теорий. Вот почему очень важно в процессе обучения обеспечить высокое качество усвоения учениками основных понятий конкретной образовательной дисциплины. Чтобы правильно организовать процесс формирования понятий, надо знать основные особенности и закономерности, которым он подчиняется.

К сожалению, при разборке учебных программ и учебников (в том числе и по математике) авторы чаще всего идут от логики формирования понятий, особенностей их усвоения у обучающихся и различных факторов, оказывающих существенное влияние на усвоение понятий. Поэтому расходуется очень много времени на формирование понятий, но уровень их усвоения обучающимися не удовлетворяет требованиям ГОСТов.

В данной работе рассматривается логические и психологодидактические основы формирования математических понятий у обучающихся общеобразовательных учебных заведений.

Введение

Программа по алгебре для 7-9 классов имеет четыре содержательные линии:

1.    Действительные числа;

2.    Тождественные преобразования;

3.    Уравнения, неравенства;

4.    Элементарные функции:

к которым в 10-11 классах добавляется еще две:

5. Элементы математического анализа;

6. Приложения математического анализа.

 

В седьмом классе закладывается фундамент четвертой содержательной линии «элементарные функции», вводится одно из важнейших математических и общенаучных понятий – понятие «функции», формируется система знаний и умений по данной теме. Поэтому первый урок введения понятия «функция» занимает одно из значительных мест в курсе алгебры 7 класса.

Современная психология рассматривает учебный процесс как активное взаимодействие учителя, с одной стороны, и учащихся с другой, в ходе которого у них формируется определенная система знаний, умений и навыков, а также убеждений, составляющих мировоззрение. Также современная психология просматривает тесную связь между обучением и развитием личности. Весьма важным для повышения эффективности обучения является вопрос о критериях умственного развития личности в целом. В замечательной книге В.П. Иржавцевой «Систематизация и обобщение знаний учащихся в процессе изучения математики» автором выделяются четыре группы критериев:

Первая группа охватывает некоторые особенности мышления, а именно:

1) самостоятельность мышления;

2) широта переноса приемов умственной деятельности;

3) проникновение в сущность изучаемых явлений;

4) быстрота умственной ориентировки при решении нестандартных задач.

Ко второй группе критериев относятся качества анализирующего наблюдения, представляющего собой синтез процессов, направленного на объект восприятия и мышления.

Третью группу составляют показатели практической деятельности учащихся.

Четвертая группа – это показатели осознанности учащимися своих мысленных операций.

Достичь всех этих критериев умственного развития и развития личности в целом помогают принципы развивающего обучения по Л. В. Занкову, которых  я и стараюсь придерживаться, строя свои уроки.

1. Повышение теоретического  уровня содержания обучения (объективно способствует интенсификации развития логической памяти, операций развития анализа и синтеза, отвлечения и обобщения)

2. Принцип обучения на высоком уровне трудности, доступном детям (раскрывает духовные силы ребенка, дает им простор и направление)

3. Быстрый темп продвижения в обучении (требует от учителя умения выделить самое главное в данном учебном материале и сосредоточить на объяснении его свое внимание учащихся)

4. Принцип осознания учащимися процесса учения.

Схема учения, как деятельности:

Осознание → Мотивы→ Способы → Контроль →Оценивание →Результат

5. Возможность развития, продвижения в обучении всех детей, даже наиболее слабых.

Одним из сложных и основных моментов в преподавании математики является работа по введению нового понятия. Читая и анализируя труды таких замечательных авторов, как Л.М.Фридман, В.П. Иржавцева, Н.И. Зильберберг, Я.И. Груденов, я стала использовать поэтапный метод введения нового понятия.

I этап – подведение под понятие;

II этап – собственно введение понятия;

III этап – закрепление понятия;

IV этап – применение понятия на практике.

Но прежде, чем раскрыть каждый этап, уточним, что такое «понятие». Всякий математический (и не только) объект обладает какими – то свойствами. Среди этих свойств имеются существенные и несущественные для его определения. Свойство является существенным, если оно присуще этому объекту и без него оно не может существовать. Несущественные свойства – это обычно случайные, их отсутствие, как правило, не влияет на существование объекта. Поэтому, чтобы понимать о каком объекте идет речь, достаточно знать его существенные свойства. В этом случае говорят, что имеется понятие об этом объекте. Следовательно, понятие- это целостная совокупность суждений о существенных свойствах соответствующего объекта. Определением понятия называется указание существенных свойств объекта понятия, которые достаточны для распознавания этого объекта.

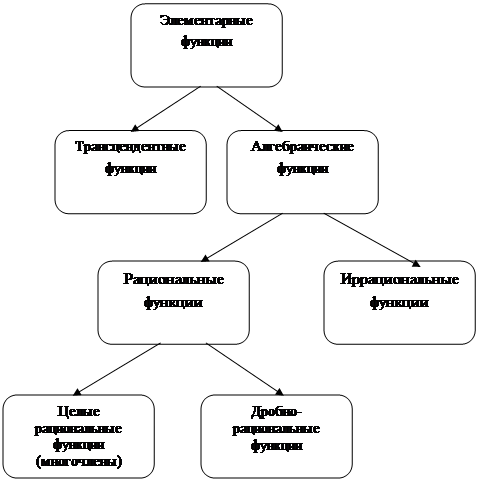
На первом этапе я показываю место данного понятия в школьном курсе математике через содержательные линии предмета, используя различные таблицы (см. приложение табл. 1.2), классифицирую понятие (см. приложение табл.3), показываю практическое применение данного понятия в других областях знаний (см. приложение). Затем в зависимости от сложности вводимого понятия:

-либо даю систему таких упражнений, чтобы на их основе учащиеся легко и быстро сформулировали определение нового понятия самостоятельно;

-либо предлагаю рассмотреть готовые примеры, выделить признаки нового понятия и сформулировать его определение;

- либо сама формулирую определение понятия. Это можно сделать двумя способами:

1.      По следующей схеме (определение через род и видовые отличия):

Название определяемого объекта → Родовое понятие + Видовые отличия,

 

где родовое понятие – более общее понятие, к которому принадлежит определяемое понятие, видовые отличия (признаки) – свойства, которые отличают данный объект от других объектов, принадлежащих данному родовому понятию.

2.          По этой же схеме, но в качестве видовых отличий указывается способ получения объектов определяемого понятия один за другим по порядку (такое определение называется индуктивным или рекуррентным).

Однако формируя определения математических понятий, нужно знать основные требования к логическому определению понятий (по Л.М.Фридману):

1) определения должны быть научно правильными;

2) определения не должны содержать порочного круга;

3) определение должно содержать указание на ближайшее родовое понятие;

4) определение не должно быть тавтологией;

5) определение должно быть достаточным;

6) определение не должно быть избыточным.

На этапе закрепления нового понятия детям предлагается обосновать либо уже готовые примеры и контрпримеры, либо самим придумать и опять же обосновать примеры введенного понятия, опираясь на родовое понятие и видовые отличия. Данный этап наиболее способствует непроизвольному запоминанию материала, которое оказывается более прочным, чем произвольное, опирающееся на пассивные способы работы.

Для применения нового понятия на практике детям предлагается (или составляется совместно) определенный алгоритм. Читая поочередно указания алгоритма, учащийся решает задачу, при этом обязательно обосновывая каждый свой шаг и проговаривая свои действия вслух. Алгоритмический метод, как мне кажется, позволяет учитывать индивидуальные особенности детей, дифференцировать работу в классе. Уменьшается списывание с доски, потому что учащиеся чувствуют себя уверенней, и как следствие, повышается степень их самостоятельности в работе.

Немного подробнее хотелось бы остановиться на понятии классификации ( I этап – подведение под понятие). Классификация играет важную роль в развитии логического мышления детей, в работе по формированию понятий, с помощью классификации осуществляется раскрытие объема понятия. Классификация помогает систематизировать учебный материал, получить более полное представление о взаимосвязях между понятиями и о системе математических понятий и, как следствие, углубить и упрочить знание и понимание детьми предмета.

В основе классификации лежит операция деления элементов родового понятия на виды по признаку, выражающему свойства элементов рода. Любая классификация должна удовлетворять следующим требованиям:

1) классификация должна проводиться по одному и тому же признаку (основание классификации);

2) образованные классы не должны пересекаться (не иметь общих элементов);

3) классификация должна быть соразмерной (все классы образуют данное понятие);

4) классификация должна быть непрерывной (классами должны быть видовые понятия по отношению к понятию, подлежащему классификации).

В классификации понятий различают три компонента:

Классифицируемое понятие – это понятие, объем которого требуется раскрыть

Основание классификации  признак, по которому производится классификация

Члены классификации т.е. образованные в результате классификации классы

 

Различают два вида классификации:

1 классификация по видоизмененному признаку	2 дихотомическая классификация
Выбор признака классификации зависит от цели квалификации. Важнейшим требованием к основанию классификации является его объективность.	Деление объема классифицируемого понятия на два противоречащих друг другу видовых понятия, один из которых обладает данным признаком, а другой не обладает.

 

В школьной программе часто применяются оба вида классификации. Первоначально объем классифицируемого понятия разбивается на базе дихотомии на два противоречащих друг другу видовых понятия, один из которых обладает данным признаком, а другой не обладает им. Затем дальнейшему исследованию в большинстве случаев подвергается то видовое понятие, которое обладает признаком разбиения.

Ниже Вашему вниманию предлагается план – конспект урока, как один из примеров воплощения всего вышесказанного на практике.

План- конспект урока.

Тема урока: Функция

Тип урока: Вводный

Вид урока: Комбинированный (проверка знаний, формирование знаний)

Методы, формы и средства.

1. Письменный контроль – индивидуальная форма - математический диктант. Позволяет быстро проверить степень усвоения знаний, умений и навыков по теме, качество выполнения домашнего задания.

2. Поэтапный метод введения нового понятия – фронтальная и индивидуальная формы -  рассказ, коллективная фронтальная эвристическая беседа, опрос, работа учащихся у доски, в справочниках и в тетрадях.

Фронтальная форма рассчитана на учащихся, имеющих примерно равный уровень подготовки. Фронтальная работа дает возможность учителю включить большую часть класса в активную учебную деятельность, организовать работу всего класса, опираясь на наиболее активных учеников, которые подают пример другим ребятам. Отвечая на вопросы учителя, приводя разнообразные примеры, доказывая свои утверждения, сами учащиеся способствуют более широкому обстоятельному анализу рассматриваемого учебного материала. В такой беседе, взаимно дополняя друг друга, ученики основательнее усваивают материал, глубже проникая в его сущность. Коллективно решая задачи, делая упражнения, учащиеся быстрее продвигаются к поставленной цели. Возникшие затруднения в познавательной деятельности разрешаются усилиями всего коллектива учащихся.

Этапы урока:

1. Организационный

2. Проверка предыдущих знаний

3. Введение новых понятий

4. Определение домашнего задания

5. Подведение итогов обучения

Цели урока.

 Учебные:

1. Проверить усвоение знаний, умений и навыков по теме « Прямоугольная система координат на плоскости»

2. Показать перспективу изучения содержательной линии «элементарные функции» и ее связь с другими линиями.

3. Показать практическое применение понятия «функция», и связь между предметами.

4. Ввести понятие функции, области определения и области значения функции, показав и обосновав зависимость данных понятий не только в седьмом классе, нои во всем курсе школьной математики.

5. Добиваться глубокого и осмысленного усвоения материала.

6. Научить применять полученные знания на практике.

Развивающие:

1. Развивать умение детей анализировать и обобщать.

2. Развивать логическое мышление.

Воспитательные:

1. Учить культуре мысли:

- правильности мышления (полноценность аргументации, полнота и выдержанность классификации);

- стилю мышления (доминирование логической схемы рассуждений, лаконизм, четкая расчлененность хода  рассуждений, точность символики);

2. Приучить детей к аккуратности, вежливости, терпимому отношению друг к другу.

Оформление доски.

  На одной из створок доски записан математический диктант.

Математический диктант (М.Д.)

           1 вариант                                                               2 вариант

 

1. Начертите прямоугольную систему координат.

2. Пронумеруйте квадранты.

3. Назовите абсциссу и ординату данных точек и укажите, каким координатным углам принадлежат эти точки.

К (5;0)	А (-1;3)
L (-6;-2)	В (0;-2)
4. Постройте отрезок по координатам его концов. М (-5;0) и N (0,5; -3)	Постройте прямую, проходящую через                                                                                точки. С (1,5;3) и Д (-2;-1)
5. Постройте точку, симметричную данной
Е (3;4)	Д (2;-2)

 

На фронтальной части доски висят схемы и таблицы.

 

(смотри приложение)

 

Ход урока

 

Организационный этап.

1. Взаимные приветствия учителя и учащихся.

2. Проверка отсутствующих.

3. Проверка подготовки учащихся к уроку.

4. Организация внимания.

5. Изложение целей данного урока.

 

Этап проверки усвоения предыдущей темы.

Учитель: Дети, прежде, чем приступить к изучению новой темы, мы проверим ваши знания, умения, навыки по теме «Прямоугольная система координат на плоскости».

Проводит математический диктант. (5-7 минут)

После того, как собраны листочки с М.Д. 1-3 мин. проходит обсуждение ответов на вопросы, возникшие у детей. Оценки за М.Д. объявляются в начале следующего урока.

 

Этап введения новых знаний

I. Подведение под понятие (4-5 мин.)

Учитель: Ребята, сегодня у нас очень важный урок, мы с вами начинаем изучение четвертого кита Математики. Его имя Функция. Функция – это одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами.

Каждая область знаний физика, химия, биология, медицина, экономика и т.д. – имеет свои объекты изучения, устанавливает свойства и, что особенно важно, взаимосвязи этих объектов, которые на математическом языке называются функциональными зависимостями или функциями. Например (Учитель показывает различные таблицы и  графики: кардиограмма, изобара, изохора  и т. д.).

А теперь давайте посмотрим, как содержательная линия «элементарные функции» пронизывает весь школьный курс математики, и узнаем какие, умения и навыки по данной теме мы получим, переходя из класса в класс (см. табл.2). За пять лет мы с вами изучим более двадцати примеров функций пяти различных видов (см. табл.3).

 

II. Введение понятия.

Учитель: А теперь мы с вами перейдем непосредственно к введению понятия функции и поработаем с таблицей 4.

Мы с вами уже знаем, что величины делятся на постоянные и переменные. Ответьте, какие величины называются постоянными, какие переменными?

Дети: Постоянные – не меняются, переменные – меняются.

Учитель: Приведите, пожалуйста, примеры таких величин и обоснуйте свой ответ.

Дети приводят примеры, объясняя свой выбор: постоянные (при определенных условиях) – температура кипения, вес какого- либо тела и т. д; переменные (при определенных условиях) – скорость и т. д.

Учитель: Теперь, пожалуйста, объясните мне, как вы понимаете, что такое зависимость?

Дети пытаются объяснить, дать определение зависимости, приводят примеры, обосновывают свои высказывания. В итоге совместной работы класс формулирует определение зависимости между величинами.

Зависимость – это связь

1. между величинами

Например: успеваемость вашего класса зависит от оценок каждого ученика, благосостояние вашей семьи зависит от заработной платы ваших родителей и т. д.

Контрпримеры: температура воздуха не зависит от вашего настроения.

Результат, примеры и контрпримеры дети записывают в свои справочники.

Учитель: Наступает важный момент, мы с вами вплотную подошли к определению функции. Я сейчас сформулирую это важное определение, а ваша задача выделить в нем родовое понятие и видовые признаки. Внимание!

Учитель формулирует определение функции, дети пытаются проанализировать его и разбить на основные составляющие.

После общего обсуждения результат записывается в справочники.

Функция – это зависимость

1. переменной y от переменной х;

2. при которой каждому значению х ставиться в соответствие единственное значение y.

х называется независимая переменная или аргумент функции;

y называется зависимая переменная или значение функции.

III Закрепление понятия.

Примеры (см. приложение, таблица 4)

Контрпримеры (см. приложение, таблица 4)

Учитель: Посмотрите на доску. Здесь записаны примеры и контрпримеры на данное понятие. Ваша задача найти функции и доказать, что данные зависимости являются функциями.

Дети отвечают, спорят, доказывают.

Учитель: Рассмотрим еще несколько примеров функции (задачи на движение S(t)=vt,    t(S) =s/v и т. д.).

Далее учащиеся самостоятельно придумывают, объясняют собственные примеры и контрпримеры (на родовое понятие и на каждый признак).

По той же схеме вводится понятие области определения и области значения функции.

Область определения функции – значения (числа)

1. которые может принимать независимая переменная.

Область значения функции значение (числа)

1. которые может принимать независимая переменная;

2. при х, принадлежащих области определения.

Примеры: Рассматривая все те задачи на движение, констатируем, что путь, скорость и время – величины положительные, для каждой функциональной зависимости определяем область определений, область значений.

S(t)=vt,   t – независимая переменная, область определений  t>0;

S – Зависимая переменная, область значений S>0.

t(S) =s/v, S – независимая переменная, область значений S>0;

t – зависимая переменная, область определений  t>0.

Контрпримеры:

S(t)=vt,   t – независимая переменная, область определений  t<0;

S – Зависимая переменная, область значений S<0.

Учитель: Вернемся к нашей основной таблице (таблица 4) и рассмотрим еще один теоретический момент. Функция может быть задана различными способами: формулой, таблицей и графиком. Например (см. таблицу 4). Все три способа более подробно мы рассмотрим на следующем уроке, сейчас же займемся решением задач, на данную тему.

IV. Применение понятия на практике.

Учитель: Дети, зная определение области значения и области определения функции, ответьте мне, пожалуйста, на следующий вопрос. Как найти значение функции при заданном значении переменной? Составьте алгоритм для решения данной задачи.

После коллективного обсуждения учащиеся приходят к общему решению и записывают результат в справочник.

Алгоритм.

1. Подставить заданное числовое значение переменной в уравнение функции вместо х.

2. Найти значение полученного числового выражения.

3. Записать ответ.

После первого теоретического блока класс приступает к решению номеров из учебника и заданий по карточкам:

- № 536 (устно) – проговаривая и доказывая вслух индивидуально;

Образец ответа: Дана функция, заданная формулой…(прочитать формулу), независимой переменной заданной функции является переменная…(назвать), зависимой – является переменная …. (назвать).

- № 537 (1,3); №538 – письменно, каждый в тетради и по вызову у доски,  на оценку отвечая по схеме: что дано, что надо сказать, как сделать, почему так,  а не иначе;

Образец ответа и записи:

№537 (1)

Что дано? Функция, заданная формулой  y =3х, где х – независимая переменная,  y – зависимая.

Что надо сделать? Вычислить значение функции при х, равном -2.

Как будем выполнять задание? С помощью алгоритма.

Первое: Поставим данное число -2 в формулу вместо аргумента,

 Y (-2) =3* (-2).

Второе: Вычислим значение полученного числового выражения,

Y (-2) = -6.

Третье: Запишем ответ.

Ответ:  y = -6, при значении аргумента, равном -2. (или Y (-2) = -6.)

№ 538 (2)

Что дано? Функция, заданная формулой S=60t,    где t  – независимая переменная, S  – зависимая.

Что надо сделать? Вычислить значение  t , если S = 240.

Как будем выполнять задание? 

Первое: Поставим данное число 220 в формулу функции, вместо зависимой переменной,

240 = 60 t.

Второе: решим полученное уравнение по алгоритму

240 = 60 t: 60

t = 4 (ч)

Третье: Запишем ответ.

- разноуровневые задания по карточкам на нахождение области определения и области значений функции, (см. приложение) – письменно, каждый в тетради и по вызову у доски на оценку.

Образец ответа и решения:

Что дано? дана функция, заданная формулой, где z-  зависимая, q – независимая переменная	Z=
Что надо сделать? Найти область определения и область значений функций
Как? 1. Т.к. дана алгебраическая дробь, следовательно, ее знаменатель не может быть равен нулю, т.е. область определения заданной функции q –любое, из множества действительных чисел, кроме q#1	1. 1- q#0 q#1 следовательно, область определения  q ЄR q# 1
2. Т.к q может принимать значения, равные нулю, отрицательные и положительные, и  может принимать отрицательные и положительные значения, следовательно, в область значений функции входят все числа из множества действительных.	2. Z Є R

 

Дети, которые решают с опережением, в конце урока сдают тетради с классной работой на проверку.

Этап определения домашнего задания.

Учитель диктует, дети записывают: запишем домашнее задание

1. § 30, стр. 121-122, выучить теоретический материал;

2. №537(2,4), № 539;

3. творческое задание: Отыскать примеры практического применения понятия «функции» (привлекая к сотрудничеству родителей).

Этап подведения итогов обучения.

Учитель: Итак, сегодня на уроке мы с вами получили следующую сумму знаний, умений и навыков:

1. Дали определение одного из важнейших математических  и общенаучных понятий  -функции.

2. Научились находить область значений и область определения функции, вычислять ее значение при заданном аргументе.

3. Рассмотрели перспективу изучения функции в старших классах.

4. Увидели где, и как применяется функциональная зависимость на практике, в других областях знаний.

Учитель сообщает оценки, благодарит всех за работу на уроке, прощается.

Заключение

Поэтапный метод подведения под понятие я использую на своих уроках (как алгебры, так и геометрии) постоянно.  Этот метод пришелся по душе и мне и моим ученикам. Дети легко усвоили схему определения понятия (через рол и видовые отличия) и, почти все, с удовольствием пользуются ею при построении определений. Учащиеся учатся самостоятельно мыслить, отстаивать свою точку зрения  и соглашаться с более точными и «красивыми» ответами своих товарищей.

Урок «Функция» был проведен мною в двух седьмых классах. Результаты проверки усвоения знаний, умений и навыков по данной теме показали, что 70% детей усвоили и успешно применяют его на практике. У 30% детей затруднение вызывают задания на определение области значений и области определения функции. Следовательно, более тщательное внимание нужно уделить подбору заданий на данный теоретический блок, разработать алгоритмы для нахождения области определения и области значения функции для слабых детей, привести индивидуальные консультации.

Список литературы:

 1. И.С. Кон «Психология ранней юности», Москва, «Просвещение». 1988.

2. Я. И. Груденев «Психолого-дидактические основы методики обучения математике», Москва, «Просвещение», 1983.

3. «Повешение эффективности обучения математики в школе», Москва, «Просвещение» , 1989.

4. Я. И. Груденев «Изучение определений, аксиом, теорем», Москва, «Просвещение», 1981.

5. В.П. Иржавцева, Л.Я. Федченко «Систематизация и обобщение знаний учащихся в процессе изучения математики», Киев, 1988.

6. Л.М. Фридман «Учись учиться математике», Москва, «Просвещение», 1985.

7. Н.И. Зильберберг «Приобщение к математическому творчеству», Уфа, 1988

8. Ш.А.Алимов и др. Учебник по алгебре для 7 класса средней школы.

9. М.Я. Выгордский. Справочник по элементарной математике. Москва, «Наука». 1965.

10.Энциклопедический словарь юного математика, Москва, «Педагогика», 1989.

11.М.Б. Волович «Ключ к пониманию алгебры», Москва, 1997г.

 

 

Приложение

Элементарные функции
Понятие о функции
7 класс	8 класс	9 класс	10 класс	11 класс
1. Область определения	5. Возрастание и убывание.	8. Четность и нечетность.	9. Непрерывность. Точки разрыва.
2.Множество значений	6. Интервалы знакопостоянства		10. Критические и экстремальные точки.
3. Способы задания.	7. Нуль функции		11. Наибольшее и наименьшее значения.
4. График.			12. Периодичность.
			13. Точки перегиба.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Но  в процессе усвоения математических понятий перед учащимися возникает ряд трудностей, которые мне, как преподавателю предстоит разрешить при дальнейшей  работе по данной теме.

Основные трудности возникают у обучающихся при формировании у них понятий об объектах, которые невозможно представить наглядно, образно в виде натуральных объектов, их моделей или условных (знаковых) изображений.. таковы, например понятие «число», «функция» и т. д. Усвоение такого рода понятий требует высокого уровня абстрактного мышления у обучающихся.

Определенные трудности вызывает у учащихся дифференцировка сходных по каким-либо признакам понятий, а также установление существенных связей и отношений между ними. Следует отметить, что в упражнениях школьных учебников и в сборниках задач не уделяется должного внимания формированию у обучающихся умения выполнять эти важные мыслительные операции.

Рассмотренные трудности в усвоении понятий могут быть преодолены на основе более глубокого изучения закономерностей процесса усвоения понятий обучающимися и совершенствования методики их формирования.

 

Карточки с разноуровневыми заданиями на нахождение

области определения функции

	В-1 1. y = 60х - 45 2. y = - 3. y =		В-2 1. y = 2. y = 3. y =

 

 

 

 

 

 

В-3 1. y = х2 - 7 2. y = 3. y =

В-4 1. y = 2. y = 3. y =

 

 

 

 

 

	В-5 1. y = (3х-5)(1-х) 2. y = 3. y =		В-6 1. y = (5-х)(3-2х) 2. y = 3. y =  +

 

 

 

 

 

 

Величины
Постоянные	Переменные
Т кипения, масса твердого тела, объем	Скорость, температура тела

 

Зависимость – это связь

1) между величинами

Ex S=5t, где V= 5 км/ч – const

S

 

 

                             t

Функция – это зависимость

1) переменной y от переменной х

2) при которой, каждому значению х ставиться в соответствии единственное значение y

х – независимая переменная или аргумент функции

y – зависимая переменная или значение функции

Ex.1		Ex.2		kEx.3
Дети	Стулья	Дети	Стулья	Дети	Стулья
Вика       →1-ый Сергей   →2-ой Юля       →3-ий Андрей  →4-ый		Вика           →1-ый Сергей           2-ой Юля           →3-ий Андрей      →4-ый		Вика           →1-ый Сергей           2-ой Юля           →3-ий Андрей      →4-ый

 

Как найти значение функции при заданном значении аргумента?

Область определения функции.

Область значений функции.

Способы задания функции

С помощью формулы.

Табличный.

Графический.