ПОНЯТИЕ СТЕПЕНИ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ

Понятие степени с целым отрицательным
показателем

Цели: ввести понятие степени с целым отрицательным показателем и формировать умение его применять.

Ход урока

I. Организационный момент.

II. Анализ результатов контрольной работы.

Проанализировать ошибки, допущенные учащимися в работе. Вынести на  доску  решение  заданий,  вызвавших  затруднения  у большинства учащихся.

III. Устная работа.

– Вычислите:

а) 2³;                    б) (–7)²;                     в) (–3)³;                      г) ;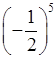

д) 5³;                    е) ;                   ж) (–2)⁴;                     з) ;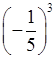

и) 6³;                    к) 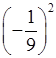;                л) (–3)⁰;                      м) 2¹.

IV. Объяснение нового материала.

Объяснение проводить по следующей схеме:

1. П о к а з  необходимости представления больших и малых чисел в обозримом и удобном для практики виде (рассмотрение примеров со с. 203–204 учебника). Можно провести аналогию с введением десятичных дробей, когда для уменьшения единиц в десять раз мы ввели запятую для отделения разрядов десятых, сотых и т. д. В случае со степенями с основанием 10 мы поступили аналогично, введя отрицательный показатель степени для выражений: 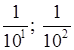 и т. д.

2. В в е д е н и е   п о н я т и я  степени с целым отрицательным показателем.

Необходимо дать определение степени с целым  отрицательным показателем и вынести на доску запись:

Затем привести несколько примеров, показывающих, как вычисляются степени  с  целым  отрицательным  числом.  При  этом  обратить  внимание  на  типичную  ошибку:  у  учащихся  степень  с  целым  отрицательным показателем может ассоциироваться с отрицательным числом (например, 2^–3 = –2³).

3. Можно вывести следствие, что числа а^п и а^–п являются взаимно-обратными. Для этого привести несколько примеров типа:

3³ = 27;    3^–3 = .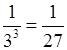

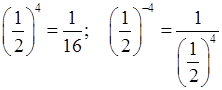 = 16.

Затем сделать общий вывод: 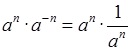 = 1.

4. Напоминаем,  что а⁰ = 1,  для а ≠ 0, выражение 0⁰ – не имеет смысла; 0ⁿ = 0 для натуральных п.

Правило: Выражение 0^п для целых отрицательных п не имеет смысла.

П р и м е р ы:                 12⁰ = 1;                                  (–3,5)⁰ = 1;

                                         0⁴ = 0;                        0¹ = 0;

                                         0⁰ – не имеет смысла;

                                         0^–3 – не имеет смысла.

V. Формирование умений и навыков.

На этом уроке необходимо начать формировать у учащихся следующие умения:

– преобразовывать выражения в дробь или произведение, используя определение степени с целым отрицательным показателем;

– вычислять степени с целым отрицательным показателем;

– представлять числа в виде степени с целым показателем.

1. № 964, № 965 – устно.

2. № 966.

Р е ш е н и е

а) 8 = 2³; 4 = 2²; 2 = 2¹; 1 = 2⁰;  = 2^–1; 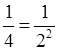 = 2^–1; 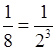 = 2^–3.

б) 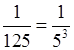 = 5^–3; 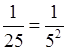 = 5^–2;  = 5^–1; 1 = 5⁰; 5 = 5¹; 25 = 5²;
125 = 5³.

3. № 968 (а; б; в; е; з; к).

Р е ш е н и е

а) 4^–2 = ;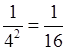

б) (–3)^–3 = ;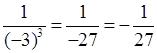

в) (–1)^–9 = 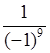 = –1;

е) ;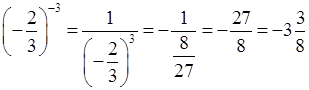

з) ;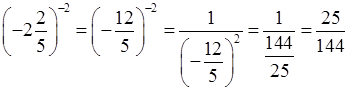

к) 1,125^–1 = .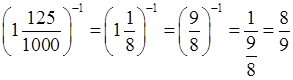

4. Многие учащиеся допускают ошибки при вычислении значений степеней с дробным основанием. И сами вычисления очень громоздкие, записываются в виде «многоэтажных» дробей. Необходимо научить учащихся рациональному приёму:

.

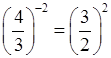Можно предложить в сильном классе самостоятельно провести доказательство:

.

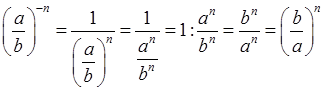Полученное равенство выносится на доску:

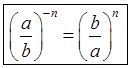
№ 970 (в, г, е).

Р е ш е н и е

в) ;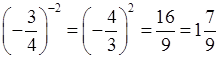

г) ;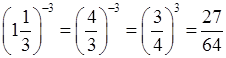

е) .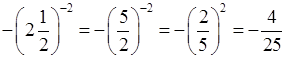

5. № 969 (а, в, д), № 971, № 972 (устно).

Эти три упражнения являются очень важными. Выводы, которые получат учащиеся, помогут им избежать ошибок в вычислении степеней, особенно «путаницы» в знаках результата.

Р е ш е н и е

№ 969.

а) –10^–4 = 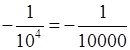 = –0,0001;

в) (–0,8)^–2 = ;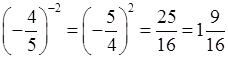

д) –(–2)^–3 = .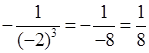

№ 971.

а) 9^–5 =  > 0;

б) 2,6^–4 =  > 0;

в) (–7,1)^–6 =  > 0;

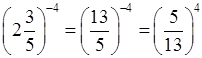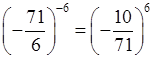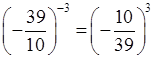г) (–3,9)^–3 =  < 0.

После выполнения упражнения № 972 полезно дать учащимся задание по составлению блок-схемы полученного  в ы в о д а:

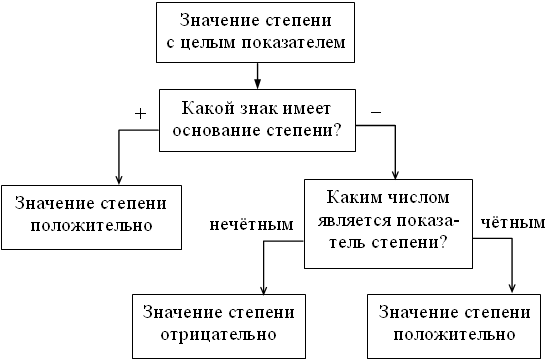
VI. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Как определяется степень с целым отрицательным показателем?

– Чему равно любое число (не равное нулю) в нулевой степени?

– Какое значение имеет выражение 0^п при целом n < 0?

– Чему равно а^п · а^–п?

– Можно ли получить отрицательный результат при возведении положительного числа в отрицательную степень?

Домашнее задание: № 967, № 968 (г, д, ж, и), № 969 (б, г, е), № 970 (а, б, д), № 983.