Пособие по геометрии 7-8 класс. Практические работы в программе Geogebra

Пособие по геометрии 7-8 класс: 

практические работы в программе Geogebra

Содержание:

1.    Простейшие геометрические построения в программе Geogebra

(построение   медиан, высот,     биссектрис,   вписанной окружности).

2.    Простейшие геометрические построения в программе Geogebra (построение серединных перпендикуляров, описанной окружности).

3.    Геометрические построения в программе Geogebra за рамками школьной геометрии (окружность Эйлера – окружность 9 точек).

ПОСТАНОВКА ЗАДАЧИ: ПОСТРОИТЬ ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК, В НЕМ ТРИ МЕДИАНЫ, ТРИ ВЫСОТЫ, ТРИ БИССЕКТРИСЫ И ВПИСАННУЮ ОКРУЖНОСТЬ.

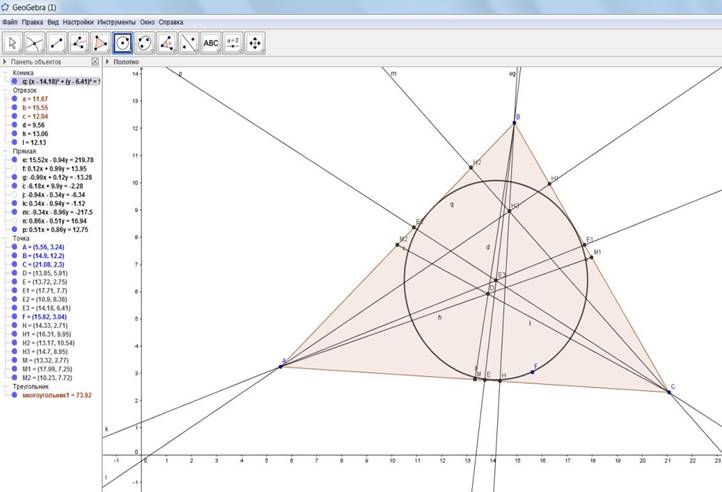
1.                        Запустите программу GeoGebra.

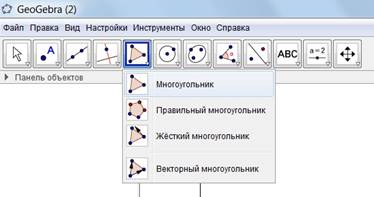
2.                        С помощью инструмента Многоугольник постройте произвольный треугольник ABC (выбираем инструмент и нажимаем в произвольных местах плоскости левой клавишей мыши ABCA не забудьте в конце нажать по первой точке, чтобы закончить контур треугольника).

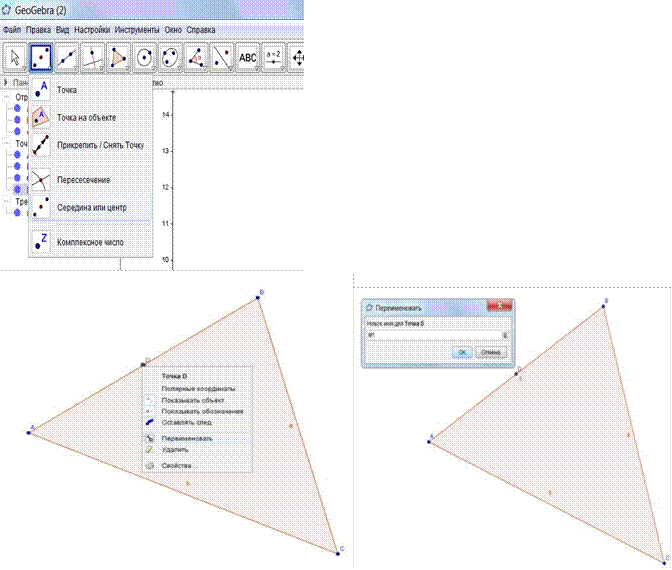
3.                        С помощью инструмента Середина или центр отметьте середины M2,M1,M отрезков AB, BC, AC (выбираем инструмент и нажимаем левой клавишей мыши по концам отрезков, наименование середин отрезков программа производит самостоятельно. Чтобы изменить название точек нажимаем на точке правой клавишей мыши и выбираем переименовать и пишем новое имя точки).

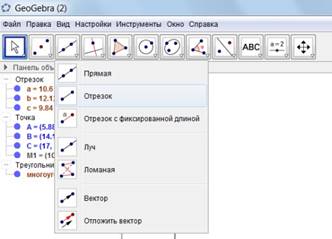
4.                        Теперь строим медианы AM1, BM, CM2 с помощью инструмента Отрезок

(выбираем инструмент и нажимаем на концах отрезка по очереди)

5.                        Находим точку пересечения всех трех медиан с помощью инструмента Пересечение (выбираем инструмент и нажимаем по очереди на две медианы, автоматически появится новая точка – точка их пересечения, которую назовем M3)

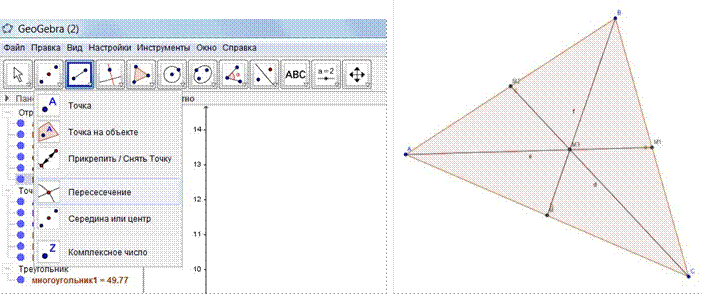
6.                        Теперь построим высоты в нашем треугольнике. Для этого выбираем инструмент Перпендикулярная прямая и нажимаем сначала на отрезок AC, к которому мы строим перпендикуляр, а потом на точку B – из какой точки он будет опущен (будет проведена прямая), а затем с помощью инструмента Пересечение найдем точку пересечения перпендикуляра и стороны AC и назовем ее H. Аналогично, построим высоты AH1, CH2. Находим точку пересечения всех трех высот с помощью инструмента Пересечение (выбираем инструмент и нажимаем по очереди на две высоты, автоматически появится новая точка – точка их пересечения, которую назовем H3)

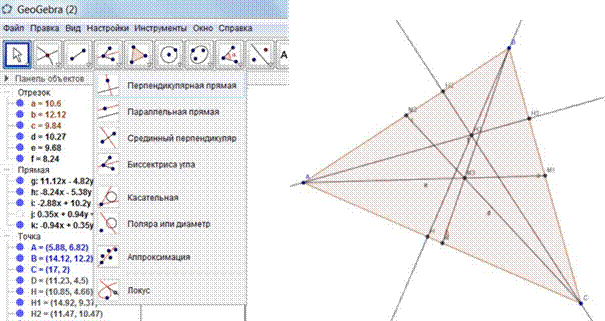
7.                        Теперь построим биссектрисы в нашем треугольнике. Для этого выбираем инструмент Биссектриса угла и нажимаем по очереди на отрезки, которые образуют угол B (т.е. AB и BC), будут проведены биссектрисы угла B (и смежного с ним угла – вторую биссектрису делаем невидимой – нажимаем на маркере этой прямой, она нам сейчас не нужна), а затем с помощью инструмента Пересечение найдем точку пересечения биссектрисы и стороны AC и назовем ее E. Аналогично, построим биссектрисы AE1, CE2. Находим точку пересечения всех трех биссектрис с помощью инструмента Пересечение (выбираем инструмент и нажимаем по очереди на две биссектрисы, автоматически появится новая точка – точка их пересечения, которую назовем Е3)

8.                       

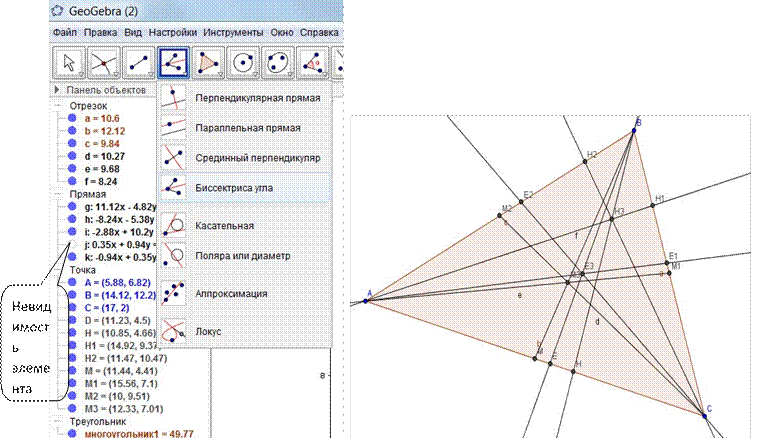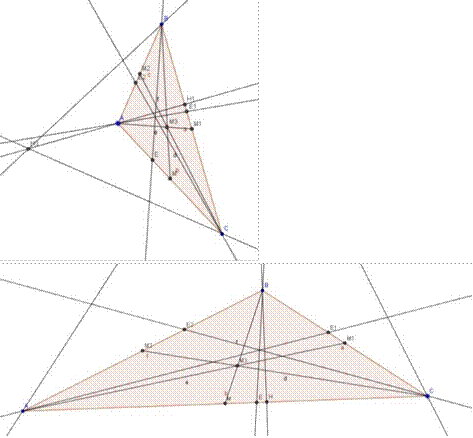
9.                        Построим вписанную окружность, зная что центр вписанной окружности всегда лежит на пересечении биссектрис треугольника (т.е. в точке Е3). Для этого используем инструмент Окружность по центру и точке, нажимаем на точку E3 и увеличиваем радиус окружности так, чтобы она касалась сторон треугольника и когда достигнет необходимого радиуса, нажимаем на левой клавише мыши. 

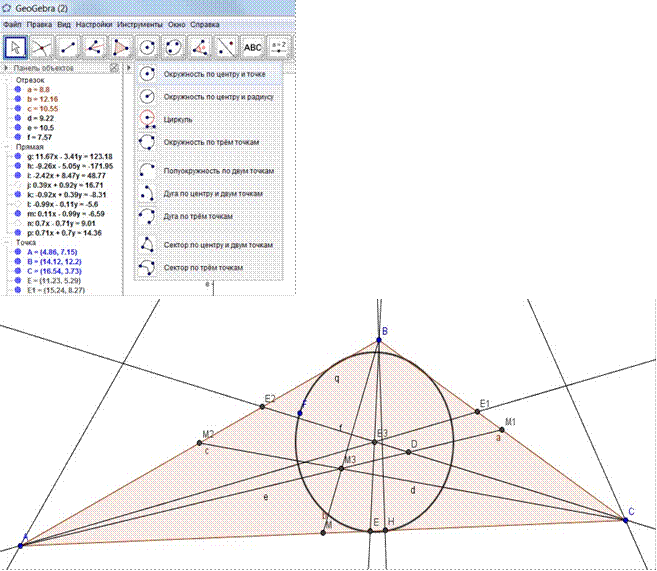
10.                   Сохраните файл в своей папке под именем практическая работа1.

Назад к содержанию…

ПОСТАНОВКА ЗАДАЧИ: ПОСТРОИТЬ ОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК, В НЕМ ТРИ СЕРЕДИННЫХ ПЕРПЕНДИКУЛЯРА И ОПИСАННУЮ ОКРУЖНОСТЬ.

1.                 Запустите программу GeoGebra.

2.                 С помощью инструмента Многоугольник постройте произвольный треугольник ABC (выбираем инструмент и нажимаем в произвольных местах плоскости левой клавишей мыши ABCA не забудьте в конце нажать по первой точке, чтобы закончить контур треугольника).

3.                 С помощью инструмента Середина или центр отметьте середины F3,F1,F2 отрезков AB, BC, AC (выбираем инструмент и нажимаем левой клавишей мыши по концам отрезков, наименование середин отрезков программа производит самостоятельно. Чтобы изменить название точек нажимаем на точке правой клавишей мыши и выбираем переименовать и пишем новое имя точки).

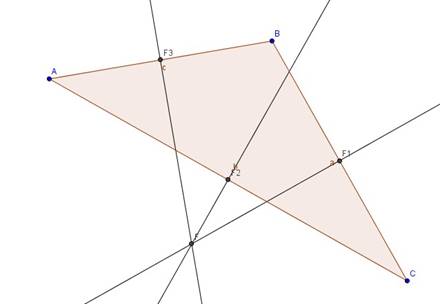
4.                 Теперь построим серединные перпендикуляры в нашем треугольнике. Для этого выбираем инструмент Перпендикулярная прямая и нажимаем сначала на отрезок AC, к которому мы строим перпендикуляр, а потом на точку F2 – из какой точки он будет проведен (будет проведена прямая). Аналогично, построим серединные перпендикуляры из точек F3 и F1. Находим точку пересечения всех трех серединных перпендикуляров с помощью инструмента Пересечение (выбираем инструмент и нажимаем по очереди на два перпендикуляра, автоматически появится новая точка – точка их пересечения, которую назовем F)

5.                 Построим описанную окружность, зная что центр описанной окружности всегда лежит на пересечении серединных перпендикуляров (т.е. в точке F). Для этого используем инструмент Окружность по центру и точке, нажимаем на точку F и увеличиваем радиус окружности так, чтобы она прошла через вершины треугольника и нажимаем на левой клавише мыши на любой вершине. 

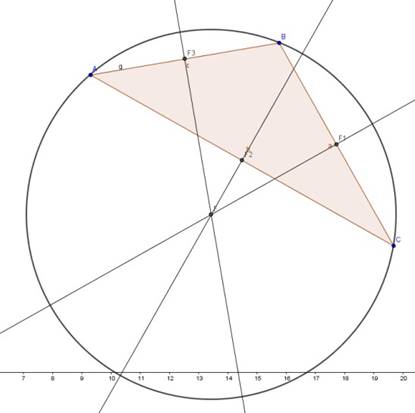
6.                 Меняем положение вершин треугольника с помощью инструмента Перемещать и наблюдаем разные чертежи.

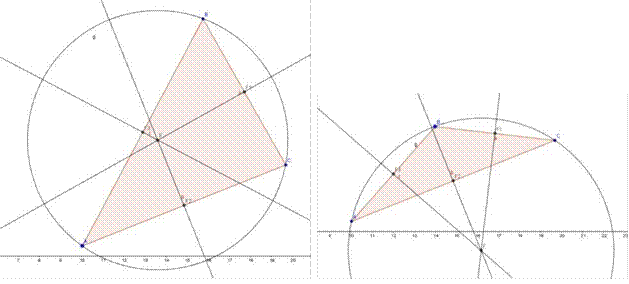
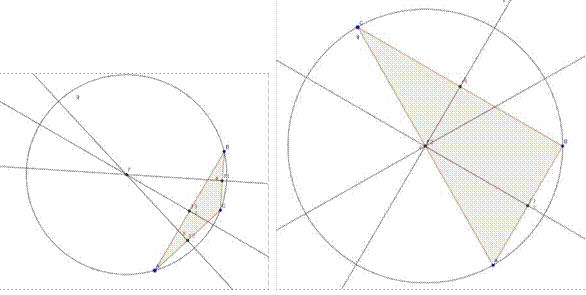
Назад к содержанию…

ПОСТАНОВКА ЗАДАЧИ: ПОСТРОИТЬ ОКРУЖНОСТЬ ЭЙЛЕРА (ИЗВЕСТНУЮ ОКРУЖНОСТЬ 9 ТОЧЕК).

Одна из красивых теорем геометрии – теорема об окружности Эйлера: в неравностороннем треугольнике середины сторон, основания высот и середины отрезков, соединяющих ортоцентр (точка пересечения высот) с вершинами треугольника, лежат на одной окружности, центром которой является середина отрезка, соединяющего ортоцентр с центром описанной окружности, а ее радиус в два раза меньше радиуса описанной окружности.

Т.е. точки А1, B1, C1, A2, B2, C2, A3, B3, C3 лежат на одной окружности, которая называется окружностью Эйлера.

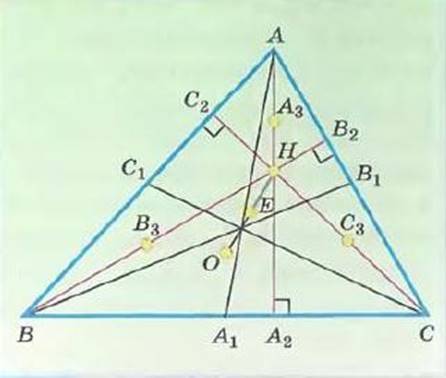
Выполнения задания:

1.                 Откройте программу GeoGebra.

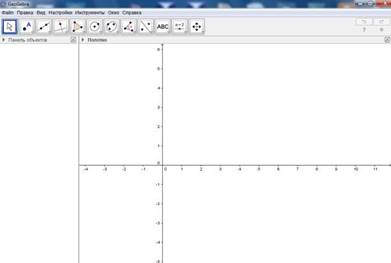
2.                 Постройте неравносторонний        треугольник        с        помощью          инструмента

Многоугольник (в 5 вкладке первый рисунок): четырьмя нажатиями клавиши мыши

3.                 Постройте в этом неравностороннем треугольнике середины сторон с помощью инструмента Середина или центр (во 2 вкладке пятый рисунок): нажатиями клавиши мыши на концы отрезков

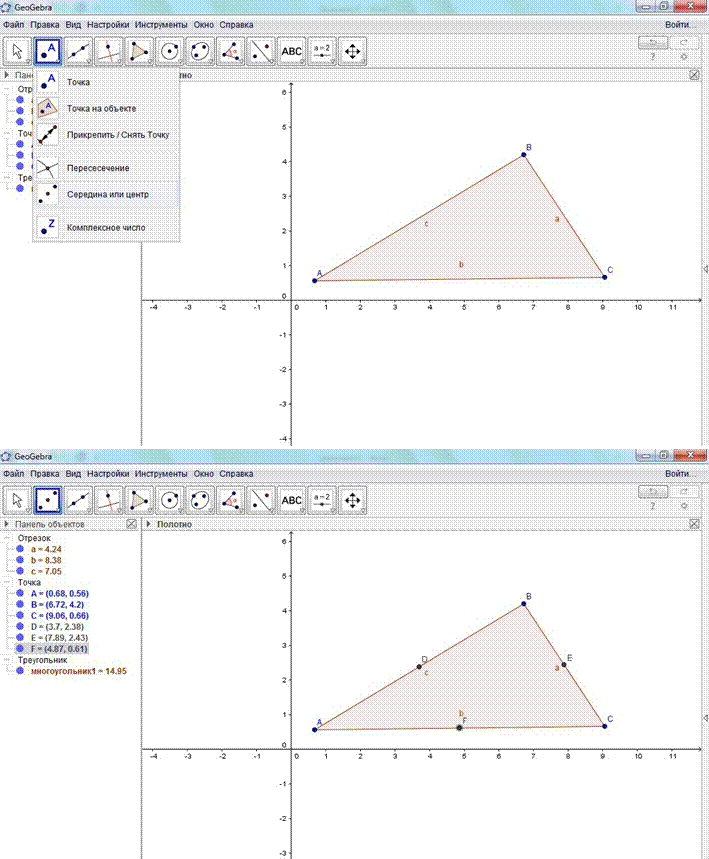
4.                 Постройте в этом неравностороннем треугольнике высоты с помощью инструмента Перпендикулярная прямая (в 4 вкладке первый рисунок): нажатиями клавиши мыши на вершину треугольника и противоположную сторону

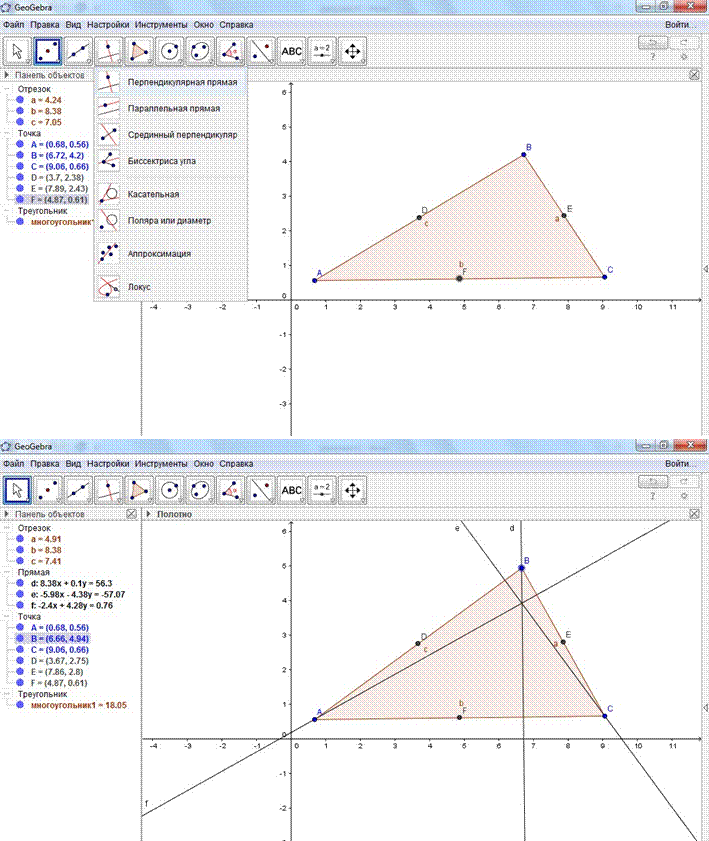
5.                 Постройте в этом неравностороннем треугольнике ортоцентр (точку пересечения высот) с помощью инструмента Пересечение (во 2 вкладке четвертый рисунок):

нажатиями клавиши мыши на две высоты треугольника

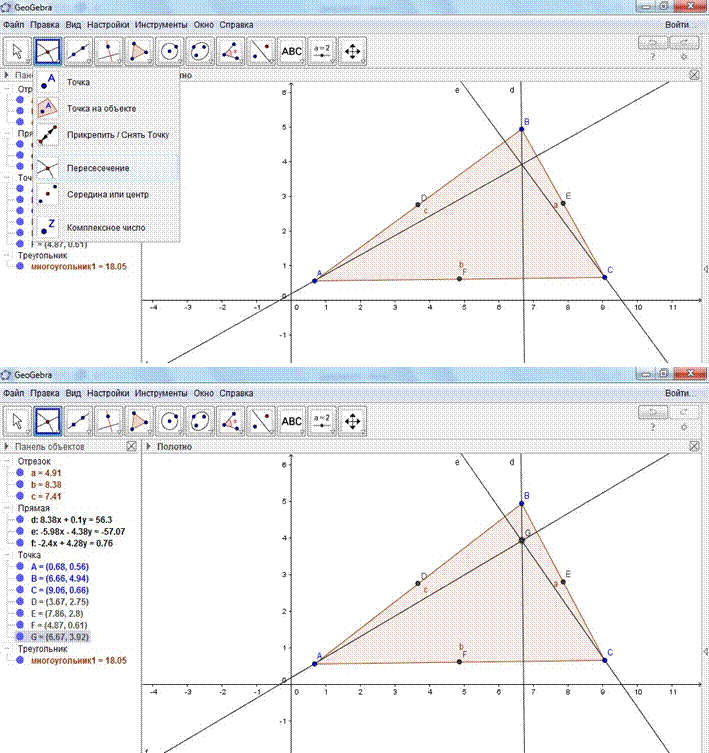
6.                 Постройте в этом неравностороннем треугольнике основания высот (точки пересечения высот со сторонами) с помощью инструмента Пересечение (во 2 вкладке четвертый рисунок): нажатиями клавиши мыши на высоту и соответствующую (противоположную) сторону треугольника

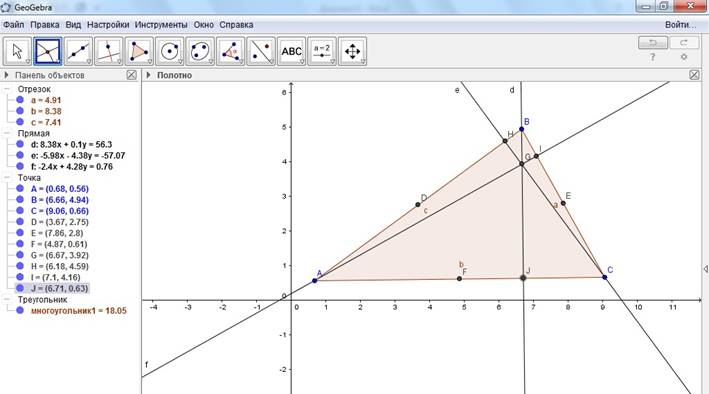
7.                 Постройте в этом неравностороннем треугольнике середины отрезков, соединяющих ортоцентр с вершинами треугольника с помощью инструмента Середина или центр (во 2 вкладке пятый рисунок): нажатиями клавиши мыши на концы отрезка (ортоцентр и вершину треугольника)

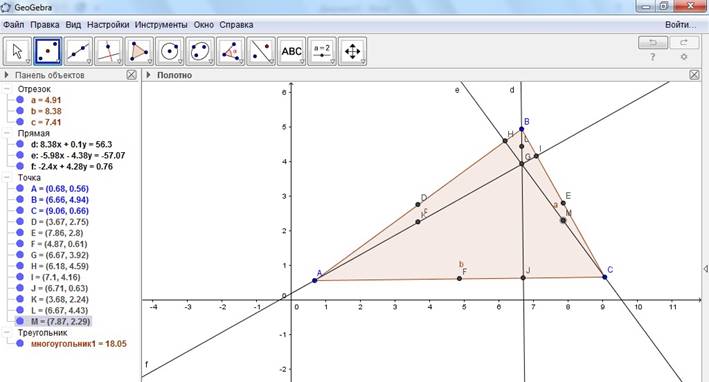
8.                 Постройте в этом неравностороннем треугольнике центр описанной окружности с помощью построения серединных перпендикуляров (инструмент Серединный перпендикуляр – в 4 вкладке третий рисунок) и точка их пересечения (инструмент Пересечение) 

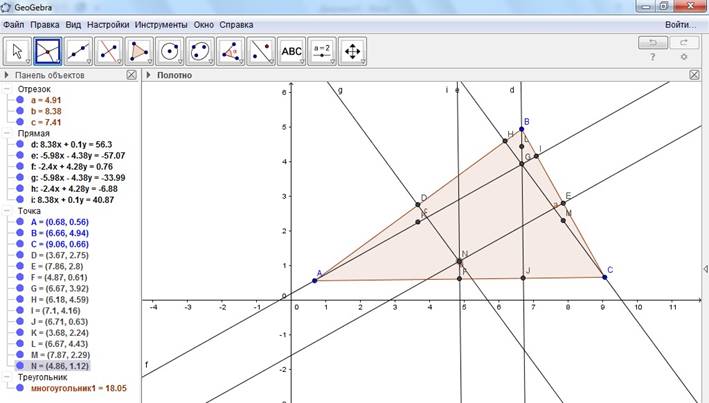
9.                 Постройте в этом неравностороннем треугольнике отрезок, концы которого – ортоцентр и центр описанной окружности с помощью инструмента Отрезок (в 3 вкладке второй рисунок) 

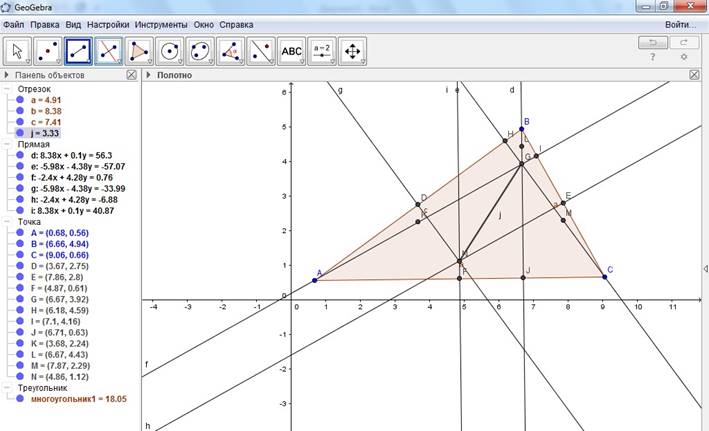
10.            Наконец, постройте в этом неравностороннем треугольнике середину отрезка, построенного в пункте 9 – ЭТО И ЕСТЬ ЦЕНТР ОКРУЖНОСТИ ЭЙЛЕРА

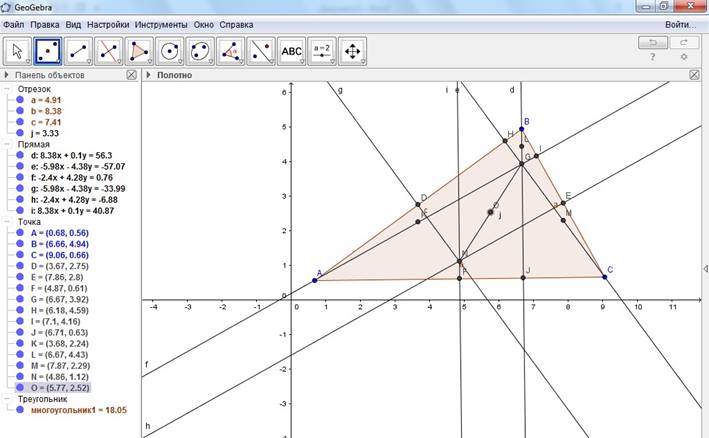
11.            И, наконец, осталось построить окружность Эйлера с помощью инструмента Окружность по центру и точке (в 6 вкладке первый рисунок) – нажатием клавиши мыши в центр и по любой из 9 построенных (описанных выше) точек

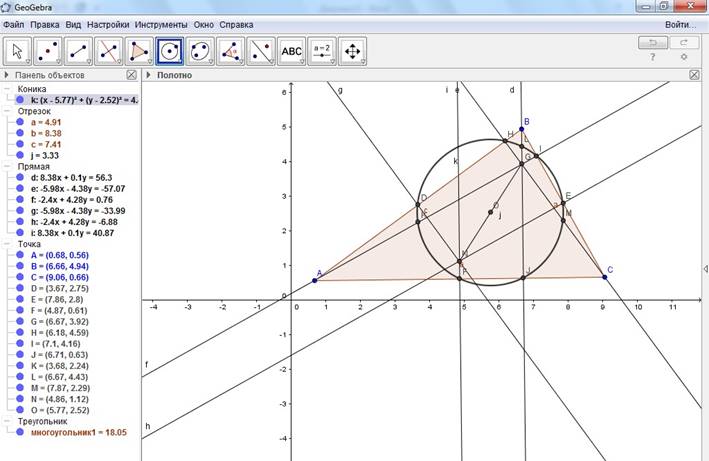
Работа выполнена.

Назад к содержанию…