"ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА по ТРЕМ СТОРОНАМ"

5.1 ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА

Урок 1/71. ПОСТРОЕНИЕ ТРЕУГОЛЬНИКА по ТРЕМ СТОРОНАМ

Цель: формировать навык построения треугольника по трем сторонам.

Ход урока

I.Организационный момент.

II. Устная работа.

    III. Объяснение нового материала.

1.    Объяснить учащимся, почему треугольник однозначно определяется тремя своими сторонами.

2.    Построение треугольника со сторонами 3 см, 4 см и 5 см с подробным объяснением каждого шага построения (согласно пункту учебника).

3.     Алгоритм построения треугольника со сторонами, а=3, b=4, с=5:

•     Начертить прямую и отложить на ней отрезок АС=5. Концы этого отрезка - вершины искомого треугольника.

•        Построить окружность с центром -  А  и радиу­сом, равным 3.

•       Построить окружность с центром -  С  и радиусом, равным 4.

•       Точка пересечения этих окружностей - есть третья вершина искомого треугольника - В.

Этот алгоритм учитель выводит вместе с учащимися. После его написания необ­ходимо, чтобы несколько учащихся проговорили вслух шаги построения треугольни­ка по трем сторонам.

Вывод 1. Окружность пересекаются в двух точках. Обозначим одну и них буквой В и проведем АВ и ВС. Получим треугольник АВС, имеющий заданные стороны.

           Понятно, что если бы мы взяли другую точку пересечения окружностей, то получили бы треугольник, равный треугольнику АВС.

4.      Неравенство треугольника.

Ø  Построим треугольник со сторонами 2 см, 3см и 4см.

Ø  После неудачных попыток попросить учащихся объяснить, почему не удается построить треугольник с такими сторонами. Так шаг за шагом прийти к в ы в о д у неравенства треугольника.

Вывод 2: Сделать это нам не удалось – окружности не пересекутся.

Этот пример показывает , что не всякие три отрезка могут быть сторонами треугольника.

Возникает вопрос: в каком случае три отрезка могут служить сторонами треугольника, а в каком – нет?

1.    В первом случае окружности пересеклись, потому что n<R+r.

2.    При втором построении окруж-ности не пересеклись, так как n>R+r.

3.    Так же ясно, что треугольник не получиться и в том случае, если n=R+r.

Таким образом, из трех отрезков можно построить треугольник, если каждый из этих трех отрезков меньше суммы  двух других. На самом деле достаточно проверить, что наибольший отрезок меньше суммы двух других.

Мы пришли к выводу, который математики называют НЕРАВЕНСТВОМ ТРЕУГОЛЬНИКА:

Любая сторона треугольника меньше суммы двух других его сторон.

 IV.   Формирование умений и навыков.

1.     № 432, №433(б), №435(1)

2.    Построение треугольника по двум сторонам и высоте, проведенной к одной из них.

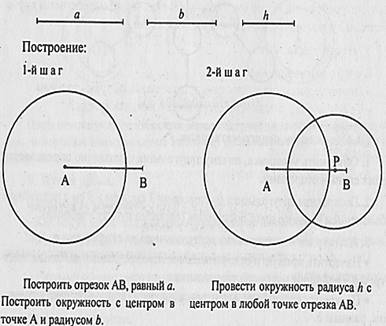
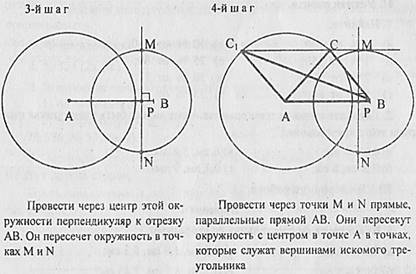
Обратить внимание учащихся, что при построении получили два разных треугольника, удовлетворяющих условию: остроугольный и тупоуголь­ный. Это говорит о том, что треугольник однозначно не определяется двумя сторонами и высотой, проведенной к одной из них.

III.  Итоги урока.

Вопросы учащимся:

-       Опишите алгоритм построения треугольника по трем сторонам.

-       Треугольник с любыми ли сторонами можно построить?

-       В чем состоит неравенство треугольника?

Домашнее задание.

№ 433(а), №435(2), п. №439(а), №440

дополнительно №436

Скачано с www.znanio.ru