Повтор Методические указания к уроку

Методические указания к уроку.

Тема " Повторение курса 5-го класса.

Действия над обыкновенными и десятичными дробями "

Цели обучения

5.1.2.20 выполнять сложение и вычитание смешанных чисел;

5.1.2.21 выполнять умножение

5.1.2.23 выполнять деление обыкновенных дробей и смешанных чисел;

5.5.2.3 решать текстовые задачи (например, задачи на совместную работу и т.д.);

5.1.2.27 выполнять сложение и вычитание десятичных дробей;

5.1.2.28 выполнять умножение десятичной дроби на натуральное число и на десятичную дробь;

5.1.2.30 выполнять деление десятичной дроби на натуральное число и на десятичную дробь.

Критерии оценивания:

Учащийся:

·                    знает правила действия с обыкновенными и  десятичными дробями;

·                    умеет выполнять действия с десятичными и обыкновенными дробями;

·                    понимает условие текстовых задач и составляет краткую запись задачи;

·                    умеет составлять математическую модель задачи;

·                    верно выполняет действия над десятичными дробями;

дает верный ответ задачи.

Теоретический материал к уроку.

1.                  Каков смысл числителя и знаменателя  обыкновенной дроби?

2.                  Что называется сокращением дроби?

3.                  Какую дробь называют несократимой дробью?

4.                  Какую дробь называют правильной дробью?

5.                  Какую дробь называют неправильной дробью?

6.                  Что называется смешанным числом?

7.                  Какая из дробей с одинаковыми знаменателями больше?

8.                  Какая из дробей с одинаковыми числителями больше?

Дробь, числитель которой меньше знаменателя, называют правильной.

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.

Чтобы сократить дробь, её  числитель и знаменатель нужно разделить на их общий делитель.

При решение задач дроби, имеющие разные знаменатели приходится заменять равными им дробями с одинаковыми знаменателями, при этом стараются подобрать наименьший общий знаменатель.

Из двух дробей с одинаковым знаменателем больше та, у которой больше числитель, и меньше та, у которой числитель меньше.

Чтобы сравнивать дроби с разными знаменателями, их сначала нужно привести к общему знаменателю.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежний.

Что бы складывать дроби  с разными знаменателями  их сначала нужно привести

к общему знаменателю.

Вычитание дробных чисел, как и натуральных, определяется на основе действий сложения: вычесть из одного числа другое- это значит найти такое число, которое при сложении со вторым даёт первое.

Чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

Чтобы находить разность дробей с разными знаменателями, их сначала нужно привести к общему знаменателю.

Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, а знаменатель на знаменатель.

Чтобы разделить дробь на дробь, нужно делимое умножить на дробь, обратную делителю.

Десятичной дробью называют обыкновенную дробь, знаменателем которой является единица с последующими нулями.

Например.

Такие дроби обычно записывают без знаменателя, а значение каждой цифры зависит от места, на котором она стоит. Для таких дробей целая часть отделяется запятой, а после запятой должно быть столько цифр, сколько нулей имеет единица в знаменателе обыкновенной дроби. Цифры дробной части называются десятичными знаками.

Например. 

Первый десятичный знак после запятой соответствует десятым, второй - сотым, третий - тысячным и т.д.

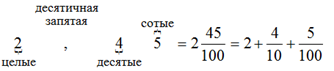
Если количество нулей в знаменателе десятичной дроби больше, чем количество цифр в числителе этой же дроби, то после десятичной запятой перед цифрами числителя дописывается нужное количество нулей.

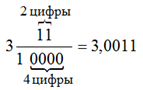
Итак, окончательно имеем: 

Ответ. 

Перевести обыкновенную дробь в десятичную можно несколькими способами.

Первый способ перевода

Чтобы превратить дробь в десятичную, нужно и числитель и знаменатель умножить на одно и то же число, так чтобы в знаменателе получилось 10, 100, 1000 и т.д.

Прежде чем приниматься за работу, не забудьте проверить, можно ли вообще превратить данную дробь в десятичную.

Примеры:

Убеждаемся, что дробь можно привести в конечную десятичную.

Умножаем числитель и знаменатель на 5. В знаменателе получим 100.

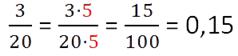
Второй способ перевода

Второй способ более сложный, но применяется чаще первого. Для того, чтобы его использовать нужно вспомнить деление уголком.

Чтобы перевести обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.

Пример: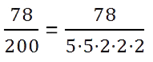  

Убеждаемся, что дробь можно перевести в конечную десятичную.

Делим уголком числитель на знаменатель.

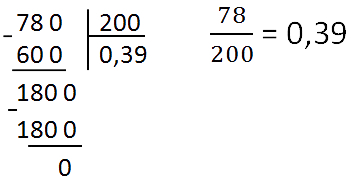
Ниже приведен список дробей со знаменателями, которые чаще других встречаются в заданиях. Вы облегчите себе работу, если их просто выучите.

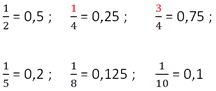
Чтобы выполнить сложение десятичных дробей столбиком, надо:

1.                   записать одну дробь под другой так, чтобы одинаковые разряды оказались друг под другом, а запятая под запятой (для удобства можно уравнять количество десятичных знаков, приписав к одной из дробей справа некоторое количество нулей);

2.                   дальше, не обращая внимания на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел;

3.                   в полученной сумме поставить десятичную запятую так, чтобы она находилась под десятичными запятыми слагаемых.

Чтобы выполнить вычитание десятичных дробей столбиком, нужно:

·                     уравнять количество десятичных знаков в записях десятичных дробей (если оно, конечно, отличается), дописав справа некоторое количество нулей к одной из дробей;

·                     вычитаемое записать под уменьшаемым так, чтобы цифры соответствующих разрядов находились друг под другом, и запятая находилась под запятой;

·                     выполнить вычитание столбиком, не обращая внимания на запятые;

·                     в полученной разности поставить запятую так, чтобы она располагалась под запятыми уменьшаемого и вычитаемого.

Умножение двух десятичных дробей выполняется так:

 1) числа перемножаются без учета запятых.

2) запятая в произведении ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых.

 Вместо умножения любого числа на 0,1; 0,01; 0,001, можно разделить это число на 10; 100; или 1000 соответственно.

При умножении десятичной дроби на натуральное число, мы должны:

1) перемножить числа, не обращая внимания на запятую;

2) в полученном произведении поставить запятую так, чтобы справа от нее было столько же цифр, сколько в десятичной дроби.

При умножении десятичной дроби на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей стоит в множителе. 

Чтобы разделить десятичную дробь на натуральное число, надо:

1) разделить дробь на это число, не обращая внимания на запятую;

2) поставить в частном запятую, когда закончится деление целой части.

При делении десятичной дроби на 10,100, 1000,  ... , надо перенести запятую в этой дроби влево на столько знаков, сколько нулей в делителе.

 При делении на десятичную дробь, сначала переносим запятую в делимом и делителе вправо на столько знаков, сколько их после запятой в делителе. А затем выполняем деление на натуральное число.

Ход урока

Организационный момент. Мотивация к учебной деятельности. Беседа.

Познакомить с требованиями, предъявляемыми к ученику 6 класса. Провести беседу о бережном отношении к учебным принадлежностям, о поведении и технике безопасности во время урока.

С помощью заданий устного счета (Приложение 1)

подвести к совместному  с учащимися определению цели урока, критериям оценивании, а также обсудить ход урока.

Приложение 1

Быстрый счет:

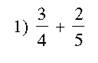
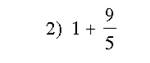
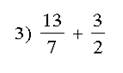
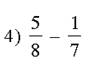
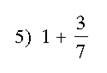
Ответы:1)     2)    3)      4)   5)   .

Работа в парах. Решение примеров и  задач.

Предложить учащимся вспомнить правила действий с дробями и решение примеров, (Презентация) работая в паре. Задания на повторение определения неправильных дробей; сокращение, сравнение, нахождения суммы, разности обыкновенных дробей;  решение уравнения. При отсутствии возможности показать презентацию провести устный опрос теории и решение примеров и задач из Приложения 2.

Приложение 2

1.    Сократите: .

2.    Сравните дроби:

а)   и  ;                          б)   и  .

3.    Выполните действия:

а)   +  ;              б)   –    +  .

в) 9  –  5 ;           г) 7  +  2 ;

4.    Найдите произведение:

а)      ×  ;                            б) 2   ×  1 ;                    в) 3   ×  1 ;  г) 1   ×  14 .

5.    Выполните действия:

а) ;           б) (4,2 : 1,2 – 1,05) × 1,6.

6.    Решите уравнение:

а) 4,72с + 2,8с = 78,96          б) 4,35 × (3,04 – с) = 6,09.

Проверить ответы по готовым решениям с помощью слайдов или ключей.

Работа в группах.

Практические задания на повторение:  действий с обыкновенными и десятичными дробями, решение уравнений и задач.

Приложение 3

1.                  Бригада выполнила в первый день  объема работы, во второй  и в третий  Бригаде осталось выполнить:

А.  объема работы.         В.  объема работы         

С.  объема работы.         D.  объема работы.      

2.                  Моторная лодка плывет по течению реки со скоростью  км/ч, а ее скорость против течения  в  раза меньше. Найти  скорость течения реки.

А)  км/ч;       В) ;                        С) ;              D) 

3.                  Семья из 3-х человек участвовали в спортивной эстафете. Отец, мать и сын пробежали 1281 м. Отец и мать пробежали 713 м, а мать и сын -631 м. На сколько метров отец пробежал больше, чем сын?

А) на 649 м       В) на 567 м       С) на 63 м        D) на 81  м  

4.                  Корень уравнения =:

А) ;                B) ;               C) ;             D) .

5.                  Решите уравнение: 96,6-(х+12,5) =53,2

А) 43,4                       В) 98               С)16,2             D) 30,9

Дополнительно

6.                  Канат проехал расстояние между городами за 3 дня. В первый день он проехал  всего пути и еще 60 км, во второй день -  всего пути и еще 20 км, в третий день - всего пути и оставшиеся 25 км. Найти расстояние между городами.

А) 400 км           В) 300 км           С) 450 км          D) 500 км        

Группы обмениваются решениями и проводят взаимооценивание.

Индивидуальная работа.

 Предложим учащимся самостоятельную работу на проверку усвоения цели обучения по вариантам.

Приложение 4

Вариант 1.

1.                  Вычислите:    () ·        

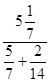
 1) 3                 2)              3)                  4)        

2.                  Выполните действия:         

1) 113              2) 11,5            3) 11,3            4) 115             

3.                  Округлите 3,24785 до сотых

1) 3,24             2) 3,25            3) 3,248          4) 3,2

4.                  Решите уравнение: 2,5х – 1,3=7,2.

1) 8,5               2) 3,4              3) 2,36            4)  6

5.                  Решите задачу. На склад привезли 250 ящиков яблок и груш, причем  из них занято грушами. Сколько ящиков яблок привезли на склад?

1) 150              2) 100             3) 125             4) 200

Дополнительное задание:

6.                  Во время автопробега спортсмены преодолели 1800 км пути. В І день -, во ІІ - того, что пройдена за І день. Сколько км спортсмены проехали за ІІІ  день?

1) 360 км       2) 1440 км       3) 1728 км      4) 72 км      

Приложение 4

Вариант 2.

1.                  Вычисли: 15-(3 + 4)

1) 12                        2) 3                         3) 13                       4) 12   

2.                  Вычисли:

1) 7           2) 1           3) 4           4)            

3.                  Округлите 7,54751 до тысячных

1). 7,547          2). 7,548         3). 7,5475       4). 7,54

4.                  Реши уравнение: 3,25х+9=35

1) 4                  2) 34                3) 13              4)  8

5.                  Решите задачу. В энциклопедии 480 страниц, Мерген пролистал   ее. Сколько ему осталось еще?

1). 120                 2). 360                             3). 240                             4). 150

Дополнительное задание:

6.                  Решите задачу. Вес трех ящиков: 27,3 кг; 30,5 кг и 18,7 кг. Найдите средний вес ящиков.

1). 27,3                2). 25,5                            3). 30,5                            4). 38,25

После выполнения учащиеся меняются тетрадями с соседом и сверяют свои ответы с заготовленными ключами.

Коллективная работа с классом. Повторив действия над различными дробями, откорректировав ошибки, связанные с правильностью применения правил, приступите к решению текстовых задач. Учебное пособие "Математика 6" или
Приложение 5. Предложить ученикам вспомнить решения типовых практических задач и при этом действия ученика: составить краткую запись задачи;  составить математическую модель задачи; верно выбрать способ решения и выполнив необходимые действия, дать верный ответ задачи. При совместной работе учитель должен следить за включением в работу и активностью каждого ученика. При наличии компьютера подготовить презентацию, видео, при отсутствии - плакаты, раздаточный демонстрационный материал.

Приложение 5

Реши задачи

1.                  В каждый час бассейн наполняется на одну пятую часть. За сколько часов наполнится весь бассейн?

Ответ: 5

2.                  Ученик покрасит лист бумаги за 3 минуты. Какая часть листа будет окрашена за 1 минуту?

Ответ:

3.                  Упаковщики в саду раскладывают яблоки в ящики. Упаковщик с опытом работы разложит по ящикам три тонны яблок за 10 дней, его помощник разложит по ящикам три тонны яблок за 15 дней. За сколько дней упаковщик и его помощник вместе справятся с этой работой?

Ответ: 6 дней

4.                  Продолжительность жизни лесной белки в среднем 6 лет, что составляет  возраста зайца. Какова продолжительность жизни зайца?

а) 12;                b) 15;             c) 10.

5.                  Предельный возраст жизни медведя 50 лет. Возраст льва составляет  возраста медведя. Каков предельный возраст льва?

а) 30;                b) 35;             c) 44.

6.                  Для приготовления 360 г коктейля потребовалось  части фруктового сока,  частей мороженого, остальное сливки. Сколько сливок потребовалось?

а) 80 г;                        b) 56 г;                      c) 45г.

Рефлексия учебной деятельности на уроке.

В конце урока учащиеся проводят рефлексию:

- что узнал, чему научился

- что осталось непонятным

- над чем необходимо работать

Учащиеся на листках записывают свои выводы.

Домашнее задание:   включите несколько примеров на закрепление и проверку темы урока и подготовку к следующим урокам.

Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а также с учетом скорости мышления и возрастных особенностей учащихся. Каждое задание оценивается согласно критериям оценивания; применяются такие формы оценивания как: самооценивание, взаимооценивание, групповое оценивание. Информация о правилах ТБ способствует осведомленности учащихся о том, как сохранить здоровье и позаботиться о безопасности окружающих.

Скачано с www.znanio.ru