Поделиться
Повт.Квадр.ур..docx
Повторение. Квадратные уравнения.
Справочный материал.
Уравнение вида: ax2 + bx + c = 0 , где a , b и с - некоторые числа и a – первый коэффициент всегда а≠0, называется квадратным. Квадратные уравнения бывают полные, где все три коэффициента a , b и с не равны нулю и неполные.
Неполные квадратные уравнения ( три вида).
1) b =0 и c=0 ax2 =0
Решение: х =0
Пример: 8х2 = 0; х=0.
2) b
0 и c=0
ax2 + bx=0
Решение: Вынести в левой части уравнения общий множитель за скобки и приравнять к нулю каждый сомножитель. x2 + bx=0 х( ах + b) =0 x=0 или ах + b =0
х=0 или х =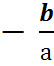
.
Пример: 3х2 -6х =0;3х ( х – 2)=0;х=0 или х -2=0;х=0 или х=2 .
3) b =0 и c≠0 ax2 +с =0 ax2 = -с
x2 = -
. Если -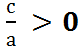
, решение
есть, уравнение
будет иметь два корня, отличающиеся своими знаками.
Если -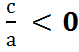
, то
уравнение не имеет решения.
Пример 1: -3х2 -
75 =0; -3х2 = 75; х2 = -
= - 25 корней нет,
т.к. нельзя извлечь квадратный корень из отрицательного числа.
Пример 2: -3х2 +
75 =0; -3х2 = -75; х2 =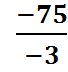 
= 25;
х=±√25; х=5 и х= - 5
Полное квадратное уравнение.
ax2 + bx + c = 0 , где a≠0 , b≠0 и с≠0.
При решении полного квадратного уравнения надо вычислить D - дискриминант.
D = b2 - 4·a·c
D >0 – квадратное уравнение имеет два корня, которые вычисляют по формулам:
Х 1,2 =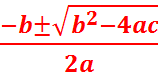 
D =0 – квадратное уравнение имеет один корень, которые вычисляют по формуле:
Х = 
D < 0 – квадратное уравнение не имеет корней, решения нет.
Пример 1. -2х2 +5х +3 =0 Выпишем коэффициенты квадратного уравнения: а = - 2; b = 5; с= 3 и вычислим D
D = 52 – 4 ·(-2) ·3= 25 +24 = 49 >0 – 2 корня
Х1=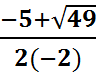 
= 
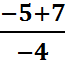= - 0,5
Х2=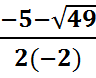 
= 
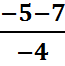= 3
Ответ: -0,5 ; 3
Пример 2. х2 -6х +9 =0 Выпишем коэффициенты квадратного уравнения: а = 1; b = -6; с= 9 и вычислим D
D =(-6)2 – 4 ·1 ·9= 36 -36 = 0 - один корень
Х =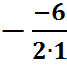 
= 3
Ответ: 3
Пример3. 8х2 +4х +3 =0 Выпишем коэффициенты квадратного уравнения: а = 8; b = 4; с= 3 и вычислим D.
D = 42 – 4 ·8 ·3= 16 - 96 = -80; D<0 не корней.
Ответ: нет решения.
Разложение квадратного трехчлена на линейные множители.
ax2 + bx + c =а·(х –х1)·(х-х2)
а – первый коэффициент, х1 и х2 – корни квадратного уравнения, х – переменная.
Пример: -5х2 -10х +15 разложить на линейные множители.
Решим квадратное уравнение -5х2 -10х +15 =0 а=-5; b=-10; c=15.
D =(-10)2 – 4 ·(-5) ·15= 100 -300 =400> 0 2 корня.
Х1=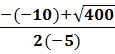 
= 
= - 3; Х2=
= 
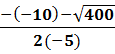=1
-5х2 -10х +15 = -5 ·( х – (- 3)) ·( х – 1)= - 5 ·( х +3) ·( х – 1).
Самостоятельная работа « Квадратные уравнения».
Вариант 1.
Решить уравнения:
1. 5х2 + 7х +2 =0 ( в ответ записать больший корень).
2. -2х2 -12х =2
3. -3х +8 +х2 =0
4. ( 3х + 1)2 =(2х+5)2 – 33 (в ответ записать меньший корень).
5. Вычислить, упростив выражение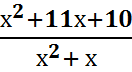 
при
х = - 5
Решить уравнения:
6. 6 х2 +18х =0 (в ответ записать меньший корень).
7. - 5 х2 - 125 =0
8. 8 х2 =0
Вариант 2.
Решить уравнения:
1. 1 + 9х2 + 6х =0 ( ответ умножить на 6 ).
2. -х2 +14х =48 (в ответ записать сумму корней)
3. -3х +7 +2х2 =0
4. ( х + 2)2 =(3х-1)2 – 13х ( в ответ записать больший корень).
5. Вычислить, упростив выражение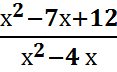 
при
х = 4
Решить уравнения:
6. 3 х2 - 27х = 0 ( в ответ записать больший корень).
7. 4 х2 - 36 = 0 ( в ответ записать меньший корень).
8. х2 +25 = 0
Вариант 3.
Решить уравнения:
1. 5 + 3х2 - 7х =0
2. -4х +4 +х2 =0
3. -2х2 +7х =5 ( в ответ записать больший корень).
4. ( 1 + 3х)2 +33=(2х+5)2 ( в ответ записать больший корень).
5. Вычислить, упростив выражение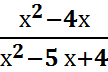 
при х = - 3
Решить уравнения:
6. х2 + 100 = 0
7. -2 х2 + 56 = 0 ( в ответ записать меньший корень).
8. 3х2 -12 = 0 ( в ответ записать больший корень).
Вариант 4.
Решить уравнения:
1. -х + 2х2 - 15 =0 ( в ответ записать меньший корень ).
2. 4х2 +12х =-9
3. -4х -5 -2х2 =0
4. 13х + ( 2 + х)2 =(1 – 3х)2 ( в ответ записать меньший корень).
5. Вычислить, упростив выражение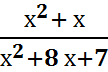 
при х = - 5
Решить уравнения:
6. 4 х2 +400 = 0
7. х2 - 400 = 0 ( в ответ записать больший корень).
8. - 6х2 +12х = 0 ( в ответ записать больший корень).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
