Практическая работа №2 Закон сохранения импульса и момента импульса. Механическая работа, мощность.

Занятие 7,   *ЕН.03 Физика

Тема: Практическая работа №2 Закон сохранения импульса и момента импульса. Механическая работа, мощность.

1.           Изучить материал №2 Закон сохранения импульса и момента импульса. Механическая работа, мощность.

2.     Посмотреть видеоурок по ссылке

https://www.youtube.com/watch?v=_zr16Phd9Sk

3.     Сделать краткий конспект лекции в рабочей тетради.

4.     Ответить на вопросы для самоконтроля.

5.     Решить задачи для самостоятельного решения.

6. Ответы, фото конспекта выслать на почту преподавателя.

Практическая работа №2 Закон сохранения импульса и момента импульса. Механическая работа, мощность.

Цель занятия - усвоить методы классической механики и научиться решать задачи динамики материальной точки, динамики поступательного движения, определять энергетические характеристики и величины.

Указания к организации самостоятельной работы студентов.

          Для достижения цели занятия необходимо изучить теорию данного раздела механики, изложенную в учебниках или в конспекте.

          Основу динамики материальной точки составляют три закона Ньютона, которые справедливы только при выполнении следующих условий: движение тела рассматривается по отношению к инерционной системы отсчета, тело должно быть материальной точкой постоянной массы, скорость тела должна быть значительно меньше скорости света в вакууме.

          При решении задач по теме используются второй закон Ньютона, который имеет вид:

F̅=ma̅, де F= ∑F̅_I - равнодействующая всех сил, приложенных к данному телу.

          В неинерциальной системе отсчета, которая движется поступательно, с ускорением а̅_o относительно инерциальной системы, второй закон Ньютона имеет вид.

F̅+F̅_in =ma̅, де  F̅_in =ma̅_o  - сила инерции,

а- ускорение тела в неинерциальной системе отсчета.

          Для решения задач с использованием второго закона Ньютона предложен метод, который включает следующие действия:

          1. Найти, или используется ли этот закон в данной задачи, и наметить рисунок-схему взаимодействующих тел.

          2. Найти и обозначить на схеме все силы, действующие на тела системы.

          Для каждого тела:

          3. Записать главное уравнение динамики в векторной форме.

          4. Выбрать подходящую инерциальную систему отсчета.

          5. Спроектировать силы на оси координат и записать второй закон Ньютона в виде системы скалярных уравнений:

           ∑F_x =ma_x,  ∑F _y=ma_y ,  ∑F_z =ma_z,

         где а_x, а_y, а_z,  - проекции вектора ускорения на соответствующие оси.

         6. Решить систему полученных уравнений по отношению к неизвестным.

          Определить ускорения тел в задачах данного типа которые называют главной задачей динамики поступательного движения.

Энергия – универсальная мера различных форм движения материальных объектов и их взаимодействия. Количественной характеристикой процесса обмена энергией между взаимодействующими телами является физическая скалярная величина – работа сил.

         Элементарная работа силы                   

         Работа силы на произвольном участке траектории 1-2   

Мощность – физическая скалярная величина, характеризующая скорость совершения работы:                                  

Мощность, развиваемая силой  в данный момент времени, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы:                          

Консервативная сила – сила, работа которой при перемещении из одного положения в другое не зависит от траектории перемещения, а зависит только от начального и конечного положений тела. Силовое поле, в котором консервативные силы совершают работу, называется потенциальным полем.

Кинетическая энергия - механическая энергия всякого свободно движущегося тела, численно равная работе, которую совершают действующие на тело силы при его торможении до полной

остановки:                                                           

Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Связь между консервативной силой  и потенциальной энергией устанавливается выражением  gradЕ_п, где gradЕ_п =

         Отсюда, как частные случаи, определяются: а) потенциальная энергия тела массой m на высоте h                                                          

         б) потенциальная энергия упругодеформированного тела          

         где k – коэффициент упругости (для пружины – жесткость).

Полная энергия механической системы – равна сумме кинетической и потенциальной энергий:                             

Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние) называются консервативными системами. В таких системах выполняется закон сохранения механической энергии:               const,

т.е. полная механическая энергия консервативной системы со временем не изменяется. Это фундаментальный закон природы, который является следствием однородности времени.

Контрольные вопросы и задания

1.  Изложить понятие инертности.

2.  Дать определение массы.

3.  Дать определение силы.

4.  Изложить первый закон Ньютона.

5.  Изложить второй закон Ньютона.

6.  Изложить третий закон Ньютона.

7.  Дать определение силы тяжести.

8. Дать определение веса тела.

9. Записать силу трения.

10. Записать закон Гука.

11.Что такое энергия, работа, мощность?

12. Как определяется работа переменной силы?

13.   Какие силы называются консервативными? Приведите примеры консервативных сил.

14.   Какие силы называются диссипативными? Приведите примеры таких сил.

15.   Дайте определения кинетической и потенциальной энергии.

16.   В чем заключается закон сохранения механической энергии?  Для каких систем он выполняется?

17.   Каким свойством времени обусловлена справедливость закона сохранения механической энергии?

18.   В чем физическая сущность закона сохранения и превращения энергии? Почему он является фундаментальным законом природы?

19.   Как на основе закона сохранения механической энергии охарактеризовать положения устойчивого и неустойчивого равновесия консервативной системы?

20.   Что такое потенциальная яма? потенциальный барьер?

Примеры решения задач

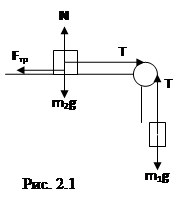Задача 1. Грузы одинаковой массы (m₁=m₂=0,5 кг) соединены нитью и перекинуты через невесомый блок, укрепленный на конце стола (рис. 2.1). Коэффициент трения груза m₂ о стол µ =0,15. Пренебрегая трением в блоке, определить: а) ускорение, с которым движутся грузы; б) силу натяжения нити.

Дано: m₁=m₂=0,5 кг; µ =0,15.

Найти: а, Т.

Решение

По второму закону Ньютона уравнения

движения грузов имеют вид:

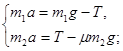
, откуда

м/с²;

 Н.

Ответ: а=4,17 м/с², Т=2,82 Н.

Задача 2. Снаряд массой 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость 300 м/с. В этой точке он разорвался на два осколка, причем больший осколок массой 3 кг полетел в обратном направлении со скоростью 100 м/с. Определить скорость второго, меньшего, осколка.

Дано: m=5 кг; v=300 м/с; m₁=3 кг; v₁=100 м/с.

Найти: v₂.

Решение

По закону сохранения импульса

 где  м/с.

Ответ: v₂=900 м/с.

Задача 3. С башни высотой 20 м горизонтально со скоростью 10 м/с брошен камень массой 400 г (рис. 2.2). Пренебрегая сопротивлением воздуха, определить кинетическую и потенциальную энергию камня через 1 с после начала движения.

Дано: H = 20 м; v₀ = 10 м/с; m = 0,4 кг; t = 1c.

Найти: E_k, E_п.

Решение

В точке А     где

Подставляя числовые данные, получим E_k  = 39,2 Дж, E_п = 59,2 Дж.

Ответ: E_k  = 39,2 Дж, E_п = 59,2 Дж.

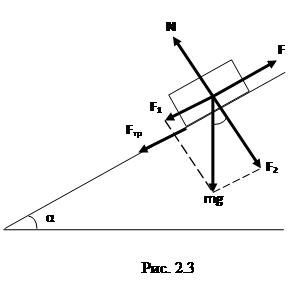
Задача 2. Автомобиль массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути (рис. 2.3). Определить: а) работу, совершаемую двигателем автомобиля на пути 5 км, если коэффициент трения равен 0,1;

 б) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.

Дано: m = 1800 кг; sinα = 0,03; s = 5000 м; μ = 0,1;

t = 300 с.

Найти: А, Р.

Решение

 где      

Подставляя числовые данные, получим: А = 11,5·10⁶ Дж, Р = 38,3·10³ Вт.

Ответ: А = 11,5 МДж, Р = 38,3·кВт.

Задачи для самостоятельного решения

1.   Тело массой 2 кг движется прямолинейно по закону , где С=2 м/с², D=0,4 м/с³. Определить силу, действующую на тело в конце первой секунды движения.

2.   Тело массой 5 кг поднимают с ускорением 2 м/с². Определить работу силы в течение первых пяти секунд.

3.   Скачано с www.znanio.ru