
Практическая работа
Тема. Решение задач линейной алгебры в MathCAD.
Цель работы. Изучение возможностей MathCAD для решения задач линейной алгебры. Приобретение навыков работы с матричными операциями в пакете.
Рекомендации к выполнению практической работы.
Рассмотрим несколько примеров.
2х1 − х2 + 5х3 = 0
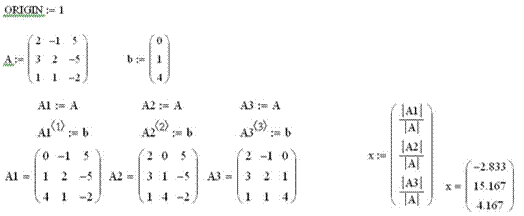
Пример 1. Решить систему линейных уравнений по формулам Крамера.{3х1 + 2х2 − 5х3 = 1 х1 + х2 − 2х3 = 4
На рис. 1 приведен фрагмент рабочего документа, содержащий решение поставленной задачи.
2х1 + х2 − 5х3 + х4 = 8
Пример 2. Решить систему линейных уравнений методом обратной матрицы { х1 − 3х2 − 6х4 = 9 2х2 − х3 + 2х4 = −5 х1 + 4х2 − 7х3 + 6х4 = 0
Решение показано на рис.2.

Пример 3. Решить систему с помощью функции lsolve и при помощи решающего блока: х1 + 2х2 + 5х3 = −9
{ х1 − х2 + 3х3 = 2 3х1 − 6х2 − х3 = 25
Решение системы при помощи функции lsolve показано на рис. 3. Фрагмент рабочего документа на рис.3 содержит пример применения решающего блока для решения системы.
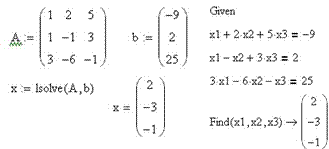
Задание 1. Решить систему уравнений методом обратной матрицы и по правилам Крамера, сделать проверку.
Задание 2. Решить систему уравнений с помощью функции lsolve и решающего блока Given. Задание 3. Выполнить действия с матрицами
|
№ вар |
Задание 1 |
Задание 2 |
Задание 3 |
|||
|
1 |
х1 + х2 + 2х3 + 3х4 = 1 3х { 1 − х2 − х3 − 2х4 = −4 2х1 + 3х2 − х3 − х4 = −6 х1 + 2х2 + 3х3 − х4 = −4 |
5𝑥 + 8𝑦 − 𝑧 = −7 { 𝑥 + 2𝑦 + 3𝑧 = 1 2𝑥 − 3𝑦 + 2𝑧 = 9
|
2(A + B)(2B - A), где 2 3 −1 −1 0 5 А = ( 4 5 2 ) , В = ( 0 1 3) −1 0 7 2 −2 4 |
|||
|
2 |
х1 + 2х2 + 3х3 − 2х4 = 6 { 1 − х2 − 2х3 − 3х4 = 8 х 3х1 + 2х2 − х3 + 2х4 = 4 2х1 − 3х2 + 2х3 + х4 = −8 |
𝑥 + 2𝑦 + 𝑧 = 4 {3𝑥 − 5𝑦 + 3𝑧 = 1 2𝑥 + 7𝑦 − 𝑧 = 8
|
3А - (А + 2В)В, где 4 5 −2 2 1 А = (3 −1 0 ) , В = (0 1 4 2 7 5 7 |
−1 3 ) 3 |
||
|
3 |
х1 + 2х2 + 3х3 + 4х4 = 5 2х { 1 + х2 + 2х3 + 3х4 = 1 3х1 + 2х2 + х3 + 2х4 = 1 4х1 + 3х2 + 2х3 + х4 = −5 |
3𝑥 + 2𝑦 + 𝑧 = 5 { 2𝑥 + 3𝑦 + 𝑧 = 1 2𝑥 + 𝑦 + 3𝑧 = 11
|
2(A - B)(A2 + В), где 5 1 7 2 4 А = (−10 −2 1) , В = (3 1 0 1 2 7 2 |
1 0) 1 |
||
|
4 |
х2 − 3х3 + 4х4 = −5 { 1 − 2х3 + 3х4 = −4 х 3х1 + 2х2 − 5х4 = 12 4х1 + 3х2 − 5х3 = 5 |
х1 + 2х2 + 4х3 = 31 {5х1 + х2 + 2х3 = 29 3х1 − х2 + х3 = 10 |
(A2 – B2)(A + В), где 7 2 0 0 2 А = (−7 −2 1) , В = (1 0 1 1 1 3 1 |
3 −2) 1 |
||
|
5 |
х1 + 3х2 + 5х3 + 7х4 = 12 3х { 1 + 5х2 + 7х3 + х4 = 0 5х1 + 7х2 + х3 + 3х4 = 4 7х1 + х2 + 3х3 + 5х4 = 16 |
4𝑥 − 3𝑦 + 2𝑧 = 9 { 2𝑥 + 5𝑦 − 3𝑧 = 4 5𝑥 + 6𝑦 − 2𝑧 = 18
|
(A – B2)(2A + В), где 5 2 0 3 6 А = (10 4 1) , В = (−1 −2 7 3 2 2 1 |
−1 0 ) 3 |
||
|
6 |
х1 + 5х2 + 3х3 − 4х4 = 20 3х { 1 + х2 − 2х3 = 9 5х1 − 7х2 + 10х4 = −9 3х2 − 5х3 = 1 |
2х1 − х2 − х3 = 4 {3х1 + 4х2 − 2х3 = 11 3х1 − 2х2 + 4х3 = 11 |
(A - B)А +2В, где 5 −1 3 3 7 А = ( 0 2 −1) , В = (1 1 −2 −1 0 0 1 |
−2 −2) 3 |
||
|
7 |
2х1 + х2 − 5х3 + х4 = 8 х { 1 − 3х2 + 6х4 = 9 2х2 − х3 + 2х4 = −5 х1 + 4х2 − 7х3 + 6х4 = 0 |
х1 + х2 + 2х3 = −1 {2х1 − х2 + 2х3 = −4 4х1 + х2 + 4х3 = −2 |
2(A – 0,5B) +АВ, где 5 3 −1 1 4 А = (2 0 4 ) , В = (−3 −2 3 5 −1 5 7 |
16 0 ) 2 |
||
|
8 |
2х1 − х2 + 3х3 + 2х4 = 4 3х { 1 + 3х2 + 3х3 + 2х4 = 6 3х1 − х2 − х3 + 2х4 = 6 3х1 − х2 + 3х3 − х4 = 6 |
3х1 − х2 = 5 { −2х1 + х2 + х3 = 0 2х1 − х2 + 4х3 = 15 |
3 А = (4 1 |
(A – B)А +3В, где 2 −5 −1 2 0 ) , В = ( 0 1 2 −1 |
2 3 −3 |
4 2) 4 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.