Практическая работа специальности 38.02.04.

Практическое занятие № 3

Тема: Вычисление предела функции в точке и в бесконечности.

Цель: приобретение практического навыка в  вычислении пределов функции, применения теорем о пределах функции; раскрытия различных видов неопределенностей.

Наглядные пособия: учебники

Литература:

1.    Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2014.

2.    Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретические сведения

Определение: Конечное число A называется пределом функции f(x) в точке x₀, если для любого положительного числа ε можно указать такое положительное δ = δ(ε), что для всех значений x, удовлетворяющих неравенству 0 < |x − x₀| < δ, соответствующие значения функции удовлетворяют неравенству |f(x) − A| < ε. Для обозначения такого предела используют символику:   

Основные свойства пределов функций:

1.  Если функция имеет конечный предел, то он единственный.

2.  Постоянный множитель можно выносить за знак предела

3.  Предел суммы (или разности) функций равен сумме (или разности) их пределов, если оба предела являются конечными

4.  Предел произведения функций равен произведению их пределов, если оба предела являются конечными

Предел отношения функций равен отношению их пределов, если оба предела являются конечными и знаменатель не обращается в нуль
 

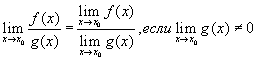
Чтобы найти предел элементарной функции  нужно предельное значение аргумента подставить в функцию и посчитать. При этом, если х=х₀ принадлежит области определения функции, то значение предела будет найдено, оно равно значению функции в точке х=х₀. При вычислении пределов полезно использовать следующие соотношения. Если  то, учитывая свойства б.б. и б.м. функций, получим:

      еслиесли a>1.

Случаи, в которых подстановка предельного значения аргумента
в функцию не дает значения предела, называют неопределенностями;
к ним относятся неопределенности видов:

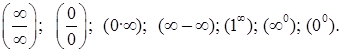
1. Правило раскрытия неопределенности типа .

Пример 1: Найти предел функции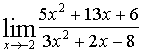
Решение: Имеем неопределенность вида   Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель x + 2, который при x → -2 не равен нулю. В результате неопределенность будет раскрыта.

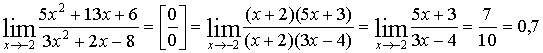
Пример 2: Найти предел функции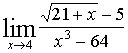

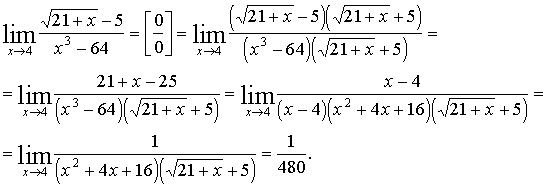
Решение: Имеем неопределенность вида . Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение, стоящее в знаменателе, на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель x - 4, который при x → 4 не равен нулю. В результате неопределенность будет раскрыта.

2. Правило раскрытия неопределенности типа.

Пример 1: Найти предел функции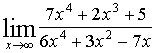
Решение: Имеем неопределенность вида []. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.

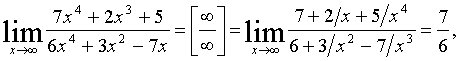
Определение. Первым замечательным пределом называется предел

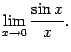
Теорема. Первый замечательный предел равен

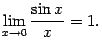
Определение: Вторым замечательным пределом называется предел

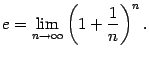
Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называют основанием натуральных логарифмов.

Теорема. Второй замечательный предел существует. Его значение – число,
лежащее между и .

Более подробное изучение числа показывает, что – иррациональное число, несколько первых десятичных знаков которого таковы:

Примеры:

Вычислить:

1) .

2) .

3)

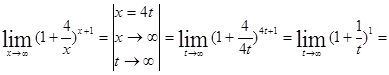
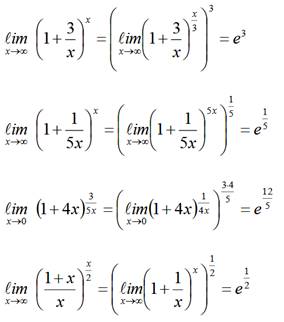
Практическая часть

Вариант 1

Вычислить пределы функций:

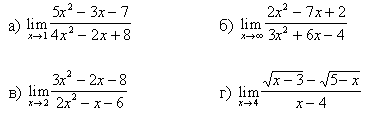
д)               е)    

 ж)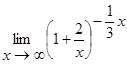

Вариант 2

Вычислить пределы функций:

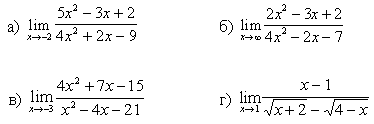
д)                     е)

ж)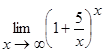

Контрольные вопросы:

1.     Что называется пределом функции в точке?

2.     Какие вы знаете основные свойства о пределах?

3.     Каковы правила раскрытия неопределенностей вида  , .

Скачано с www.znanio.ru