Практическая работа специальности 38.02.04.

Практическое занятие № 10

Тема: Решение задач на применение формул комбинаторики

Цель занятия: сформировать навыки решения задач на применение формул комбинаторики

Наглядные пособия: учебники

Литература:

1.     Григорьев С.Г. Математика: учебник для СПО. – М.: Изд. центр «Академия», 2019.

2.       Гусев В.А. Математика для профессий и специальностей соц.-экон. профиля: учебник для образовательных учреж. нач. и сред. проф. образ. – М.: Изд. центр «Академия», 2013.

Теоретические сведения

Большинство комбинаторных задач решается с помощью двух основных правил –правила суммы и правила произведения.

Пример: В магазине «Все для чая» есть 6 разных чашек и 4 разных блюдца. Сколько вариантов чашки и блюдца можно купить?

Решение.

Чашку мы можем выбрать 6-ю способами, а блюдце 4-я способами. Так как нам надо купить пару чашку и блюдце, то это можно сделать 6 · 4 = 24 способами (по правилу произведения).Ответ: 24.

Для успешного решения комбинаторных задач надо еще и правильно выбрать формулу, по которой искать количество нужных соединений. В этом поможет следующая схема.

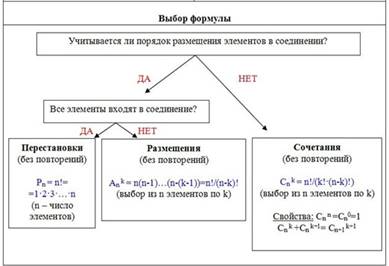
Задача 1. Найдите количество трехзначных чисел, которые можно составить из цифр 1, 2, 3, 4, 5, 6, 7, если цифры в числе повторяться не могут.

Решение.

Для выбора формулы выясняем, что для чисел, которые мы будем составлять, порядок учитывается и не все элементы одновременно выбираются. Значит, это соединение – размещение из 7 элементов по 3. Воспользуемся формулой для числа размещений: A₇³ = 7(7 – 1)(7 – 2) = 7 · 6 · 5 = 210 чисел.

Ответ: 210.

Задача 2. Сколько существует семизначных телефонных номеров, в которых все цифры разные, а номер не может начинаться с нуля?

Решение.

На первый взгляд эта задача такая же, как и предыдущая, но сложность в том, что надо не учитывать те соединения, которые начинаются с нуля. Значит необходимо из существующих 10-ти цифр составить все семизначные номера телефонов, а потом от полученного числа отнять количество номеров, начинающихся с нуля. Формула будет иметь вид:

A₁₀⁷ – A₉⁶ = 10 · 9 · 8 · 7 · 6 · 5 · 4 – 9 · 8 · 7 · 6 · 5 · 4 = 544 320.

Ответ: 544 320.

Задача 3. Сколькими способами можно расставить на полке 12 книг, из которых 5 книг – это сборники стихотворений, так, чтобы сборники стояли рядом?

Решение.

Сначала примем 5 сборников условно за одну книгу, потому что они должны стоять рядом. Так как в соединении существенным есть порядок, и все элементы используются, значит  это перестановки из 8 элементов (7 книг + условная 1 книга). Их количество Р₈. Далее будем переставлять между собой только сборники стихотворений. Это можно сделать Р₅ способами. Поскольку нам нужно расставить и сборники, и другие книги, то воспользуемся правилом произведения. Следовательно, Р₈ · Р₅ = 8! · 5!. Число способов будет большим, поэтому ответ можно оставить в виде произведения факториалов.

Ответ: 8! · 5!

Задача 4.  В классе 16 мальчиков и 12 девочек. Для уборки территории возле школы нужно 4 мальчика и 3 девочки. Сколькими способами можно их выбрать со всех учеников класса?

Решение.

Сначала отдельно выберем 4 мальчика из 16 и 3 девочки из 12. Так как порядок размещения не учитывается, то соответственные соединения – сочетания без повторений. Учитывая необходимость одновременного выбора и мальчиков, и девочек, используем правило произведения. В результате число способов будет вычисляться таким образом:

С₁₆⁴ · С₁₂³ = (16!/(4! · 12!)) · (12!/(3! · 9!)) = ((13 · 14 · 15 · 16) / (2 · 3 · 4)) ·((10 · 11 · 12) / (2 · 3)) = 400 400.

Ответ: 400 400.

Таким образом, успешное решение комбинаторной задачи зависит от правильного анализа ее условия, определения типа соединений, которые будут составляться, и выбора подходящей формулы для вычисления их количества.

Практическая часть

Контрольные вопросы:

1.    Что такое комбинаторика?

2.    Правило суммы и произведения.

3.    Что такое перестановка? Как вычислить число перестановок n предметов?

4.    Что называется размещениями из n элементов по k элементов? По какой формуле можно вычислить число всевозможных размещений из n элементов по k элементов?

5.    Что называется сочетанием без повторений из n элементов по k? По какой формуле можно вычислить число всевозможных сочетаний из n элементов по k   элементов?

6.