
ЗАДАНИЕ № 1. Проведите анализ КИМ, позволяющий выявить отмену старых заданий, включение новых, смену минимальных проходных баллов и продолжительности экзамена по плану:
1) Определите цель изменения КИМ.
Цель КИМ: усиление деятельностной составляющей КИМ: применение умений и навыков анализа различной информации, решения задач, в том числе практических, развернутого объяснения, аргументации и др.
2) Общий формат экзаменационной работы остался прежним, однако в работу внесены несколько поправок.
Какие? Предложите список, состоящий из не менее 3-х положений базового уровня и не менее 4-х положений профильного уровня
В работу профильной математики внесены следующие изменения:
В работу базовой математики внесены следующие изменения.
3) Заполните сводную таблицу изменений в ЕГЭ по предмету «Математика»
Базовый уровень
|
№ нового задания |
№ старого задания |
Что проверяется? |
|
|
1 |
№1 |
Умение выполнять вычисления и преобразования: выполнять арифметические действия, сочетая устные и письменные приёмы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма |
|
|
2 |
удалено |
Умение выполнять вычисления и преобразования: выполнять арифметические действия, сочетая устные и письменные приёмы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции |
|
|
3 |
№ 3 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни: анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчётах |
|
|
4 |
№ 4 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни: описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках; определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций |
|
|
5 |
Новое задание |
умение выполнять действия с геометрическими фигурами: решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы |
|
|
6 |
№ 6 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни: решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения |
|
|
7 |
№ 2 |
умение выполнять вычисления и преобразования: выполнять арифметические действия, сочетая устные и письменные приёмы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции |
|
|
8 |
№ 8 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни: описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках; определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций |
|
|
9 |
№ 9 |
Уметь решать уравнения и неравенства: решать рациональные, иррациональные, пока зательные, тригонометрические и логарифмические уравнения, их системы |
|
|
10 |
№ 10 |
умение выполнять действия с геометрическими фигурами: моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; решать планиметрические задачи на нахож дение геометрических величин (длин, углов, площадей) |
|
|
11 |
№ 11 |
Уметь строить и исследовать простейшие математические модели: моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий |
|
|
12 |
№ 12 |
Уметь строить и исследовать простейшие математические модели: моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры; анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчётах; описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках. |
|
|
13 |
№13 |
Уметь выполнять действия с геометрическими фигурами: моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы. |
|
|
14 |
№ 14 |
Уметь выполнять действия с функциями: исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции; описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках; решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения. |
|
|
15 |
№ 15 |
уметь выполнять действия с геометрическими фигурами: решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) |
|
|
16 |
№16 |
уметь выполнять действия с геометрическими фигурами: решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы |
|
|
17 |
№ 17 |
Уметь решать уравнения и неравенства: анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчётах; решать рациональные, показательные и логарифмические неравенства, их системы |
|
|
18 |
№ 18 |
Уметь строить и исследовать простейшие математические модели: проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения |
|
|
19 |
№ 19 |
умение выполнять вычисления и преобразования: выполнять арифметические действия, сочетая устные и письменные приёмы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма |
|
|
20 |
Новое задание |
умение строить и исследовать простейшие математические модели: решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы; решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков, использовать для приближённого решения уравнений и неравенств графический метод; решать рациональные, показательные и логарифмические неравенства, их системы; моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры |
|
|
21 |
№ 21 |
умение строить и исследовать простейшие математические модели: моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры. |
Профильный уровень
|
№ нового задания |
№ старого задания |
Что проверяется? |
|
1 |
№ 5 |
Уметь решать уравнения и неравенства: решать рациональные, иррациональные, пока |
|
2 |
№ 4 |
умение строить и исследовать
простейшие математические модели:
моделировать реальные ситуации на языке |
|
3 |
Новое задание |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами: моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; решать планиметрические задачи на
нахож площадей) |
|
4 |
№ 6 |
умение выполнять вычисления и
преобразования: выполнять арифметические
действия, сочетая устные и письменные приёмы;
находить значения корня натуральной степени, степени вычислять значения числовых и
буквенных проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции |
|
5 |
№ 9 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами: решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы |
|
6 |
№8 |
Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций; вычислять производные и
первообразные монотонность, находить наибольшее и наименьшее значения функции |
|
7 |
№ 7 |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни: анализировать реальные числовые
данные, ин социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения |
|
8 |
№ 10 |
умение строить и исследовать простейшие математические модели: моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры |
|
9 |
№ 11 |
Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций; моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры |
|
10 |
новое задание из блока «Элементы комбинаторики, статистики и теории вероятностей» повышенного уровня сложности. |
Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни: моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий. |
|
11 |
новое задание |
Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций; вычислять производные и первообразные элементарных функций; исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции |
|
12 |
№ 12 |
Уметь решать уравнения и неравенства: решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы; решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод; решать рациональные, показательные и логарифмические неравенства, их системы |
|
13 |
№ 13 без отбора корней(2б) |
умение выполнять действия с геометрическими фигурами, координатами и векторами: решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы; определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами; моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения |
|
14 |
№ 14 |
Уметь решать уравнения и неравенства: решать рациональные, показательные и логарифмические неравенства, их системы |
|
15 |
№15 система из уравнения и неравенства (3б) |
умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни: анализировать реальные числовые данные, информацию статистического характера; осуществлять практические расчёты по формулам; пользоваться оценкой и прикидкой при практических расчётах ; решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения |
|
16 |
№17 экономическая(2б) |
умение выполнять действия с геометрическими фигурами, координатами и векторами: решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей); определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами; моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения |
|
17 |
№16планиметрическая(3б) |
Уметь решать уравнения и неравенства: решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы; решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод; решать рациональные, показательные и логарифмические неравенства, их системы; моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры |
|
18 |
№ 18 (4б) |
умение строить и исследовать простейшие математические модели: моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры; проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения |
ЗАДАНИЕ № 2. Изучите задание № 12 профильного уровня КИМ ЕГЭ по математике, определите правильность его выполнения согласно критериям и указаниям по оцениванию.
|
Содержание критерия |
Баллы |
Выставляемые баллы |
|
Обоснованно получены верные ответы в обоих пунктах |
2 |
|
|
Обоснованно получен верный ответ в пункте а ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б |
1 |
1 балл |
|
Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
|
|
Максимальный балл 2 |
|
|
|
12. а) Решите уравнение 2 sin (𝑥 + 𝜋) + cos 2𝑥 = 3 cos 𝑥 + 1
![]() 3
3
![]() б) Укажите
корни этого уравнения, принадлежащие отрезку [−3𝜋; −
3𝜋]
б) Укажите
корни этого уравнения, принадлежащие отрезку [−3𝜋; −
3𝜋]
2
Решение. а) Запишем исходное уравнение в виде:
![]()
![]()
sin 𝑥 + √3 cos 𝑥 + 1 − 2 sin2 𝑥 = √3 cos 𝑥 + 1; sin 𝑥 − 2 sin2 𝑥 = 0
sin 𝑥 ∙ (2 sin 𝑥 − 1)=0
![]() Значит sin 𝑥 = 0, откуда x=𝜋𝑘, k ∈ Z, или sin 𝑥=1
Значит sin 𝑥 = 0, откуда x=𝜋𝑘, k ∈ Z, или sin 𝑥=1
2
откуда x=𝜋+2𝜋𝑛, n∈ Z или
![]() 6
6
x=5𝜋+2𝜋𝑚, m∈ Z
6
Б) с помощью числовой окружности отберем корни принадлежащие отрезку
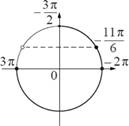 [−3𝜋; −
3𝜋].
[−3𝜋; −
3𝜋].
2
![]() Получим числа: -3𝜋; 2 𝜋; -11𝜋
Получим числа: -3𝜋; 2 𝜋; -11𝜋
6
![]()
![]() Ответ: a) 𝜋𝑘, k ∈ Z; 𝜋+2𝜋𝑛, n∈ Z;5𝜋+2𝜋𝑚, m∈ Z
Ответ: a) 𝜋𝑘, k ∈ Z; 𝜋+2𝜋𝑛, n∈ Z;5𝜋+2𝜋𝑚, m∈ Z
6 6
![]() б) -3𝜋; 2 𝜋; -11𝜋
б) -3𝜋; 2 𝜋; -11𝜋
6
ЗАДАНИЕ № 3. Заполните матрицу проектного замысла «Сложные задания ЕГЭ по математике», содержащую необходимую и достаточную информацию о проектном замысле.
Матрица проектного замысла состоит из:
· краткого описания проблемы;
· разделов и тем, определяемых как «сложные»;
· описания проектной идеи: что, как и с помощью каких механизмов, способов и средств будет изменено;
· ресурсной карты проектного замысла: какие задания убрать из КИМ, варианты альтернативных заданий (не менее 2х).
1) Описание проблемы: Задачи с параметрами № 17(по-новому) являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа. По статистике многие из выпускников не приступают к решению задач. В школе такие задачи практически не рассматриваются, а типовых задач этого вида очень много и они требуют большого количества времени на изучение. Одна из проблем решения данного задания – проблема выбора способа, который быстрее всего приведет к правильному результату.
2) Сложные темы:
Преобразование графиков различных функций и приёмы построения графиков
Графический способ решения задач с параметрами: использование чётности функции
Условия касания и метод оценки в задачах с параметрами
3) Особенность задач с параметрами заключается в возможности привлечь к их решению различные идеи и методы: построение изображения множества решений в координатах или использование знаний видов и свойств элементарных функций. Эти задачи сложно классифицировать и дать общий алгоритм решения, поскольку каждая из них является нестандартной, но можно изучить основные приемы и методы. Не забывайте про особенности функций: монотонность, непрерывность, четность/нечетность, ограниченность, инвариантность и т. д. Для того чтобы осилить задачу с параметром, необходимо произвести несложные, но последовательные рассуждения и составить логическую схему решения. Самое главное в этом задании — логика. Чтобы подготовиться к заданиям с параметрами, рекомендуется решать задачи из учебников С.А. Шестакова «Задачи с параметрами», А.И. Козко и В.Г. Чирского «Задачи с параметрами для абитуриентов».
4) В задании № 6 – убрать задание ПЕРВООБРАЗНАЯ и заменить на любое задание с производной, например на применение уравнения касательной; в задании № 10 теория вероятности повышенной сложности заменить на действия в алгебраической или геометрической форме с КОМПЛЕКСНЫМИ числами
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.