
Задача 1. Двое рабочих выполняют некоторую работу. После 45 минут совместной работы первый рабочий был переведен на другую работу, и второй рабочий закончил оставшуюся часть работы за 2 часа 15 минут. За какое время мог бы выполнить работу каждый рабочий в отдельности, если известно, что второму для этого понадобится на 1 час больше, чем первому.
Решение:
Пусть х – время работы первого по выполнению всей работы.
у – время работы второго рабочего.
По условию х=у–1, и первое уравнение составлено.
Пусть объем всей работы равен 1.
Тогда ![]() – производительность труда первого
рабочего,
– производительность труда первого
рабочего,
![]() – производительность труда второго
рабочего.
– производительность труда второго
рабочего.
Так как они работали 45 мин.=3/4 часа совместно, то
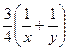 – объем работы, выполненной
рабочими за 45 минут.
– объем работы, выполненной
рабочими за 45 минут.
Так как второй рабочий работал один 2 часа 15 минут=2¼=9/4 часа, то
![]() – объем работы, выполненной вторым
рабочим за 2 часа 15 минут.
– объем работы, выполненной вторым
рабочим за 2 часа 15 минут.
По условию 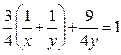 .
.
Таким образом, мы получили систему двух уравнений
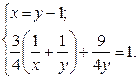
Решим ее, для этого выражение для х из первого уравнения подставим во второе
![]() Þ
Þ ![]() Þ 4у2–19у+12=0
Þ 4у2–19у+12=0
![]() ч.
и у2=4 ч.
ч.
и у2=4 ч.
Из двух значений для
у выберем то, которое подходит по смыслу задачи у1=45
мин., но 45 мин. рабочие работали вместе, а потом второй рабочий работал еще
отдельно, поэтому ![]() не подходит по смыслу
задачи. Для полученного у2=4 ч. найдем из первого уравнения
первоначальной системы значение х
не подходит по смыслу
задачи. Для полученного у2=4 ч. найдем из первого уравнения
первоначальной системы значение х
х=4–1 Þ х=3 ч.
Ответ: первый рабочий выполнит работу за 3 часа, второй – за 4 часа.
Замечание: эту задачу можно было решить, не вводя вторую переменную у, а выразить время работы второго рабочего через х, тогда нужно было составить одно уравнение и решить его.
Задача 2. Две бригады рабочих начали работу в 8 часов. Сделав вместе 72 детали, они стали работать раздельно. В 15 часов выяснилось, что за время раздельной работы первая бригада сделала на 8 деталей больше, чем вторая. На другой день первая бригада делала за 1 час на одну деталь больше, а вторая бригада за 1 час на одну деталь меньше. Работу бригады начали вместе в 8 часов и, сделав 72 детали, снова стали работать раздельно. Теперь за время раздельной работы первая бригада сделала на 8 деталей больше, чем вторая, уже к 13 часам. Сколько деталей в час делала каждая бригада?
Решение:
Пусть х деталей в час изготовляет первая бригада (производительность первой бригады).
у – производительность второй бригады.
х+у – совместная производительность бригад.
Так как вместе они сделали 72 детали, то
![]() – время совместной работы бригад.
– время совместной работы бригад.
Так как бригады работали с 8 до 15 часов, всего 7 часов, то
![]() – время работы бригад раздельно,
тогда
– время работы бригад раздельно,
тогда
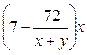 – число деталей, которое
изготовила первая бригада, работая отдельно
– число деталей, которое
изготовила первая бригада, работая отдельно
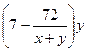 – число деталей, которое
изготовила вторая бригада, работая отдельно
– число деталей, которое
изготовила вторая бригада, работая отдельно
По условию 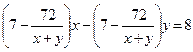 или
или 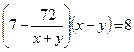
Составим второе уравнение. По условию:
х+1 – производительность труда первой бригады на другой день.
у–1 – производительность труда второй бригады на другой день.
х+1+у–1=х+у – совместная производительность (такая же, как и в первый день).
Так как бригады работали с 8 до 13 часов – всего 5 часов, то
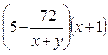 – число деталей, которые
изготовила первая бригада, работая отдельно, во второй день.
– число деталей, которые
изготовила первая бригада, работая отдельно, во второй день.
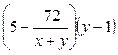 – число деталей, которые
изготовила вторая бригада, работая отдельно, во второй день.
– число деталей, которые
изготовила вторая бригада, работая отдельно, во второй день.
По условию 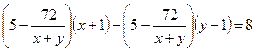 или
или 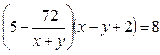 .
.
Таким образом, мы составили систему двух уравнений:
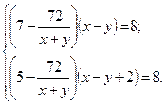
Решим эту систему методом замены переменных:
Пусть ![]() ...................(V)
...................(V)
Тогда имеем:
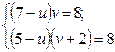 Þ
Þ 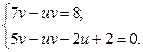
Выразим из первого
уравнения ![]() и подставим во второе уравнение
и подставим во второе уравнение
![]() Þ v2+2v–8=0 Þ v1=2,
v2=–4.
Þ v2+2v–8=0 Þ v1=2,
v2=–4.
Значение v2=–4 не подходит по смыслу задачи (из условия ясно, что производительность первой бригады выше, чем второй, а значит х–у=v>0). Найдем значение u, соответствующее v2=2, подставив значение v2 в выражение для u:
![]() .
.
Так как нам нужно найти значения х и у, подставим полученные значения для u и v в (V)
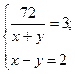 Þ
Þ 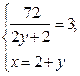 Þ
Þ 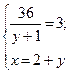 Þ
Þ 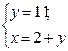 Þ
Þ 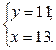
Ответ: 13 деталей в час изготавливала первая бригада; 11 деталей в час изготавливала вторая бригада.
Задача 3. Один насос может наполнить бассейн на 24 часа быстрее, чем другой. Через 8 часов после того, как был включен второй насос, включили первый, и через 20 часов совместной работы оказалось, что заполнено 2/3 бассейна. За сколько часов может наполнить бассейн каждый насос, работая самостоятельно?
Решение:
Примем весь бассейн за 1. Пусть I насос, работая самостоятельно, может наполнить весь бассейн за x часов, тогда II — за x+24 часа.
|
Время работы |
Производительность труда |
Объем работы |
|
|
I насос |
x |
|
1 |
|
II насос |
x+24 |
|
1 |
Известно, что II насос был включен 8+20=28 часов, а I — 20 часов, и за это время они наполнили 2/3 бассейна. Составим и решим уравнение:
![]()
Обе части уравнения делим почленно на 2 и переносим все слагаемые в левую часть:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Второй корень — посторонний. Значит, I насос может наполнить бассейн самостоятельно за 60 часов, а II — за 60+24=84 часа.
Ответ: за 60 часов и 84 часа.
Домашнее задание
№616. Предложить задачу на дом.
Две бригады, работая совместно, закончили отделку квартир в доме за 6 дней. Сколько дней потребовалось бы каждой бригаде на выполнение этой работы, если одной для этого требуется на 5 дней больше чем другой?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (дни) |
Производительность
|
|
Первая бригада |
1 |
X |
|
|
Вторая бригада |
1 |
Х+5 |
|
|
Совместно |
1 |
6 |
|
Заметив по таблице, что совместная производительность выражается
как ![]() или
как
или
как ![]() ,
составим и решим уравнение.
,
составим и решим уравнение.
1) ![]() =
=![]() ;
;
Ответ: 10 дней, 15 дней.
Используя этот способ, можно решить задачу.
№703*.
Два хлопкоуборочных комбайна могут собрать хлопок с поля на 9 дней скорее, чем один первый комбайн, и на 4 дня скорее, чем один второй. За сколько дней каждый комбайн может собрать весь хлопок?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (дни) |
Производительность
|
|
Первый комбайн |
1 |
X+9 |
|
|
Второй комбайн |
1 |
Х+4 |
|
|
Совместно |
1 |
6 |
|
1) Составим и решим уравнение
![]() =
=![]() ;
умножив на Х (Х+9) + (Х+4) ? 0, получим:
;
умножив на Х (Х+9) + (Х+4) ? 0, получим:
2Х2 + 13Х = Х2 + 4Х +9Х + 36,
Х2 = 36;
Х1,2 = +6;
2) - 6 не удовлетворяет условию задачи. За 6 дней соберут весь хлопок два комбайна; за 10 дней - второй комбайн и за 15 дней - первый.
Ответ: 15 и 10 дней.
№704*.
Для наполнения бассейна через первую трубу потребуется на 9ч. больше времени, чем при пополнении через первую и вторую трубы, и на семь меньше, чем через одну вторую трубу. За сколько часов наполниться бассейн через обе трубы?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность
|
|
Первая труба |
1 |
X+9 |
|
|
Вторая труба |
1 |
(Х+9)+7 |
|
|
Совместно |
1 |
6 |
|
1) Составим и решим уравнение
![]() =
=![]() ;
;
![]()
![]()
![]()
![]()
х1,2 = +12.
x = -12 - не удовлетворяет условию задачи. За 12 часов наполнится бассейн.
Ответ: 12ч.
№706*.
Два слесаря получили заказ. Сначала 1ч работал первый слесарь, затем 4ч они работали вместе. В результате было выполнено 40% заказа. За сколько часов мог выполнить заказ каждый слесарь, если первому для этого понадобилось бы на 5 ч больше, чем второму?
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность
|
|
Первый слесарь |
1 |
X |
|
|
Второй слесарь |
1 |
(Х - 9) |
|
|
Совместно |
|
4 |
|
1) Первый слесарь, работая один, за 1 час выполнил работу ![]() ,
и работая совместно, выполнили работу
,
и работая совместно, выполнили работу ![]() ,
что по условию равно 40% всего заказа, т.е.
,
что по условию равно 40% всего заказа, т.е.
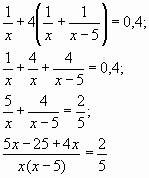
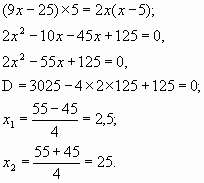
2,5 не удовлетворяет условию задачи, т.к. второй слесарь работал на 5 ч меньше, то есть 2,5 - 5 = - 2,5, что не выполнимо.
2) За 25 ч. может выполнить заказ первый слесарь и за 20 ч. второй слесарь.
Ответ: 25ч и 20ч.
Алгебра 9 класс. Учебник авторов Ю.Н. Макарычев, Н.Г. Миндюк, К.И Нешков, СБ. Суворова.
№1150. (Задачи повышенной трудности).
За сколько часов может выполнить работу каждый из трех рабочих, если производительность труда третьего рабочего равна полусумме производительностей труда первого и второго? Известно, что если бы третий рабочий проработал один 48 ч., то для окончания работы первому требовалось бы 10ч., а второму 15ч.
Проведем анализ задачи, составив таблицу.
|
Вид деятельности |
Работа (1) |
Время (ч) |
Производительность
|
|
Первый рабочий |
1 |
10 |
Х |
|
Второй рабочий |
1 |
15 |
Y |
|
Третий рабочий |
1 |
48 |
|
1) ![]() работа,
выполненная вторым и третьим рабочими.
работа,
выполненная вторым и третьим рабочими.
![]() работа,
выполненная первым и третьим рабочими.
работа,
выполненная первым и третьим рабочими.
Составим и решим систему:
![]()
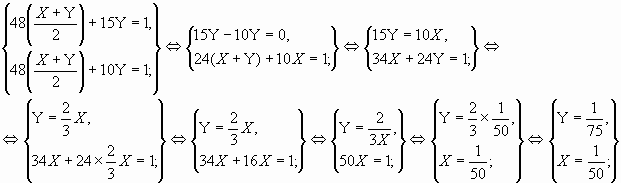
2) ![]()
Таким образом,
![]() -
производительность первого рабочего,
-
производительность первого рабочего,
![]() -
производительность второго рабочего,
-
производительность второго рабочего,
![]() -
производительность третьего рабочего.
-
производительность третьего рабочего.
3) ![]() =
50ч - время первого рабочего,
=
50ч - время первого рабочего,
![]() = 75ч
- время второго рабочего,
= 75ч
- время второго рабочего,
![]() = 60ч
- время третьего рабочего.
= 60ч
- время третьего рабочего.
Ответ: 50ч; 75ч; 60ч.
Источник.
http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/584346/
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.