Приложение 3 (1)

1.Найти сопротивление между точками A и D, если каждое из трех сопротивлений равно 1 Ом. ( Сопротивлением соединительных проводов пренебречь)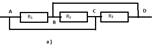                                                   

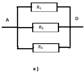
Т.к. точки А и С, В и D соединены проводниками, значит  схему а) можно заменить на в).  Общее сопротивление  при этом вычисляется по формуле 

Все три сопротивления одинаковы, значит общее сопротивление вычисляется по формуле:

                              R=1/3 Ом = 0, 3 Ом

2.Найти общее сопротивление на участке цепи, если все сопротивления равны по 2 Ом.                                                                   

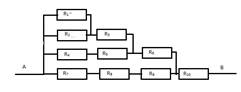
А. Найдем сопротивление R’ . Сопротивление R₁   и R₂ соединены параллельно, значит  R’ ищем по формуле 

                          R’=1 Ом

Б.  R’ и R₃ соединены последовательно и их общее сопротивление равно

 R’’ =R’+R ₃                     R’’= 3 Ом

В. Находим сопротивление R’’’ = R₄+ R₅        R’’’=4 Ом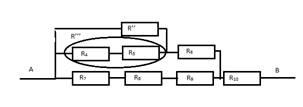

Г. Сопротивление R’’’’ определяем по формуле

    R’’’’= 1,7 Ом;    R’’’’’ = R’’’’ + R₆;            R’’’’’ = 3,7  Ом

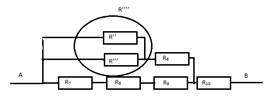
Д.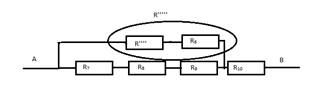 

Е.  R’’’’’’ = R₇ +R₈ +R₉

      R’’’’’’ = 6 Ом

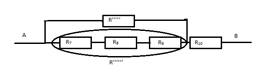
Ж.      R’’’’’’’  определим по формуле  

                      R= 2,3 Ом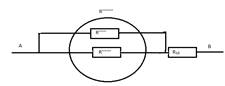       

З.  Общее сопротивление всей цепи равна R= R’’’’’’’+ R₁₀

                   R = 4,3  Ом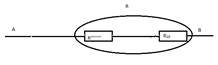       

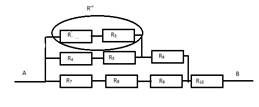
3.Найти сопротивление цепи  если R₁ = 2 Ом,  R₂ = 4 Ом, R₃ =1,5 Ом,  R₄ = 2 Ом,  R₅ = 3 Ом,      R₆ = 4 Ом, R₇ = 1 Ом,  R₈ = R₉ = R₁₀ =7,5 Ом,  R₁₁ = 1,5 Ом 

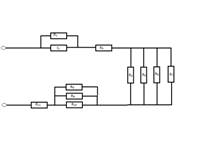
Рассмотрим соединение проводников. Оно смешанное и значит,  ищем группы одинаково соединенных проводников и заменим их эквивалентной схемой.

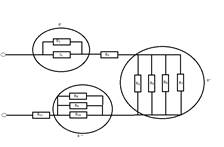             Находим промежуточные сопротивления R^’,   R^’’,  R^’’’  

R^’   =  ,   R^’ =1,3 Ом,                       =  +  +  + ,    R^’’ = 0,48 Ом,

Поскольку  три сопротивления R₈, R₉, R₁₀  имеют одинаковое значение то  сопротивление R^’’’  рассчитываем по формуле

                       R^’’’ =  ,        R^’’’ = 2,5  Ом,

 И наконец получили упрощенную схему

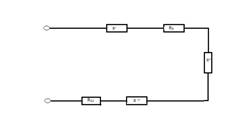
 Все сопротивления соединены последовательно.

R = R’ + R₃ + R’’ + R’’’ + R₁₁,                             R = 7,31 Ом

1.                  Найти сопротивление каркаса куба, составленного из проволочек одинакового сопротивления.

   В силу симметрии потенциал вершин куба 2, 3, 6 равны и вершин 4, 5, 7, значит вершины 2,3,6 и 4,5,7 соединим проводниками, лишенными сопротивления, - «шинами». Сопротивление куба  от этого не изменится. Таким образом, шины соединены друг с другом шестью проводниками: 2 – 7, 2 – 4, 3 – 5, 3 – 4, 6 – 7, 6 – 5.Общее сопротивление можно вычислить по формуле   R = R’ + R’’ + R’’’

R’, R’’, R’’’ вычисляем по формулам:

    R’ =  ;                       R’’ =  ;                 R’’’ =  ;

Конечное значение сопротивление ребер куба равна

                            R =  R₁

4.Найдите эквивалентное сопротивление бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый

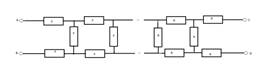
Для нахождения эквивалентного сопротивления цепи необходимо выделить общую секцию, которая бесконечно повторяется. Вполне очевидно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится, т.к. число элементов (секций) бесконечно. В силу вышесказанного, выделив повторяющуюся секцию в цепи и заменив сопротивление, остальной цепи искомым сопротивлением R_х, получим эквивалентную схему. Найдем сопротивление цепи, предварительно записав выражение для R_х через R_x. Опуская промежуточные выкладки, получим:                                  

Или