Приложения 4. правила кирхгофа (1) (3) (1)

Задача 2

Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найтитоки в ветвях, используя законы Кирхгофа.

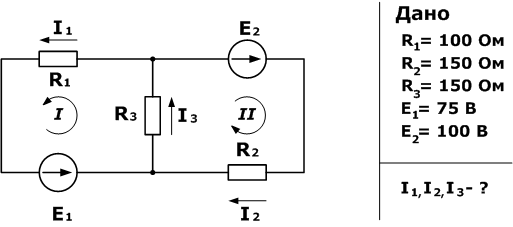
Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.

Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи 

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.

На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.

Уравнения для первого и второго контуров по второму закону будут: 

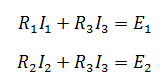
Все эти три уравнения образуют систему

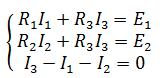
Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым). 

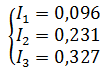
Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.

Задача 3

Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

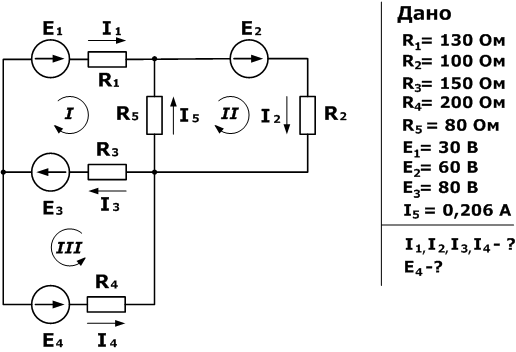
Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2 

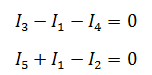Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче. 

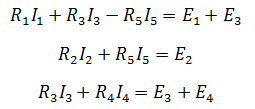
На основании этих уравнений составляем систему с 5-ью неизвестными 

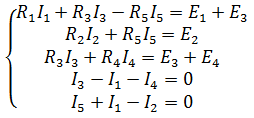
Решив эту систему любым удобным способом, найдем неизвестные величины 

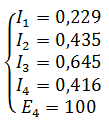Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками. 

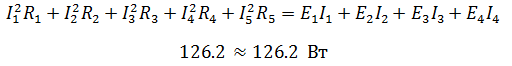
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно. 

1.Три  источника  тока  с  электродвижущими  силами  ℰ₁ =
= 2,5 В; ℰ₂ = 2 В; ℰ₃ = 15 В и резисторами R₁ = 2 Ом; R₂ = 3 Ом; R₃ = 8 Ом соединены, как показано на рисунке 14. Определите токи через эти резисторы. Внутренним сопротивлением источников пренебречь.

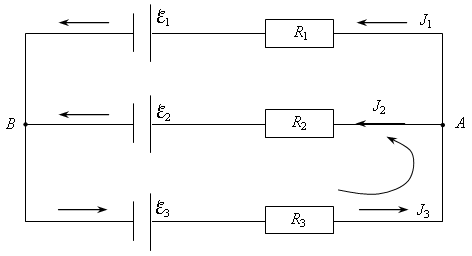
Рис. 14

По первому правилу Кирхгофа: для узла А:

– J₁ – J₂ + J₃ = 0

По второму правилу Кирхгофа для контура Аℰ₂Вℰ₁А:

– ℰ₁ + ℰ₂ = J₁R₁ – J₂R₂;

для контура Аℰ₃Вℰ₂А:

–ℰ₂ + ℰ₃ = J₂R₂ + J₃R₃;

для контура AE₃BE₁A:

ℰ₁ – ℰ₃ = –J₁R₁ – J₃R₃.

Подставим в эти формулы численные значения из условия задачи:

J₁ + J₂ = J₃

– 0,5 = – 3J₂ + 2J₁

13 = 3J₂ + 8J₃

12,5= –2J₁ –8J₃

13 = 3J₂ + 8(J₁ + J₂) = 3J₂ + 8J₁ + 8J₂ = 11J₂ + 8J₁.

Далее решаем систему: 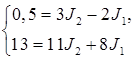 и находим  J₂ =  = 0,65A,
J₁ = 0,73 A,    J₃ = 1,38 A.

Проверяем решение по первому правилу Кирхгофа:

0,65 + 0,73 = 1,38 (А).

2.Два элемента с ЭДС ℰ₁ = 1,25 В и ℰ₂ = 1,5 В, имеющие одинаковые внутренние сопротивления r₁ = r₂ = 0,4 Ом, соединены параллельно и замкнуты резистором, сопротивление которого R = 10 Ом. Найти силы токов в резисторе и в каждом элементе (рис. 15).

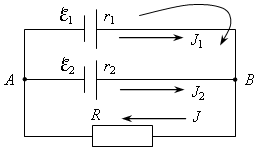
Рис. 15

Решение. Обозначим направления токов и выберем направление обхода контуров так, как показано на рисунке.

По первому правилу Кирхгофа: для узла А:  J – J₁ – J₂ = 0.

По второму правилу Кирхгофа: для контура Aℰ₁BRA:  J₁r₁ + JR = ℰ₁ для контура Aℰ₁Bℰ₂A:   J₁r₁ – J₂r₂ = ℰ₁ – ℰ₂.

Подставив числовые значения ЭДС и сопротивления, получим систему уравнений:

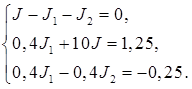
Решив эту систему, получим: J ≈ 0,135 A, J₁ ≈ – 0,245 A, J₂ ≈ 0,38 А.

Значение силы тока J₁ получилось отрицательным, это указывает на то, что  действительное  направление  данного  тока  противоположно  обозначенному.

Задачи для самостоятельного решения.

1. Две  батареи  (ℰ₁ = 10 В, r₁ = 1 Ом; ℰ₂ = 8 В, r₂ = 2 Ом)  и  резистор
R = 6 Ом соединены, как показано на рисунке 16. Определить силу тока в батареях и резисторе.

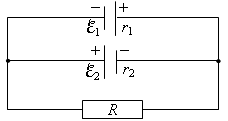
Рис. 16

Ответ: J₁ = 6,4 A; J₂ = 5,8 A; J₃ = 0,6 А.

2. Два источника тока (ℰ₁ = 8 В, r₁ = 2 Ом, ℰ₂ = 6 В, r₂ = 1,5 Ом) и резистор R = 10 Ом соединены, как показано на рисунке 17. Определить силу тока, текущего через реостат.

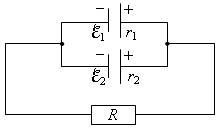
Рис. 17

Ответ: J = 0,63 A.

Скачано с www.znanio.ru