Применение теоремы о трёх перпендикулярах,на угол между прямой и плоскостью

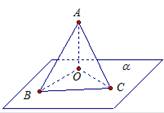
1.Из точки А, не принадлежащей плоскости α, проведены к этой плоскости перпендикуляр АО и две равные наклонные АВ и АС. Известно, что ∠ОАВ = ∠ВАС = 60°, АО = 1,5 см. Найдите расстояние между основаниями наклонных, угол между прямой АВ и плоскостью α.

Дано: АВ = АС,

∠ОАВ = ∠ВАС = 60°,

АО = 1,5 см.

Найти: ВС, ∠(АВ, α)

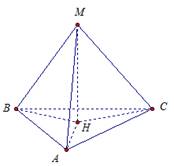
2. Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см. Найдите расстояние от точки М до плоскости АВС, если АВ = 6 см. Чему равен угол между прямой МС и плоскостью АВС?

Дано:

АВ = ВС =СА = 6 см;

МА = МВ = МС = 4 см.

Найти:

ρ (М, АВС);

∠ (МС, АВС).

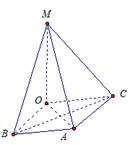
3. Прямая р проведенная из центра О описанной около треугольника АВС окружности, есть геометрическое место точек (ГМТ), равноудаленных от вершин треугольника.

Дано: 

Доказать:

МА = МВ = МС.

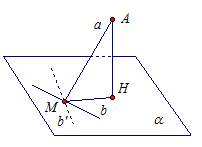
4.Прямая а пересекает плоскость α в точке М и не перпендикулярна к этой плоскости. Докажите, что в плоскости α через точку М проходит прямая, перпендикулярная к прямой а, и притом только одна.

Дано: МА = а – наклонная к α.

Доказать: 1) существует 

2) b – единственная.

5. Прямая АК перпендикулярна к плоскости равностороннего треугольника АВС, точка М – середина стороны ВС.

1) Докажите, что МК ⊥ ВС

2) Найдите угол между прямой КМ и плоскостью АВС, если АК = а, ВС = 2а.

1) Дано:

AB = BC = CA,

AK ⊥ ABC,

BM = MC.

Доказать: МК ⊥ ВС.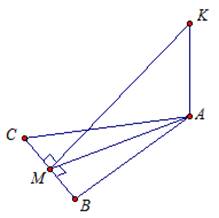 

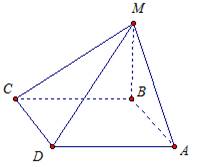
6. Из точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD.

1) Докажите, что треугольники АМD и МСD – прямоугольные.

2) Найдите угол между прямой МD и плоскостью АВС, если СD = 3см,

АD = 4 см, МВ=5 см.