Примеры закона сложения скоростей_приложение

Примеры решения задач

1. Лодка двигается по реке с собственной скоростью 8 м/с, так, как показано на рисунке. Скорость течения реки составляет 1 м/с. Определите скорость лодки относительно берега.

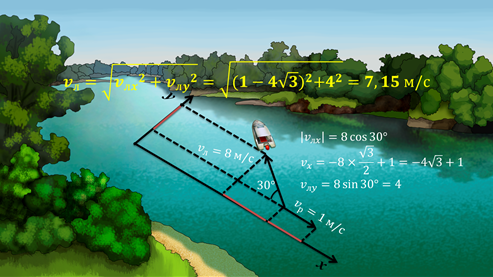
Расположим оси координат так, чтобы направление оси х совпадало с направлением течения реки. Тогда проекция скорости на ось х будет равна, т.к. на рисунке нам указан угол между направлением течения и скоростью лодки. Обратите внимание, что эта проекция будет отрицательной. В этом можно убедиться при построении проекции, да и чисто логически ясно, что лодка плывет против течения, а значит, одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения на ось х, конечно же, будет равна 1 м/с, поскольку направление течение совпадает с направлением оси х. Тогда скорость движения лодки по оси х относительно берега равна:

 Проекция вектора скорости лодки на ось у равна

Разумеется, проекция скорости течения на ось у будет равна нулю, потому что вектор скорости течения перпендикулярен этой оси. С помощью геометрической суммы проекций мы можем найти модуль скорости лодки, относительно берега:

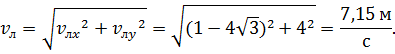
2.

Найдём скорость машины, относительно самолёта в заданной системе координат. Сначала найдем проекции скорости машины на оси х и у. Точно так же, как и в предыдущем примере, проекция на ось х равна:, а проекция на ось у равна. Точно так же находим проекции скорости самолёта на координатные оси:

Напомним, что проекции являются скалярными величинами, поэтому их мы складываем алгебраически:

Теперь, когда мы нашли проекции скорости машины относительно самолёта на оси х и у, мы можем найти модуль скорости с помощью геометрической суммы:

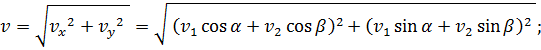
Таким образом, мы получили расчётную формулу для вычисления модуля скорости одного движущегося тела, относительно другого движущегося тела. Эта формула справедлива для тех случаев, когда оба тела двигаются в одной плоскости.