Проект "Подготовка к ЕГЭ-19 задание."

Задание 19. Арифметическая прогрессия составлена из n различных натуральных чисел, причем .

а) Возможно ли, чтобы сумма всех n членов этой прогрессии была бы равна 18?

б) Определите наибольшее число членов арифметической прогрессии, если сумма всех ее чисел меньше 850.

в) Определите все возможные значения n, если сумма всех чисел данной прогрессии равна 235.

Решение.

а) Арифметическая прогрессия определяется выражением , где d – разность прогрессии. Пусть d=3, а первый член равен , тогда получим три таких члена прогрессии:

3, 6, 9

которые в сумме дают 18.

б) Сумму S всех первых n членов арифметической прогрессии можно определить по формуле

          (1)

из которой видно, что наименьшее значение суммы достигается при d=1 (так как наименьшая разность между двумя различными натуральными числами равна 1),  (так как наименьшее натуральное число есть 1). Подставляет это в формулу, имеем, что

Так как S < 850, то получаем неравенство:

откуда

Здесь можно простым подбором найти наибольшее n, при котором выполняется последнее неравенство. Это значение будет равно 40, так как , а следующее значение 41 уже дает превышение значения 1700.

в) Используя формулу (1) для S=235 можно записать равенство:

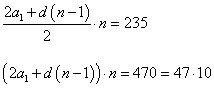
Здесь число 47 – простое, то есть, оно не раскладывается на более мелкие множители, следовательно, чтобы левая часть равенства была равна 470, необходимо, чтобы множитель n был делителем 10. Так как n – натуральное число, то имеем следующие возможные значения (для n>2): 5 и 10. Значение n=47 не подойдет, т.к. в п б. показано, что при n=40 минимальная сумма равна 1640, что больше 235. Проверим, подойдут ли числа 5 и 10. При n=5, получаем:

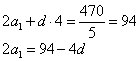
Можно ли подобрать такие целые , чтобы выполнялось равенство? Да, можно, это числа d=1 и .

Теперь проверим значение n=10:

подходит при d=1 и .

Ответ: а) да; б) 40; в) 5 и 10.

Задание 19. Число 704 можно представить в виде произведения натуральных чисел. Можно ли из них образуют геометрическую прогрессию, состоящую из:

а) пяти членов;

б) четырех членов;

в) трех членов.

Решение.

Сначала разложим число 704 на простые множители, получим:

Можно ли из этих чисел получить геометрическую прогрессию. Очевидно, можно записать множители в таком виде:

где последовательность 1, 2, 4, 8 – геометрическая прогрессия  с q=2 и . То есть, можно образовать геометрическую прогрессию из 3-х и 4-х членов.

Ответ: а) нет; б) да; в) да

Задание 19. Пусть имеются два натуральных числа, связанных между собой выражением , и пусть q – их наименьшее общее кратное, а d – их наибольший общий делитель.

а) Может ли  быть равен 110?

б) Может ли  быть равен 3?

в) Найдите наименьшее значение .

Решение.

Представим числа x и y в виде произведений , где a, b – взаимно простые числа (иначе d не будет наибольшим общим делителем). Кроме того, из формулы  следует, что при x=1, имеем . Наименьшее общее кратное можно записать в виде  или так:

а) Чтобы  число 110 должно представляться в виде произведения двух взаимно простых чисел a и b. Получаем вариант a=10, b=11, d=1, тогда x=10, y=11. Но эти числа не удовлетворяет равенству . Можно заметить, что остальные варианты (например, a=11, b=20, d=2) будут только отдаляться от этого равенства.

б)-в) Равенство  выполняется при наименьших x=1, y=4 (см. начало решения), следовательно, минимальное значение (при a=1, b=4, d=1)

Простым перебором можно убедиться, что при  и a=1, b=2, d=1 имеем x=1, y=2 выражение  не выполняется. Аналогично и при x=1, y=3.

Ответ: а) нет; б) нет; в) 4.

Задание 19. Арифметическая прогрессия составлена из n различных натуральных чисел, причем .

а) Возможно ли, чтобы сумма всех n членов этой прогрессии была бы равна 12?

б) Определите наибольшее число членов арифметической прогрессии, если сумма всех ее чисел меньше 435.

в) Определите все возможные значения n, если сумма всех чисел данной прогрессии равна 305.

Решение.

а) Арифметическая прогрессия определяется выражением , где d – разность прогрессии. Пусть d=3, а первый член равен , тогда получим три таких члена прогрессии:

1, 4, 7

которые в сумме дают 12.

б) Сумму S всех первых n членов арифметической прогрессии можно определить по формуле

          (1)

из которой видно, что наименьшее значение суммы достигается при d=1 (так как наименьшая разность между двумя различными натуральными числами равна 1),  (так как наименьшее натуральное число есть 1). Подставляет это в формулу, имеем, что

Так как S < 435, то получаем неравенство:

откуда

Здесь можно простым подбором найти наибольшее n, при котором выполняется последнее неравенство. Это значение будет равно 28, так как , а следующее значение 29 уже дает точное значение 870.

в) Используя формулу (1) для S=305 можно записать равенство:

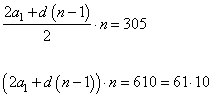
Здесь число 61 – простое, то есть, оно не раскладывается на более мелкие множители, следовательно, чтобы левая часть равенства была равна 610, необходимо, чтобы множитель n был делителем 10. Так как n – натуральное число, то имеем следующие возможные значения (для n>2): 5 и 10. Значение n=61 не подойдет, т.к. в п б. показано, что при n=29 минимальная сумма равна 870, что больше 305. Проверим, подойдут ли числа 5 и 10. При n=5, получаем:

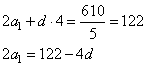
Можно ли подобрать такие целые , чтобы выполнялось равенство? Да, можно, это числа d=1 и .

Теперь проверим значение n=10:

подходит при d=1 и .

Ответ: а) да; б) 28; в) 5 и 10.

Задание 19. На каждой из восьми карточек записаны числа в следующем порядке: 3, -5, -6, 7, -8, 10, -11, 12. Затем, карточки перевернули, перемешали и на их чистых сторона снова записывают эти числа (по одному на каждой) в этом же порядке. Затем, полученные числа на каждой карточке складывают, а восемь сумм – умножают.

а) Может ли в результате получиться 0?

б) Может ли в результате получиться 2?

в) Какое наименьшее целое неотрицательное число может в результате получиться?

Решение.

а) Можно заметить, что какие бы два числа не были бы записаны на карточке, в сумме они никогда не дадут 0. А произведение ненулевых множителей дает число отличное от нуля.

б-в) Минимальные по модулю суммы получаются, если на каждой карточке записаны соседние числа:

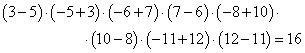
Ответ: а) нет; б) нет; в) 16.

Вариант 6.

Задание 19. Пусть имеются два натуральных числа, связанных между собой выражением , и пусть q – их наименьшее общее кратное, а d – их наибольший общий делитель.

а) Может ли  быть равен 104?

б) Может ли  быть равен 15?

в) Найдите наименьшее значение .

Решение.

Представим числа x и y в виде произведений , где a, b – взаимно простые числа (иначе d не будет наибольшим общим делителем). Кроме того, из формулы  следует, что наименьшее x=6, при котором имеем целое . Наименьшее общее кратное можно записать в виде  или так:

а) Чтобы  число 104 должно представляться в виде произведения двух взаимно простых чисел a и b. Получаем вариант a=13, b=8, d=1, тогда x=13, y=8 и эти числа удовлетворяет равенству .

б)-в) Равенство  выполняется при наименьших x=6, y=5 (см. начало решения), следовательно, минимальное значение (при a=6, b=5, d=1)

Ответ: а) да; б) нет; в) 30.

Задание 19. Трое друзей играли в теннис. В каждой игре участвовало два игрока. Один из них сыграл 18 игр, а другой — 11 игр. Мог ли третий участник сыграть 

а) 19;

б) 28;

в) 31 игр?

Решение.

а) Да, например, первый с третьим сыграли 13 игр, второй с первым 6 игр и первый со вторым 5 игр. Получается, что третий сыграл 13+6=19 игр.

б) Общее число сыгранных партий будет равно

не целое число, следовательно, третий игрок не мог сыграть 28 игр.

в) Максимальное число партий, которые мог сыграть третий игрок, равно 18+11=29, что меньше числа 31. Следовательно, третий игрок не мог сыграть 31 раз.

Ответ: а) да; б) нет; в) нет.

Задание 19. Носки 40-го размера стоят 60 рублей, а носки 30-го размера — 35 рублей. Нужно купить носки, имея всего 1499 рублей и соблюдая дополнительное условие: число носков 40-го размера не должно отличаться от числа носков 30-го размера больше чем на шесть.

а) Можно ли купить 30 носков?

б) Можно ли купить 35 носков?

в) Какое наибольшее число носков можно купить?

Решение.

а) Да, например, можно купить 12 носков 40-го размера и 18 носков 30-го:

 рублей.

б) Нет. Наименьшая сумма получится, если купить наибольшее число носков 30-го размера и наименьшего 40-го, то есть, 20 и 15 штук соответственно:

 рублей.

в) Обозначим через n число носков 40-го размера, а через m – число носков 30-го размера. Общее число носков должно быть

Также заметим, что максимальное число носков может быть куплено при n<m, то есть, когда носков 30-го размера больше (они дешевле). Получаем условие:

                (1)

Общая сумма затрат, равна , которая не должна превышать 1499 рублей:

     (2)

Подставим в (2) вместо , получим:

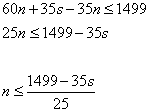
А из условия (1), имеем:

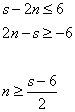
Объединяя два последних выражения, имеем:

значит

откуда

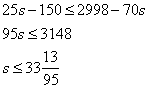
Здесь нужно проверить: можно ли взять крайнее значение s=33. В этом случае n=14, m=19, имеем:

не подходит, значит, наибольшее число носков равно 32.

Ответ: а) да; б) нет; в) 32.

Задание 19. Имеется несколько двухзначных натуральных чисел, не обязательно различных. Известно, что сумма этих чисел равна 396. Затем эти же числа записали наоборот (например, было 23, стало 32).

а) Может ли сумма чисел, записанных наоборот, быть в 4 раза больше исходной суммы чисел?

б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?

в) Найдите наибольшее возможное значение суммы получившихся чисел.

Решение.

а) Исходные двухзначные числа можно записать в виде

и пусть

В этих обозначениях сумма исходных чисел, равна , а записанных наоборот , которая должна равняться . Получаем систему:

Умножим первое уравнение на 10 и вычтем из него второе, получим:

И, подставляя это значение во второе уравнение, имеем:

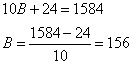
Следовательно, можно взять 18 чисел, например, семнадцать 19 и последнее 73. Проверяем:

Все верно.

б) Аналогичными рассуждениями, получаем:

Значит, можно взять, например, 11 чисел: десять 37 и последнее 26. Проверяем:

Все верно.

в) Требуется определить, для какого наибольшего S имеет натуральные решения следующая система уравнений:

Выразим отсюда S, умножив первое уравнение на 10 и вычитая второе:

Число A – это сумма натуральных цифр, значит оно натуральное. Нужно найти такое наименьшее A, при котором , где n – количество двухзначных чисел. Так как минимальная сумма A получается при сложении единиц, то A=n, а , получаем:

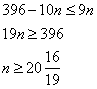
то есть, наименьшее целое n=21 и максимальная сумма

Ответ: а) да; б) да; в) 1881.

Задание 19. Число 3645 можно представить в виде произведения натуральных чисел. Можно ли из них образуют геометрическую прогрессию, состоящую из:

а) пяти членов;

б) четырех членов;

в) трех членов.

Решение.

Сначала разложим число 3645 на простые множители, получим:

Можно ли из этих чисел получить геометрическую прогрессию. Очевидно, можно записать множители в таком виде:

где последовательность 1, 3, 9, 27 – геометрическая прогрессия  с q=3 и . То есть, можно образовать геометрическую прогрессию из 3-х и 4-х членов.

Ответ: а) нет; б) да; в) да.

В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого, один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.

а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?

б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?

в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.

Решение.

а) Пусть в школе № 1 писали тест два учащихся, один из них набрал 1 балл, а второй набрал 19 баллов и перешёл в школу № 2. Тогда средний балл в школе № 1 уменьшился в 10 раз.

б) Пусть в школе № 2 писали тест m учащихся, средний балл равнялся B, а прошедший в неё учащийся набрал u баллов. Тогда получаем

u=0,9(m+1)B-mB  , 10u=(9-m)B

Если B = 7, то(9-m)B не делится на 10, а 10u делится на 10. Но это невозможно, поскольку 10u=(9-m).

в) Пусть в школе № 1 средний балл равнялся A. Тогда получаем:

u=(9-m)A-0,9(8-m)A, 10u=(18-m)A=(9-m)B

Заметим, что если B = 1 или B = 3, то 10u=(9-m)B не делится на 10. Если B = 2 или B = 4, то m = 4. В первом случае 14A = 10, а во втором 14A = 20. Значит, ни один из этих случаев не возможен.

При B = 5 и m = 3 получаем u = 3 и A = 2. Этот случай реализуется, например, если в школе № 1 писали тест 6 учащихся, 3 из них набрали по 1 баллу, а 3 — по 3 балла, в школе № 2 писали тест 3 учащихся и каждый набрал по 5 баллов, а у перешедшего из одной школы в другую учащегося 3 балла.

 Ответ: а) да; б) нет; в) 5.

В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом, причём в школе №1 средний балл равнялся 42.

Один из учащихся, писавших тест, перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах. В результате средний балл в школе №1 вырос на 25%, средний балл в школе №2 также вырос на 25%.

а) Сколько учащихся могло писать тест в школе №1 изначально?

б) В школе №1 все писавшие тест набрали разное количество баллов. Какое наибольшее количество баллов мог набрать учащийся этой школы?

в) Известно, что изначально в школе №2 писали тест более 10 учащихся. Какое наименьшее количество учащихся могло писать тест в школе №2 изначально?

Решение.

а) Пусть в школе №1 писали тест n учащихся. Тогда суммарный балл всех учащихся этой школы равнялся 42n , а после перехода одного учащегося в школу №2 суммарный балл стал равняться 52,5(n − 1). Таким образом, суммарный балл уменьшился на 10,5(5 − n). Это число должно быть натуральным, поскольку равняется количеству баллов перешедшего в школу №2 учащегося. Значит, этот учащийся набрал 21 балл и n = 3.

б) В школе №1 тест писали 3 учащихся, один из которых набрал 21 баллов. При этом суммарно они набрали 126 баллов. Значит, наибольшее количество баллов у учащегося с лучшим результатом могло быть тогда, когда суммабаллов остальных двух учащихся была наименьшей, то есть когда они набрали 1 и 21 баллов. В этом случае наибольший балл равен 104

.в) Пусть в школе №2 писали тест m учащихся, а средний балл равнялся B. Тогда получаем:1,25(m+1)B-mB=2,  (m+5)B=84 Таким образом, число 84 должно делиться на m + 5. При этом m + 5 > 15, поскольку m > 10. Число 84 имеет 4 делителя, больших 15: 21, 28, 42 и 84. Значит, m + 5 ≥ 21, откуда m ≥ 16.Покажем, что число m может равняться 16. Этот случай реализуется, например, если в школе №1 писали тест 3 учащихся, один учащийся набрал 21 балл, один учащийся набрал 63 баллa и один учащийся набрал 42 баллов, в школе №2 писали тест 16 учащихся и каждый набрал по 4 балла, а у перешедшего из одной школы в другую учащегося 21 балл.

 

Ответ: а) 3; б) 104; в) 16.