Проект "Подготовка к ЕГЭ" Тождества по теме Обратные тригонометрические функции"

Проект  «Подготовка к ЕГЭ»

Обучающихся 10А класса

Востриковой Алёны

Агапова Данилы

Учитель Зарьянцева Виктория Павловна

Тождества с арккосинусом, арксинусом, арктангенсом и арккотангенсом.

Перечень вопросов, рассматриваемых в теме:

·         Тождества, связывающие обратные тригонометрические функции и тождества, связывающие тригонометрические и обратные тригонометрические функции

·         Применение тождеств на несложных примерах и для вычисления выражений, включающих арккосинус, арксинус, арктангенс и арккотангенс

·         Применение тождеств с арккосинусом, арксинусом, арктангенсом и арккотангенсом для преобразования выражений.

Глоссарий по теме

Арккосинусом числа m  называется такое число α, что:  и . Арккосинус числа m обозначают: .

Арксинусом числа m  называется такое число α, что:  и . Арксинус числа m обозначают: .

Арктангенсом числа m называется такое число α, что:  и . Арктангенс числа m обозначают: 

Арккотангенсом числа n называется такое число α, что:  и .

Арккотангенс числа n обозначают: .

Основная литература:

Фёдорова Н.Е., Колягин Ю.М., Ткачёва М.В., Шабунин М.И. под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 4-е изд. – М.: Просвещение, 2020г. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс. 310-322.

Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс», 2019. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс. сс. 286-321, 327-354.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

На предыдущих уроках мы познакомились с понятиями арксинуса, арккосинуса, арктангенса и арккотангенса и с самыми простыми тождествами, которые связывают их с тригонометрическими функциями:

 для любого значения m:;

 для любого значения m;

1.    для любого α: 

2.    для любого α: .

3.    для любого α: .

4.    для любого α: 

Однако, эти тождества не позволяют вычислять значения более сложных выражений, например, таких:

1)

2)

3)

На этом уроке мы рассмотрим несколько тождеств, которые позволят нам вычислять значения выражений и преобразовывать достаточно сложные выражения с обратными тригонометрическими функциями.

Задание.

Попробуйте вычислить значение выражения:

Решение:

В этом случае мы не можем воспользоваться тождеством, так как . Но в этом случае мы имеем табличные значения:

Ответ:

Задание

Вычислим значение выражения

Решение:

В этом случае мы также имеем табличные значения:

Ответ: 

1. Рассмотрим сначала задачи, связанные с вычислением табличных значений обратных тригонометрических функций.

Пример 1.

Найдите значение: .

Решение:

При решении данной задачи будем пользоваться табличными значениями аркфункций тождеством:

Ответ: .

Пример 2.

Вычислить: 

Решение:

На первый взгляд, использование тождества приводит к получению ответа:. Но заметим, что аргумент синуса не удовлетворяет промежутку . Поэтому ответ является неверным. Таким образом, нужно найти такое значение a , что:. Таким значением является . Значит, ответом является число .

2 вариант. Найдем численное значение . Оно равно . Теперь найдем . Оно равно.

Заметим, что второй вариант решения возможен в том случае, когда мы имеем дело с табличными значениями тригонометрических функций.

Ответ: .

Пример 3.

Вычислить: 

Решение:

В этом примере возможен только ход рассуждений по первому варианту, так как мы имеем дело не с табличными значениями косинуса. Очевидно, что число 10 не является правильным ответом, поскольку оно не принадлежит промежутку . Таким образом, нам нужно найти такое число a из промежутка , косинус которого равен косинусу 10. Таким значением a является число , так как значит,  и, с учетом формул приведения: .

Ответ: 1

Тождества, связывающие тригонометрические и обратные тригонометрические функции

и , если   и   и , если   и , если   и   и

2. Рассмотрим некоторые тождества

С использованием тождеств, связывающих тригонометрические и обратные тригонометрические функции, рассмотрим решение некоторых примеров:

Пример 4.

Вычислите: .

Решение:

При решении этой задачи используется только знание табличных значений тригонометрических и обратных тригонометрических функций:

.

Ответ: 0.

Пример 5.

Вычислить: 

Решение:

Для вычисления значения данного выражения воспользуемся тождеством (22):

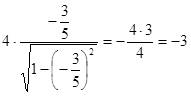
Ответ: -3

Пример 6.

Вычислить: 

Решение:

Сначала воспользуемся табличными значениями обратных тригонометрических функций и заменим . Теперь воспользуемся для преобразования формулой тангенса двух аргументов:

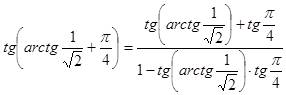. Теперь, используя тождества для арктангенса и табличные значения тангенса, получим результат: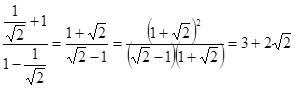 

Ответ: 

Решение задачи 2

Вычислить: .

Решение:

Данное выражение вообще не содержит табличных значений тригонометрических функций, поэтому при решении этой задачи будем использовать тождества второй группы. Но сначала воспользуемся формулой косинуса суммы аргументов. Таким образом, получим:

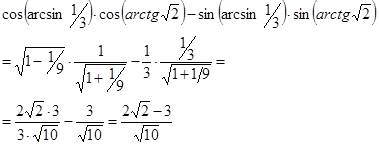
Ответ:.

Решение задачи 3

Вычислить 

Решение:

Воспользуемся для начала формулой синуса двойного аргумента и получим:

.

Теперь, используя тождества и преобразуя полученное выражение, получим окончательный результат:

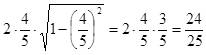
Ответ: 

3. Рассмотрим более сложные задачи.

Пример 7

Вычислить: .

Решение:

Найдем . Для этого воспользуемся формулой тангенса суммы аргументов:

Поэтому сумма арктангенсов – это такое число, тангенс которого равен -1. Для того чтобы найти окончательно это число, определим, какому промежутку оно должно принадлежать. и принадлежат промежутку , поскольку в силу монотонности функции арктангенс (он монотонно возрастает) каждый из рассматриваемых арктангенсов больше чем , который равен . А в силу ее ограниченности каждый из них меньше чем . Поэтому сумма этих арктангенсов принадлежит промежутку . В этом промежутке содержится единственное число, тангенс которого равен -1. Это . Таким образом значение выражения равно: .

Ответ: 0,75

Пример 8

Найдите  в виде целого числа, если .

Решение:

Сначала воспользуемся формулой, связывающей значения тангенса и котангенса одного аргумента:

. Это позволяет вычислить . Теперь, подставив найденное значение в выражение, значение которого нужно найти, получим искомый результат:

Ответ: 5.

Пример 9

Вычислить: 

Решение:

При вычислении значения данного выражения прежде всего воспользуемся формулами синуса двойного аргумента, выражающего его через тангенс, и тангенса половинного аргумента:

.

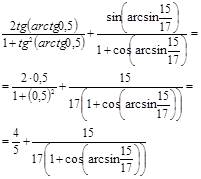Теперь воспользуемся тождеством (19) и получим окончательный результат:

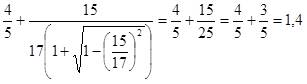
Пример 10

Вычислить: 

Решение:

Заметим, что при вычислении значения данного выражения можно использовать формулы котангенса суммы и разности аргументов, а затем формулы котангенса половинного аргумента. Но мы будем использовать другой путь. Один из аргументов  и другой . Сумма и разность аргументов представляют собой очень привлекательные выражения:  и . Попробуем это использовать. Преобразуем данное выражение, воспользовавшись формулой суммы котангенсов: . И далее используя в знаменателе формулу преобразования произведения синусов в разность косинусов:. Таким образом получим: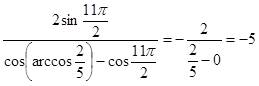 

Примеры и разбор решения заданий тренировочного модуля

1. Упростить выражение: , где 

Решение:

При выполнении преобразования данного выражения воспользуемся формулой синуса двойного аргумента, а также тождествами, позволяющими выразить и. В результате получим:

.

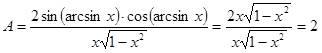Ответ: 2.

2. Упростите выражение: .

Решение:

Воспользуемся формулой преобразования косинуса суммы аргументов, а затем тождествами:

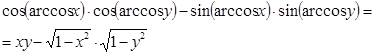Ответ: .

3. Найдите значение выражения: 

Решение:

С одной стороны, можно попытаться воспользоваться тождеством: . Но в этом случае мы получим в качестве значения выражения: , значение которого вычислять не очень удобно. Поэтому мы будем действовать другим способом: сначала вычислим значение , а затем – значение косинуса в найденной точке.

Для вычисления  воспользуемся выражением косинуса через котангенс половинного аргумента: . Используя этот результат, получим: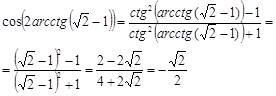

Теперь найдем 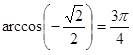, Ответ: