
Публикация является частью публикации:
МУНИЦИПАЛЬНОЕ БЮЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 22»
Тема работы
«Решение задач на смешение веществ различными способами».
номинация
«Математическое исследование»
Автор: Пыхтина Анна, Морозкина Александра,
Леньшина Александра , 8 класс
МБОУ «СОШ № 22»
Научный руководитель: Крымкина Наталья Васильевна
учитель математики высшей категории
г. Сергиев Посад
2017 год.
Оглавление
1. Введение…………………………………………………………………………3
2. Основная часть………………………………………………………………….3-11
3. Заключение……………….……………………………………………………...11
4. Литература………………………………………………………………………12
1. Введение.
На уроках математики, начиная с начальной школы, мы постоянно сталкиваемся с задачами на смешение различных веществ. С каждым годом эти задачи усложняются, но принцип их решения не меняется – мы берем одну часть за «x» и отталкиваемся от нее.
Но недавно мы узнали, что раньше такие задачи можно было решать, не вводя переменные.
Такие способы подробно описаны в книге Леонтия Филипповича Магницкого.
ЦЕЛЬ РАБОТЫ:
· найти новые способы решения задач на смешение.
Задачи работы:
![]() поиск
различных способов решения задач на смешение;
поиск
различных способов решения задач на смешение;
![]() знакомство
с «Арифметикой» Магницкого.
знакомство
с «Арифметикой» Магницкого.
Актуальность работы заключается в том, что изучение различных способов решения задач, позволит нам лучше подготовиться к сдаче экзаменов. Ведь способы, описанные в «Арифметике» Магницкого упрощают решение задач.
Практическая значимость: материал может быть использован как дополнительный источник для изучения жизни и творчества великих математиков.
2.Основная часть.
2.1.Леонтий Филиппович Магницкий - замечательный русский математик
Лео́нтий Фили́ппович Магни́цкий (при рождении Теляшин; 9 июня 1669, Осташков — 19 октября 1739, Москва) — русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первого в России учебного справочника по математике. Родился в Осташковской патриаршей слободе. По одной версии, был сыном крестьянина Филиппа Телятина. С юных лет работал с отцом на пашне, самостоятельно обучаясь чтению и письму, и был страстным охотником читать и разбирать мудрёное и трудное. По другой версии, был родным племянником архимандрита Нектария, устроителя Ниловой пустыни близ Осташкова Тверской губернии и потому имел доступ к церковным книгам. В 1684 году отправлен в Иосифо-Волоколамский монастырь как возчик для доставки рыбы монахам. Поразил монахов своей грамотностью и умом, оставлен при обители в роли чтеца. Затем переведён в Московский Симонов монастырь. Монастырское начальство решило готовить незаурядного юношу в священнослужители. 1685—1694 годах — учится в Славяно-греко-латинской академии. Математика там не преподавалась. По-видимому свои математические познания он приобрёл путем самостоятельного изучения.
Знания Леонтия Филипповича в области математики удивляли многих.
При встрече он произвёл на царя Петра I очень сильное впечатление незаурядным
умственным развитием и обширными познаниями. В знак почтения и признания
достоинств Пётр I «жаловал» ему фамилию Магницкий «в сравнении того, как магнит
привлекает к себе железо, так он природными и самообразованными способностями
своими обратил внимание на себя». В
1701 году по распоряжению Петра I был назначен преподавателем школы
«математических и навигацких, то есть мореходных хитростно наук учения»,
помещавшейся в здании Сухаревой башни. Начал работать помощником учителя
математики — Андрея Фарварсона, а затем — учителем арифметики и, по всей
вероятности, геометрии и тригонометрии; ему было поручено написать учебник по
математике и кораблевождению. В 1703 году
Магницкий составил первую в России учебную энциклопедию по математике под
заглавием «Арифметика, сиречь наук числительная, с разных диалектов на
словенский язык переведённая и во едино собрана и на две книги
разделена…Сочинися сия книга чрез труды Леонтия Магницкого». Как
учебник эта книга более полувека употреблялась в школах благодаря
научно-методическим и литературным достоинствам. В 1704 году Магницкому царским указом было пожаловано дворянство. Пётр
I был особенно расположен к Леонтию Филипповичу, жаловал его деревнями во
Владимирской и Тамбовской губерниях, приказал выстроить ему дом на Лубянке, а
за «непрестанные и прилежные в навигацких школах во учении труды» наградил  «саксонским кафтаном» и другой одеждой. В 1715 году в Петербурге была открыта Морская академия,
куда было перенесено обучение военным наукам, а в московской Навигатской школе
стали учить только арифметике, геометрии и тригонометрии. С этого момента
Магницкий становится старшим учителем школы и руководит её учебной частью.
Умер в Москве в октябре 1739 года в возрасте 70 лет.
Похоронен в Москве в церкви Гребневской Иконы Божией Матери у
Никольских ворот (в 1927 году церковь была разобрана). 27 мая 1932 года при постройке первой линии московского
метрополитена на глубине одного метра обнаружилась плита из крепкого известняка
на обратной стороне которой оказалась тонко выбита «эпитафия» надгробия Л. Ф.
Магницкого, написанная его сыном Иваном (её текст опубликован в 1836 году в
газете «Московские ведомости»). На другой
день под плитой-памятником на глубине четырёх метров обнаружена была гробница.
Она была выложена из хорошего кирпича и залита со всех сторон известью. В
могиле находилась дубовая колода, в ней лежал невредимый скелет Леонтия
Филипповича с некоторыми сохранившимися на нём покровами, под головой
находилась стеклянная чернильница, имевшая форму лампадки, и рядом лежало
полуистлевшее гусиное перо.
«саксонским кафтаном» и другой одеждой. В 1715 году в Петербурге была открыта Морская академия,
куда было перенесено обучение военным наукам, а в московской Навигатской школе
стали учить только арифметике, геометрии и тригонометрии. С этого момента
Магницкий становится старшим учителем школы и руководит её учебной частью.
Умер в Москве в октябре 1739 года в возрасте 70 лет.
Похоронен в Москве в церкви Гребневской Иконы Божией Матери у
Никольских ворот (в 1927 году церковь была разобрана). 27 мая 1932 года при постройке первой линии московского
метрополитена на глубине одного метра обнаружилась плита из крепкого известняка
на обратной стороне которой оказалась тонко выбита «эпитафия» надгробия Л. Ф.
Магницкого, написанная его сыном Иваном (её текст опубликован в 1836 году в
газете «Московские ведомости»). На другой
день под плитой-памятником на глубине четырёх метров обнаружена была гробница.
Она была выложена из хорошего кирпича и залита со всех сторон известью. В
могиле находилась дубовая колода, в ней лежал невредимый скелет Леонтия
Филипповича с некоторыми сохранившимися на нём покровами, под головой
находилась стеклянная чернильница, имевшая форму лампадки, и рядом лежало
полуистлевшее гусиное перо.
2.2.«Арифметика» Магницкого.
Книга эта содержит начала математических знаний того времени: арифметики, алгебры, геометрии и тригонометрии. В конце книги имеется снабженный большим числом таблиц отдел, посвященный морскому делу. Большую часть места, как указывает и заглавие книги, автор посвящает арифметике.
 Использовав, кроме
русской рукописной литературы, то, что ему казалось полезным из иностранных
источников, Магницкий весь материал приспосабливает к потребностям русского
читателя и придает своему изложению во многом характер русских рукописных
математических книг, в связи с которыми и нужно рассматривать
"Арифметику" Магницкого. М. В. Ломоносов называл эту книгу вратами
своей учености" и знал ее наизусть. "Вратами учености" эта книга
была для всех русских людей первой половины XVIII века, стремившихся к
образованию.
Использовав, кроме
русской рукописной литературы, то, что ему казалось полезным из иностранных
источников, Магницкий весь материал приспосабливает к потребностям русского
читателя и придает своему изложению во многом характер русских рукописных
математических книг, в связи с которыми и нужно рассматривать
"Арифметику" Магницкого. М. В. Ломоносов называл эту книгу вратами
своей учености" и знал ее наизусть. "Вратами учености" эта книга
была для всех русских людей первой половины XVIII века, стремившихся к
образованию.
2.3.« Задачи на смешение веществ».
Такие задачи часто встречаются в жизни – в металлургии, химическом производстве, в медицине и фармакологии и даже в обычной жизни, например, кулинарии.
В металлургии такие задачи возникают, когда нужно знать состав различных сплавов, в химии – количество вещества, вступающего в реакцию, в медицине и фармакологии часто от дозы лекарственного вещества и его составляющих зависит результат лечения, а в кулинарии - вкус полученного блюда.
Обычно нам нужно узнать, как из двух растворов получить вещество нужной концентрации, что и в каких количествах, добавить, какова доля каждого из составляющих веществ.
Как мы сейчас решаем такие задачи?
Одну часть берем за «X», составляем уравнения, если нужно, вводим вторую переменную, решаем и получаем нужные значения.
Магницкий Л. Ф. еще в начале восемнадцатого века, когда еще не было принято использование переменных, предложил остроумный графический метод решения таких задач.
Рассмотрим метод Магницкого, который мы условно назвали «рыбкой» на примере задачи смешения масел.
Как смешать масла?
ЗАДАЧА.У некоторого человека были продажные масла. Одно - ценою десять гривен за ведро, а другое - шесть гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою семь гривен за ведро.
Вопрос: в каких пропорциях нужно смешать эти два масла?
Современный способ решения задачи.
Возьмем одну часть дешевого масла за «X». А часть дорогого масла - за «Y» и получим вот такое уравнение:
• 7( x+y) = 6x+10y
• 7x+7y=6x+10y
• 7x-6x=10y-7y
• x=3y
• 1/3=x/y
Мы получили, что масла нужно смешать в пропорции 1 к 3
Старинный способ решения задачи.
Приведем способ решения этой задачи Магницким Л. Ф. (Рис. 2).
В центре пишем цену первого масла – 6. Под ним, отступя вниз, пишем цену второго масла. Слева, примерно посередине между верхней и нижней цифрами пишем стоимость желаемого масла. Соединяем три цифры отрезками прямых. Получаем картинку рис.2 –а.
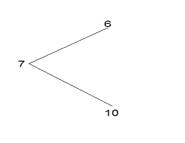 Рис.
2-а
Рис.
2-а
Первую цену, поскольку она меньше цены желаемого масла, вычтем из цены смешанного масла, и результат поставим справа от второй цены по диагонали относительно первой цены. Затем из второй цены, которая больше цены желаемого масла, вычтем цену смешанного масла, а то, что останется, напишем справа от первой цены по диагонали ко второй цене. Соединим точки отрезками, и получим вот такую картину – Рис. 2-б.
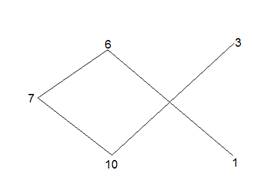 Рис.
2-б.
Рис.
2-б.
Затем определяем соотношение полученных справа величин между собой. Мы видим, что рядом с ценой дешевого масла стоит цифра 3, а рядом с ценой дорогого масла – цифра 1. Это означает, что дешевого масла нужно взять втрое больше, чем дорогого, т. е. для получения масла ценою 7 гривен, нужно взять масла в пропорции 1 к 3, т.е. дешевого масла должно быть втрое больше, чем дорогого масла.
Сравнивая оба способа – современный и старинный (Магницкого), мы видим, что ответы, полученные двумя способами, идентичны, значит, такой способ вполне применим к решению данной задачи на смешение веществ.
Правило креста или квадрат Пирсона.
Вот еще один из способов решения. Он называется «квадрат Пирсона».
Допустим, нужно приготовить раствор определенной концентрации, имея два раствора разной концентрации. Обозначим массу первого раствора через m1 , а второго- m2 .Пусть массовая доля растворенного вещества в первом растворе - k1 , во втором- k2 , а в их смеси – k3. Общая масса растворенного вещества в смеси будет скалываться из масс растворенного вещества в исходных растворах:
m1 k1
+
m2 k2 =
k3 (m1
+
m2 )
Откуда ![]() =
=![]()
Видно, что отношение массы первого вещества к массе второго раствора есть отношение разности массовых долей растворенного вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.
При решении задач на растворы с разными концентрациями применяют диагональную схему.
![]()
![]() k1
k3 -
k2
k1
k3 -
k2
![]()
![]() k3
k3
k2 k1- k3
Данный способ может использоваться при решении задач на смеси и сплавы.
Например . Морская вода содержит 5 % соли. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5 %.
![]()
![]() 5 %
1,5 % 30 кг
5 %
1,5 % 30 кг
![]()
![]() 1,5
%
1,5
%
0% 3,5 % х кг
Ответ: 7 кг
Задача на смешение веществ в повседневной жизни.
Может ли данная методика пригодиться в современной жизни? Конечно, может, вот, например, в парикмахерской.
У нас есть два раствора перекиси водорода: 30% и 3% . Нужно получить 12 % раствор. Как правильно подсчитать пропорции?
Попробуем решить эту задачу.
Вот два способа, какими можно решить задачу.
1 способ.
Обозначим искомую часть 30% раствора – х, а 3% -раствора - y. Соответственно, надо получить 0,12 (х+у).
Запишем уравнение:
0,03у+0,3х=0.12(x+y)
0,3х-0,12х=0,12у-0,03у
0,18х=0,09у
х=2у
Ответ: для получения 12%-го раствора нужно взять одну часть 30% раствора и две части 3%-го раствора перекиси.
Второй способ - метод Магницкого.
В центре пишем концентрацию первого раствора – 30 %. Под ним, отступя вниз, пишем концентрацию второго раствора- 3% или 0, 03. Слева, примерно посередине между верхней и нижней цифрами пишем концентрацию желаемого раствора – 12% или 0, 2. Соединяем три цифры отрезками прямых.
Из первой концентрации, поскольку она больше желаемой, вычтем 0,12, подпишем, справа от 0,03 результат 0, 18, который оказался по диагонали от 0,3. Из 0, 12 вычитаем 0, 03 и подписываем, справа от 0,3 результат – 0,09, который тоже, оказывается, по диагонали от значения 0, 03. Соединяем все отрезками и получаем «рыбку» (рис. 3).
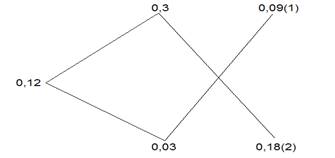 Рис.
3.
Рис.
3.
Соотношение полученных величин – 0, 09 и 0,018 – составляет 1 к 2, т. е. первого раствора концентрацией 30 % надо взять в 2 раза меньше, чем 3%-го раствора.
Подобные задачи встречаются и на экзаменах в ОГЭ и ЕГЭ.
Вот и сама задача из открытого банка ФИПИ.
Имеется два сплава с разным содержанием золота. В первом сплаве – 35% золота, а во втором 60% , в каком отношении надо взять первый и второй сплав, чтобы получить из них новый, содержащий 40% золота.
Решим и эту задачу двумя способами.
Пусть часть первого сплава – х, а второго – у
Тогда количество золота в первом сплаве составляет 0, 35х, а во втором 0,6у. Масса нового сплава равна х+у, а кол-во золота составляет 0,4( х+у).
Составим уравнение:
• 0, 35х+0,6у=0,4(х+у)
• 35х+60у=40х+40у
• 20у=5х
• х/у=4/1
Ответ: для получения сплава, содержащего 40% золота из двух сплавов с содержанием 35% и 60%, нужно взять в 4 раза больше 35%-го сплава.
2 способ – метод Магницкого.
Аналогично методу рыбки, описанному выше, формируем изображение, показанное на рисунке 4.
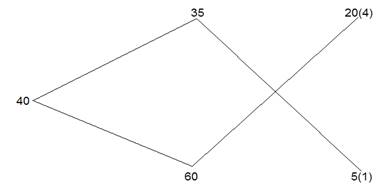 Рис.
4
Рис.
4
Результат: соотношение полученных величин составляет 1 к 4, значит 35%-го сплава надо взять в 4 раза больше, чем 60%-го.
Как вы снова смогли убедиться, способ Леонтия Филипповича Магницкого проще для понимания.
Применение такого способа может помочь быстро и правильно решить эту довольно сложную задачу.
3.Заключение
На представленных примерах видно, что изящный метод решения задач на смешение веществ Магницкого Л. Ф. актуален и сегодня.
Данное математическое исследование поможет нашим сверстникам при подготовке к экзаменам. Работу можно будет использовать для внеклассной работы по математике.
4.Литература
1. С. Н. Олехник, Ю. В. Нестеренко, М. К. Потапов. Старинные занимательные задачи. Москва, «Наука», главная редакция Физико-математической литературы, 1985.
2. Магницкий Леонтий Филиппович // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб.: 1890—1907.
3. Шикман А. П. Деятели отечественной истории. Биографический справочник. Москва, 1997 г.
4. http://www.etudes.ru/ru/mov/magn/index.php
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.