
Шифры и математика
В процессе работы над индивидуальным исследовательским проектом по математике на тему "Шифры и математика" автором была поставлена цель, изучить применение основ математики в криптологии и криптографии. В своем проекте учащийся школы выясняет, что такое шифр, какие виды шифра существуют и какое они имеют отношение к математике.
Подробнее о работе:
В ученической исследовательской работе по математике "Шифры и
математика" автором были рассмотрены вариации шифров, в том числе
и шифр перестановки, а также проведена практическая работа по применению одного
из видов шифрования на примере шифра Цезаря и продемонстрирован пример
дешифровки шифра Цезаря. Также в проекте дано определение книжного шифра и
проведена дешифровка на примере книжного шифра.
Учебная исследовательская работа по математике на тему "Шифры и математика" будет интересна учащимся 10 и 11 класса, представляет собой изучение истории криптографии, знакомит с разными видами шифров, рассматривает способы шифрования, применяющие математику, и приводит примеры на шифровку и дешифровку текста.
Оглавление
Введение
1. Виды шифров.
1.2 Шифры замены.
1.3 Шифры перестановки.
2. Применение одного из видов шифрования на примере шифра Цезаря.
3. Пример дешифровки шифра Цезаря.
4. Дешифровка на примере книжного шифра.
Заключение
Список использованной литературы
Введение
В данной работе описываются виды шифров, методы их применения на практике, а
также история криптографии и криптологии. Вместе с тем, приведены примеры на
шифровку текста всеми видами представленных шифров. Возможность и умение
использовать знания о математике и ее роли в шифровании в частности, поможет
людям начать меньше беспокоиться за сохранность важных данных. Кроме того,
применение подобных знаний помогает в развитии логического мышления и
приобретения навыков исследовательской деятельности.
Цель проекта: изучить применение основ математики в криптологии и криптографии.
Задачи проекта:
1. изучить историю криптографии;
2. познакомиться с разными видами шифров;
3. рассмотреть способы шифрования, применяющие математику;
4. рассмотреть примеры на шифровку и дешифровку текста;
5. создать продукт.
Вопросы проекта:
1. Выяснить, что включают в себя понятия «криптология» и «криптография»
2. Какие математические понятия используются при шифровании информации?
3. Какие исторические личности и события связаны с шифрами?
Актуальность: Данная проблема актуальна в наше время, так как криптография и стеганография востребованы повсеместно из-за потребности в сокрытии важных данных и информации от третьих лиц.
Продукт проекта: Буклет, в котором дана краткая информация о шифрах и их применении на практике.
Виды шифров
Еще в древние времена, люди начали задумываться над тем, как донести сообщение
до определенного человека, исключив из этого процесса посторонних. Именно тогда
начали зарождаться науки «криптография» и «криптология».
Криптология — учение об искусстве секретности и наука о методах шифрования и расшифровывания и их проектировании.
В свою очередь, Криптография — практический способ применения методов шифрования.
А Шифр – какая-либо система преобразования текста с секретом для обеспечения секретности передаваемой информации.
В современном обществе шифры применяются для тайной переписки дипломатических представителей со своими правительствами, в вооруженных силах для передачи текста секретных документов по техническим средствам связи, банками для обеспечения безопасности транзакций, а также некоторыми интернет-сервисами.
Помимо того, как зашифровать сообщение, необходимо найти способ его расшифровать. Методы чтения шифров и зашифрованных текстов изучает наука «криптоанализ».
Несмотря на то, что методы криптографии и криптоанализа до недавнего времени были не очень тесно связаны с математикой, математики всегда участвовали в расшифровке важных сообщений. И зачастую именно они добивались заметных успехов, ведь математики в своей работе постоянно имеют дело с разнообразными сложными задачами, а каждый шифр — это серьезная логическая задача. Постепенно роль математических методов в криптографии стала возрастать, и за последнее столетие они существенно изменили эту древнюю науку.
Шифры замены
Наиболее простейшими из криптографических шифров являются шифры замены или подстановки, когда одни символы сообщения заменяются другими символами, согласно некоторому правилу.
Рассмотрим наиболее древний и популярный шифр замены - шифр Цезаря, его называют в честь Юлия Цезаря, который использовал его, чтобы защищать военные сообщения. Суть его состояла в том, что буква алфавита заменялась другой с помощью сдвига по алфавиту на одно и то же число позиций. Например, при шифровке слова ТАЙНОПИСЬ, используя сдвиг на три буквы по алфавиту. Получим «ХГМРСТЛФЯ».
|
П |
Э |
Ж |
К |
Л |
М |
Ё |
О |
Щ |
|
Р |
Ю |
З |
Л |
М |
Н |
Ж |
П |
Ъ |
|
С |
Я |
И |
М |
Н |
О |
З |
Р |
Ы |
|
Т |
А |
Й |
Н |
О |
П |
И |
С |
Ь |
|
У |
Б |
К |
О |
П |
Р |
Й |
Т |
Э |
|
Ф |
В |
Л |
П |
Р |
С |
К |
У |
Ю |
|
Х |
Г |
М |
Р |
С |
Т |
Л |
Ф |
Я |
Гай Юлий Цезарь (100 или 102 до н. э. – 44 до н. э.) – древнеримский государственный и политический деятель, диктатор, полководец, писатель. Хотя Цезарь был первым зафиксированным человеком, использующим эту схему, другие шифры подстановки, как известно, использовались и ранее. Его племянник, Август, также использовал этот шифр, но со сдвигом вправо на один, и он не повторялся к началу алфавита.
Обратите внимание на строки 4 и 7. В них содержится слово до шифровки и его шифр. Легко дать математическое описание шифра замены. Пусть A= {a1, a2, a3, …, a35} – множество букв алфавита и знаков препинания,
B= {b1, b2, b3, …, b35} – множество знаков шифра. Пусть также f: A → B – взаимно-однозначное отображение A в B. Это значит, что каждой букве ax алфавита A сопоставляется однозначно определенная буква bx алфавита B, которую мы обозначаем символом f(ax), причем разным буквам сопоставляются разные буквы. Тогда шифр замены действует так: открытый текст a1 a2...ax преобразуется в шифрованный текст f(x1) f(x2) ...f(xx). Для русского языка можно обойтись 35 знаками; 31 буква (е, ё, и ь, ъ не различаются), пробел, точка, запятая, тире. Если число знаков, используемых при шифровании, тоже равно 35, то каждый такой шифр задается взаимно-однозначным отображением одного множества из 35 элементов на другое такое же множество.
Число таких отображений равно 1×2×3×…×35 = 35!
Это число примерно равно 1040. Иметь дело с произвольными отображениями f не слишком удобно: запомнить такое отображение трудно, а хранить при себе таблицу отображения – «ключ» шифра – нежелательно. Лучше иметь какое-нибудь простое правило, позволяющее по x найти f (x). А такие правила дают методы математики.
Шифры перестановки
При составлении таких шифров весь текст разбивается на группы, состоящие из
одинакового числа букв, и внутри каждой группы буквы некоторым образом
переставляются. Число различных преобразований шифра перестановки,
предназначенного для шифрования сообщения, состоящего из x символов меньше либо
равно x! (в это число входит и вариант преобразования, оставляющий все символы
на своих местах). Число возможных перестановок очень велико, отсюда большое
разнообразие перестановочных криптограмм.
Типичным и древнейшим примером шифра перестановки является шифр «Сциталь». Этот шифр известен со времен войны Спарты и Персии против Афин. Спартанский полководец Лисандр подозревал персов в возможной измене, но не знал их тайных планов. Его агент в стане персов прислал шифрованное сообщение, которое позволило Лисандру опередить персов и разгромить их.
Шифрованное сообщение было написано на поясе официального гонца от персов следующим образом: агент намотал пояс на сциталь (деревянный цилиндр определенного диаметра) и написал на поясе сообщение вдоль сциталя; потом он размотал пояс, и получилось, что поперек пояса в беспорядке написаны буквы. Гонец не догадывался, что узор на его красивом поясе на самом деле содержит зашифрованную информацию.
Лисандр взял сциталь такого же диаметра, аккуратно намотал на него пояс и вдоль сциталя прочитал сообщение от своего агента. Например, если роль сциталя выполняет карандаш с шестью гранями, то открытый текст «КРИПТОГРАФИЯ» может быть преобразован в шифртекст «РПОРФЯКИТГАИ». Шифртекст может быть и другим, так как он зависит не только от диаметра карандаша. Для реализации такого шифра использовалась специальное шифрующее устройство.
По описанию Плутарха (род. до 50 — ум. после 120 гг. н. э.), оно состояло из двух палок одинаковой длины и толщины. Одну оставляли себе, а другую отдавали отъезжающему. Эти палки называли сциталами. Когда правителям нужно было сообщить какую-нибудь важную тайну, они вырезали длинную и узкую, вроде ремня, полоску папируса, наматывали ее на свою сциталу, не оставляя на ней никакого промежутка, так чтобы вся поверхность палки была охвачена полосой. Затем, оставляя папирус на скитале в том виде, как он есть, писали на нем все, что нужно, а написав, снимали полосу и без палки отправляли адресату.
Так как буквы на ней разбросаны в беспорядке, то прочитать написанное он мог, только взяв свою скиталу и намотав на нее без пропусков эту полосу. Аристотелю (384 до н. э. – 322 до н. э.) принадлежит способ дешифрования этого шифра. Надо изготовить длинный конус и, начиная с основания, обертывать его лентой с шифрованным сообщением, сдвигая ее к вершине. В какой-то момент начнут просматриваться куски сообщения.
Шифр «Сцитала», реализует не более n перестановок (n – длина сообщения). Имеются еще и чисто физические ограничения, накладываемые реализацией шифра «Сцитала». Естественно предположить, что диаметр жезла не должен превосходить 10 сантиметров. При высоте строки в 9, 1 сантиметр на одном витке такого жезла уместится не более 32 букв (10π < 32). Таким образом, число перестановок, реализуемых «Сциталой», вряд ли превосходит 32.
Шифр маршрутной перестановки
Широкое распространение получили шифры перестановки, использующие некоторую
геометрическую фигуру. Преобразования из этого шифра состоят в том, что в
фигуру исходный текст вписывается по ходу одного «маршрута», а затем по
ходу другого выписывается с нее. Такой шифр называют маршрутной перестановкой.
Например, можно вписывать исходное сообщение в прямоугольную таблицу, выбрав такой маршрут: по горизонтали, начиная с левого верхнего угла, поочередно слева направо и справа налево. Выписывать же сообщение будем по другому маршруту: по вертикали, начиная с верхнего левого угла и двигаясь поочередно сверху вниз и снизу-вверх. Зашифруем, например, указанным способом фразу:
«ПРИМЕР МАРШРУТНОЙ ПЕРЕСТАНОВКИ» используя прямоугольник размера 4х7:
|
П |
Р |
И |
М |
Е |
Р |
М |
|
Н |
Т |
У |
Р |
Ш |
Р |
А |
|
О |
Й |
П |
Е |
Р |
Е |
С |
|
И |
К |
В |
О |
Н |
А |
Т |
Зашифрованная фраза выглядит так: «ПНОИКЙТРИУПВОЕРМЕШРНАЕРРМАСТ»
Теоретически маршруты могут быть значительно более изощренными, однако запутанность маршрутов усложняет использование таких шифров. В пункте 2 рассмотрим описание трех разновидностей шифров перестановки.
Шифр «Решетка Кардано»
Для использования шифра, называемого поворотной решеткой, изготавливается трафарет из прямоугольного листа клетчатой бумаги размера 2m х 2k клеток. В трафарете вырезано m*k клеток так, что при наложении его на чистый лист бумаги того же размера четырьмя возможными способами его вырезы полностью покрывают всю площадь листа. Буквы сообщения последовательно вписываются в вырезы трафарета (по строкам, в каждой строке слева направо) при каждом из четырех его возможных положений в заранее установленном порядке. Поясним процесс шифрования на примере. Пусть в качестве ключа используется решетка 6 х 10, приведенная на рис. 1. Зашифруем с ее помощью текст:

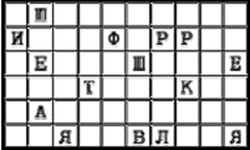
«ШИФР РЕШЕТКА ЯВЛЯЕТСЯ ЧАСТНЫМ СЛУЧАЕМ ШИФРА МАРШРУТНОЙ ПЕРЕСТАНОВКИ»

Наложив решетку на лист бумаги, вписываем первые 15 (по числу вырезов) букв сообщения: ШИФРРЕШЕТКАЯВЛЯ... Сняв решетку, мы увидим текст, представленный на рис. 2. Поворачиваем решетку на 180°. В окошечках появятся новые, еще не заполненные клетки. Вписываем в них следующие 15 букв. Получится запись, приведенная на рис. 3. Затем переворачиваем решетку на другую сторону и зашифровываем остаток текста аналогичным образом (рис. 4, 5).
Получатель сообщения, имеющий точно такую же решетку, без труда прочтет исходный текст, наложив решетку на шифртекст по порядку четырьмя способами. Можно доказать, что число возможных трафаретов, то есть количество ключей шифра «решетка», составляет Т = 4mk. Этот шифр предназначен для сообщений длины n = 4mk. Число всех перестановок в тексте такой длины составит (4mk)!, что во много раз больше числа Т. Однако, уже при размере трафарета 8x8 число возможных решеток превосходит 4 миллиарда ((4×8×8)! =256!)
Далее возникает вопрос: «Как запомнить уже составленную, изготовленную решетку? На случай экстренной ситуации» Есть несколько путей решения вопроса.
Например, можно запомнить таблицу, в которой отмечены числа (табл.) в каждой
строке (рис. 6).
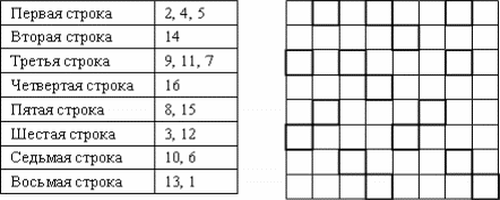
Есть и другой способ. Записать окошки в двоичной системе и в каждое окошко подставить 1.
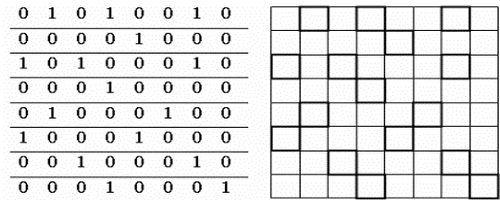
Чтобы не запоминать большие числа в двоичной системе счисления, можно перевести их в десятичную. Здесь пригодяться математические знания.
Например:
01010010 = 10100102 = 1×26 + 0×25 + 1×24 + 0×23 + 0×22 + 1×21 + 0×20 =
= 6410 + 1610 + 210 = 8210
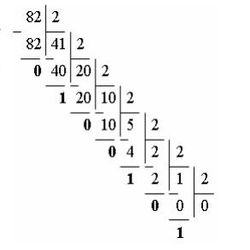
Чтобы восстановить зашифрованные данные необходимо перевести эти числа из десятичной системы в двоичную. Этот перевод можно осуществить с помощью деления на 2 пока частное не станет равно 0. А потом записывают остатки, начиная с последнего.
Книжный шифр
Книжный шифр, является еще одним примером шифра перестановки. До конца не известно, кто изобрел данный шифр, однако наиболее ранним примером является шифр Энея, который использовался еще в четвертом столетии до нашей эры, и описал его в сочинении «Об обороне укрепленных мест». Эней предложил прокалывать малозаметные дырки в книге или в другом документе над буквами секретного сообщения. Интересно отметить, что в первой мировой войне германские шпионы использовали аналогичный шифр, заменив дырки на точки, наносимые симпатическими чернилами на буквы газетного текста.
Книжный шифр в современном варианте имеет несколько другой вид. Суть этого шифра состоит в каждая буква в сообщении определяется тремя цифрами: первая - порядковый номер страницы, вторая – порядковый номер строки сверху или снизу в зависимости от того, как договорятся стороны, а третья – порядковый номер буквы в строке. Предположим, что ключом к шифру будет отрывок из первой главы Откровения Иоанна Богослова. (Чаще всего для шифра использовали именно Библию).
«Откровение Иисуса Христа, которое дал Ему Бог, чтобы показать рабам Своим, чему надлежит быть вскоре. И Он показал, послав оное через Ангела Своего рабу Своему Иоанну, который свидетельствовал слово Божие и свидетельство Иисуса Христа и что он видел. Блажен читающий и слушающие слова пророчества сего и соблюдающие написанное в нем; ибо время близко.
Иоанн семи церквам, находящимся в Асии: благодать вам и мир от Того, Который есть и был и грядет, и от семи духов, находящихся перед престолом Его, и от Иисуса Христа, Который есть свидетель верный, первенец из мертвых и владыка царей земных. Ему, возлюбившему нас и омывшему нас от грехов наших Кровию Своею и соделавшему нас царями и священниками Богу и Отцу Своему, слава и держава во веки веков, аминь. Се, грядет с облаками, и узрит Его всякое око и те, которые пронзили Его; и возрыдают пред Ним все племена земные.
Ей, аминь. Я есмь Альфа и Омега, начало и конец, говорит Господь, Который есть и был и грядет, Вседержитель. Я, Иоанн, брат ваш и соучастник в скорби и в царствии, и в терпении Иисуса Христа, был на острове, называемом Патмос, за слово Божие и за свидетельство Иисуса Христа.»
И зашифруем слово: «Криптография». Первая буква слова – «К», мы её обозначаем 1/3. (Числитель – порядковый номер строки, знаменатель – номер буквы.). Рекомендуется вносить побольше разнообразия, заимствуя букву из разных мест ключа, чтобы затруднить расшифрование написанного для посторонних.
Таким образом, один из вариантов шифртекста для слова «Криптография» выглядит так - «1/3, 2/1, 3/32, 5/40, 8/2, 9/11, 9/16, 10/3, 11/14, 15/39, 16/18, 17/13».
Применение одного из видов шифрования на примере шифра Цезаря
Зашифруем пословицу: «Что посеешь, то и пожнешь» с помощь шифра Цезаря со сдвигом на 5. Так, первая буква – «Ч», перейдет в «Ь», «Т» перейдет в «Ч» и так далее.
Таким образом, исходный алфавит будет выглядеть как «АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ»,
А шифрованный как «ЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ».
Так, оригинальный текст «Что посеешь, то и пожнешь».
Перейдет в «Ьчу фуцййэб, чу н фултйэб». Он получается путем замены каждой буквы оригинального текста соответствующей буквой шифрованного алфавита.
Пример дешифровки шифра Цезаря
Допустим, дана задача расшифровать латинскую пословицу. При этом, известно, что был произведен сдвиг на 5.
Зашифрованная пословица выглядит так:
XN ANX UFHJR, UFWF GJQQZR
Зашифрованный алфавит: «FGHIJKLMNOPQRSTUVWXYZABCDE»
Исходный алфавит: «ABCDEFGHIJKLMNOPQRSTUVWXYZ»
Если заменить каждую букву зашифрованного текста на соответствующую ему букву алфавита со сдвигом -5, то получим:
SI VIS PACEM, PARA BELLUM
Что значит: «Хочешь мира, готовься к войне».
Дешифровка на примере книжного шифра
Заключение
Во время написания данного проекта, я взялся за детальное рассмотрение связи математики, криптографии и шифров в частности. Поскольку в современных реалиях, люди встречаются с шифрами гораздо чаще, чем думают и лишь единицы интересуются, тем, как они появились, какую роль сыграли в мировой истории и как, в принципе, они работают.
Несколько примеров их применения в сферах жизни общества:
|
Где используется |
Назначение |
|
Военное дело, политика, флот |
Передача секретных сообщений и информации, Азбука Морзе, Международный свод сигналов с помощью флагов, семафорная азбука |
|
Экономика и бизнес |
Передача секретных сообщений и информации, передача документов в электронном виде, шифровка платежей |
|
История |
Шифр Цезаря, Августа, Полибия, заговорщиков, революционеров, тайная переписка монархов, взлом Сигмы |
|
Интернет и ИТ |
Криптосистема RSA |
|
Математика |
Теория чисел, логические задачи |
|
Литература |
Шифровка черновиков известных писателей, например Пушкина |
|
Личная жизнь |
Тайная переписка, переписка через Интернет, передача документов в электронном виде, оплата услуг |
Выполняя данную работу, я ставил цель изучить применение основ математики в криптографии. Внимательно изучая данную тему, я осознал, что основы математики используются практически в любом шифре, а также, что криптография и стеганография будут востребованы повсеместно, так как потребность в сокрытии важных данных и информации становится только более актуальной и необходимой. А знание основ сможет помочь людям уберечь важную информацию и обезопасить себя.
Список использованной литературы
1. Виленкин Н.Я Математика и шифры. - Квант, № 8, 1997.
2. Аршинов М.Н., Садовский Л.Е. Коды и математика. - М.: Наука, 1983.
3. Гонина Е.Е. Шифры, коды, тайны. - Живая математика, № 1, 2008.
4. Дориченко С.А., Ященко В.В. 25 этюдов о шифрах: Популярно о современной криптографии - М.: Теис, 1994.
5. Ященко В.В., ред. Введение в криптографию. - М: МЦНМО, 2000.
6. К. Шеннон. Работы по теории информации и кибернетике. - М., ИЛ, 1963.
7. Жельников В. Криптография от папируса до компьютера. - М.: "АВF", 1996 -335с.
8. А.Н. Лебедев. Криптография с «открытым ключом» и возможности ее практического применения. «Защита информации», выпуск 2, 1992.
9. Фелкон Тэвис, Джуди Хиндлей, Рут Томисон, Хизер Эмери. Краткий курс юного шпиона Авт. лит. обработки Анна Данковцева. - М.: Педагогика, 1985.
10. Г. Фролов. Тайны тайнописи. - М., 1992.
11. М. Гарднер. От мозаик Пенроуза к надежным шифрам. - М.; Мир, 1993.
12. М. Масленников. Практическая криптография. Санкт-Петербург: БХВ - Петербург, 2003.
13. Виноградов И. М. Основы теории чисел. М.: Наука. 1972.
14. Серов Е., Волгин В. Тайны военной разведки (1918 -1945). // Армия. - М., 1994 - № 7 - с. 52 -55.
15. Виленкин Н.Я., Депман И.Я. За страницами учебника математики - М.: Просвещение, 1986.
16. Зельманзон М., Хлобыстова Л. Самосовмещение квадрата и тайнопись - «Квант», № 12, 1980.
17. Гатчин Ю.А., Коробейников А.Г. Основы криптографических алгоритмов. Учебное пособие. - СПб.: СПбГИТМО(ТУ), 2002.
18. Коробейников А. Г. Математические основы криптографии. Учебное пособие. - СПб: СПб ГИТМО (ТУ), 2002.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.