Происхождение понятия интеграла

Происхождение понятия интеграла

Понятие интеграла и интегральное исчисление возникли из потребности вычислять площади любых фигур и поверхностей и объемы произвольных тел. Предыстория интегрального исчисления восходит к глубокой древности. Идея интегрального исчисления была древними учеными предвосхищена гораздо в большей мере, чем идея дифференциального исчисления. Мы уже говорили о методе исчерпывания Евдокса. Ниже пойдет речь о формировании понятия интеграла в XVII в. и о его дальнейшем развитии. Чтобы дать общий обзор проблемы об интегральном исчислении, начнем с постановки вопроса.

Пусть требуется найти площадь S криволинейной фигуры A'C'B'D' (рис. 1). Отнесем ее к декартовой прямоугольной системе координат XOY и опустим из крайних точек А' и В' (имеющих наименьшую и наибольшую абсциссы) нашей фигуры  перпендикуляры А'А и В'В на ось Ох. Площадь S представится тогда как разность между площадью S₁ фигуры АА'СВ'В и площадью S₂ фигуры AA'D'B'B. Отсюда ясно, что задачу вычисления площади произвольной фигуры можно свести к задаче вычисления площади фигуры вроде АА'СВ'В, ограниченной дугой некоторой  кривой, двумя ординатами А'А и В'В и отрезком АВ оси абсцисс, заключенным между этими ординатами. Такую фигуру принято называть криволинейной трапецией.

Итак, пусть требуется найти площадь S криволинейной трапеции  ABCD (рис. 2), где DC — дуга линии у = f(x). Для этого разделим точками основание АВ нашей трапеции на п (вообще неравных) частей:

а = x₀<x₁<x₂< …  <x_k<x_k+1<  …  <x_n = b.                                           (1)

Длины участков х₁ - х₀, х₂ - х₁, ... , x_n - x_n-1 обозначим через Δ х₁, Δх₂, ... , Δx_n. Проведя ординаты, соответствующие точкам деления, мы разбиваем трапецию на п полосок с основаниями  Δ х₁, Δх₂, … , Δ x_k, Δ x_k+1, … , Δx_n. Заменяя каждую полосу некоторым прямоугольником, в котором основанием

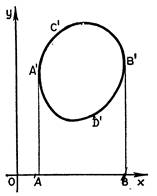
            Рис.1                                            рис. 2

служит  основание соответствующей полосы, а высотой — одна из ординат

(допустим, левая) полосы, мы как бы заменяем нашу фигуру ABCD другой, ступенчатой фигурой  Т  площадь которой равна сумме S_n площадей построенных n прямоугольников. Площадь каждого из последних равна произведению высоты на основание, т. е. f(x_k)Δx_k, или y_k Δx_k, где k = 1, 2, ..., n. Итак,

S_n  =  f(x₁)Δx₁  +  f(x₂)Δx₂ + …+  f(x_n)Δx_n,                       (2)

Формула (2) дает лишь приближенную площадь  криволинейной трапеции, но с неограниченным увеличением числа n, т. е. с неограниченным убыванием длин участков Δx_k, ступенчатая фигура Т неограниченно приближается к фигуре ABCD, и мы можем достигнуть любой степени приближения. Поэтому точное значение S мы получим как предел суммы S_n, когда наибольшая из длин  Δx_k  стремится к нулю. Этот предел и называется определенным интегралом от функции  f(x) на отрезке [а, b] и обозначается символом   (3)  или  . Символ   был введен Лейбницем в 1686 г. В нем знак  представляет как бы удлиненную букву S (первая в латинском слове Summa — сумма); ydx напоминает структуру слагаемых суммы.

Термин «интеграл» (от латинского integer — целый, т. е. целая, вся — площадь) был предложен в 1696 г. Иоганном Бернулли и одобрен, хотя < и неохотно, Лейбницем, который до этого пользовался выражением «сумма всех ydx».

Последнее обозначение для определенного интеграла ввел Ж.Фурье. Числа а и b называют соответственно нижним и верхним  пределами интеграла. Если функция  f(x), называемая подынтегральной, непрерывна, то предел, о котором идет речь, существует и не зависит ни от способа разбиения отрезка [а, b] на участки Δx_i  ни от выбора на них точек. Функцию f(x) называют в этом случае интегрируемой. В такой общей форме  (3)  это определение  интеграла было впервые сформулировано немецким математиком Б. Риманом примерно в середине прошлого века. Поэтому интегральную сумму иногда называют римановой суммой.