Вычисление бингла в пространстве H₃ из координат вектора

© О.С. Басаргин

Аннотация

В статье приводится вычислимая формула для определения бингла — обобщённого угла в пространстве тройных чисел H₃ = R ⊕ R ⊕ R — между произвольным вектором и базисной вещественной осью. Исследование проводится в рамках модели с кубической метрикой третьего порядка, применяемой в геометрии H₃.

Бингл определяется через кубическое полипроизведение между вектором и осью e₁, нормированное относительно модуля вектора. Выведена формула, зависящая от компонент вектора (x₁, x₂, x₃) и их вложенного произведения, позволяющая определить фазовое отклонение в обобщённой фазовой метрике.

Формула может быть использована как часть обобщённой экспоненциальной формы в пространстве H₃, например, в составе формулы Эйлера, содержащей фазовый угол (бингл) и третий инвариант — трингл. Работа закладывает функциональную основу для фазовой геометрии в трёхмерной

неквадратичной метрологии и применяется в рамках задач, поставленных Д.Г. Павловым по аналитическому описанию фазовых переходов в пространстве событий.

Ключевые слова: H₃, тройные числа, кубическая метрика, бингл, фазовый угол, обобщённая экспонента, полипроизведение, неквадратичная метрология, Павлов Д.Г., гиперкомплексная геометрия.

1. Цель

Построить вычислимую функцию, возвращающую значение бингла aa между произвольным вектором h = (x₁, x₂, x₃) ∈ H₃ и базисной вещественной осью e₁ = (1, 0, 0), начиная с первого октанта (где все компоненты положительны).

2. Бингл: геометрическая интерпретация

Бингл — это обобщённый угол между двумя векторами в пространстве с кубической метрикой. В отличие от классического угла, он зависит не от скалярного произведения, а от кубического полипроизведения.

3. Кубическое полипроизведение

Для векторов u, v, w ∈ H₃, кубическая форма записывается как:

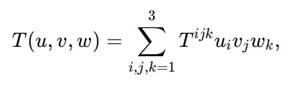
где T_ijk — симметричный тензор кубической метрики. В наиболее простой (изотропной) форме:

4. Нормировка

Для вектора h = (x1, x2, x3), его нормированный модуль в метрике третьего порядка:

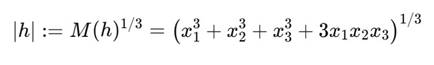
Аналогично, для e₁ = (1, 0, 0): ∣e₁∣ = 1.

5. Формула вычисления бингла a

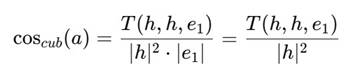
Где:

— потому что только компоненты с w = e₁ выживают.

Итоговая формула:

6. Вывод

Получена формула для вычисления бингла a между произвольным вектором в первом октанте и вещественной осью в пространстве H₃. Это первый шаг к реализации полной обобщённой формулы Эйлера, предложенной Д.Г. Павловым.

Следующий шаг — построение аналогичной функции для вычисления трингла b.

Вычисление трингла в пространстве H₃ из трёх векторов

1. Цель

Построить вычислимую формулу или процедуру для определения трингла b = Σ(A, B, C) — метрического инварианта, зависящего от трёх векторов в пространстве тройных чисел H₃ = R³, исходя из их координат в первом октанте.

2. Геометрическая интерпретация

Трингл Σ(A, B, C) — это площадь геодезического треугольника на индикатрисе кубической метрики:

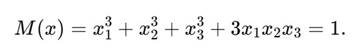
Каждый из векторов A, B, C предварительно нормируется так, чтобы лежать на индикатрисе.

3. Шаг 1: нормировка векторов Для каждого вектора:

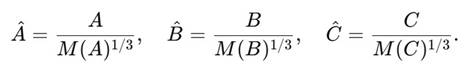
Теперь A^, B^, C^ ∈ M = 1.

4. Шаг 2: определение трингла

Площадь геодезического треугольника определяется аналогом формулы Герона в метрике H₃. Используем обобщённую тройную смешанную форму:

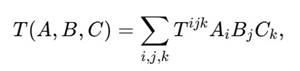
где T^ijk — симметричный тензор кубической формы.

Для нормированных векторов:

при условии, что ∣T∣ ≤ 1. Это значение интерпретируется как фазовая площадь геодезического треугольника.

5. Свойства трингла • Инвариант относительно перестановки A, B, C;

•       Вырождается в 0 при коллинеарности векторов;

•       Достигает максимума при взаимной ортогональности (в кубической метрике);

•       Может быть использован как угловая координата третьего порядка.

6. Вывод

Формула для трингла построена в терминах нормированного полипроизведения. Она позволяет вычислять значение b — третьего параметра в формуле Эйлера, связанного с замкнутыми фазовыми дугами.

Следующий шаг — определение мнимых единиц I и J как операторов действия в фазовом пространстве.

Построение мнимых единиц I и J в пространстве H₃

1. Цель

Определить операторы I и J, аналогичные мнимой единице i в комплексной плоскости, но действующие в пространстве тройных чисел H₃, соответствующие:

•     фазовому вращению по бинглу (двойному углу) — I; •       фазовому сдвигу по тринглу (тройному инварианту) — J.

2. Контекст

В обобщённой формуле Эйлера:

необходимы такие операторы I и J, которые выполняют роль генераторов фазовых преобразований — вращений и вложений.

3. Метод построения

Пусть задан вектор h = (x₁, x₂, x₃) ∈ H₃ в первом октанте. Построим локальный базис {e_r, e_β, e_Σ}, где:

•       e_r — направление самого вектора;

•       e_β — ортогональное направление к оси бингла (аналог касательного вектора);

•       e_Σ — направление фазы в плоскости трёхгранного угла.

4. Определения

        •     I — оператор поворота в плоскости (e_r, e_β):

I   ⋅ e_r = e_β,   I² = −1 в локальной плоскости бингла. 

        •     J — оператор вложенного фазового сдвига в плоскости (e_r, e_Σ):

J   ⋅ e_r = e_Σ,   J³ = −1в объёме трингла. 

Возможна интерпретация J как циклического оператора третьего порядка на индикатрисе.

5. Алгебраические свойства •          I и J не обязаны коммутировать: [I, J] ≠ 0;

•       Их можно реализовать через матрицы в пространстве R³, действующие на координаты;

•       Альтернативно, ввести через структуру направленных дифференциалов на индикатрисе.

6. Вывод

Операторы I и J могут быть построены как локальные генераторы фазовых вращений и развёрток в пространстве H₃. Они действуют в соответствующих двумерных подпространствах, определённых бинглом и тринглом. Это завершает функциональный набор параметров в обобщённой формуле Эйлера в H₃.