Промежуточная аттестация по алгебре за 9 класс

итоговая контрольная работа по алгебре за 9 класс

Описание

контрольно-измерительных материалов (КИМ) для проведения в 2023-2024 уч.г. промежуточной аттестации по алгебре

для 9 класса

1. Назначение контрольно-измерительных материалов (КИМ)

Промежуточная аттестация обучающихся — процедура, проводимая с целью определения степени освоения обучающимися содержания учебных предметов/курсов за год в соответствии с образовательным стандартом.

Цель работы – оценить уровень достижения планируемых предметных и метапредметных результатов по алгебре согласно ФГОС и ФОП обучающимися 9 класса.

2. Документы, определяющие содержание КИМ для проведения промежуточной аттестации

· приказ Минобрнауки от 17.12.2010 № 1987 «Об утверждении федерального государственного образовательного стандарта основного общего образования» с изменениями, утвержденными приказом Минобрнауки России от 29 декабря 2014 года №1644, приказом Минобрнауки России от 31 декабря 2015 года № 1577, приказом Минпросвещения России от 11 декабря 2020 года № 712,

· приказ Минпросвещения РФ от 18.05.2023 № 370 «Об утверждении федеральной образовательной программы основного общего образования»,

· ООП ООО МБОУ СОШ № 90 с углубленным изучением предметов ХЭЦ,

· содержания учебников, включённых в Федеральный перечень.

3. Подходы к отбору содержания, разработке структуры КИМ для проведения промежуточной аттестации

КИМ для проведения промежуточной аттестации основаны на системно-деятельностном, компетентностном и уровневом подходах.

В рамках данной процедуры наряду с предметными результатами освоения основной образовательной программы основного общего образования оценивается также достижение метапредметных результатов, в том числе уровень сформированности универсальных учебных познавательных, коммуникативных и регулятивных действий (УУД) и овладения межпредметными понятиями.

Тексты заданий в КИМ в целом соответствуют формулировкам, принятым в учебниках, включенных в Федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.

4. Форма проведения промежуточной аттестации

Письменная форма – контрольная работа

5. Структура КИМ для проведения промежуточной аттестации

Промежуточная аттестация проходит в письменной форме – контрольная работа, которая содержит 9 заданий. Задания 1-9 подразумевают запись решения и ответ.

6. Распределение заданий по проверяемым в КИМ элементам содержания

№ задания	Раздел программы	Элементы содержания, проверяемые заданиями КИМ	Код проверяемого элемента содержания
1	Числа и вычисления.	Рациональные числа, иррациональные числа, десятичные дроби.	1.1
2	Уравнения и неравенства.	Решение дробно-рациональных уравнений.	2.1
3		Решение линейных неравенств с одной переменной.	2.2
4		Решение систем линейных неравенств с одной переменной	2.3
5	Функции	Графики функций и их свойства.	3.1
6	Числовые последовательности	Арифметическая прогрессия	4.1
7		Геометрическая прогрессия	4.2
8	Вероятность и статистика	Чтение таблиц и диаграмм	5.1
9		Случайная величина и распределение вероятностей	5.2

7. Проверяемые требования к результатам (предметным и метапредметным) обучения

№ задания	Код проверяемого элемента содержания	Проверяемые требования к предметным результатам обучения	Проверяемые требования к метапредметным результатам обучения	Уровень сложности
1	1.1	Выполнять арифметические действия с рациональными числами, сочетая устные и письменные приёмы, выполнять вычисления с иррациональными числами. Находить значения степеней с целыми показателями, вычислять значения числовых выражений.		базовый
2	2.1	Решать линейные уравнения, уравнения, сводящиеся к ним, простейшие дробно-рациональные уравнения. Решать системы двух линейных уравнений с двумя переменными и системы двух уравнений, в которых одно уравнение не является линейным. Решать линейные неравенства.		Повышенный
3	2.2			базовый
4	2.3			базовый
5	3.1	Распознавать функции изученных видов. Показывать схематически расположение на координатной плоскости графиков функций вида: y = kx, y = kx + b, y = k/x, y = ax2 + bx + c, y = x3, y = √x, y = \|x\|, в зависимости от значений коэффициентов, описывать свойства функций.		базовый
6	4.1	Выполнять вычисления с использованием формул n-го члена арифметической и геометрической прогрессий, суммы первых n членов. Решать задачи, связанные с числовыми последовательностями, в том числе задачи из реальной жизни.		базовый
7	4.2			базовый
8	5.1	Извлекать и преобразовывать информацию, представленную в различных источниках в виде таблиц, диаграмм, графиков, представлять данные в виде таблиц, диаграмм, графиков. Находить вероятности случайных событий в изученных опытах, в том числе в опытах с равновозможными элементарными событиями.		базовый
9	5.2			базовый

8. Система оценивания заданий и работы в целом

\Максимальная сумма, которую может получить учащийся, правильно выполнивший все задания - 9 баллов. За верное выполнение каждого заданий выставляется 1 балл. За неверный ответ или его отсутствие выставляется 0 баллов. Выполнение заданий №5 и №8 оценивается так: отмечены все верные ответы – 1 балл, допущена хотя бы одна ошибка – 0 баллов.

9. Шкала перевода баллов (% выполнения работы) в отметку (на основе ОГЭ)

% выполнения работы	Баллы (могут быть разное количество баллов за работы)	Отметка	Уровень достижения проверяемых результатов
88 – 100	8– 9	5	Повышенный
68 – 87	6-7	4	Базовый
45 – 67	4-5	3	Базовый
0 – 44	0-4	2	Недостаточный

10. Время выполнения работы – 45минут.

11. Описание дополнительных материалов и оборудования, необходимых для проведения работы

1 вариант

1. Найдите значение выражения 2,7 × 10² - 0,3 × 10³

2. Решите уравнение: . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

3. Решите неравенство 20-3(x-5)≤19-7х

4. Найдите наименьшее целое число, являющееся решением системы неравенств

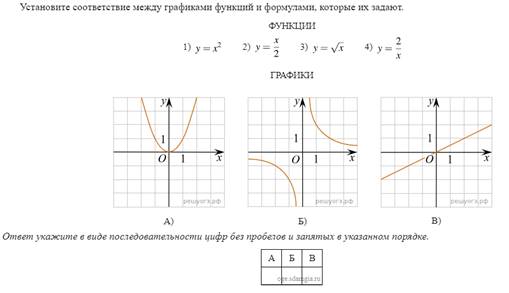
6. Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.

7. Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т. д. Сколько бактерий окажется в организме через 4 часа, если по истечении четвертого часа в организм из окружающей среды попала еще одна бактерия?

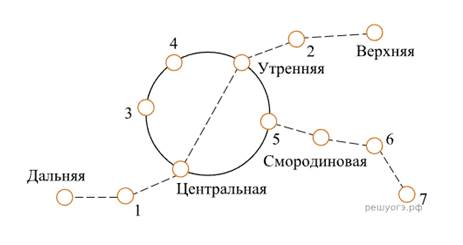
8. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырех цифр.

Станции	Веселая	Ветреная	Звездная	Птичья
Цифры

На рисунке изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Веселая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звездная. Всего в метрополитене города N есть три станции, от которых тоннель ведет только в одну сторону  — это станции Дальняя, Верхняя и Звездная. Антон живет недалеко от станции Надежда.

9. В коробке 14 пакетиков с черным чаем и 6 пакетиков с зеленым чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зеленым чаем?

Скачано с www.znanio.ru

Описание контрольно-измерительных материалов (КИМ) для проведения в 2023-2024 уч

Числа и вычисления. Рациональные числа, иррациональные числа, десятичные дроби

Решать системы двух линейных уравнений с двумя переменными и системы двух уравнений, в которых одно уравнение не является линейным

Выполнять вычисления с использованием формул n-го члена арифметической и геометрической прогрессий, суммы первых n членов

Промежуточная аттестация по алгебре за 9 класс

Найдите значение выражения 2,7 × 10 2 - 0,3 × 10 3 2

В коробке 14 пакетиков с черным чаем и 6 пакетиков с зеленым чаем

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

19.06.2024