Поделиться
ПА геометрия 8 кл.docx
Описание
контрольно-измерительных материалов (КИМ) для проведения в 2023-2024 уч.г. промежуточной аттестации по геометрии
для 8 класса
1. Назначение контрольно-измерительных материалов (КИМ)
Промежуточная аттестация обучающихся — процедура, проводимая с целью определения степени освоения обучающимися содержания учебных предметов/курсов за год в соответствии с образовательным стандартом.
Цель работы – оценить уровень достижения планируемых предметных и метапредметных результатов по геометрии согласно ФГОС и ФОП обучающимися 8 класса.
2. Документы, определяющие содержание КИМ для проведения промежуточной аттестации
· приказ Минобрнауки от 17.12.2010 № 1987 «Об утверждении федерального государственного образовательного стандарта основного общего образования» с изменениями, утвержденными приказом Минобрнауки России от 29 декабря 2014 года №1644, приказом Минобрнауки России от 31 декабря 2015 года № 1577, приказом Минпросвещения России от 11 декабря 2020 года № 712,
· приказ Минпросвещения РФ от 18.05.2023 № 370 «Об утверждении федеральной образовательной программы основного общего образования»,
· ООП ООО МБОУ СОШ № 90 с углубленным изучением предметов ХЭЦ,
· содержания учебников, включённых в Федеральный перечень.
3. Подходы к отбору содержания, разработке структуры КИМ для проведения промежуточной аттестации
КИМ для проведения промежуточной аттестации основаны на системно-деятельностном, компетентностном и уровневом подходах.
В рамках данной процедуры наряду с предметными результатами освоения основной образовательной программы основного общего образования оценивается также достижение метапредметных результатов, в том числе уровень сформированности универсальных учебных познавательных, коммуникативных и регулятивных действий (УУД) и овладения межпредметными понятиями.
Тексты заданий в КИМ в целом соответствуют формулировкам, принятым в учебниках, включенных в Федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.
4. Форма проведения промежуточной аттестации
Устная форма промежуточной аттестации: экзамен по билетам.
5. Структура КИМ для проведения промежуточной аттестации
Промежуточная аттестация проходит в устной форме – экзамен (по билетам). Составлено 13 билетов и 20 задач к ним.. В каждом билете 2 части: теоретическая (два вопроса, требующих устного ответа) и практическая (решение практико-ориентированной задачи на применение математической грамотности). Для оценивания выполнения теоретической и практической частей экзамена используются критерии, прописанные в Положении о нормах оценивания по учебным предметам (п.4.3.1 и 4.3.2).
6. Распределение заданий по проверяемым в КИМ элементам содержания
|
№ раздела |
Раздел программы
|
Элементы содержания, проверяемые заданиями КИМ
|
Код проверяемого элемента содержания
|
|
1 |
Четырехугольники |
Четырёхугольники. Параллелограмм, его признаки и свойства. Частные случаи параллелограммов (прямоугольник, ромб, квадрат), их признаки и свойства. Трапеция, равнобокая трапеция, её свойства и признаки. Прямоугольная трапеция.
|
1.1 |
|
2 |
Теорема Фалеса и теорема о пропорциональных отрезках, подобные треугольники |
Подобие треугольников, коэффициент подобия. Признаки подобия треугольников. Применение подобия при решении практических задач. Теорема Фалеса.
|
2.1 |
|
3 |
Площадь. Нахождение площадей треугольников и многоугольных фигур. Площади подобных фигур |
Формулы для площади треугольника, параллелограмма, ромба и трапеции. Отношение площадей подобных фигур. Вычисление площадей треугольников и многоугольников на клетчатой бумаге.
|
3.1 |
|
4 |
Теорема Пифагора и начала тригонометрии |
Теорема Пифагора. Применение теоремы Пифагора при решении практических задач. Синус, косинус, тангенс острого угла прямоугольного треугольника. |
4.1 |
|
5 |
Углы в окружности. Вписанные и описанные четырехугольники. Касательные к окружности. Касание окружностей |
Вписанные и центральные углы, угол между касательной и хордой. Вписанные и описанные четырёхугольники. Взаимное расположение двух окружностей. Касание окружностей. Общие касательные к двум окружностям.
|
5.1 |
7. Проверяемые требования к результатам (предметным и метапредметным) обучения
|
№ билета |
Код проверяемого элемента содержания
|
Проверяемые требования к предметным результатам обучения
|
Проверяемые требования к метапредметным результатам обучения
|
Уровень сложности
|
|
1 |
5.1
3.1
|
Иметь представление о касательной, ее свойстве, свойстве отрезков касательных. Уметь вычислять площадь треугольника различными способами. |
Выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями, формулировать определения понятий, устанавливать существенный признак классификации; воспринимать, формулировать и преобразовывать суждения: утвердительные и отрицательные, единичные, частные и общие; выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях, предлагать критерии для выявления закономерностей и противоречий; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат.
|
базовый |
|
2 |
1.1
5.1 |
Распознавать основные виды четырёхугольников, их элементы и свойства. Владеть понятиями вписанного и центрального угла, знать теоремы о вписанных углах. |
базовый |
|
|
3 |
1.1
4.1
|
Иметь представление о выпуклом многоугольнике, уметь находить сумму внешних и внутренних углов. Пользоваться теоремой Пифагора для решения геометрических задач. |
базовый |
|
|
4 |
2.1, 3.1
5.1 |
Иметь представление о подобных треугольниках, знать теорему об отношении площадей подобных треугольников. Иметь представление о касательной к окружности |
базовый |
|
|
5 |
1.1
3.1
|
Распознавать основные виды четырёхугольников, их элементы и свойства. Иметь представление о подобных треугольниках. |
базовый |
|
|
6 |
1.1, 3.1
4.1
|
Распознавать основные виды четырёхугольников, их элементы и свойства. Уметь вычислять площади четырехугольников по формулам. Владеть понятиями синуса, косинуса и тангенса острого угла прямоугольного треугольника
|
базовый |
|
|
7 |
1.1, 3.1
2.1 |
Распознавать основные виды четырёхугольников, их элементы и свойства. Уметь вычислять площади четырехугольников по формулам. Владеть понятием средней линии треугольника, ее свойствами. |
базовый |
|
|
8 |
1.1, 3.1
5.1 |
Распознавать основные виды четырёхугольников, их элементы и свойства. Уметь вычислять площади четырехугольников по формулам. Владеть понятиям вписанного угла, его свойством. |
базовый |
|
|
9 |
1.1, 3.1
5.1
|
Распознавать основные виды четырёхугольников, их элементы и свойства. Уметь вычислять площади четырехугольников по формулам. Владеть понятием описанного четырёхугольника, его свойством. |
|
базовый |
|
10 |
5.1
1.1, 3.1 |
Уметь применять теорему Фалеса для решения практических задач. Распознавать основные виды четырёхугольников, их элементы и свойства. Уметь вычислять площади четырехугольников по формулам |
базовый |
|
|
11 |
5.1
3.1 |
Иметь представление об окружности, ее элементах, взаимном расположении окружности и прямой. Уметь вычислять площадь треугольника различными способами. |
базовый |
|
|
12 |
5.1
1.1, 2.1 |
Иметь представление об окружности, ее элементах, касательной к окружности. Распознавать основные виды четырёхугольников, их элементы и свойства. Владеть понятием средней линии трапеции, ее свойствами. |
базовый |
|
|
13 |
5.1
3.1 |
Владеть понятием вписанного в окружность четырёхугольника, его свойством. Уметь вычислять площадь треугольника различными способами. |
базовый |
Задачи к билетам по геометрии
|
№ задачи |
Код проверяемого элемента содержания
|
Проверяемые требования к предметным результатам обучения
|
Проверяемые требования к метапредметным результатам обучения
|
Уровень сложности
|
|
1,8 |
1.1 |
Распознавать основные виды четырёхугольников, их элементы, пользоваться их свойствами при решении геометрических задач.
|
Выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев); проводить самостоятельно несложные доказательства математических фактов, выстраивать аргументацию, обосновывать собственные рассуждения; оценивать достоверность полученных результатов, выводов и обобщений; выявлять недостаточность и избыточность информации, данных, необходимых для решения задачи; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи.
|
базовый |
|
2,7 |
5.1 |
Владеть понятием описанного четырёхугольника, применять свойства описанного четырёхугольника при решении задач.
|
базовый |
|
|
3,4,6, 15,17, 18 |
3.1 |
Вычислять площади многоугольных фигур. Применять полученные умения в практических задачах.
|
базовый |
|
|
5, 20 |
2.1 |
Владеть понятием средней линии треугольника и трапеции, применять их свойства при решении геометрических задач. |
базовый |
|
|
9,10,19 |
4.1 |
Владеть понятиями синуса, косинуса и тангенса острого угла прямоугольного треугольника. Пользоваться этими понятиями для решения практических задач. Пользоваться теоремой Пифагора для решения геометрических и практических задач. |
базовый |
|
|
11,12, 13,14 |
5.1 |
Владеть понятиями вписанного и центрального угла, использовать теоремы о вписанных углах, ( угле между касательной и хордой при решении геометрических задач.
|
базовый |
|
|
16 |
3.1 |
Вычислять (различными способами) площадь треугольника Применять полученные умения в практических задачах.
|
базовый |
8. Система оценивания заданий и работы в целом
Оценка устного ответа обучающегося
Ответ оценивается отметкой «5», если обучающийся:
· полно раскрыл содержание материала в объёме, предусмотренном программой учебника;
· изложил материал грамотным языком в определённой логической последовательности, точно используя математическую терминологию и символику;
· правильно выполнил рисунок, чертёж, сопутствующий ответу;
· показал умение иллюстрировать теоретические положения конкретными примерами;
· продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе навыков и умений;
· отвечал самостоятельно без наводящих вопросов учителя.
Ответ оценивается отметкой «4», если обучающийся ответил по требованиям на отметку «5», но при этом имеет один из недостатков:
· в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;
· допущены 1-2 недочёта при освещении основного содержания ответа, исправление по замечанию учителя;
· допущены ошибки или более двух недочётов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Ответ оценивается отметкой «3», если обучающийся:
· неполно или непоследовательно раскрыл содержание материала, но показал общее понимание вопроса и продемонстрировал умения, достаточные для дальнейшего усвоения программного материала;
· имел затруднения или допустил ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
· не справился с пониманием теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
· при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Ответ оценивается отметкой «2», если обучающийся:
· не раскрыл основное содержание учебного материала;
· обнаружил незнание и непонимание большей или меньшей важной части учебного материала;
· допустил ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменного ответа обучающегося
Ответ оценивается отметкой «5», если обучающийся:
· выполнил работу полностью;
· не допустил пробелов и ошибок в логических рассуждениях и обосновании;
· не допустил математических ошибок в решении.
Ответ оценивается отметкой «4», если обучающийся:
· выполнил работу полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являются специальным объектом проверки);
· допустил ошибку или 2-3 недочёта в выкладках, рисунках, чертежах или графиках.
Ответ оценивается отметкой «3», если обучающийся:
· владеет обязательными умениями по проверяемой теме;
· допустил более одной ошибки или более 2-3 недочетов в выкладках, чертеже.
Ответ оценивается отметкой «2», если обучающийся:
· не владеет обязательными умениями по данной теме в полной мере;
· допустил существенные ошибки.
9. Шкала перевода баллов (% выполнения работы) в отметку (на основе ОГЭ)
Каждое из трех заданий билета оценивается по пятибалльной шкале. Отметка за экзамен выставляется как среднее арифметическое трех полученных за ответ отметок.
|
Отметка |
Уровень достижения проверяемых результатов |
|
5 |
Повышенный |
|
4 |
Базовый |
|
3 |
|
|
2 |
Недостаточный |
10. Время на подготовку к ответу по билету – 20 минут.
11. Описание дополнительных материалов и оборудования, необходимых для проведения работы
Билеты к экзамену по геометрии 8 класс
Билет № 1
1. Касательная к окружности: определение и свойство. Свойство отрезков касательных.
2. Треугольник: определение и виды. Формулы для вычисления площади треугольника.
Билет № 2
1. Трапеция. Определение. Виды трапеций. Свойство равнобедренной трапеции.
2. Дуга окружности. Центральный и вписанный угол. Теорема о вписанном угле.
Билет № 3
1. Выпуклый многоугольник. Сумма углов выпуклого n-угольника. Сумма внешних углов выпуклого многоугольника.
2. Теорема Пифагора. Примеры для нахождения неизвестного катета, неизвестной гипотенузы. Пифагоровы треугольники.
Билет № 4
1. Подобные треугольники: определение, коэффициент подобия. Теорема об отношении площадей подобных треугольников.
2. Касательная к окружности: определение и признак касательной.
Билет № 5
1. Параллелограмм: определение и признаки.
2. Определение подобных треугольников. Признаки подобия.
Билет № 6
1. Параллелограмм: определение и свойства. Формула площади параллелограмма.
2. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника
Билет № 7
1. Прямоугольник: определение, свойства и признак. Формула площади прямоугольника.
2. Средняя линия треугольника. Теорема о средней линии треугольника
Билет № 8
1. Ромб: определение и свойства. Формула площади ромба.
2. Вписанный угол: определение и свойства.
Билет № 9
1. Трапеция: определение и виды. Формула площади трапеции.
2. Окружность, вписанная в многоугольник. Свойство описанного четырехугольника.
Билет № 10
Билет № 11
1. Окружность (определение). Центр, радиус, диаметр окружности. Взаимное расположение окружности и прямой.
2. Треугольник: определение и виды. Формула Герона.
Билет № 12
1. Окружность (определение). Хорда окружности. Касательная к окружности: определение и свойства.
2. Трапеция. Средняя линия трапеции. Свойство средней линии трапеции.
Билет № 13
1. Окружность, описанная около многоугольника. Свойство вписанного четырехугольника.
2. Треугольник: определение и виды. Формулы площадей.
Задачи к билетам по геометрии 8 класс
1. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
2. В
параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна
из его сторон равна 6.
3. Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите бо́льшую высоту.
4. Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.
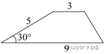5. Основания трапеции равны
4 см и 10 см. Диагональ трапеции делит среднюю линию на два
отрезка. Найдите длину большего из них.
6. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если ее основания равны 3 и 9.
7. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
8. Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.
9. В
треугольнике ABC угол C прямой, BC = 8 , sin A =
0,4. Найдите AB. 
10. Катеты
прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого
треугольника.
11. Найдите
градусную меру центрального ∠MON,
если известно, NP — диаметр, а градусная мера ∠MNP равна 18°.
12. Найдите ∠DEF, если градусные меры дуг DE и EF равны 150° и 68° соответственно.
13. Прямоугольный
треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен
радиус этой окружности?
14. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.
15. Из
квадрата вырезали прямоугольник (см. рис.). Найдите площадь получившейся
фигуры.
16.
Найдите площадь треугольника, изображенного на рисунке.
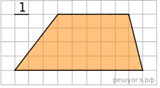
17. Найдите площадь трапеции, изображенной на рисунке.
18. Одна
из сторон параллелограмма равна 12, другая равна 5, а один из
углов — 45°. Найдите площадь параллелограмма.
19. Найдите тангенс угла A треугольника ABC, изображенного на рисунке.
20. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 66, сторона BC равна 37, сторона AC равна 74. Найдите MN.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
