Теория

Логарифм положительного числа b по основанию a - это показатель степени, в которую надо возвести a, чтобы получить b.

𝑙𝑜𝑔_𝑎𝑏 = 𝑐  ⇔  𝑎^𝑐 = 𝑏.

При этом 𝑏 > 0, 𝑎 > 0, 𝑎 ≠ 1.

Например:

𝑙𝑜𝑔₂8 = 3,           таккак     2³ = 8;

так.

Логарифм определен только для положительных чисел. Например, число 𝑙𝑜𝑔₂(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим - 4.

Основание логарифма должно быть положительным и не равным единице. В самом деле, выражение 𝑙𝑜𝑔₁7 не имеет смысла: в какую бы степень мы ни возвели число 1, мы не получим 7.

Свойства логарифмов

1)  Основное логарифмическое тождество:

𝑎^{𝑙𝑜𝑔𝑎𝑏} = 𝑏,     𝑙𝑜𝑔_𝑎𝑎^𝑐 = 𝑐.

2)  Логарифм произведения:

𝑙𝑜𝑔_𝑎(𝑏𝑐) = 𝑙𝑜𝑔_𝑎𝑏 + 𝑙𝑜𝑔_𝑎𝑐.

3)  Логарифм частного:

.

2

4)  Логарифм степени:

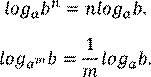
5)  Формула перехода к новому основанию:

,

* полезно запомнить: 𝑙𝑜𝑔_𝑎𝑏 ∙ 𝑙𝑜𝑔_𝑏𝑐 = 𝑙𝑜𝑔_𝑎𝑐.

6**) 𝑎𝑙𝑜𝑔_𝑏𝑐 = 𝑐𝑙𝑜𝑔_𝑏𝑎.

3

В каких заданиях ЕГЭ мы встретим логарифмы?

Начнем с ЕГЭ базового уровня: 

задание 16 - преобразования числовых логарифмических

выражений (рассмотрены в РТ),  задание 17 - логарифмические уравнения (рассмотрены в РТ), задание 18 - простейшие логарифмические неравенства.

В ЕГЭ профильного уровня:

задание 6 - простейшие уравнения (логарифмические уравнения)

(рассмотрены в РТ),,

задание 7 - вычисления и преобразования (преобразования

буквенных логарифмических выражений), (рассмотрены в РТ),

задание 9 - задачи с прикладным содержанием (логарифмические

уравнения и неравенства),

задание 11 - графики функций (показательные и логарифмические

функции),

задание 12 - наибольшее и наименьшее значение функций

(исследование показательных и логарифмических функций),

задание 13 - уравнения (логарифмические уравнения, уравнения

смешанного типа)

задание 15 - неравенства (логарифмические неравенства,

неравенства с логарифмами по переменному основанию), задание 18 - параметры.

В этой рабочей тетради мы рассмотрим: как применять свойства логарифмов для вычисления логарифмов, для решения простейших  логарифмических уравнений.

Остальные задания будут разобраны в следующих рабочих тетрадях.

Преобразование числовых логарифмических выражений 

(логарифм произведения и логарифм частного, логарифм степени, формула перехода к новому основанию)

I.  𝑙𝑜𝑔₂24 − 𝑙𝑜𝑔₂0,75 = 𝑙𝑜𝑔₂(24 ∶ 0,75) = 𝑙𝑜𝑔₂32 = 5,       таккак  2⁵ = 32; 𝑙𝑜𝑔₃6,75 + 𝑙𝑜𝑔₃4 = 𝑙𝑜𝑔₃(6,75 ∙ 4) = 𝑙𝑜𝑔₃27 = 3,            таккак   3³ = 27.

Задания для самостоятельного решения

II.    

.

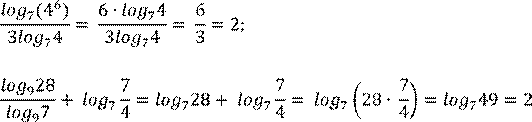Задания для самостоятельного решения

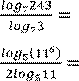
1.                   6.

2.                    7.       

3.                     

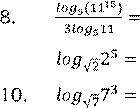
4.                  9.    

5.                   

III.    𝑙𝑜𝑔₃5 ∙ 𝑙𝑜𝑔₅81 = 𝑙𝑜𝑔₃81 = 4;

.

Задания для самостоятельного решения

1.       𝑙𝑜𝑔₂7 ∙ 𝑙𝑜𝑔₇32 =

2.       𝑙𝑜𝑔₅2 ∙ 𝑙𝑜𝑔₂125 =

3.       𝑙𝑜𝑔₅9 ∙ 𝑙𝑜𝑔₃25 =

4.       7𝑙𝑜𝑔_2,511 ∙ 𝑙𝑜𝑔₁₁0,4 =

5.       𝑙𝑜𝑔_0,83 ∙ 𝑙𝑜𝑔₃1,25 =

6.       𝑙𝑜𝑔₅7 ∙ 𝑙𝑜𝑔₇25 =

Простейшие логарифмические уравнения

I.     𝑙𝑜𝑔₂(𝑥 + 2) = 𝑙𝑜𝑔₂11

Основания логарифмов равны, сами логарифмы тоже равны - значит, равны и числа, от которых они берутся! Пользуясь свойством монотонности логарифмической функции "отбрасываем" логарифмы. Получаем:

𝑥 + 2 = 11;

𝑥 = 11 − 2;

𝑥 = 9.

Не забывайте делать проверку!!

Ответ: 9

Задания для самостоятельного решения

1.  𝑙𝑜𝑔₅(8 − 𝑥) = 𝑙𝑜𝑔₅2,

2.  𝑙𝑜𝑔₇(1 − 𝑥) = 𝑙𝑜𝑔₇5,

3.  𝑙𝑜𝑔₃(𝑥 + 4) = 𝑙𝑜𝑔₃16, 4. 𝑙𝑜𝑔₂(𝑥 − 2) = 𝑙𝑜𝑔₂11,

5.                  𝑙𝑜𝑔₃(15 − 𝑥) = 𝑙𝑜𝑔₃7,

6.                  𝑙𝑜𝑔₄(𝑥 + 13) = 𝑙𝑜𝑔₄24,

7.                  𝑙𝑜𝑔₅(8 − 𝑥) = 𝑙𝑜𝑔₅5,

8.                  𝑙𝑜𝑔₇(1 − 𝑥) = 𝑙𝑜𝑔₇2,

9.                  𝑙𝑜𝑔₁₇(29 − 6𝑥) = 𝑙𝑜𝑔₁₇5,

10.              𝑙𝑜𝑔₁₁(7𝑥 − 12) = 𝑙𝑜𝑔₁₁23,

11.              𝑙𝑜𝑔₇(3𝑥 − 19) = 𝑙𝑜𝑔₇11,

12.              𝑙𝑜𝑔₅(24 − 7𝑥) = 𝑙𝑜𝑔₅3,

13.              𝑙𝑜𝑔₂(5𝑥 − 23) = 𝑙𝑜𝑔₂17,

14.              𝑙𝑜𝑔₂₂(4𝑥 − 33) = 𝑙𝑜𝑔₂₂3.

II.  𝑙𝑜𝑔₅(𝑥 + 4) = 2

Применим основное логарифмическое тождество:

𝑙𝑜𝑔₅(𝑥 + 4) = 𝑙𝑜𝑔₅5²;

𝑥 + 4 = 25;

𝑥 = 25 − 4;

𝑥 = 21.

Ответ: 21

Задания для самостоятельного решения

III.  2𝑙𝑜𝑔₄(2𝑥+5) = 4

Перейдем от логарифма по основанию 4 (в показателе степени) к логарифму по основанию 2. Так же учитываем, что

2𝑥 + 5 > 0;

𝑥 > −2,5;

;

;

;

Возведем обе части уравнения в квадрат

2𝑥 + 5 = 16;

2𝑥 = 16 − 5; 2𝑥 = 11; 𝑥 = 5,5.

5,5 > −2,5

Ответ: 5,5

Задания для самостоятельного решения

1.       3𝑙𝑜𝑔9(4𝑥+1) = 9,   6. 𝑙𝑜𝑔₉3^5𝑥−5 = 4,

2.       2𝑙𝑜𝑔4(2𝑥+2) = 4,   7. 𝑙𝑜𝑔₈₁3^2𝑥−6 = 2, 

3.       3𝑙𝑜𝑔27(2𝑥−9) = 3, 8. 𝑙𝑜𝑔₁₆2^2𝑥−3 = 3,  4. 5𝑙𝑜𝑔25(2𝑥−1) = 5,       9. 𝑙𝑜𝑔₂₇3^5𝑥+5 = 2, 

                                          5. 4𝑙𝑜𝑔16(8𝑥−4) = 4,                                10. 𝑙𝑜𝑔₄2^8𝑥+8 = 4. 

IV. Логарифмические уравнения (с дополнительным применением свойств логарифма)

𝑙𝑜𝑔₄(𝑥 + 2) + 𝑙𝑜𝑔₄3 = 𝑙𝑜𝑔₄15;

𝑥 + 2 > 0;

𝑥 > −2;

Представим сумму логарифмов в левой части уравнения как логарифм произведения

𝑙𝑜𝑔₄((𝑥 + 2) ∙ 3) = 𝑙𝑜𝑔₄15;

(𝑥 + 2) ∙ 3 = 15;

3𝑥 + 6 = 15;

3𝑥 = 15 − 6;

3𝑥 = 9;

𝑥 = 3,                   (3 > −2).

Ответ: 3.

Задания для самостоятельного решения

1.  𝑙𝑜𝑔₄(8𝑥 − 7) − 𝑙𝑜𝑔₄5 = 𝑙𝑜𝑔₄21;

2.  𝑙𝑜𝑔₂(𝑥 − 1) + 𝑙𝑜𝑔₂6 = 𝑙𝑜𝑔₂18;

3.  𝑙𝑜𝑔₅(2𝑥 − 6) − 𝑙𝑜𝑔₅2 = 𝑙𝑜𝑔₅3;

4.  𝑙𝑜𝑔₃(2𝑥 + 4) − 𝑙𝑜𝑔₃2 = 𝑙𝑜𝑔₃5. 

Удачи на экзамене!!!